Кристаллография, 2020, T. 65, № 2, стр. 281-287

ВВЕДЕНИЕ

Структурные фазовые переходы (ФП) $\bar {3}m$ – 2/m – 2 происходят с понижением симметрии и возникновением спонтанной деформации. Высокотемпературная ромбоэдрическая фаза является фазой прототипа [1]. Эти ФП являются несобственными [2, 3]. Первая низкотемпературная фаза (2/m) может быть только сегнетоэластической, вторая может быть и сегнетоэлектрической [4]. В сегнетоэластиках, как и в сегнетоэлектриках, при полиморфных ФП с понижением симметрии образуется доменная структура с различными ориентационными состояниями (ОС), которые разделены доменными стенками [5–8]. В сегнетоэластической фазе возникают небольшие спонтанные повороты кристаллографических осей, обусловленные смещениями атомов и поворотами групп атомов при изменении спонтанной деформации [9–11]. Это приводит к расщеплению каждого возможного ОС на группу близких, субориентационных состояний. Количество субориентационных состояний зависит от симметрии низкотемпературной фазы. Угол и знак спонтанного поворота можно определить из уравнений доменной стенки, полученных в системе координат параэластической и сегнетоэластической фаз [12, 13]. Общее количество возможных ОС зависит от симметрии параэластической фазы и не изменяется при последующих ФП [14].

При ФП $\bar {3}m$ – 2/m возможно образование трех групп ОС, которые подразделяются на два субориентационных состояния [15].

В [16] предложен метод определения температурной зависимости параметров решетки при структурном ФП второго рода 4/m – 2/m, основанный на условии сохранения макросимметрии параэластической фазы в полидоменном кристалле. Интересно применить этот метод для двух последовательных ФП $\bar {3}m$ – 2/m – 2. В работе анализ полученных решений сделан на примере сегнетоэластиков Pb₃(VO₄)₂ и Pb₃(PO₄)₂.

ОПРЕДЕЛЕНИЕ ТЕМПЕРАТУРНЫХ ЗАВИСИМОСТЕЙ ПАРАМЕТРОВ РЕШЕТКИ В ПАРАЭЛАСТИЧЕСКОЙ И СЕГНЕТОЭЛАСТИЧЕСКОЙ ФАЗАХ ПРИ СТРУКТУРНОМ ФП $\bar {3}m$–$2{\text{/}}m$

Ромбоэдрическую γ-фазу определим как псевдомоноклинную [17]. Обозначим параметры решетки в параэластической γ-фазе ${{a}_{0}}$, ${{b}_{0}}$, ${{c}_{0}}$, β₀, в β-фазе – ${{a}_{1}}$, ${{b}_{1}}$, ${{c}_{1}}$, β₁, в α-фазе – ${{a}_{2}}$, ${{b}_{2}}$, ${{c}_{2}}$, β₂. Выберем следующую кристаллофизическую систему координат (СК): Х₁ совпадает с направлением оси с, Х₂ – с осью b, Х₃ образует угол ($\beta - \pi {\text{/}}2$) с осью а.

Тензор теплового расширения сегнетоэластической фазы в СК параэластической фазы без учета спонтанных поворотов имеет вид:

где ${{e}_{{11}}} = ({{c}_{1}}{\text{/}}{{с}_{0}}) - 1$; ${{e}_{{22}}} = ({{b}_{1}}{\text{/}}{{b}_{0}}) - 1$; ${{e}_{{33}}} = ({{a}_{1}}\cos {{\beta }_{1}}{\text{/}}{{a}_{0}}\cos {{\beta }_{0}}) - 1$; ${{e}_{{13}}} = \frac{{{{c}_{1}} + 3{{a}_{1}}\cos {{\beta }_{1}}}}{{6{{a}_{1}}\sin {{\beta }_{1}}}}$.

В [15] получены матрицы преобразования СК, соответствующие двум субориентационным состояниям S₁₁ и S₁₂:

Тензоры теплового расширения, которые соответствуют этим субориентационным состояниям, в СК параэластической фазы имеют вид где $e_{{ij}}^{/} = {{a}_{{ik}}}{{a}_{{jm}}}{{e}_{{km}}}$.

Тензоры теплового расширения остальных ОС можно получить из (3), применяя операцию поворота вокруг оси симметрии третьего порядка на угол ±120°.

Из условия сохранения макросимметрии в полидоменном кристалле при структурном ФП [18] получен усредненный тензор теплового расширения E_u для шести возможных ОС в β-фазе:

где $e_{{{\text{11}}}}^{{\text{/}}}\, = \,a_{{11}}^{2}{{e}_{{11}}}\, + \,2{{a}_{{11}}}{{a}_{{13}}}{{e}_{{13}}}\, + \,a_{{12}}^{2}{{e}_{{22}}}\, + \,a_{{13}}^{2}{{e}_{{33}}}$, $e_{{{\text{22}}}}^{{\text{/}}} = a_{{21}}^{2}{{e}_{{11}}} + $ $ + \;2{{a}_{{21}}}{{a}_{{23}}}{{e}_{{13}}} + a_{{22}}^{2}{{e}_{{22}}} + a_{{23}}^{2}{{e}_{{33}}}$, $e_{{{\text{33}}}}^{{\text{/}}} = a_{{13}}^{2}{{e}_{{11}}} + 2{{a}_{{31}}}{{a}_{{33}}}{{e}_{{13}}} + $ $ + \;a_{{32}}^{2}{{e}_{{22}}} + a_{{33}}^{2}{{e}_{{33}}}$. Тензор Е_u соответствует симметрии параэластической ромбоэдрической фазы.

С учетом спонтанных поворотов компоненты тензора E_u при комнатной температуре отличаются от ранее полученных [12] на величины Δ₁ и Δ₂:

где для Pb₃(PO₄)₂${{\Delta }_{1}} = 1.7 \times {{10}^{{ - 4}}}$, ${{\Delta }_{2}} = - {\text{3}}{\text{.02}} \times {\text{1}}{{{\text{0}}}^{{ - {\text{5}}}}}$, а для Pb₃(VO₄)₂${{\Delta }_{1}} = 1.{\text{1}} \times {\text{1}}{{{\text{0}}}^{{ - {\text{3}}}}}$, ${{\Delta }_{2}} = - {\text{3}}{\text{.02}} \times {\text{1}}{{{\text{0}}}^{{ - {\text{6}}}}}$. Поскольку тензор спонтанной деформации зависит от E_u [19]: то где $a = {\text{0}}{\text{.5(}}{{e}_{{{\text{22}}}}} - {{e}_{{11}}})$, $c = e_{{{\text{13}}}}^{s}$.

Таким образом, с учетом спонтанных поворотов изменяются соотношения между компонентами $e_{{{\text{11}}}}^{s}$ и $e_{{{\text{22}}}}^{s}$ и появляется еще одна не нулевая компонента спонтанной деформации $e_{{33}}^{s}$. Поэтому ориентация доменной стенки W^/ должна зависеть от величины четырех компонент спонтанной деформации, а не только от a и c, как получено в [12].

Поскольку ${{\Delta }_{i}}$ малы, то с целью упрощения вида функциональных температурных зависимостей параметров решетки в сегнетоэластических фазах далее не учитывались спонтанные повороты при определении величин компонент тензора $E_{u}^{{}}$

Из тензора $E_{u}^{{\text{1}}}$ получаем величину усредненного параметра a_1u ромбоэдрической решетки в полидоменном кристалле: где с₁(t) и b₁(t) – моноклинные параметры β-фазы, зависящие от температуры t.

Из анализа экспериментальных температурных зависимостей кристаллографических параметров решетки Pb₃(PO₄)₂, Pb₃(VO₄)₂, BiVO₄ и BaTiO₃ установлено, что зависимость от температуры усредненного параметра а_u, как и параметров парафазы, близка к линейной [16, 20]. В [16] предложено такую температурную зависимость описывать экспоненциальной функцией. Следуя [16], запишем температурные зависимости параметров решетки в виде экспоненциальных функций:

Параметр ${{a}_{{{\text{1}}pv}}}$ псевдоромбоэдрической решетки, соответствующий моноклинной фазе, можно определить с небольшой погрешностью из формулы Он немного меньше соответствующих значений ${{a}_{{1u}}}(t)$ в сегнетоэластической фазе, но они равны при температуре ФП второго рода ${{t}_{{f{\text{1}}}}}$ (или гипотетического ФП второго рода). Поэтому температурная зависимость ${{a}_{{{\text{1}}pv}}}$(t) также соответствует экспоненциальной функции, близкой к линейной Для определения коэффициентов k₀, k₁, … k₁₁ необходимо знать экспериментальные значения параметров γ- и β-фаз при двух произвольных температурах в каждой фазе: ${{t}_{1}}({{a}_{{{\text{01}}}}},{{b}_{{01}}},{{c}_{{01}}},{{\beta }_{{01}}})$, (${{t}_{2}}({{a}_{{{\text{02}}}}},{{b}_{{02}}},{{c}_{{02}}},{{\beta }_{{02}}})$, ${{t}_{3}}({{a}_{{{\text{11}}}}},{{b}_{{11}}},{{c}_{{11}}},{{\beta }_{{11}}})$, ${{t}_{4}}({{a}_{{{\text{12}}}}},{{b}_{{12}}},{{c}_{{12}}},{{\beta }_{{12}}})$. С учетом предложенных обозначений получаем: где ${{a}_{{1u1}}} = 0.5\sqrt[4]{3}\left( {\frac{{{{c}_{{11}}}}}{{\sqrt 3 }} + {{b}_{{11}}}} \right)$, ${{a}_{{1u2}}} = 0.5\sqrt[4]{3}\left( {\frac{{{{c}_{{12}}}}}{{\sqrt 3 }} + {{b}_{{12}}}} \right)$, ${{a}_{{{\text{1}}pr{\text{1}}}}} = \sqrt {{{c}_{{11}}}{{b}_{{11}}}} $, ${{a}_{{{\text{1}}pr{\text{2}}}}} = \sqrt {{{c}_{{12}}}{{b}_{{12}}}} $.

Поскольку температурные зависимости в пределах фазы близки к линейным зависимостям, выбор температурных точек, соответствующих экспериментальным данным, принципиального значения не имеет. Получен алгоритм для минимального количества экспериментальных данных, но если данных больше двух в пределах фазы, лучше выбирать их поближе к краям температурного интервала. Если наблюдается значительный разброс экспериментальных данных, то для определения параметров функций необходимо применить метод наименьших квадратов, предварительно преобразуя (10)–(12) в линейные функции с помощью логарифмирования уравнений и соответствующей замены переменных [21].

Из (9), (11) получаем систему уравнений

которая имеет два решения: где $D = a_{{1u}}^{2}(t) - 4mna_{{1pv}}^{2}$, $m = 0.5{\text{/}}\sqrt[4]{3},$ $n = 0.5\;\sqrt[4]{3}.$

Температура ФП второго рода ${{t}_{{f{\text{1}}}}}$ определяется из условия

Из (10), (12), (17) получаем В [22] показано, что в Pb₃(PO₄)₂ и Pb₃(VO₄)₂ существует линейная зависимость параметров решетки от параметра с в пределах фазы. Это позволяет определить, используя (15) или (16), температурные зависимости параметров ${{a}_{{\text{1}}}}(t)$ и ${{{\beta }}_{1}}(t)$: где ${{k}_{{{\text{13}}}}} = \frac{{{{a}_{{11}}} - {{a}_{{12}}}}}{{{{c}_{{11}}} - {{c}_{{12}}}}}$, ${{k}_{{12}}} = {{a}_{{11}}} - {{k}_{{13}}}{{c}_{{11}}}$, ${{k}_{{{\text{15}}}}} = \frac{{{{{\beta }}_{{11}}} - {{{\beta }}_{{12}}}}}{{{{c}_{{11}}} - {{c}_{{12}}}}}$, ${{k}_{{14}}} = {{\beta }_{{11}}} - {{k}_{{15}}}{{c}_{{11}}}$.

ОПРЕДЕЛЕНИЕ ТЕМПЕРАТУРНЫХ ЗАВИСИМОСТЕЙ ПАРАМЕТРОВ РЕШЕТКИ В СЕГНЕТОЭЛАСТИЧЕСКОЙ α-ФАЗЕ

Температурные зависимости параметров решетки в $\alpha $-фазе определяются так же, как в $\beta $-фазе, только необходимо в уравнения (1)–(20) подставить соответствующие параметры решетки при двух произвольных температурах в пределах α-фазы: ${{t}_{{\text{5}}}}({{a}_{{21}}},{{b}_{{21}}},{{c}_{{21}}},{{{\beta }}_{{21}}})$, ${{t}_{{\text{6}}}}({{a}_{{22}}},{{b}_{{22}}},{{c}_{{22}}},{{{\beta }}_{{22}}})$. C учетом предложенных обозначений получаем температурные зависимости ${{a}_{{{\text{2}}u}}}(t)$ и ${{a}_{{{\text{2}}pv}}}(t)$:

где ${{k}_{{{\text{17}}}}} = \frac{{\ln {{a}_{{2u1}}} - \ln {{a}_{{2u2}}}}}{{{{t}_{5}} - {{t}_{6}}}}$, ${{k}_{{16}}} = \frac{{{{a}_{{2u1}}}}}{{\exp ({{k}_{{17}}}{{t}_{5}})}}$, ${{k}_{{{\text{19}}}}} = \frac{{\ln {{a}_{{2{\text{p}}v1}}} - \ln {{a}_{{2pv2}}}}}{{{{t}_{5}} - {{t}_{6}}}}$, ${{k}_{{18}}} = \frac{{{{a}_{{2pv1}}}}}{{\exp ({{k}_{{19}}}{{t}_{5}})}}$, ${{a}_{{2u1}}} = 0.5\sqrt[4]{3}\left( {\frac{{{{c}_{{21}}}}}{{\sqrt 3 }} + {{b}_{{21}}}} \right)$, ${{a}_{{2u2}}} = 0.5\sqrt[4]{3}\left( {\frac{{{{c}_{{22}}}}}{{\sqrt 3 }} + {{b}_{{22}}}} \right)$, ${{a}_{{{\text{2}}pr{\text{1}}}}} = \sqrt {{{c}_{{21}}}{{b}_{{21}}}} $, ${{a}_{{{\text{2}}pr{\text{2}}}}} = \sqrt {{{c}_{{22}}}{{b}_{{22}}}} $.

Из (21) и (22) получаем систему уравнений, аналогичную (14), которая имеет два решения:

где ${{D}_{2}}(t) = a_{{2u}}^{2}(t) - 4mna_{{2pv}}^{2}(t{\text{)}}$, $m = 0.5{\text{/}}\sqrt[4]{3}$, $n = 0.5\sqrt[4]{3}$.

Температуру ФП второго рода ${{t}_{{f2}}}$ можно определить из условия

Из уравнений (21), (22), (25) получаем Температурные зависимости параметров ${{a}_{{\text{2}}}}(t)$ и ${{\beta }_{2}}(t)$ определяются аналогично (19), (20) с учетом их линейной зависимости от величины ${{c}_{2}}({\text{t}})$: где ${{k}_{{{\text{21}}}}} = \frac{{{{a}_{{21}}} - {{a}_{{22}}}}}{{{{c}_{{21}}} - {{c}_{{22}}}}}$, ${{k}_{{20}}} = {{a}_{{21}}} - {{k}_{{21}}}{{c}_{{21}}}$, ${{k}_{{{\text{23}}}}} = \frac{{{{{\beta }}_{{21}}} - {{{\beta }}_{{22}}}}}{{{{c}_{{21}}} - {{c}_{{22}}}}}$, ${{k}_{{22}}} = {{\beta }_{{21}}} - {{k}_{{23}}}{{c}_{{21}}}$.

Качество аппроксимации экспериментальных значений в α-, β- и γ-фазах определялось с использованием средней абсолютной процентной ошибки МАРЕ [23]:

где $E{\text{(}}t{\text{)}} = K{\text{(}}t{\text{)}} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{K} {\text{(}}t{\text{)}}$; $K(t)$ – экспериментальное значение параметров ячейки, а $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{K} (t)$ – соответствующее ему теоретическое значение при той же температуре.

АНАЛИЗ ТЕМПЕРАТУРНЫХ ЗАВИСИМОСТЕЙ ПАРАМЕТРОВ РЕШЕТКИ В СЕГНЕТОЭЛАСТИКЕ Pb₃(VO₄)₂

Ортованадат свинца Pb₃(VO₄)₂ является несобственным сегнетоэластиком, в котором наблюдаются два ФП первого рода: при 377 K из γ-фазы ($R\bar {3}m$) в β-фазу (P2₁/c), при 275 K – в α-фазу (P2₁) [16]. В этом кристалле при ФП $\gamma \to \beta $ образуется нетипичная для сегнетоэластиков очень мелкая доменная структура (доменная сетка). Причина ее образования окончательно не выяснена.

После подстановки экспериментальных значений параметров решеток при двух произвольных температурах в каждой фазе [24] были получены значения параметров функций (10), (12), (15), (16), (19), (20–24), (27), (28) (табл. 1, 2, 3).

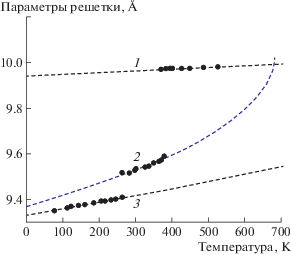
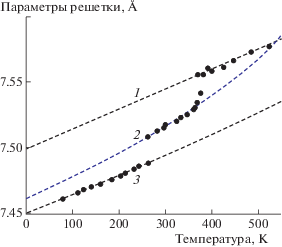
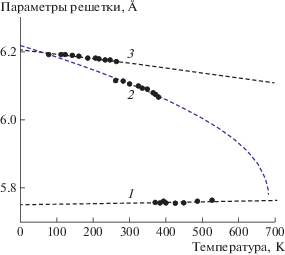
Из анализа полученных решений установлено, что экспериментальным температурным зависимостям параметра с₁ в β-фазе [24] соответствует второй корень ${{c}_{{{\text{12}}}}}(t)$ решения системы (14) (рис. 1), следовательно, остальным параметрам решетки соответствуют функции ${{a}_{{{\text{12}}}}}(t)$, ${{b}_{{12}}}(t)$, ${{{\beta }}_{{12}}}(t)$ (рис. 2, 3). Температура гипотетического ФП ${{t}_{{f{\text{1}}}}} = 675.{\text{5}}$ K, что на ∼300 K больше температуры ФП первого рода Т₁.

Аналогично в α-фазе экспериментальным температурным зависимостям параметра c₂ также соответствует второй корень ${{c}_{{22}}}(t)$ (24), а остальным параметрам решетки – функции ${{a}_{{{\text{22}}}}}(t)$, ${{b}_{{22}}}(t)$, ${{{\beta }}_{{22}}}(t)$(рис. 1–3). Температура гипотетического ФП ${{t}_{{f{\text{2}}}}} = {\text{1492}}{\text{.8}}$ K, что значительно больше ${{t}_{{f1}}}$.

Относительное различие между теоретическими и экспериментальными значениями параметров ячейки в Pb₃(VO₄)₂ в γ-, β- и α-фазах MAPE < < 0.037%.

ТЕМПЕРАТУРНЫЕ ЗАВИСИМОСТИ ПАРАМЕТРОВ РЕШЕТКИ В СЕГНЕТОЭЛАСТИКЕ Pb₃(PO₄)₂

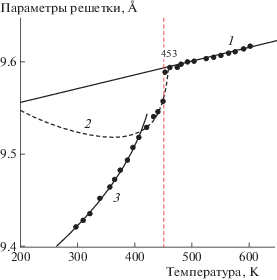
Ортофосфат свинца Pb₃(PO₄)₂ является чистым несобственным сегнетоэластиком, в котором при 453 K наблюдается ФП первого рода из параэластической ромбоэдрической фазы $(R\bar {3}m)$ в сегнетоэластическую моноклинную фазу $C2{\text{/}}c$ [25] или С2 [26]. В [27] установлено, что в ортофосфате свинца в районе 363 K наблюдается небольшое структурное изменение в виде небольшого скачка в температурной зависимости параметра b, которое не получило подтверждения при последующих исследованиях. Ниже будет показано, что немного выше этой температуры наблюдается излом усредненного параметра ${{a}_{u}}(t)$, что указывает на наличие еще одного структурного ФП. Поэтому параэластическую фазу обозначим как $\gamma $-фазу, а сегнетоэластические фазы – как β- и α-фазы аналогично ортованадату свинца.

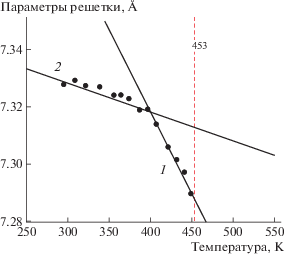
Значения параметров функций в параэластической и сегнетоэластических фазах, полученные с использованием экспериментальных данных параметров решеток при двух произвольных температурах в каждой фазе [28], представлены в табл. 4–6. Температурная зависимость усредненного параметра ${{a}_{u}}(t)$ имеет излом при температуре 401 K (рис. 4)

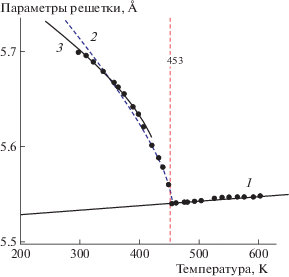
Экспериментальной температурной зависимости параметров ${{c}_{1}}$ и ${{c}_{2}}$ в обеих сегнетоэластических фазах, как и в Pb₃(VO₄)₂, соответствовал второй корень решения системы (14) (${{c}_{{{\text{12}}}}}(t)$ и ${{c}_{{{\text{22}}}}}(t)$ соответственно). Следовательно, остальным параметрам решетки в β-фазе соответствуют функции ${{a}_{{{\text{12}}}}}(t)$, ${{b}_{{12}}}(t)$, ${{{\beta }}_{{12}}}(t)$, в α-фазе – функции ${{a}_{{{\text{22}}}}}(t)$, ${{b}_{{22}}}(t)$, ${{{\beta }}_{{22}}}(t)$ (рис. 5, 6). Температура гипотетического ФП из $\gamma $ в $\beta $-фазу ${{t}_{{f{\text{1}}}}} = 454.{\text{07}}$ K, что на один градус больше температуры ФП первого рода t₁. Температура гипотетического ФП из β в α-фазу ${{t}_{{f{\text{2}}}}} = 439.{\text{8}}$ K. В [29] показано, что в параэластической фазе вплоть до температуры 468 K существуют локальные моноклинные микрообласти.

Относительное различие между теоретическими и экспериментальными значениями параметров ячейки в Pb₃(PO₄)₂ в трех фазах MAPE < < 0.039%.

ЗАКЛЮЧЕНИЕ

Таким образом, при фазовом переходе $\bar {3}m - {\text{2/}}m$ образуется сегнетоэластическая фаза, которая имеет четыре различных компоненты тензора спонтанной деформации. Увеличение числа ненулевых компонент обусловлено спонтанными поворотами кристаллографических осей. Аналогичная ситуация наблюдается при последующем ФП $2{\text{/}}m - 2$. В этих фазах при изменении температуры в основном происходит перераспределение величин между параметрами решетки b и с (увеличение одного за счет уменьшения другого), однако и другие параметры решетки сегнетоэластических фаз незначительно влияют на это перераспределение из-за наличия спонтанных поворотов.

Предложенный метод определения температурной зависимости параметров решетки сегнетоэластических фаз при двух последовательных ФП $\bar {3}m - 2{\text{/}}m - 2$ имеет два решения. Анализ полученных решений в Pb₃(VO₄)₂ и Pb₃(PO₄)₂ показал, что только одно решение соответствует экспериментальным данным. Установлено, что температурная зависимость усредненного параметра псевдоромбоэдрической фазы ${{a}_{u}}(t)$ в сегнетоэластической фазе Pb₃(PO₄)₂ имеет излом, соответствующий еще одному структурному ФП, возможно, ${\text{2/}}m - {\text{2}}$.

Предложенный метод позволяет также вычислить температуру ФП второго рода или гипотетического ФП второго рода. Если в кристалле реализуется структурный ФП первого рода, то ему предшествует гипотетический ФП второго рода, который определяет температурную зависимость параметров решетки как в сегнетоэластической фазе, так и в ее зародышах.

В Pb₃(PO₄)₂ вследствие малого отличия температуры гипотетического ФП из $\gamma $- в $\beta $-фазу от температуры ФП первого рода при экспериментальных исследованиях не наблюдается температурного гистерезиса ФП. Второй гипотетический ФП в α-фазу на 14 K ниже первого.

В Pb₃(VO₄)₂ особенностью гипотетического ФП из $\beta $- в $\alpha $-фазу является то, что он значительно выше температуры гипотетического ФП из γ- в $\beta $-фазу. Можно предположить, что в этом кристалле зародыши β-фазы образуются из зародышей α-фазы при температуре ${{t}_{{f{\text{1}}}}}$.