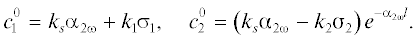Кристаллография, 2020, T. 65, № 3, стр. 470-476
Фототермическое преобразование бесселевых световых пучков в периодически поляризованных нелинейных кристаллах
Г. С. Митюрич 1, *, Е. В. Лебедева 2, П. А. Хило 3, Д. Г. Митюрич 4, А. Н. Сердюков 1
1 Гомельский государственный университет им. Ф. Скорины
Гомель, Беларусь
2 Белорусский торгово-экономический университет потребительской кооперации
Гомель, Беларусь
3 Гомельский государственный технический университет им. П.О. Сухого
Гомель, Беларусь
4 БелНИПИнефть РУП “Производственное объединение “Беларуcнефть”
Гомель, Беларусь
* E-mail: george_mityurich@mail.ru
Поступила в редакцию 24.10.2019
После доработки 24.10.2019
Принята к публикации 25.11.2019
Аннотация
Рассмотрен механизм формирования фотодефлекционного отклика, возникающего в периодически поляризованном нелинейном кристалле, облучаемом бесселевым световым пучком. Найдено распределение тепловых полей, получено точное решение системы уравнений теплопроводности с использованием интегральных преобразований Фурье–Бесселя и Лапласа для трехслойной системы, состоящей из нелинейного кристалла, подложки и окружающей среды. Предложен способ управления амплитудой фотодефлекционного сигнала на основе применения аксиконов с регулируемым углом конусности или использования оптических схем, обеспечивающих изменение конусности бесселевых световых пучков.
ВВЕДЕНИЕ
Воздействие мощного лазерного излучения на кристаллические среды позволяет существенно расширить область применения фотоакустических методов исследования вещества [1–4]. Рассмотрению нелинейных режимов импульсной генерации звука посвящено достаточно большое количество публикаций [5–10], однако интерес к практическим вопросам нелинейной фотоакустики не ослабевает.
Нелинейное взаимодействие световых волн в периодически поляризованных структурах, как отмечается в [11, 12], обладает большими потенциальными возможностями для эффективной генерации второй гармоники (ГВГ), а также для реализации параметрических эффектов генерации волн суммарной и разностной частот. Разработка параметрического генератора света на основе веерных периодически поляризованных структур ниобата лития с плавной перестройкой длины волны излучения описана в [13]. Там же рассмотрена возможность использования генератора света в лазерном оптико-акустическом газоанализаторе медицинского назначения.
Цель настоящей работы – изучение особенностей фототермического преобразования бесселевых световых пучков (БСП) в нелинейных периодически поляризованных кристаллах и установление зависимости величины углов фотодефлекции от теплофизических и диссипативных параметров нелинейной среды и пространственного распределения светового поля.
ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ ПРИ КВАЗИСИНХРОННОМ ВЗАИМОДЕЙСТВИИ БЕССЕЛЕВЫХ СВЕТОВЫХ ПУЧКОВ
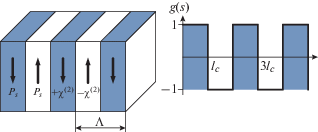
Рассмотрим нормальное падение амплитудно-модулированного на частоте Ω БСП на периодически поляризованный нелинейный кристалл, вырезанный перпендикулярно оси третьего порядка [111] (рис. 1). В соответствии с [14] вдоль оси третьего порядка кристаллов кубической симметрии может возникать ГВГ. В [15] исследованы особенности удвоения частоты БСП при квазисинхронном взаимодействии световых пучков в периодически поляризованных кристаллах. Были рассмотрены кристаллические образцы с идеальной периодической структурой, состоящей из противоположно поляризованных доменов, толщины которых равны когерентной длине, а эффективные коэффициенты нелинейной связи меняют знак при переходе от одной области к другой.
В рассматриваемом случае предполагается, что волна основной частоты распространяется в области прозрачности кристалла, а амплитудно-модулированное излучение второй гармоники интенсивно поглощается. Ситуация реализуема, например, в кристаллах типа селенитов, германате висмута, силикате висмута, которые прозрачны для излучения рубинового лазера (λ ≈ 0.694 мкм), но интенсивно поглощают излучение на частоте второй гармоники [16]. Отметим, что реализация условий фазового синхронизма в гиротропных кристаллах кубической симметрии возможна, как показано в [14], благодаря явлению естественной или вынужденной (эффект Фарадея) оптической активности кристалла. Кроме этого, наличие в нелинейных кристаллах периодической доменной структуры позволяет реализовать режим квазисинхронизма [15], что ведет к эффективной генерации излучения на удвоенной частоте.
Таким образом, фотоакустический сигнал возникает в кристаллической пространственно поляризованной пластинке вследствие поглощения модулированного по амплитуде БСП на частоте второй гармоники. Под воздействием пучка света исследуемый неоднородный образец периодически нагревается модулированным излучением, что приводит к возбуждению термоакустических колебаний поверхности, освещаемой поляризационными модами БСП. Это приводит к отклонению зондирующего пучка на угол дефлекции (рассматривается случай трансверсальной геометрии взаимодействия возбуждающего и зондирующего пучков (рис. 2)), величина которого зависит от термоупругих, нелинейных, оптических и дихроичных свойств исследуемого образца, а также поляризационных и энергетических параметров БСП.
Рис. 2.
Схема регистрации фотодефлекционного сигнала: 1 – модулятор, 2 – аксикон, 3 – БСП, 4 – “термическая” линза, 5 – зондирующий луч, 6 – позиционно-чувствительный фотодетектор, 7 – нелинейный периодически поляризованный кристалл, 8 – подложка.
Пусть на нелинейный кристалл вдоль оси третьего порядка падает мощный БСП основной частоты, электрическое поле которого E1(ρ, z) задается соотношением
(1)
${{E}_{1}}{\kern 1pt} \left( {{\rho },z} \right) = {{A}_{1}}{\kern 1pt} \left( z \right){{J}_{0}}{\kern 1pt} \left( {{{q}_{1}},{\rho }} \right){{{\text{e}}}^{{i{{k}_{{{{1}_{z}}}}}z}}},$Электромагнитное поле второй гармоники представим в виде ряда Фурье–Бесселя:
(2)
${{E}_{2}}{\kern 1pt} \left( {{\rho },z} \right) = \sum\limits_{m = 1}^M {{{A}_{{{{2}_{m}}}}}{\kern 1pt} \left( z \right){{J}_{0}}{\kern 1pt} \left( {{{q}_{{{{2}_{m}}}}},{\rho }} \right){{{\text{e}}}^{{i{{k}_{{{{2}_{m}}}}}z}}},} $(3)
${{j}_{0}}{\kern 1pt} \left( {{{q}_{{{{2}_{m}}}}},{\rho }} \right) = \left\{ {\begin{array}{*{20}{l}} {\frac{{{{J}_{0}}{\kern 1pt} \left( {{{q}_{{{{2}_{m}}}}},{\rho }} \right)}}{{\sqrt {\pi } {{R}_{{{{2}_{m}}}}}{{J}_{1}}{\kern 1pt} \left( {{{q}_{{{{2}_{m}}}}},{{R}_{B}}} \right)}}{\text{,}}\quad {\text{при}}\quad {\rho } < {{R}_{B}},} \\ {0,\quad {\text{при}}\quad {\rho } \geqslant {{R}_{B}}.} \end{array}} \right.$При $\rho = {{R}_{B}}$ и ${{q}_{{{{2}_{m}}}}}{{R}_{B}} = \left( {m - 0.25} \right){\pi }$ функция Бесселя обращается в нуль, т.е., согласно (2), (3), поле ${{E}_{2}}\left( {\rho ,z} \right)$ представляет собой разложение по модам цилиндрической области радиусом RB.
В (3) ${{J}_{1}}{\kern 1pt} \left( {{{q}_{{{{2}_{m}}}}},{{R}_{B}}} \right)$ – функция Бесселя первого порядка, ${{R}_{B}} = \left( {m{\pi } - {{\pi } \mathord{\left/ {\vphantom {{\pi } 4}} \right. \kern-0em} 4}} \right)q_{{{{2}_{m}}}}^{{ - 1}}$ – радиус локализованного излучения БСП. Из (3) также следует условие нормировки
(4)
$2{\pi }\int\limits_0^{{{R}_{B}}} {J_{0}^{2}{\kern 1pt} \left( {{{q}_{{{{2}_{m}}}}},{\rho }} \right)} {\kern 1pt} {\rho }d{\rho } = 1.$Удобство нормировки (4) состоит, в частности, в возможности описания нелинейного взаимодействия в кристаллах единым интегралом перекрытия взаимодействующих мод БСП.
Процесс ГВГ в поглощающих кристаллах может быть описан системой укороченных уравнений [15, 17]:
Представляя поля посредством рядов Фурье, несложно привести систему уравнений (5) для амплитуд взаимодействующих волн к виду:
(6)
$\left\{ {\begin{array}{*{20}{l}} {\frac{{d{{A}_{1}}}}{{dz}} = i{{{\sigma }}_{1}}A_{1}^{*}\sum\limits_m {{{q}_{m}}{{A}_{{2m}}}} {{{\text{e}}}^{{i\Delta {{k}_{z}}z}}},} \\ {\frac{{d{{A}_{{2m}}}}}{{dz}} + {{{\delta }}_{2}}{{A}_{{2m}}} = i{{{\sigma }}_{2}}{{q}_{m}}A_{1}^{2}{{{\text{e}}}^{{ - i\Delta {{k}_{z}}z}}},} \end{array}} \right.$(7)
${{A}_{{2m}}}{\kern 1pt} \left( z \right) = \frac{{i{\sigma }{{q}_{m}}}}{{{{p}_{1}}}}{{\left| {{{A}_{1}}} \right|}^{2}}{{{\text{e}}}^{{ - \frac{{{{{\delta }}_{2}}}}{2}z}}}{{{\text{e}}}^{{ - i\frac{{\Delta {{k}_{z}}z}}{r}}}}\sin {{p}_{1}}z,$Как следует из (7), интенсивность электрического поля на частоте второй гармоники ${{J}_{{2\omega }}}\sim {{\left| {{{A}_{{2m}}}} \right|}^{2}}$, возбужденной БСП, определяется интегралами перекрытия qm парциальных световых пучков накачки, а также общим числом M генерируемых мод. Кроме того, амплитуда поля удвоенной гармоники A2m при увеличении коэффициента поглощения δ2 может достаточно сильно затухать, уменьшаясь по экспоненте, что экспериментально наблюдалось в [16] для кристаллов типа селенитов.
РЕШЕНИЕ ТЕПЛОВОЙ ЗАДАЧИ. АМПЛИТУДА ФОТОДЕФЛЕКЦИОННОГО СИГНАЛА
Модулированное воздействие излучения второй гармоники на поглощающий в данном частотном диапазоне кристалл с регулярной доменной структурой приводит к возникновению периодической составляющей температурного поля, изменение которого описывается неоднородным уравнением теплопроводности [19]. Выделим временнýю часть системы уравнений теплопроводности для трехслойной системы окружающая среда–нелинейный периодически поляризованный кристалл–подложка
(8)
$\left\{ \begin{gathered} {{\nabla }^{2}}{{T}_{1}} - {{{\sigma }}_{1}}T = 0,\quad z < 0, \hfill \\ {{\nabla }^{2}}T - \frac{1}{{{{{\beta }}_{S}}}}\frac{{\partial T}}{{\partial t}} = - \frac{1}{{2{{k}_{S}}}}{{Q}_{{2\omega }}}(1 + {{{\text{e}}}^{{i\Omega t}}}), \hfill \\ {{\nabla }^{2}}{{T}_{2}} - {{{\sigma }}_{2}}T = 0,\quad z > l, \hfill \\ \end{gathered} \right.\quad 0 \leqslant z \leqslant l,$(9)
${{Q}_{{2\omega }}} = \frac{{\omega }}{{8{\pi }}}{\varepsilon ''}\sum\limits_{m = 1}^M {{{{\left| {A_{{2\omega }}^{0}} \right|}}^{2}}{{J}_{0}}{\kern 1pt} \left( {{{q}_{{2\omega }}},{\rho }} \right)J_{0}^{*}} {\kern 1pt} \left( {{{q}_{{2\omega }}},{\rho }} \right){{{\text{e}}}^{{ - 2{{k}_{{2\omega }}}z}}},$Выражение (9) содержит сложную зависимость амплитуды поля A2ω от пространственной координаты z и интегралов перекрытия qm взаимодействующих мод. При этом неоднородное уравнение теплопроводности (8) принимает трансцендентную форму. В том случае, когда толщина образца d удовлетворяет условию
Решение системы уравнений теплопроводности (8) выполнено с использованием интегральных преобразований Фурье–Бесселя и Лапласа аналогично [21, 22] (Приложение). Для угла фотодефлекции Ф получено выражение
(11)
$\begin{gathered} \Phi {\kern 1pt} \left( {{\rho },z,t} \right) = \frac{{{{{\pi }}^{2}}{{w}_{0}}}}{{4{{n}_{{eff}}}}}\frac{{d{{n}_{{eff}}}}}{{dT}}\bar {T} \times \\ \times \;\int\limits_0^t {\frac{{\left( {1 + \cos \Omega t} \right)x}}{{{{{[w_{0}^{2} + 8{{{\beta }}_{s}}(t - {\tau })]}}^{{3/2}}}}}{{e}^{{ - \frac{{({{x}^{2}} + {{y}^{2}})}}{{w_{0}^{2} + 8{{{\beta }}_{{\text{s}}}}(t - {\tau })}}}}}{{e}^{{ - {\alpha }_{{2{\omega }}}^{2}{{{\beta }}_{s}}(t - {\tau })}}}d{\tau },} \\ \end{gathered} $Выражение (11) показывает, что пространственное распределение температурного поля и амплитуды фотодефлекционного отклика в нелинейных средах сложным образом зависит от диссипативных, геометрических теплофизических и нелинейных параметров среды, а также энергетически временных и поляризационных свойств квазибездифракционного излучения.
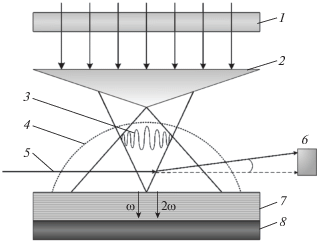
Как видно на рис. 3, влияние подложки обусловливает смещение положений максимумов амплитуды фотодефлекционного сигнала в направлении больших углов конусности. При этом общий характер зависимости Ф(α) сохраняется, а величина амплитуды результирующего отклика уменьшается, что является следствием проникновения температурного поля в область подложки и окружающей среды (расплывания за пределы образца). Зависимость угла фотодефлекции от радиальной координаты является экспоненциально убывающей и одновременно осциллирующей (рис. 4), что обусловлено модулирующим воздействием функций Бесселя.
Рис. 3.
Зависимость величины фотодефлекции от угла конусности α: 1 – с учетом свойств подложки, 2 – без учета влияния подложки.
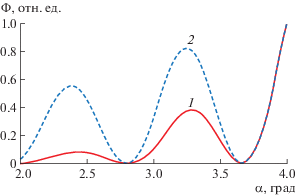
Рис. 4.
Сравнение зависимостей фотодефлекционного сигнала от радиальной координаты ρ: 1 – с учетом свойств подложки, 2 – без учета влияния подложки.
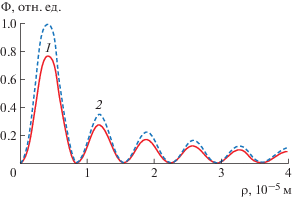
Это обстоятельство важно учитывать для правильной интерпретации экспериментальных данных, полученных в результате прецизионных измерений амплитудно-фазовых характеристик фотодефлекционного отклика от нелинейных периодически поляризованных кристаллических структур.
Квадрат интеграла перекрытия $q_{m}^{2}$ имеет два максимума: при m = m1 = 1 и m = m2 = (2q1RBm)/π [15, 18]. Следовательно, наибольший вклад в эффективность ГВГ вносят две группы мод, локализованные в окрестности обозначенных максимумов. Вблизи m1 и m2 происходят наибольшее выделение тепловой энергии и генерация термоупругих волн, при этом амплитуда фотодефлекционного сигнала достигает своего максимального значения. Также отметим, что из аналитического выражения (11) и приведенных выше графических зависимостей видно, что существует возможность эффективного влияния на амплитуду фотодефлекционного сигнала путем изменения угла конусности БСП.
ЗАКЛЮЧЕНИЕ
Построена модель фототермического преобразования бесселевых световых пучков в периодически поляризованных нелинейных кристаллах. В рамках этой модели получено точное решение системы уравнений теплопроводности для трехслойной системы, включающей в себя нелинейный кристалл, облучаемый квазибездифракционным излучением, подложку и окружающую среду. Установлено, что величина фотодефлекционного отклика от образца нелинейного кристалла при учете параметров подложки и окружающей среды приблизительно на 0.22 отн. ед. ниже значения, полученного при расчетах, проведенных без учета этих параметров. Графический анализ также показывает, что при увеличении времени воздействия БСП на нелинейный кристалл происходит уменьшение амплитуды фотодефлекционного сигнала, что объясняется размыванием поля температур в исследуемом образце вследствие теплообмена с окружающей средой и диэлектрической подложкой. Отметим, что существует возможность эффективного управления амплитудой фотодефлекционного отклика от нелинейного кристалла, которая может быть реализована при использовании аксиконов с регулируемым углом конусности, созданных, например, на основе кристаллов, обладающих эффектом Поккельса [23, 24]. Импульсное возбуждение ультразвуковых волн управляемыми БСП в образцах горных пород экспериментально продемонстрировано в [25]. В [21, 22, 26] исследована термооптическая управляемая генерация звука квазибездифракционным излучением в плотном слое хиральных и ахиральных углеродных нанотрубок, а также в магнитоактивных сверхрешетках, что подтверждает практическую значимость использования поляризационных мод БСП.
Список литературы
Mandelis A., Salnik A., Opsal J., Rosencwaig A. // J. Appl. Phys. 1999. V. 85. P. 1811.
Ошурко В.Б. // Квантовая электроника. 2004. Т. 35. № 2. С. 185.
Gusev V., Mandelis A., Bleiss R. // Int. J. Thermophys. 1993. V. 14. № 2. P. 321.
Мадвалиев У., Салихов Т.Х., Шарифов Д.М. // ЖТФ. 2004. Т. 74. № 2. С. 17.
Ахманов С.А., Гусев В.Э. // Успехи физ. наук. 1992. Т. 162. № 3. С. 3.
Kopylova D.S., Pelivanov I.M. // J. Acoust. Soc. Am. 2011. V. 130. № 4. P. 213.
Yelleswarapu C.S., Kothapalli S.R. // Optics Express. 2010. V. 18. № 9. P. 9020.
Blackman F., Antonolli L. // Appl. Opt. 2005. V. 44. № 1. P. 103.
Greogoire G., Tournat V., Gusev V. // Eur. Phys. J. Special Topics. 2008. V. 153. P. 313.
Митюрич Г.С. // ЖТФ. 1989. Т. 59. Вып. 9. С. 118.
Хило П.А., Петрова Е.С., Хило Н.А. // Проблемы физики, математики и техники. 2013. Т. 15. № 2. С. 25.
Аветисян Ю.О. // Изв. НАН Армении. Физика. 2006. Т. 41. № 1. С. 8.
Колкер Д.Б., Бойко А.А., Духовникова Н.Ю. // Приборы и техника эксперимента. 2014. № 1. С. 85.
Бокуть В.Б., Сердюков А.Н. // Журн. прикл. спектроскопии. 1970. Т. 12. Вып. 1. С. 65.
Хило П.А. // Журн. прикл. спектроскопии. 2000. Т. 67. № 5. С. 595.
Батог В.Н., Бурков В.И., Кизель В.А. и др. // Кристаллография. 1971. Т. 16. Вып. 6. С. 1044.
Дмитриев В.Г., Тарасов Л.В. Прикладная нелинейная оптика. М.: Радио и связь, 1982. 352 с.
Mityurich G.S., Aleksiejuk M., Astakhov P.V. et al. // Int. J. Thermophys. 2011. V. 32. № 4. P. 844.
Mityurich G.S., Chernenok E.V., Serdyukov A.N. // J. Appl. Spect. 2015. V. 82. № 2. P. 254.
Ландау Л.Д. Электродинамика сплошных сред. М.: Наука, 1982. 624 с.
Митюрич Г.С., Лебедева Е.В., Сердюков А.Н. // Проблемы физики, математики и техники. 2016. Т. 27. № 4. С. 19.
Митюрич Г.С., Лебедева Е.В., Сердюков А.Н. // Проблемы физики, математики и техники. 2017. Т. 33. № 4. С. 17.
Митюрич Г.С., Черненок Е.В., Сердюков А.Н. // Афiцыйны бюл. 2015. № 4. С. 146.
Митюрич Г.С., Черненок Е.В., Сердюков А.Н. // Афiцыйны бюл. 2016. № 2. С. 162.
Mityurich G.S., Kozhushko V.V., Mityurich D.G. et al. // 20th Int. Conf. Photoacoustic and Photothermal Phenomena. Moscow. 2019. P. 72.
Митюрич Г.С., Черненок Е.В., Свиридова В.В. и др. // Кристаллография. 2015. Т. 60. № 2. С. 299.
Бейтман Г., Эрдейи А. Таблицы интегральных преобразований: М.: Наука, 1969. Т. 1. 344 с.
Дополнительные материалы отсутствуют.
Инструменты
Кристаллография