Кристаллография, 2020, T. 65, № 4, стр. 515-521

ВВЕДЕНИЕ

Дифракция Лауэ рентгеновской сферической волны в монокристаллическом образце в форме пластины наблюдается, когда отраженный пучок выходит из образца через ту же поверхность, что и прошедший пучок. Эта поверхность называется выходной. Впервые дифракцию такого типа экспериментально исследовали в 1959 г. [1]. Для получения когерентных изображений авторы [1] использовали узкую щель перед кристаллом, которая фактически являлась вторичным источником излучения с малым поперечным сечением. Указанный экспериментальный метод широко используется в течение многих лет для исследования качества монокристаллов и получил название рентгеновской секционной топографии.

Теория для схемы эксперимента [1] разработана в [2, 3] для нулевого расстояния от источника до кристалла. Был использован метод преобразования Фурье для представления падающей сферической волны в виде суперпозиции плоских волн. Угловая зависимость амплитуд прохождения и отражения при дифракции плоской волны находится аналитически. Оказалось, что дифракционная картина на выходной поверхности кристалла формируется в треугольнике Бормана, который образуют направления падающего и отраженного пучков. Затем эта картина переносится без изменения в плоскость регистрации.

Почти одновременно Такаги [4] предложил другой вариант теории, в основе которого лежит система дифференциальных уравнений. Эти уравнения сейчас носят его имя. Численное решение уравнений Такаги позволяет не только рассмотреть произвольный тип падающей волны, но и искажения кристаллической решетки вблизи дефектов, а также произвольную форму кристалла. В случае совершенного кристалла система дифференциальных уравнений имеет решение в виде свертки волновой функции на границе кристалла с пропагатором кристалла, который аналитически выражается через функции Бесселя. Решения для кристаллов с границами разных типов и разных схем отражения получены в [5–11].

В [12–14] была развита обобщенная теория дифракции сферической волны, которая дополнительно учитывала расстояние от источника до детектора. Одним из основных результатов стало предсказание дифракционной фокусировки расходящегося излучения кристаллом в форме пластины. Экспериментальная проверка этого эффекта выполнена в [15–18].

Для кристаллов с дефектами структуры предложен эффективный численный метод решения уравнений Такаги (например, [19]) и выполнены расчеты для различных дефектов при разных условиях облучения, описание которых приведено в [20]. В [21–27] исследована неоднородная структура излучения при дифракции в кристаллах специальной формы (параллелепипеда или цилиндра), причем использовали как аналитические, так и численные методы.

В настоящей работе теоретически исследована дифракция сферической рентгеновской волны в толстом совершенном кристалле с наклонной ступенькой на выходной поверхности. Использованы два способа решения задачи, а именно, преобразование Фурье угловой зависимости волновой функции для падающей плоской волны и кристалла в форме пластины и численное решение уравнений Такаги в области ступеньки, где параметры дифракции зависят от координаты вдоль поверхности образца. Аналитическое решение уравнений Такаги представлено во второй части работы [28]. Интерес к такой форме образца определяется тем, что при угле наклона ступеньки меньше угла Брэгга в узкой переходной области толстого кристалла сильно изменяется почти однородное пространственное распределение интенсивности отраженного пучка, причем интенсивность в максимуме возрастает более чем в 7 раз. Эффект очень слабо зависит от расстояния между источником и кристаллом, за исключением области дифракционной фокусировки. Анализируется зависимость эффекта от угла наклона ступеньки. Полученные результаты дают мотивацию к экспериментальному изучению эффекта и могут быть практически использованы для разных целей, в частности для прецизионного определения дифракционных параметров, зависящих от структуры кристалла.

ФОРМУЛИРОВКА ЗАДАЧИ И МЕТОД ЧИСЛЕННОГО РЕШЕНИЯ

Схема численного эксперимента показана на рис. 1. Монохроматическая сферическая волна от точечного источника рентгеновских лучей, расположенного на расстоянии L от монокристалла, падает под углом Брэгга и имеет конечную угловую расходимость. Кристалл имеет форму пластины толщиной t (максимальная толщина), на выходной поверхности которой находится наклонная ступенька высотой t₀.

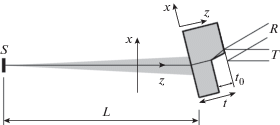
Такая формулировка задачи обусловлена тем, что при правильном описании любого источника рентгеновского излучения (синхротронный или лабораторный) каждую точку поперечного сечения источника нужно рассматривать независимо от других точек, поскольку как электроны на орбите синхротронного источника, так и атомы анода рентгеновской трубки излучают спонтанно, и корреляция между разными микроисточниками отсутствует. Монохроматизация излучения реализуется стандартными способами и не влияет на форму поперечного сечения падающей волны. На рисунке монохроматор не показан. Эффективный поперечный размер источника учитывается суммированием интенсивности от всех точек поперечного сечения.

Наклонная ступенька на выходной поверхности монокристалла приводит к пространственной неоднородности интенсивности прошедшего и отраженного пучков в поперечном сечении. Эти пучки детекторы измеряют независимо. Они расположены на небольшом расстоянии от кристалла для того, чтобы пучки разделились в пространстве и не интерферировали. Для простоты будем вычислять интенсивности пучков на выходной поверхности кристалла в его толстой части (толщина t).

Задачу удобно разбить на два этапа. На первом этапе вычислим распределение волнового поля на толщине кристалла t₁ = t – t₀. На этой толщине ступенька отсутствует, и кристалл однородный вдоль поверхности (вдоль оси x). Неоднородность интенсивности возникает только вследствие неоднородности падающей волны и эффекта дифракции. В этом случае задачу удобно решать методом преобразования Фурье, используя аналитическое решение для падающей плоской волны.

Будем считать, что ограничение угловой расходимости пучка из-за релятивистких эффектов невелико и нет необходимости вводить поправки в пропагатор Френеля, как это было сделано в [29]. Волновую функцию падающего излучения в параксиальном приближении удобно записать в виде

где координата z отсчитывается вдоль направления от источника к кристаллу (оси слева на рис. 1), λ – длина волны рентгеновского излучения, K = = 2π/λ, пропагатор Френеля имеет вид От координаты y в направлении, перпендикулярном плоскости дифракции, интенсивность не зависит. Представим (1) в виде интеграла Фурье по q и учтем, что q = Kθ описывает малую угловую расходимость падающего излучения вблизи угла Брэгга, т.е. падающая волна представляет собой суперпозицию из плоских волн с волновым вектором k₀ = (q, 0, K).

Рассмотрим симметричную дифракцию Лауэ на системе атомных плоскостей, соответствующих вектору обратной решетки h. Известно, что волновой вектор проходящей волны не меняется при дифракции на совершенном кристалле в форме пластины [20, 30]. Используя аналитическое решение для плоской волны, можно сразу написать решение для первого этапа в виде

Здесь и далее опускаем множитель exp(iKz), так как он не влияет на интенсивность. Фурье-образ пропагатора Френеля имеет следующее аналитическое выражение: а решение задачи для плоской волны хорошо известно [20, 30, 31]. Запишем его в виде, удобном для расчетов: где Параметр g имеет положительную мнимую часть, χ₀, χ_h, χ_–h – компоненты Фурье поляризуемости кристалла для векторов обратной решетки 0, h, ‒h соответственно, θ_B – угол Брэгга, параметр q₀ = = Kθ₀ описывает возможное отклонение кристалла от угла Брэгга.

Аналогичное решение можно написать для отраженной волны:

где Здесь X_h = Kχ_h. В данном случае волновой вектор плоских волн k₀ + h, а отраженная волна распространяется в направлении, составляющем удвоенный угол Брэгга с направлением прошедшей волны.

На втором этапе решим другую задачу, а именно, задачу дифракции в кристалле, имеющем форму пластины, в случае произвольной падающей волны и произвольной неоднородности структуры кристалла в плоскости xz. На этом этапе используем другую систему координат (рис. 1 справа). То есть ось x идет вдоль поверхности пластины, а ось z – по нормали к поверхности. Будем численно решать уравнения Такаги [4]:

Здесь X_–h = Kχ_–h, s₀ и s_h – координаты вдоль направлений проходящей и отраженной волн, u – вектор смещения из-за возможной деформации кристаллической решетки, параметр отклонения от условия Брэгга α_q определен в (8).

Для решения уравнений Такаги в случае дифракции Лауэ удобно сделать подстановку E_h = = $E_{h}^{'}$exp(–ihu) и записать уравнения в другой форме:

где Параметры p и q определяются методом приближенного решения уравнений Такаги. Будем рассматривать слои в кристалле толщиной d_z, параллельные оси x. Параметры p и q равны отрезкам вдоль направлений проходящей и отраженной волн, соответствующих одному слою. В случае симметричной дифракции p = q = d_z/γ₀. В настоящей модели кристалл без деформаций, т.е. u = 0, но параметры U₀, U, V₀, V зависят от координат x и z.

Для численного решения уравнений (13) необходимо заменить производные отношением разностей. Используя метод, предложенный в [19], будем вычислять производные и функции в середине слоя по схеме:

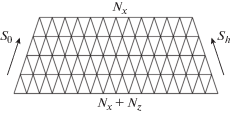
Заменяя производные и функции в уравнениях (13) в середине каждого слоя по схеме (16), (17) , получим систему линейных уравнений для амплитуд проходящей и отраженной волн в случае системы точек с периодом d_z вдоль оси z и с периодом d_x = = 2d_ztg θ_B вдоль оси x (рис. 2).

Решение этой системы $E_{2}^{{(n)}}$ можно представить в виде произведения матрицы M_2,4 на вектор $E_{4}^{{(o)}}$, т.е.

где Здесь $s_{0}^{ - }$ = s₀ – p, $s_{h}^{ - }$ = s_h – q, Метод решения состоит в следующем. Начнем с входной поверхности первого слоя, где амплитуды E₀ и $E_{h}^{'}$ известны из граничных условий, и применим (18) для получения значений на выходной поверхности слоя, которая является входной поверхностью для следующего слоя и так далее. В итоге получим значения во всех точках сетки рис. 2. Число точек сетки N_x вдоль оси x уменьшается на единицу при каждом шаге итераций. Поэтому для получения решения в области с размерами N_xd_x вдоль оси x необходимо знать граничные условия в области (N_x + N_z)d_x, а полная толщина кристалла во второй части равна t₀ = N_zd_z (рис. 2), где N_z – число слоев.

Матрица (21) написана для кристалла с деформированной решеткой. Если кристалл имеет аморфные области, в которых дифракция отсутствует, то в таких областях матрица имеет вид

где Здесь χ₁ – нулевая компонента Фурье поляризуемости кристалла в аморфной области, которая может иметь другой химический состав. В частности, это может быть пустое место, где χ₁ = 0. В симметричном случае V₁ = U₁.

В настоящей работе решение задачи на первом этапе формирует граничные условия для второго этапа. Так как сетки точек, используемые на разных этапах, разные, необходимые значения получим интерполяцией. Кроме того, нужно проектировать ось x первого этапа на ось x второго этапа, учитывая, что эти оси образуют угол Брэгга. Конкретные расчеты выполнены для кристалла кремния, параметры χ₀, χ_h, χ_–h вычисляли с помощью онлайн-программы [32].

Компьютерная программа была написана на языке ACL [33]. Интегралы Фурье (3) и (9) вычисляли с помощью процедуры быстрого преобразования Фурье, встроенной в язык ACL. Код этой процедуры на языке Фортран известен с середины прошлого века как часть библиотеки NAG [34]. В расчетах использовано число точек N = 16 384. Шаг d_x сетки точек задается, шаг d_q = Kd_θ = = 2π/(Nd_x), и расчетная область Nd_q в обратном пространстве должна быть достаточно большой, чтобы подынтегральная функция была равна нулю на концах области.

Отметим, что амплитуда (5) равна exp(iX₀t₁/2γ₀), и в пределе |q| → ∞ в тонком кристалле отлична от нуля. В настоящей работе кристалл толстый, модуль этой функции близок к нулю, и проблемы нет. Важно также контролировать позицию треугольника Бормана в пространстве. Интегралы Фурье (3) и (9) для нулевого расстояния (L = 0) отличны от нуля только в области x < 0, так как точка x = 0 соответствует всем лучам, угловое положение которых выходит за область дифракции Брэгга. Удобно сдвинуть начало координат на оси x таким образом, чтобы оно соответствовало середине треугольника Бормана. Дополнительный сдвиг на расстояние x_s = –Lθ₀ необходимо выполнить в случае конечного расстояния, чтобы скорректировать изменение брэгговского направления при угловом смещении кристалла.

Правильный выбор центра пучка особенно важен в случае толстого кристалла, потому что вследствие эффекта Бормана (аномальное прохождение с минимальным поглощением) через кристалл проходит только часть пучка, соответствующая середине треугольника Бормана. Ось легко сдвинуть, умножая подынтегральную функцию на множитель

Здесь дополнительно введено возможное смещение x₀ начала ступеньки относительно середины треугольника Бормана. Именно начало ступеньки выбрано в качестве центра на оси x координатной системы второго этапа расчетов.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

На рис. 3 показаны результаты расчета распределения интенсивности в неоднородной части кристалла, т.е. в слое, содержащем ступеньку. Значения параметров: энергия фотонов E = ћω = = 10 кэВ (λ = 0.124 нм); расстояние от источника до кристалла L = 2 м; толщина однородной части кристалла t₁ = 1 мм; высота ступеньки на выходной поверхности t₀ = 0.2 мм; угол θ наклона ступеньки определяется из условия R = tg θ/tg θ_B = = 0.5; кристалл кремния, отражение 220. Для этих условий θ_B = 18.84°, следовательно, θ = 9.68°. Используемое в расчете расстояние легко реализовать в экспериментах с помощью узкой щели или составной преломляющей линзы, которые формируют вторичный источник на нужном расстоянии.

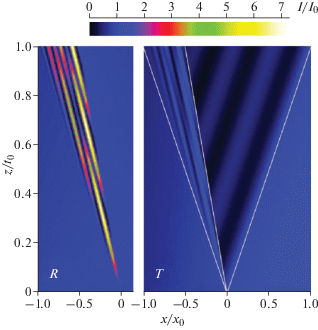
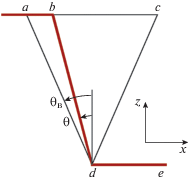
Схематически граница ступеньки и указанные углы обозначены на рис. 4. Граница ступеньки соответствует линии abde. Эта граница приводит к изменению интенсивности внутри треугольника Бормана acd. Интенсивность отраженного пучка (на рис. 3 левая панель, обозначена буквой R) сильно изменяется только в треугольнике abd, в то время как интенсивность проходящего пучка (на рис. 3 правая панель, обозначена буквой T) изменяется во всем треугольнике Бормана, но по-разному в областях abd и bcd. Обе панели показаны в одной и той же цветовой шкале для лучшего сравнения. За единицу принята средняя интенсивность отраженного пучка на нижней границе рисунка, т.е. при толщине t₁. Отметим, что для рассмотренного расстояния толщина дифракционной фокусировки [12, 36] равна t_df = = L|χ_h|F = 60.8 мкм, где F = 1/(sin θ_Bsin 2θ_B). Следовательно, часть излучения при слабом поглощении на этой толщине максимально сжимается, а потом снова расходится и в области ступеньки имеет уже почти однородную интенсивность по оси x (вдоль поверхности). На рис. 3 смещение x₀ = 0. Карта цветов не позволяет показать очень слабые изменения интенсивности из-за поглощения справа от ступеньки в вертикальном направлении. Но можно заметить слабые изменения интенсивности в проходящем пучке в горизонтальном направлении. Из рисунка следует, что интенсивность проходящего пучка в области треугольника Бормана около ступеньки заметно изменяется, но не так сильно, как интенсивность отраженного пучка. В частности, интенсивность проходящего пучка в области bcd изменяется только в направлении, поперечном относительно проходящего пучка. Фактически она переносится с линии bd в направлении проходящего пучка. В области abd распределение интенсивности более сложное, но максимальная интенсивность значительно меньше, чем интенсивность отраженного пучка в той же области.

Наиболее интересно поведение интенсивности отраженного пучка. Оно носит выраженный интерференционный характер, максимум более чем в 7 раз превышает интенсивность перед ступенькой. Можно предположить, что такое поведение связано с тем фактом, что граница ступеньки ближе к левой стороне треугольника Бормана, т.е. к направлению отраженного пучка. Налицо очень сильное перераспределение интенсивности, которое напоминает отражение проходящей волны на границе ступеньки.

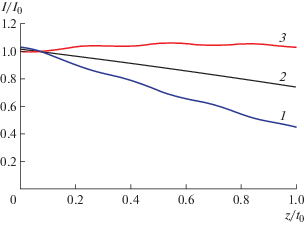
На рис. 5 показаны зависимости средних по ширине полосы, равной основанию треугольника Бормана, интенсивностей от координаты z в области ступеньки для проходящего пучка (кривая 1), половины суммарной интенсивности (кривая 2) и отраженного пучка (кривая 3). Интенсивности нормированы на первую точку кривой 3 для отраженного пучка. Видно, что средняя интенсивность отраженного пучка даже немного возрастает. Однако средняя интенсивность проходящего пучка (кривая 1) резко падает. Средняя суммарная интенсивность обоих пучков (кривая 2) уменьшается линейно. Для кривой 2 можно вычислить коэффициент поглощения по нормали к поверхности: μ = 15.8 см^–1. Для сравнения нормальный коэффициент поглощения μ₀/γ₀ = = 80.0 см^–1, а аномальный коэффициент поглощения для плоской волны под углом Брэгга равен μ_a/γ₀ = 2.5 см^–1. То еcть ступенька частично ликвидирует условия, необходимые для эффекта Бормана. Полная волновая функция излучения не равна нулю в точке расположения атомов, и поглощение увеличивается. Заметим, что в большей части рассматриваемой области вещества нет, значит, и поглощение нулевое. В основном все поглощение происходит в треугольнике abd. Одновременно интенсивность перераспределяется таким образом, что часть излучения проходящей волны трансформируется в отраженную волну, что и приводит к возрастанию интенсивности отраженной волны.

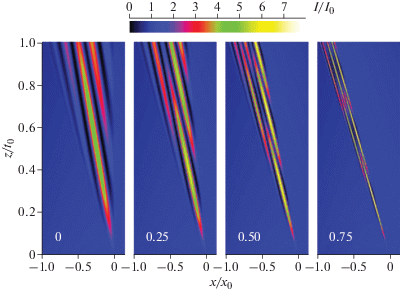
На рис. 6 показаны четыре фрагмента распределения интенсивности по высоте ступеньки для различных углов ее наклона. Фактически варьировался параметр R, который был равен 0, 0.25, 0.5 и 0.75. Все фрагменты нарисованы для одной и той же цветовой шкалы. Интересно, что при уменьшении ширины переходной области от границы ступеньки к границе треугольника Бормана ширина интерференционных полос также уменьшается, а их число изменяется незначительно. Самый высокий максимум как раз соответствует самой узкой переходной области. Более того, в узкой переходной области уменьшается период осцилляций и по вертикальной оси, соответствующей изменению толщины кристалла.

Этот результат очень сложно объяснить на качественном уровне. Во второй части работы будет представлено аналитическое решение задачи, приводящее к такому же результату. Вместе с тем наличие интерференционных полос с малым периодом открывает возможность прецизионных измерений различных величин, в том числе параметров дифракции.

В настоящей работе рассмотрен вариант с углом наклона ступеньки в сторону отраженного пучка. При угле наклона в сторону проходящего пучка роли проходящего и отраженного пучков меняются. Картины типа тех, что показаны на рис. 6, появляются в случае проходящего пучка. Это было показано в [37], где рассмотрен треугольный вырез на выходной поверхности. Расчеты показывают, что распределения на рис. 3 и 6 не очень сильно зависят от расстояния (они практически одни и те же при нулевом и предельно большом расстояниях). Исключение составляют лишь расстояния, близкие к расстоянию дифракционной фокусировки. Для толщины кристалла 1 мм это расстояние равно 32.9 м.