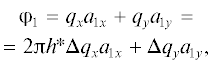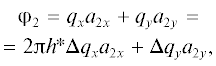Кристаллография, 2020, T. 65, № 5, стр. 804-810
Теоретический формализм для анализа дифракционного рассеяния рентгеновского излучения на двумерных кристаллах
М. А. Чуев 1, Г. В. Пруцков 2, Н. Н. Новикова 2, *, Э. М. Пашаев 2, О. В. Коновалов 3, Н. Д. Степина 4, А. В. Рогачев 2, С. Н. Якунин 2
1 Физико-технологический институт им. К.А. Валиева РАН
Москва, Россия
2 Национальный исследовательский центр “Курчатовский институт”
Москва, Россия
3 Европейский центр синхротронного излучения (ESRF)
Гренобль, Франция
4 Институт кристаллографии им. А.В. Шубникова ФНИЦ “Кристаллография и фотоника” РАН
Москва, Россия
* E-mail: nn-novikova07@yandex.ru
Поступила в редакцию 27.04.2020
После доработки 27.04.2020
Принята к публикации 12.05.2020
Аннотация
Разработан теоретический формализм для количественного описания рентгеновской дифракции в условиях полного внешнего отражения на ленгмюровских монослоях. Предложенный подход основан на использовании приближения искаженной волны и позволяет включать в рассмотрение физические механизмы формирования кривых и карт (в обратном пространстве) дифракции для реальных монослоев, а также самосогласованно описывать особенности брэгговских пиков. Результирующий алгоритм легко реализуется на персональном компьютере, что дает возможность проводить численное моделирование экспериментальных двумерных карт дифракционного рассеяния и надежно определять как средние значения структурных параметров исследуемых слоев, так и их среднеквадратичные отклонения.
ВВЕДЕНИЕ
Уникальные свойства синхротронного излучения, в первую очередь высокая интенсивность и когерентность, дают возможность значительно увеличить пространственное разрешение, чувствительность и точность рентгеновских исследований. Современные поверхностно-чувствительные методы позволяют получать структурную информацию о границах раздела и поверхностях отдельных нанообъектов, а также изучать кинетику процессов структурообразования в двумерных ансамблях различной природы. Эти исследования не только существенно расширяют знания о строении наноразмерных систем, но и способствуют взрывному развитию технологического прогресса, поскольку границы раздела и ультратонкие слои становятся ключевыми элементами перспективных функциональных материалов и наноустройств.
Особый интерес к двумерным ансамблям на жидких границах раздела связан с тем, что в этом случае наблюдается высокая подвижность ионов, молекул и наночастиц вблизи поверхности. Используя принципы самосборки, можно формировать на поверхности жидкости сложноорганизованные ультратонкие пленки и регулировать наноархитектуру подобных систем на молекулярном уровне. Параметры таких пленок можно модифицировать в широких пределах, изменяя химические и физические характеристики жидкой субфазы, что позволяет контролируемым образом создавать принципиально новые, не существующие в природе биоорганические наноматериалы. Основные функциональные свойства таких материалов (оптические, электрические, магнитные и другие) определяются коллективной динамикой молекул на межфазных границах, поэтому выявление иерархических взаимосвязей между химией молекулярного уровня и структурообразованием в двумерных системах на жидкости имеет важное значение для разработки новых методов целенаправленного “конструирования” нанообъектов [1, 2].
Изучение механизмов, управляющих процессами самоорганизации молекул на жидких границах раздела, остается одним из приоритетных направлений фундаментальных исследований для целого ряда наук, в том числе для коллоидной химии, физики конденсированного состояния, физической химии поверхностей [3, 4]. В последние годы в биомедицинских исследованиях резко вырос интерес к биоорганическим наносистемам на жидкости. Согласно современным представлениям реальная биохимия в клетке чаще всего протекает не в трехмерном, а в двумерном пространстве [5]. Различные микро- и наноструктуры в клетке организованы таким образом, что на них или постоянно закреплены биомакромолекулы, или эти молекулы оседают на поверхностях, образуя двумерные супрамолекулярные ансамбли. Структуру и функции таких природных систем можно изучать в экспериментах in vitro, используя белково-липидные пленки на жидкости в качестве модельных объектов.
Ключевыми проблемами при исследовании двумерных наносистем на жидких границах раздела остаются разработка и адаптация структурных рентгеновских методик для изучения таких систем, а также развитие адекватных методов анализа и интерпретации экспериментальных данных. В настоящей работе предложен теоретический формализм для количественного описания рассеяния рентгеновского излучения на ленгмюровских пленках. Метод Ленгмюра–Блоджетт относится к наиболее эффективным способам формирования двумерных наносистем на жидких поверхностях и широко применяется как для создания функциональных материалов, так и в научных исследованиях. Поскольку толщина ленгмюровских пленок не превышает несколько нанометров, для получения структурной информации о таких системах используют методики, естественным образом ограничивающие глубину проникновения излучения в исследуемый образец, в частности, в условиях скользящего падения рентгеновских лучей. К числу наиболее информативных методов анализа структуры молекулярных пленок относится рентгеновская дифракция в скользящей геометрии, когда в случае идеальной двумерной кристаллической решетки и произвольного направления падения рентгеновских лучей образуется целая совокупность дифрагированных волн [6, 7]. Для адекватного анализа экспериментальных двумерных карт дифракционного рассеяния необходимо разработать формализм реализации численных процедур усреднения интенсивности дифракционного отражения по хаотической ориентации кристаллитов в плоскости пленки. Решению этой задачи посвящена настоящая работа.
ПРИБЛИЖЕНИЕ ИСКАЖЕННОЙ ВОЛНЫ В УСЛОВИЯХ ПОЛНОГО ВНЕШНЕГО ОТРАЖЕНИЯ
Качественные особенности метода рентгеновской дифракции в скользящей геометрии хорошо известны [6–9]. Поскольку в этом случае компонента вектора рассеяния qz вдоль нормали к пленке ничем не ограничена, дифракционное рассеяние имеет место вдоль непрерывных линий (брэгговских стержней), проходящих через узлы двумерной обратной решетки перпендикулярно поверхности пленки, а брэгговские пики определяются “двумерным” условием Вульфа–Брэгга:
где dhk – расстояние между соответствующими цепочками атомов в двумерной кристаллической решетке, θhk – угол Брэгга в плоскости пленки, λ − длина волны излучения.Формирование кривых рентгеновской дифракции в условиях полного внешнего отражения от мономолекулярных слоев обычно описывают простейшей моделью. Каждый домен монослоя рассматривают как двумерный кристалл, состоящий из одинаково ориентированных жестких молекул. Дифракционная картина в обратном пространстве определяется произведением двух факторов: структурным фактором вследствие трансляционной симметрии центров молекул в плоскости монослоя и формфактором индивидуальной молекулы. Такой подход к анализу экспериментальных данных в целом позволяет оценивать средние значения структурных характеристик этих монослоев, и в силу своей простоты он получил довольно широкое распространение [8]. Однако используемая в этом подходе стандартная теория дифракции на малых кристаллитах в борновском приближении (рассеяния на отдельных атомах) не адекватна сути самого экспериментального метода, поскольку в этом случае дифракция в кристаллитах существенно ограничена эффектом полного внешнего отражения, который обусловлен как раз многократным рассеянием. В принципе проблему можно решить в рамках динамической теории рассеяния рентгеновских лучей. Однако в условиях скользящего падения эту теорию несложно реализовать лишь в случае совершенных кристаллов. При ее применении в реальной ситуации (в частности, для описания дифракции на мономолекулярных слоях) сложность конкретной реализации сильно перевешивает простоту самого экспериментального метода [7, 9].
Для количественного описания экспериментальных кривых рентгеновской дифракции в условиях полного внешнего отражения от монослоев разумно использовать приближение искаженной волны [10]. В этом приближении диэлектрическая проницаемость среды представляется в виде
(2)
${\delta }({\mathbf{r}}) = {{{\delta }}_{1}}({\mathbf{r}}) + {{{\delta }}_{2}}({\mathbf{r}}){\text{,}}$В наиболее общем случае многоатомной кристаллической пленки c элементарной ячейкой, характеризуемой базисом (а1, а2, а3), в котором векторы а1 и а2 лежат в плоскости кристаллической пленки
nz – единичный вектор вдоль нормали к пленке, средние положения j-го атома в ячейке определяются выражением(4)
${{{\mathbf{r}}}_{j}} = {{c}_{{j1}}}{{{\mathbf{a}}}_{1}} + {{c}_{{j2}}}{{{\mathbf{a}}}_{2}} + {{c}_{{j3}}}{{{\mathbf{a}}}_{3}}.$(5)
$\begin{gathered} I({\mathbf{q}}{\kern 1pt} ') = {{\left| {\frac{{e_{0}^{2}{\text{exp}}(--i{\omega }t)(\tilde {I} - {\mathbf{s}} \times {\mathbf{s}})}}{{{{m}_{e}}{{c}^{2}}R}}{\kern 1pt} E_{0}^{'}} \right|}^{2}}{\kern 1pt} M({\mathbf{q}}{\kern 1pt} '){{\left| {F({\mathbf{q}}{\kern 1pt} ')} \right|}^{2}} \times \\ \times \;\frac{{N_{{3z}}^{2}}}{{1 + 4N_{{3z}}^{2}{{{\sin }}^{2}}{{{{\tilde {\varphi }}}}_{3}}}}\mathop \prod \limits_{i = 1}^2 \frac{{{{{\sin }}^{2}}\left( {\frac{{{{{\varphi }}_{i}}{{N}_{i}}}}{2}} \right)}}{{{{{\sin }}^{2}}({{{\varphi }}_{i}})}}, \\ \end{gathered} $(7)
$\begin{gathered} F({\mathbf{q}}{\kern 1pt} ') = \mathop \sum \limits_{j = 1}^m \,{{f}_{j}}\exp (i{\mathbf{q}}{\kern 1pt} '{{{\mathbf{r}}}_{j}}) = \\ = \mathop \sum \limits_{j = 1}^m \,{{f}_{j}}\exp (i(с_{1}^{j}{{{\varphi }}_{2}} + c_{2}^{j}{{{\varphi }}_{2}} + c_{3}^{j}{{{{\tilde {\varphi }}}}_{3}})), \\ \end{gathered} $(8)
${\mathbf{q}}{\kern 1pt} {\text{'}} = {\mathbf{\tilde {k}}} - {\mathbf{k}}{\kern 1pt} {\text{'}} = {\mathbf{\tilde {k}}} - {\mathbf{k}}s,$где αс – критический угол полного внешнего отражения, α – угол скольжения рентгеновского излучения. В то же время q' можно определить через отклонение Δq от вектора дифракции qhk для выбранного отражения hk, поэтому компоненты φ1, φ2, ${{{\tilde {\varphi }}}_{3}}$ могут быть выражены как
(11в)
$\begin{gathered} {{{{\tilde {\varphi }}}}_{3}} = {\pi }l + {{q}_{x}}{{a}_{{3x}}} + {{q}_{y}}{{a}_{{3y}}} - k{{s}_{z}}{{a}_{{3z}}} = \\ = {\Delta }{{q}_{x}}{{a}_{{3x}}} + {\Delta }{{q}_{y}}{{a}_{{3y}}} - {\Delta }{{q}_{z}}{{a}_{{3z}}}. \\ \end{gathered} $Из (5) следует, что профили интенсивности в плоскости пленки xy представляют собой брэгговские пики в двумерном обратном пространстве с центрами в узлах обратной решетки
(12)
${{{\mathbf{q}}}_{{hk}}} = \left( {\frac{{2{\pi }(h{{a}_{{2y}}} - k{{a}_{{1y}}})}}{{{{a}_{{1x}}}{{a}_{{2y}}} - {{a}_{{2x}}}{{a}_{{1y}}}}},\;~\frac{{2{\pi }(h{{a}_{{1x}}} - k{{a}_{{2x}}})}}{{{{a}_{{1x}}}{{a}_{{2y}}} - {{a}_{{2x}}}{{a}_{{1y}}}}}} \right)$с пиковой интенсивностью, пропорциональной $N_{1}^{2}N_{2}^{2}$, а нормальные компоненты брэгговских пиков в обратном пространстве определяются выражением
(13)
$k{{s}_{{hklz}}} = \frac{{{{q}_{{hkx}}} + {{q}_{{hky}}}{{a}_{{3y}}} - {\pi }l}}{{{{a}_{{3z}}}}}.$Поскольку ленгмюровские монослои фактически представляют собой 2D “порошок”, т.е. суперпозицию двумерных кристаллитов, равновероятно ориентированных на поверхности воды, при измерении дифракционной картины проводится сканирование только по углу 2θ в плоскости пленки (или qxy-сканирование). В этом случае качественный анализ дифракционной картины осуществляют по схеме стандартной (трехмерной) порошковой дифракции, когда угловые положения брэгговских пиков 2θhk, соответствующие векторам двумерной обратной решетки (13), определяют расстояния между цепочками атомов dhk двумерной кристаллической решетки. Скорректированная на аппаратную функцию ширина наблюдаемого брэгговского пика Δθhk в плоскости двумерной решетки определяет среднюю длину когерентности L двумерных кристаллитов по формуле Шеррера.
Однако для количественного анализа кривых и карт дифракции на мономолекулярных слоях в условиях полного внешнего отражения рентгеновских лучей такой подход не годится как в силу весьма приближенного характера самой формулы Шеррера, так и из-за ее полного несоответствия в случае эффективного вектора рассеяния (8) и (9). Необходимо разработать формализм для реализации численных процедур усреднения интенсивности дифракционного отражения (5) по хаотической ориентации кристаллитов в плоскости пленки и учета аппаратной функции рентгеновского дифрактометра.
УСРЕДНЕНИЕ ИНТЕНСИВНОСТИ ДИФРАКЦИОННОГО ОТРАЖЕНИЯ ПО ХАОТИЧЕСКОЙ ОРИЕНТАЦИИ КРИСТАЛЛИТОВ
Усреднить интенсивность дифракционного отражения можно, если перейти в приведенных выше формулах от представления в терминах компонент эффективного вектора рассеяния к угловому представлению. Согласно (11) интенсивность дифракционного отражения hk может быть рассчитана через отклонение вектора рассеяния от вектора обратной решетки qhkl. В силу узости распределения интенсивности отражения (5) в окрестности брэгговских пиков (12) (с шириной распределения вдоль базисных векторов решетки a1 и a2, обратно пропорциональных N1 и N2) расчеты карт поверхностной дифракции можно проводить только в ближайшей окрестности Δq' этих пиков, так что интенсивность дифракционного отражения можно представить в виде суммы по брэгговским пикам:
(14)
$I({\mathbf{q}}{\kern 1pt} ') = \sum\limits_{hkl} {{{I}_{{hkl}}}({{{\mathbf{q}}}_{{hkl}}} + {\Delta }{\mathbf{q}}{\kern 1pt} ')} .$(18)
$k_{{hklxy}}^{'}\sin {\theta }_{{hk}}^{'} = k\sqrt {{{{\sin }}^{2}}{{{\theta }}_{{hk}}} - s_{{hklz}}^{2}} $выражения (17) позволяют определить угол Брэгга θhk (угол между волновым вектором k и нормалью к вектору обратной решетки (12) для заданного отражения) по формуле
(19a)
$\sin {{{\theta }}_{{hk}}} = \frac{{q_{{hk}}^{2} + {{k}^{2}}s_{{hklz}}^{2}}}{{2k{{q}_{{hk}}}}},$(19б)
$\sin {\theta }_{{hk}}^{'} = \frac{{q_{{hk}}^{2} - {{k}^{2}}s_{{hklz}}^{2}}}{{2k_{{hklxy{\kern 1pt} '}}^{'}{\kern 1pt} {{q}_{{hk}}}}}.$С помощью набора формул (17)–(19) можно провести учет хаотической ориентации кристаллитов в плоскости пленки, переписав выражения (5) и (14) в угловом представлении, удобном для сравнения и подгонки теории и эксперимента:
(20)
$\begin{gathered} I({\mathbf{q}}) = \sum\limits_{hkl} {\int\limits_{ - {\pi }}^{\pi } {{{I}_{{hkl}}}({{{\mathbf{q}}}_{{hkl}}} + {\Delta }{{{\mathbf{q}}}_{{xy}}}({\Delta }{{{\theta }}_{{xy}}},~{\theta })} } + \\ + \;{\Delta }{{q}_{z}}({\Delta }{{{\theta }}_{z}}){{{\mathbf{n}}}_{z}})d{\theta ,} \\ \end{gathered} $(21a)
${\Delta }{{{\theta }}_{{xy}}} \equiv {\Delta }{{{\theta }}_{{hkxy}}} = {{{\theta }}_{{xy}}} - {{{\theta }}_{{hk}}} - {\theta }_{{hk}}^{'},$(21б)
${\Delta }{{{\theta }}_{z}} \equiv \Delta {{{\theta }}_{{hkz}}} = {{{\theta }}_{z}} - {\text{co}}{{{\text{s}}}^{{ - 1}}}{{s}_{{hklz}}},$(22a)
$\begin{gathered} \Delta {{{\mathbf{q}}}_{{xy}}}(\Delta {{{\theta }}_{{xy}}},{\theta }) = \Delta {{q}_{{hkl}}}(\Delta {{{\theta }}_{{xy}}},{\theta })\frac{{{{{\mathbf{q}}}_{{hk}}}}}{{{{q}_{{hk}}}}} + \\ + \;\Delta {{q}_{ \bot }}(\Delta {{{\theta }}_{{xy}}},~{\theta }){{n}_{ \bot }}, \\ \end{gathered} $(22б)
$\begin{gathered} {\Delta }{{q}_{{hkl}}}({\Delta }{{{\theta }}_{{xy}}},{\theta }) = k_{{hklxy}}^{'}[\sin ({\theta }_{{hk}}^{'} + {\Delta }{{{\theta }}_{{xy}}} - {\theta }) - \\ - \;\sin {\theta }_{{hk}}^{'}] + k[\sin ({{{\theta }}_{{hk}}} + {\theta }) - \sin {{{\theta }}_{{hk}}}], \\ \end{gathered} $(22в)
$\begin{gathered} {\Delta }{{q}_{ \bot }}({\Delta }{{{\theta }}_{{xy}}},{\theta }) = {{k}_{{hklxy}}}\cos ({\theta }_{{hk}}^{'} + {\Delta }{{{\theta }}_{{hk}}} - {\theta }) - \\ - \;k\cos ({{{\theta }}_{{hk}}} + {\theta }). \\ \end{gathered} $(23)
$\begin{gathered} {\Delta }{{q}_{{x,y}}} \equiv {\Delta }{{q}_{{hkx}}}({\Delta }{{{\theta }}_{{xy}}},{\theta }) = {\Delta }{{q}_{{hkl}}}({\Delta }{{{\theta }}_{{xy}}},{\theta })\frac{{{{q}_{{hkx,y}}}}}{{{{q}_{{hk}}}}} \pm \\ \pm \;{\Delta }{{q}_{ \bot }}(\Delta {{{\theta }}_{{xy}}},{\theta })\frac{{{{q}_{{hky,x}}}}}{{{{q}_{{hk}}}}}. \\ \end{gathered} $Представленные формулы позволяют моделировать карты дифракционного рассеяния на двумерных ансамблях молекул цилиндрической формы в условиях полного внешнего отражения рентгеновских лучей и проводить численный анализ экспериментальных данных исследования ленгмюровских монослоев методом дифракции в скользящей геометрии.
ПРИМЕР АНАЛИЗА ЭКСПЕРИМЕНТАЛЬНОЙ КАРТЫ ДИФРАКЦИОННОГО РАССЕЯНИЯ С ИСПОЛЬЗОВАНИЕМ ПРЕДЛОЖЕННОГО ТЕОРЕТИЧЕСКОГО ФОРМАЛИЗМА
На основе описанного формализма разработана программа для обработки экспериментальных двумерных карт дифракционного рассеяния. Изменение параметров модели ленгмюровской пленки, таких как размеры элементарной ячейки, наклоны и повороты молекул, размеры областей когерентного рассеяния и среднеквадратичные смещения атомов из положения равновесия, позволяет проводить количественный анализ экспериментальных результатов и получать численные значения структурных параметров монослоя.
Возможности разработанной программы продемонстрированы на примере анализа экспериментальных карт рассеяния для липидного монослоя, сформированного на поверхности жидкой субфазы при различном поверхностном давлении. В качестве тестового объекта выбран монослой фосфолипида дипальмитоилфосфатидилхолин (ДПФХ) – 1,2-Dipalmitoyl-sn-glycero-3-phospho-choline (Sigma).
Для приготовления всех растворов была использована вода высокой степени очистки (сопротивление более 18 мОм/см), полученная на установке Millipore Corp. Все измерения проводили при температуре 21°С. Для формирования фосфолипидного монослоя раствор ДПФХ в хлороформе (концентрации 0.45 мг/мл) наносили на поверхность водной субфазы в ленгмюровской ванне и поджимали до рабочего давления, которое поддерживали постоянным в процессе рентгеновских измерений. Было выполнено несколько измерений при различных значениях поверхностного давления.
Измерения проведены на станции ID10 (ESRF), оборудованной ленгмюровской ванной и предназначенной для исследований на поверхности жидкости [11]. Использовано излучение с длиной волны 0.564 Å. При измерении картин двумерной дифракции угол падения излучения на поверхность воды составлял 0.8θС (θС – критический угол полного внешнего отражения для воды). Интенсивность дифракционного отражения в направлении qz регистрировали с помощью линейного позиционно-чувствительного детектора (Mythen 1K, Dectris) с вертикальным размером стрипа 50 мкм.
Экспериментальные и расчетные карты дифракционного рассеяния на монослое ДПФХ при давлении π = 5 и 25 мН/м представлены на рис. 1 и 2 соответственно. При моделировании двумерных карт дифракционного рассеяния учитывали аппаратные поправки – дисперсию длин волн и уширение пиков на щелях Соллера. Из сравнения рис. 1 и 2 видно, что при увеличении поверхностного давления изменяются положения рефлексов как по оси qxy, так и по оси qz. Смещение пиков в область больших qxy однозначно указывает на уменьшение параметров двумерной решетки при увеличении давления в ленгмюровском слое. Сдвиг пиков 10 и 01 в сторону меньших qz связан с уменьшением угла наклона молекул ДПФХ. Основные средние параметры двумерной решетки так же, как тип и угол наклона молекул, могут быть получены простым преобразованием координат рефлексов в обратном пространстве [12]. Для анализа тонких эффектов на картине дифракции на двумерной решетке требуется проведение моделирования распределения интенсивности рассеяния в обратном пространстве.
Рис. 1.
Двумерная карта дифракционного рассеяния на монослое ДПФХ, сформированном на поверхности водной субфазы при давлении π =5 мН/м: а – экспериментальные данные, б – численное моделирование.
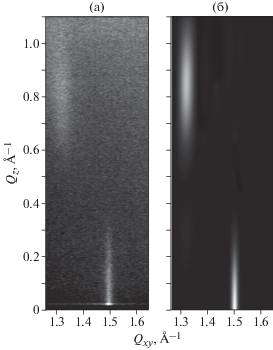
Рис. 2.
Двумерная карта дифракционного рассеяния на монослое ДПФХ, сформированном на поверхности водной субфазы при давлении π = 25 мН/м: а – экспериментальные данные, б – численное моделирование.
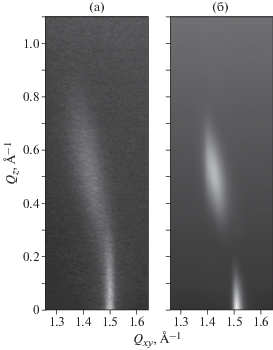
Принципиальное различие экспериментальных данных, представленных на рис. 1 и 2, состоит в заметном изменении формы рефлексов 10 и 01: на рис. 1 (низкое давление) брэгговский стержень при qz ≠ 0 расположен практически вертикально, тогда как на рис. 2 (высокое давление) он становится наклонным и вытянутым в направлении рефлекса 1$\bar {1}$ при qz = 0.
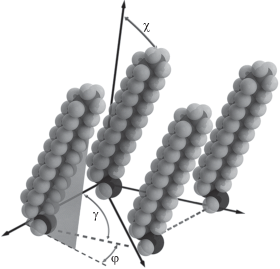
Математическое моделирование двумерных карт дифракционного рассеяния с использованием представленного теоретического формализма позволяет получить хорошее качественное совпадение с экспериментом, соответствующие структурные параметры монослоя представлены в табл. 1. Согласно полученным данным параметры упорядоченной фазы монослоя ДПФХ при низком давлении соответствуют искаженной гексагональной решетке с параметрами a = 5.28 Å, γ = = 69.6°, угол наклона углеводородных цепей относительно нормали к плоскости пленки χ = = 39.3°, азимут 55.2°, молекулы наклонены в сторону следующего ближайшего соседа (обозначения параметров элементарной решетки приведены на рис. 3). Форма рефлексов (в частности, характерные размеры в направлениях qz и qxy) эффективно регулируется длиной молекул и размером областей когерентного рассеяния, которые были заданы как 25 и 95 Å соответственно. Для монослоя ДПФХ при повышенном давлении была использована модель более плотной упаковки молекул с решеткой, близкой к гексагональной, с параметрами a = 5.05 Å, γ = 64.4°. Угол наклона углеводородных цепочек заметно уменьшился и составил χ = 27.6°. Для моделирования специфичной формы рефлексов 10 и 01 использована модель ленгмюровского слоя, которая предполагает наличие кристаллитов с некоторой дисперсией параметров решетки и углов наклона молекул и подчиняется закону нормального распределения. В таком случае результирующая картина дифракции будет представлять собой суперпозицию интенсивностей дифракции на кристаллитах с различными параметрами решетки, взятую с соответствующим весовым коэффициентом. Наилучшее согласие расчетной дифракционной картины с экспериментальной было получено при использовании полуширины распределения параметра решетки Δa ∼ 0.18 Å и дисперсии угла наклона хвостов Δχ ∼ 11°.
Таблица 1.
Сравнение параметров кристаллической решетки монослоя ДПФХ при различных значениях поверхностного давления π
| π, мН/м | a1 = a2, Å | γ, град | χ, град | φ, град | Площадь на углеводородную цепь, Å2 |
|---|---|---|---|---|---|
| 5 | 5.28 | 69.6° | 39.3° | –55.2 | 26.1 |
| 25 | 5.05 | 64.4° | 27.6° | –57.8 | 23 |
Большой разброс параметра решетки и углов наклона углеводородных цепочек молекул ДПФХ, наблюдаемый при поджатии монослоя, можно объяснить особенностями структурообразования монослоя этого фосфолипида. Известно, что в монослое ДПФХ при малых давлениях реализуется фазовый переход из состояния “растянутой” жидкости в конденсированную фазу. На изотерме сжатия наблюдается характерное плато – при уменьшении площади слоя давление в монослое остается постоянным. Многочисленные исследования монослоя ДПФХ методом брюстеровской микроскопии показали, что при фазовом переходе в монослое ДПФХ одновременно существуют две фазы – жидкая (неупорядоченная) и конденсированная (упорядоченная). На начальной стадии фазового перехода в жидкой фазе образуются отдельные домены упорядоченной фазы размером 10 мкм, по мере уменьшения площади монослоя упорядоченные домены растут и достигают размеров 40–50 мкм [13]. При дальнейшем сжатии слоя домены сливаются друг с другом, фракция упорядоченной фазы в монослое заметно увеличивается, на изотерме наблюдается резкий рост давления. Понятно, что такие сложные процессы носят неравновесный характер и могут заметно повлиять на упаковку молекул ДПФХ: при увеличении давления в монослое негидростатическое давление соседних кристаллитов друг на друга приводит к дефектам упаковки, которые выражаются в разбросе угла наклонов молекул и их азимутов.
ЗАКЛЮЧЕНИЕ
Разработан теоретический формализм для количественного описания экспериментальных карт дифракционного рассеяния на двумерных кристаллах. Использовано приближение искаженной волны, которое, с одной стороны, существенно проще в практической реализации, чем решение задачи в рамках динамической теории рассеяния рентгеновских лучей; с другой стороны, оно позволяет надежно определять при моделировании экспериментальных данных как средние значения структурных параметров, так и их среднеквадратичные отклонения. В рамках предложенного подхода рассеивающая среда на первом этапе характеризуется более простым, однородным распределением рассеивающих атомов, что позволяет точно рассчитать волновое поле внутри материала в условиях полного внешнего отражения рентгеновских лучей. На втором этапе рассматривается рассеяние именно этого поля (т.е. искаженной волны) на всех атомах реально исследуемой структуры. Используя полученные в работе формулы, можно проводить самосогласованный расчет интенсивности дифракционного отражения в условиях полного внешнего отражения от ленгмюровских монослоев и выполнять количественный анализ экспериментальных данных, полученных для таких систем методом дифракции в скользящей геометрии.
Работа выполнена в рамках Государственного задания ФТИАН им. К.А. Валиева РАН Минобрнауки РФ (тема № 0066-2019-0004). Анализ экспериментальных данных проведен в рамках Государственного задания ФНИЦ “Кристаллография и фотоника” РАН.
Список литературы
Hinderhofer A., Heinemeyer U., Gerlach A. et al. // J. Chem. Phys. 2007. V. 127. P. 194705.
Yang S., Yan Y., Huang J. et al. // Nat. Commun. 2017. V. 8. № 1. P. 1.
Stefaniu C., Brezesinski G., Möhwald H. // Adv. Colloid Int. Sci. 2014. V. 208. P. 197.
Zheludeva S.I., Novikova N.N., Konovalov O.V. et al. // X-Ray Standing Wave Technique: Principles and Applications. N. Y.: World Scientific Publishing, 2013. V. 1. P. 355.
Minsky A., Shimoni E., Frenkiel-Krispin D. // Nat. Rev. Mol. Cell Biol. 2002. V. 3. P. 50.
Pershan P.S., Schlossman M. Liquid Surfaces and Interfaces: Synchrotron X-ray Methods. Cambridge: Cambridge University Press, 2012. 315 p.
Daillant J., Alba M. // Rep. Prog. Phys. 2000. V. 63. № 10. P. 1725.
Kaganer V.M., Möhwald H., Dutta P. // Rev. Mod. Phys. 1999. V. 71. P. 779.
Cantin S., Pignat J., Daillant J. et al. // Soft Matter. 2010. V. 6. P. 1923.
Vineyard J.H. // Phys. Rev. B. 1982. V. 26. № 8. P. 4146.
Smilgies D.M., Boudet N., Struth B. et al. // J. Synchrotron Rad. 2005. V. 12. P. 329.
Kjaer K. // Physica B. 1994. V. 198. P. 100.
Kim K., Choi S.Q., Zell Z.A. et al. // PNAS. 2013. V. 110. P. 3054.
Дополнительные материалы отсутствуют.
Инструменты
Кристаллография