Кристаллография, 2020, T. 65, № 6, стр. 851-856

ВВЕДЕНИЕ

Создание гибридных органо-неорганических планарных систем на основе молекул белков – актуальная проблема современного материаловедения в области природоподобных технологий. Разнообразие функций белковых молекул в живых организмах открывает большие возможности использования подобных систем при разработке различных биоэлектронных устройств: биосенсоров, биокаталитических систем, гибридных устройств микро- и наноэлектроники. Для эффективного функционирования такого рода устройств белковые молекулы должны формировать сплошные упорядоченные слои или пленки с технологически контролируемыми параметрами структуры: толщиной, плотностью, требуемой ориентацией, упорядоченностью молекул и т.д. [1]. Последнее определяет важность как разработки новых, так и адаптации уже существующих методов формирования белковых слоев с воспроизводимыми параметрами, а также неразрушающих методов анализа и контроля их структуры.

Одним из эффективных методов получения упорядоченных органических пленок с контролируемыми параметрами на твердых подложках является ленгмюровская технология [2] (методы Ленгмюра–Блоджетт и Ленгмюра–Шеффера (ЛШ)). Указанная технология состоит в формировании на поверхности жидкости мономолекулярного слоя с его дальнейшим однократным или многократным переносом на поверхность подложки, что позволяет с высокой точностью контролировать толщину полученной пленки или слоистой структуры.

Ранее [3, 4] на примере лизоцима был предложен и апробирован принципиально новый подход к получению белковых пленок на твердых подложках, основанный на модификации метода ЛШ. В предложенном подходе для формирования ленгмюровского монослоя используется предварительно подготовленный белковый раствор, параметры которого соответствуют условиям кристаллизации белка (тип растворителя и буфера, pH раствора, концентрация белка, состав и концентрация осадителя). Добавление осадителя, например хлористого натрия, в раствор лизоцима приводит к изменению гидратной оболочки белковых молекул и смене межмолекулярного взаимодействия от отталкивания к притяжению [5]. Также при соответствии параметров раствора условиям кристаллизации в нем образуется предшествующая кристаллизации промежуточная фаза, которая характеризуется наличием в растворе устойчивых олигомеров белка [6, 7]. С применением методов рентгеновской рефлектометрии (РР) и атомно-силовой микроскопии было показано, что пленки лизоцима, полученные модифицированным методом ЛШ, являются гомогенными и имеют более высокую плотность в сравнении с пленками островкового типа, полученными из раствора белка без добавления осадителя. Это свидетельствует о том, что образующиеся в растворе олигомеры частично участвуют в формировании ленгмюровского монослоя как отдельные упорядоченные структурные единицы. Вместе с тем в [3, 4, 8] методом стоячих рентгеновских волн в области полного внешнего отражения (СРВ в ПВО) [9] показано наличие и определено расположение слоев ионов осадителя в полученных планарных системах, что представляется важным с точки зрения изучения механизма взаимодействия молекул белка с осадителем.

В [3, 4, 8] с целью обработки экспериментальных данных рентгеновской рефлектометрии и СРВ в ПВО применялся модельный подход, требующий использования заданной параметрической модели распределения электронной плотности (ЭП) в исследуемой структуре. В качестве такой модели была выбрана слоистая структура, в которой белковая пленка представлялась в виде гомогенного слоя с постоянным по толщине значением ЭП и двух переходных слоев, характеризующих несовершенство границ пленка–подложка и пленка–вакуум.

Развивая модельное представление о структуре ленгмюровской пленки лизоцима, можно считать, что распределение ЭП по ее толщине (в случае мономолекулярной пленки) не может быть однородным, а должно быть сходным с распределением ЭП в молекуле белка. В связи с этим уточнение особенностей строения сформированных на твердых подложках пленок лизоцима с использованием модели, основанной на атомарном строении его молекулы, представляется интересным как с методической точки зрения, так и с целью получения новой информации о структуре такого рода планарных систем.

В настоящей работе методом РР проведено исследование тонких пленок лизоцима, сформированных на кремниевых подложках с применением модифицированного метода ЛШ с использованием хлорида калия в качестве осадителя. На основании расчета распределения ЭП в молекулах лизоцима предложена слоистая модель структуры исследуемых пленок, которая была использована в ходе обработки экспериментальных данных РР.

МАТЕРИАЛЫ И МЕТОДЫ

Подготовка образцов. Для приготовления растворов использовали: белок лизоцима куриного яйца (HEWL) (CAS #12650–88–3, Sigma-Aldrich); ацетат натрия (CAS #6131–90–4, Helicon); хлорид калия (CAS #7447-40-7, aber GmbH); сверхчистую воду (удельное сопротивление 18 МОм⋅см), полученную с помощью системы Simplicity 185 (Millipore). В качестве буферного раствора использовался натрий-ацетатный буфер (0.2 М CH₃COONa/CH₃COOH, pH 4.5).

Растворы белка с осадителем получены из двух первичных растворов: маточного раствора лизоцима с концентрацией 80 мг/мл в натрий-ацетатном буфере и раствора хлорида калия с концентрацией 50 мг/мл в том же буфере. Оба первичных раствора фильтровали с использованием мембранных фильтров (Millex) с диаметром пор 0.22 мкм; маточный раствор белка дополнительно центрифугировали в течение 10 мин с частотой 10 000 об./мин. В полученном смешанном растворе белка с осадителем концентрации лизоцима и хлорида калия составляли 40 и 25 мг/мл соответственно.

Монослои лизоцима формировали при температуре 18.5 ± 0.5°C в ленгмюровской ванне KSV 5000 LB (KSV Instruments) с двумя барьерами и рабочей площадью 750 см²; в качестве субфазы использовали сверхчистую воду. Поверхностное давление измеряли с помощью весов Вильгельми с платиновой пластиной; точность измерения составляла ±0.1 мН/м. Раствор белка с осадителем объемом 1000 мкл наносили на предварительно очищенную поверхность субфазы с помощью автоматической пипетки Eppendorf по истечении 30 мин после смешивания первичных растворов. Сразу после нанесения монослой поджимался подвижными барьерами со скоростью 20 мм/мин до достижения значения поверхностного давления 14 мН/м.

Перенос сформированного монослоя на твердую подложку осуществлялся методом ЛШ путем однократного касания поверхностью подложки поверхности субфазы с монослоем. Подложки были изготовлены из кремниевых пластин толщиной 380 ± 15 мкм, ориентации [100] с гидрофильной поверхностью (“Протон Альфа”). После переноса монослоя подложку помещали в герметичную кристаллизационную ячейку [10], в специальное углубление которой наливали 1 мл раствора осадителя с концентрацией 50 мг/мл для медленного высыхания капли субфазы, захваченной с монослоем.

Измерения методом РР. Экспериментальные данные РР получены с использованием рентгеновского дифрактометра SmartLab (Rigaku), оснащенного источником излучения с вращательным анодом (Mo) мощностью 9 кВт; использовали спектральную линию MoK_α1 (λ = 0.07093 нм). Регистрацию интенсивности рассеянного излучения проводили с помощью NaI-детектора.

Съемку кривых зеркального отражения осуществляли путем сканирования обратного пространства вдоль направления q_z, перпендикулярного поверхности исследуемых пленок (стандартное θ/2θ-сканирование). При этом падающий пучок засвечивал практически всю поверхность образца; приемные щели обеспечивали угловое разрешение в плоскости рассеяния 0.012°.

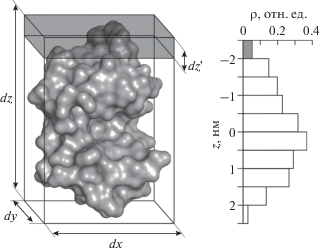
Анализ экспериментальных данных РР. Расчет профилей распределения ЭП в мономере лизоцима проводили исходя из трехмерной атомной структуры данного белка, взятой из банка данных PDB (PDB ID: 4WLD). Для расчета профиля распределения объем dxdydz (рис. 1) разбивали на насколько элементарных объемов dxdydz', по каждому из которых рассчитывали электронную плотность ρ в соответствии с уравнением:

где x_k – число атомов k-го сорта, Z_k – атомный номер, $f_{k}^{'}$ – действительная часть атомного фактора рассеяния, dxdy – площадь на молекулу, dz' – шаг расчета профиля распределения вдоль направления dz. Путем вращения молекулы внутри объема dxdydz проводили расчет профилей распределения ЭП в различных направлениях в мономере лизоцима.

В соответствии с проведенными расчетами был выбран модельный профиль распределения ЭП в исследуемых пленках, отражающий специфику распределения ЭП в мономере лизоцима. Данный профиль, характеризующийся набором параметров и описываемый гладкой функцией от координаты по глубине структуры, разбивали на достаточно тонкие слои (в пределах которых изменением электронной плотности можно пренебречь) с идеально гладкими границами.

Расчет теоретической кривой зеркального отражения от такой слоистой системы выполняли в соответствии с рекуррентными соотношениями Парратта [11]. Уточнение параметров модели и соответственно профиля распределения ЭП проводили путем минимизации расхождения между экспериментальными и расчетными данными (критерия χ²) с использованием алгоритма Левенберга–Марквардта [12]. Оценку ошибки полученных параметров и соответствующего им профиля распределения ЭП выполняли с применением подхода, описанного в [13].

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

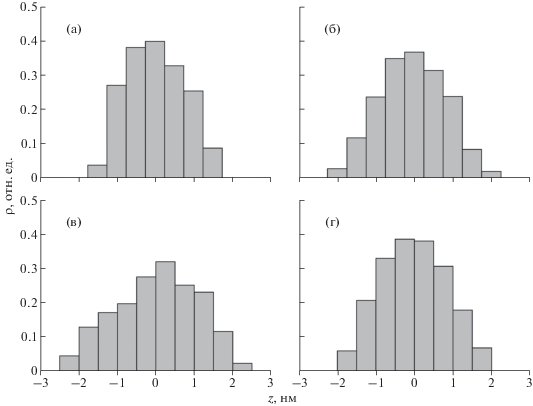
На рис. 2 представлены рассчитанные профили распределения ЭП для трех взаимно перпендикулярных направлений в произвольно ориентированном в пространстве мономере белка лизоцима, а также профиль ЭП, усредненный по всем возможным направлениям. Представленные на рисунке профили рассчитаны с шагом dz' = 0.5 нм, нормированы на ЭП кремния и соответствуют площади на молекулу dxdy = $4R_{g}^{2}$ ≈ ≈ 12.25 нм², где R_g ≈ 1.75 нм – радиус инерции мономера [14]. Из рисунка видно, что для произвольного положения мономера лизоцима в пространстве распределение ЭП можно условно описать некоторой гладкой функцией с одним максимумом. В таком случае распределение ЭП для системы в виде монослоя молекул на поверхности твердой подложки может быть представлено слоистой моделью с тремя переходными слоями, характеризующими изменение плотности на двух границах пленки и границе подложки. В настоящей работе в качестве функции, описывающей переходные слои, была выбрана функция ошибок (функция Лапласа) [13]. Использованный при расчетах шаг dz' = 0.5 нм является достаточно мелким для выявления специфики распределения ЭП в мономере лизоцима и построения слоистой модели для обработки данных РР в виде трех переходных слоев. Использование более мелкого шага не приводило к значительным изменениям в теоретических профилях распределения.

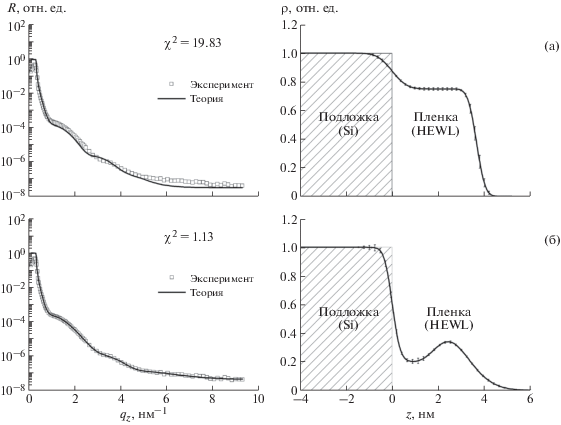
На рис. 3 представлено сравнение результатов обработки экспериментальных данных РР при использовании предложенной модели и модели, применявшейся ранее [3, 4, 8]. Видно, что использование модели с тремя переходными слоями приводит к значительному снижению расхождения между экспериментальными и расчетными данными, о чем свидетельствует уменьшение критерия χ² до значения, близкого к единице.

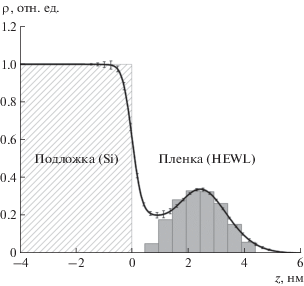
На рис. 4 показано соответствие между полученным в результате обработки экспериментальных данных профилем распределения ЭП в исследуемых пленках и его теоретическим распределением в мономере лизоцима. Представленное на рисунке теоретическое распределение соответствует площади на молекулу dxdy = 12.96 нм², что лишь незначительно больше величины dxdy = = $4R_{g}^{2}$ ≈ 12.25 нм². Таким образом, исследуемые пленки представляют собой сплошной слой мономеров лизоцима, т.е. являются гомогенными.

ЗАКЛЮЧЕНИЕ

Проведены исследования тонких пленок лизоцима, сформированных на кремниевых монокристаллических подложках, модифицированным методом Ленгмюра–Шеффера. Исходя из моделирования теоретического распределения электронной плотности в мономере лизоцима, предложена слоистая модель ленгмюровской монослойной пленки лизоцима. Использование предложенной модели в качестве стартовой при обработке экспериментальных данных РР позволило снизить расхождение между расчетными и экспериментальными данными и уточнить специфику структуры исследуемых пленок, в том числе оценить их степень гомогенности.

Отметим, что в случае анизотропной структуры элементов, составляющих пленку белка (таких как молекулярные комплексы, олигомеры и другие), данный подход может быть применен с целью определения их преимущественной ориентации в пленке относительно поверхности подложки.

Работа выполнена при поддержке Министерства науки и высшего образования РФ в рамках выполнения работ по Государственному заданию ФНИЦ “Кристаллография и фотоника” РАН с использованием оборудования ЦКП (проект RFMEFI62119X0035).