Кристаллография, 2021, T. 66, № 2, стр. 214-229
Дифракция поляризованных нейтронов в исследованиях на монокристаллах
1 Петербургский институт ядерной физики им. Б.П. Константинова – НИЦ “Курчатовский институт”
Санкт-Петербург, Россия
* E-mail: Zobkalo_IA@pnpi.nrcki.ru
Поступила в редакцию 27.05.2020
После доработки 27.05.2020
Принята к публикации 28.05.2020
Аннотация
Обзор посвящен различным методам использования дифракции поляризованных нейтронов, с последующим поляризационным анализом или без него. Представлены теоретические основы различных методов дифракции поляризованных нейтронов для исследования магнитных свойств вещества. Продемонстрирована эффективность использования поляризованных нейтронов для определения магнитных свойств структуры, разделения магнитных и ядерных вкладов, изучения распределения плотности намагниченности в кристаллах, изучения киральных эффектов. Приводятся примеры экспериментальных работ, результаты которых подтверждают уникальность этой методики для решения задач физики магнитных явлений в твердом теле.
ОГЛАВЛЕНИЕ
Введение
1. Уравнения Малеева–Блюма
2. Дифракция поляризованных нейтронов без анализа поляризации после рассеяния – полуполяризционный эксперимент
2.1. Классическая дифракция поляризованных нейтронов
2.2. Применение полуполяризационного метода для исследования магнитной киральности
3. Поляризационный анализ
3.1. Продольный поляризационный анализ
3.2. XYZ-поляризационный анализ
3.3. Сферическая нейтронная поляриметрия
Заключение
ВВЕДЕНИЕ
Наличие у нейтрона спина и магнитного момента определяет уникальное значение нейтронного рассеяния для исследования магнитных свойств конденсированного вещества. Взаимодействие магнитного момента нейтрона с незаполненными электронными оболочками атомов дает доступ к микроскопическим свойствам соединений. Наиболее распространено использование неполяризованных пучков нейтронов для определения магнитных структур, т.е. определение направлений магнитных моментов и их величины. Начиная с пионерского эксперимента на MnO К. Шалла и Дж. Смарта в 1949 г. [1], в котором получено доказательство антиферромагнетизма, предсказанного Л. Неелем, было определено множество магнитных структур, в том числе магнитные конфигурации, гораздо более сложные, чем простые ферромагнитные или антиферромагнитные упорядочения.
Процесс рассеяния может оказывать влияние на спиновое состояние нейтронного пучка. Следовательно, можно ожидать, что контроль спинового состояния нейтрона в эксперименте может дать дополнительную ценную информацию. С теоретической точки зрения возможность использования поляризованного пучка нейтронов предполагалась с самого начала нейтронных исследований [2–5]. В 1937 г. Дж. Швингер разработал детальную теорию неполяризованного пучка нейтронов, который будет частично поляризован после прохождения через ферромагнетик [2], что экспериментально было подтверждено в 1938 г. О. Фришем и др. [6]. В это же время О. Халперн и М. Джонсон развивали теорию магнитного рассеяния нейтронов, где особое внимание уделялось вопросам поляризации [3–5]. Общая теория рассеяния поляризованных нейтронов была опубликована С.В. Малеевым и М. Блюмом в 1963 г. одновременно и независимо друг от друга [7, 8] (С.В. Малеев и др. опубликовали работу [7] в 1962 г., а переведенный вариант статьи [8] вышел только в 1963 г.). В этих статьях теоретически показано, что при работе с поляризованными нейтронами и поляризационным анализом можно разделить вклады в рассеяние структурного или магнитного происхождения, а кроме того, обнаружить рассеяние, которое остается скрытым в обычных экспериментах по рассеянию неполяризованных нейтронов.
Экспериментальные возможности и успехи в этой области, как нередко бывает, обусловлены техническим развитием, в частности в области способов получения поляризованных нейтронов. Это подразумевает как увеличение потока поляризованных нейтронов на позиции образца, так и снижение затрат на производство такого потока. В 1951 г. был получен полностью поляризованный пучок нейтронов при отражении нейтронов от намагниченных зеркал [9]. В том же году была достигнута полная поляризация нейтронов методом брэгговского рассеяния на антиферромагнитном магнетите (Fe3O4) [10]. Развитие техники производства поляризованных нейтронов открыло новое экспериментальное пространство, и в 1959 г. [11] были проведены первые эксперименты, в которых поляризованные нейтроны использовались как исследовательский инструмент. Они продемонстрировали высокую чувствительность поляризованных нейтронов к слабым магнитным сигналам, что позволило очень точно отобразить карты распределения намагниченности и определить магнитные форм-факторы никеля и железа [11]. В 1964 г. Г.М. Драбкиным и др. была экспериментально обнаружена поляризационная зависимость магнонного рассеяния на железе [12]. В 1969 г. Р. Мун, Т. Рист и В. Келер в Ок-Ридже впервые оснастили трехосный спектрометр оборудованием для работы как с падающими поляризованными нейтронами, так и с анализом поляризации после рассеяния, что дает возможность получения новой информации благодаря анализу изменения поляризации после рассеяния [13]. Благодаря сравнительно небольшим затратам этот вариант поляризационного продольного анализа получил широкое распространение в настоящее время; им оснащено большинство современных спектрометров, что делает данный метод доступным для все большего числа пользователей. В 1989 г. Ф. Тассэ обобщил продольный поляризационный анализ на полностью сферический [14].
1. УРАВНЕНИЯ МАЛЕЕВА–БЛЮМА
Для начала полезно определить, что означает понятие “поляризованные нейтроны”. Проекция спина нейтрона на выделенную ось z может принимать значения sz = ±1/2. Проекция на другое направление, перпендикулярное z, будет равна 0. Это связано с тем, что спин нейтрона – это трехмерный векторный оператор s = $1{\text{/}}2{\mathbf{\sigma }}$, где ${\mathbf{\sigma }}$ – матрицы Паули:
(1)
${{{\sigma }}_{x}} = \left( {\begin{array}{*{20}{c}} 0&1 \\ 1&0 \end{array}} \right),\quad {{{\sigma }}_{y}} = \left( {\begin{array}{*{20}{c}} 0&i \\ { - i}&0 \end{array}} \right),\quad {{{\sigma }}_{z}} = \left( {\begin{array}{*{20}{c}} 1&0 \\ 0&{ - 1} \end{array}} \right).$(2)
$\begin{gathered} {\mathbf{p}} = \left\langle {2{\mathbf{s}}{\text{/}}\hbar } \right\rangle = \left\langle {\mathbf{\sigma }} \right\rangle ,\quad {{p}_{x}} = \left\langle {{{{\sigma }}_{x}}} \right\rangle ,\quad {{p}_{y}} = \left\langle {{{{\sigma }}_{y}}} \right\rangle , \\ {{p}_{z}} = {{{\sigma }}_{z}}, \\ \end{gathered} $Для определения поляризации пучка нейтронов необходимо задать ось квантования внешним полем, что дает возможность определить средние значения проекций спина нейтронов на это направление. Для заданной оси квантования спин нейтрона может быть направлен либо параллельно (+), либо антипараллельно (–). Поляризация пучка нейтронов относительно произвольно выбранной оси (i = x, y, z) определяется как
где $N_{i}^{ + }$ ($N_{i}^{ - }$) – число нейтронов со спином, параллельным (антипараллельным) оси i. В полностью неполяризованном пучке существует равное количество обеих спиновых конфигураций, следовательно, P = 0. Полностью поляризованный пучок имеет поляризацию P = ±1. Вектор поляризации уже представляет собой классический псевдовектор.В отличие от предыдущей теории Халперна–Джонсона, ограниченной ферромагнитной и простой антиферромагнитной структурами, в теории Малеева–Блюма никаких ограничений на тип магнитного упорядочения не накладывается. Таким образом была продемонстрирована возможность изучать любые поляризационные эффекты, в том числе при рассеянии спиральными спиновыми структурами. Фундаментальные уравнения рассеяния поляризованных нейтронов Малеева–Блюма в настоящее время рассматривают в несколько упрощенном виде:
(5)
$\begin{gathered} {\sigma } = (NN{\kern 1pt} {\text{*}}) + ({{{\mathbf{M}}}_{ \bot }}{\mathbf{M}}_{ \bot }^{*}) + i{\mathbf{P}} \cdot ({\mathbf{M}}_{ \bot }^{*} \times {{{\mathbf{M}}}_{ \bot }}) + \\ + \;{\mathbf{P}} \cdot ({{{\mathbf{M}}}_{ \bot }}N{\kern 1pt} {\text{*}} + {\mathbf{M}}_{ \bot }^{*}N), \\ \end{gathered} $(6)
$\begin{gathered} {\mathbf{P}}{\kern 1pt} '{\kern 1pt} {\sigma } = {\mathbf{P}}NN{\kern 1pt} {\text{*}} - {\mathbf{P}}({{{\mathbf{M}}}_{ \bot }}{\mathbf{M}}_{ \bot }^{*}) + {{{\mathbf{M}}}_{ \bot }}({\mathbf{PM}}_{ \bot }^{*}) + \\ + \;{\mathbf{M}}_{ \bot }^{*}({\mathbf{P}}{{{\mathbf{M}}}_{ \bot }}) - i({\mathbf{M}}_{ \bot }^{*} \times {{{\mathbf{M}}}_{ \bot }}) + \\ + \;N{\mathbf{M}}_{ \bot }^{*} + N{\kern 1pt} {\text{*}}{{{\mathbf{M}}}_{ \bot }} - i(N{\mathbf{M}}_{ \bot }^{*} - N{\kern 1pt} {\text{*}}{{{\mathbf{M}}}_{ \bot }}) \times {\mathbf{P}}. \\ \end{gathered} $(7)
${{{\mathbf{M}}}_{ \bot }} = ({\mathbf{Q}} \times {{{\mathbf{F}}}_{{\text{M}}}} \times {\mathbf{Q}}).$Уравнение (5) представляет зависимость сечения рассеяния от поляризации пучка падающих нейтронов P. Первое слагаемое в уравнении (5) – это чисто ядерный вклад. Второе – обычный магнитный вклад, который учитывается таким же образом, как при анализе данных неполяризованных нейтронов. Эти два элемента не зависят от поляризации падающих на образец нейтронов. Третий член уравнения (5) – это так называемый магнитный киральный вклад, тогда как четвертый отражает вклад от интерференции между ядерным и магнитным рассеянием. Оба последних зависят от поляризации падающего пучка нейтронов. Интерференционный вклад не равен нулю в тех случаях, когда периодичность магнитной структуры совпадает с периодичностью кристаллической, т.е. магнитное и ядерное рассеяние появляются в одних и тех же точках обратного пространства.
Уравнение (6) отражает изменение поляризации при рассеянии в магнитной среде, в нем поляризация рассеянного пучка нейтронов P' представлена как функция начальной поляризации P. Первое слагаемое в уравнении (6) – ядерный вклад, он не изменяет поляризацию (P' = P). Действие некирального магнитного вклада (второй, третий, четвертый члены уравнения (6)) – это прецессия падающей поляризации на 180° вокруг ${{{\mathbf{M}}}_{ \bot }}$: падающая поляризация обращается, за исключением компоненты вдоль ${{{\mathbf{M}}}_{ \bot }}$. Изучение интерференционных вкладов (последние три слагаемых уравнения (6)) показывает, что поляризация может быть создана вдоль ${{{\mathbf{M}}}_{ \bot }}$, когда магнитный и ядерный вклады находятся в фазе. Поскольку интерференционный вклад зависит от P, поляризация вращается по конусу вокруг ${{{\mathbf{M}}}_{ \bot }}$. Киральный магнитный вклад (пятый член уравнения (6)) создает поляризацию вдоль вектора рассеяния Q.
В магнитном рассеянии участвуют только компоненты ${{{\mathbf{M}}}_{ \bot }}$, перпендикулярные вектору рассеяния Q, что задает специфическую систему координат, удобную для различных вычислений, связанных с рассеянием поляризованных нейтронов. Обычно Q направлен вдоль оси X, ось Y направлена перпендикулярно X в плоскости рассеяния, Z – перпендикулярно X и Y так, чтобы сформировать правую систему координат. При таком выборе вектор магнитного взаимодействия по определению не имеет компонент вдоль X, так как он перпендикулярен вектору рассеяния.
2. ДИФРАКЦИЯ ПОЛЯРИЗОВАННЫХ НЕЙТРОНОВ БЕЗ АНАЛИЗА ПОЛЯРИЗАЦИИ – ПОЛУПОЛЯРИЗАЦИОННЫЙ ЭКСПЕРИМЕНТ
2.1. Классическая дифракция поляризованных нейтронов
Поскольку в первых экспериментах Р. Натанса и К. Шалла [11] с использованием поляризованных нейтронов применялся этот метод, то именно он сейчас называется “классической дифракцией поляризованных нейтронов”. Идея его сравнительно проста, хотя реализация часто вызывает серьезные технические затруднения. В таком эксперименте на образец падает поток поляризованных нейтронов, а поляризация рассеянных нейтронов не анализируется. Для переворота поляризации падающих нейтронов используется флиппер. Образец намагничивается магнитным полем, приложенным вдоль вертикальной оси Z' (заметим, что поскольку плоскость рассеяния не всегда лежит в горизонтальной плоскости, то направление Z не всегда совпадает с Z'). Так как это поле используется и в качестве ведущего, поляризация нейтронов также направлена вдоль оси Z'. В эксперименте измеряются интенсивности рассеянных нейтронов при двух возможных состояниях падающей поляризации; затем рассчитывается их отношение R, которое обычно называют флип-отношение (flipping ratio). Такую конфигурацию эксперимента часто называют “полуполяризованным экспериментом”. Этот метод демонстрирует колоссальное повышение чувствительности для слабых магнитных сигналов. Выражение для интенсивности (5) для этого случая можно переписать в виде
(8)
$\begin{gathered} {{I}^{ \pm }} = {{\left| N \right|}^{2}} + {{\left| {{{{\mathbf{M}}}_{ \bot }}} \right|}^{2}} \pm P \cdot (M_{ \bot }^{z}{\text{'}}N{\kern 1pt} {\text{*}} + M_{ \bot }^{z}{\text{'*}}N) + \\ + \;iP \cdot {{({\mathbf{M}}_{ \bot }^{*} \times {{{\mathbf{M}}}_{ \bot }})}^{z}}{\text{'}}. \\ \end{gathered} $Тогда измеряемое флип-отношение записывается следующим образом:
(9)
$R = \frac{{{{{\left| N \right|}}^{2}} + {{{\left| {{{{\mathbf{M}}}_{ \bot }}} \right|}}^{2}} + P \cdot (M_{ \bot }^{z}{\text{'}}N{\text{*}} + M_{ \bot }^{z}{\text{'*}}N) + iP \cdot {{{({\mathbf{M}}_{ \bot }^{*} \times {{{\mathbf{M}}}_{ \bot }})}}^{z}}{\text{'}}}}{{{{{\left| N \right|}}^{2}} + {{{\left| {{{{\mathbf{M}}}_{ \bot }}} \right|}}^{2}} - P \cdot (M_{ \bot }^{z}{\text{'}}N{\text{*}} + M_{ \bot }^{z}{\text{'*}}N) + iP \cdot {{{({\mathbf{M}}_{ \bot }^{*} \times {{{\mathbf{M}}}_{ \bot }})}}^{z}}{\text{'}}}}.$(10)
$R = \frac{{{{N}^{2}} + F_{M}^{2}{{{\sin }}^{2}}\alpha + 2P{{F}_{M}}N{{{\sin }}^{2}}\alpha }}{{{{N}^{2}} + F_{M}^{2}{{{\sin }}^{2}}\alpha - 2P{{F}_{M}}N{{{\sin }}^{2}}\alpha }}.$Если структура точно известна (т.е. N), то из измеренного R можно получить магнитный структурный фактор FM, решая уравнение второй степени. Это уравнение имеет два корня, но выбор между двумя корнями, как правило, очевиден.
Необходимо обратить внимание на следующий важный фактор: для центросимметричных структур это уравнение дает не только амплитуду магнитного структурного фактора, но и его фазу. Классическая дифракция поляризованных нейтронов, таким образом, является одним из очень немногих методов, способных дать фазу структурного фактора, которая обычно теряется в дифракционном эксперименте, где измеряется интенсивность, т.е. квадрат структурного фактора. Однако если кристаллическая структура нецентросимметрична, то структурный фактор является комплексной величиной, и знания флип-отношения недостаточно для решения этой проблемы. Действительно, мы сталкиваемся с одним уравнением для двух неизвестных величин (действительной и мнимой частей магнитного структурного фактора). В этом случае приходится работать непосредственно с флип-отношениями.
Чтобы понять, почему чувствительность повышается по сравнению с неполяризованными нейтронами, традиционно приводят простой, но впечатляющий пример. Представим, что нужно измерить магнитный сигнал, на порядок меньший, чем ядерный (FM = 0.1N). При неполяризованном пучке интенсивность такого смешанного отражения составляет (измеряется в горизонтальной плоскости, т.е. α = 90°):
То есть магнитный вклад составляет всего лишь 1% от полной интенсивности. Для рассеяния поляризованных нейтронов получим следующие выражения (считаем пучок полностью поляризованным, |P| = 1):
(12)
$\begin{gathered} {{I}^{ + }} = ~{{N}^{2}} + F_{M}^{2} + 2N{{F}_{M}} = {{N}^{2}} + {{(0.1N)}^{2}} + \\ + \;2 \cdot 0.1{{N}^{2}} = 1.21{{N}^{2}}, \\ \end{gathered} $(13)
$\begin{gathered} {{I}^{ - }} = ~{{N}^{2}} + F_{M}^{2} - 2N{{F}_{M}} = ~{{N}^{2}} + {{(0.1N)}^{2}} - \\ - \;2 \cdot 0.1{{N}^{2}} = 0.81{{N}^{2}}. \\ \end{gathered} $Существует ряд ограничений на класс соединений, которые могут быть исследованы с помощью этой методики: это могут быть парамагнетики, насыщенные ферромагнетики, или насыщенные ферримагнетики. Этот метод применим для антиферромагнетиков только в некоторых частных случаях: ядерный и магнитный структурный факторы должны быть в фазе и необходимо нарушить баланс 180°-ных доменов. В ином случае этот метод обеспечивает информацию о ферромагнитной составляющей, индуцированной внешним полем, а не об антиферромагнитной, вклад от которой погашается доменами. Важно отметить, что метод основан на интерференции магнитных и ядерных сигналов, т.е. магнитные и ядерные пики должны появляться в одном и том же месте в обратном пространстве, а это значит, что можно исследовать только магнитные структуры с вектором распространения k = 0.
Для того чтобы извлечь результат из полученных измерений, используются следующие соображения. В эксперименте получаются магнитные структурные факторы FM для различных брэгговских отражений h, k, l. Они являются фурье-компонентами распределения намагниченности ρ(r) в прямом пространстве, которые также могут быть определены как произведение магнитного момента mν атома ν и его форм-фактора fν(Q) (в обратном пространстве):
(14)
${{{\mathbf{F}}}_{M}}({\mathbf{Q}}) = \mathop \sum \limits_{\nu } \,{{f}_{{\nu }}}({\mathbf{Q}}){{{\mathbf{m}}}_{{\nu }}}{{e}^{{i{\mathbf{Q}}{{{\mathbf{r}}}_{{\nu }}}}}} = \int {{\mathbf{\rho }}({\mathbf{r}}){{e}^{{i{\mathbf{Qr}}}}}d{\mathbf{r}}} .$Поскольку в эксперименте измеряются непосредственно фурье-компоненты распределения намагниченности, то естественно восстановить это распределение в реальном пространстве обратным фурье-преобразованием:
(15)
${\mathbf{\rho }}({\mathbf{r}}) = \frac{1}{V}\sum\limits_{\mathbf{Q}} {{{{\mathbf{F}}}_{{\text{M}}}}({\mathbf{Q}}){{e}^{{ - i{\mathbf{Qr}}}}}} .$Этот метод широко применялся в прошлом, однако имеет ряд существенных недостатков. Главным образом это связано с ограничением на количество измеренных отражений – количество коэффициентов Фурье. Отсутствующие измерения считаются равными нулю, что влечет за собой некоторое искажение карт распределения спиновой плотности, фальшивые максимумы. Отметим, что этот метод применим только к центросимметричным структурам, поскольку может работать только с магнитными структурными факторами.
Серьезный прогресс в обработке данных классического эксперимента по дифракции поляризованных нейтронов был достигнут при подходе в рамках метода “Максимальной Энтропии” (MaxEnt). Этот метод основан на байесовских статистических методах, для реконструкции распределения намагниченности некоторое время назад он был адаптирован Р. Папуляром и Б. Жийон [15]. Поскольку измеряется ограниченное количество магнитных структурных факторов, то существует много возможных карт распределения спиновой плотности, которые с ними согласуются. MaxEnt определяет вероятность для каждой из карт и выбирает карту с наибольшей вероятностью с учетом наблюдений и их стандартных отклонений. Это тот вариант, который максимизирует энтропию Больцмана. Одно из преимуществ этого метода заключается в том, что никаких предположений о ненаблюдаемых коэффициентах Фурье не делается. Качество реконструкций при этом намного лучше по сравнению с классической инверсией Фурье. Разница в полученных результатах хорошо видна на рис. 1, где показано сравнение распределения намагниченности в Cr, полученное методом инверсии Фурье и методом MaxEnt [16]. Как Фурье, так и MaxEnt показывают асимметрию распределения плотности намагниченности вдоль направления [1 1 0].
Рис. 1.
Карты распределения спиновой плотности в Cr, восстановленные методом инверсии Фурье (а); методом MaxEnt (б) [16].
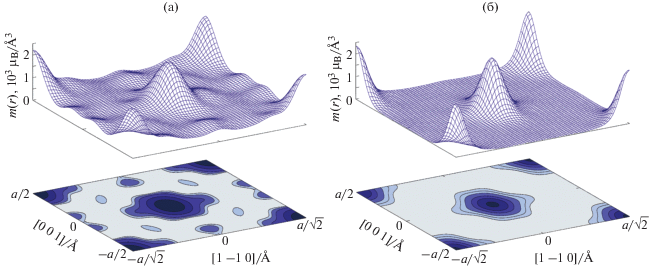
По сравнению с картой MaxEnt карта Фурье показывает дополнительные особенности, в действительности являющиеся артефактами, которые появились из-за конечного числа измеренных FM. Все артефакты, присутствующие в карте Фурье, подавляются в реконструкции MaxEnt. Таким образом, использование MaxEnt приводит к распределению, которое наименее подвержено влиянию недостающей информации. Этот метод дает свободное от модели описание плотности намагничивания. Наконец, еще одно преимущество метода MaxEnt заключается в том, что его применение может быть распространено на нецентросимметричные структуры [17], и, таким образом, его можно применять непосредственно к флип-отношениям.
В магнитных материалах-изоляторах распределение намагниченности обычно представляет собой сумму вкладов от отдельных атомов, каждый из которых является характеристикой определенной конфигурации свободного атома или иона. Вырождение различных орбитальных состояний устраняется кристаллическим полем, в результате чего магнитные моменты хорошо локализованы возле атомов и форме распределения соответствуют конкретные атомные орбитали. В этом случае для изолированных магнитных ионов могут быть выполнены строгие расчеты Q-зависимости форм-фактора из первых принципов [18]. Однако полученные формулы достаточно сложны и в большинстве случаев можно перейти к так называемому “дипольному приближению”. В нем используются только сферические гармоники низшего порядка, описывающие форму иона. Электронная плотность ионов в дипольном приближении считается сферически симметричной. В этом случае форм-фактор выражается как
(16)
$f({\mathbf{Q}}) = \left\langle {{{j}_{0}}({\mathbf{Q}})} \right\rangle + {{C}_{2}}\left\langle {{{j}_{2}}({\mathbf{Q}})} \right\rangle ,$Показательным примером исследования форм-фактора является работа [20], выполненная на SmCo5 (рис. 2). Самарий представляет собой такой частный случай, где орбитальный и спиновый вклады в намагниченность имеют противоположные знаки и практически компенсируют друг друга в некоторой точке. Это приводит к форм-фактору, который имеет максимум в положении, отличном от Q = 0. Интересный эффект также заключается в том, что первые возбужденные состояния кристаллического поля располагаются на относительно низком энергетическом уровне, при температуре 300 К они заселены. Таким образом, магнитный момент на Sm при комнатной температуре составляет всего m ∼ 0.04 μB и увеличивается до m ∼ 0.38 μB при T = 4.2 K [20]. Очевидно также, что для всех температур форм-фактор самария имеет в основном орбитальный характер.
Рис. 2.
Экспериментально полученный форм-фактор Sm в SmCo5 при температурах 300 (а) и 4.2 K (б). Сплошные линии – результат расчета [20].
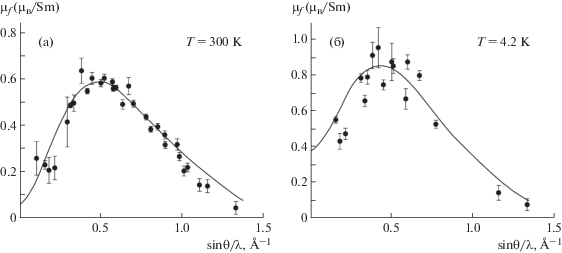
Отметим, что намагниченность в сильно анизотропных кристаллах направлена не вдоль магнитного поля. Чтобы учесть это обстоятельство, в [21] было предложено использовать тензор магнитной восприимчивости каждого магнитного атома χij, тогда магнитный момент на каждом атоме выражается как
и эта формула затем используется в форумуле (14).Безмодельный подход дает отличные результаты для хорошо локализованных магнитных моментов. Это справедливо для ионных соединений, состоящих из магнитных катионов и диамагнитных анионов. В этих соединениях некоторая часть намагниченности с катиона может быть перенесена на лиганды, однако, как правило, эта часть невелика и не сильно влияет на характер магнитной орбитали на металле. В последнее время большой интерес вызывают молекулярные магнетики. В отличие от ионных систем магнитная плотность органических соединений распределена по всем молекулам из-за ковалентных эффектов. Эффект делокализации еще более выражен, когда в молекуле нет магнитного иона и магнетизм обусловлен только 2p-электронами [22]. Для таких систем используется модельный подход, для которого также возможны два решения.
Первое – это метод мультипольного разложения, он более гибкий. Распределение намагниченности ρ(r) представляется в виде разложения по базису реальных сферических гармонических функций с центром на позициях атомов
а функции ρi(ri) – выражаются через радиальные Слэйтеровские волновые функции, реальные сферические функции, и их заселенности. Тогда выражение для магнитного структурного фактора получается подстановкой полученного выражения ${\rho }({\mathbf{r}})$ в (15).Можно использовать и “подход волновой функции”, где магнитная волновая функция Хартрее–Фока составляется из стандартных атомных орбиталей на каждом магнитном атоме
(20)
$\left| {\Psi } \right\rangle = \mathop \sum \limits_i \,{{\alpha }_{i}}{{{\psi }}_{i}}({\mathbf{r}}),$(21)
${{F}_{M}}({\mathbf{Q}}) = \left\langle {\Psi \left| {{{e}^{{i{\mathbf{Qr}}}}}} \right|\Psi } \right\rangle = \int {\Psi {\kern 1pt} *{\kern 1pt} {{e}^{{i{\mathbf{Qr}}}}}\Psi d{\mathbf{r}}} .$Как мультипольное разложение, так и подход волновой функции хорошо адаптированы к описанию молекулярного магнетизма.
Молекулярный магнетизм является быстро растущей областью в материаловедении с высоким технологическим потенциалом применения в электронных устройствах. Магнитные взаимодействия могут быть настроены путем построения блоков молекул, содержащих магнитные центры, и цель состоит в том, чтобы синтезировать органические соединения, которые упорядочиваются при комнатной температуре. Для этой цели необходимо хорошее понимание механизма магнитных связей 2р-электронов.
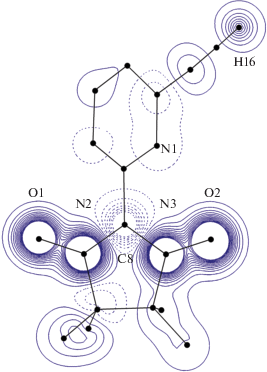
Метод классической дифракции поляризованных нейтронов дает непосредственно распределение электронов, ответственных за магнетизм в органических веществах материалов, которые в свою очередь могут быть сопоставлены с теоретическими расчетами электронных волновых функций и химических связей. Спиновая плотность в молекулярных соединениях также может быть использована для отслеживания обменных путей в молекулах в случаях, когда обнаруживается спиновая поляризация на атомах, которые в принципе немагнитны. Так, например, обстоит дело со свободными радикалами нитронил нитроксида NitPy (C≡C–H). Это соединение состоит из зигзагообразных цепочек, соединенных C≡C–H⋅⋅⋅О-комплексами, где водород соединяет две молекулы. Значительная спиновая плотность обнаружена на позиции водорода: m ≈ 0.04 μB (рис. 3), что указывает на то, что водородная связь участвует в ферромагнитном обменном взаимодействии между молекулами [23].
2.2. Применение полуполяризационного метода для исследования магнитной киральности
Обратимся к выражению (2), описывающему зависимость сечения рассеяния от поляризации падающего пучка нейтронов. Если направить поляризацию вдоль вектора рассеяния Q (т.е. вдоль оси X в принятых обозначениях), то очевидно, что интерференционный член уходит из выражения, поскольку ${{{\mathbf{M}}}_{ \bot }}$ не имеет x-компоненты. Таким образом, если измерить интенсивности рассеяния с поляризацией вдоль и против вектора рассеяния, соответственно $I_{x}^{ + }$ и $I_{x}^{ - }$, то их разность будет соответствовать вкладу кирального рассеяния
(22)
$I_{x}^{ + } - I_{x}^{ - } = 2i \cdot ({\mathbf{M}}_{ \bot }^{*} \times {{{\mathbf{M}}}_{ \bot }}).$Рис. 4.
Зависимость разности в заселенности правых и левых спиралей от деформации кручения. Открытые кружки – поляризация направлена вдоль вектора рассеяния Q, закрытые – поляризация против Q [26].
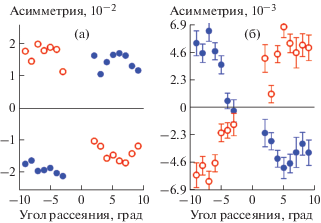
В [26] методом дифракции поляризованных нейтронов на металлическом гольмии показано, что деформация кручения приводит к изменению заселенности “правых” и “левых” спиралей. Эксперименты проводились при температуре 77 K на многодетекторной установке с “белым” пучком тепловых нейтронов на текстурированном образце гольмия с разориентацией гексагональной оси ±7° (она же – ось магнитного геликоида). На рис. 5 показаны результаты дифракции на сателлитах (0 0 0)± при скручивании образца влево – рис. 5а, а затем вправо – рис. 5б. Асимметрия рассеяния рассчитывалась как
(23)
$A( \pm {\mathbf{k}}) = \frac{{{{I}^{ + }}( \pm {\mathbf{k}}) - {{I}^{ - }}( \pm {\mathbf{k}})}}{{{{I}^{ + }}( \pm {\mathbf{k}}) + {{I}^{ - }}( \pm {\mathbf{k}})}}~\sim {{n}_{{L~}}} - {{n}_{{R~}}}~,$Рис. 5.
Результаты сканирования сателлита (0 0 1)+k2 вдоль направления l при температурах 1.5, 30, 38 К и поляризации нейтронов, направленной параллельно и антипараллельно вектору рассеяния [29].
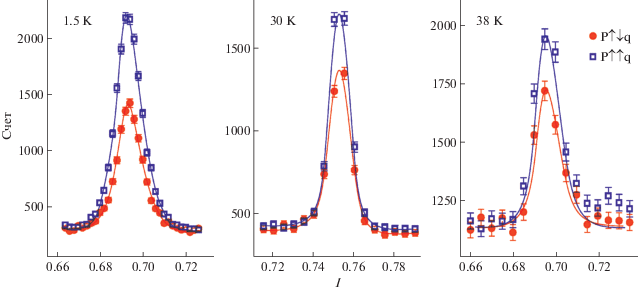
Таким образом, показано, что деформация кручения приводит к появлению вектора Дзялошинского, что, в свою очередь, индуцирует разницу в заселенности правых и левых спиралей [26].
С помощью полуполяризационного метода при исследовании CsMnBr3 В.П. Плахтий и соавт. в 2000 г. впервые получили экспериментальное доказательство существования кирального класса универсальности [27]. Несколько ранее, в 1992 г. Х. Кавамурой было выдвинуто предположение о том, что антиферромагнетики с треугольной решеткой и спиральные магнетики должны принадлежать новым, киральным классам универсальности [28]. Как известно, поведение системы в критической области определяется небольшим набором параметров, определяющим класс универсальности, к которому принадлежит эта система. Соответственно, для кирального класса критические индексы теплоемкости, намагниченности, восприимчивости и корреляционной длины должны отличаться от индексов гейзенберговских магнетиков. То есть спиновая киральность является критической величиной, флуктуации которой определяются новыми критическими индексами βc, γc, νc. В [27] были получены значения критической киральной экспоненты βc = 0.44(2) ≈ 2β, что совпадает с теоретически предсказанным результатом [28].
Примером эффективного использования полуполяризационного метода для исследований киральной заселенности могут служить эксперименты на мультиферроике TbMn2O5 [29]. В этом соединении реализуется магнитная структура с вектором k = (0.5 – δx, 0, 0.25 + δz), температурная эволюция δx, δz приводит к смене магнитных фаз от высокотемпературной несоразмерной фазы к соразмерной и затем к низкотемпературной несоразмерной. При этом в соразмерной магнитной фазе в соединении наблюдается сегнетоэлектрическая поляризация, а несоразмерным магнитным фазам соответствует слабая сегнетоэлектрическая поляризация. Измерения показали, что разность в заселенности “правых” и “левых” магнитных киральных доменов существует во всех магнитоупорядоченных фазах. Этот вывод можно сделать исходя из результатов сканирования магнитного сателлита (0 0 1)+k2 (рис. 5), где также видно, что эта разность сохраняет свою величину (с учетом наложения рассеяния от конфигурационных доменов) при трех температурах, соответствующих трем различным магнитным и ферроэлектрическим фазам. Эти результаты позволили сделать вывод о том, что в TbMn2O5 антисимметричное взаимодействие ДМ отчетливо проявляется во всех магнитных фазах, и, таким образом, вклад в сегнетоэлектрическую поляризацию обеспечивают как обменно-стрикционный механизм, так и обратный эффект ДМ [29].
3. ПОЛЯРИЗАЦИОННЫЙ АНАЛИЗ
3.1. Продольный поляризационный анализ
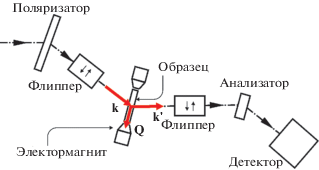
Обратимся к выражению (6), описывающему изменение поляризации при рассеянии нейтронов на магнетике. Экспериментального воплощения потенциала поляризационного анализа, продемонстрированного в (6), пришлось ждать несколько лет. Классической работой по поляризационному анализу считается работа 1969 г., выполненная Р. Муном, Т. Ристом и В. Келером [13], в которой определялось спиновое состояние нейтронов после рассеяния. Однако отметим, что об экспериментах по малоугловому рассеянию, в которых анализировалась поляризация прошедшего через образец пучка, докладывалось еще раньше, в 1964 г. Г.М. Драбкиным и соавт. [12]. Первые эксперименты с поляризационным анализом нейтронов далеко не полностью раскрывали все его возможности, однако сразу продемонстрировали уникальные особенности методики при исследовании магнитных свойств вещества. Схема эксперимента Р. Муна показана на рис. 6. Трехосный нейтронный спектрометр был дополнен поляризатором и флиппером (устройством для переворота спина нейтрона) до образца, флиппером и анализатором после образца, а также электромагнитом, который мог создавать поле на образце в горизонтальном и вертикальном направлениях [13]. При такой схеме эксперимента нейтроны находятся в постоянном или адиабатически меняющемся поле на протяжении всего пути от поляризатора до анализатора. Из-за прецессии вектора поляризации вокруг магнитных полей сохраняется только компонента вдоль направляющего поля (“продольная”). После взаимодействия с образцом спин нейтрона попадает в то же ведущее поле, что и до акта рассеяния. Таким образом, если нейтроны поляризованы в определенном направлении, то анализ проводится в том же направлении. Поэтому данный метод называется “одноосным” или “продольным”.
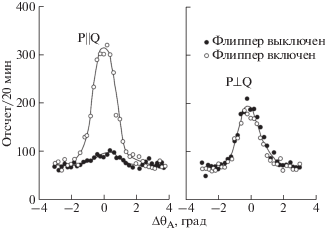
При двух возможных состояниях падающей поляризации и двух возможных состояниях рассеянной можно измерить четыре различных интенсивности: $I_{x}^{{ + + }}$, $I_{x}^{{ + - }}$, $I_{x}^{{ - + }}$ и $I_{x}^{{ - - }}$. Обращаясь к уравнению (6), можно видеть, что в нем есть члены, пропорциональные Pi, т.е. они не изменяют падающую поляризацию и члены, пропорциональные –Pi, они переворачивают падающую поляризацию. Обычно используется терминология, в которой первые обеспечивают non spin-flip (NSF), а вторые – спин-флип (SF). Очевидно, что процесс SF всегда имеет магнитное происхождение. NSF-процесс может быть либо ядерным, либо магнитным, поскольку магнитные компоненты, параллельные Pi, дают NSF, в то время как магнитные компоненты, перпендикулярные Pi, – SF. В частном случае, когда Pi||Q, т.е. вдоль X, магнитное рассеяние полностью SF, т.е. с переворотом спина (выражение (7)), а ядерное рассеяние дает вклад исключительно в NSF. Другими словами, при Pi⊥Q существует полное разделение ядерных и магнитных вкладов. Сканирование рефлекса в двух каналах – SF и NSF – в этой конфигурации сразу даст информацию о природе этого отражения: чисто ядерное, чисто магнитное или смешанное ядерное/магнитное. Именно это свойство чаще всего используется в экспериментах с поляризационным анализом. В пионерской работе по поляризационному анализу [13] были эффектно и эффективно продемонстрированы возможности поляризационного анализа для исследования вкладов различных видов магнитного и немагнитного рассеяния. Показателен пример парамагнитного рассеяния на MnF2. В парамагнитном состоянии средние величины проекций магнитных моментов на оси X, Y, Z равны друг другу. При этом проекция вдоль X не участвует в рассеянии. Это означает, что для поляризации P⊥Q все рассеяние происходит с переворотом спина, а для P⊥Q интенсивности рассеяния с переворотом спина и без переворота – равны. Именно такая ситуация наблюдалась в эксперименте [13] и отображена на рис. 7, где приведены поляризационные зависимости парамагнитного рассеяния на MnF2. Здесь приведены результаты сканирования через позицию упругого ядерного пика. “Flipper-off” соответствует I++, позиция “flipper-on” дает интенсивность ${{I}^{{-- + }}}$.
3.2. XYZ-поляризационный анализ
Дальнейшее развитие метода продольного поляризационного анализа приводит к третьему ортогональному направлению, вдоль которого может быть ориентирована поляризация нейтронов. Обычно в методе XYZ-поляризационного анализа поляризацию ориентируют вдоль осей X, Y, Z, которые образуют систему координат, определенную во Введении. Для реализации этого метода обычно используют конструкцию из трех ортогональных пар колец (XYZ-кольца), создающих ведущее поле на образце в любом направлении величиной порядка 20–30 Гс, чего вполне достаточно для того, чтобы контролировать поляризацию нейтронного пучка. При такой схеме измерений можно получить все диагональные члены тензора поляризации, что очень часто дает достаточно информации для экспериментаторов. В результате в современных нейтронных установках этот метод поляризационного анализа применяется наиболее часто. Анализ выражения (6) для случая XYZ-поляризационного анализа позволяет выразить эти диагональные члены следующим образом (здесь вновь считаем величину поляризации |P| равной единице):
(24)
$I_{y}^{{ - - }}\sim {{N}^{2}} + {{\left| {M_{ \bot }^{y}} \right|}^{2}} - (M_{ \bot }^{y}N{\kern 1pt} {\text{*}} + M_{ \bot }^{y}{\text{*}}N),$Измеряя эти интенсивности, можно получить информацию не только о магнитном рассеянии, но и об интерференционном магнитно-ядерном рассеянии, а также выяснить существование магнитного кирального рассеяния. Для этого можно не использовать поляризованные нейтроны, а лишь проанализировать созданную поляризацию пучка при рассеянии. В этом случае поляризация вдоль направления X происходит от кирального рассеяния, тогда как поляризация вдоль Y, Z – от соответствующих компонент магнитно-ядерного интерференционного вклада.
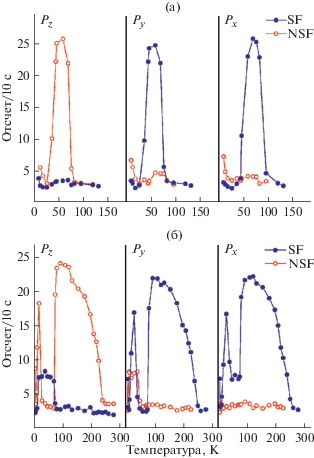
Использование XYZ-поляризационного анализа позволяет быстро определить важные детали, связанные с исследованиями магнетизма в веществе. Иногда возникает ситуация, когда одного–двух измерений, сделанных с поляризационным анализом, хватает для того, чтобы определить направление магнитного момента и его температурную эволюцию в кристалле, как это было сделано, например, в [30]. На рис. 8 показаны результаты измерений температурных зависимостей магнитных отражений в Nd2CuO4, полученные методом XYZ-поляризационного анализа. Кристаллическая структура этого соединения – тетрагональная, I4/mmm, вектор магнитной структуры k = = (1/2 1/2 0). Как видно, наблюдается совершенно различное поведение интенсивностей с четными и нечетными по l индексами. Это связано с тем, что отражения с четным и нечетным l происходят от двух типов ориентационных доменов, соответствующих 90°-ному вращению вокруг оси c. Анализ соотношения SF- и NSF-интенсивностей в диапазоне температур 75–245 K для рефлекса с нечетным l (1/2 1/2 1) показывает, что спины в этом домене (домен 1) ориентированы вертикально (в условиях эксперимента – вдоль оси (1 –1 0)). Это следует из того факта, что рассеяние в этом диапазоне температур полностью NSF для P||Z, тогда как для P||Y наблюдается SF-рассеяние, так же, как и для P||X. В то же время для отражения (1/2 1/2 0) интенсивность отсутствует, поскольку в этом домене (домен 2) спины ориентированы вдоль оси (1 1 0), а это направление совпадает с направлением вектора рассеяния Q. Таким образом, магнитные моменты этого домена не принимают участия в рассеянии. При этом в обоих доменах спин параллелен вектору магнитной структуры k. Изменение соотношения интенсивностей для всех режимов измерений T ≈ ≈ 75 K свидетельствует об ориентационном переходе. Теперь уже в домене 2 спины меди направлены вдоль оси (1 –1 0), а в домене 1 – вдоль оси (1 1 0), т.е. в обоих доменах магнитные моменты Cu2+ разворачиваются перпендикулярно вектору k. При 30 K происходит обратный ориентационный переход.
Рис. 8.
Температурные зависимости магнитных рефлексов (0.5 0.5 0) (а), (0.5 0.5 1) (б), измеренные методом XYZ-поляризационного анализа [30].
3.3. Сферическая нейтронная поляриметрия
При всех своих достоинствах продольный поляризационный анализ все же имеет ряд серьезных недостатков. Так, он дает доступ только к диагональным членам тензора поляризации, которым может быть выражено уравнение (6) Малеева–Блюма. В этом методе не могут быть измерены недиагональные члены, которые очень важны для некоторых задач (в частности, они дают высочайшую точность для определения малых поворотов магнитных моментов). Важно отметить, что, поскольку анализируется только одна компонента конечной поляризации, а две остальные теряются (например, из-за доменов), невозможно отличить чистый поворот поляризации от деполяризации. Таким образом, теряется часть информации, и, как следствие, трудно обнаружить слабые эффекты. С самого начала развития поляризационного анализа было ясно, что очень желательно проводить измерения всех членов тензора. Для этого необходимо иметь возможность поляризовать падающие нейтроны в одном направлении и независимо анализировать их в другом направлении; это является чрезвычайно сложной задачей из-за сильного влияния любого магнитного поля на вектор поляризации. Один из путей решения этой проблемы – использование камеры с нулевым полем, в котором вектор поляризации нейтронов распространяется без изменений от входного ведущего поля к образцу и от образца к выходному ведущему полю. Переход от ведущего поля в область с нулевым полем должен быть полностью неадиабатичным. Разделение пути нейтронов на различные магнитные области было достигнуто с помощью использования сверхпроводящих ниобиевых экранов Мейснера. Такой экран обеспечивает точное сохранение направления спина, обеспечивает неадиабатический переход спина из одной магнитной области в другую.
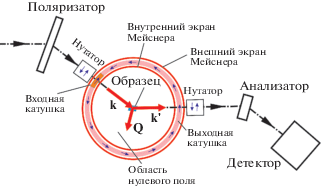
Эта идея была реализована Ф. Тассэ в устройстве с нулевым полем CryoPAD (Cryogenic Polarization Analysis Device, рис. 9) [14]. CryoPAD оснащен двумя сверхпроводящими экранами Мейснера. Оба экрана имеют форму длинных вертикальных трубок. Падающий и рассеянный пучки нейтронов проходят через адиабатические вращатели спинов (нутаторы). Между двумя экранами Мейснера помещены две катушки – входная, занимающая небольшой сектор в районе падающего пучка, и выходная, распределенная в угловом диапазоне, близком к 2π. При такой организации можно независимо ориентировать поляризацию падающих на образец нейтронов в любом направлении и анализировать ее в любом другом направлении. Это дает экспериментальную возможность полностью задействовать весь потенциал поляризационного анализа, отраженный в уравнении Малеева–Блюма (3). Уравнения (20) можно дополнить недиагональными членами, которые описывают поворот поляризации, и получить таким образом полный комплект уравнений для интенсивностей, которые можно измерить методом сферической нейтронной поляриметрии (SNP). Обычно этим методом проводят измерение элементов матрицы поляризации. В матричном виде изменение поляризации записывается как
где ${{\mathcal{P}}_{{ij}}}$ – тензор, описывающий поворот поляризации, а $P_{i}^{{{\text{''}}}}$ – вектор поляризации, созданной в процессе рассеяния. Индексы i и j принимают значения x, y, z для поляризации рассеянных и падающих нейтронов соответственно. Элементы поляризационной матрицы ${{\mathcal{P}}_{{ij}}}$ соответствуют поляризации нейтронов вдоль оси i при начальной поляризации вдоль j и вычисляются следующим образом:(26)
${{\mathcal{P}}_{{ij}}} = {\text{\;}}\frac{{{{I}_{{ij}}} - {{I}_{{\bar {i}j}}}}}{{{{I}_{{ij}}} + {{I}_{{\bar {i}j}}}}}.$(27)
$\mathcal{P} = \left( {\begin{array}{*{20}{c}} {\frac{{({{N}^{2}} - {\mathbf{M}}_{ \bot }^{2})}}{{{{{\sigma }}_{x}}}}}&{\frac{{2\operatorname{Im} (NM_{ \bot }^{z}{\text{*}})}}{{{{{\sigma }}_{x}}}}}&{\frac{{2\operatorname{Im} (NM_{ \bot }^{y}{\text{*}})}}{{{{{\sigma }}_{x}}}}} \\ {\frac{{ - 2\operatorname{Im} (NM_{ \bot }^{z}{\text{*}})}}{{{{{\sigma }}_{y}}}}}&{\frac{{\left( {{{N}^{2}} + {{{\left| {M_{ \bot }^{y}} \right|}}^{2}} - {{{\left| {M_{ \bot }^{z}} \right|}}^{2}}} \right)}}{{{{{\sigma }}_{y}}}}}&{\frac{{2{\text{Re}}(M_{ \bot }^{y}M_{ \bot }^{z}{\text{*}})}}{{{{{\sigma }}_{y}}}}} \\ {\frac{{ - 2\operatorname{Im} (NM_{ \bot }^{y}{\text{*}})}}{{{{{\sigma }}_{z}}}}}&{\frac{{2\operatorname{Re} (M_{ \bot }^{z}M_{ \bot }^{y}{\text{*}})}}{{{{{\sigma }}_{z}}}}}&{\frac{{\left( {{{N}^{2}} + {{{\left| {M_{ \bot }^{z}} \right|}}^{2}} - {{{\left| {M_{ \bot }^{y}} \right|}}^{2}}} \right)}}{{{{{\sigma }}_{z}}}}} \end{array}} \right)~,~~$(28)
$P{\kern 1pt} {\text{''}} = \left( {\begin{array}{*{20}{c}} {\frac{{ - 2\operatorname{Im} (M_{ \bot }^{y}M_{ \bot }^{z}{\text{*}})}}{{\sigma }}} \\ {\frac{{2\operatorname{Re} (NM_{ \bot }^{y}{\text{*}})}}{{\sigma }}} \\ {\frac{{2\operatorname{Re} (NM_{ \bot }^{z}{\text{*}})}}{{\sigma }}} \end{array}} \right),$(29)
${{{\sigma }}_{z}} = {{N}^{2}} + {\mathbf{M}}_{ \bot }^{2} + {{P}_{z}} \times 2\operatorname{Im} (NM_{ \bot }^{z}{\text{*}})~,$С первых применений SNP зарекомендовал себя как чрезвычайно мощное и эффективное средство исследования магнетизма. Иногда этот метод является единственным способом разрешить сложные экспериментальные проблемы.
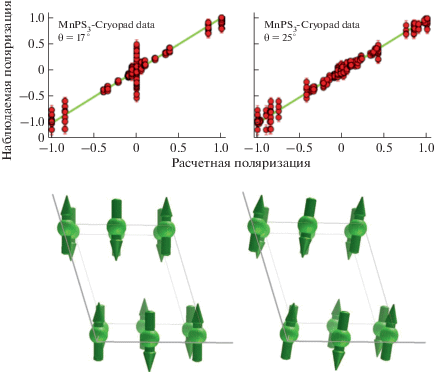
В качестве демонстрации эффективности техники SNP можно рассмотреть интересный пример исследований MnPS3 [31]. Это соединение со слоистой структурой, кристаллизующееся в моноклинной пр. гр. С2/m, моноклинная ось составляет угол 17.3° с вертикалью к плоскости (a, b). При TN = 78 K происходит упорядочение спинов на марганце в антиферромагнитную коллинеарную фазу с вектором магнитной структуры k = (0 0 0), каждый ион Mn2+ антиферромагнитно связан со своим ближайшим соседом. Вначале магнитная структура уточнялась по интегральным интенсивностям, при этом хороший результат подгонки давала структура с магнитными моментами, перпендикулярными плоскости (a, b). Однако из-за того, что анизотропия вызывала вопросы, было решено исследовать это соединение с помощью SNP. Для нескольких рефлексов вида (0 k l) были измерены коэффициенты поляризационной матрицы Pij. Для полученных измерений была выполнена процедура фиттирования, в которой варьировались заселенность 180°-ных доменов и амплитуда магнитного момента (рис. 10, левая колонка). Затем было выполнено фиттирование, при котором также варьировался угол между направлением магнитных моментов и осью c*. В итоге лучший результат был получен для θ = –25.4°, что с учетом моноклинности оси c составляет угол ∼8° с осью c* (рис. 10, правая колонка). Как видно, отклонение моментов на небольшой угол значительно изменяет качество подгонки результатов SNP, в то время как неполяризованный эксперимент это не чувствует. Наклон магнитных моментов относительно естественных симметричных направлений указывает на наличие конкурирующих анизотропий. Без SNP этот наклон, безусловно, никогда бы не был обнаружен.
Рис. 10.
Наблюдаемые и рассчитанные матричные элементы поляризационной матрицы для магнитной структуры, слева – магнитные моменты вдоль c*; справа – моменты Mn2+ под углом 8° от c*. Соответствующие магнитные конфигурации показаны внизу [31].
Отметим, что работа в режиме SNP требует значительного приборного времени, поскольку поляризация пучка нейтронов и последующий анализ спинового состояния значительно снижают поток нейтронов на регистрирующем устройстве. Необходимо иметь в виду, что для набора матрицы из девяти элементов требуется провести 18 измерений (SF, NSF для каждого сочетания i, j). Поэтому для каждого конкретного эксперимента надо выбирать разумную стратегию измерений, поскольку очень часто нет необходимости в измерениях всех компонент поляризационной матрицы. Примером такого подхода может служить работа по исследованию эволюции магнитной структуры NdMn2O5 [32]. NdMn2O5 является слабым мультиферроиком, несоразмерная магнитная структура с вектором (0.5 0 kz) в нем формируется при TN = 30 K, а сегнетоэлектрическая поляризация наблюдается ниже TCE = 20 K. В этой работе изучалась температурная зависимость магнитной структуры, влияние на нее внешнего электрического поля. Магнитную структуру NdMn2O5 можно описать как эллиптический геликоид:
(30)
${\mathbf{M}}({{{\mathbf{r}}}_{{n~}}}) = {\mathbf{u}}{{{\mu }}_{{\text{u}}}}\cos ({{{\mathbf{r}}}_{n}} \cdot {\mathbf{k}}) + {\mathbf{v}}{{{\mu }}_{{\text{v}}}}\sin ({{{\mathbf{r}}}_{n}} \cdot {\mathbf{k}}),$Измерялись элементы поляризационной матрицы Pyy, Pzz, Pyx, Pzx для нескольких магнитных сателлитов при температурах 4, 18, 20 K. Дифракция на несоразмерной магнитной структуре дает отражения, свободные от ядерного вклада. Диагональные элементы в этом случае дают эллиптичность магнитной структуры, а недиагональные определяют среднюю киральность:
(31)
${{P}_{{yy}}} = - {{P}_{{zz}}}\sim \frac{{{{{\mu }}_{{\text{u}}}}^{2}{\text{co}}{{{\text{s}}}^{2}}{\beta } - {{{\mu }}_{{\text{v}}}}^{2}}}{{{{{\mu }}_{{\text{u}}}}^{2}{\text{co}}{{{\text{s}}}^{2}}{\beta } + {{{\mu }}_{{\text{v}}}}^{2}}} = \frac{{{{R}^{2}}{\text{co}}{{{\text{s}}}^{2}}{\beta } - 1}}{{{{R}^{2}}{\text{co}}{{{\text{s}}}^{2}}{\beta } + 1}},$(32)
${{P}_{{yx}}} = {{P}_{{zx}}}\sim \frac{{2(1 - 2{{n}_{r}}){{{\mu }}_{{\text{u}}}}{{{\mu }}_{{\text{v}}}}}}{{{\mu }_{{\text{u}}}^{2} + {\mu }_{{\text{v}}}^{2}}} = \frac{{2(1 - 2{{n}_{r}})R\cos {\beta }}}{{{{R}^{2}}{{{\cos }}^{2}}{\beta } + 1}},$Таблица 1.
Элементы поляризационных матриц магнитных сателлитов (2 0 0)–k2 и (0 0 0)+k1 NdMn2O5 при температурах 4, 18 K [32]
| 4 K | (2 0 0)–k2 | (0 0 0)+k1 | ||||
|---|---|---|---|---|---|---|
| x | y | z | x | y | z | |
| x | –1.041(14) | –0.98(4) | ||||
| y | –0.19(5) | –0.316(13) | –0.20(2) | –0.20(2) | ||
| z | –0.08(4) | 0.292(14) | –0.19(2) | 0.19(2) | ||
| 18 К | (2 0 0)–k2 | (0 0 0)+k1 | ||||
| x | y | z | x | y | z | |
| x | –0.98(7) | –0.98(10) | ||||
| y | –0.580(22) | 0.35(2) | ||||
| z | 0.584(24) | –0.36(2) | ||||
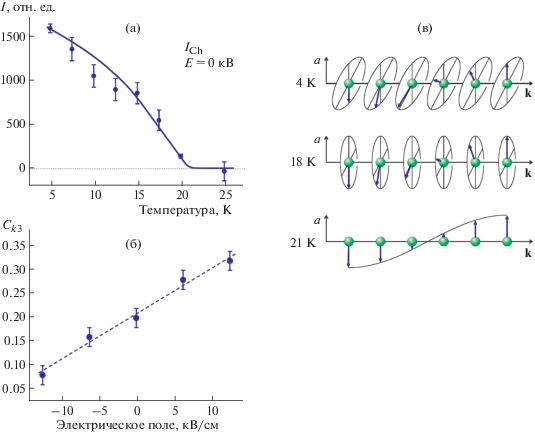
Рис. 11.
Температурная зависимость кирального рассеяния в NdMn2O5 (а); зависимость средней киральности от приложенного электрического поля в режиме FC (б); схема температурной трансформации эллиптической спирали в структуру “спиновая волна” (в). По материалам работы [32].
ЗАКЛЮЧЕНИЕ
В обзоре представлены фундаментальные аспекты дифракции поляризованных нейтронов, разобраны теоретические основы различных методов для исследования магнитных свойств вещества. Приводятся также практические детали применения этих методов, показано, как их использование помогает получить уникальную информацию. Продемонстрирован высокий потенциал дифракции поляризованных нейтронов и уникальность этой методики в решении задач физики конденсированных сред, в основном связанных с магнетизмом. Это обстоятельство определяет увеличение количества нейтронных экспериментальных установок, предоставляющих возможности использования поляризованных нейтронов, что, в свою очередь, предполагает увеличение количества экспериментов с их использованием. Изложенный материал может служить для планирования экспериментов и понимания их результатов. Поскольку измерения с поляризованными нейтронами требуют значительного времени, то, планируя эксперимент, важно понимать, какие методы будут наиболее эффективны в решении той или иной задачи, как при необходимости комбинировать различные подходы. При этом нужно помнить три простых факта: спины нейтронов переворачиваются при рассеянии ядерными или атомными спиновыми компонентами, перпендикулярными поляризации нейтронов, и не переворачиваются при рассеянии на магнитных компонентах, параллельных поляризации нейтронов; магнитные компоненты, параллельные вектору рассеяния, не участвуют в нейтронном рассеянии; спин нейтронов не переворачивается при ядерном рассеянии.
Спектр современных экспериментальных методик исследования магнитных свойств вещества очень широк: от сквидов до вынужденного комбинационного рассеяния, от магнитной мессбауэрографии до синхротронного излучения. Год от года растет и совершенство используемого в них оборудования, что дает возможности совершенно различных подходов к изучению магнитных явлений. Во всем этом разнообразии нейтронное рассеяние занимает особое место, подобно торту на празднике магнитных исследований. Ну а дифракция поляризованных нейтронов – вишенка на этом торте.
Автор выражает благодарность А.Н. Матвеевой и О.В. Усманову за помощь в подготовке материалов обзора.
Список литературы
Shull C.G., Smart J.S. // Phys. Rev. 1949. V. 76. P. 1256.
Schwinger J. // Phys. Rev. 1937. V. 51. P. 544.
Halpern O., Johnson M. // Phys. Rev. 1937. V. 51. P. 992.
Halpern O., Johnson M. // Phys. Rev. 1937. V. 52. P. 52.
Halpern O., Johnson M. // Phys. Rev. 1939. V. 55. P. 898.
Frisch O., von Halban H., Koch J. // Phys. Rev. 1938. V. 53. P. 719.
Малеев С.В., Барьяхтар В.Г., Сурис Р.А. // ФТТ. 1962. Т. 4. С. 3461.
Blume M. // Phys. Rev. 1963. V. 130. P. 1670.
Hughes D., Burgy M. // Phys. Rev. 1951. V. 81. P. 498.
Shull C., Wollan E., Koehler W. // Phys. Rev. 1951. V. 84. P. 912.
Nathans R., Shull C., Shirane G. et al. // J. Phys. Chem. Solids. 1959. V. 10. P. 138.
Драбкин Г.М., Забидаров Е.И., Касман Я.А. и др. // ЖЭТФ. 1964. Т. 47. С. 2316.
Moon R.M., Riste T., Koehler W.C. // Phys. Rev. 1969. V. 181. P. 920.
Tasset F. // Physica B. 1989. V. 156–157. P. 627.
Papoular R.J., Gillon B. // Europhys. Lett. 1990. V. 13. P. 429.
Strempfer J., Bruckel Th., Mcintyre G.J. et al. // Physica B. 1999. V. 267–268. P. 56.
Schleger P., Puig-Molina A., Ressouche E. et al. // Acta Cryst. A. 1997. V. 53. P. 426.
Lovesey S.W. Theory of neutron scattering from condensed matter. V. 2. Oxford: Clarendon Press, 1984. 360 p.
Brown P.J. International Tables for Crystallography. V. C. Dordrecht: Kluwer Academic Publishers, 1992. 1000 p.
Givord D., Laforest J., Schweizer J. et al. // J. Appl. Phys. 1979. V. 50. P. 2008.
Gukasov A., Brown P.J. // J. Phys. Condens. Matter. 2002. V. 14. P. 8831.
Schweizer J. // Physica B. 1997. V. 234–236. P. 772.
Ressouche E. // Physica B. 1999. V. 267–268. P. 27.
Ishida M., Endoh Y., Matsuda S. et al. // J. Phys. Soc. Jpn. 1985. V. 54. P. 2975.
Siratori K., Akimitsu J., Kita E. et al. // J. Phys. Soc. Jpn. 1980. V. 48. P. 1111.
Fedorov V.I., Gukasov A.G., Kozlov V. et al. // Phys. Lett. A. 1997. V. 224. P. 372.
Plakhty V.P., Kulda J., Visser D. et al. // Phys. Rev. Lett. 2000. V. 85. P. 3942.
Kawamura H. // J. Phys. Soc. Jpn. 1992. V. 61. P. 1299.
Zobkalo I.A., Gavrilov S.V., Sazonov A. et al. // J. Phys.: Condens. Matter. 2018. V. 30. P. 205804.
Zobkalo I.A., Gukasov A.G., Kokovin S.Yu. et al. // Solid State Commun. 1991. V. 80. P. 921.
Ressouche E., Loire M., Simonet V. et al. // Phys. Rev. B. 2010. V. 82. P. 100408R.
Zobkalo I.A., Matveeva A.N., Sazonov A. et al. // Phys. Rev. B. 2020. V. 101. P. 064425.
Дополнительные материалы отсутствуют.
Инструменты
Кристаллография