Кристаллография, 2021, T. 66, № 5, стр. 730-737
Поиск эффективного алгоритма для восстановления решений при анализе данных малоуглового рассеяния от раствора кремнезоля
А. Е. Крюкова 1, 2, *, П. В. Конарев 1, 2, В. В. Волков 1
1 Институт кристаллографии им. А.В. Шубникова, ФНИЦ “Кристаллография и фотоника” РАН
Москва, Россия
2 Национальный исследовательский центр “Курчатовский институт”
Москва, Россия
* E-mail: KrukovaAE@yandex.ru
Поступила в редакцию 08.06.2020
После доработки 17.06.2020
Принята к публикации 19.06.2020
Аннотация
Представлено сравнение устойчивости восстановления решения задачи определения объемных распределений частиц по размерам на примере данных малоуглового рассеяния от раствора кремнезоля, состоящего из монодисперсных растворов TM-50 и SM. Исследован ряд итеративных алгоритмов: квазиньютоновский градиентный метод минимизации в варианте Бройдена–Флетчера–Голдфарба–Шанно с простыми ограничениями на параметры, метод имитации отжига, их комбинация, а также симплекс-метод Нелдера–Мида. В результате сравнения границ устойчивости для трех пар параметров раствора кремнезоля (радиусов и полидисперсностей частиц) методы выстроены в порядке возрастания их эффективности. Наиболее подходящим из предложенных подходов оказалась комбинация градиентного метода минимизации и имитации отжига для двухкомпонентной полидисперсной системы раствора кремнезоля с малоперекрывающимся объемным распределением частиц по размерам. Подход применим к исследованию систем различной природы, в том числе растворов белковых комплексов.
ВВЕДЕНИЕ
Подавляющее большинство систем в природе, представляющих интерес для научных исследований в различных отраслях, в частности медицине, биологии и промышленности, являются многокомпонентными и полидисперсными. Описание и расшифровка структуры такого рода систем, не исследованных ранее, в настоящее время являются актуальной задачей. Одним из эффективных методов по восстановлению структуры исследуемого объекта является метод малоуглового рассеяния (МУР) [1–5]. Для анализа полидисперсных объектов в растворе по данным МУР разработан ряд программ, таких как MIXTURE [1], GNOM [6], SASFIT [7], SASVIEW [8], McSAS [9] и другие.
Ранее для оценки качества работы программы MIXTURE (с реализованным методом переменной метрики в варианте Бройдена–Флетчера–Голдфарба–Шанно с простыми ограничениями на параметры [10], от англ. Broyden–Fletcher–Goldfarb–Shanno algorithm, BFGS) было проведено исследование на устойчивость решения задачи определения структурных параметров наночастиц для теоретических данных МУР, рассчитанных от различных модельных систем [11, 12]. Использовались системы, состоящие из сферических частиц двух типов, имеющих перекрывающиеся и неперекрывающиеся объемные распределения по размерам. Кроме того, к наборам данных добавлялся шум двух типов (гауссовский и пуассоновский) с различным относительным уровнем и исследовалась степень отклонения найденного решения от заданной теоретической модели. Было показано, что диапазон области стартовых значений параметров, позволяющий восстановить истинное решение, зависит от многих факторов, в частности от относительного вклада параметров компонентов смеси в общую кривую рассеяния и от уровня и вида шума, содержащегося в данных.
На следующем этапе полученный результат проверяли на примере реальной экспериментальной системы – раствора кремнезолей, представляющего собой смесь частиц TM-50 и SM [13]. Предварительно с помощью программы GNOM [6] было выявлено наличие двух типов полидисперсных компонентов. Далее в рамках двухкомпонентной модели сферических частиц исследовалась возможность восстановления решений программой MIXTURE. Установлено, что характеры границ устойчивости решений схожи для теоретических и экспериментальных данных, что свидетельствует о стабильности работы алгоритма, реализованного в программе MIXTURE. В то же время ограничения областей стартовых значений параметров, при которых возможно восстановление, указывает на попадание в локальные минимумы в процессе поиска решения.
Вследствие этого возникла идея проверить эффективность работы модифицированной версии программы MIXTURE, в алгоритме которой реализован метод имитации отжига (англ. Simulated annealing, SA) [14], в ряде случаев позволяющий находить глобальный минимум целевой функции. Результаты такого исследования приведены в [15]. В качестве объекта исследования был выбран тот же раствор кремнезоля, что и в [13]. Анализ сходимости решения проводили при одновременном варьировании только одной пары параметров – средних радиусов частиц кремнезоля R1 и R2. В результате было установлено, что обе модификации программы (с использованием BFGS- и SA-процедур) дали схожие результаты, но при этом границы для BFGS-процедуры оказались шире.
Далее была рассмотрена возможность комбинированного использования упомянутых выше алгоритмов минимизации: квазиньютоновского градиентного спуска и метода имитации отжига [16]. Предполагалось, что это улучшит возможности восстановления распределений частиц по размерам. Действительно, такой подход позволил расширить границы параметров, при старте с которых могут быть найдены истинные значения системы.
Цель данной работы – систематическое сравнение границ устойчивого приближения для программы с различными минимизационными схемами. Для этого провели исследования на устойчивость упомянутых выше модификаций программы MIXTURE (BFGS, SA, BFGS + SA) для трех пар параметров: (R1, R2), (dR1, R2) и (R1, dR2), где dR1 и dR2 – полидисперсности двух типов частиц кремнезоля. Помимо этого исследовали возможности алгоритма с применением симплекс-метода Нелдера–Мида (англ. Nelder–Mead, NM) [17]. Исследования проводили на примере экспериментальных данных МУР от полидисперсного раствора кремнезоля.
КРЕМНЕЗОЛИ
Раствор, выбранный в качестве объекта исследования, получен путем смешения монодисперсных растворов кремнезолей Ludox TM-50TM и SMTM. Образцы ТМ-50 (50 мас. % SiO2 и 0.3 мас. % Na) и SM (30 мас. % SiO2 и 0.2 мас. % Na) изготовлены компанией Grace Davidson [18]. Несмотря на то что размеры (диаметры) частиц, заявленные производителем (для сухих образцов), составляют 70 Å для SM и 220 Å для ТМ-50, ранее было показано [19], что в растворе они увеличиваются до 100 Å для SM и 270 Å для ТМ-50. Раствор кремнезоля разводили водой в соотношении 1:100, чтобы избежать эффекта межчастичного взаимодействия, при этом центрифугирование не использовали, так как растворы изначально стабилизировались с использованием гидроксида натрия NaOH для предотвращения агрегации.
ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА
Эксперимент по исследованию раствора кремнезоля выполнен на установке “АМУР-К” [20] (ФНИЦ “Кристаллография и фотоника” РАН, Москва, Россия) и проведен следующим образом: образец кремнезоля помещали в стеклянный капилляр, а затем в вакуумную камеру. Расстояние образец–детектор составляло 700 мм. Время измерений одного образца составляло 10 мин. Экспериментальные данные нормировали на интенсивность падающего пучка, после чего в них вводили поправку на коллимационные искажения.
Установка “АМУР-К” оснащена однокоординатным позиционно-чувствительным детектором ОД3М при фиксированной длине волны излучения λ, равной 0.1542 нм (CuKα-линия острофокусной трубки, монохроматор из пиролитического графита), и коллимационной системой Кратки. Сечение рентгеновского пучка составляло 0.2 × 8 мм2, область углов рассеяния соответствовала диапазону значений модуля вектора рассеяния
(1)
$\begin{gathered} 0.1 < s < 10.0\;{\text{н}}{{{\text{м}}}^{{--1}}} \\ \left( {\left| s \right| = \frac{{4{{\pi }}\sin {{\theta }}}}{{{\lambda }}},\;2\theta --{\text{угол}}\;{\text{рассеяния}}} \right). \\ \end{gathered} $Рис. 1.
Экспериментальная кривая МУР от раствора кремнезоля (точки). Наилучшее приближение к экспериментальным данным, рассчитанное программой MIXTURE (сплошная линия). Приближение, при котором решение не попало в глобальный минимум функции (пунктирная линия) (а). Объемное распределение по радиусам сферических частиц, найденное программой MIXTURE, соответствующее наилучшему приближению (б).
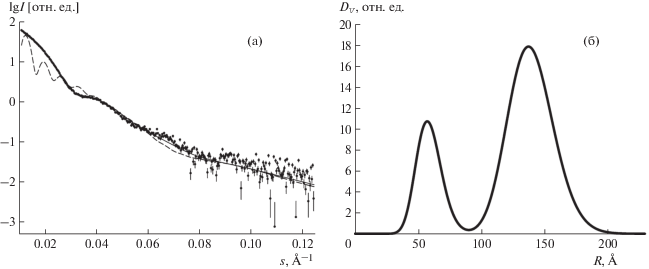
Таблица 1.
Найденные структурные параметры системы, состоящей из двух типов сферических наночастиц кремнезоля – ТМ-50 и SM
| ТМ-50 | SM | |||
|---|---|---|---|---|
| R1, Å | dR1, Å | R2, Å | dR2, Å | |
| Метод Нелдера–Мида (NM) | 59.8 | 10.0 | 140.0 | 17.9 |
| Метод имитации отжига (SA) | 58.7 | 13.1 | 139.4 | 17.9 |
| Квазиньютоновский градиентный метод (BFGS) | 58.8 | 10.0 | 139.4 | 17.9 |
| BFGS + SA | 58.8 | 10.0 | 139.4 | 17.9 |
МЕТОД РАСЧЕТА ИНТЕНСИВНОСТИ МАЛОУГЛОВОГО РАССЕЯНИЯ ОТ МНОГОКОМПОНЕНТНОЙ ПОЛИДИСПЕРСНОЙ СИСТЕМЫ
Интенсивность рассеяния многокомпонентной системы в случае разбавленной системы можно представить в виде
где суммирование проводится по разным компонентам, ${{{v}}_{k}}$ – относительная объемная доля k-го компонента, Ik(s) – интенсивность k-го компонента.Для полидисперсной системы частиц интенсивность каждого компонента можно представить в виде
(3)
${{I}_{k}}(s) = \int {{{D}_{k}}(R){{V}_{k}}(R){{{[\Delta {{\rho }_{k}}(R)]}}^{2}}} {\kern 1pt} {{i}_{{0k}}}(s,R)dR,$Для расчета функции объемного распределения k-го компонента использовали распределение Шульца:
(4)
$D(R) = \frac{1}{{{{R}_{0}}}}{{(z + 1)}^{{z + 1}}}\frac{1}{{{\text{Г}}(z + 1)}}{{\left( {\frac{R}{{{{R}_{0}}}}} \right)}^{z}}\exp \left[ { - \frac{{(z + 1)R}}{{{{R}_{0}}}}} \right],$Критерием качества решения системы служит значение квадратичной невязки χ2, которое в результате поиска распределения частиц по размерам минимизируется:
(5)
${{\chi }^{2}} = \frac{1}{{N - 1}}{{\sum\limits_j {\left[ {\frac{{I({{s}_{j}}) - c{{I}_{{{\text{calc}}}}}({{s}_{j}})}}{{\sigma ({{s}_{j}})}}} \right]} }^{2}},$Алгоритм, использующий формулы (2)–(4), реализован в программе MIXTURE. Такой подход применим к исследованию систем различной природы, в частности он успешно использовался для количественного описания температурного структурного перехода в трехкомпонентных микроэмульсиях [21], анализа ансамбля состояний самособирающихся икосаэдрических капсул фермента люмазинсинтазы в нативном состоянии и при наличии мутаций [22], а также изучения олигомерного состава ассоциатов наночастиц оксида железа, внедренных в капсулы вируса мозаики Бром [23].
Основным фактором, затрудняющим поиск глобального минимума функции, является нелинейная зависимость расчетных данных от параметров модели. При стандартном анализе для каждого параметра задают диапазон возможных значений, в пределах которого ищут решения. В зависимости от сложности используемой модели, стартовых значений параметров и шума экспериментальных данных решения могут существенно различаться. Поэтому анализ устойчивости и возможности восстановления теоретических данных приобретает исключительно важный характер.
ИСПОЛЬЗУЕМЫЕ МЕТОДЫ МИНИМИЗАЦИИ
В ходе работы проводили исследование на устойчивость алгоритмов четырех модификаций программы MIXTURE. В каждой из которых использовали различные минимизационные схемы: метод BFGS [10], SA [14], комбинация этих методов (BFGS + SA), а также NM [17].
Алгоритм BFGS является итерационным методом, относится к классу квазиньютоновских методов, в которых матрица вторых производных (гессиан) функции вычисляется не напрямую, а в некотором приближении, основываясь на сделанных до этого шагах. Метод достаточно эффективен, не требует больших временных затрат для поиска решения, но при этом решение может остановиться в локальном минимуме целевой функции, находящемся далеко от глобального экстремума целевой функции.
Метод SA является стохастическим методом поиска глобального экстремума. Он является наиболее подходящим для минимизации функций с большим числом переменных, что идеально подходит для многих задач МУР. Алгоритм основан на методе случайных испытаний, запускается с произвольной модели, параметры которой затем изменяются случайным образом в соответствии со схемой Метрополиса [24] до тех пор, пока решение не станет соответствовать экспериментальным данным, например, по критерию χ2. В отличие от метода квазиньютоновского градиентного спуска, где на каждом следующем шаге принимается решение с меньшим χ2 (5), в методе SA с определенной долей вероятности (определяемой так называемой “температурой отжига”) может приниматься худшее решение, это дает возможность программе выходить из локальных минимумов и продолжать спуск. По мере продолжения поиска значение температуры монотонно снижается, с использованием шкалирующего коэффициента 0.93–0.95 после каждых 1000–10 000 вариаций модели. Однако поиск решения с помощью такого алгоритма занимает длительное время (так как требуется достаточно большое количество температурных итераций).
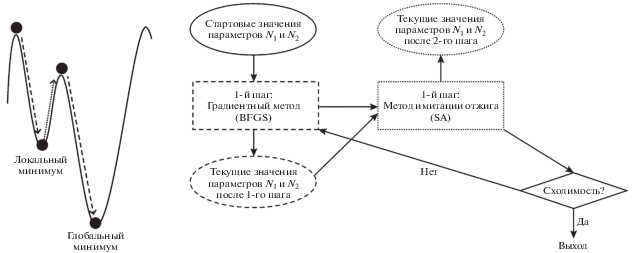
Комбинация BFGS и SA представляет собой поочередное использование этих алгоритмов минимизации. Схема поиска минимума показана на рис. 2. В целях поиска первого (возможно, локального) минимума нелинейной целевой функции (1) проводят старт программы MIXTURE, использующей градиентный метод минимизации, с некоторых значений параметров двухкомпонентной полидисперсной модели N1 и N2 (где N – один из структурных параметров R1, R2, dR1 либо dR2). Далее с оптимизированных методом BFGS значений проводится запуск модифицированной версии MIXTURE с использованием метода имитации отжига для того, чтобы вывести систему «из равновесия», причем со всего лишь одной итерацией по температуре, поэтому вычисления не занимают длительного времени. После этого с новых полученных значений программа запускается вновь с градиентным методом и так повторяется до тех пор, пока параметры модели не перестанут изменяться. За пороговое значение их изменчивости брали 1–5% от величины, полученной на предыдущей итерации.
Рис. 2.
Схема поиска глобального минимума целевой функции при комбинированном использовании методов BFGS и SA.
Метод NM, известный как метод деформируемого многогранника (часто используемое название “симплекс-метод” неверно, так как этот термин относится к другому, конфигурационному методу поиска), простой и в то же время эффективный, позволяющий оптимизировать функции многих переменных без вычисления градиентов. Суть метода заключается в последовательном перемещении вершин многогранника в пространстве параметров модели в сторону точки экстремума. Однако если метод находит локальный экстремум типа “плоского узкого оврага”, то многогранник может сжаться настолько, что поиск экстремума прекратится из-за ограниченной точности вычислений. В этом случае достаточно эффективным оказывается повторный запуск с новой конфигурации вершин. Метод отличается высокой надежностью и позволяет после нескольких запусков найти решение, более точное, чем ранее рассмотренные алгоритмы, хотя и требует длительных расчетов.
Несмотря на то что все эти методы являются достаточно эффективными, в ряде случаев только экспериментальным путем можно определить, будет ли используемый метод подходить для поставленной задачи. Поэтому с целью нахождения наиболее эффективного алгоритма для решения задачи восстановления объемного распределения частиц по размерам для двухкомпонентной полидисперсной системы были протестированы все упомянутые выше модификации программы MIXTURE.
ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ ВОССТАНОВЛЕНИЯ РЕШЕНИЙ
Приближение проводили в рамках модели, состоящей из двух типов сферических частиц с радиусами R1, R2, полидисперсностями dR1, dR2 и объемными долями V1, V2. Исследовали сходимость расчетов к правильному решению при одновременном варьировании стартовых значений следующих пар параметров: (R1, R2), (dR1, R2), (R1, dR2), тогда как остальные параметры фиксировались на истинных значениях, найденных программой MIXTURE (табл. 1) с относительными объемными долями V1 = 0.25 для меньших частиц кремнезоля (SM) и V2 = 0.75 для больших частиц кремнезоля (TM-50). В табл. 1 эти значения не приведены, так как алгоритмы всех исследуемых модификаций программы MIXTURE устойчивы к изменению объемных долей во всем диапазоне от 0 до 1.
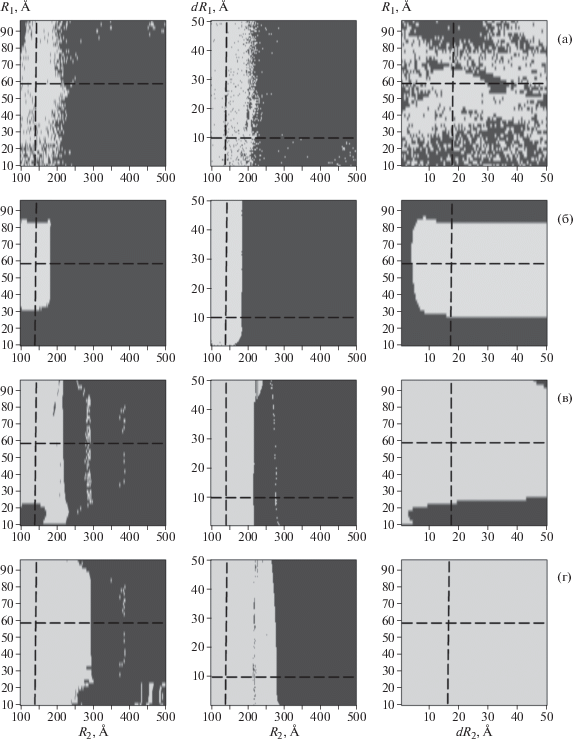
Диапазоны, в пределах которых выбирали стартовые значения параметров, были следующими: для радиусов R1 10.0–96.0 Å и R2 100.0–500.0 Å, для полидисперсностей dR1 и dR2 0.5–50.0 Å. Диапазоны были выбраны таким образом, чтобы радиусы меньших и бóльших частиц не коррелировали друг с другом. При этом шаг расчетной сетки по R1 и R2 составлял 2 Å, шаг сетки по dR1 и dR2 – 0.5 Å. Таким образом, для пары параметров (R1, R2) были посчитаны 8844 точки, для (dR1, R2) – 20 100 точек, для (R1, dR2) – 4400 точек. На основе этих данных построены двумерные карты, представленные на рис. 3. Верхняя панель соответствует результатам, полученным модифицированной версией программы MIXTURE с реализованным методом NM, вторая – программе с методом SA, третья – с BFGS, четвертая (нижняя) панель – комбинации методов BFGS и SA. Первый столбец (слева) – для пары параметров (R1, R2), второй – для (dR1, R2), третий – для (R1, dR2). Область светлого цвета соответствует нахождению истинного решения (в случае, когда значения параметров, полученных в результате моделирования программой MIXTURE, находились в пределах 5% от найденных ранее оптимальных значений). Область темного цвета соответствует всем остальным решениям, существенно отличающимся от истинного решения. Пунктирной линией отмечены истинные (оптимальные) значения параметров, восстановленные программой MIXTURE, указанные в табл. 1.
Рис. 3.
Контурные графики устойчивости восстановления решения программой MIXTURE в зависимости от стартовых значений радиусов сферических частиц кремнезоля и их полидисперсностей (R1, R2) , (dR1, R2), (R1, dR2). Пересечение пунктирных линий соответствует точным (истинным) значениям параметров. Области темного цвета – “неудача” (отличие от истинных параметров более чем на 5%), области светлого цвета – “успешное” нахождение решения (найденные параметры находятся в пределах 5% от истинных). Использованные алгоритмы минимизации: NM (а), SA (б), BFGS (в), BFGS + SA (г).
ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
Анализ двумерных карт позволил установить, что самые широкие границы устойчивости соответствуют комбинации методов BFGS и SA для всех трех пар параметров. При этом можно выстроить ряд алгоритмов в порядке возрастания их эффективности: NM, SA, BFGS, BFGS + SA, поэтому на рис. 3 они расположены в соответствующем порядке, сверху вниз.
Помимо этого, в некоторых случаях области нахождения правильных решений имеют достаточно сложные границы фрактального вида, с отдельными «очагами» неустойчивости внутри данных диапазонов, что свидетельствует о разной чувствительности методов минимизации к определенным параметрам модели.
Анализируя двумерные карты, отметим, что метод NM оказался наименее эффективным по сравнению с другими использовавшимися методами. Несмотря на то что его границы устойчивости шире, чем для метода SA, сравнительно легко попасть в область неустойчивости при незначительном отклонении от истинного значения. Для других трех методов можно говорить об имеющихся тенденциях. Для параметров R1 и R2 прослеживаются следующие закономерности: стартовые значения допустимо варьировать в пределах 50, 65 и 80% для R1 и 15, 65, 100% для R2 от истинного значения для методов SA, BFGS, BFGS + SA соответственно. Во всех случаях при значении R2 более 300 Å не удалось добиться восстановления данных. То есть стартовое значение данного параметра может не более чем в 2 раза превышать его истинное значение. При этом решения являются устойчивыми к варьированию параметров dR1 и dR2 во всем исследуемом диапазоне.
Также отметим, что метод SA теоретически мог бы позволить найти более широкие границы устойчивости, если бы существенно увеличили число вариаций модели при каждой итерации по температуре, но это на порядок увеличило бы время расчетов, что, как полагаем, неприемлемо с практической точки зрения. Кроме того, метод SA требует длительной работы по поиску оптимального режима снижения температуры, общего рецепта для этого до сих пор не выработано. В случае комбинированной схемы BFGS + SA метод SA используется исключительно с целью выхода из локального минимума и последующего продолжения поиска градиентным методом, для этой цели достаточно использования одной итерации по температуре.
ЗАКЛЮЧЕНИЕ
Исследована устойчивость решений программы MIXTURE для двухкомпонентного раствора кремнезоля с использованием следующих методов минимизации: градиентного метода (BFGS), метода имитации отжига (SA), сочетания этих двух методов (BFGS + SA), а также симплекс-метода Нелдера–Мида (NM). Анализ полученных данных позволяет расположить методы в порядке возрастания их эффективности: NM, SA, BFGS, BFGS + SA. Таким образом, алгоритм поиска с последовательным комбинированием методов минимизации BFGS и SA для систем сферических частиц с малоперекрывающимися объемными распределениями частиц по размерам позволяет максимально эффективно восстанавливать функцию ${{D}_{{v}}}(r)$ в более широких диапазонах стартовых значений параметров, чем с использованием других предложенных алгоритмов. Развитые подходы применимы к исследованию систем различной природы, в том числе для растворов белковых комплексов.
Работа выполнена при поддержке Министерства науки и высшего образования РФ в рамках выполнения работ по Государственному заданию ФНИЦ “Кристаллография и фотоника” РАН, a также при частичной финансовой поддержке Российского фонда фундаментальных исследований (грант № 19-32-90190 Аспиранты) и Программы деятельности НИЦ КИ на 2018–2022 г. Малоугловые измерения выполнены с использованием оборудования ЦКП ФНИЦ “Кристаллография и фотоника” РАН при поддержке Министерства науки и высшего образования России (проект RFMEFI62119X0035).
Список литературы
Svergun D.I., Konarev P.V., Volkov V.V. et al. // J. Chem. Phys. 2000. V. 113. P. 1651. https://doi.org/10.1063/1.481954
Konarev P.V., Petoukhov M.V., Volkov V.V., Svergun D.I. // J. Appl. Cryst. 2006. V. 39. P. 277. https://doi.org/10.1107/S0021889806004699
Petoukhov M.V., Franke D., Shkumatov A.V. et al. // J. Appl. Cryst. 2012. V. 45. P. 342. https://doi.org/10.1107/S0021889812007662
Konarev P.V., Volkov V.V., Sokolova A.V. et al. // J. Appl. Cryst. 2003. V. 36. P. 1277. https://doi.org/10.1107/S0021889803012779
Svergun D.I., Feigin L.A. X-Ray and Small-AngleNeutron Scattering. Moscow: Nauka, 1986.
Svergun D.I. // J. Appl. Cryst. 1992. V. 25. P. 495. https://doi.org/10.1107/S0021889892001663
Bressler I., Kohlbrecher J., Thünemann A.F. // J. Appl. Cryst. 2015. V. 48. P. 1587. https://doi.org/10.1107/S1600576715016544
Doucet M., Cho J.H., Gervaise A. et al. // SasView version 4.2.2. Zenodo. 2019. https://doi.org/10.5281/zenodo.2652478
Bressler I., Pauw B.R., Thünemann A.F. // J. Appl. Cryst. 2015. V. 48. P. 962. https://doi.org/10.1107/S1600576715007347
Gill P.E., Murray W., Wright M.H. Practical Optimizationт. London: Academic Press, 1981.
Kryukova A.E., Konarev P.V., Volkov V.V. // J. Physics: Conf. Ser. 2017. V. 941. P. 012069. https://doi.org/10.1088/1742-6596/941/1/012069
Крюкова А.Е., Конарев П.В., Волков В.В. // Кристаллография. 2018. Т. 63. № 1. С. 32. https://doi.org/10.7868/S0023476118010113
Крюкова А.Е., Козлова А.С., Конарев П.В. и др. // Кристаллография. 2018. Т. 63. № 4. С. 524. https://doi.org/10.1134/S002347611804015X
Kirkpatrick S., Gelatt C.D., Vecci M.P. // Science. 1983. V. 220. P. 671. https://doi.org/10.1126/science.220.4598.671
Kryukova A.E., Konarev P.V., Volkov V.V., Asadchikov V.E. // J. Mol. Liquids. 2019. V. 283. P. 221. https://doi.org/10.1016/j.molliq.2019.03.070
Kryukova A.E., Konarev P.V., Volkov V.V., Asadchikov V.E. // Phys. Atomic Nuclei. 2019. V. 82. P. 1576. https://doi.org/10.1134/S1063778819110097
Nelder J.A., Mead R. // Computer J. 1965. V. 7. P. 308. https://doi.org/10.1093/comjnl/7.4.308
Dumont F., Warlus J., Watillon A. et al. // Interface Sci. 1990. V. 138. P. 543. https://doi.org/10.1016/0021-9797(90)90236-H
Asadchikov V.E., Volkov V.V., Volkov Yu.O. et al. // JETF Lett. 2011. V. 94. P. 625. https://doi.org/10.1134/S0021364011190040
Mogilevskii L.Yu., Dembo A.T., Svergun D.I., Feigin L.A. // Crystallography Reports. 1984. V. 29. P. 587.
Svergun D.I., Konarev P.V., Volkov V.V. et al. // J. Chem. Phys. 2000. V. 113. P. 1651. https://doi.org/10.1063/1.481954
Zhang X., Konarev P.V., Petoukhov M.V. et al. // J. Mol. Biol. 2006. V. 362. P. 753. https://doi.org/10.1016/j.jmb.2006.07.037
Malyutin A.G., Cheng H., Sanchez-Felix O.R. et al. // ACS Appl. Mater. Interfaces. 2015. V. 7. P. 12089. https://doi.org/10.1021/acsami.5b02278
Metropolis N., Rosenbluth A.W., Rosenbluth M.N. et al. // J. Chem. Phys. 1953. V. 21. P. 1087. https://doi.org/10.1063/1.1699114
Дополнительные материалы отсутствуют.
Инструменты
Кристаллография


