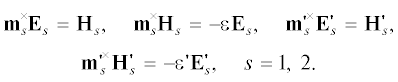Кристаллография, 2023, T. 68, № 1, стр. 62-67

ВВЕДЕНИЕ

В последнее время наряду с поверхностными электромагнитными волнами (поверхностными поляритонами и плазмонами) [1] на границах раздела изотропных сред широко изучаются бездисперсионные поверхностные поляритоны или волны Дьяконова. Эти волны теоретически предсказаны в [2, 3] и экспериментально обнаружены сравнительно недавно [4]. Существование таких поверхностных волн обусловлено различием в анизотропии пограничных сред, и они все более привлекают внимание исследователей [5–8].

Условием возникновения волн Дьяконова может быть не только разная анизотропия пограничных сред, но и различие таких характеристик сред, как гиротропия, хиральность и др. Например, в [9, 10] теоретически предсказаны поверхностные волны на границах сдвоенных непоглощающих гиротропных сред с противоположно направленными векторами гирации, перпендикулярными к плоскости раздела. Как известно, для описания монохроматических электромагнитных полей в прозрачных гиротропных средах используются эрмитовы тензоры диэлектрической и магнитной проницаемостей ε и μ [11–13]. В [9] рассматривались полубесконечные пограничные среды с тензорами диэлектрической проницаемости

которые различаются лишь знаками мнимых антисимметричных частей, ответственных за гиротропию. Здесь c^× – антисимметричный тензор, дуальный вектору c [11], перпендикулярному к границе раздела, знак $ \otimes $ обозначает тензорное произведение векторов, G – параметр гирации, ±Gc – векторы гирации. Гиротропные свойства, описываемые тензорами (1), характерны для магнитоупорядоченных сред [13]. Все направления распространения поверхностных волн равноправны в силу осевой симметрии рассматриваемой структуры, а характерная глубина проникновения поверхностных волн в каждую из пограничных сред при малых значениях параметра G, как показано в [9], обратно пропорциональна G².

Систему сред, описываемых тензорами (1), можно отнести к PT-симметричным системам, которые сейчас интенсивно изучаются [14–17] и имеют большие перспективы для практического применения в качестве одномодовых лазеров, когерентных идеальных поглотителей, сенсоров. Неоднородная среда является PT-симметричной, если выполняется условие

где r – радиус-вектор, а звездочка обозначает комплексное сопряжение. Очевидно, что для системы непоглощающих сред с тензорами (1) соотношение (2) выполняется. Отметим, что в литературе, как правило, рассматриваются PT-симметричные структуры, включающие в себя одновременно поглощающие и усиливающие изотропные негиротропные среды, подчиняющиеся условию (2) для скалярной комплексной диэлектрической проницаемости. В [18] условие (2) дополняется условием κ(–r)= –κ*(r) для параметра киральности κ, который предоставляет дополнительную степень свободы для управления рассеивающими свойствами PT-симметричной системы, в том числе для детектирования энантиомеров [19]. Поверхностные плазмон-поляритоны не могут возникнуть на границе раздела PT-симметричной системы полубесконечных негиротропных сред в силу (2), но могут возникнуть в многослойных структурах и на метаповерхности [20]. Исследования поверхностных электромагнитных волн на границах раздела анизотропных сред, образующих РТ-симметричную систему, в литературе не представлены.

Осевая симметрия распространения поверхностных электромагнитных волн нарушается, если вектор c не перпендикулярен границе раздела сред. Здесь исследуем случай, когда этот вектор лежит в плоскости раздела пограничных гиротропных сред. Вводя базис из единичных векторов b, q и a = [bq], связанный с поверхностной волной, можно записать

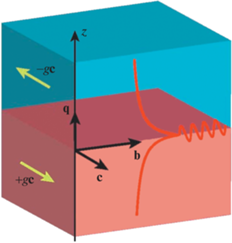
где квадратные скобки обозначают векторное произведение, вектор b определяет направление распространения поверхностной волны, q – вектор нормали к плоскости раздела, а α – угол между b и c. Одним из простейших является случай, когда α = ±π/2 (c = ±a или b = ±[qc], т.е. поверхностная волна распространяется перпендикулярно c, как показано на рис. 1). На примере этого случая в данной работе устанавливается важное свойство поверхностных волн в сдвоенных PT-симметричных гиротропных структурах – однонаправленность их распространения. А именно, если поверхностная волна может распространяться в некотором направлении, задаваемом вектором b, то в противоположном направлении –b она распространяться не может. Таким образом, гиротропная структура выступает оптическим вентилем в отношении поверхностных волн. Данный эффект является следствием невзаимных свойств гиротропных сред. Ранее вентильный эффект для поверхностных электромагнитных волн обсуждался в [21] в случае фарадеевской среды, граничащей с изотропной средой. В [22] с использованием формализма матриц импеданса обсуждалась проблема существования поверхностных электромагнитных волн на плоских границах бианизотропных бикристаллов. Был рассмотрен пример с двумя поверхностными волнами в магнитооптически активном бикристалле, распространяющимися в заданном направлении, при невозможности распространения таких волн в противоположном направлении. В [23] подробно анализировалась возможность существования в магнитооптических структурах нескольких поверхностных волн с одинаковыми значениями тангенциального волнового числа.

В работе выведено дисперсионное уравнение для поверхностных волн, из которого следует указанная выше однонаправленность их распространения. Показано, что для случая α = +π/2 (b = = +[qc]) поверхностная волна оказывается линейно поляризованной, а ее характерная глубина проникновения в каждую из пограничных сред при малых значениях параметра гирации G обратно пропорциональна этому параметру. В то же время при α = –π/2 (b = –[qc]) волна распространяться не может.

ГРАНИЧНЫЕ УСЛОВИЯ И ДИСПЕРСИОННОЕ УРАВНЕНИЕ. ПОЛЯРИЗАЦИЯ ПОВЕРХНОСТНОЙ ВОЛНЫ

Пусть ось z декартовой системы координат направлена вдоль единичного вектора q нормали к границе раздела гиротропных сред, а начало отсчета лежит на границе. Предполагаем, что среды с тензорами ε и ε' (1) располагаются в полупространствах z < 0 и z > 0 соответственно (далее все величины, относящиеся к среде в полупространстве z > 0, обозначим штрихами). Удобно вместо диэлектрических тензоров ε и ε' использовать обратные к ним тензоры

где материальные параметры a, b и g несложным образом выражаются через ε_o, ε_e и G. Считаем, что величины a и b при заданной частоте электромагнитного поля ω положительны. Знак параметра гирации g в общем случае может быть как отрицательным, так и положительным. Не теряя общности, выбираем g > 0, поскольку при g < 0 можно воспользоваться преобразованиями g → –g, c → → ‒c, не изменяющими вид тензоров (4).

Рассматриваемая здесь PT-симметричная структура получается из образца однородного гиротропного материала при его разрезании плоскостью, содержащей вектор c, и последующем развороте на 180° одной из получившихся половин вокруг направления q, перпендикулярного c.

Электромагнитное поле поверхностной электромагнитной волны является суперпозицией полей двух парциальных волн:

где единичный вектор b определяет направление распространения волны, k – волновое число, C_s – весовые коэффициенты парциальных волн, H_s и E_s – их векторные амплитуды. Комплексные параметры η_s характеризуют локализацию поля неоднородных парциальных волн вблизи границы раздела, и для того, чтобы при z → –∞ (z < 0) электромагнитное поле исчезало, необходима отрицательность мнимых частей этих параметров – $Im{{\eta }_{s}} < 0.$

В полупространстве z > 0 электромагнитное поле описывается напряженностями H'(r, t) и E'(r, t), выражения для которых такие же, как и (5), с заменой величин C_s, η_s, H_s и E_s на штрихованные, при этом $Im\eta _{s}^{'} > 0.$

Уравнения (5) могут быть записаны с использованием комплексных векторов рефракции [11]:

характеризующих парциальные волны и принимающих вид Здесь введена безразмерная фазовая скорость поверхностной волны ν = ω/(ck) (т.е. фазовая скорость в единицах скорости света в вакууме c).

Уравнения Максвелла для волны с вектором рефракции m записываются в виде

откуда [11]: Подставляя в первое из уравнений (9) обратный тензор ε^–1 (4), а также учитывая соотношения ${{{\mathbf{m}}}^{ \times }}{{{\mathbf{m}}}^{ \times }} = {\mathbf{m}} \otimes {\mathbf{m}} - {{{\mathbf{m}}}^{2}}$, ${{{\mathbf{m}}}^{ \times }}{{{\mathbf{c}}}^{ \times }} = {\mathbf{c}} \otimes {\mathbf{m}} - {\mathbf{cm}}$ и ${\mathbf{mH}} = 0,$ получим

В данной работе рассмотрим только отдельные взаимно противоположные направления распространения волн. Они перпендикулярны вектору c, лежащему в плоскости раздела сред, и характеризуются углами α = +π/2 и α = –π/2 (см. (3)). Тогда c = ±a = ±[bq]. Так как согласно (7) mc = = ±ma = 0, уравнение (10) упрощается:

Его решения легко отыскиваются и отвечают следующим напряженностям магнитного поля парциальных волн: при условии, что соответственно $1 - a{\mathbf{m}}_{1}^{2} = 0$ и $1 - a{\mathbf{m}}_{2}^{2} - (b - a){{[{{{\mathbf{m}}}_{2}}{\mathbf{a}}]}^{2}} = 0$ (или $1 - b{\mathbf{m}}_{2}^{2} = 0$). С учетом (7) имеем $1 - a(1 + \eta _{1}^{2}){\text{/}}{{\nu }^{2}} = 0$ и $1\, - \,b(1\, + \,\eta _{2}^{2}){\text{/}}{{\nu }^{2}}\, = $ $ = 0,$ откуда находим параметры локализации, выбирая их мнимые части отрицательными: Используя второе из уравнений (9), рассчитываем напряженности электрического поля парциальных волн: Верхние и нижние знаки в (13) соответствуют взаимно противоположным направлениям распространения поверхностной волны b = +[qc] и b = = ‒[qc], отвечающим углам α = +π/2 и α = –π/2 в (3).

Переходя к рассмотрению волн в полупространстве z > 0, в полученных выше соотношениях следует заменить g на –g, поскольку тензор $\varepsilon {\kern 1pt} {{'}^{{ - 1}}}$ отличается от ${{\varepsilon }^{{ - 1}}}$ лишь знаком перед g. Параметры локализации (12) от g не зависят, однако $\eta _{1}^{'}$ и $\eta _{2}^{'}$ должны быть выбраны с положительными мнимыми частями:

Получаем следующие результаты для напряженностей полей:

Дисперсионное уравнение находится из граничных условий, состоящих в том, что тангенциальные составляющие электрического и магнитного полей непрерывны на границе раздела. Иными словами, ${{\left. {{{{\mathbf{H}}}_{\tau }}({\mathbf{r}},t)} \right|}_{{z = 0}}} = {\mathbf{H}}_{\tau }^{'}{\kern 1pt} {{\left. {({\mathbf{r}},t)} \right|}_{{z = 0}}}_{{}}$ и ${{\left. {{{{\mathbf{E}}}_{\tau }}({\mathbf{r}},t)} \right|}_{{z = 0}}} = $ $ = {\mathbf{E}}_{\tau }^{'}{\kern 1pt} {{\left. {({\mathbf{r}},t)} \right|}_{{z = 0}}}$, или в развернутом виде с учетом (5) и (6):

Тангенциальные составляющие полей парциальных волн легко определяются из соотношений (11), (13) и (15): Подставляя (17) в (16), получим систему уравнений для весовых коэффициентов парциальных волн: Из нее следует, что ${{C}_{2}} = C_{2}^{'} = 0,$ а коэффициенты ${{C}_{1}}$ и $C_{1}^{'}$ совпадают и отличны от нуля при условии $a{{\eta }_{1}} \pm ig = 0,$ которое с учетом (12) записывается в виде

Уравнение (18) является дисперсионным и имеет решение только тогда, когда в правой части выбирается положительный знак. Это означает, что в направлении b = +[qc] возможно возбуждение поверхностной электромагнитной волны, а в противоположном направлении b = –[qc] она распространяться не может. Таким образом, PT-симметричная гиротропная структура, характеризуемая обратными тензорами диэлектрической проницаемости (4), проявляет вентильные свойства по отношению к поверхностным электромагнитным волнам.

Решением уравнения (18), определяющим квадрат фазовой скорости поверхностной волны, является

Поскольку ${{C}_{2}} = C_{2}^{'} = 0,$ волна является однопарциальной, причем в соответствии с (14) и (19) параметры локализации равны Распределение напряженностей электромагнитного поля (5) с учетом (19) и (20), а также (11), (13) и (15) принимает вид для $z \in ( - \infty , + \infty ).$ Здесь весовые коэффициенты ${{C}_{1}}$ и $C_{1}^{'}$ равны напряженности магнитного поля на границе раздела сред H₀, которая может быть произвольной.

Характеристики рассматриваемой поверхностной электромагнитной волны не зависят от материального параметра b – этот параметр не входит в выражения (19)–(21). Она является TEM-модой (т.е. поперечной волной), поскольку ${\mathbf{bH}}({\mathbf{r}},t) = {\mathbf{bE}}({\mathbf{r}},t) = 0.$ Поляризация волны является линейной на любом расстоянии от границы раздела, так как $\left[ {{\mathbf{H}}({\mathbf{r}},t),{\mathbf{H}}{\kern 1pt} *{\kern 1pt} ({\mathbf{r}},t)} \right] = \left[ {{\mathbf{E}}({\mathbf{r}},t),{\mathbf{E}}{\kern 1pt} *{\kern 1pt} ({\mathbf{r}},t)} \right] = 0$ [11]. Очевидно, что плотность энергии электромагнитного поля пропорциональна $exp\left( { - 2gk\left| z \right|{\text{/}}a} \right),$ поэтому характерная глубина проникновения волны, на которой ее интенсивность ослабевает в e раз по сравнению с интенсивностью на границе раздела, оказывается равной

Глубина проникновения обратно пропорциональна параметру гирации g при условии, что g ≪ ≪ a. Таким образом, чем меньше параметр гирации, тем слабее локализована поверхностная электромагнитная волна вблизи границы раздела сдвоенной гиротропной структуры.

СИММЕТРИЙНЫЙ АНАЛИЗ ВОЛНОВЫХ УРАВНЕНИЙ

Кратко обсудим причины вентильных свойств сдвоенных гиротропных структур на основе анализа симметрий волновых уравнений. При этом предполагаем, что направление распространения волн по отношению к вектору c любое, т.е. угол α в соотношении (3) произвольный.

Согласно (8) векторные амплитуды парциальных волн подчиняются следующим соотношениям:

Если существует решение дисперсионного уравнения, следующего из (22), то формально существует аналогичное решение, получающееся из комплексно сопряженных соотношений (22): Здесь учтено то, что $\varepsilon {\kern 1pt} * = \varepsilon {\kern 1pt} '$ (см. (1)). При этом в соответствии с (7)

Рассмотрим операцию поворота на 180° вокруг вектора единичной нормали к границе раздела q. Эта операция приводит к следующим преобразованиям векторов:

а для тензоров диэлектрической проницаемости имеем ε ⇄ ε'. Применяя данную операцию к уравнениям (23) и обозначая преобразованные векторы шляпками, получим причем из (24) и (25) следует, что

Из сравнения уравнений (22) и (26) видно, что сдвоенная гиротропная структура симметрична относительно комбинированной операции сопряжения и поворота на 180° вокруг q (т.е. $\varepsilon \to \varepsilon ,$ $\varepsilon {\kern 1pt} ' \to \varepsilon {\kern 1pt} '$). Преобразованные векторы рефракции (27) описывают парциальные волны, распространяющиеся в направлении, противоположном вектору b. Однако, поскольку в (27) входят комплексно сопряженные параметры локализации, амплитуды этих волн экспоненциально возрастают при удалении от границы раздела. Понятно, что такие волны физически нереализуемы. Формально дисперсионное уравнение для нефизической поверхностной волны, распространяющейся в направлении –b, имеет такое же решение ν = = ν_S, что и для обычной поверхностной волны, распространяющейся в направлении b.

Таким образом, приходим к следующему общему заключению (при дополнительном условии единственности решений дисперсионного уравнения): если в сдвоенной гиротропной структуре, описываемой обратными диэлектрическими тензорами (4), в некотором направлении b вдоль границы раздела возможно распространение поверхностной электромагнитной волны, то в противоположном направлении –b поверхностная волна распространяться не может. В предыдущем разделе этот вывод продемонстрирован для частного случая поверхностных электромагнитных волн, распространяющихся в направлении, перпендикулярном c.

Обратимся к операции поворота на 180° вокруг единичного вектора b в направлении распространения поверхностной волны. При ее выполнении пограничные среды меняются местами с заменой вектора с в (4) на ${\mathbf{\hat {c}}} = {\mathbf{b}}cos\alpha - {\mathbf{a}}sin\alpha $ (см. (3)). Тогда

или где $ - {\mathbf{\hat {c}}} = - {\mathbf{b}}cos\alpha + {\mathbf{a}}sin\alpha .$ Очевидно, что вектор $ - {\mathbf{\hat {c}}}$ получается из c (3) при замене угла α на π – α. Отсюда заключаем, что если возможно возбуждение поверхностной волны, направленной под углом α по отношению к вектору c, то также возможно распространение поверхностной волны под углом π – α по отношению к этому вектору. Иными словами, разрешенные направления распространения поверхностных волн расположены зеркально симметрично относительно плоскости с вектором нормали с, перпендикулярной границе раздела гиротропных сред.

ЗАКЛЮЧЕНИЕ

Установлено важное свойство сдвоенных PT-симметричных гиротропных структур с обратными диэлектрическими тензорами (4), состоящее в однонаправленности распространения в них поверхностных электромагнитных волн. А именно, если в некотором направлении b вдоль границы раздела пограничных комплементарных гиротропных сред возможно распространение поверхностной электромагнитной волны, то в противоположном направлении –b поверхностная волна распространяться не может. Здесь подробно рассматривался только случай распространения волн перпендикулярно к оси c гиротропных сред. Установлено, что разрешенным направлением распространения является ${\mathbf{b}} = + [{\mathbf{qc}}],$ а запрещенным – ${\mathbf{b}} = - [{\mathbf{qc}}],$ где q – вектор нормали к границе раздела сред (при условии, что g > 0). При малых значениях параметра гирации g поверхностные волны являются слабо локализованными, а их характерная глубина проникновения обратно пропорциональна g. Анализ общего случая произвольных направлений распространения волн вдоль границы раздела математически более сложен и будет проведен в отдельной работе.

Полученные результаты могут оказаться важными для фотоники на чипе и направленного резонансного переноса энергии между удаленными донорной и акцепторной молекулами, расположенными вблизи границы раздела двух гиротропных сред.

Работа выполнена при финансовой поддержке Белорусского республиканского фонда фундаментальных исследований, грант Ф21ИЗР-003.