1. На главную
  2. Электронные версии
  3. Лесоведение
  4. № 2, 2019

Лесоведение, 2019, № 2, стр. 105-114

Построение кривых хода роста древостоев на основе обобщенной модели Берталанфи по данным государственного лесного реестра

М. Д. Корзухин *

Институт глобального климата и экологии Росгидромета и РАН
107258 Москва, ул. Глебовская, 20Б, Россия

* E-mail: mdkorz@gmail.com

Поступила в редакцию 10.01.2018
После доработки 10.04.2018
Принята к публикации 03.12.2018

Полный текст (PDF)

Аннотация

Сформулирована модель роста древостоя, примененная к данным Государственного лесного реестра за 2013 г. в разрезе субъектов РФ. Определена динамика удельных запасов древесины с возрастом t, V(t) (м3 га–1): построены кривые хода роста (КХР) пород по наблюдаемым значениям удельных запасов Uk, м3 га–1 в шести группах возраста. Модель имеет вид двух динамических уравнений и выведена из физически правдоподобных предположений; за основу взята модель роста Берталанфи. Отличие предлагаемой модели от имеющихся в литературе – способность описывать немонотонную динамику, а именно, часто наблюдаемое падение Uk в старших возрастах (для спелых и перестойных древостоев). Полученные интерполирующие кривые (1326 шт.) предполагается использовать при подготовке Национального доклада о кадастре парниковых газов, где применяется алгоритм модели РОБУЛ (Региональная оценка баланса углерода лесов).

Ключевые слова: кривая хода роста, Государственный лесной реестр, модель роста древостоя.

Отчетные данные Государственного лесного реестра содержат величины: Vk – запас древесины, м3, Sk – площади преобладающей породы, га; k = 1, .., 6 – номер группы возраста. В совокупности они позволяют найти значения удельных запасов Uk = Vk/Sk, м3 га–1. Существенно, что Uk – это возрастные распределения, измеренные в некоторый момент времени, а не собственно кривые хода роста (КХР) (развитие во времени). Считать непоредственно по ним, например, прирост биомассы (а это частое испольование КХР) некорректно ввиду отсутствия данных в некоторых группах, немонотонности по возрасту или очевидного измерительного “шума”. Единственная допускаемая немонотонность – это падение Uk в старших возрастах (для спелых и перестойных древостоев). Независимо от экологических причин этого падения есть все основания считать его не измерительным артефактом, а реальным явлением; на это, в частности, указывают модальные таблицы хода роста (ТХР) (Швиденко и др., 2008), индивидуальные пробные площади (Кузьмичев, 1977), ТХР для Онтарио, Канада (Penner et al., 2008).

Прямые наблюдения хода роста на протяжении развития древостоя затруднены из-за низкой скорости процесса. В такой ситуации применяется эргодическая гипотеза: средние по пространству значения Uk, измеренные в некоторый момент времени, в разумной мере дают возможность оценить развитие древостоя с возрастом k (подробнее см. (Карев, 2001)). Эргодическая гипотеза (явно или неявно) широко применяется в естественных науках.

Для получения КХР из величин Uk последние необходимо интерполировать гладкими кривыми того или иного типа. Лесоведение изобилует формулами, используемыми для этой цели; большинство из них является формально-регрессионными кривыми, почти или совсем не имеющими физической интерпретации. Часть моделей имеет механизменную (“рrocess based”) и экофизиологическую основу. Большинство моделей динамики насаждений основываются на формализации углеродного баланса (Карев, 2001; Суховольский, Иванова, 2013; Aleksandrov, Golitsyn, 2015), в более реалистических случаях дополняемого балансом Н2О и введением климатических, почвенных и биотических факторов (см. обзоры в работах (Jorgensen, 2011; Pretzsch et al, 2015)). Предложены также модели, основанные на термодинамических гипотезах, предлагающие целостное описание леса (в частности – интересующих лесников одновозрастных насаждений) небольшим числом макроскопических параметров (Alexandrov, 2008; Александров, Голицын, 2012; Aleksandrov, Golitsyn, 2015). Однако до сих пор связь между регрессионным и экофизиологическим типами описаний слаба – КХР строятся тем или иным “сглаживанием” натурных данных, а экологические модели ограничиваются точечными примерами. Экофизиологическую основу имеют все DGVMs (Dynamical global vegetation models), однако их цель не состоит в решении достаточно специальной задачи нахождения КХР (см. сравнительно полные обзоры в работах (Методы оценки .., 2012, гл. 6; Корзухин, 2015)).

Специфика предлагаемой статьи заключается в применении физически обоснованной модели к массовому материалу по удельным запасам Uk, содержащихся в данных ГЛР. Прикладной аспект работы состоит в стремлении приобрести опыт интерполяции отчетных данных, с возможным формированием в будущем банка данных кривых хода роста для основных лесообразующих пород списка ГЛР.

МАТЕРИАЛЫ И МЕТОДИКА

Для ислледования привлечены отчетные данные по площадям и запасам насаждений для покрытых лесом земель по состоянию на 01.01.2014 г. (форма 4-ДЛР “Распределение площади лесов и запасов древесины по преобладающим породам и группам возраста” ГЛР). Структура данных, использованных в расчетах, соответствовала принятой в методике РОБУЛ (Региональная оценка бюджета углерода лесов) для расчета баланса углерода лесов (Замолодчиков и др., 2011), а именно, площади и запасы исходных 66 пород списка ГЛР были сгруппированы в 12 индивидуальных и 4 обобщенных породы c заданными размерами возрастных классов (табл. 1). Данные дифференцированы по преобладающим породам, группам возраста, категории землепользования (леса защинтые, резервные, эксплуатационные), субъекту Российской Федерации и широтной полосе. Каждый субъект Российской Федерации сопоставлен с макрорегионом (Европейско-Уральская часть, Западная Сибирь, Восточная Сибирь, Дальний Восток) и широтной полосой (северная – северные редколесья и северная тайга, средняя – средняя тайга и южная – южная тайга, смешанные, широколиственные леса и лесостепь).

Таблица 1.  

Список пород (мета-пород) РОБУЛ с сопутствующими параметрами, данные ГЛР за 2013 г.

№ п/п Название породы Код породы
ГЛР 		Код породы РОБУЛ Площадь занимаемая породой, км2 Доля в полной облесенной площади
(“Всего”) 		Число записей в банке данных Размер возрастного класса, лет
1 Сосна 101 101 1 194 931 0.155060 139 20
2 Ель 102 102 777 069 0.100836 128 20
3 Пихта 103 103 142 959 0.018551 72 20
4 Лиственница 104 104 2 753 201 0.357267 126 20
5 Сосна кедровая 105 105 388 825 0.050456 63 40
6 Можжевельник 106 106 22 0.000003 1 20
7 Дуб выcoкocтвoльный 110 110 36 788 0.004774 70 20
8 Дуб низкocтвoльный 111 111 31 815 0.004128 75 10
9 Бepeзa кaмeннaя 117 117 88 898 0.011536 14 20
10 Прочие твердолиственные 112..116, 120..121 122 24 134 0.003132 81 20
11 Береза 124 124 1 175 952 0.152597 143 10
12 Осина 125 125 240 420 0.031198 138 10
13 Прочие мягколиственные 126..132 133 94 356 0.012244 139 10
14 Прочие древесные породы 141..180 135 7584 0.000984 48 20
15 Кeдpoвый стлaник 191 191 385 710 0.050051 29 20
16 Прочие кустарники 181..190, 193..204 139 363 543 0.047175 99 5
  Всего     7 706 207 1.000000 1326  

Всего получено 1326 ненулевых независимых возрастных распределений Uk, каждое из которых рассматривается как оценка соответствующей КХР. Полнота данных ГЛР, имеющих отношение к задаче, приведена в табл. 2; число ненулевых точек среди Uk для каждого случая (записи в банке данных) обозначено как Pn.

Таблица 2.  

Встречаемость записей в баке данных с различным числом ненулевых точек среди Uk и другие характеристики данных ГЛР за 2013 г.

Число Pn ненулевых точек среди Uk Число записей в банке данных Площадь, км2 Доля в полной площади
6 741 7 422 430 0.9632
5 175 239 477 0.0311
4 128 29 514 0.0038
3 85 7042 0.0009
2 89 4307 0.0006
1 108 3437 0.0004
Сумма 1326 7 706 207 1.0000

Расположение эмпирических точек радикально влияет на вид получаемой кривой хода роста V(t). В частности, особый интерес представляет расположение точек Uk в старших группах возраста. Некоторые характеристики этого случая для информационно значимых 5 и 6 точек приведены в табл. 3. Как видим, суммарная площадь и число случаев с падением запасов в старших возрастах заметны среди всех вариантов. Прочие немонотонности (в младших группах) естественно считать измерительным шумом.

Таблица 3.  

Анализ монотонности–немонотонности величин Uk

Тип расположения Число случаев Площадь, км2 Доля в полной площади
Pn = 6
Все случаи 741 7 422 430  
Монотонный рост 317 2 563 070 0.345
Немонотонный рост для любых групп 424 4 859 360 0.655
U5 > U6 среди последних случаев 327 3 081 209 0.415
Pn = 5
Все случаи 175 239 477  
Монотонный рост 34 27 160 0.113
Немонотонный рост для любых групп 141 212 317 0.887
U5 > U6 среди последних случаев 82 106 826 0.446

Модель Берталанфи (Bertalanffy, 1957) (утвердившееся в литературе название; в реальности модель имеет длительную предысторию с 20-х годов ХХ в.) состоит из одного динамического уравнения для биомассы организма m, описывающего рост за счет поглощения ресурса и ограничение роста за счет расхода ресурса:

(1)
${{dm} \mathord{\left/ {\vphantom {{dm} {dt}}} \right. \kern-0em} {dt}} = fg{{m}^{q}} - rm.$

Поглощение пропорционально поглощающей поверхности организма s (или соответствующей ей биомассе):

(2)
$s = g{{m}^{q}}.$

В уравнениях (1), (2) f – удельная скорость поглощения ресурса; g, q – аллометрические параметры, связывающие биомассу m и поглощающую поверхность s; ресурс расходуется пропорционально полной биомассе с удельной скоростью r. Согласно обзору L. von Bertalanffy (1957) для животных в зависимости от типа метаболизма 2/3 ≤ ≤  q ≤ 1.0. В случае, когда рассматривается рост дерева, s – это его листовая поверхность, а расход состоит из опада, отмирания корней, некоторых компонентов дыхания. В то время как первое слагаемое имеет серьезные биологические основания, второе, ограничивающее рост, по существу полуэмпирично, поскольку причины ограничения роста дерева достоверно неизвестны, не говоря о том, что описание набора сложных процессов одним слагаемым r × m – сильное огрубление.

Такое же по структуре уравнение применяется для описания динамики биомассы М единицы площади древостоя (например, Zeide, 1989; в популярной модели TRIFFID-Cox, 2001; Shvidenko et al., 2007; West et al., 2009; Aleхandrov, Golitsyn, 2015; и др.), иногда – с обобщениями (Day, Taylor, 1997):

(3)
${{dM} \mathord{\left/ {\vphantom {{dM} {dt}}} \right. \kern-0em} {dt}} = p{{M}^{q}} - rM,$

где p = f × g. Этот переход с методической точки зрения далеко не тривиален, так как М = m × N (N – число деревьев) и описание динамики М требует по крайней мере двух уравнений (см. (Корзухин, Семевский, 1992)). Мощная теория роста организмов, структуры и динамики леса (реально – древостоя) MST (Metabolic Scale Theory-Enquist et al., 2009; Kerkhoff and Enquist, 2006; West et al., 2009) предсказывает, что в соотношении (2) для организма q = 3/4, и что при определенных предположениях (в частности, при сомкнутом пологе) прирост биомассы древостоя также пропорционален поглощающей поверхности:

(4)
${{dM} \mathord{\left/ {\vphantom {{dM} {dt}}} \right. \kern-0em} {dt}} = f{\kern 1pt} S,$
(5)
$S = g{{M}^{q}},$
где S – площадь листвы, соответствующая биомассе М) но уже со степенью q = 3/5 (Enquist et al., 2009). Все указывает на то, что величина q меняется в ходе развития насаждения.

В нашем случае в качестве исходного будет использоваться уравнение (3), с напоминанием, что оно менее обосновано, чем (1) и по существу является его аналогом. Общее решение уравнения (3) с начальным условием М(0) = М0 имеет вид:

(6)
$M(t) = {{\left[ {{{e}^{{ - r(1 - q)t}}}\left( {M_{0}^{{1 - q}} - {p \mathord{\left/ {\vphantom {p r}} \right. \kern-0em} r}} \right) + {p \mathord{\left/ {\vphantom {p r}} \right. \kern-0em} r}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 {(1 - q)}}} \right. \kern-0em} {(1 - q)}}}}}.$

Очевидно, что это монотонная функция, которая непригодна для описания важного для нас случая немонотонности Uk в старших возрастах. Более того, никакая немонотонная кривая X(t) не может быть решением любого одного (автономного) уравнения, поэтому искомая модель должна состоять по меньшей мере из двух динамических уравнений. Предлагаемое обобщение уравнения Берталанфи, преодолевающее недостаточность одного уравнения, состоит: а) в разбиении популяции деревьев на несколько возрастных когорт; б) во введении конкурентного подавления роста младших когорт старшими.

В простейшем случае вводим две когорты. Подавление роста описываем типичным для лесной экологии множителем, пропорциональным количеству света, проходящему через слой листвы толщиной LAI при коэффициенте поглощения k:

(7)
$Q\sim \exp ( - k \times {\text{LAI}}).$

Поскольку LAI = S (равенство (5)), можно записать два динамических уравнения, правые части которых формализуют введенные выше процессы. Проще всего принять, что все особи старшей когорты выше особей младшей, тогда LAI в (7) – это полная листовая поверхность старшей когорты; в противном случае это ее часть. Натурные данные ГЛР приведены в переменных запаса стволовой древесины (м3 га–1), так что КХР будут получены в тех же единицах. Поэтому, считая, что запасы пропорциональны биомассе, модель запишем в переменных запасов младшей (V1), и старшей (V2) когорт; единица времени – 1 год:

(8a)
${{d{{V}_{1}}} \mathord{\left/ {\vphantom {{d{{V}_{1}}} {dt}}} \right. \kern-0em} {dt}} = {{p}_{2}}\exp \left( { - {{p}_{3}}V_{2}^{{p4}}} \right)V_{1}^{{p4}} - {{p}_{5}}{{V}_{1}} - {{p}_{6}}{{V}_{1}};$
(8b)
${{d{{V}_{2}}} \mathord{\left/ {\vphantom {{d{{V}_{2}}} {dt}}} \right. \kern-0em} {dt}} = {{p}_{2}}V_{2}^{{p4}} + {{p}_{5}}{{V}_{1}} - {{p}_{7}}{{V}_{2}}.$

Смысл первых двух слагаемых ясен из предыдущего изложения; слагаемое р5V1 описывает демографический переход из младшей когорты в старшую; слагаемые р6V1, р7V2 – потери углерода на дыхание и гибель деревьев в каждой когорте.

Система уравнений (8) применялась для построения КХР при наличии 4, 5 или 6 ненулевых значений Uk. Случаи Pn = 1, 2 и 3, несмотря на ничтожную представленность в общей площади (табл. 2), из обсчета не устранялись, но к ним применялось базовое уравнение Берталанфи

(9)
${{d{{V}_{1}}} \mathord{\left/ {\vphantom {{d{{V}_{1}}} {dt}}} \right. \kern-0em} {dt}} = {{p}_{2}}V_{1}^{{p4}} - {{p}_{5}}{{V}_{1}},$
решавшееся с начальным условием V1(0) = p1. При Pn = 1 свободным считался параметр p1 – начальное условие; следуя (Enquist et al. (2009)), бралось р4 = 3/5; назначался максимум V1(t → ∝) = = V1max = 1.2 × Uk (Uk > 0 – единственное ненулевое значение); р5 бралось как характерное время пребывания в состоянии 1, р5 = 1/Tmax, где Tmax – старший возраст группы 6; окончательно из формулы, дающей максимум V1:

(10)
${{V}_{{1\max }}} = {{({{{{p}_{2}}} \mathord{\left/ {\vphantom {{{{p}_{2}}} {{{p}_{5}}}}} \right. \kern-0em} {{{p}_{5}}}})}^{{{1 \mathord{\left/ {\vphantom {1 {(1 - p4)}}} \right. \kern-0em} {(1 - p4)}}}}},$
(11)
${{p}_{2}} = {{V_{{1\max }}^{{1 - p4}}} \mathord{\left/ {\vphantom {{V_{{1\max }}^{{1 - p4}}} {{{T}_{{\max }}}}}} \right. \kern-0em} {{{T}_{{\max }}}}}.$

Целью всех этих манипуляций было добиться прохождения траектории в точности через значение Uk: V1(tk) = Uk (tk – середина возрастного интервала группы k). При Pn = 2 схема оставалась той же, но траектория проводилась через значение Uaver = (Uk1 + Uk2)/2, где два значения U – единственные ненулевые величины, а Uaver соответствует возрасту taver = (tk1 + tk2)/2. При Pn = 3 свободными считались параметры р1, р2, р5 (при р4 = 3/5).

Система уравнений (8) решалась численно с начальными условиями:

(12)
${{V}_{1}}(0) = {{p}_{1}};\,\,\,\,{{V}_{2}}(0) = 0$
на промежутке времени [0, Tmax]. Расчетная кривая хода роста V(t) находилась как суммарный запас обеих когорт:

(13)
$V(t) = {{V}_{1}}(t) + {{V}_{2}}(t).$

Параметры получены минимизацией среднеквадратического отклонения

$SD = {{\left[ {\sum\limits_{{\text{k}} = 1}^{{\text{k}} = 6} {{{{{{({{U}_{{\text{k}}}} - {{V}_{{\text{k}}}})}}^{2}}} \mathord{\left/ {\vphantom {{{{{({{U}_{{\text{k}}}} - {{V}_{{\text{k}}}})}}^{2}}} {Pn}}} \right. \kern-0em} {Pn}}} } \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}.$

Сумма берется только для Uk > 0; Vk – значения V(t) в моменты времени, равные серединам возрастных интервалов групп возраста.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Собственно результаты состоят в найденных семи параметрах р1..р7 для каждого из 1326 набора эмпирических точек U1..U6. Качество описания задается абсолютной величиной стандартного отклонения SD (см. уравнение (14)) в м3 га–1 на одну точку, точностью интерполяции и безразмерным критерием “эффективности модели” МЕ (“model efficiency” – по (Nash, Sutcliffe, 1970), который регулярно используется в современных экологических работах):

(15)
$ME = 1 - \frac{{\sum {{{{({{U}_{{\text{k}}}} - {{V}_{{\text{k}}}})}}^{2}}} }}{{\sum {{{{({{U}_{{\text{k}}}} - {{U}^{{{\text{mean}}}}})}}^{2}}} }}.$

Значение МЕ может находиться в интервале (‒∞, 1), где 1 соответствует наилучшему описанию данных моделью, 0 – качеству описания, совпадающему с описанием эмпирическим средним, МЕ < 0 – непригодности используемой модели.

Прямым счетом до больших t были также найдены Vmax – равновесные значения V(t).

Распределение значений МЕ (15) для наиболее информационно надежных случаев с Pn = 5, 6 дано в табл. 4.

Таблица 4.

Качество подгонки модели (8) к данным ГЛР при 5 и 6 ненулевых значениях удельного запаса в группах возраста

МЕ 0 0.2 0.4 0.8 0.9 0.99 0.999 0.9999 1.0*
nn    13       5      32     51    333      384         95             3

* Получено округлением МЕ > 0.99995 до 1. Примечание. Всего проанализировано 916 кривых. ME – эффективность модели (формула (15)); nn – число случаев в банке данных (кривых хода роста), имеющих ME в указанном интервале.

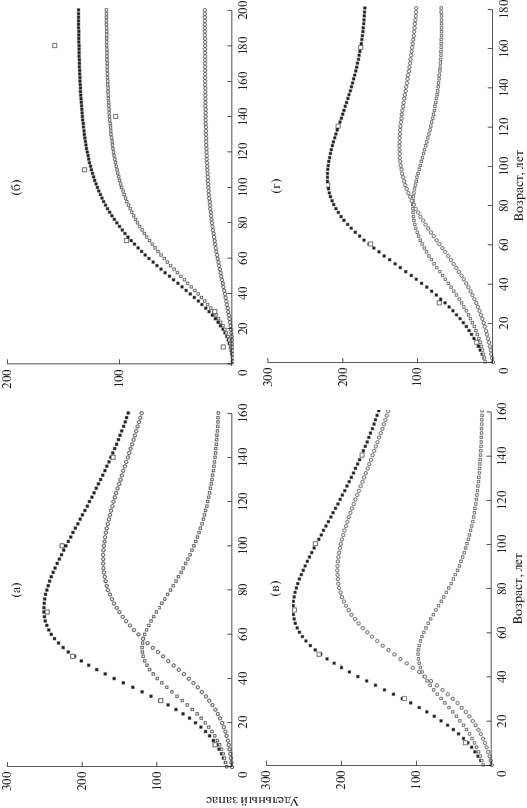
Примеры полученных КХР приведены на рисунке. А, В, Г – случаи с немонотонным ростом; Б – случай монотонного роста, с которым прекрасно справляется модель.

Возможны два взгляда на уравнение (8).

Оно рассматривается только как инструмент интерполяции. В этом случае исследователь не обращает внимания на полученные значения параметров и вид кривых, но лишь на точность описания данных.

Таблица 5.  

Параметры для примеров интерполяции КХР, приведенных на рисунке

Параметр Рис. (а) Рис. (б) Рис. (с) Рис. (д)
Субъект Федерации Алтайский край Красноярский край Нижегородская обл. Пермская обл.
Порода Сосна Лиственница Сосна Ель
Площадь, занятая породой, га 1 042 900 21 103 500 815 000 4 501 600
Категория земель лесного фонда Защитная Эксплуатационная Эксплуатационная Эксплуатационная
р1, м3 га–1 7.068970 0.221740 11.426892 10.149989
р2, м3(1–р4) гар4–1 год–1 0.143978 0.328352 0.182715 0.175568
р3, м3р4 га–р4 0.010393 0.012665 0.004406 0.003682
р4, безразм. 0.990003 0.814332 0.990000 0.989536
р5, год–1 0.039546 0.018336 0.056431 0.043010
р6, год–1 0.009971 0.096691 0.046486 0.073705
р7, год–1 0.140527 0.167454 0.139587 0.124363
Точность интерполяции SD 3.26 15.47 2.25 3.22
Эффективность модели МЕ 0.9983 0.9218 0.9992 0.9980
Рис. 1.

Примеры интерполяции удельных запасов по данным ГЛР моделью (8): ◻ − эмпирические значения, ◻ − V1(t), ⚪ − V2(t), ◼ − V(t). Подробную информацию см. в табл. 5.

Также его можно рассмотреть и как инструмент интерполяции, и как физическую модель. В этом случае приходится оценивать реалистичность полученных величин параметров и вида кривых, корректировать их в случае нереалистичности; эта процедура существенно неформальна. Для Pn = 1, 2 алгоритм подгонки исключал возможность “патологических” результатов; в остальных 1129 случаях эта ситуация встретилась примерно в 30 из них, и почти всегда нереально большим оказывалось значение Vmax в результате вырожденных случаев, когда найденные величины р3 или р5 равнялись нулю. Для устранения “патологии” достаточно было зафиксировать р3 = = р3min ~ 0.1 (близко к типичным значениям для остальных случаев) или р5 = р5min = 1/Tmax и пересчитать случай с небольшой потерей точности. Таким образом, исследователь всегда будет стоять перед альтернативой: предпочесть ли более высокую точность описания при нереалистических результатах или уменьшить ее в пользу физического правдоподобия.

Применение модели с семью параметрами для интерполяции эмпирической кривой, заданной шестью (а тем более меньшим числом) точек выглядит модельным излишеством. Распространено мнение, что если число параметров равно или более больше числа точек, то модель может с идеальной точностью описать “любые” данные; это очевидное заблуждение, легко опровергаемое примерами. В нашем случае численные эксперименты показали, что любое упрощение модели (8), например, положение р3 ≡ 0 (устранение конкурентного подавления), взятие р6 ≡ р7 или фиксация р4 = 3/5 (строгое следование MST), лишает ее возможности описать падение Uk в старших возрастах – кривые V(t) становятся монотонными. Конечно, справедлив тезис, что в принципе возможна другая модель с нужными свойствами, но с меньшим числом параметров; однако пока ее нет.

Представляет серьезный интерес сравнение значений найденных параметров с таковыми, измеряемыми в лесной экологии. Возможны следующие сопоставления:

Параметр р2 пропорционален произведению удельной скорости ассимиляции f и морфологического параметра g в равенстве (5); введя конверсионный коэффициент [запас → биомасса] h, нетрудно получить, что p2 = f × g × h p4–1.

Произведение р3 × V p4 равно произведению коэффициента экстинкции k и S = LAI (листового индекса), откуда нетрудно получить, что p3 = = k × g × h p4.

Параметр аллометрии р4 (q в (2)) многократно измерялся в лесной экологии для отдельных деревьев, имеется также его теоретическая оценка; в нашем случае р4 (q в (5)) относится к насаждению и также может быть сопоставлен с соответствующими результатами.

При известных g, р4 и биомассе М можно найти величину LAI (5).

В итоге, четыре экологически важнейшие величины (f, k, q, LAI) возможно сравнить с результатами их измерений и вычислений, содержащихся в огромной экологической литература по проблеме. Однако данное сравнение достаточно объемно и не могло быть предпринято в рамках решавшейся в настоящей статье задачи.

Была испытана модель, аналогичная (8), но с бóльшим числом возрастных когорт, конкретно – с четырьмя, и теми же параметрами р1…р7. Качество описания данных практически не улучшилось, однако ввиду большей гибкости модель чаще стала вести себя как формально проведенный интерполяционный полином, т.е. фактически стала менее устойчивой (при использовании модели (8) встретилось лишь несколько таких случаев). В качестве базового рабочего варианта была оставлена модель (8).

Нам известны два модельных описания падения удельного запаса U в старших возрастах – W.A. Kurz, M.J. Apps (1999) (модель СВМ) и A. Shvidenko et al. (2007); оба используют эмпирически введенное экспоненциальное уменьшение V(t). Две недавние модели динамики насаждения (Ogawa, 2017, 2018) сформулированы в механизменных терминах, однако описывают уменьшение в старших возрастах только биомассы листвы и дыхания насаждения.

Специфика отчетных данных ГЛР такова, что они игнорируют многопородность насаждений, сводя их к однопородной ситуации так называемой “преобладающей” породы (которая может представлять меньше половины суммарного запаса). В этом случае применение формально однопородной модели (8) означает, что мы описываем динамику некоторой обобщенной породы, состоящей из суммы реально наличествующих пород; соответственно, и полученные параметры являются обобщенными.

Любая модель или подразумевает, или явно использует какие-либо экологические механизмы. В нашем случае – это конкурентное подавление меньших деревьев бóльшими. Это возможный (Binkley et al., 2002), но не единственный механизм, могущий объяcнить падение запасов в старших возрастах. Например, М.В. Рогозин и Г.С. Разин (2015) указывают на возможные изменения классов бонитета, в частности, в старших возрастах насаждений, и для этого есть реальные экологические основания; тогда же могут ухудшаться условия воспроизводства насаждений или повышаться вероятность гибели деревьев. Скорее всего, имеют место разные причины эффекта, реализующиеся в различных ситуациях, их обзор выходит за рамки данной публикации.

Заключение. Динамическая модель использована для описания кривых хода роста, полученных по данным ГЛР. Все слагаемые в правых частях уравнений имеют прямую физическую интерпретацию. При построении модели использован один из возможных механизмов, объясняющих падение запасов в спелых и перестойных древостоях, а именно, конкурентное подавление когорты второго яруса старшей когортой. Полученное высокое качество описания всех 1326 описания кривых хода не исключает других вариантов описания немонотонной динамики.

Список литературы

  1. Александров Г.А., Голицын Г.С. Критерий подобия для роста лесных насаждений // Доклады Академии наук. 2012. Т. 446. С. 110–113.

  2. Замолодчиков Д.Г., Грабовский В.И., Краев Г.Н. Динамика бюджета углерода лесов России за два последних десятилетия // Лесоведение. 2011. № 6. С. 16–28.

  3. Карев Г.П. Системное моделирование лесных сообществ // Сибирский экологический журн. 2001. № 4. С. 518–528.

  4. Корзухин М.Д. Возможные расчетные оценки влияния климата на продуктивность лесов (обзор подходов) // Проблемы экологического мониторинга и моделирования экосистем. М.: 2015. Т. XXVI. № 2. С. 33–58.

  5. Корзухин М.Д., Семевский Ф.Н. Синэкология лесa. – СПб.: Гидрометеоиздат, 1992. 192 с.

  6. Кузьмичев В.В. Закономерности роста древостоев. Новосибирск: Наука, 1977. 160 с.

  7. Методы оценки последствий изменения климата для физических и биологических систем. Под ред. С.М. Семенова, М.: Росгидромет, 2012. 508 с.

  8. Рогозин М.В., Разин Г.С. Модели динамики и моделирование развития древостоев // Сибирский лесной журн. 2015. № 2. С. 50–70.

  9. Суховольский В.Г., Иванова Ю.Д. Оценка первичной продуктивности лесных насаждений с использованием модели распределения фитомассы по фракциям // Лесоведение. 2013. № 5. С. 20–28.

  10. Швиденко А.З., Щепащенко Д.Г., Нильссон С., Булуй Ю.И. Таблицы и модели роста и биологической продуктивности насаждений основных лесообразующих пород Северной Евразии (нормативно-справочные материалы). Изд. 2-е. М.: Рослесхоз, Международный институт прикладного системного анализа, 2008. 886 с.

  11. Alexandrov G.A. Forest growth in the light of the thermodynamic theory of ecological systems // Ecological Modelling. 2008. V. 216. № 2. P. 102–106.

  12. Alexandrov G.A., Golitsyn G.S. Biological age from the viewpoint of the thermodynamic theory of ecological systems // Ecological Modelling. 2015. V. 313. № 2. P. 103–108.

  13. Bertalanffy L., von. Quantitative laws in metabolism and growth // The Quarterly Review of Biology. 1957. V. 32. P. 217–231.

  14. Binkley D., Stape J.L., Ryan M.G., Barnard H.R., Fownes J. Age-related decline in forest ecosystem growth: an individual-tree, stand-structure hypothesis // Ecosystems. 2002. V. 5. № 1. P. 58–67.

  15. Cox P.M. Description of the ‘TRIFFID’ dynamic global vegetation model // (Hadley Centre Technical note 24). London, UK: Hadley Centre, Meteorological Office, 2001. 16 p.

  16. Day T., Taylor P.D. Von Bertalanffy’s growth equation should not be used to model age and size at maturity // The American Naturalist. 1997. V. 149. № 2. P. 381–393.

  17. Enquist B.J., West G.B., Brown J.H. (II) Extensions and evaluations of a general quantitative theory of forest structure and dynamics // Proceedings of the National Academy of Sciences of the USA. 2009. V. 106. № 17. P. 7046–7051.

  18. Jorgensen S.E. Chapter 6 Models of forest ecosystems // Handbook of ecological models used in ecosystem and environmental management / Ed. by S.E. Jorgensen, Boca Raton, Florida, USA: CRC Press, Taylor & Francis Group. 2011. P. 161–174.

  19. Kerkhoff A.J., Enquist B.J. Ecosystem allometry: the scaling of nutrient stocks and primary productivity across plant communities // Ecology Letters. 2006. V. 9. № 4. P. 419–427.

  20. Kurz W.A., Apps M.J. A 70-year retrospective analysis of carbon fluxes in the Canadian forest sector // Ecological Applications. 1999. V. 9 (2). P. 526–547.

  21. Nash J.E., Sutcliffe J.V. River flow forecasting through conceptual models part I – A discussion of principles // J. Hydrology. 1970. V. 10. № 3. P. 282–290.

  22. Ogawa K. Modeling age-related stand respiration changes in forest stands under the self-thinning law // Ecological Modelling. 2017. V. 349. № 1. P. 62–68.

  23. Ogawa K. Mathematical consideration of the age-related decline in leaf biomass in forest stands under the self-thinning law // Ecological Modelling. 2018. V. 372. № 1. P. 64–69.

  24. Penner M., Woods M., Parton J., Stinson A. Validation of empirical yield curves for natural-origin stands in boreal Ontario // The Forestry Chronicle. 2008. V. 84. № 5. P. 704–717.

  25. Pretzsch H., Forrester D.I., Rötzera T. Representation of species mixing in forest growth models. A review and perspective // Ecological Modelling. 2015. V. 313. P. 276–292.

  26. Shvidenko A., Schepschenko D., Nilsson S., Bouloui Y. Semi-empirical models for assessing biological productivity of Northern Eurasian forests // Ecological Modeling. 2007. V. 204. № 1–2. P. 163–179.

  27. West G.B., Enquist B.J., Brown J.H. (I) A general quantitative theory of forest structure and dynamics // Proceedings of the National Academy of Sciences of the USA. 2009. V. 106. № 17. P. 7040–7045.

  28. Zeide B. Accuracy of equations describing diameter growth // Canadian J. Forest Research. 1989. V. 19. № 10. P. 1283–1286.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Лесоведение

Архивы выпусков Информация о журнале Отправить рукопись в журнал