Известия РАН. Механика твердого тела, 2019, № 2, стр. 101-110

КОНТАКТНОЕ ВЗАИМОДЕЙСТВИЕ ПЛАСТИНКИ С НЕЛИНЕЙНО-УПРУГИМ СТРИНГЕРОМ

О. М. Джохадзе^a, С. С. Харибегашвили^a, Н. Н. Шавлакадзе^a, *, **

^a Тбилисский государственный университет, математический институт им. А. Размадзе
Тбилиси, Грузия

^* E-mail: nusha@rmi.ge
^** E-mail: nusha1961@yahoo.com

Поступила в редакцию 10.06.2017
После доработки 06.02.2018
Принята к публикации 06.02.2018

DOI: 10.1134/S0572329919010033

Аннотация

Рассматривается задача определения механического поля в однородной полуплоскости, подкрепленной конечным однородным стрингером, материал которого подчиняется нелинейному закону Гука. Поставленная задача редуцируется к нелинейному сингулярному интегродифференциальному уравнению. Используя принцип неподвижной точки Шаудера доказывается существование решения этого уравнения. При помощи метода малого параметра получается система рекуррентных линейных сингулярных интегральных уравнений первого рода.

Ключевые слова: контактная задача, нелинейное интегродифференциальное уравнение, принцип Шаудера, метод малого параметра

Введение. В работах [1–4] были получены точные и приближенные решения статических и динамических контактных задач для разных областей, усиленных упругими тонкими накладками как постоянной, так и переменной жесткости, изучено поведение контактных напряжений в концах линии контакта в зависимости от закона изменения геометрических и физических параметров задачи. Библиография различных контактных задач приводится в монографии [1], где рассматриваются плоские контактные задачи о передаче нагрузки от полубесконечного или конечного стрингера (включения) к упругой полуплоскости или плоскости. Задачи сведены к интегродифференциальному уравнению Прандтля, получены различные аналитические методы его решения. В [4] расматривается контактная задача для анизотропной полуплоскости с упрочняющимися накладками конечной длины, она сводится к решению нелинейного сингулярного интегро-дифференциального уравнения при определенных граничных условиях. Контактные задачи для изотропной и ортотропной кусочно-однородной плоскости, а также для клиновидной анизотропной пластины с полубесконечной и конечной накладкой были решены в [5–8]. При нашей постановке задачи рассматривается упругая полубесконечная пластинка, которая на конечном отрезке своей границы усилена стрингером из нелинейно-упругого материала общего вида. Доказывается существование и единственность решения полученного нелинейного интегродифференциального уравнения. Для конкретного случая “нелинейности” получено условие относительно малого параметра, при выполнении которого решение полученной системы рекуррентных линейных уравнений представляется в виде сходящегося ряда по степеням этого параметра.

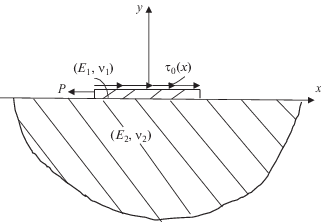
1. Постановка задачи и ее редукция к нелинейному сингулярному интегродифференциальному уравнению (НСИДУ). Пусть линейно-упругая полубесконечная пластинка с модулем упругости ${{E}_{2}}$ и коэффициентом Пуассона ${{{\nu }}_{2}}$ на конечном отрезке [–1, 1] оси $Ox$ усилена нелинейно-упругим стрингером в виде накладки конечной длины и достаточно малой толщины ${{h}_{1}}$, модулем упругости ${{E}_{1}}$ и коэффициентом Пуассона ${{{\nu }}_{1}}$, загруженной тангенциальной силой интенсивности ${{{\tau }}_{0}}(x)$. Пусть далее, к одному из концов стрингера приложена сосредоточенная горизонтальная сила $P$ (фиг. 1).

В условиях плоского напряженного состояния требуется определить контактные напряжения, действующие на отрезке соединения стрингера с пластинкой.

Материал стрингера удовлетворяет нелинейному закону Гука [1, 4]

(1.1)

${\varepsilon }_{x}^{{(1)}}(x) = \frac{{d{{u}_{1}}(x)}}{{dx}} = \frac{1}{E}g({\sigma }_{x}^{{(1)}}(x))$

где ${\varepsilon }_{x}^{{(1)}}(x)$ и ${{u}_{1}}(x)$ – соответственно деформация и перемещение точек стрингера, ${\sigma }_{x}^{{(1)}}(x)$ – осевое напряжение по направлению оси $Ox$, $E = {{{{E}_{1}}} \mathord{\left/ {\vphantom {{{{E}_{1}}} {(1 - {\nu }_{1}^{2}}}} \right. \kern-0em} {(1 - {\nu }_{1}^{2}}})$.

Из условия равновесия любой конечной части стрингера имеем

(1.2)

${\sigma }_{x}^{{(1)}}(x) = \frac{1}{{{{S}_{0}}}}\left[ {P - d\int\limits_{ - 1}^x {{\tau }(t)dt - \int\limits_{ - 1}^x {{{{\tau }}_{0}}(t)} } dt} \right]$

где ${\tau }(x)$ – неизвестное тангенциальное контактное напряжение, отнесенное к единице ширины стрингера, ${{S}_{0}}$ – площадь его поперечного сечения, $d$ – эффективная ширина, по которой он контактируется с основанием.

Основываясь на равенства (1.1) и (1.2), деформацию точек стрингера можно выразить в виде

(1.3)

$\begin{array}{*{20}{c}} {{\varepsilon }_{x}^{{(1)}} = \frac{1}{E}g({\varphi }(x)),\quad }&{\left| x \right| < 1} \end{array}$

${\varphi }(x) = \frac{1}{{{{S}_{0}}}}\left[ {P - d\int\limits_{ - 1}^x {{\tau }(t)dt - \int\limits_{ - 1}^x {{{{\tau }}_{0}}(t)} dt} } \right]$

Условие равновесия стрингера имеет вид

(1.4)

${\varphi }(1) = 0$

На основе известных результатов (см., например, [9]), деформация граничных точек пластинки по оси $Ox$, вызванной распределенными по интервалу (–1, 1) тангенциальными напряжениями интенсивности ${\tau }(x)$, представляется в виде

(1.5)

${\varepsilon }_{x}^{{(2)}}(x): = \frac{{d{{u}_{2}}(x,0)}}{{dx}} = - \frac{2}{{{\pi }{{E}_{2}}}}\int\limits_{ - 1}^1 {\frac{{{\tau }(t)dt}}{{t - x}}} \begin{array}{*{20}{c}} {,\quad }&{\left| x \right| < 1} \end{array}$

где ${{u}_{2}}(x,y)$ – перемещения точек пластинки вдоль оси $Ox$.

На основании условия контакта

(1.6)

${\varepsilon }_{x}^{{(1)}}(x) = {\varepsilon }_{x}^{{(2)}}(x),\quad \left| x \right| \leqslant 1$

вдоль линии соединения стрингера с основанием с учетом (1.3) и (1.5) получим

(1.7)

$ - \frac{2}{{{\pi }{{E}_{2}}}}\int\limits_{ - 1}^1 {\frac{{{\tau }(t)dt}}{{t - x}}} = \frac{1}{E}g({\varphi }(x)),\quad \left| x \right| < 1$

В обозначениях

${\lambda } = \frac{{2{{S}_{0}}E}}{{{{E}_{2}}d}},$ $f(x) = \frac{{\lambda }}{{{\pi }{{S}_{0}}}}\int\limits_{ - 1}^1 {\frac{{{{{\tau }}_{0}}(t)dt}}{{t - x}}} $

уравнение (1.7) перепишем в виде

(1.8)

$g({\varphi }(x)) - \frac{\lambda }{{\pi }}\int\limits_{ - 1}^1 {\frac{{{\varphi '}(t)dt}}{{t - x}}} = f(x),\quad \left| x \right| < 1$

при условиях

(1.9)

${\varphi }( - 1) = {P \mathord{\left/ {\vphantom {P {{{S}_{0}}}}} \right. \kern-0em} {{{S}_{0}}}},\quad {\varphi }(1) = 0$

Здесь интегралы в (1.8) понимаются в смысле главного значения по Коши.

Таким образом, поставленная гранично-контактная задача для упругой изотропной полубесконечной пластинки, усиленной на своей границе нелинейно-упругим стрингером конечной длины, эквивалентно сведена к решению нелинейного сингулярного интегродифференциального уравнения (1.8) при граничных условиях (1.9). Решение задачи (1.8), (1.9) ищется в классе непрерывных функций в смысле Гельдера $(H)$ на сегменте [–1,1] , производная которых принадлежит классу $H{\text{*}}$ [9, 10]. Относительно $f(x)$ будем предполагать, что она также принадлежит классу $H{\text{*}}$ на сегменте [–1,1].

2. Существование решения задачи (1.8), (1.9). Нелинейное сингулярное интегродифференциальное уравнение (1.8) при граничных условиях (1.9) преобразуем теперь к эквивалентному нелинейному интегральному уравнению. С этой целью воспользовавшись известной формулой обращения сингулярного интегрального уравнения с ядром Коши в классе функций, неограниченных на обеих концах сегмента [10, 11], получим

(2.1)

${\varphi '}(x) = - \frac{1}{{{\pi \lambda }\sqrt {1 - {{x}^{2}}} }}\int\limits_{ - 1}^1 {\frac{{\sqrt {1 - {{t}^{2}}} g({\varphi }(t))dt}}{{t - x}} + \frac{1}{{{\pi \lambda }\sqrt {1 - {{x}^{2}}} }}\int\limits_{ - 1}^1 {\frac{{\sqrt {1 - {{t}^{2}}} f(t)dt}}{{t - x}}} + \frac{{{{C}_{0}}}}{{\sqrt {1 - {{x}^{2}}} }}} $

Интегрируя обе части уравнения (10) будем иметь

(2.2)

$\begin{gathered} {\varphi }(x) = - \frac{1}{{2{\pi \lambda }}}\int\limits_{ - 1}^1 {\ln \frac{{1 - xt + \sqrt {(1 - {{t}^{2}})(1 - {{x}^{2}})} }}{{1 - xt - \sqrt {(1 - {{t}^{2}})(1 - {{x}^{2}})} }}g({\varphi }(t))dt + } \\ + \;\frac{1}{{2{\pi \lambda }}}\int\limits_{ - 1}^1 {\ln \frac{{1 - tx + \sqrt {(1 - {{t}^{2}})(1 - {{x}^{2}})} }}{{1 - tx - \sqrt {(1 - {{t}^{2}})(1 - {{x}^{2}})} }}} f(t)dt + {{C}_{0}}{\text{arcsin}}\,x + C \\ \end{gathered} $

Здесь постоянные ${{C}_{0}}$ и $C$ определяются из граничных условии (1.9):

${{C}_{0}} = - \frac{P}{{{\pi }{{S}_{0}}}},\quad C = \frac{P}{{2{{S}_{0}}}}$

Замена переменных $x = \cos {\pi }\,s,t = \cos {\pi }\,u,0 \leqslant s,u \leqslant 1$, в уравнении (2.2), после элементарных преобразованный, дает

$\begin{gathered} {\psi }(s) - \frac{1}{{\lambda }}\int\limits_0^1 {\sin {\pi }u\left[ {\ln \left| {\frac{{\sin \frac{{\pi }}{2}(s + u)}}{{\sin \frac{{\pi }}{2}(s - u)}}} \right|} \right]g({\psi }(u))du = } \\ = \; - \frac{1}{{\lambda }}\int\limits_0^1 {\left[ {\ln \left| {\frac{{\sin \frac{{\pi }}{2}(s + u)}}{{\sin \frac{{\pi }}{2}(s - u)}}} \right|} \right]} {{f}_{1}}(u)du + \frac{P}{{{{S}_{0}}}}s \\ \end{gathered} $

где $\psi (s) = {\varphi }(\cos {\pi }s),{{f}_{1}}(s) = f(\cos {\pi }s)\sin {\pi }s$. Уравнение (2.3) представляет собой уравнение типа Гаммерштейна. Перепишем ее следующем в операторном виде

${\psi } = A{\psi }$

$\begin{gathered} A{\psi } = \frac{1}{{\lambda }}\int\limits_0^1 {\sin {\pi }u\left[ {\ln \left| {\frac{{\sin \frac{{\pi }}{2}(s + u)}}{{\sin \frac{{\pi }}{2}(s - u)}}} \right|} \right]g({\psi }(u))du - } \\ - \;\frac{1}{{\lambda }}\int\limits_0^1 {\left[ {\ln \left| {\frac{{\sin \frac{{\pi }}{2}(s + u)}}{{\sin \frac{{\pi }}{2}(s - u)}}} \right|} \right]} {{f}_{1}}(u)du + \frac{P}{{{{S}_{0}}}}s \\ \end{gathered} $

Пусть,

(2.5)

$\begin{gathered} \left| {g({\xi })} \right| \leqslant {{M}_{1}}{{\left| {\xi } \right|}^{{\alpha }}} + {{M}_{2}},\quad \begin{array}{*{20}{c}} {{\alpha } \geqslant 0,}&{\quad {\xi } \in R} \end{array}, \\ \begin{array}{*{20}{c}} {{{M}_{i}} = {\text{const}} \geqslant 0,}&{\quad i = 1,2} \end{array} \\ \end{gathered} $

Вводя обозначение $Q(s,u) = \left| {\frac{{\sin ({{\pi } \mathord{\left/ {\vphantom {{\pi } 2}} \right. \kern-0em} 2})(s + u)}}{{\sin ({{\pi } \mathord{\left/ {\vphantom {{\pi } 2}} \right. \kern-0em} 2})(s - u)}}} \right|,s,u \in [0,1]$ выражение $A{\psi }$ из формулы (2.4) оценивается следующим образом:

(2.6)

$\begin{gathered} \left| {A{\psi }} \right| \leqslant \frac{1}{{\lambda }}\int\limits_0^1 {\left| {\ln Q(s,u)} \right|} \left| {g({\psi }(u)} \right|du + \frac{1}{{\lambda }}\int\limits_0^1 {\left| {\ln Q(s,u)} \right|} \left| {{{f}_{1}}(u)} \right|du + \frac{P}{{{{S}_{0}}}} \leqslant \\ \leqslant \;\frac{1}{{\lambda }}\left\{ {{{M}_{1}}\int\limits_0^1 {\left| {\ln Q(s,u)} \right|{{{\left| {{\psi }(u)} \right|}}^{{\alpha }}}du + {{M}_{2}}\int\limits_0^1 {\left| {\ln Q(s,u)} \right|du} } } \right\} + \\ + \;\frac{1}{{\lambda }}\int\limits_0^1 {\left| {\ln Q(s,u)} \right|} \left| {{{f}_{1}}(u)} \right|du + \frac{P}{{{{S}_{0}}}} \leqslant \\ \leqslant \frac{1}{{\lambda }}\left\{ {({{M}_{1}}\left\| {\psi } \right\|_{C}^{{\alpha }} + {{M}_{2}} + {{{\left\| {{{f}_{1}}} \right\|}}_{C}})\int\limits_0^1 {\left| {\ln Q(s,u)} \right|du} } \right\} + \frac{P}{{{{S}_{0}}}} \\ \end{gathered} $

Теперь оценим следующий интеграл $\int\limits_0^1 {\left| {\ln Q(s,u)} \right|} ds$. С этой целью рассмотрим функцию $q(x) = {{x}^{{\varepsilon }}}\ln x,0 < x \leqslant 1,{\varepsilon } > 0$, находим ее критическую точку ${{x}_{0}} = {{e}^{{ - {{\text{1}} \mathord{\left/ {\vphantom {{\text{1}} {\varepsilon }}} \right. \kern-0em} {\varepsilon }}}}}$ и учитывая, что $q({{e}^{{ - {1 \mathord{\left/ {\vphantom {1 {\varepsilon }}} \right. \kern-0em} {\varepsilon }}}}}) = - {1 \mathord{\left/ {\vphantom {1 {{\varepsilon }e}}} \right. \kern-0em} {{\varepsilon }e}}$, заключаем:

(2.7)

$\mathop {\sup }\limits_{0 < x \leqslant 1} \left| {q(x)} \right| = \frac{1}{{e{\varepsilon }}} = :{{M}_{{\varepsilon }}},\quad 0 < {\varepsilon } < 1$

Так как

(2.8)

$\sin x \geqslant \left\{ \begin{gathered} \frac{2}{{\pi }}x,\begin{array}{*{20}{c}} {}&{0 \leqslant x \leqslant \frac{{\pi }}{2}} \end{array} \hfill \\ \frac{2}{{\pi }}({\pi } - x),\begin{array}{*{20}{c}} {}&{\frac{{\pi }}{2} \leqslant x \leqslant {\pi }} \end{array} \hfill \\ \end{gathered} \right.$

получим

(2.9)

${{\left| {\sin \frac{{\pi }}{2}(t + s)} \right|}^{{ - {\varepsilon }}}} \leqslant \left\{ \begin{gathered} {{(t + s)}^{{ - {\varepsilon }}}},\begin{array}{*{20}{c}} {}&{0 \leqslant s \leqslant 1 - t} \end{array} \hfill \\ {{(2 - (t + s))}^{{ - {\varepsilon }}}},\begin{array}{*{20}{c}} {}&{s \geqslant 1 - t} \end{array} \hfill \\ \end{gathered} \right.$

(2.10)

${{\left| {\sin \frac{{\pi }}{2}(t - s)} \right|}^{{ - {\varepsilon }}}} \leqslant {{\left| {t - s} \right|}^{{ - {\varepsilon }}}},\begin{array}{*{20}{c}} {}&{0 \leqslant s,t \leqslant 1} \end{array}$

Из (2.7) и (2.9) следует

(2.11)

$\begin{gathered} \int\limits_0^1 {\left| {\ln \left| {\sin \frac{{\pi }}{2}(t + s)} \right|} \right|} ds \leqslant \int\limits_0^1 {\frac{1}{{{{{\left| {\sin \frac{{\pi }}{2}(t + s)} \right|}}^{{\varepsilon }}}}}} \left| {{{{\left| {\sin \frac{{\pi }}{2}(t + s)} \right|}}^{{\varepsilon }}}\ln \left| {\sin \frac{{\pi }}{2}(t + s)} \right|} \right|ds \leqslant \\ \leqslant \;{{M}_{{\varepsilon }}}\int\limits_0^1 {\frac{{ds}}{{{{{\left| {\sin \frac{{\pi }}{2}(t + s)} \right|}}^{{\varepsilon }}}}}} \leqslant \frac{{{{M}_{{\varepsilon }}}}}{{1 - {\varepsilon }}}[2 - {{t}^{{1 - {\varepsilon }}}} - {{(1 - t)}^{{1 - {\varepsilon }}}}] \\ \end{gathered} $

Из (2.7) и (2.10) имеем

(2.12)

$\begin{gathered} \int\limits_0^1 {\left| {\ln \left| {\sin \frac{{\pi }}{2}(t - s)} \right|} \right|} ds \leqslant \int\limits_0^1 {\frac{1}{{{{{\left| {\sin \frac{{\pi }}{2}(t - s)} \right|}}^{{\varepsilon }}}}}} \left| {{{{\left| {\sin \frac{{\pi }}{2}(t - s)} \right|}}^{{\varepsilon }}}\ln \left| {\sin \frac{{\pi }}{2}(t - s)} \right|} \right|ds \leqslant \\ \leqslant \;{{M}_{{\varepsilon }}}\int\limits_0^1 {\frac{{ds}}{{{{{\left| {t - s} \right|}}^{{\varepsilon }}}}}} = \frac{{{{M}_{{\varepsilon }}}}}{{1 - {\varepsilon }}}[{{t}^{{1 - {\varepsilon }}}} + {{(1 - t)}^{{1 - {\varepsilon }}}}] \\ \end{gathered} $

Но так как, при ${\varepsilon } = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},$ величина ${\varepsilon }(1 - {\varepsilon })$ достигает максимума, поэтому учитывая (2.11) и (2.12), получим

(2.13)

$\begin{gathered} \int\limits_0^1 {\left| {\ln Q(s,t)} \right|} ds \leqslant \int\limits_0^1 {\left| {\ln \left| {{\text{sin}}\frac{{\pi }}{2}(s + t)} \right|} \right|} ds + \int\limits_0^1 {\left| {\ln \left| {\sin \frac{{\pi }}{2}(s - t)} \right|} \right|} ds \leqslant \frac{{{{M}_{{\varepsilon }}}}}{{1 - {\varepsilon }}}[2 - {{t}^{{1 - {\varepsilon }}}} - {{(1 - t)}^{{1 - {\varepsilon }}}}] + \\ + \frac{{{{M}_{{\varepsilon }}}}}{{1 - {\varepsilon }}}[{{t}^{{1 - {\varepsilon }}}} + {{(1 - t)}^{{1 - {\varepsilon }}}}] = \frac{{2{{M}_{{\varepsilon }}}}}{{1 - {\varepsilon }}} \\ \end{gathered} $

Поэтому в силу (2.7) из (2.13) будем иметь

(2.14)

$\int\limits_0^1 {\left| {\ln Q(s,u)} \right|} ds \leqslant \frac{8}{e}$

Учитывая (2.13), из (2.6) получим

(2.15)

${{\left\| {A{\psi }} \right\|}_{C}} \leqslant \frac{{8{{M}_{1}}}}{{e{\lambda }}}\left\| {\psi } \right\|_{C}^{{\alpha }} + \frac{8}{{e{\lambda }}}({{M}_{2}} + {{\left\| {{{f}_{1}}} \right\|}_{C}}) + \frac{P}{{{{S}_{0}}}}$

Рассмотрим неравенство

(2.16)

$a + b{{r}^{{\alpha }}} \leqslant r$

относительно $r \geqslant 0$, где $a,b = {\text{const}} > 0,\begin{array}{*{20}{c}} {}&{{\alpha } = {\text{const}} \geqslant 0} \end{array}.$

Как известно [12, 13]

1) если $0 \leqslant {\alpha } < 1$, то для любых $a$ и $b$ всегда существует $r > 0$, удовлетворяющий неравенству (2.16);

2) если ${\alpha } = 1$, то достаточно потребовать, чтобы $b < 1,$ тогда неравенство (2.16) имеет решение $r \geqslant \frac{a}{{1 - b}}$;

3) если ${\alpha } > 1$ и имеет место неравенство $a \leqslant \frac{{{\alpha } - 1}}{{\alpha }}{{({\alpha }b)}^{{ - {{{({\alpha } - 1)}}^{{ - 1}}}}}}$, то тогда существует хотя бы одно положительное решение неравенства (2.16).

Опираясь на эти заключения, связанные с неравенством (2.16), в котором

$a = \frac{8}{{e{\lambda }}}({{M}_{2}} + {{\left\| {{{f}_{1}}} \right\|}_{C}}) + \frac{P}{{{{S}_{0}}}}$, $b = \frac{{8{{M}_{1}}}}{{e{\lambda }}}$

получим, что в силу (2.15) оператор $A:C([0,1]) \to C([0,1]),$ действующий по формуле (2.4), переводит шар $B(0,r): = \{ {\psi } \in C([0,1]):{{\left\| {\psi } \right\|}_{{C([0,1])}}} \leqslant r\} $ в себя:

а) для достаточно большого фиксированного $r$ в случае $0 \leqslant {\alpha } < 1$;

б) для произвольного $r \geqslant {a \mathord{\left/ {\vphantom {a {(1 - b)}}} \right. \kern-0em} {(1 - b)}}$ в случае ${\alpha } = 1$ и $b < 1,$ то есть

$r \geqslant \frac{{\frac{8}{e}({{M}_{2}} + {{{\left\| {{{f}_{1}}} \right\|}}_{{C([0,1])}}}) + \frac{P}{{{{S}_{0}}}}{\lambda }}}{{{\lambda } - \frac{8}{e}{{M}_{1}}}}$

в случае ${\lambda } > ({8 \mathord{\left/ {\vphantom {8 e}} \right. \kern-0em} e}){{M}_{1}};$

в) при ${\alpha } > 1$ в случае

${\lambda } > \max \left\{ {\frac{8}{e}({{M}_{2}} + {{{\left\| {{{f}_{1}}} \right\|}}_{{C([0,1])}}},\frac{{8{\alpha }{{M}_{1}}}}{e}{{{\left( {\frac{{\alpha }}{{{\alpha } - 1}}} \right)}}^{{\alpha }}}{{{\left( {1 + \frac{P}{{{{S}_{0}}}}} \right)}}^{{{\alpha } - 1}}}} \right\}$

Поскольку оператор $A:C([0,1]) \to C([0,1])$ является компактным, то по принципу неподвижной точки Шаудера [13] интегральное уравнение (2.3) имеет хотя бы одно непрерывное решение, которое, опираясь на результаты, изложенные в работе [10, стр. 175], будет принадлежать также классу $H.$

3. Единственность решения поставленной задачи. Теперь покажем, что если задача (1.1)–(1.6) имеет решение, то оно единственное.

Действительно, предположим, что задача допускает два решения ${{u}^{{(1)}}}(x,y)$ и ${{u}^{{(2)}}}$(x, y), граничные значения которых на границе пластинки $u_{0}^{{(j)}}(x) = {{u}^{{(j)}}}(x,0)$, с учетом условия контакта (1.6), удовлетворяют следующим соотношениям

$\frac{{du_{0}^{{(j)}}(x)}}{{dx}} = \frac{1}{E}g({{{\varphi }}_{j}}(x)),\quad \left| x \right| < 1$

${{{\varphi }}_{j}}(x) = \frac{1}{{{{S}_{0}}}}[P - d\int\limits_{ - 1}^x {{{{\tau }}_{j}}(t)dt - } \int\limits_{ - 1}^x {{{{\tau }}_{0}}(t)dt],} \quad j = 1,2$

где ${{{\tau }}_{1}}(x)$ и ${{{\tau }}_{2}}(x)$ – соответствующие искомые контактные напряжения. Разность этих решений $u(x,y) = {{u}^{{(1)}}}(x,y) - {{u}^{{(2)}}}(x,y)$ удовлетворяет основным уравнениям теории упругости при отсутствии внешних сил, а для ее граничного значения имеем

(3.1)

$E\frac{{du(x,0)}}{{dx}} = - \frac{d}{{{{S}_{0}}}}\left( {\int\limits_{ - 1}^x {{{{\tau }}^{0}}(t)dt} } \right)K(x)$

${{{\tau }}^{0}}(t) = {{{\tau }}_{1}}(t) - {{{\tau }}_{2}}(t)$, $K(x) = \int\limits_0^1 {g'[{{{\varphi }}_{1}}(x) + {\omega }({{{\varphi }}_{2}}(x) - {{{\varphi }}_{1}}(x)]d{\omega }} $

Как известно, согласно формуле Остроградского–Грина имеет место следующее соотношение [9]

(3.2)

$\int\limits_L {({{X}_{n}}u + {{Y}_{n}}v)dl = \iint\limits_S {({\lambda }{{{\theta }}^{2}} + 2{\mu }(e_{{xx}}^{2} + e_{{yy}}^{2} + e_{{zz}}^{2} + 2e_{{xy}}^{2}))}} dxdy$

где ${{X}_{n}},{{Y}_{n}},u,v$ – соответственно, компоненты внешних напряжений и смещений на границе$L$ пластинки, ${\theta } = {{e}_{{xx}}} + {{e}_{{yy}}} + {{e}_{{zz}}}$, а ${{e}_{{xx}}}$, ${{e}_{{yy}}}$, ${{e}_{{xy}}}$, ${{e}_{{zz}}}$ – компоненты деформации.

Учитывая (3.1), интеграл в левой части формулы (3.2) имеет вид

(3.3)

$\begin{gathered} \int\limits_L {({{X}_{n}}u + {{Y}_{n}}v)dl = } - \int\limits_{ - 1}^1 {{{{\tau }}^{0}}(t){{u}_{0}}(t)dt = - \int\limits_{ - 1}^1 {{{u}_{0}}(t)d\left( {\int\limits_{ - 1}^t {{{{\tau }}^{0}}(\eta )d\eta } } \right)} } = \\ - \;[{{u}_{0}}(t)\int\limits_{ - 1}^t {{{{\tau }}^{0}}(\eta )d\eta ]_{{ - 1}}^{1}} + \int\limits_{ - 1}^1 {u_{0}^{'}(t)\left( {\int\limits_{ - 1}^t {{{{\tau }}^{0}}(\eta )d\eta } } \right)} dt = - \frac{{{{S}_{0}}E}}{d}\int\limits_{ - 1}^1 {u_{0}^{{'2}}(t)\frac{{dt}}{{K(t)}}} \\ {{u}_{0}}(x) = u(x,0) \\ \end{gathered} $

Так как подинтегральная функция правой части формулы (3.2) представляет собой положительно определенную квадратичную форму, имея в виду представление (3.3), можно заключить, что если $g' > 0$, оба решения ${{u}^{{(1)}}}(x,y)$ и ${{u}^{{(2)}}}(x,y)$ дают одинаковые компоненты деформации и одинаковые компоненты напряжения. Это означает, что задача (1.1)–(1.6) имеет единственное решение.

4. Построение решения при помощи метода малого параметра. Уравнение (1.8) перепишем в виде

(4.1)

$\begin{gathered} {{{\lambda }}_{0}}g({\varphi }(x)) - \frac{1}{{\pi }}\int\limits_{ - 1}^1 {\frac{{{\varphi '}(t)dt}}{{t - x}}} = {{f}_{0}}(x),\quad {\text{|}}x{\text{|}} < 1 \\ {{{\lambda }}_{0}} = \frac{1}{{\lambda }},\quad {{f}_{0}}(x) = \frac{1}{{{\pi }{{S}_{0}}}}\int\limits_{ - 1}^1 {\frac{{{{{\tau }}_{0}}(t)dt}}{{t - x}}} \\ \end{gathered} $

Когда ${{\lambda }_{0}}$ является малым параметром, то есть материал стрингера является жестким, представим решение уравнения (4.1) в виде ряда по степеням малого параметра ${{\lambda }_{0}}$:

(4.2)

${\varphi }(x) = \sum\limits_{k = 0}^\infty {{\lambda }_{0}^{k}{{{\varphi }}_{k}}(x)} = {{{\varphi }}_{0}}(x) + {{{\lambda }}_{0}}{{{\varphi }}_{1}}(x) + {\lambda }_{0}^{2}{{{\varphi }}_{2}}(x) + {\lambda }_{0}^{3}{{{\varphi }}_{3}}(x) + O({\lambda }_{0}^{4}).$

В предположении, что функция $g$ является аналитической функцией, разлагающаяся в ряд Маклорена: $g(x) = \sum\limits_{k = 0}^\infty {\frac{{{{g}^{{(k)}}}(0)}}{{k!}}} {{x}^{k}}$ на всей действительной оси, будем иметь

(4.3)

$g({\varphi }(x)) = g(0) + \frac{{g'(0)}}{1}{\varphi }(x) + \frac{{g''(0)}}{{1 \cdot 2}}{{{\varphi }}^{2}}(x) + \frac{{g'''(0)}}{{1 \cdot 2 \cdot 3}}{{{\varphi }}^{3}}(x) + \cdot \cdot \cdot $.

Подставляя (4.2) и (4.3) в (4.1), приравнивая коэффициенты при одинаковых степенях ${{{\lambda }}_{0}}$, получим

$\frac{1}{{\pi }}\int\limits_{ - 1}^1 {\frac{{{\varphi }_{0}^{'}(t)dt}}{{t - x}}} = - {{f}_{0}}(x),\quad \left| x \right| < 1$

$\frac{1}{{\pi }}\int\limits_{ - 1}^1 {\frac{{{\varphi }_{1}^{'}(t)dt}}{{t - x}}} = g(0) + g'(0){{{\varphi }}_{0}}(x) + \frac{1}{2}g''(0){\varphi }_{0}^{2}(x) + \frac{1}{6}g'''(0){\varphi }_{0}^{3}(x),\quad \left| x \right| < 1$

$\frac{1}{{\pi }}\int\limits_{ - 1}^1 {\frac{{{\varphi }_{2}^{'}(t)dt}}{{t - x}}} = g'(0){{{\varphi }}_{1}}(x) + g''(0){\varphi }_{0}^{{}}(x){{{\varphi }}_{1}}(x) + \frac{1}{2}g'''(0){\varphi }_{0}^{2}(x){{{\varphi }}_{1}}(x),\quad \left| x \right| < 1$

$\begin{gathered} \frac{1}{{\pi }}\int\limits_{ - 1}^1 {\frac{{{\varphi }_{3}^{'}(t)dt}}{{t - x}}} = g'(0){{{\varphi }}_{2}}(x) + \frac{1}{2}g''(0){\varphi }_{{\text{1}}}^{{\text{2}}}(x) + g''(0){{{\varphi }}_{0}}(x){{{\varphi }}_{2}}(x) + \frac{1}{2}g'''(0){\varphi }_{0}^{{}}(x){\varphi }_{1}^{2}(x) \\ + \;\frac{1}{2}g'''(0){\varphi }_{0}^{2}(x){{{\varphi }}_{{\text{2}}}}(x),\quad \left| x \right| < 1 \\ \end{gathered} $

при условиях

(4.5)

${{{\varphi }}_{0}}( - 1) = {P \mathord{\left/ {\vphantom {P {{{S}_{0}}}}} \right. \kern-0em} {{{S}_{0}}}},\quad {{{\varphi }}_{0}}(1) = 0$

(4.6)

${{{\varphi }}_{k}}( - 1) = 0,\quad {{{\varphi }}_{k}}(1) = \begin{array}{*{20}{c}} {0,}&{\quad k \geqslant 1} \end{array}$

Таким образом, решение уравнения (1.8) при условии (1.9) сводится к решению системы рекуррентных линейных сингулярных интегральных уравнений (4.4) первого рода при условиях (4.5) и (4.6). Решения каждого из этих уравнений с учетом (4.5), (4.6) представляются в явном виде с применением формулы обращения интеграла типа Коши [10, 11] в классе функций, неограниченных на обеих концах линии интегрирования.

В качестве примера рассмотрим случай $g(u) = {{u}^{2}}.$ Тогда система рекуррентных уравнений (4.4) принимает вид:

$L{{{\varphi }}_{0}}(x) = - {{f}_{0}}(x),$

откуда в силу (2.2) и (4.5):

${{{\varphi }}_{0}}(x) = \frac{1}{{2{\pi }}}\int\limits_{ - 1}^1 {\ln } \frac{{1 - tx + \sqrt {(1 - {{t}^{2}})(1 - {{x}^{2}})} }}{{1 - x - \sqrt {(1 - {{t}^{2}})(1 - {{x}^{2}})} }}{{f}_{0}}(t)dt - \frac{P}{{{\pi }{{S}_{0}}}}\arcsin x + \frac{P}{{2{{S}_{0}}}}$

$L{{{\varphi }}_{1}}(x) = {\varphi }_{0}^{2}(x)$

$L{{{\varphi }}_{2}}(x) = 2{{{\varphi }}_{0}}(x){{{\varphi }}_{1}}(x)$

$L{{{\varphi }}_{3}}(x) = 2{{{\varphi }}_{0}}(x){{{\varphi }}_{2}}(x) + {\varphi }_{1}^{2}(x)$

$L{{{\varphi }}_{4}}(x) = 2{{{\varphi }}_{0}}(x){{{\varphi }}_{3}}(x) + 2{{{\varphi }}_{1}}(x){{{\varphi }}_{2}}(x)...$

(4.7)

$L{{{\varphi }}_{k}}(x) = \sum\limits_{i + j = k - 1}^{} {} {{{\varphi }}_{i}}(x){{{\varphi }}_{j}}(x),\begin{array}{*{20}{c}} {}&{\left| x \right| < 1} \end{array}...$

$L{\psi }(x) = \frac{1}{{\pi }}\int\limits_{ - 1}^1 {\frac{{{\psi '}(t)dt}}{{t - x}}} $

Из (4.7) следует, что ${{\left\| {{{{\varphi }}_{n}}} \right\|}_{C}} \leqslant {{4}^{{n - 1}}}{\text{||}}{{L}^{{ - 1}}}{\text{||}}_{{H{\text{*}} \to C}}^{{2n + 1}}\left\| {{{f}_{0}}} \right\|_{{H{\text{*}}}}^{{n + 1}},$ и ряд (4.2) сходится при условии

(4.8)

${{{\lambda }}_{0}} \leqslant \frac{{\delta }}{{4{\text{||}}{{L}^{{ - 1}}}{\text{|}}{{{\text{|}}}^{2}}\left\| {{{f}_{0}}} \right\|}},\quad 0 < {\delta } = {\text{const}} < 1$

Заключение. Для нелинейных дифференциальных уравнений нам известна общая теорема Пуанкаре [14] о разложении решения по степеням малого параметра. Для нелинейного интегрального уравнения вида (4.1) при конкретных нелинейных функциях $g$ из достаточно широкого класса функций можно получить условие вида (4.8) относительно малого параметра ${{{\lambda }}_{0}}$, при котором ряд (4.2) сходится. Соответственно, решение уравнении (4.1) при условиях (1.9) можно построить в виде ряда (4.2).

Работа выполнена при финансовой поддержке национального научного фонда им. Ш. Руставели (грант № FR/86/5-109/14).

Фиг. 1

Список литературы

Александров В.М., Мхитарян С.М. Контактные задачи для тел с тонкими покрытиями и прослойками. М.: Наука, 1983. 487 с.
Банцури Р.Д. Контактная задача для анизотропного клина с упругим креплением // Докл. АН СССР. 1975. Т. 222. № 3. С. 568–571.
Нуллер Б.М. О деформации упругой клиновидной пластинки, подкрепленной стержнем переменной жесткости и об одном методе решения смешанных задач // ПММ. 1976. Т. 40. Вып. 2. С. 306–316.
Саркисян В.С. Некоторые задачи математической теории упругости анизотропного тела. Ереван: ЕГУ, 1983. 534 с.
Shavlakadze N. The contact problems of the mathematical theory of elasticity for plates with an elastic inclusion // Acta Appl. Math. 2007. V. 99. № 1. P. 29–51.
Банцури Р.Д., Шавлакадзе Н.Н. Контактная задача для кусочно-однородной плоскости с конечным включением // ПММ. 2011. Т. 75. Вып. 1. С. 133–139.
Bantsuri R., Shavlakadze N. The boundary-contact problems electroelasticity for piezo-electric plate with inclusion and half space with cut. (Russian) Prikl. Mat. i Mech. 78, 2014. № 4. P. 583–594. Eng. Transl // J. Appl. Math. Mech. 78, 2014. № 4. P. 93–97.
Shavlakadze N. The effective solution of two–dimensional integro-differential equations and their applications in the theory of viscoelasticity // J. of Appl. Mathem. and Mechs. ZAMM. Z. Angew. Math. Mech. 1–10, 2015. https://doi.org/10.1002/zamm.201400091
Мусхелишвили Н.И. Некоторые основные задачи математической теории упругости. М.: Наука, 1966. 707 с.
Мусхелишвили Н.И. Сингулярные интегральные уравнения. М.: Наука, 1968. 511 с.
Гахов Ф.Д. Краевые задачи. Изд. физ. мат. лит. 1963. 487 с.
Краснов М.Л. Интегральные уравнения. М.: Наука. 1975.
Треногин В.А. Функциональный анализ. М.: Наука, 1980. 495 с.
Голубев В.В. Лекции по аналитической теории дифференциальных уравнении. Изд. технико-теорет. лит. 1950. 436 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал