Известия РАН. Механика твердого тела, 2019, № 2, стр. 126-139
О РЕШЕНИИ ОДНОЙ СМЕШАННОЙ ГРАНИЧНОЙ ЗАДАЧИ НЕЛИНЕЙНОЙ ТЕОРИИ ПОЛЗУЧЕСТИ
С. М. Мхитарян *
Институт механики НАН Армении
Ереван, Армения
* E-mail: smkhitaryan39@rambler.ru
Поступила в редакцию 26.10.2017
После доработки 15.10.2018
Принята к публикации 19.10.2018
Аннотация
При антиплоской деформации рассматривается одна смешанная граничная задача нелинейной теории установившейся ползучести (НТУП) при степенном законе связи между напряжениями и скоростями деформаций для полупространства, когда на одной части его граничной плоскости заданы скорости деформаций, а на остальной части касательные напряжения равны нулю. Построено замкнутое решение задачи. Для сравнительного анализа построено также ее приближенное решение. Рассмотрен частный случай.
Введение. В работах [1, 2] в постановке НТУП при степенной зависимости между интенсивностями напряжений и скоростей деформаций или в постановке деформационной теории пластичности со степенным упрочнением материала исследована плоская контактная задача о сжатии двух тел. При этом, исходя из точного решения обобщенной задачи Фламана в перемещениях, в указанных работах для определения зависимости перемещений или скоростей деформаций граничных точек деформируемых полуплоскостей, которыми заменяются сжимаемые тела, от распределенных нормальных сил применяется обобщенный принцип суперпозиции перемещений (ОПСП) или скоростей деформаций. Некоторые оценки точности этого принципа приведены в [3]. Оценке ОПСП посвящены также работы [4, 5], причем в [5] проведен сравнительный анализ точного решения нелинейной контактной задачи о взаимодействии штампа с плоским основанием с полупространством при антиплоской деформации, полученного методом годографа, с приближенным решением этой же задачи по ОПСП. Метод годографа, приводящий к линейному дифференциальному уравнению для потенциала в плоскости деформаций, применительно к задачам о трещинах предложен в [6]. Метод годографа позволяет получить неограниченные на концах характерного интервала решения рассматриваемых нелинейных по степенному закону граничных задач. Другой подход к линеаризации, основанный на введении функции псевдонапряжений в плоской задаче при степенном законе, развит в [7]. Метод функции псевдонапряжений позволяет получить только ограниченные на концах интервала решения таких задач. Оба метода вместе расширяют возможности исследования граничных задач НТУП при степенном законе. В нелинейных по степенному закону задачах при антиплоской деформации функция псевдонапряжений введена в работе [8], там же этим методом построено точное решение первой граничной задачи НТУП для полупространства при антиплоской деформации. Отметим еще, что многие результаты по исследованию контактных и смешанных задач подытожены в [9, 10].
Степенным законом между напряжениями и скоростями деформаций, известным как закон Глена, адекватно описывается механическое поведение морских льдов и покровов, ледников, мерзлых грунтов и других материалов. Теоретическому и экспериментальному обоснованию и обобщению закона Глена посвящены многочисленные исследования. В этом направлении из новых исследований укажем на работы [11–13].
В настоящей статье на основании результатов работы [8] построено замкнутое ограниченное на концах интервала решение смешанной граничной задачи НТУП при степенной зависимости между напряжениями и скоростями деформаций для полупространства при антиплоской деформации, когда на полосе граничной плоскости полупространства заданы скорости деформаций, а вне полосы на остальной части границы касательные напряжения равны нулю. Решение этой задачи, как в [8], сводится к решению нелинейного сингулярного интегрального уравнения (НСИУ). Для сравнительного анализа эта же задача решается также на основании ОПСП. Рассмотрен частный случай, когда на полосе скорости деформации заданы параболическим законом.
1. Постановка задачи и вывод основных уравнений. Пусть отнесенное к правой прямоугольной системе координат $0xyz$ полупространство $y < 0$ находится в условиях установившейся ползучести при антиплоской деформации в направлении оси $0z$ с базовой плоскостью $0xy.$ Для материала полупространства примем степенной физический закон [14, 15]:
(1.1)
$\begin{gathered} {{{\tau }}_{{xz}}} = \frac{{{\rm T}\left( \Gamma \right)}}{\Gamma }{{{\gamma }}_{{xz}}},\quad {{{\tau }}_{{yz}}} = \frac{{{\rm T}\left( \Gamma \right)}}{\Gamma }{{{\gamma }}_{{yz}}},\quad {\rm T} = {\rm T}\left( \Gamma \right) = {{K}_{0}}{{\Gamma }^{m}} \\ \left( {{{K}_{0}} > 0,0 < m \leqslant 1} \right),\quad {\rm T} = \sqrt {{\tau }_{{xz}}^{2} + {\tau }_{{yz}}^{2}} ,\quad \Gamma = \sqrt {{\gamma }_{{xz}}^{2} + {\gamma }_{{yz}}^{2}} \\ {{{\gamma }}_{{xz}}} = {{\partial w} \mathord{\left/ {\vphantom {{\partial w} {\partial x}}} \right. \kern-0em} {\partial x}},\quad {{{\gamma }}_{{yz}}} = {{\partial w} \mathord{\left/ {\vphantom {{\partial w} {\partial y}}} \right. \kern-0em} {\partial y}} \\ \end{gathered} $Здесь ${\rm T}$ и $\Gamma $ – интенсивности касательных напряжений и скоростей деформаций, соответственно, K0 – физическая постоянная материала полупространства, m – показатель ползучести, ${{{\tau }}_{{xz}}}$ и ${{{\tau }}_{{yz}}}$ – компоненты касательных напряжений, ${{{\gamma }}_{{xz}}}$ и ${{{\gamma }}_{{yz}}}$ – компоненты скоростей деформаций, а $w = w\left( {x,y} \right)$ – единственная отличная от нуля компонента скорости в направлении оси $0z$ при антиплоской деформации.
Для полупространства $y < 0$ или для базовой полуплоскости Π– = $\{ - \infty < x < \infty ;\, - {\kern 1pt} \infty $ < < y < 0}, подчиняющихся степенному закону (1.1), ставим следующую граничную задачу:
(1.2)
$\left\{ \begin{gathered} {{\left. {w(x,y)} \right|}_{{y = - 0}}} = f(x) - {\delta }\,\,(x \in L),\quad {{\left. {{{{\tau }}_{{yz}}}} \right|}_{{y = - 0}}} = 0\quad (x \in L';L' = \{ y = 0;\left| x \right| \geqslant a\} = R{\backslash }L) \hfill \\ w\left( {x,y} \right) \to 0\quad {\text{п р и }}\quad {{x}^{2}} + {{y}^{2}} \to \infty ,\quad L = \left\{ {y = 0; - a \leqslant x \leqslant a} \right\} \hfill \\ \end{gathered} \right.$Здесь $f\left( x \right)$ $\left( {x \in \left[ { - a,a} \right]} \right)$ – заданная достаточно гладкая функция, ${\delta }$ – абсолютная величина жесткой составляющей компоненты скорости в отрицательном направлении оси $0z$, подлежащая определению, $L$ – след полосы ω = {y = 0; $ - a \leqslant x \leqslant a; - \infty < z < \infty \} $ на замкнутой полуплоскости ${{\bar {\Pi }}_{ - }} = \left\{ { - \infty < x < \infty ,y \leqslant 0} \right\}$.
Граничная задача (1.2) должна быть дополнена условием
где ${\rm T}$ – наперед заданная величина, а ${\tau }\left( x \right)$ – неизвестные на $L$ касательные напряжения с обратным знаком: ${{\left. {{{{\tau }}_{{yz}}}} \right|}_{{y = - 0}}} = - {\tau }(x)\,\,\,(x \in [ - a,a]).$Решение задачи (1.2)–(1.3) сведем к решению НСИУ. С этой целью воспользуемся результатами работы [8], где исходя из уравнения равновесия введена функция напряжений $\Phi \left( {x,y} \right)$ и сделан переход к комплексным числам $z = x + iy,$ $\bar {z} = x - iy$. Предполагается, что функция $\Phi \left( {x,y} \right)$, как в [8], вместе со своими частными производными до второго порядка включительно непрерывна в замкнутой полуплоскости. Далее введем функцию псевдонапряжений $\Lambda \left( {x,y} \right) = \,\Lambda \left( {z,\bar {z}} \right)$ [8] и ключевую функцию:
(1.4)
$w\left( {x, - 0} \right) = - \frac{{K\left( m \right)}}{2}\int\limits_{ - \infty }^\infty {{\text{sign}}\left( {x - u} \right)} {\varphi }\left( u \right)du\quad \left( { - \infty < x < \infty } \right),\quad K\left( m \right) = \frac{1}{2}{{\left( {{2 \mathord{\left/ {\vphantom {2 {{{K}_{0}}}}} \right. \kern-0em} {{{K}_{0}}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 m}} \right. \kern-0em} m}}}}$(1.5)
$\frac{{dw\left( {x, - 0} \right)}}{{dx}} = - K\left( m \right){\varphi }\left( x \right)\quad \left( { - \infty < x < \infty } \right)$(1.6)
${\varphi }\left( x \right) = \frac{{{{2}^{{{{\left( {m - 1} \right)} \mathord{\left/ {\vphantom {{\left( {m - 1} \right)} m}} \right. \kern-0em} m}}}}}}{{\pi }}\int\limits_{ - a}^a {\frac{{{\tau }\left( u \right)du}}{{u - x}}} {{\left\{ {{{{\tau }}^{2}}\left( x \right) + {{{\left[ {\frac{1}{\pi }\int\limits_{ - a}^a {\frac{{{\tau }\left( u \right)du}}{{u - x}}} } \right]}}^{2}}} \right\}}^{{{{\left( {1 - m} \right)} \mathord{\left/ {\vphantom {{\left( {1 - m} \right)} {\left( {2m} \right)}}} \right. \kern-0em} {\left( {2m} \right)}}}}}$Теперь при помощи (1.5)–(1.6) реализуем первое граничное условие из (1.2), предварительно продифференцировав это условие по $x$. В результате придем к следующему определяющему НСИУ:
(1.7)
$\frac{1}{{\pi }}\int\limits_{ - a}^a {\frac{{{\tau }\left( s \right)ds}}{{s - x}}} {{\left\{ {{{{\tau }}^{2}}\left( x \right) + {{{\left[ {\frac{1}{{\pi }}\int\limits_{ - a}^a {\frac{{{\tau }\left( s \right)ds}}{{s - x}}} } \right]}}^{2}}} \right\}}^{{{{\left( {1 - m} \right)} \mathord{\left/ {\vphantom {{\left( {1 - m} \right)} {\left( {2m} \right)}}} \right. \kern-0em} {\left( {2m} \right)}}}}} = - \frac{{{{2}^{{{{\left( {1 - m} \right)} \mathord{\left/ {\vphantom {{\left( {1 - m} \right)} m}} \right. \kern-0em} m}}}}}}{{K\left( m \right)}}f'\left( x \right)\quad \left( { - a < x < a} \right)$Решение НСИУ должно удовлетворять условию (1.3).
2. Решение определяющего НСИУ (1.7). В соответствии с функциональными свойствами функций $\Phi \left( {x,y} \right)$ и $\Lambda \left( {x,y} \right)$ необходимо построить ограниченное на концах интервала (–a, a) решение НСИУ (1.7). Поступив совершенно аналогично сделанному в [8] и воспользовавшись известным методом нахождения ограниченного решения краевой задачи Римана [16], искомое решение (1.7) можем представить в форме
(2.1)
${\tau }(x) = \frac{{2\sqrt {{{a}^{2}} - {{x}^{2}}} }}{{{\pi }{{{\left[ {2K(m)} \right]}}^{m}}}}{\kern 1pt} {\kern 1pt} \int\limits_{ - a}^a {\frac{{f'\left( s \right)ds}}{{\sqrt {{{a}^{2}} - {{s}^{2}}} (s - x)}}} {{\left\{ {{{{\left[ {f'(x)} \right]}}^{2}} + \left. {\frac{{{{a}^{2}} - {{x}^{2}}}}{{{{{\pi }}^{2}}}}{{{\left[ {\int\limits_{ - a}^a {\frac{{f'(s)ds}}{{s - x}}} } \right]}}^{2}}} \right\}} \right.}^{{\frac{{m - 1}}{2}}}}\quad \left( {\left| x \right| \leqslant a} \right)$Рассмотрим важный частный случай когда $f\left( x \right) = {\rm A}{{x}^{2}}$ $\left( {{\rm A} > 0} \right)$. Очевидно, что в этом случае условие (2.2) удовлетворяется автоматически, а из (2.1) после элементарных вычислений находим
(2.3)
${\tau }\left( x \right) = \left( {{2 \mathord{\left/ {\vphantom {2 a}} \right. \kern-0em} a}} \right){{\left[ {{{a{\rm A}} \mathord{\left/ {\vphantom {{a{\rm A}} {K\left( m \right)}}} \right. \kern-0em} {K\left( m \right)}}} \right]}^{m}}\sqrt {{{a}^{2}} - {{x}^{2}}} \quad \left( { - a \leqslant x \leqslant a} \right)$Подставляя теперь (2.3) в условие (1.3), придем к соотношению
(2.4)
${{\left[ {{{a{\rm A}} \mathord{\left/ {\vphantom {{a{\rm A}} {K\left( m \right)}}} \right. \kern-0em} {K\left( m \right)}}} \right]}^{m}} = {{\rm T} \mathord{\left/ {\vphantom {{\rm T} {\left( {{\pi }a} \right)}}} \right. \kern-0em} {\left( {{\pi }a} \right)}}$Отметим, что в рассматриваемом частном случае для линейно-упругого полупространства, когда m = 1, НСИУ (1.7) переходит в линейное СИУ, которое после замены в нем упругой константы ${{K}_{0}} = G$ ($G$ – модуль сдвига материала полупространства) на соответствующую упругую константу, совпадает с СИУ линейной плоской контактной задачи о вдавливании жесткого штампа с параболическим основанием в упругую полуплоскость [17]. Оказывается, и это важно подчеркнуть, что в разбираемом частном случае эпюры распределений касательных напряжений с обратным знаком (2.3) в обсуждаемой нелинейной смешанной граничной задаче (1.2)–(1.3) и в указанной линейной контактной задаче представляют собой подобные эллипсы. Кроме того, получающаяся из (2.4) при m = 1 формула для a после идентификации соответствующих обозначений совпадает с формулой для полудлины контактного участка в линейной плоской контактной задаче [17].
Несколько подробнее остановимся на вопросе подобия, когда распределения касательных напряжений в любой точке отрезка [–a, a] в указанных линейной и нелинейной задачах пропорциональны между собой. Исходя из (1.5)–(1.7) можно утверждать, что для того чтобы имело место такое подобие необходимо и достаточно, чтобы выполнялось условие
(2.5)
${{{\tau }}^{2}}\left( x \right) + {{\left[ {\frac{1}{{\pi }}\int\limits_{ - a}^a {\frac{{{\tau }\left( s \right)ds}}{{s - x}}} } \right]}^{2}} = C = {\text{const}},\quad x \in \left[ { - a,a} \right]$(2.6)
$F\left( z \right) = \frac{1}{{2{\pi }i}}\int\limits_{ - a}^a {\frac{{{\tau }\left( s \right)ds}}{{s - z}}} \quad \left( {z = x + iy} \right)$Отсюда по формулам Сохоцкого–Племеля для граничных значений ${{F}^{ \pm }}\left( x \right)$ будем иметь
(2.7)
${{F}^{ + }}\left( x \right) = \frac{1}{2}{\tau }\left( x \right) + \frac{1}{{2{\pi }i}}\int\limits_{ - a}^a {\frac{{{\tau }\left( s \right)ds}}{{s - x}}} ,\quad {{F}^{ - }}\left( x \right) = - \frac{1}{2}{\tau }\left( x \right) + \frac{1}{{2{\pi }i}}\int\limits_{ - a}^a {\frac{{{\tau }\left( s \right)ds}}{{s - x}}} \quad \left( {\left| x \right| \leqslant a} \right)$Так как здесь ${\tau }\left( { \pm a} \right) = 0,$ то граничные значения ${{F}^{ \pm }}\left( x \right)$ существуют также в концевых точках отрезка [–a, a] [16] (стр. 246–247), причем
Из (2.7) очевидно, что
(2.8)
${{F}^{ - }}\left( x \right) = - \overline {{{F}^{ + }}\left( x \right)} \quad \left( { - a \leqslant x \leqslant a} \right)$Теперь перемножением равенств (2.7) для определения функции F(z) получим следующую граничную задачу:
(2.9)
${{F}^{ + }}\left( x \right){{F}^{ - }}\left( x \right) = {{\left[ {F\left( a \right)} \right]}^{2}}\quad \left( { - a \leqslant x \leqslant a} \right),\quad C = - 4{{\left[ {F\left( a \right)} \right]}^{2}} = - 4{{\left[ {F\left( { - a} \right)} \right]}^{2}}$Таким образом, введенная кусочно голоморфная функция (2.6) обладает свойствами:
1) функция F(z) голоморфна во всей комплексной плоскости $z = x + iy,$ разрезанной по отрезку [–a, a] вещественной оси;
2) функция F(z) в любой точке этой области конечна и отлична от нуля;
3) на разрезе [–a, a] ее граничные значения удовлетворяют соотношению (2.9);
4) согласно условию (1.3) функция F(z) на бесконечности обладает асимптотическим поведением
(2.10)
${{F}^{ + }}\left( z \right) \sim - \frac{T}{{2{\pi }iz}}\quad \left( {z \to \infty } \right)$Далее введем функцию
(2.11)
${{\Omega }^{ + }}\left( x \right){{\Omega }^{ - }}\left( x \right) = 1\quad \left( { - a \leqslant x \leqslant a} \right)$При этом согласно (2.8):
(2.12)
${\text{|}}{{\Omega }^{ + }}(x)\,{{{\text{|}}}^{2}} = {\text{|}}{{\Omega }^{ - }}(x){{{\text{|}}}^{2}} = 1,\quad {{\Omega }^{ + }}(x) = {1 \mathord{\left/ {\vphantom {1 {\overline {{{\Omega }^{ + }}(x)} }}} \right. \kern-0em} {\overline {{{\Omega }^{ + }}(x)} }}\quad \left( { - a \leqslant x \leqslant a} \right)$Но свойствами (2.12) обладают только точки единичной окружности с центром в начале координат комплексной плоскости ${\zeta } = u + i{\text{v}} = \Omega \left( z \right).$ Кроме того, функция Ω(z) обладает всеми перечисленными выше 1)–4) свойствами функции F(z), только вместо (2.10) имеет асимптотику
(2.13)
$\Omega \left( z \right) \sim - \frac{T}{{2{\pi }iF\left( a \right)z}}\quad \left( {z \to \infty } \right)$Следовательно, функция ${\zeta } = \Omega \left( z \right)$ всю комплексную плоскость $z = x + iy,$ разрезанную по отрезку [–a, a] вещественной оси, конформно отображает на единичный круг с центром в начале координат комплексной плоскости ${\zeta } = u + i{\text{v}}.$ Но по известной теореме Римана из теории конформных отображений такая функция единственная. Поэтому она должна совпадать с той однозначной ветвью обратной к функции Жуковского
которая согласно (2.13) исчезает на бесконечности. В итоге(2.14)
$\Omega \left( z \right) = {{(z - \sqrt {{{z}^{2}} - {{a}^{2}}} )} \mathord{\left/ {\vphantom {{(z - \sqrt {{{z}^{2}} - {{a}^{2}}} )} z}} \right. \kern-0em} z}$Для этой ветви
(2.15)
${{\Omega }^{ \pm }}\left( x \right) = \frac{1}{a}(x \mp i\sqrt {{{a}^{2}} - {{x}^{2}}} )\quad \left( {z \to x \pm i0, - a \leqslant x \leqslant a} \right),\quad \Omega \left( z \right) \sim \frac{a}{{2z}}\quad \left( {z \to \infty } \right)$Из (2.13) и (2.15) вытекает, что ${{\Omega }^{ \pm }}\left( x \right)$ удовлетворяют соотношению (2.11) и
(2.16)
$F\left( a \right) = {{iT} \mathord{\left/ {\vphantom {{iT} {\left( {{\pi }a} \right)}}} \right. \kern-0em} {\left( {{\pi }a} \right)}}\quad (C = {{4{{T}^{2}}} \mathord{\left/ {\vphantom {{4{{T}^{2}}} {({{{\pi }}^{2}}{{a}^{2}})}}} \right. \kern-0em} {({{{\pi }}^{2}}{{a}^{2}})}})$Теперь из (2.14) и (2.16) окончательно находим
Далее при помощи (2.17) и (2.15) из (2.7) находим решение исходного НСИУ (2.5):
(2.18)
${\tau }\left( x \right) = {{F}^{ + }}\left( x \right) - {{F}^{ - }}\left( x \right) = \frac{{2T}}{{{\pi }{{a}^{2}}}}\sqrt {{{a}^{2}} - {{x}^{2}}} \quad \left( { - a \leqslant x \leqslant a} \right)$Исходя из (1.7), (2.5) и (2.18), вычислим также функцию $f'(x){\text{:}}$
Отсюда, как и следовало ожидать
где снова учтено соотношение (2.4).Теперь обратно, пусть распределения касательных напряжений в линейной $\left( {{{{\tau }}_{1}}\left( x \right)} \right)$ и нелинейной $\left( {{{{\tau }}_{2}}\left( x \right)} \right)$ задачах подобны, т.е. ${{{\tau }}_{2}}\left( x \right) = q{{{\tau }}_{1}}\left( x \right)$ $\left( {q = {\text{const}}, - a \leqslant x \leqslant a} \right)$, где q – коэффициент подобия. Эти функции согласно (1.7) удовлетворяют следующим СИУ:
(2.20)
$\begin{gathered} {\tau }_{1}^{2}\left( x \right) + {{\left[ {\frac{1}{{\pi }}\int\limits_{ - a}^a {\frac{{{{{\tau }}_{1}}\left( s \right)ds}}{{s - x}}} } \right]}^{2}} = C\quad \left( { - a \leqslant x \leqslant a} \right) \\ C = \frac{4}{{{{q}^{{{2 \mathord{\left/ {\vphantom {2 {\left( {1 - m} \right)}}} \right. \kern-0em} {\left( {1 - m} \right)}}}}}}}{{\left[ {\frac{{K\left( 1 \right)}}{{K\left( m \right)}}} \right]}^{{{{2m} \mathord{\left/ {\vphantom {{2m} {\left( {1 - m} \right)}}} \right. \kern-0em} {\left( {1 - m} \right)}}}}},\quad q = \frac{{K\left( 1 \right)}}{{{{{\left( {aA} \right)}}^{{1 - m}}}{{{\left[ {K\left( m \right)} \right]}}^{m}}}} \\ \end{gathered} $Далее в (2.3) и (2.4) введем безразмерные величины
В результате формула (2.3) примет вид
(2.21)
${\tau }_{0}^{{\left( m \right)}}\left( {\xi } \right) = {{(2{\rm A}_{0}^{{\left( m \right)}})}^{{1 - {\mu }}}}\sqrt {1 - {{{\xi }}^{2}}} \quad \left( { - 1 \leqslant {\xi } \leqslant 1,\;{\mu } = 1 - m} \right)$(2.22)
${\rm A}_{0}^{{\left( m \right)}} = {{({{2}^{{\mu }}}{{S}_{0}})}^{{{1 \mathord{\left/ {\vphantom {1 {\left( {2 - {\mu }} \right)}}} \right. \kern-0em} {\left( {2 - {\mu }} \right)}}}}}\quad \left( {0 \leqslant {\mu } < 1} \right)$Теперь рассмотрим вопрос определения параметра δ. С этой целью сначала при помощи (2.3) по формуле (1.6) вычислим ключевую функцию ${\varphi }\left( x \right)$. При этом будем считать, согласно постановке задачи, ${\tau }\left( x \right) = 0$ при $\left| x \right| \geqslant a$. Воспользовавшись выражением известного интеграла из [18] (стр.175, ф-лы (19)), находим
(2.23)
$\varphi \left( x \right) = \left\{ \begin{gathered} - {{({{2{\rm T}} \mathord{\left/ {\vphantom {{2{\rm T}} {({\pi }{{a}^{2}})}}} \right. \kern-0em} {({\pi }{{a}^{2}})}})}^{{{1 \mathord{\left/ {\vphantom {1 m}} \right. \kern-0em} m}}}}{{\left( {{{\rm T} \mathord{\left/ {\vphantom {{\rm T} {\left( {{\pi }a} \right)}}} \right. \kern-0em} {\left( {{\pi }a} \right)}}} \right)}^{{{{\left( {1 - m} \right)} \mathord{\left/ {\vphantom {{\left( {1 - m} \right)} m}} \right. \kern-0em} m}}}}x\quad \left( {\left| x \right| \leqslant a} \right) \hfill \\ - {{({{2{\rm T}} \mathord{\left/ {\vphantom {{2{\rm T}} {({\pi }{{a}^{2}})}}} \right. \kern-0em} {({\pi }{{a}^{2}})}})}^{{{1 \mathord{\left/ {\vphantom {1 m}} \right. \kern-0em} m}}}}{{2}^{{^{{{{\left( {m - 1} \right)} \mathord{\left/ {\vphantom {{\left( {m - 1} \right)} m}} \right. \kern-0em} m}}}}}}{\text{sign}}x{\text{|sign}}x\sqrt {{{x}^{2}} - {{a}^{2}}} - x{{{\text{|}}}^{{{1 \mathord{\left/ {\vphantom {1 m}} \right. \kern-0em} m}}}}\quad \left( {\left| x \right| \geqslant a} \right) \hfill \\ \end{gathered} \right.$Далее формулу (1.4) представим в форме
(2.24)
$\begin{gathered} w_{0}^{{\left( m \right)}}\left( {{\xi }, - 0} \right) = {\rm A}_{0}^{{\left( m \right)}}{{{\xi }}^{2}} - {\delta }_{0}^{{\left( m \right)}}\quad \left( {{\xi } = {x \mathord{\left/ {\vphantom {x a}} \right. \kern-0em} a}, - 1 \leqslant {\xi } \leqslant 1} \right),\quad w_{0}^{{\left( m \right)}}\left( {{\xi }, - 0} \right) = w{{\left( {a{\xi }, - 0} \right)} \mathord{\left/ {\vphantom {{\left( {a{\xi }, - 0} \right)} a}} \right. \kern-0em} a} \\ {\delta }_{0}^{{\left( m \right)}} = {{\delta } \mathord{\left/ {\vphantom {{\delta } a}} \right. \kern-0em} a} = {\rm A}_{0}^{{\left( m \right)}}\frac{{1 + {{m}^{2}}}}{{1 - {{m}^{2}}}} = {\rm A}_{0}^{{\left( m \right)}}\frac{{{{{\mu }}^{2}} - 2{\mu } + 2}}{{{\mu }\left( {2 - {\mu }} \right)}}\quad \left( {{\mu } = 1 - m} \right) \\ \end{gathered} $Таким образом, в рассматриваемом частном случае точные выражения основных величин поставленной нелинейной смешанной граничной задачи в безразмерной форме выражаются формулами (2.21)–(2.22) и (2.24).
3. Решение нелинейной смешанной граничной задачи по ОПСП. Методом ОПСП построим также приближенное решение рассматриваемой нелинейной смешанной задачи. Для получения основных уравнений сначала найдем решение задачи типа Фламана для нелинейного по степенному закону полупространства при антиплоской деформации, когда на границе полупространства в начале координат по отрицательному направлению оси 0z действует касательная сосредоточенная сила Q. С этой целью в формулу
(3.1)
$ - w\left( {x, - 0} \right) = {{\left( {\frac{Q}{{\pi }}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 m}} \right. \kern-0em} m}}}}K\left( m \right){{2}^{{{{\left( {m - 1} \right)} \mathord{\left/ {\vphantom {{\left( {m - 1} \right)} m}} \right. \kern-0em} m}}}}\frac{m}{{1 - m}}{{\left| x \right|}^{{{{\left( {m - 1} \right)} \mathord{\left/ {\vphantom {{\left( {m - 1} \right)} m}} \right. \kern-0em} m}}}}\quad \left( { - \infty < x < \infty } \right)$Отсюда, вводя, как в [1, 2], обобщенные перемещения $\left( {w\left( {x, - 0} \right) < 0} \right)$ или скорости ${{w}_{{о б }}} = {{[ - w(x, - 0)]}^{m}},$ из (3.1) будем иметь
(3.2)
${{w}_{{о б }}} = \frac{Q}{{\pi }}{{\left[ {\frac{{K\left( m \right)m}}{{1 - m}}} \right]}^{m}}{{2}^{{m - 1}}}{{\left| x \right|}^{{m - 1}}}\quad \left( { - \infty < x < \infty } \right)$Теперь, исходя из (3.2), для распределенных касательных сил интенсивности ${\tau }\left( x \right)$, опять как в [1, 2], применим обычный линейный принцип суперпозиции, а затем вернемся к $w\left( {x, - 0} \right)$. В итоге получим
(3.3)
$ - w\left( {x, - 0} \right) = {{\left[ {\frac{{{\rm H}\left( m \right)}}{{\pi }}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 m}} \right. \kern-0em} m}}}}{{\left[ {\int\limits_{ - a}^a {\frac{{{\tau }\left( s \right)ds}}{{{{{\left| {x - s} \right|}}^{{1 - m}}}}}} } \right]}^{{{1 \mathord{\left/ {\vphantom {1 m}} \right. \kern-0em} m}}}}\quad \left( { - \infty < x < \infty } \right),\quad {\rm H}\left( m \right) = \frac{1}{{{{K}_{0}}}}{{\left( {\frac{m}{{1 - m}}} \right)}^{m}}$Далее при помощи (3.3) реализуем первое условие граничной задачи (1.2). В результате после простых преобразований относительно ${\tau }\left( x \right)$ придем к интегральному уравнению (ИУ) Карлемана:
(3.4)
$\frac{{{\rm H}\left( m \right)}}{{\pi }}\int\limits_{ - a}^a {\frac{{{\tau }\left( s \right)ds}}{{{{{\left| {x - s} \right|}}^{{1 - m}}}}}} = {{\left[ {{\delta } - f\left( x \right)} \right]}^{m}}\quad \left( { - a < x < a} \right)$Решение этого уравнения должно удовлетворять условию (1.3). При предельном переходе $m \to 1$ ИУ (3.4) с точностью до упругой константы перейдет в ИУ линейной плоской контактной задачи о вдавливании жесткого штампа, основание которого характеризуется функцией f(x), в упругую полуплоскость [17]:
В ИУ (3.4) и в условии (1.3) перейдем к безразмерным величинам, полагая
В результате они перейдут соответственно в ИУ
(3.5)
$\begin{gathered} \frac{1}{{\pi }}\int\limits_{ - 1}^1 {\frac{{{{{\tau }}_{0}}\left( {\eta } \right)d{\eta }}}{{{{{\left| {{\xi } - {\eta }} \right|}}^{{\mu }}}}}} = {{g}_{0}}\left( {\xi } \right)\quad \left( { - 1 < {\xi } < 1,\;0 < {\mu } < 1} \right) \\ {{g}_{0}}\left( {\xi } \right) = {{\left( {\frac{{\mu }}{{1 - {\mu }}}} \right)}^{{1 - {\mu }}}}{{\left[ {{{{\delta }}_{0}} - {{f}_{0}}\left( {\xi } \right)} \right]}^{{1 - {\mu }}}},\quad {{f}_{0}}\left( {\xi } \right) = f{{\left( {a{\xi }} \right)} \mathord{\left/ {\vphantom {{\left( {a{\xi }} \right)} {a,}}} \right. \kern-0em} {a,}}\quad {{{\delta }}_{0}} = {{\delta } \mathord{\left/ {\vphantom {{\delta } a}} \right. \kern-0em} a} \\ \end{gathered} $(3.6)
$\int\limits_{ - 1}^1 {{{{\tau }}_{0}}} \left( {\xi } \right)d{\xi } = {{{\rm T}}_{0}}\quad \left( {{{{\rm T}}_{0}} = {{\rm T} \mathord{\left/ {\vphantom {{\rm T} {a{{K}_{0}}}}} \right. \kern-0em} {a{{K}_{0}}}}} \right)$Считая функцию f(x) четной, решение ИУ (3.5) можно представить в форме бесконечного ряда
(3.7)
$\begin{gathered} \int\limits_{ - 1}^1 {\frac{{C_{n}^{{{{\mu } \mathord{\left/ {\vphantom {{\mu } 2}} \right. \kern-0em} 2}}}\left( {\eta } \right)d{\eta }}}{{{{{\left| {{\xi } - {\eta }} \right|}}^{{\mu }}}{{{(1 - {{{\eta }}^{2}})}}^{{{{\left( {1 - {\mu }} \right)} \mathord{\left/ {\vphantom {{\left( {1 - {\mu }} \right)} 2}} \right. \kern-0em} 2}}}}}}} = {{{\mu }}_{n}}C_{n}^{{{{\mu } \mathord{\left/ {\vphantom {{\mu } 2}} \right. \kern-0em} 2}}}\left( {\xi } \right)\quad \left( { - 1 < {\xi } < 1,\;n = 0,1,2,\;...} \right) \\ {{{\mu }}_{n}} = {\pi }\Gamma {{\left( {n + {\mu }} \right)} \mathord{\left/ {\vphantom {{\left( {n + {\mu }} \right)} {n!\Gamma \left( {\mu } \right)\cos \left( {{{{\pi \mu }} \mathord{\left/ {\vphantom {{{\pi \mu }} 2}} \right. \kern-0em} 2}} \right)}}} \right. \kern-0em} {n!\Gamma \left( {\mu } \right)\cos \left( {{{{\pi \mu }} \mathord{\left/ {\vphantom {{{\pi \mu }} 2}} \right. \kern-0em} 2}} \right)}} \\ \end{gathered} $Однако для простоты здесь такое решение построим в указанном выше частном случае, когда
Для упрощения вычислений функцию ${{g}_{0}}\left( {\xi } \right)$ из (3.5) разложим в ряд Маклорена по степеням ${\xi }$ и в этом разложении ограничимся членами порядка ${{{\xi }}^{2}}$. В результате
(3.8)
${{g}_{0}}\left( {\xi } \right) = {{\left( {\frac{{\mu }}{{1 - {\mu }}}} \right)}^{{1 - {\mu }}}}[{\delta }_{0}^{{1 - {\mu }}} - {{{\rm A}}_{0}}\left( {1 - {\mu }} \right){\delta }_{0}^{{ - {\mu }}}{{{\xi }}^{2}}]\quad \left( { - 1 \leqslant {\xi } \leqslant 1} \right)$Чтобы найти решение ИУ (3.5) при правой части (3.8), воспользуемся спектральными соотношениями (3.7) при n = 0 и n = 2:
(3.9)
$\begin{gathered} \frac{1}{{\pi }}\int\limits_{ - 1}^1 {\frac{{d{\eta }}}{{{{{\left| {{\xi } - {\eta }} \right|}}^{{\mu }}}{{{(1 - {{{\eta }}^{2}})}}^{{{{\left( {1 - {\mu }} \right)} \mathord{\left/ {\vphantom {{\left( {1 - {\mu }} \right)} 2}} \right. \kern-0em} 2}}}}}}} = \frac{1}{{\cos \left( {{{{\pi \mu }} \mathord{\left/ {\vphantom {{{\pi \mu }} 2}} \right. \kern-0em} 2}} \right)}}\quad \left( { - 1 < {\xi } < 1} \right) \\ \frac{1}{{\pi }}\int\limits_{ - 1}^1 {\frac{{C_{2}^{{{{\mu } \mathord{\left/ {\vphantom {{\mu } 2}} \right. \kern-0em} 2}}}\left( {\eta } \right)d{\eta }}}{{{{{\left| {{\xi } - {\eta }} \right|}}^{{\mu }}}{{{(1 - {{{\eta }}^{2}})}}^{{{{\left( {1 - {\mu }} \right)} \mathord{\left/ {\vphantom {{\left( {1 - {\mu }} \right)} 2}} \right. \kern-0em} 2}}}}}}} = \frac{{\Gamma \left( {{\mu } + 2} \right)}}{{2\Gamma \left( {\mu } \right)\cos \left( {{{{\pi \mu }} \mathord{\left/ {\vphantom {{{\pi \mu }} 2}} \right. \kern-0em} 2}} \right)}}C_{2}^{{{{\mu } \mathord{\left/ {\vphantom {{\mu } 2}} \right. \kern-0em} 2}}}\left( {\xi } \right) \\ C_{2}^{{{{\mu } \mathord{\left/ {\vphantom {{\mu } 2}} \right. \kern-0em} 2}}}\left( {\xi } \right) = {\mu }\left( {1 + {{\mu } \mathord{\left/ {\vphantom {{\mu } 2}} \right. \kern-0em} 2}} \right){{{\xi }}^{2}} - {{\mu } \mathord{\left/ {\vphantom {{\mu } 2}} \right. \kern-0em} 2} \\ \end{gathered} $Тогда искомое решение при помощи (3.9) можно представить следующей формулой:
Последнее после простых преобразований примет вид
(3.10)
$\begin{gathered} {{{\tau }}_{0}}\left( {\xi } \right) = {{\left( {\frac{{\mu }}{{1 - {\mu }}}} \right)}^{{1 - {\mu }}}}\frac{{\cos \left( {{{{\pi \mu }} \mathord{\left/ {\vphantom {{{\pi \mu }} 2}} \right. \kern-0em} 2}} \right)}}{{{\delta }_{0}^{{\mu }}}}{{(1 - {{{\xi }}^{2}})}^{{{{\left( {{\mu } - 1} \right)} \mathord{\left/ {\vphantom {{\left( {{\mu } - 1} \right)} 2}} \right. \kern-0em} 2}}}} \times \\ \times \;\left\{ {{{{\delta }}_{0}} - \frac{{\left( {1 - {\mu }} \right){{{\rm A}}_{0}}}}{{{\mu }\left( {1 + {\mu }} \right)\left( {2 + {\mu }} \right)}}[2\left( {2 + {\mu }} \right){{{\xi }}^{2}} - 2 + {\mu }\left( {1 + {\mu }} \right)]} \right\} \\ \left( { - 1 < {\xi } < 1} \right) \\ \end{gathered} $Чтобы получить ограниченное на концах интервала (–1, 1) решение, в (3.10) потребуем чтобы выполнялось условие
Отсюда находим параметр ${{{\delta }}_{0}}$:
(3.11)
${{{\delta }}_{0}} = \left( {1 - {\mu }} \right){{{{{\rm A}}_{0}}} \mathord{\left/ {\vphantom {{{{{\rm A}}_{0}}} {\mu }}} \right. \kern-0em} {\mu }}$Подставляя выражение ${{{\delta }}_{0}}$ из (3.11) в (3.10), окончательно получим
(3.12)
${{{\tau }}_{0}}\left( {\xi } \right) = \frac{{2{\rm A}_{0}^{{1 - {\mu }}}}}{{1 + {\mu }}}\cos \left( {{{{\pi \mu }} \mathord{\left/ {\vphantom {{{\pi \mu }} 2}} \right. \kern-0em} 2}} \right){{(1 - {{{\xi }}^{2}})}^{{{{\left( {{\mu } + 1} \right)} \mathord{\left/ {\vphantom {{\left( {{\mu } + 1} \right)} 2}} \right. \kern-0em} 2}}}}\quad \left( { - 1 \leqslant {\xi } \leqslant 1} \right)$Для определения безразмерной полудлины ${{{\rm A}}_{0}} = a{\rm A}$ интервала, при котором имеет место ограниченное решение (3.12), подставим (3.12) в условие (3.6). После несложных выкладок будем иметь
(3.13)
${{{\rm A}}_{0}} = {{\left[ {\frac{{\sqrt {\pi } {\mu }\left( {{\mu } + 2} \right)\Gamma \left( {{{\mu } \mathord{\left/ {\vphantom {{\mu } 2}} \right. \kern-0em} 2}} \right){{S}_{0}}}}{{4\Gamma \left( {{{\left( {1 + {\mu }} \right)} \mathord{\left/ {\vphantom {{\left( {1 + {\mu }} \right)} 2}} \right. \kern-0em} 2}} \right)\cos \left( {{{{\pi \mu }} \mathord{\left/ {\vphantom {{{\pi \mu }} 2}} \right. \kern-0em} 2}} \right)}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 {\left( {2 - {\mu }} \right)}}} \right. \kern-0em} {\left( {2 - {\mu }} \right)}}}}}$Отметим, что при предельном переходе ${\mu } \to 0$ из (3.13), а также из (2.4) или (2.22), получается известный результат из [17]: $a = \sqrt {{{\rm T} \mathord{\left/ {\vphantom {{\rm T} {{\pi }{\rm A}{{K}_{0}}}}} \right. \kern-0em} {{\pi }{\rm A}{{K}_{0}}}}} .$
Чтобы оценить отклонение перемещений или скоростей, полученных методом ОПСП, от заданных там же соответствующих величин, (2.3) подставим в (3.3). В результате, после перехода к безразмерным величинам, получим
(3.14)
${{w}_{0}}\left( {{\xi }, - 0} \right) = \frac{{2\left( {1 - {\mu }} \right){{{\rm A}}_{0}}}}{{{\mu }{{{\pi }}^{{{1 \mathord{\left/ {\vphantom {1 {\left( {1 - {\mu }} \right)}}} \right. \kern-0em} {\left( {1 - {\mu }} \right)}}}}}}}\int\limits_{ - 1}^1 {\frac{{\sqrt {1 - {{{\eta }}^{2}}} d{\eta }}}{{{{{\left| {{\xi } - {\eta }} \right|}}^{{\mu }}}}}} \quad \left( { - 1 < {\xi } < 1} \right),\quad {{w}_{0}}\left( {{\xi }, - 0} \right) = - \frac{{w(a{\xi }, - 0)}}{a}$Для вычисления интеграла в (3.14) воспользуемся билинейным разложением ядра:
(3.15)
$\begin{gathered} {{w}_{0}}\left( {{\xi }, - 0} \right) = \left[ {{{2\left( {1 - {\mu }} \right){{{\rm A}}_{0}}} \mathord{\left/ {\vphantom {{2\left( {1 - {\mu }} \right){{{\rm A}}_{0}}} {\mu }}} \right. \kern-0em} {\mu }}} \right]{{\left[ {{{I}_{{\mu }}}\left( {\xi } \right)} \right]}^{{{1 \mathord{\left/ {\vphantom {1 {\left( {1 - {\mu }} \right)}}} \right. \kern-0em} {\left( {1 - {\mu }} \right)}}}}}\quad \left( { - 1 \leqslant {\xi } \leqslant 1} \right) \\ {{I}_{{\mu }}}\left( {\xi } \right) = {{\left[ {2\Gamma \left( {{{\left( {1 + {\mu }} \right)} \mathord{\left/ {\vphantom {{\left( {1 + {\mu }} \right)} 2}} \right. \kern-0em} 2}} \right)\cos \left( {{{{\pi \mu }} \mathord{\left/ {\vphantom {{{\pi \mu }} 2}} \right. \kern-0em} 2}} \right)} \right]}^{{ - 1}}}\sum\limits_{n = 0}^\infty {\left( {2n + {{\mu } \mathord{\left/ {\vphantom {{\mu } 2}} \right. \kern-0em} 2}} \right)} {{g}_{n}}C_{{2n}}^{{{{\mu } \mathord{\left/ {\vphantom {{\mu } 2}} \right. \kern-0em} 2}}}\left( {\xi } \right) \\ {{g}_{n}} = {{\sum\limits_{k = 0}^n {\left( { - 1} \right)} }^{k}}\frac{{{{2}^{{2\left( {n - k} \right)}}}\Gamma \left( {2n - k + {{\mu } \mathord{\left/ {\vphantom {{\mu } 2}} \right. \kern-0em} 2}} \right)\Gamma \left( {n - k + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}} \right)}}{{k!\left( {n - k + 1} \right)!\left( {2n - 2k} \right)!}} \\ \end{gathered} $При этом точные перемещения или скорости здесь согласно (2.24) имеют вид
(3.16)
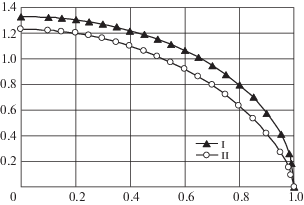
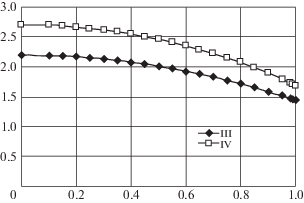
$w_{0}^{{\left( m \right)}}\left( {{\xi }, - 0} \right) = {\delta }_{0}^{{\left( m \right)}} - {\rm A}_{0}^{{\left( m \right)}}{{{\xi }}^{2}}\quad \left( { - 1 \leqslant {\xi } \leqslant 1} \right)$4. Анализ числовых результатов. Для сравнительного анализа точного и приближенного решений обсуждаемой нелинейной задачи проведена численная реализация формул (2.21), (2.22) и (2.24) для точного решения и формул (3.11)–(3.13) и (3.15)–(3.16) для приближенного решения. Результаты численного эксперимента подытожены в табл. 1, 2, 3 и представлены на графиках (фиг. 1, 2 ).
Таблица 1
| S0|µ | 0.01 | 0.05 | 0.1 | 0.2 | 0.3 | 0.5 | 0.7 | 0.9 |
|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.3155 | 0.3125 | 0.3087 | 0.3005 | 0.2916 | 0.2714 | 0.2471 | 0.2174 |
| 0.3163 | 0.3168 | 0.3182 | 0.3232 | 0.3329 | 0.3773 | 0.5152 | 1.3672 | |
| 0.2 | 0.4469 | 0.4459 | 0.4446 | 0.4417 | 0.4385 | 0.4309 | 0.4211 | 0.4082 |
| 0.4481 | 0.4521 | 0.4582 | 0.4751 | 0.5005 | 0.5989 | 0.8780 | 2.5675 | |
| 0.3 | 0.5479 | 0.5490 | 0.5504 | 0.5533 | 0.5566 | 0.5646 | 0.5753 | 0.5901 |
| 0.5494 | 0.5566 | 0.5672 | 0.5951 | 0.6353 | 0.7848 | 1.1994 | 3.7119 | |
| 0.5 | 0.7083 | 0.7134 | 0.7201 | 0.7349 | 0.7517 | 0.7937 | 0.8522 | 0.9389 |
| 0.7101 | 0.7233 | 0.7422 | 0.7904 | 0.8579 | 1.1032 | 1.7767 | 5.9057 | |
| 0.7 | 0.8388 | 0.8478 | 0.8596 | 0.8859 | 0.9162 | 0.9933 | 1.1039 | 1.2749 |
| 0.841 | 0.8595 | 0.8860 | 0.9529 | 1.0457 | 1.3807 | 2.3015 | 8.0189 | |
| 0.9 | 0.9517 | 0.9644 | 0.9812 | 1.0187 | 1.0622 | 1.1745 | 1.3394 | 1.6021 |
| 0.9542 | 0.9777 | 1.0113 | 1.0956 | 1.2123 | 1.6325 | 2.7924 | 10.0771 | |
| 1 | 1.0034 | 1.0179 | 1.0372 | 1.0801 | 1.1301 | 1.2599 | 1.4524 | 1.7632 |
| 1.0061 | 1.0320 | 1.0689 | 1.1617 | 1.2898 | 1.7513 | 3.0281 | 11.0901 | |
| 2 | 1.4216 | 1.4524 | 1.4938 | 1.5874 | 1.6990 | 2 | 2.4755 | 3.3110 |
| 1.4253 | 1.4725 | 1.5395 | 1.7074 | 1.9391 | 2.7800 | 5.1610 | 20.8257 | |
| 5 | 2.2529 | 2.3236 | 2.4195 | 2.6410 | 2.9126 | 3.6840 | 5.0091 | 7.6160 |
| 2.2587 | 2.3558 | 2.4936 | 2.8405 | 3.3242 | 5.1208 | 10.4433 | 47.9030 | |
| 8 | 2.8531 | 2.9569 | 3.0985 | 3.4290 | 3.8402 | 5.0397 | 7.1908 | 11.6758 |
| 2.8604 | 2.9978 | 3.1935 | 3.6881 | 4.3829 | 7.0052 | 14.9918 | 73.4389 | |
| 10 | 3.1917 | 3.3154 | 3.4847 | 3.8815 | 4.3788 | 5.8480 | 8.5374 | 14.3017 |
| 3.1999 | 3.3613 | 3.5914 | 4.1748 | 4.9977 | 8.1288 | 17.7992 | 89.9551 |
Таблица 2
| S0|µ | 0.01 | 0.05 | 0.1 | 0.2 | 0.3 | 0.5 | 0.7 | 0.9 |
|---|---|---|---|---|---|---|---|---|
| 0.1 | 31.393 | 6.0984 | 2.9407 | 1.3691 | 0.8521 | 0.452 | 0.2960 | 0.2218 |
| 31.314 | 6.0203 | 2.8634 | 1.2930 | 0.7767 | 0.377 | 0.2208 | 0.1519 | |
| 0.2 | 44.473 | 8.7015 | 4.2354 | 2.0122 | 1.2811 | 0.718 | 0.5044 | 0.4164 |
| 44.362 | 8.5900 | 4.1240 | 1.9003 | 1.1678 | 0.598 | 0.3763 | 0.2853 | |
| 0.3 | 54.524 | 10.712 | 5.2429 | 2.5206 | 1.6262 | 0.941 | 0.6891 | 0.6021 |
| 54.387 | 10.575 | 5.1050 | 2.3804 | 1.4823 | 0.784 | 0.5140 | 0.4124 | |
| 0.5 | 70.481 | 13.92 | 6.8601 | 3.3477 | 2.1962 | 1.322 | 1.0207 | 0.9579 |
| 70.304 | 13.742 | 6.6797 | 3.1616 | 2.0019 | 1.103 | 0.7614 | 0.6562 | |
| 0.7 | 83.465 | 16.542 | 8.1892 | 4.0358 | 2.6768 | 1.655 | 1.3223 | 1.3007 |
| 83.255 | 16.330 | 7.9738 | 3.8114 | 2.44 | 1.38 | 0.9864 | 0.8910 | |
| 0.9 | 94.7 | 18.818 | 9.3473 | 4.6405 | 3.1033 | 1.957 | 1.6043 | 1.6345 |
| 94.462 | 18.576 | 9.1015 | 4.3825 | 2.8288 | 1.632 | 1.1967 | 1.1197 | |
| 1 | 99.849 | 19.862 | 9.8803 | 4.9203 | 3.3017 | 2.099 | 1.7397 | 1.7988 |
| 99.598 | 19.608 | 9.6204 | 4.6467 | 3.0096 | 1.751 | 1.2978 | 1.2322 | |
| 2 | 141.45 | 28.34 | 14.23 | 7.2315 | 4.9638 | 3.333 | 2.9651 | 3.3779 |
| 141.1 | 27.977 | 13.855 | 6.8294 | 4.5247 | 2.78 | 2.2118 | 2.3140 | |
| 5 | 224.17 | 45.340 | 23.048 | 12.031 | 8.5094 | 6.14 | 6.0000 | 7.7698 |
| 223.61 | 44.759 | 22.442 | 11.362 | 7.7566 | 5.12 | 4.4757 | 5.3226 | |
| 8 | 283.89 | 57.698 | 29.517 | 15.62 | 11.219 | 8.399 | 8.6132 | 11.911 |
| 283.18 | 56.958 | 28.741 | 14.752 | 10.226 | 7.005 | 6.4251 | 8.1599 | |
| 10 | 317.58 | 64.693 | 33.195 | 17.682 | 12.793 | 9.746 | 10.226 | 14.591 |
| 316.78 | 63.8644 | 32.3228 | 16.699 | 11.6613 | 8.1288 | 7.6282 | 9.9950 |
Таблица 3
| ξ|µ | 0.01 | 0.05 | 0.1 | 0.2 | 0.3 | 0.5 | 0.7 | 0.9 |
|---|---|---|---|---|---|---|---|---|
| 0 | 1.09494 | 1.0929 | 1.0902 | 1.0844 | 1.0780 | 1.0627 | 1.043 | 1.0167 |
| 1.09426 | 1.0883 | 1.078 | 1.0465 | 0.9978 | 0.8352 | 0.564 | 0.1877 | |
| 0.1 | 1.08945 | 1.0874 | 1.0847 | 1.079 | 1.0726 | 1.0573 | 1.0377 | 1.0116 |
| 1.08873 | 1.0826 | 1.0721 | 1.0402 | 0.9913 | 0.8290 | 0.5592 | 0.1860 | |
| 0.2 | 1.07282 | 1.0708 | 1.0682 | 1.0625 | 1.0562 | 1.0412 | 1.0219 | 0.9962 |
| 1.07194 | 1.0653 | 1.0541 | 1.0212 | 0.9717 | 0.8101 | 0.5448 | 0.1806 | |
| 0.3 | 1.04451 | 1.0426 | 1.04 | 1.0345 | 1.0283 | 1.0137 | 0.9949 | 0.9699 |
| 1.04337 | 1.0358 | 1.0235 | 0.9889 | 0.9385 | 0.7782 | 0.5206 | 0.1717 | |
| 0.4 | 1.00353 | 1.0017 | 0.9992 | 0.9939 | 0.988 | 0.9739 | 0.9559 | 0.9318 |
| 1.00204 | 0.9931 | 0.9795 | 0.9425 | 0.8909 | 0.7329 | 0.4864 | 0.1591 | |
| 0.5 | 0.94825 | 0.9465 | 0.9441 | 0.9391 | 0.9335 | 0.9203 | 0.9032 | 0.8805 |
| 0.9463 | 0.9358 | 0.9203 | 0.8806 | 0.8276 | 0.6731 | 0.4417 | 0.1428 | |
| 0.6 | 0.87596 | 0.8743 | 0.8722 | 0.8675 | 0.8624 | 0.8501 | 0.8344 | 0.8134 |
| 0.87346 | 0.8610 | 0.8434 | 0.8006 | 0.7465 | 0.5976 | 0.386 | 0.1229 | |
| 0.7 | 0.78195 | 0.7805 | 0.7786 | 0.7744 | 0.7698 | 0.75889 | 0.7448 | 0.7261 |
| 0.77884 | 0.7643 | 0.7444 | 0.6987 | 0.6441 | 0.5041 | 0.3182 | 0.099 | |
| 0.8 | 0.65697 | 0.6557 | 0.6541 | 0.6506 | 0.6468 | 0.6376 | 0.6258 | 0.61 |
| 0.65321 | 0.6365 | 0.6146 | 0.5669 | 0.5136 | 0.3882 | 0.2367 | 0.0711 | |
| 0.9 | 0.47728 | 0.4764 | 0.4752 | 0.4727 | 0.4699 | 0.4632 | 0.4546 | 0.4432 |
| 0.47304 | 0.4551 | 0.4325 | 0.3864 | 0.3390 | 0.2404 | 0.1375 | 0.0388 |
В табл. 1 приведены значения величин $A_{0}^{{\left( m \right)}}$ (точные) и A0 (приближенные) при различных значениях параметров ${\mu }$ и ${{S}_{0}},$ причем в каждой клетке таблицы на первом месте записаны значения $A_{0}^{{\left( m \right)}},$ а на втором месте – A0. Анализ данных этой таблицы показывает, что при ${{S}_{0}} = 0.1,$ ${{S}_{0}} = 0.2$ по мере возрастания ${\mu }$ величина $A_{0}^{{\left( m \right)}}$ убывает, а A0 возрастает. При малых ${\mu }$ их значения весьма близки между собой, но при больших ${\mu }$ они значительно расходятся друг от друга. Например, при ${{S}_{0}} = 0.2$ и ${\mu } = 0.2$ их расхождение составляет 3.3%, а при ${{S}_{0}} = 0.2,$ ${\mu } = 0.7$ – около 45%. При фиксированных же ${{S}_{0}}$ их значения при малых ${\mu }$ весьма близки между собой, а при больших ${\mu }$ они опять сильно расходятся друг от друга.
В табл. 2 в указанной выше последовательности для различных ${\mu }$ и ${{S}_{0}}$ приведены значения ${\delta }_{0}^{{\left( m \right)}}$ (точные) и ${{{\delta }}_{0}}$ (приближенные). Здесь при фиксированном ${{S}_{0}}$ при возрастании ${\mu }$ эти величины убывают, причем при малых ${\mu }$ эти величины выражаются довольно большими, но весьма близкими между собой числами. Это объясняется тем, что малые ${\mu }$ характеризуют линейную задачу, где жесткие перемещения (или скорости) весьма большие числа. При фиксированных же ${\mu }$ величины ${\delta }_{0}^{{\left( m \right)}}$ а ${{{\delta }}_{0}}$ при возрастании параметра ${{S}_{0}}$ возрастают, оставаясь однако довольно близко друг другу.
В табл. 3 в упомянутой выше последовательности приведены значения ${\tau }_{0}^{{\left( m \right)}}\left( {\xi } \right)$ (точные) и ${{{\tau }}_{0}}\left( {\xi } \right)$ (приближенные) для различных μ и точек ${\xi },$ когда ${{S}_{0}} = 0.3.$ Здесь при малых ${\mu }$ их значения близки между собой, а при больших μ они сильно расходятся. Например, в центре отрезка ${\xi } = 0$ при μ = 0.2 их отклонение составляет 4%, а при ${\mu } = 0.5$–17% При фиксированном ${\mu },$ когда ${\xi }$ возрастает ${\tau }_{0}^{{\left( m \right)}}$ и ${{{\tau }}_{0}}\left( {\xi } \right)$ убывают. При ${\mu }$ близких к единице расхождения между ними в каждой точке интервала (0, 1) значительны.
На фиг. 1 по данным таблицы построены графики изменения ${\tau }_{0}^{{\left( m \right)}}\left( {\xi } \right)$ (верхний график) и ${{{\tau }}_{0}}\left( {\xi } \right)$(нижний график). В окрестности точки ξ = 1 они с большой точностью совпадают, а в центре ξ = 0 заметно расходятся друг от друга.
Наконец, на фиг. 2 представлены графики изменения $w_{0}^{{\left( m \right)}}\left( {\xi } \right)$ (нижний график) и ${{w}_{0}}\left( {\xi } \right)$ (верхний график). Здесь наблюдается та же закономерность что и на фиг. 1.
5. Заключение. Таким образом, при антиплоской деформации построено точное решение смешанной граничной задачи НТУП при степенном законе связи между напряжениями и скоростями деформаций для полупространства, когда на одной части его граничной плоскости заданы скорости деформаций, а на остальной части касательные напряжения равны нулю. Для сравнительного анализа построено также ее приближенное решение, в результате чего показано, что отклонения между точными и приближенными характеристиками задачи при показателях ползучести m, близких к нулю (при ${\mu } = 1 - m$, близких к 1) значительны, а по мере приближения m к 1 (${\mu }$ к 0) эти отклонения заметно уменьшаются.
Список литературы
Арутюнян Н.Х. Плоская контактная задача теории ползучести // ПММ. 1959. Т. 23. Вып. 5. С. 901–924.
Арутюнян Н.Х. Плоская задача теории пластичности со степенным упрочнением материала // Изв АН Арм. ССР. Сер. физ.-мат. наук. 1959. Т. 12. № 2. С. 77–105.
Atkinson C. A note on crack problems in power- law elastic materials and contact problems in non-linear creep // Int. I. Engng. Sci. 1971. V. 9. № 8. P. 729–739.
Александров В.М., Сумбатян М.А. Об одном решении контактной задачи нелинейной установившейся ползучести для полуплоскости // Изв. РАН. МТТ. 1983. № 1. С. 107–113.
Александров В.М., Брудный С.Р. О методе обобщенной суперпозиции в контактной задаче антиплоского сдвига // Изв. РАН. МТТ. 1986. № 1. С. 71–78.
Rice J. R. Mathematical Analysis in the Mechanics of Fracture, Chapter 3 of Fracture: An Advanced Treatise (Vol. 2, Mathematical Fundamentals) (ed. H. Liebowitz), Academic Press, N.Y., 1968, P. 191–311. = Райс Дж. Математические методы в механике разрушения. Под редакцией Г. Либовица. Разрушение. Т. 2. М.: Мир. 1973. С. 204–335.
Lee Y.S., Gong H. Application of complex variables and pseudostress function to power-law materials and stress analisys of single rigid inclusion in power-law materials subjected to simple tension and pure shear // Int. J. Mech. Sci. 1987. V. 29. № 10/11. P. 669–694.
Мхитарян С.М. О решении первой граничной задачи нелинейной теории установившейся ползучести для полупространства при антиплоской деформации // Изв. РАН. МТТ. 2012. № 6. С. 58–66.
Арутюнян Н.Х., Манжиров А.В. Контактные задачи теории ползучести. Ереван: Изд-во Ин-та Механики НАН РА, 1999. 320 с.
Развитие теории контактных задач в СССР. М.: Наука, 1976. 493 с.
Budd W.F., Warner R.C., Jacka T.H., Jun Li, Treverrow A. Ice flow relations for stress and strain–rate components from combined shear and compression Laboratory experiments. Journal of Glaciology. 2013. V. 59. № 214. P. 374–392.
Graham F.S., Morlighem M., Warner R.Gh., Treverrow A. Implementing an empirical scalar constitutive relation for ice with flow-induced polycrystalline anisotropy in large–scale ice sheet models. The Crysphere. March 2018. V. 12 (3). P. 1047–1067.
Bons P.D., Kleiner T., Llorens M.-G., Prior D.I., Sachau T., Weikusat I. and Jansen D. Greenland Ice Sheet: Higher Nonlinearity of Ice Flow Significantly Reduces Estimated Basal Motion. AGU100. Advancing Earth and Space Science. Geophysical Research Letters, June 2018. P. 6542–6547.https://doi.org/10.1029/2018GL078356
Качанов Л.М. Теория ползучести. М.: Физматгиз, 1960. 455 с.
Качанов Л.М. Основы механики разрушения. М.: Наука, 1974. 312 с.
Мусхелишвили Н.И. Некоторые основные задачи математической теории упругости. М.: Наука, 1966. 708 с.
Штаерман И.Я. Контактная задача теории упругости. М.; Л.: Гостехтеориздат, 1949. 270 с.
Bateman H. and Erdalyi A. Tables of Integral Transforms, Vol. II McGraw–Hill Book Co., New York, 1954. = Бейтмен Г., Эрдейи А. Таблицы интегральных преобразований. Том II. М.: Наука, 1970. 328 с.
Попов Г.Я. Некоторые свойства классических многочленов и их применение к контактным задачам // ПММ. 1963. Т. 27. Вып. 5. С. 821–832.
Мхитарян С.М. О некоторых спектральных соотношениях, связанных с интегральным уравнением Карлемана, и их приложениях к контактным задачам // ПММ. 1983. Т. 47. Вып. 2. С. 219–227.
Bateman H. and Erdalyi A. Higher Transcendental Functions, Vol. 2 McGraw– Hill Book Co., New York, 1953. = Бейтмен Г., Эрдейи А. Высшие трансцендентные функции Т. 2. М.: Наука, 1974. 295 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела