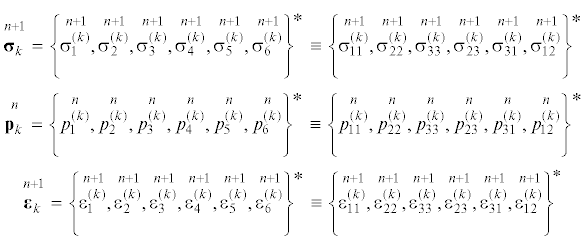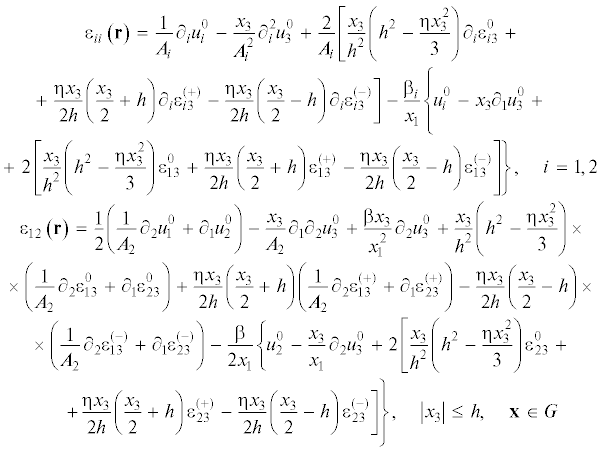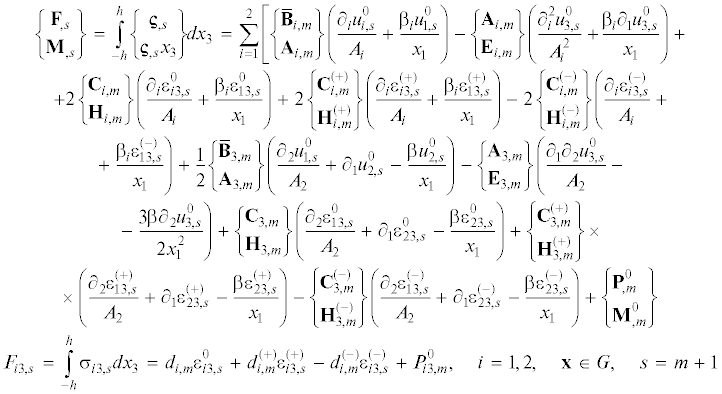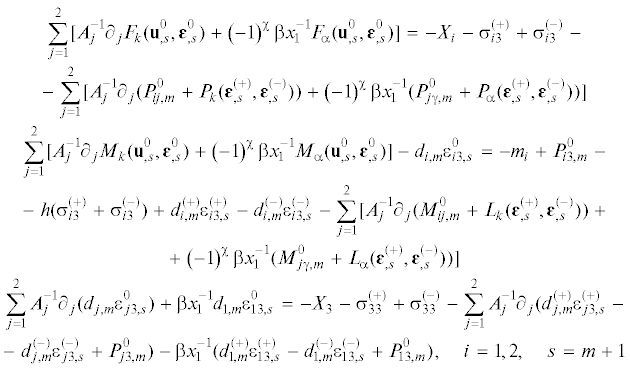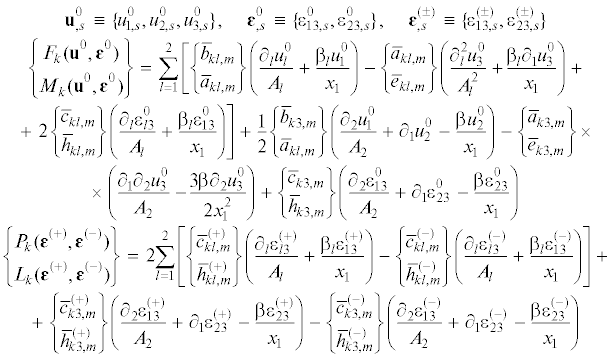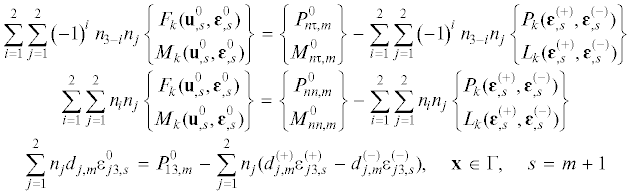Известия РАН. Механика твердого тела, 2019, № 2, стр. 3-28

1. Введение. Композиционные материалы находят все более широкое применение в инженерной практике, особенно при создании тонкостенных элементов конструкций типа балок, пластин и оболочек. Так как все материалы, в том числе и используемые в качестве компонентов композиций, проявляют реономные свойства [1, 2], актуальной является проблема математического моделирования и изучения особенностей механического поведения армированных тонкостенных конструкций, работающих в условиях неустановившейся ползучести. При решении этой проблемы, с одной стороны, нужно опираться на адекватную структурную модель рассматриваемой композитной среды, материалы фаз композиции которой обладают определенными реономными свойствами, а с другой стороны, при поперечном нагружении тонкостенных композитных элементов конструкций необходимо обоснованно использовать те или иные кинематические соотношения их изгибного деформирования.

Так, в [3, 4] исследована реология зернистых (наполненных) композитных сред, в [5, 6] моделировались вязкоупругие свойства однонаправленно армированных композитов (однако такие композиты редко используются на практике, разве что в конструкциях стержневого типа). В [7, 8] были построены структурные модели вязкоупругого поведения перекрестно-армированных композитных сред. Недостаток моделей, предложенных в [7, 8], заключается в том, что монолитное в реальности композитное тело представляется в виде отдельных однонаправленно армированных стержней, ориентация которых соответствует заданным направлениям армирования. При этом указанные армированные стержни получаются несвязанными между собой в единое целое (в монолитный материал). В [9] предложена структурная модель, лишенная указанного недостатка.

В перечисленных публикациях поведение материалов компонентов композиции предполагается линейно- или нелинейно-наследственным, что свойственно в основном полимерным материалам. Структурные же модели, описывающие реономное поведение металлокомпозитов на основе технических теорий, на сегодняшний день отсутствуют. Однако известно, что нелинейно-наследственная теория ползучести Ю.Н. Работнова описывает механическое поведение не только полимерных материалов, но и некоторых металлических сплавов и сталей на стадиях их упрочнения и установившейся ползучести при активном нагружении [1, 10–13], поэтому на базе этой теории можно с единых позиций описать реономное поведение композитных конструкций, состоящих как из полимерных, так и металлических материалов.

В работе [14] была исследована неустановившаяся ползучесть продольно армированных балок-стенок, механическое поведение материалов компонентов композиции которых описывается нелинейно-наследственной теорией Ю.Н. Работнова. В [14] показано, что при изгибе таких конструкций необходимо учитывать их ослабленное сопротивление поперечным сдвигам. До настоящего времени ползучесть тонкостенных композитных элементов конструкций в основном изучалась в рамках классических теорий [15], не учитывающих ослабленное сопротивление поперечным сдвигам. В [16, 17] исследовалось линейно-упругое поведение армированных пластин и оболочек на основе второго варианта теории Тимошенко. В этих работах построены структурные теории линейно-упругого деформирования композитных сред, на основе которых с применением принципа Вольтерра [12] предлагается получение определяющих уравнений для армированных тонкостенных элементов конструкций из линейно-вязкоупругих материалов фаз композиции. Однако в [16, 17] никакие решения для композитных пластин и оболочек из вязкоупругих материалов получены не были. В работах [18, 19] исследовалось линейно-вязкоупругое поведение изотропных оболочек, подкрепленных системой ребер, с учетом их ослабленного сопротивления поперечным сдвигам. Особенности же деформирования армированных оболочек из таких материалов не изучались.

Исследованные в [14] армированные балки-стенки являются простейшими типами тонкостенных элементов конструкций, в которых реализуется обобщенное плоское напряженное состояние. В тонкостенных же элементах более сложной геометрии (пластинах и оболочках) при учете их ослабленного сопротивления поперечным сдвигам имеет место объемное напряженное состояние, поэтому в силу нелинейного поведения материалов фаз композиции (в рамках нелинейно-наследственной теории ползучести Ю.Н. Работнова [1, 10–12]) деформирование пластин и оболочек в условиях неустановившейся ползучести может обладать специфическими особенностями, которые не проявляются при изгибе армированных балок-стенок.

В связи с этим, настоящая работа посвящена изучению реономного поведения изгибаемых армированных пластин, механическое поведение материалов компонентов композиции которых описывается соотношениями нелинейно-наследственной теории ползучести Ю.Н. Работнова, с учетом их (пластин) ослабленного сопротивления поперечным сдвигам.

2. Метод шагов по времени. Предполагается, что материалы всех фаз композиции армированной пластины однородны, изотропны и их механическое поведение описывается соотношениями нелинейно-наследственной теории ползучести Ю.Н. Работнова [1, 10–13]:

$\sigma _{{ij}}^{{(k)}}$, $\varepsilon _{{ij}}^{{(k)}}$ – компоненты тензоров напряжений и деформаций в k-м компоненте композиции (индексом k = 0 помечаются характеристики связующего материала, а индексом $k \geqslant 1$ – характеристики материала k-го семейства армирующих волокон); $g_{1}^{{(k)}}(\varepsilon _{ * }^{{(k)}},\varepsilon _{0}^{{(k)}})$ – известная из эксперимента функция, являющаяся при умножении на 3/2 коэффициентом пропорциональности между интенсивностями напряжений $\sigma _{ * }^{{(k)}}$ и деформаций $\varepsilon _{ * }^{{(k)}}$ в k-м компоненте композиции; $g_{0}^{{(k)}}(\varepsilon _{ * }^{{(k)}},\varepsilon _{0}^{{(k)}})$ – известная из эксперимента зависимость утроенного объемного модуля k-го составляющего композиции от $\varepsilon _{ * }^{{(k)}}$, $\varepsilon _{0}^{{(k)}}$ (функции $g_{0}^{{(k)}}(\varepsilon _{ * }^{{(k)}},\varepsilon _{0}^{{(k)}})$, $g_{1}^{{(k)}}(\varepsilon _{ * }^{{(k)}},\varepsilon _{0}^{{(k)}})$ или $\sigma _{ * }^{{(k)}}(\varepsilon _{ * }^{{(k)}},\varepsilon _{0}^{{(k)}})$ известны из диаграмм мгновенного деформирования материала k-го компонента композиции; зависимость этих функций от обоих аргументов позволяет учитывать свойство разносопротивляемости материалов фаз, которое часто наблюдается в экспериментах [1, 12, 13, 20]); $K_{0}^{{(k)}}$(t – τ), $K_{1}^{{(k)}}\left( {t - \tau } \right)$ – известные разностные ядра ползучести для шарового тензора ${{\delta }_{{ij}}}\sigma _{0}^{{(k)}}$ и девиатора $s_{{ij}}^{{(k)}}$ напряжений k-го компонента композиции, в частности, эти ядра могут быть слабосингулярными (см. (2.3)); $B_{l}^{{(k)}}\left( t \right)$ – регулярные функции (возможно, постоянные), характеризующие ядра ползучести; $\alpha _{l}^{{(k)}}$ – показатели сингулярности ядер ползучести; N – количество семейств армирующих волокон; ${{\delta }_{{ij}}}$ – символ Кронекера; t – время.

Как обычно, предполагается, что до начального момента времени $t = {{t}_{0}} = 0$ все материалы фаз и композиция в целом находятся в естественном состоянии, т.е. функции $\sigma _{{ij}}^{{(k)}}$ принадлежат классу Хевисайда [1, 12, 13, 20], что отражено в нижних пределах интегралов в правых частях соотношений (2.1).

Соотношениями (2.1)–(2.3) хорошо описывается нелинейно-наследственное поведение не только полимерных материалов [1, 12, 21], но и упругопластическая наследственность некоторых металлов на стадии их активного нагружения, например алюминиевых сплавов [13, 22], некоторых марок сталей [1, 22] и др.

Так как даже простейшие задачи неустановившейся ползучести для изотропных элементов конструкций требуют привлечения численных методов интегрирования по времени [1, 18, 19, 23, 24], то тем более это касается армированных композитных конструкций и сред [25]. Поэтому в настоящем исследовании используем численно-аналитический подход к моделированию нелинейно-наследственного поведения армированных пластин, базирующийся на идее метода шагов по времени [1, 20, 23, 24]. С этой целью дискретизируем задачу по времени, то есть будем рассматривать ее решения в моменты времени ${{t}_{m}}$, причем предполагаем, что при $m = 0,1,2,\,...,\,n$ решение задачи уже известно, т.е. известны значения величин (см. (2.1), (2.2)):

Повторяя рассуждения из [14, 26], на основании соотношений (2.1)–(2.4) для рассматриваемого момента времени ${{t}_{{n + 1}}}$ определяющие уравнения для материала k-го компонента композиции можно записать в матричной форме

$\mathop {{{A}_{k}}}\limits^{n + 1} $ – симметричные 6 × 6-матрицы, ненулевые компоненты которых $\mathop {A_{{ij}}^{{(k)}}}\limits^{n + 1} $ ($i,\,\,j = 1,\,\,...,\,\,6$) определяются равенствами (10) в [14]; $\mathop {{{\sigma }_{k}}}\limits^{n + 1} $, $\mathop {{{\varepsilon }_{k}}}\limits^{n + 1} $ – шестикомпонентные вектор-столбцы напряжений и деформаций в материале k-го составляющего композиции; $\mathop {{{{\mathbf{p}}}_{k}}}\limits^n $ – известный в момент времени ${{t}_{{n + 1}}}$ шестикомпонентный вектор-столбец в том же материале, который можно трактовать как вектор “начальных напряжений” и компоненты которого $\mathop {p_{{ij}}^{{(k)}}}\limits^n $ определены равенствами (9) в [14]; звездочка в верхнем индексе означает операцию транспонирования. Отметим: в работе [9] было получено выражение для величин $\mathop {p_{{ij}}^{{(k)}}}\limits^n $ в предположении, что ядра ползучести в (2.1) являются регулярными ($\alpha _{l}^{{(k)}} = 0$, см. (2.3)) и представляют собой линейную комбинацию экспоненциальных функций.

Соотношения (2.5) с учетом равенств (9), (10) из [14] в момент времени ${{t}_{{n + 1}}}$ можно трактовать как определяющие соотношения для k-го компонента композиции, механическое поведение которого характеризуется зависимостями нелинейно-упругого изотропного тела с начальным напряженным состоянием.

Линеаризуем соотношения (2.5), предполагая, что левые части соотношений (2.1) с учетом (2.2) удовлетворяют достаточным условиям сходимости метода последовательных приближений (см. стр. 199 в [20]). При этом считаем, что в момент времени ${{t}_{{n + 1}}}$ на некоторой m-й итерации известны приближения деформаций $\mathop {\varepsilon _{{ij,m}}^{{(k)}}}\limits^{n + 1} $ во всех компонентах композиции, тогда в силу соотношений (2.2) известны и m-е приближения величин $\mathop {\varepsilon _{{ * ,m}}^{{(k)}}}\limits^{n + 1} $, $\mathop {\varepsilon _{{0,m}}^{{(k)}}}\limits^{n + 1} $. Для следующего же s-го приближения деформаций $\mathop {\varepsilon _{{ij,s}}^{{(k)}}}\limits^{n + 1} $ и напряжений $\mathop {\sigma _{{ij,s}}^{{(k)}}}\limits^{n + 1} $ справедливо линейное матричное равенство (см. (2.5)):

где $\mathop {{{\sigma }_{{k,s}}}}\limits^{n + 1} $, $\mathop {{{\varepsilon }_{{k,s}}}}\limits^{n + 1} $ – шестикомпонентные вектор-столбцы, имеющую структуру, аналогичную (2.6), и подлежащие определению; $\mathop {{{A}_{{k,m}}}}\limits^{n + 1} $ – симметричные 6 × 6-матрицы, компоненты которых $\mathop {A_{{ij,m}}^{{(k)}}}\limits^{n + 1} $ известны на s-й итерации и вычисляются по формулам (10) из [14] при замене $\mathop {\varepsilon _{ * }^{{(k)}}}\limits^{n + 1} $, $\mathop {\varepsilon _{0}^{{(k)}}}\limits^{n + 1} $ их m-ми приближениями $\mathop {\varepsilon _{{ * ,m}}^{{(k)}}}\limits^{n + 1} $, $\mathop {\varepsilon _{{0,m}}^{{(k)}}}\limits^{n + 1} $; вектор $\mathop {{{{\mathbf{p}}}_{k}}}\limits^n $ от номера итерации не зависит.

В работе [9] на основе соотношений (2.7) в момент времени ${{t}_{{n + 1}}}$ на s-й итерации были получены линейные определяющие соотношения для композитной среды, имеющие матричный вид:

где $\mathop {{{\sigma }_{{,s}}}}\limits^{n + 1} $, $\mathop {{{\varepsilon }_{{,s}}}}\limits^{n + 1} $ – шестикомпонентные вектор-столбцы, характеризующие s-е приближения осредненных напряжений и деформаций в композиции (имеют структуру, аналогичную (2.6)); $\mathop {{{{\mathbf{p}}}_{{,m}}}}\limits^{n + 1} $ – известный шестикомпонентный вектор-столбец, определяемый векторами $\mathop {{{{\mathbf{p}}}_{k}}}\limits^n $, компонентами матриц $\mathop {{{A}_{{k,m}}}}\limits^{n + 1} $ и структурой армирования (направлением и плотностью армирования волокнами k-го семейства), который в момент времени ${{t}_{{n + 1}}}$ на s-й итерации можно трактовать как вектор “начальных напряжений” в композиции; $\mathop {{{A}_{{,m}}}}\limits^{n + 1} $ – известная на s-й итерации $6 \times 6$-матрица, компоненты которой $\mathop {{{A}_{{ij,m}}}}\limits^{n + 1} $ ($i,\,\,j = 1,\,\,...,\,\,6$) можно трактовать как “эффективные жесткости” композиции и которая определяется компонентами матриц $\mathop {{{A}_{{k,m}}}}\limits^{n + 1} $ и структурой армирования.

Далее в настоящем исследовании предполагаем, что в каждой точке композитного тела в момент времени ${{t}_{{n + 1}}}$ на s-й итерации в соотношении (2.8) известны все компоненты вектора $\mathop {{{{\mathbf{p}}}_{{,m}}}}\limits^{n + 1} $ и матрицы $\mathop {{{A}_{{,m}}}}\limits^{n + 1} $ (см. [9]).

Так как ниже все соотношения записываются при $t = {{t}_{{n + 1}}}$, для сокращения записи будем опускать верхний индекс $n + 1$, означающий этот момент времени (см. обозначения (2.4)).

3. Изгиб армированных пластин, изготовленных из нелинейно-наследственных материалов фаз композиции. В ортогональной (декартовой прямоугольной или цилиндрической) системе координат ${{x}_{1}},\,\,{{x}_{2}},\,\,{{x}_{3}}$ рассмотрим тонкостенный плоский элемент толщиной 2h, состоящий из регулярно чередующихся армированных слоев, параллельных отсчетной плоскости $({{x}_{1}},\,\,{{x}_{2}})$, которую совместим со срединной плоскостью элемента, а ось ${{x}_{3}}$ направим по толщине элемента (фиг. 1). Армирование в направлении ${{x}_{3}}$ является квазиоднородным.

Как показано в [14] на примерах простейших тонкостенных элементов – армированных балок-стенок, выполненных из нелинейно-наследственных материалов, при изгибе тонкостенных элементов композитных конструкций, армированных в плоскостях, параллельных срединной плоскости, необходимо учитывать их ослабленное сопротивление поперечным сдвигам. В связи с этим, сдвиговые деформации в поперечном направлении ${{x}_{3}}$ в момент времени ${{t}_{{n + 1}}}$ зададим распределенными по толщине пластины в следующем виде:

где $\varepsilon _{{i3}}^{0}$, $\varepsilon _{{i3}}^{{( \pm )}}$ – функции только двух пространственных переменных ${{x}_{1}},\,\,{{x}_{2}}$, подлежащие определению и имеющие следующий смысл: $\varepsilon _{{i3}}^{{( + )}}$, $\varepsilon _{{i3}}^{{( - )}}$ – деформации поперечного сдвига на верхней (${{x}_{3}} = h$) и нижней (${{x}_{3}} = - h$) лицевых поверхностях пластины, при $\varepsilon _{{i3}}^{{( \pm )}} \equiv 0$ функции $\varepsilon _{{i3}}^{0}$ определяют деформации поперечного сдвига в срединной плоскости ${{x}_{3}} = 0$ в момент времени ${{t}_{{n + 1}}}$; G – область, занимаемая пластиной в плане; $\eta $ – параметр переключения, позволяющий выбирать тот или иной вариант теории деформирования пластины.

Если в (3.1) принять $\eta = 0$, $\varepsilon _{{i3}}^{0} \equiv 0$, то в дальнейшем получим соотношения, основанные на классической теории Кирхгофа, использующей кинематическую гипотезу недеформируемой нормали [2, 16, 18]. Если же $\eta = 0$ при $\varepsilon _{{i3}}^{0} \ne 0$, то из (3.1) следуют соотношения первого варианта теории Тимошенко, базирующегося на кинематической гипотезе независимой ротации нормали, остающейся прямолинейной [18, 27, 28]. В случае же $\eta = 1$ и $\varepsilon _{{i3}}^{0} \ne 0$ из (3.1) вытекают соотношения второго варианта теории Тимошенко, учитывающего в процессе деформирования искривление нормали к срединной плоскости [16–18, 29].

Согласно гипотезам классической теории и теорий типа Тимошенко, обжатием тонкостенного элемента пренебрегаем, то есть считаем, что прогиб ${{u}_{3}}$ в момент времени ${{t}_{{n + 1}}}$ не зависит от координаты ${{x}_{3}}$:

При этом соотношения, связывающие между собой деформации ${{\varepsilon }_{{ij}}}$ и перемещения u_i, имеют вид [1, 2, 16, 29] (в настоящем исследовании ограничимся геометрически линейной постановкой задачи изгиба относительно толстых пластин)

где $\beta $ – параметр переключения, позволяющий записывать соответствующие соотношения в декартовой прямоугольной ($\beta = 0$) или цилиндрической ($\beta = 1$) системах координат; ${{A}_{i}}$ – параметры Ламе: ${{A}_{1}} = {{A}_{2}} \equiv 1$ при $\beta = 0$ и ${{A}_{1}} \equiv 1$, ${{A}_{2}} = {{x}_{1}}$ при $\beta = 1$ (в этом случае ${{x}_{1}}$ – полярный радиус, ${{x}_{2}}$ – полярный угол); ${{\partial }_{i}}$ – оператор частного дифференцирования по переменной ${{x}_{i}}$.

На основании равенств (3.3) с учетом (3.1) и (3.2) получим [29, 30]

где $u_{i}^{0}$ – перемещения точек срединной плоскости (${{x}_{3}} = 0$).

Таким образом, в момент времени ${{t}_{{n + 1}}}$ в соотношениях (3.1), (3.4) и (3.5) неизвестными являются функции $u_{i}^{0}$, $u_{3}^{0}$, $\varepsilon _{{i3}}^{0}$, $\varepsilon _{{i3}}^{{( \pm )}}$ ($i = 1,\,\,2$), зависящие только от двух пространственных переменных ${{x}_{1}},\,\,{{x}_{2}}$.

В качестве статической гипотезы используем традиционное приближенное равенство, верное как в рамках теории Кирхгофа, так и в рамках теорий типа Тимошенко [2, 16–18, 27–30]:

Так как материалы фаз композиции предполагаются изотропными, то при плоском армировании (фиг. 1) матрица ${{A}_{{,m}}}$ в (2.8) имеет блочную структуру. За счет этого линейные определяющие соотношения (2.8) с учетом (3.6) и (2.6) можно записать в более простом виде, исключив предварительно из рассмотрения ${{\varepsilon }_{{33,s}}}$ (ср. с (1.15) и (1.16) в [30]):

${{B}_{{,m}}}$ – 3 × 3-матрица, компоненты которой, согласно соотношениям (2.8), (3.6) и (3.9), определяются так: ${{A}_{{ij,m}}}$, ${{p}_{{ij,m}}}$ – компоненты матрицы ${{A}_{{,m}}}$ и вектор-столбца ${{{\mathbf{p}}}_{{,m}}}$ (имеющего структуру, аналогичную (2.6)) в соотношении (2.8), которые предполагаются известными из решения на предыдущей итерации.

На основании соотношений (3.7) и (3.8) с учетом равенств (3.1), (3.5), (3.9) и (3.10) в момент времени ${{t}_{{n + 1}}}$ на s-й итерации можем определить все внутренние силовые факторы в пластине:

${{{\mathbf{A}}}_{{i,m}}}$, ${{{\mathbf{\bar {B}}}}_{{i,m}}}$, ${{{\mathbf{C}}}_{{i,m}}}$, ${\mathbf{C}}_{{i,m}}^{{( \pm )}}$, ${{{\mathbf{E}}}_{{i,m}}}$, ${{{\mathbf{H}}}_{{i,m}}}$, ${\mathbf{H}}_{{i,m}}^{{( \pm )}}$ – трехкомпонентные векторы-столбцы, элементы которых совпадают с компонентами i-х столбцов 3 × 3-матриц ${{\bar {A}}_{{,m}}} = \left( {{{{\bar {a}}}_{{ji,m}}}} \right)$, ${{\bar {B}}_{{,m}}} = \left( {{{{\bar {b}}}_{{ji,m}}}} \right)$, ${{\bar {C}}_{{,m}}} = \left( {{{{\bar {c}}}_{{ji,m}}}} \right)$, $\bar {C}_{{,m}}^{{( \pm )}} = \left( {\bar {c}_{{ji,m}}^{{( \pm )}}} \right)$, ${{\bar {E}}_{{,m}}} = \left( {{{{\bar {e}}}_{{ji,m}}}} \right)$, ${{\bar {H}}_{{,m}}} = \left( {{{{\bar {h}}}_{{ji,m}}}} \right)$, $\bar {H}_{{,m}}^{{( \pm )}} = (\bar {h}_{{ji,m}}^{{( \pm )}})$, $i,\,\,j = 1$, 2, 3, определяемых, согласно равенствам (3.1), (3.5), (3.7), (3.8) и (3.11), так: ${{F}_{{ij,s}}}$, ${{F}_{{i3,s}}}$ – s-е приближения мембранных и поперечных усилий в пластине в момент времени ${{t}_{{n + 1}}}$; ${{M}_{{ij,s}}}$ – s-е приближения изгибающих и крутящих моментов; $P_{{ij,m}}^{0}$, $P_{{i3,m}}^{0}$, $M_{{ij,m}}^{0}$ ($i,\,\,j = 1,\,\,2$) имеют смысл “начальных” силовых факторов, известных на s-й итерации в момент времени ${{t}_{{n + 1}}}$.

В квазистатической постановке задачи внутренние силовые факторы (3.11) и (3.12) в момент времени ${{t}_{{n + 1}}}$ должны удовлетворять уравнениям равновесия [1, 18, 27, 29]:

$\sigma _{{i3}}^{{( \pm )}}\left( {\mathbf{x}} \right) = {{\sigma }_{{i3}}}\left( {{\mathbf{x}},\,\, \pm h} \right)$ – заданные напряжения на верхней (+) и нижней (–) лицевых поверхностях пластины; ${{X}_{i}}$ – приведенные распределенные внешние нагрузки, действующие в направлении ${{x}_{i}}$ ($i = 1,\,\,2,\,\,3$) и порожденные объемными силами; ${{m}_{i}}$ – приведенные распределенные внешние моменты от объемных сил.

К уравнениям (3.14) необходимо добавить по два статических граничных условия на лицевых поверхностях пластины [16–18, 30] (см. (3.1) и (3.8)):

$p_{{i3,m}}^{{( \pm )}}$ известны как “начальные” напряжения в момент времени ${{t}_{{n + 1}}}$ на s-й итерации. Из соотношений (3.16) вытекает т.е. в момент времени ${{t}_{{n + 1}}}$ на текущей s-й итерации приближения для функций $\varepsilon _{{i3}}^{{( \pm )}}\left( {\mathbf{x}} \right)$ в равенствах (3.1), (3.4), (3.5) и в выражениях для внутренних силовых факторов (3.11) известны, так как функции $b_{{i,m}}^{{( \pm )}}\left( {\mathbf{x}} \right)$ предполагаются уже известными из решения на предыдущей m-й итерации.

После подстановки внутренних силовых факторов (см. (3.11) и (3.12)) в уравнения равновесия (3.14) с учетом равенств (3.15) получим

${{\bar {a}}_{{kl,m}}}$, ${{\bar {b}}_{{kl,m}}}$, ${{\bar {c}}_{{kl,m}}}$ и т.д. – компоненты матриц (3.13). Согласно равенствам (3.17), (3.12) и (3.19), правые части системы (3.18) – известные функции.

Система пяти разрешающих уравнений (3.18) с учетом (3.19) и (3.20) содержит пять неизвестных кинематических переменных $u_{{i,s}}^{0}\left( {\mathbf{x}} \right)$, $u_{{3,s}}^{0}\left( {\mathbf{x}} \right)$ и $\varepsilon _{{i3,s}}^{0}\left( {\mathbf{x}} \right)$ ($i = 1,\,\,2$). Для однозначного интегрирования этой системы в момент времени ${{t}_{{n + 1}}}$ необходимо использовать квазистатические [18, 27, 29, 30]

и кинематические (см. (3.2) и (3.4)) граничные условия, где ${{F}_{{nn}}}$ и ${{F}_{{n\tau }}}$ – заданные на контуре Г нормальная и касательная мембранные силы; ${{F}_{{n3}}}$ – заданная на Г поперечная сила; ${{M}_{{nn}}}$ и ${{M}_{{n\tau }}}$ – заданные на Г изгибающий и крутящий моменты; ${{u}_{{30}}}$ – заданный на Г прогиб; ${{u}_{{i0}}}$ – заданные на торцевой поверхности пластины перемещения в тангенциальных направлениях ${{x}_{i}}$ ($i = 1,\,\,2$); Г – контур, ограничивающий область G, занимаемую пластиной в плане; δ – угол, задающий направление внешней нормали к контуру Г и отсчитываемый от направления ${{x}_{1}}$.

Согласно равенствам (3.4), граничные условия (3.23) нельзя удовлетворить в каждой точке r торцевой поверхности пластины при произвольной зависимости функций ${{u}_{{i0}}}$ от координаты ${{x}_{3}}$, поэтому по аналогии со статическими граничными условиями (см. (3.21), (3.11) и (3.12)) кинематические условия (3.23) на кромке пластины будем удовлетворять в интегральном смысле, а именно: проинтегрируем равенства (3.23) по толщине пластины с весами 1 и ${{x}_{3}}$, тогда с учетом (3.4) в момент времени ${{t}_{{n + 1}}}$ получим

Для получения статических граничных условий в перемещениях необходимо подставить в (3.21) выражения (3.11), тогда с учетом (3.12), (3.15) и (3.19) будем иметь

$P_{{ij,m}}^{0}$, $P_{{i3,m}}^{0}$, $M_{{ij,m}}^{0}$ ($i,\,\,j = 1,\,\,2$) определены в (3.12). Согласно соотношениям (3.17), (3.19) и (3.27) правые части в (3.26) известны на текущей s-й итерации в рассматриваемый момент времени ${{t}_{{n + 1}}}$.

Подстановка выражений (3.19) в (3.18) приводит к системе уравнений с частными производными десятого порядка [18, 27, 29, 30], поэтому для ее однозначного интегрирования в каждой точке контура Г необходимо задать пять статических (3.26) (с учетом выражений (3.19) и (3.27)) или пять кинематических (3.22) и (3.24) (с учетом обозначений (3.25)) граничных условий. Возможно и задание пяти смешанных из (3.22), (3.24) и (3.26) граничных условий (например при шарнирном опирании пластины на кромке Г).

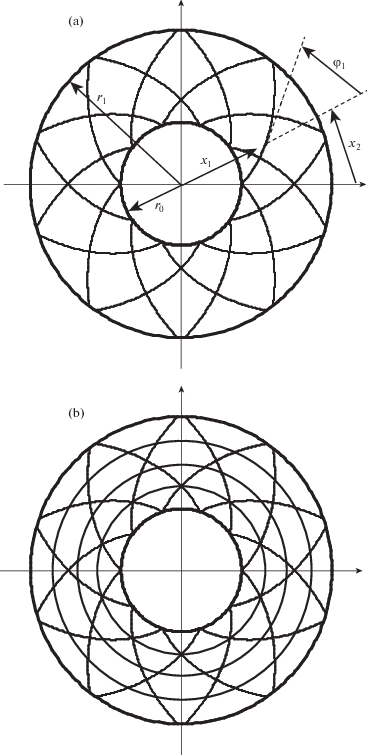
4. Модельная задача. Рассмотрим изгиб кольцевой пластины постоянной толщины 2h с кромками радиусов ${{r}_{0}}$ и ${{r}_{1}}$. Нагружение и закрепление пластины не зависят от окружного направления ${{x}_{2}}$, внешние силы в этом направлении отсутствуют. Пластина усилена осесимметрично: 1) двумя ($N = 2$) семействами волокон с одинаковыми плотностями армирования (${{\omega }_{1}}\left( {{{x}_{1}}} \right) = {{\omega }_{2}}\left( {{{x}_{1}}} \right)$), уложенных по радиально-симметричным направлениям (${{\varphi }_{1}}\left( {{{x}_{1}}} \right) = - {{\varphi }_{2}}\left( {{{x}_{1}}} \right)$, где ${{\varphi }_{k}}$ – угол армирования волокнами k-го семейства, отсчитываемый от полярного радиуса ${{x}_{1}}$) – спиральное армирование (фиг. 2,а); 2) тремя (N = 3) семействами волокон, два из которых по-прежнему уложены радиально-симметрично (${{\varphi }_{1}}\left( {{{x}_{1}}} \right) = - {{\varphi }_{2}}\left( {{{x}_{1}}} \right)$) с одинаковыми плотностями армирования (${{\omega }_{1}}({{x}_{1}}) = {{\omega }_{2}}({{x}_{1}})$), а третье семейство уложено в окружном направлении (${{\varphi }_{3}}\left( {{{x}_{1}}} \right) = \pi {\text{/}}2$) с плотностью ${{\omega }_{3}}\left( {{{x}_{1}}} \right)$ (${{r}_{0}} \leqslant {{x}_{1}} \leqslant {{r}_{1}}$) – спирально-окружное армирование (фиг. 2,b). В обоих случаях арматура спиральных семейств ($k = 1,\,\,2$) изготовлена из одного и того же материала.

В силу указанных особенностей нагружения, закрепления и армирования рассматриваемых пластин решение задачи об их неупругом деформировании не зависит от окружной координаты ${{x}_{2}}$, то есть реализуется случай осесимметричного изгиба. При этом во всех разрешающих уравнениях и соответствующих им граничных условиях следует принять $\beta = 1$ (см. (3.3)) и отбросить производные от функций по переменной ${{x}_{2}}$, а частные производные по полярному радиусу ${{x}_{1}}$ нужно заменить обычными производными.

Предполагается, что на лицевых поверхностях ${{x}_{3}} = \pm h$ касательные напряжения отсутствуют ($\sigma _{{i3}}^{{( \pm )}} \equiv 0$), поэтому из равенств (3.17) при $t = {{t}_{{n + 1}}}$ имеем

Получающаяся при этом на каждой s-й итерации в момент времени ${{t}_{{n + 1}}}$ линейная двухточечная граничная задача (3.18), (3.22), (3.24) и (3.26) с учетом (3.19), (3.25), (3.27), (3.20), (3.15) и (4.1) может быть проинтегрирована численно методом пристрелки [31].

Если эта граничная задача решена, то при $t = {{t}_{{n + 1}}}$ известны s-е приближения функций $u_{3}^{0}$, $u_{i}^{0}$, $\varepsilon _{{i3}}^{0}$ ($i = 1,\,\,2$). При этом по формулам (3.1) и (3.5) можно определить s-е приближения осредненных деформаций композиции в каждой точке пластины в момент времени ${{t}_{{n + 1}}}$. Зная приближения этих деформаций, по известным структурным формулам [9] можно вычислить s-е приближения деформаций во всех компонентах композиции в каждой точке тонкостенной конструкции и построить следующее приближение матрицы ${{A}_{{,s}}}$ и вектора-столбца ${{{\mathbf{p}}}_{{,s}}}$ в определяющем соотношении (2.8). По известным же компонентам ${{A}_{{ij,s}}}$, ${{p}_{{i,s}}}$ матрицы ${{A}_{{,s}}}$ и вектора ${{{\mathbf{p}}}_{{,s}}}$ на основании соотношений (3.9) и (3.10) можно определить в каждой точке пластины следующие приближения матрицы ${{B}_{{,s}}}$ и вектора-столбца ${\mathbf{p}}_{{,s}}^{0}$, коэффициентов ${{b}_{{i,s}}}$ и “начальных напряжений” ${{p}_{{i3,s}}}$ ($s = m + 1$) в соотношениях (3.7) и (3.8) и построить следующее ($s + 1$)-е приближение решения рассматриваемой задачи неупругого изгиба армированных пластин и т.д., пока итерационный процесс не сойдется с требуемой точностью.

Если в момент времени ${{t}_{{n + 1}}}$ итерационный процесс сошелся с требуемой точностью, т.е. в каждой точке пластины известны деформации $\varepsilon _{{ij}}^{{(k)}}$ каждого компонента композиции, то на основании (2.5) с учетом (2.6) можно определить и напряженное состояние $\sigma _{{ij}}^{{(k)}}$ ($0 \leqslant k \leqslant N$) во всех материалах фаз композиции. Следовательно, с учетом (2.2) все величины, указанные в (2.4), становятся известными в каждой точке пластины в момент времени ${{t}_{{n + 1}}}$. Повторяя проведенные выше рассуждения, можем получить решение рассматриваемой задачи для следующего момента времени ${{t}_{{n + 2}}}$ и т.д. Учитывая, что до начального момента времени $t = {{t}_{0}} = 0$ конструкция находится в естественном состоянии, т.е. при $m = 0$ все величины в (2.4) равны нулю, можно последовательно по описанной выше схеме получить в дискретные моменты времени ${{t}_{n}}$ ($n = 0,\,\,1,\,\,2...$) решение о ползучести армированных пластин, выполненных из нелинейно-наследственных материалов компонентов композиции.

5. Обсуждение результатов расчетов. В качестве конкретных примеров исследуем особенности изгибного деформирования в условиях ползучести кольцевых пластин толщиной $2h = 10$ см, ограниченных кромками радиусов ${{r}_{0}} = 1$ м, ${{r}_{1}} = 2$ м и изготовленных из алюминиевого сплава Д16Т. Нелинейно-наследственное поведение этого материала описывается соотношениями (2.1)–(2.3) при следующих механических характеристиках [13]:

Пластины осесимметрично армированы двумя ($N = 2$, фиг. 2,а) или тремя ($N = 3$, фиг. 2,b) семействами борных волокон с механическими характеристиками [32]

Здесь: ${{E}^{{(k)}}}$, ${{\mu }^{{(k)}}}$ ($0 \leqslant k \leqslant N$) – модуль Юнга и коэффициент Пуассона материала k-го компонента композиции. Согласно равенствам (5.1) и (5.2), в рассматриваемых условиях борные волокна не ползут и ведут себя линейно-упруго [32], для сплава же Д16Т связь между шаровыми тензорами напряжений и деформаций является также линейно-упругой.

На внутренних кромках ${{r}_{0}}$ пластины жестко закреплены: ${{u}_{{30}}} = 0$, ${{u}_{{i0}}} = 0$, $i = 1,\,\,2$ (см. (3.22)–(3.25)), а на внешних кромках ${{r}_{1}}$ свободны от нагружения (${{F}_{{nn}}} = {{F}_{{n\tau }}} = {{F}_{{n3}}} = 0$, ${{M}_{{nn}}} = {{M}_{{n\tau }}}$ = 0, ${{x}_{1}} = {{r}_{1}}$). Пластины равномерно нагружены только поперечной распределенной нагрузкой $\sigma _{{33}}^{{( + )}}$ ($\sigma _{{33}}^{{( - )}} \equiv 0$, $\sigma _{{i3}}^{{( \pm )}} \equiv 0$, ${{m}_{i}} \equiv 0$, ${{X}_{j}} \equiv 0$, $i = 1,\,\,2$, $j = 1,\,\,2,\,\,3$), которая прикладывается к их верхним лицевым поверхностям в виде функции класса Хевисайда:

Согласно модельной задаче, пластины осесимметрично армированы: 1) двумя ($N = 2$) семействами борных волокон по логарифмическим спиралям (фиг. 2,а), т.е.

2) тремя ($N = 3$) семействами борных волокон, причем первые два семейства ($k = 1,\,\,2$) также уложены радиально-симметрично по логарифмическим спиралям, т.е. для них выполняются равенства (5.3), а третье семейство уложено в окружном направлении (${{\varphi }_{3}} = \pi {\text{/}}2$) с плотностью армирования ${{\omega }_{3}}\left( {{{x}_{1}}} \right)$ (фиг. 2,b).

Так как борные волокна имеют постоянные поперечные сечения [32], то плотности армирования ${{\omega }_{k}}$ в осесимметричном случае при армировании по логарифмическим спиралям под любыми углами ψ изменяются по закону [16, 30]

где ${{\omega }_{{0k}}}$ – плотность армирования волокнами k-го семейства, заданная на внутренней кромке ${{x}_{1}} = {{r}_{0}}$.

Из соотношений (5.4) следует, что при любых углах армирования ψ (см. равенства (5.3)) общий расход волокон спиральных семейств в пластинах фиксированных размеров при одинаковых ${{\omega }_{{0k}}}$ ($k = 1,\,\,2$) будет одним и тем же. Далее в расчетах для спирально армированных пластин (N = 2, фиг. 2,а) принимается ${{\omega }_{{01}}} = {{\omega }_{{02}}} = 0.35$, при этом суммарная плотность армирования на внутренних кромках пластин (${{\omega }_{{01}}} + {{\omega }_{{02}}}$ = 0.7) равна предельно допустимой величине, так как на практике это значение примерно равно именно 0.7 [33].

Согласно формуле (5.4), при спиральной укладке волокон (фиг. 2,а) суммарная плотность армирования $\omega \left( {{{x}_{1}}} \right) = {{\omega }_{1}}\left( {{{x}_{1}}} \right) + {{\omega }_{2}}\left( {{{x}_{1}}} \right) = 2{{\omega }_{1}}\left( {{{x}_{1}}} \right)$ монотонно убывает от внутренней кромки ${{x}_{1}} = {{r}_{0}}$ к внешней ${{x}_{1}} = {{r}_{1}}$. Так как при окружной укладке арматуры (${{\varphi }_{3}} = \pi {\text{/}}2$, см. фиг. 2b) плотность армирования ${{\omega }_{3}}\left( {{{x}_{1}}} \right)$ может быть задана произвольной функцией от ${{x}_{1}}$ [16], то выберем ${{\omega }_{3}}\left( {{{x}_{1}}} \right)$ так, чтобы при спирально-окружной укладке волокон суммарная плотность армирования ω(x₁) = ${{\omega }_{1}}({{x}_{1}}) + {{\omega }_{2}}({{x}_{1}}) + {{\omega }_{3}}({{x}_{1}})$ = = 2ω₁(x₁) + ω₃(x₁) была величиной постоянной, причем потребуем выполнения равенства $\omega \left( {{{x}_{1}}} \right) = 2{{\bar {\omega }}_{{01}}} = {\text{const}}$, где ${{\bar {\omega }}_{{01}}} = {{\omega }_{1}}\left( {{{r}_{0}}} \right) = {{\omega }_{2}}\left( {{{r}_{0}}} \right)$ в случае спирально-окружной укладки волокон. При этом плотности армирования первых двух (спиральных) семейств определяются по-прежнему из (5.4) при замене ${{\omega }_{{0k}}} \to {{\bar {\omega }}_{{0k}}}$ ($k = 1,\,\,2$). Кроме того, потребуем, чтобы общий расход арматуры в случаях обоих типов армирования, изображенных на фиг. 2, был одинаков, т.е.

где согласно (5.4) правая часть пропорциональна общему расходу арматуры в пластине со спиральным армированием (фиг. 2,а).

Из последнего равенства следует

Таким образом, если в случае спирально-окружной укладки волокон плотности армирования спиральных семейств вычисляются по формулам (5.4) с учетом равенств (5.5) (при замене в (5.4) ${{\omega }_{{0k}}} \to {{\bar {\omega }}_{{0k}}}$, $k = 1,\,\,2$), а плотность армирования окружным семейством волокон (${{\varphi }_{3}} = \pi {\text{/}}2$) определяется соотношением

то общий расход арматуры, пропорциональный величине $\Omega $, в пластинах со спиральной (фиг. 2,а) и спирально-окружной (фиг. 2,b) укладкой волокон при любых углах армирования ψ (см. (5.3)) будет один и тот же, причем в случае спирально-окружной укладки волокон суммарная плотность армирования в пластинах будет постоянной ($\omega \left( {{{x}_{1}}} \right) = 2{{\bar {\omega }}_{{01}}} = {\text{const}}$, где величина ${{\bar {\omega }}_{{01}}}$ известна из (5.5) при ${{\omega }_{{01}}} = 0.35$).

При указанных условиях закрепления, нагружения и армирования кольцевых пластин в них реализуется случай осесимметричного изгиба.

На фиг. 3–5 приведены результаты расчетов податливостей изгибаемых композитных пластин с различными структурами армирования. Кривые с номерами 1, 2 на этих фигурах рассчитаны на основе первого и второго вариантов теории Тимошенко соответственно (см. (3.1) при $\eta = 0$ и $\eta = 1$ при $\varepsilon _{{i3}}^{0} \ne 0$), а кривые с номерами 3 – на основе классической теории (см. (3.1) при $\eta = 0$, $\varepsilon _{{i3}}^{0} \equiv 0$). Кривые, номера которых помечены одним штрихом, определены для спирально армированных пластин (фиг. 2,а), а линии, номера которых помечены двумя штрихами, рассчитаны для пластин со спирально-окружной укладкой волокон (фиг. 2,b) при разных углах армирования ψ (см. (5.3)).

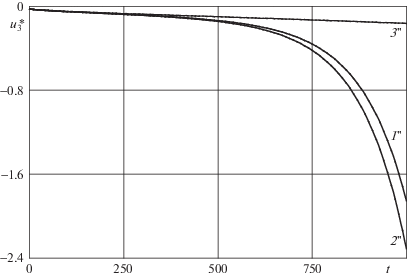
На фиг. 3 изображены зависимости прогиба точек внешней кромки пластины $u_{3}^{ * }\left( t \right) = {{u}_{3}}\left( {{{r}_{1}},t} \right)$ (в мм) от времени t (в часах), рассчитанные с шагом по времени $\Delta t = 10$ ч при радиально-окружной структуре армирования конструкции (см. фиг. 2,b при ψ = 0). Дополнительные расчеты показали, что, как и в [14], поведение функции $u_{3}^{ * }\left( t \right)$ в случае рассматриваемых материалов компонентов композиции (см. (5.1) и (5.2)) практически не зависит от выбора шага $\Delta t$, по крайней мере в интервале $\Delta t \in $ [0.1, 100]. (Более подробно этот вопрос обсуждается в [14, 34].)

Из фиг. 3 видно, что в случае радиально-окружного армирования пластины после $t = 400$ ч прогибы, рассчитанные по классической теории, существенно отличаются от прогибов, определенным по теориям Тимошенко, причем это различие возрастает со временем. В окрестности начального момента времени $t \approx 0$ на всех кривых фиг. 3 наблюдается стадия упрочнения (плохо заметная при выбранном масштабе по оси ординат), быстро переходящая в стадию установившейся ползучести, которая для кривой 3'' наблюдается вплоть до $t = 1000\,\,{\text{ч }}$. Однако, согласно поведению кривых 1''и 2'', после $t = 400$ ч наблюдается ускорение ползучести армированных пластин, рассчитанных по теориям типа Тимошенко.

Следует отметить, что нелинейно-наследственная теория ползучести Ю.Н. Работнова описывает только первую и вторую стадию ползучести, но не описывает третью стадию ускоренной ползучести, предшествующую разрушению материала [1, 12]. В силу этого, ускорение ползучести, наблюдаемое согласно поведению кривых 1''и 2'' на фиг. 3 после $t = 400$ ч, объясняется не началом и развитием предразрушения материалов компонентов композиции, а активным и ускоренным развитием деформаций поперечного сдвига, так как линии 1''и 2'' рассчитаны с учетом ослабленного сопротивления армированной пластины именно этим сдвигам (подробнее см. ниже).

Напомним, что в случае изгибного деформирования балок-стенок, армированных в продольном направлении и выполненных из нелинейно-наследственных материалов, зависимости, аналогичные $u_{3}^{ * }\left( t \right)$ и рассчитанные ранее как по классической теории, так и по второму варианту теории Тимошенко, качественно подобны кривой 3'' на фиг. 3 (см. рис. 3 в [14]), т.е. для армированных балок-стенок ускорение ползучести не имеет места даже при учете их ослабленного сопротивления поперечным сдвигам. Следовательно, наблюдаемое, согласно поведению кривых 1''и 2'' на фиг. 3, ускорение ползучести армированной пластины объясняется более сложным видом напряженно-деформированного состояния (НДС) в компонентах композиции (см. (3.7) и (3.8)) по сравнению с НДС в фазах композиции армированных балок-стенок, а также нелинейным поведением материала связующего (см. (5.1)).

Следует отметить, что и при других структурах армирования (при $0 < \psi \leqslant \pi {\text{/}}2$ как в случае спиральной укладки волокон (фиг. 2,а), так и в случае спирально-окружной укладки арматуры (фиг. 2,b)) наблюдается поведение зависимостей $u_{3}^{ * }\left( t \right)$, качественно подобное кривым, изображенным на фиг. 3. А значит, исследование простейших тонкостенных композитных элементов (продольно армированных балок-стенок) не позволяет выявить все особенности деформирования тонкостенных армированных элементов конструкций более сложной геометрии (пластин и оболочек), работающих в условиях неустановившейся ползучести.

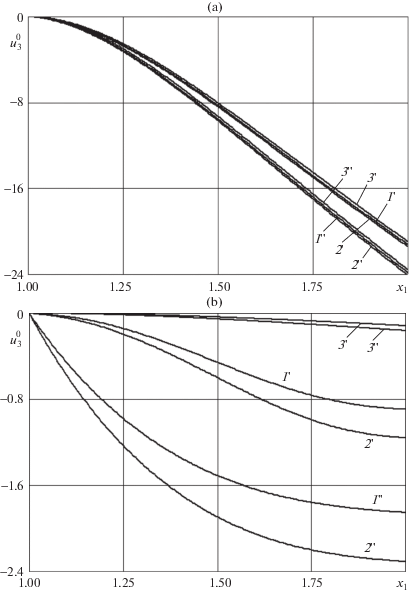
На фиг. 4 изображены эпюры прогибов, определенные в начальный момент времени $t = + 0$ (фиг. 4,а) и при $t = 1000$ ч (фиг. 4,b). По оси абсцисс на фиг. 4 отложен полярный радиус ${{x}_{1}}$ (в метрах), а по оси ординат – прогиб $u_{3}^{0}$ (в мкм на фиг. 4,а и в мм на фиг. 4,b). Кривые 1'–3' на этой фигуре рассчитаны для пластины с радиальной структурой армирования (см. фиг. 2,а при ψ = 0), а линии 1''–3'' – для пластины с радиально-окружной структурой (см. фиг. 2,b при ψ = 0). Линии на фиг. 4,а образуют два пучка близко лежащих кривых; в каждом из этих пучков верхние линии рассчитаны по классической теории (кривые 3' и 3''), средние и нижние линии – по первому (кривые 1' и 1'') и второму (кривые 2' и 2'') вариантам теории Тимошенко соответственно. Дополнительные расчеты показали, что и при других структурах армирования (см. фиг. 2 при $0 < \psi \leqslant \pi {\text{/}}2$) в начальный момент времени $t = + 0$ получаются качественно аналогичные и близко лежащие кривые $u_{3}^{0}\left( {{{x}_{1}},\,\, + 0} \right)$, рассчитанные по разным теориям. Следовательно, согласно фиг. 4,а, в начальный момент времени все три сравниваемых теории предсказывают примерно одну и ту же податливость рассматриваемых армированных пластин. Действительно, отношение модулей упругости волокон бора и алюминиевого связующего равно 6.4 (см. (5.1) и (5.2)), то есть анизотропия исследуемой бороалюминиевой композиции является слабой, а значит, классическая теория при кратковременном нагружении (в частности, в рамках линейно-упругого поведения фаз композиции) должна хорошо описывать механическое поведение рассматриваемых пластин [16, 27, 29], что и нашло свое отражение на фиг. 4,а.

Однако в соответствии с поведением кривых на фиг. 3 к моменту времени $t = 1000$ ч значения прогибов, предсказываемых разными теориями, существенно различаются, причем согласно фиг. 4,b эпюры прогибов в этот момент времени различаются не только количественно, но и качественно. А именно: кривизна линий 1', 2' на фиг. 4,b в отличие от кривой 3' является знакопеременной; линии же 1'', 2'' имеют кривизну, знак которой противоположен знаку кривизны кривой 3''. Как было показано в [30, 35], необычное поведение кривых 1'', 2'' на фиг. 4,b объясняется именно тем, что в окрестности внутренней, жестко закрепленной кромки (${{x}_{1}} = {{r}_{0}}$) в связующем получают значительное развитие деформации поперечных сдвигов и их скорости в условиях ползучести.

В силу того, что кривые 1'–3' и 1''–3'' на фиг. 4,b существенно различны, при расчетах ползучести армированных пластин целесообразно использовать второй вариант теории Тимошенко (см. кривые 2' и 2'' на фиг. 3 и 4) как наиболее точный (с точки зрения математического моделирования [16–18, 29, 36]) из всех обсуждаемых теорий.

Исследуем влияние углов армирования ψ волокнами спиральных семейств (см. (5.3) и фиг. 2) на податливость композитных пластин в разные моменты времени. С этой целью в качестве меры податливости изгибаемых пластин примем следующую величину

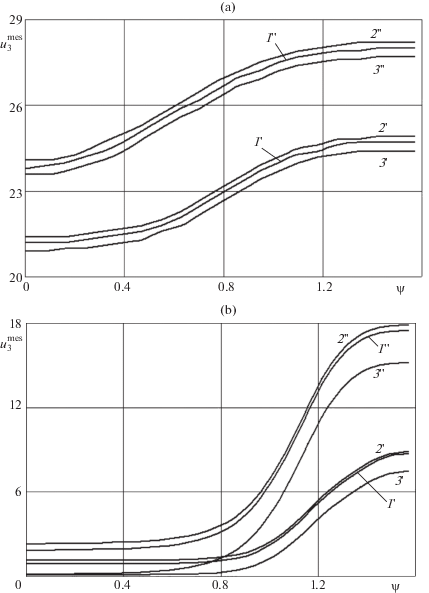
На фиг. 5 изображены зависимости (5.6) от угла спирального армирования ψ в начальный момент времени $t = + 0$ (фиг. 5,а) и при $t = 1000$ ч (фиг. 5,b). По оси абсцисс на фиг. 5 отложен угол спирального армирования ψ (в радианах), а по оси ординат – величина $u_{3}^{{{\text{mes}}}}$ (в мкм на фиг. 5,а и в мм на фиг. 5,b). Как видно из этой фигуры, в оба рассматриваемых момента времени зависимости (5.6) являются возрастающими по ψ, т.е. наименьшей податливостью обладают пластины либо с радиальным армированием (см. кривые 1'–3' на фиг. 5 при $\psi \to 0$, а также фиг. 2,а при $\psi \to 0$), либо с радиально-окружным армированием (см. кривые 1''–3'' на фиг. 5 при $\psi \to 0$, а также фиг. 2,b при $\psi \to 0$); наибольшей же податливостью обладают пластины, армированные в окружном направлении (см. кривые на фиг. 5 при $\psi \to \pi {\text{/}}2$ и фиг. 2 при $\psi \to \pi {\text{/}}2$). Однако, согласно фиг. 5, в разные моменты времени изменяемость зависимости (5.6) по ψ количественно существенно разная. Для относительной количественной оценки этой изменяемости рассмотрим величины

В табл. 1 приведены значения (5.7), рассчитанные для двух моментов времени $t = + 0$ и $t = 1000$ ч по трем осуждаемым теориям изгибного деформирования пластин при двух типах их армирования, изображенных на фиг. 2. Как видно из фиг. 5 и табл. 1, с течением времени изменяемость податливости пластин (рассчитанная по всем сравниваемым теориям) в зависимости от угла спирального армирования ψ резко возрастает, и при $t = 1000$ ч она на порядок больше, чем в начальный момент времени.

Согласно поведению кривых, изображенных на фиг. 5,а, классическая теория (см. кривые 3' и 3'') при всех углах армирования волокнами спиральных семейств ($0 \leqslant \psi \leqslant \pi {\text{/}}2$) в начальный момент времени обеспечивает вполне приемлемую точность определения податливости рассматриваемых армированных пластин, так как кривые 1', 2' и 1'', 2'' лежат близко к кривым 3' и 3'' соответственно. (Этот результат вполне согласуется с эпюрами прогибов, изображенных на фиг. 4,а.)

Согласно же поведению кривых на фиг. 5,b, изменяемость податливости рассматриваемых армированных пластин в момент времени $t = 1000$ ч при $0 \leqslant \psi \leqslant 0.6$ рад незначительна, а существенная зависимость $u_{3}^{{{\text{mes}}}}$ от ψ (см. (5.6)) в этот момент времени наблюдается при достаточно больших углах спирального армирования: $\pi {\text{/}}4 < \psi \leqslant \pi {\text{/}}2$. Кроме того, при этих же углах армирования наблюдается увеличение точности вычисления податливости пластин, определенной на базе классической теории (кривые 3' и 3'') и первого варианта теории Тимошенко (кривые 1', 1'') по сравнению с расчетами по второму варианту теории Тимошенко (кривые 2', 2''). Так, значение $u_{3}^{{{\text{mes}}}}$, рассчитанное по классической теории для пластины со спирально-окружной структурой армирования при $\psi \to \pi {\text{/}}2$ (см. кривую 3'' на фиг. 5,b), отличается от аналогичной величины, определенной по второму варианту теории Тимошенко (см. кривую 2'' на фиг. 5,b при $\psi \to \pi {\text{/}}2$), всего на 15.1%. При радиально-окружном же армировании ($\psi \to 0$) это различие составляет 93% (см. кривые 2'' и 3'' на фиг. 4,b). Как уже отмечалось, последний факт объясняется развитием в окрестности внутренней, жестко закрепленной кромки значительных деформаций поперечных сдвигов в связующем материале.

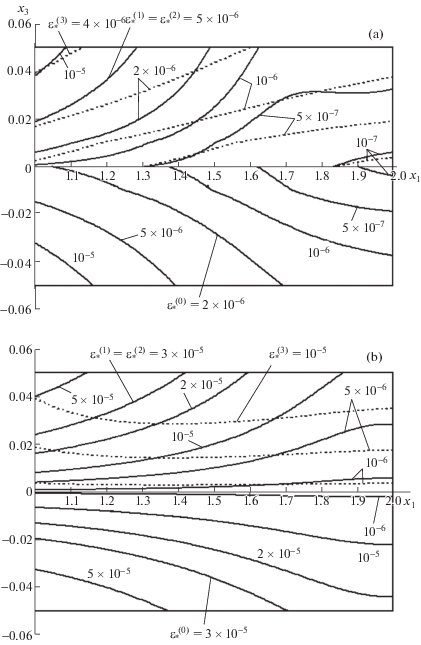
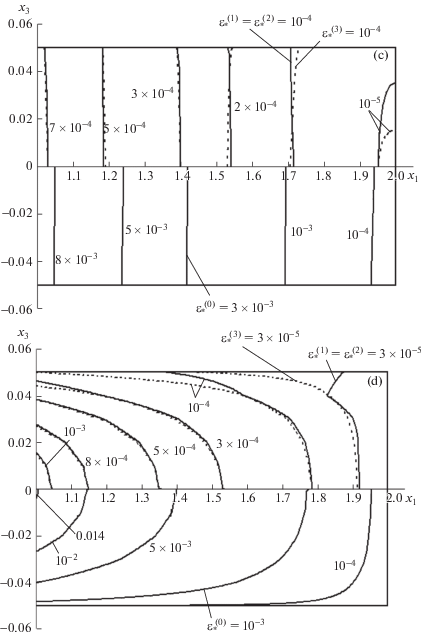
Для демонстрации этого факта на фиг. 6 изображены радиальные сечения пластины (с радиально-окружной структурой армирования; см. фиг. 2,b при $\psi \to 0$) и изолинии, на которых интенсивность деформаций $\varepsilon _{ * }^{{(k)}}$ (см. (2.2)) в k-м компоненте композиции ($k = 0,...,3$) имеет постоянное значение. По оси абсцисс на фиг. 6 отложен полярный радиус ${{x}_{1}}$ (в метрах), а по оси ординат – осевая координата ${{x}_{3}}$ (в метрах). В силу отсутствия нагружения пластины в радиальном и окружном направлениях, а также в силу предположения о равносопротивляемости материалов фаз композиции растяжению и сжатию “картины” деформирования компонентов композиции симметричны относительно срединной плоскости ${{x}_{3}} = 0$, поэтому ради экономии места на нижних половинах фиг. 6 изображены изолинии деформирования связующего ($\varepsilon _{ * }^{{(0)}} = {\text{const}}$), а на верхних половинах – армирующих волокон, причем сплошные кривые соответствуют радиально уложенным волокнам бора ($\varepsilon _{ * }^{{(1)}} = \varepsilon _{ * }^{{(2)}} = {\text{const}}$), а пунктирные линии – волокнам бора, уложенным в окружном направлении ($\varepsilon _{ * }^{{(3)}}$ = const).

На фиг. 6,а приведены картины деформирования материалов фаз композиции в начальный момент времени $t = + 0$, рассчитанные по второму варианту теории Тимошенко. Классическая теория и первый вариант теории Тимошенко для этого момента времени приводят примерно к таким же изолиниям $\varepsilon _{ * }^{{(k)}} = {\text{const}}$, что и изображенные на фиг. 6,а (поэтому они не приведены на фиг. 6). Это обстоятельство и объясняет близость кривых 1'', 2'', 3'' на фиг. 4,а.

На фиг. 6b–d приведены картины деформирования, рассчитанные при $t = 1000$ ч по классической теории (фиг. 6,b), первому (фиг. 6,c) и второму (фиг. 6,d) вариантам теории Тимошенко. Сравнение изолиний на этих фигурах показывает, что на момент времени $t = 1000$ ч классическая теория и первый вариант теории Тимошенко предсказывают совершенно разные картины деформирования материалов фаз композиции пластины, которые как качественно, так и количественно существенно отличаются от картин деформирования, рассчитанных по второму варианту теории Тимошенко. Этот факт и объясняет значительное отличие кривых 1'' и 3'' от кривой 2'' на фиг. 4,b.

Кроме того, сравнение изолиний, изображенных на фиг. 6а и 6d и рассчитанных по одной и той же теории, но в разные моменты времени, указывает на то, что с течением времени картины деформирования материалов фаз композиции существенно изменяются как качественно, так и количественно. При этом, согласно фиг. 6d, во всех компонентах композиции в окрестности внутренней, жестко закрепленной кромки (${{x}_{1}} = {{r}_{0}}$) в процессе ползучести активно развиваются именно деформации поперечного сдвига (об этом свидетельствует поведение кривых $\varepsilon _{ * }^{{(k)}} = {\text{const}}$, $k = 0,\,\,...,\,\,3$ в окрестности заделки, где они по форме близки к параболам, что полностью согласуется с (3.1) при $\eta = 1$), в начальный же момент времени (см. фиг. 6,а) деформации поперечных сдвигов пренебрежимо малы.

В приведенных выше расчетах прогибы по модулю не превосходят 1/5 толщины пластины (см. правый участок кривой 2'' на фиг. 5,b), а интенсивность деформаций материалов компонентов композиции не превосходит 5% (см., например, нижнюю часть фиг. 6,d). Кроме того, в упруго-хрупких волокнах бора интенсивность напряжений $\sigma _{ * }^{{(k)}}$ (см. (2.2)) не превосходит предела прочности этих волокон ($\sigma _{ * }^{{(k)}} < {{\sigma }_{{\text{в }}}}$ = = 3150 МПа [32], $k = 1,\,\,2,\,\,3$). Следовательно, все результаты, полученные в настоящем исследовании в рамках геометрически линейной постановки, являются вполне корректными с механической точки зрения.

6. Заключение. Применение метода шагов по времени с привлечением соответствующих структурных соотношений механики композитов позволило решить задачу о механическом поведении армированных пластин из нелинейно-наследственных материалов, подчиняющихся теории ползучести Ю.Н. Работнова.

Проведенный анализ неупругого изгиба кольцевых бороалюминиевых пластин, поведение связующего которых описывается указанной теорией ползучести, показал, что при кратковременном нагружении таких конструкций для их расчета вполне можно использовать классическую теорию Кирхгофа. Однако при длительном нагружении в связующем рассматриваемых тонкостенных конструкций активно развиваются деформации поперечного сдвига, поэтому расчет ползучести бороалюминиевых пластин, армированных в плоскостях, параллельных срединным поверхностям, необходимо проводить с учетом их ослабленного сопротивления поперечным сдвигам на базе теорий типа Тимошенко. Расчеты показали, что в рамках этих теорий наблюдается ускорение ползучести армированных пластин при достаточно длительных временах их нагружения, что не имеет места, например, при изгибе простейших тонкостенных конструкций типа продольно-армированных балок-стенок, выполненных из тех же материалов компонентов композиции. С увеличением длительности времени нагружения изгибаемых композитных пластин наблюдается существенное увеличение зависимости их податливости от параметров структуры армирования (плотности и направления). Расчеты, выполненные по классической теории и по первому варианту теории Тимошенко, показывают, что при длительном нагружении эти теории предсказывают неоправданно заниженную (на десятки процентов и даже в разы) податливость армированных пластин по сравнению с более точным (в смысле математического моделирования) вторым вариантом теории Тимошенко, который и рекомендуется применять для расчетов механического поведения таких тонкостенных конструкций.