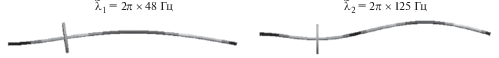Известия РАН. Механика твердого тела, 2019, № 3, стр. 100-107

О ПОДХОДЕ К ОПРЕДЕЛЕНИЮ СОБСТВЕННЫХ ЧАСТОТ ГИРОСКОПИЧЕСКОЙ СИСТЕМЫ С ТРЕНИЕМ В ОБЩЕМ ВИДЕ

А. Н. Брысин^a, А. Н. Никифоров^a, *

^a Институт машиноведения им. А.А. Благонравова РАН
Москва, Россия

Поступила в редакцию 10.07.2018
После доработки 10.07.2018
Принята к публикации 19.11.2018

DOI: 10.1134/S0572329919030061

Аннотация

Работа о приложении методов теории возмущений, приведения массы и теории сопротивления материалов к аналитическому решению задачи о зависимости собственных частот реального ротора от скорости вращения. Полученное приближенное решение сопоставляется с численным.

Ключевые слова: ротор, колебания, характеристическое уравнение, малый параметр

Различные задачи механики твердого тела по праву решаются все чаще численными методами. Их достоинства, в частности лидера по использованию – метода конечных элементов: универсальность (любая система по геометрии и физике), точность и качество конечных результатов (при необходимости в каждой точке системы), получение и/или выявление новых эффектов взаимодействия и переходных процессов. Тем не менее, их совокупный “минус” в математической непрозрачности системы и невозможности получения обозримого решения для быстрого и простого понимания сути происходящего относительно интересующего системного параметра. Отсюда по-прежнему развиваются аналитические методы, в т.ч. для анализа динамики вращающегося тела.

Частоты вращения в машинах и механизмах редко когда превышают вторые собственные частоты роторов. Пусть реальный ротор сведен к безинерционному упруго-гистерезисному валу с массивным диском, т.е. к гироскопической системе с частотно-независимым трением, характеристическое уравнение которой имеет вид [1]:

(1)

$\left| {\begin{array}{*{20}{c}} { - m{{\Omega }^{2}} + {{k}_{{11}}} + {i\eta }{{k}_{{11}}}}&{{{k}_{{12}}} + {i\eta }{{k}_{{12}}}} \\ {{{k}_{{21}}} + {i\eta }{{k}_{{21}}}}&{ - I{{\Omega }^{2}} + {{I}_{0}}\omega \Omega + {{k}_{{22}}} + {i\eta }{{k}_{{22}}}} \end{array}} \right| = 0$

где m – приведенная масса ротора, I – приведенный момент инерции ротора (относительно перпендикуляра к его оси в точке приведения), I₀ – полярный момент инерции ротора (вокруг его оси), k_ij – коэффициенты жесткости ротора в точке приведения, ω – скорость вращения, Ω или Ω_i – некоторая или i-я комплексная круговая частота собственных колебаний (прецессии) ротора, ReΩ – угловая скорость прецессии, η = = η × sgn$\tfrac{{\operatorname{Re} \Omega - \omega }}{{\left| {\operatorname{Re} \Omega - \omega } \right|}}$ – коэффициент гистерезисных потерь (упругой энергии).

В развернутой форме:

(2)

$mI{{\Omega }^{4}} - m{{I}_{0}}\omega {{\Omega }^{3}} - (1 + {i\eta })(m{{k}_{{22}}} + I{{k}_{{11}}}){{\Omega }^{2}} + (1 + {i\eta }){{k}_{{11}}}{{I}_{0}}\omega \Omega + {{(1 + {i\eta })}^{2}}({{k}_{{11}}}{{k}_{{22}}} - k_{{12}}^{2}) = 0$

Данное уравнение дает две положительные и две отрицательные частоты:

${{\Omega }_{{1,2}}} = {{L}_{{1,2}}} + i{{D}_{{1,2}}},{{\Omega }_{{3,4}}} = --{{L}_{{3,4}}}--i{{D}_{{3,4}}}$, где D_i – точная диссипативная (пропорциональная η) добавка к точной круговой собственной частоте ротора L_i.

Положительные частоты собственных колебаний не что иное, как угловые скорости прямой затухающей собственной (невынужденной) прецессии ротора, отрицательные – соответствуют его обратной затухающей собственной прецессии.

Вычисление корней характеристического уравнения вращающейся системы с трением представляет собой нетривиальную задачу. Четвертая степень для алгебраических уравнений является наивысшей, при которой существует решение общего вида, т.е. для любых значений коэффициентов при Ω и свободного члена. В то же время члены, содержащие ω, делают аналитическое решение весьма громоздким. Для получения “обозримых” частот допустимо пренебречь явлениями, связанными с трением и вращением, т.е. диссипативными и гироскопическим.

Пусть Λ_i – i-й корень частотного уравнения вращающейся системы без трения:

(3)

$mI\Lambda _{i}^{4} - m{{I}_{0}}\omega \Lambda _{i}^{3} - \left( {m{{k}_{{22}}} + I{{k}_{{11}}}} \right)\Lambda _{i}^{2} + {{k}_{{11}}}{{I}_{0}}\omega {{\Lambda }_{i}} + {{k}_{{11}}}{{k}_{{22}}} - k_{{12}}^{2} = 0$

а λ_i – i-й корень уравнения частот невращающегося, недемпфированного ротора:

(4)

$mI\lambda _{i}^{4} - \left( {m{{k}_{{22}}} + I{{k}_{{11}}}} \right)\lambda _{i}^{2} + {{k}_{{11}}}{{k}_{{22}}} - k_{{12}}^{2} = 0$

причем λ_3,4 = –λ_1,2, |Λ₃| < λ₁ < Λ₁ и |Λ₄| < λ₂ < Λ₂.

Для пользования методом теории возмущений [2, 3] возможно представление:

${{\Lambda }_{i}} = {{\lambda }_{i}} + {{\Delta }_{\omega }}_{i}$

где Δ_ωi – некоторая гироскопическая добавка (пропорциональная ω) к точной круговой собственной частоте невращающегося ротора λ_i, или:

${{\Lambda }_{i}} = {{\lambda }_{i}}({\text{1}} + {{\varepsilon }_{{\omega i}}}),\;\;{\text{г д е }}\;\;{{\varepsilon }_{{\omega i}}} = {{\Delta }_{\omega }}_{i}{\text{/}}{{\lambda }_{i}}.$

Вследствие малости ε_ωi допустимы приближения:

$\Lambda _{i}^{2} \approx \lambda _{i}^{2}({\text{1}} + {\text{2}}{{\varepsilon }_{{\omega i}}}),\quad \Lambda _{i}^{3} \approx \lambda _{i}^{3}({\text{1}} + {\text{3}}{{\varepsilon }_{{\omega i}}}),\quad \Lambda _{i}^{4} \approx \lambda _{i}^{4}({\text{1}} + {\text{4}}{{\varepsilon }_{{\omega i}}})$

Вставляя эти равенства в (3), приравнивая к нулю сумму членов, содержащих ε_ωi и ω, а также сумму оставшихся членов, можно получить порождающее уравнение (4) и малую гироскопическую добавку к λ_i:

(5)

${{\varepsilon }_{{\omega i}}} = {{I}_{0}}\omega {{\lambda }_{i}}\frac{{m\lambda _{i}^{2} - {{k}_{{11}}}}}{{{\text{4}}mI\lambda _{i}^{4} - {\text{3}}m{{I}_{0}}\omega \lambda _{i}^{3} - {\text{2}}\left( {m{{k}_{{22}}} + I{{k}_{{11}}}} \right)\lambda _{i}^{2} + {{k}_{{11}}}{{I}_{0}}\omega {{\lambda }_{i}}}}$

По аналогии:

$\begin{gathered} {{\Omega }_{i}} \approx {{\Lambda }_{i}} + {\text{i}}{{\Delta }_{i}}, \\ {{\Omega }_{i}} \approx {{\Lambda }_{i}}({\text{1}} + {\text{i}}{{\varepsilon }_{{\eta i}}}),\quad \Omega _{i}^{2} \approx \Lambda _{i}^{2}({\text{1}} + {\text{i2}}{{\varepsilon }_{{\eta i}}}),\quad \Omega _{i}^{3} \approx \Lambda _{i}^{3}({\text{1}} + {\text{i3}}{{\varepsilon }_{{\eta i}}}),\quad \Omega _{i}^{4} \approx \Lambda _{i}^{4}({\text{1}} + {\text{i4}}{{\varepsilon }_{{\eta i}}}) \\ \end{gathered} $

Здесь и далее Λ_i – приближенная круговая собственная частота вращающегося ротора с трением, Δ_i и ε_ηi = Δ_i/Λ_i – приближенная и малая диссипативные добавки к ней.

Подставляя эти выражения в характеристическое уравнение (1), отбрасывая члены, содержащие квадраты малых величин и разделяя действительную и мнимую части, можно выразить малую диссипативную добавку:

(6)

${{\varepsilon }_{{\eta i}}} = \eta \frac{{(m{{k}_{{22}}} + I{{k}_{{11}}})\Lambda _{i}^{2} - {{k}_{{11}}}{{I}_{0}}\omega {{\Lambda }_{i}} - 2({{k}_{{11}}}{{k}_{{22}}} - k_{{12}}^{2})}}{{4mI\Lambda _{i}^{4} - 3m{{I}_{0}}\omega \Lambda _{i}^{3} - 2\left( {m{{k}_{{22}}} + I{{k}_{{11}}}} \right)\Lambda _{i}^{2} + {{k}_{{11}}}{{I}_{0}}\omega {{\Lambda }_{i}}}}$

На числовых примерах можно убедиться, что входящая в формулу (5) дробь всегда положительна, в т.ч. при отрицательных λ_i и значениях ω > λ₂, а дробь формулы (6) положительна, пока ω не превышает некоторого достаточно значительного предела. В результате знак ε_ωi зависит только от знака λ_i, поэтому произведение ε_ωiλ_i неизменно положительно, а знак ε_ηi фактически – от знака η, по которому может быть сделан вывод об устойчивости (о затухании или нарастании) собственной прецессии ротора. Прямая – устойчива, пока η > 0, т.е. затухает, пока ω < ReΩ. Обратная – устойчива, если η < 0, т.е. затухает при любой скорости вращения.

Искомые комплексные собственные частоты ротора:

$\begin{gathered} {{\Omega }_{{\text{1}}}} \approx {{\lambda }_{{\text{1}}}}({\text{1}} + {{\varepsilon }_{\omega }}_{{\text{1}}})({\text{1}} + {\text{i}}{{\varepsilon }_{{\eta {\text{1}}}}}),\quad {{\Omega }_{{\text{2}}}} \approx {{\lambda }_{{\text{2}}}}({\text{1}} + {{\varepsilon }_{\omega }}_{{\text{2}}})({\text{1}} + {\text{i}}{{\varepsilon }_{{\eta {\text{2}}}}}), \\ {{\Omega }_{{\text{3}}}} \approx {{\lambda }_{{\text{3}}}}({\text{1}} + {{\varepsilon }_{\omega }}_{{\text{3}}})({\text{1}} + {\text{i}}{{\varepsilon }_{{\eta {\text{3}}}}}),\quad {{\Omega }_{{\text{4}}}} \approx {{\lambda }_{{\text{4}}}}({\text{1}} + {{\varepsilon }_{\omega }}_{{\text{4}}})({\text{1}} + {\text{i}}{{\varepsilon }_{{\eta {\text{4}}}}}) \\ \end{gathered} $

Погрешность предложенного аналитического решения задачи о зависимости частот собственных колебаний гироскопической системы с трением от скорости вращения оценена графически на примере материализованного вала с диском (табл. 1).

Таблица 1.

Данные экспериментальной роторной системы	Обозначение и значение
Диаметр вала	8 мм
Длина вала	l = 645 мм
Погонная масса вала	m₀ = 0.4 кг/м
Изгибная жесткость вала	EJ = 40 Нм²
Радиус диска	R = 42 мм
Масса диска	m₁ = 270 г
Осевой момент инерции диска	I₀ = 2.38 · 10^–4 кгм²
Расстояние между защемленным концом и диском	l₁ = 1/4l

Результаты модального анализа невращающегося опытного ротора в зависимости от условий опирания на одном из концов вала иллюстрируют фиг. 1 и фиг. 2. Первая иллюстрация охватывает две низшие частоты и формы собственных колебаний консольного ротора (с защемленным и свободным концами), а вторая – две низшие собственные частоты и формы ротора с опорами на концах (с защемленным и свободно опертым концами).

Фиг. 1

Фиг. 2

Приведенные инерционно-упругие характеристики экспериментальной системы (для точки симметрии диска) получены с использованием методов конечных элементов, а именно в программе Ansys [4, 5], приведения массы [6, 7] и теории сопротивления материалов [7–9].

Как известно, коэффициенты жесткости балки с закрепленным и свободным концами на расстоянии l₁ от конца-заделки:

${{k}_{{11}}} = \frac{{12EJ}}{{l_{1}^{3}}},\quad {{k}_{{12}}} = {{k}_{{21}}} = - \frac{{6EJ}}{{l_{1}^{2}}},\quad {{k}_{{22}}} = \frac{{4EJ}}{{{{l}_{1}}}}{\text{,}}\quad {{K}_{{11}}} = {{k}_{{11}}} - \frac{{k_{{12}}^{2}}}{{{{k}_{{22}}}}} = \frac{{3EJ}}{{l_{1}^{3}}}$

Значения k_ij для опытного консольного ротора (таблица, фиг. 1):

(7)

${{k}_{{11}}} = {\text{11}}{\text{.51}} \cdot {\text{1}}{{{\text{0}}}^{4}}{\text{Н /м }},\quad {{k}_{{12}}} = {{k}_{{21}}} = - 9.28 \cdot {\text{1}}{{{\text{0}}}^{3}}{\text{Н }},\quad {{k}_{{22}}} = {\text{1}}{{{\text{0}}}^{3}}{\text{Н м ,}}\quad {{K}_{{11}}} = {\text{2}}{\text{.88}} \cdot {\text{1}}{{{\text{0}}}^{4}}{\text{Н /м }}$

Вместе с тем в одноименном методе исходят из того, что приведенная масса – это такая сосредоточенная масса, которая, двигаясь со скоростью центра приведения, имеет такую же кинетическую энергию W, какой обладают все движущиеся массы системы:

$W = \int {\frac{{v_{{{\text{d}}m}}^{2}{\text{d}}m}}{2}} + \sum\limits_{i = 1}^n {\frac{{{{m}_{i}}v_{i}^{2}}}{2}} $

где интеграл распространен на всю распределенную массу системы, ${{v}_{{{\text{d}}m}}}$ – скорость элемента dm распределенной массы, ${{v}_{i}}$ – скорость i-й сосредоточенной массы m_i системы.

Этому тождеству умножением и делением правой его части на общую массу M системы, а также на квадрат скорости ${{v}_{0}}$ заранее выбранной в ней точки (приведения) придают вид:

$W = \frac{{{\kappa }Mv_{0}^{2}}}{2},$ где ${\kappa } = \frac{1}{M}\left[ {\int {{{{\left( {\frac{{{{v}_{{{\text{d}}m}}}}}{{{{v}_{0}}}}} \right)}}^{2}}{\text{d}}m} + \sum\limits_{i = 1}^n {{{m}_{i}}{{{\left( {\frac{{{{v}_{i}}}}{{{{v}_{0}}}}} \right)}}^{2}}} } \right]$

Произведение ${\kappa }M$ = m называют приведенной массой, а безразмерную величину ${\kappa }$ – коэффициентом приведения массы. Отношение скоростей равно отношению перемещений точек системы при движении, поэтому:

$m = \int {{{{\left( {\frac{{{{x}_{{{\text{d}}m}}}}}{{{{x}_{0}}}}} \right)}}^{2}}{\text{d}}m} + \sum\limits_{i = 1}^n {{{m}_{i}}{{{\left( {\frac{{{{x}_{i}}}}{{{{x}_{0}}}}} \right)}}^{2}}} $

В приложении к роторной системе dm = m₀dz, где dz – элемент длины l вала:

$m = {{m}_{0}}\int\limits_0^l {{{{\left( {\frac{{x(z)}}{{{{x}_{0}}}}} \right)}}^{2}}dz} + \sum\limits_{i = 1}^n {{{m}_{i}}{{{\left( {\frac{{{{x}_{i}}}}{{{{x}_{0}}}}} \right)}}^{2}}} $

Так как x(z) это функция, описывающая вид осевой линии ротора при его колебаниях по собственной форме, x₀ – значение функции x(z) в точке приведения, x_i – значение функции x(z) в центре прикрепления i-го диска, то в качестве функции x(z) может быть выбрано уравнение упругой линии балки (вала) со статически приложенной к ней (к нему) в точке приведения силой.

Согласно теории сопротивления материалов прогибы консольной балки при действии сосредоточенной поперечной силы F_x на расстоянии l₁ от заделанного конца:

$x(z) = \frac{{{{F}_{x}}}}{{6EJ}}(3{{l}_{1}}{{z}^{2}} - {{z}^{3}})\quad {\text{п р и }}\quad z \leqslant {{l}_{1}},\quad x(z) = \frac{{{{F}_{x}}}}{{6EJ}}(3l_{1}^{2}z - l_{1}^{3})\quad {\text{п р и }}\quad z \geqslant {{l}_{1}}$

Если распределенная и сосредоточенная массы консольного ротора приводятся к точке z = l₁, т.е. к точке симметрии насаженного на вал диска, то: ${{x}_{0}} = {{x}_{1}} = \frac{{{{F}_{x}}l_{1}^{3}}}{{3EJ}}$ и

$m = {{m}_{0}}\int\limits_0^{{{l}_{1}}} {{{{\left( {\frac{{3{{l}_{1}}{{z}^{2}} - {{z}^{3}}}}{{2l_{1}^{3}}}} \right)}}^{2}}{\text{d}}z} + {{m}_{0}}\int\limits_{{{l}_{1}}}^l {{{{\left( {\frac{{3l_{1}^{2}z - l_{1}^{3}}}{{2l_{1}^{3}}}} \right)}}^{2}}{\text{d}}z} + {{m}_{1}}$

или

$m = \frac{{33}}{{140}}{{m}_{0}}{{l}_{1}} + \left[ {\frac{1}{4} + \frac{3}{4}{{{\left( {\frac{l}{{{{l}_{1}}}}} \right)}}^{2}}} \right]{{m}_{0}}{{l}_{2}} + {{m}_{1}}$

где l₂ = l – l₁.

Приведенный поперечный момент инерции ротора (относительно перпендикуляра к его оси в точке приведения) может быть выражен из порождающего уравнения (4):

$I = \frac{{{{k}_{{22}}}}}{{\lambda _{2}^{2}}}\frac{{\lambda _{2}^{2} - {{{{K}_{{11}}}} \mathord{\left/ {\vphantom {{{{K}_{{11}}}} m}} \right. \kern-0em} m}}}{{\lambda _{2}^{2} - {{{{k}_{{11}}}} \mathord{\left/ {\vphantom {{{{k}_{{11}}}} m}} \right. \kern-0em} m}}}$.

Соответствующие значения для экспериментального консольного ротора (табл. 1, фиг. 1):

(8)

$m = 2.62\;{\text{к г ,}}\quad I = 86 \cdot {\text{1}}{{0}^{{ - {\text{4}}}}}\;{\text{к г }}{{{\text{м }}}^{{\text{2}}}}$

Коэффициент демпфирования η для экспериментального консольного (η) и опертого (${\tilde {\eta }}$) на статор обоими концами вала с диском найден опытным путем – измерением затухающих собственных колебаний ротора в результате ударного их возбуждения с последующим определением логарифмического их декремента:

$d = \frac{1}{n}\ln \frac{{{{A}_{i}}}}{{{{A}_{{i + n}}}}},\quad \eta = d{\text{/}}\pi ,$

где A_i – амплитуда i-го колебания, A_i ₊_n – амплитуда i + n-го колебания, n – общее число отслеженных колебаний.

Для минимизации влияния на результаты опытов случайных ошибок и факторов ударное испытание “каждого” ротора проводилось четыре раза. За окончательные значения η и ${\tilde {\eta }}$ принимались средние арифметические, вычисленные после всех испытаний:

(9)

$\eta = 0.0{\text{29}},\quad {\tilde {\eta }} = 0.032$

По данным (7–9) определены как точные Ω_i = L_i + iD_i непосредственно из (1), так и приближенные Ω_i = Λ_i + iΔ_i, где Λ_i = λ_i(1 + ε_ωi), Δ_i = ε_ηiΛ_i, с помощью (3), (4). Различие значений по действительной части получилось менее 2%, по мнимой – менее 5%. Сопоставимая с погрешностями аналитического округления точность, конечно, во многом обусловлена отношением I₀/I, много меньшим единицы.

Приняв за приемлемую точность 5%-е несовпадение Λ_i с L_i и 15%-е несовпадение Δ_i с D_i при скоростях вращения ω вплоть до второй критической частоты невращающегося ротора λ₂, установлен предел применимости разработанного подхода, т.е. предельное значение для показателя гироскопического действия в случае консольной роторной системы:

I₀/I ≈ 0.05

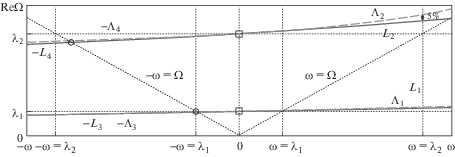
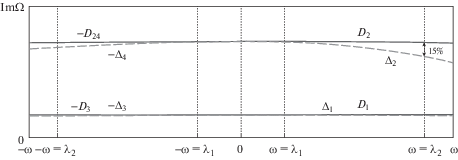
По (7–9) и при I₀ = 4 ⋅ 10^–4 кгм² построены зависимости L_i(ω), Λ_i(ω) и D_i(ω), Δ_i(ω), представленные на фиг. 3 и фиг. 4. Ввиду кососимметричного расположения кривых используется не правая полуплоскость с осью абсцисс ω (диаграмма Кэмпбелла), а верхняя полуплоскость с осью абсцисс от –ω до +ω (отвечающая положительным значениям Ω), что несколько удобнее. Сплошными кривыми показаны точные, а пунктирными – приближенные вещественные и мнимые части круговых собственных частот экспериментального консольного ротора. Также посредством обозначений “◻” и “○” указаны критические частоты соответственно невращающегося ротора и в случае его обратной прецессии.

Фиг. 3

Фиг. 4

Как видно, все частоты и их мнимые составляющие хорошо согласуются, пока скорость вращения ω локализуется в окрестности первой критической частоты невращающегося ротора λ₁. Это вполне ожидаемо от “первого приближения”. В то же время нетривиально, что и когда ω близка к λ₂, лишь действительная и мнимая части второй точной частоты прямой прецессии (L₂ и D₂) существенно расходятся с соответствующими компонентами приближенной (Λ₂ и Δ₂).

Когда вал с дисками имеет опоры в концевых сечениях, влияние гироскопических моментов дисков на амплитудно-частотную характеристику обычно оказывается слабее, чем в случае консольного ротора. Данный факт должен сопровождаться расширением пределов применимости разработанного подхода в приложении к роторным системам без консольных свесов. Однако в случае ухода от схем с консольными вылетами низшие собственные частоты роторов обычно повышаются, и при близких к ним скоростях вращения гироскопические члены (с множителем I₀ω) будут больше, а пределы применимости – уже. Для понимания результирующей тенденции на практике, выполнен соответствующий расчет.

В работе [9] показано, что коэффициенты жесткости невращающегося вала с защемленным и свободно опертым концами на расстоянии l₁ от защемленного конца:

${{\tilde {k}}_{{11}}} = 3EJ\frac{{l_{1}^{3} + 4l_{2}^{3}}}{{l_{1}^{3}l_{2}^{3}}},\quad {{\tilde {k}}_{{12}}} = {{\tilde {k}}_{{21}}} = - 3EJ\frac{{2l_{2}^{2} - l_{1}^{2}}}{{l_{1}^{2}l_{2}^{2}}},\quad {{\tilde {k}}_{{22}}} = EJ\frac{{3l + {{l}_{2}}}}{{{{l}_{1}}{{l}_{2}}}}{\text{,}}\quad {{\tilde {K}}_{{11}}} = \frac{{12EJ{{l}^{3}}}}{{l_{1}^{3}l_{2}^{2}(3l + {{l}_{2}})}}$

а его прогибы при действии сосредоточенной поперечной силы F_x в этом же месте:

$x(z) = \frac{{{{R}_{{\text{A}}}}}}{{6EJ}}{{z}^{3}} - \frac{{{{M}_{{\text{A}}}}}}{{2EJ}}{{z}^{2}}\quad {\text{п р и }}\quad z \leqslant {{l}_{1}}$, $x(z) = \frac{{{{R}_{{\text{A}}}}}}{{6EJ}}{{z}^{3}} - \frac{{{{M}_{{\text{A}}}}}}{{2EJ}}{{z}^{2}} + \frac{{{{F}_{x}}}}{{6EJ}}{{(z - {{l}_{1}})}^{3}}\quad {\text{п р и }}\quad z \geqslant {{l}_{1}}$

где ${{R}_{{\text{A}}}} = {{F}_{x}}\frac{{3l_{1}^{2}l - l_{1}^{3} - 2{{l}^{3}}}}{{2{{l}^{3}}}}$, ${{M}_{{\text{A}}}} = {{F}_{x}}\frac{{3l_{1}^{2}l - l_{1}^{3} - 2{{l}_{1}}{{l}^{2}}}}{{2{{l}^{2}}}}$ – реакции “опоры-заделки”.

В случае приведения роторных масс к точке z = l₁:

${{x}_{0}} = {{x}_{1}} = \frac{{{{F}_{x}}l_{1}^{3}l_{2}^{2}(3l + {{l}_{2}})}}{{12EJ{{l}^{3}}}}$

Величина приведенной массы ротора с защемленным и свободно опертым концами определяется по формуле:

$\begin{array}{*{20}{c}} {\tilde {m} = {{m}_{0}}\int\limits_0^{{{l}_{1}}} {{{{\left( {\frac{{(l_{2}^{3} - 3{{l}^{2}}{{l}_{2}}){{z}^{3}} + 3l{{l}_{2}}({{l}^{2}} - l_{2}^{2}){{z}^{2}}}}{{l_{1}^{3}l_{2}^{2}(3l + {{l}_{2}})}}} \right)}}^{2}}dz} + } \\ { + \;{{m}_{0}}\int\limits_{{{l}_{1}}}^l {{{{\left( {\frac{{(l_{2}^{3} - 3{{l}^{2}}{{l}_{2}}){{z}^{3}} + 3l{{l}_{2}}({{l}^{2}} - l_{2}^{2}){{z}^{2}} + 2{{l}^{3}}{{{(z - {{l}_{1}})}}^{3}}}}{{l_{1}^{3}l_{2}^{2}(3l + {{l}_{2}})}}} \right)}}^{2}}dz} + {{m}_{1}}} \end{array}$

Интегрируя и переписывая соответствующим образом формулу для приведенного поперечного момента инерции, получится:

$\tilde {m} = \frac{{{{m}_{0}}{{l}^{3}}(24{{l}^{4}} - 24{{l}^{3}}{{l}_{1}} - 4{{l}^{2}}l_{1}^{2} + 8ll_{1}^{3} - l_{1}^{4})}}{{35l_{1}^{2}{{{(4{{l}^{2}} - 5l{{l}_{1}} + l_{1}^{2})}}^{2}}}} + {{m}_{1}},\quad \tilde {I} = \frac{{{{{\tilde {k}}}_{{22}}}}}{{\tilde {\lambda }_{2}^{2}}}\frac{{\tilde {\lambda }_{2}^{2} - {{{{{\tilde {K}}}_{{11}}}} \mathord{\left/ {\vphantom {{{{{\tilde {K}}}_{{11}}}} {\tilde {m}}}} \right. \kern-0em} {\tilde {m}}}}}{{\tilde {\lambda }_{2}^{2} - {{{{{\tilde {k}}}_{{11}}}} \mathord{\left/ {\vphantom {{{{{\tilde {k}}}_{{11}}}} {\tilde {m}}}} \right. \kern-0em} {\tilde {m}}}}}$

При рассматриваемых условиях опирания концов экспериментального ротора на статор (табл. 1, фиг. 2) значения его приведенных характеристик:

(10)

$\begin{gathered} {{{\tilde {k}}}_{{11}}} = {\text{11}}{\text{.62}} \cdot {\text{1}}{{{\text{0}}}^{4}}\;{\text{Н /м }},\quad {{{\tilde {k}}}_{{12}}} = {{{\tilde {k}}}_{{21}}} = - 8.76 \cdot {\text{1}}{{{\text{0}}}^{3}}\;{\text{Н }},\quad {{{\tilde {k}}}_{{22}}} = 1.25 \cdot {\text{1}}{{{\text{0}}}^{3}}\;{\text{Н м ,}} \\ {{{\tilde {K}}}_{{11}}} = 5.46 \cdot {\text{1}}{{{\text{0}}}^{4}}\;{\text{Н /м ,}}\quad \tilde {m} = 0.53\;{\text{к г ,}}\quad \tilde {I} = 26 \cdot {\text{1}}{{0}^{{ - {\text{4}}}}}\;{\text{к г }}{{{\text{м }}}^{{\text{2}}}} \\ \end{gathered} $

В то же время условия опирания не влияют на осевой момент инерции ротора I₀ и практически не сказываются на коэффициенте трения ${\eta } \approx {\tilde {\eta }} \approx 0.03$.

Отвечающие параметрам (10), точные и приближенные комплексные частоты Ω показали, что расхождение между L_i и Λ_i менее чем на 5%, а также между D_i и Δ_i менее чем на 15% в диапазоне 0 < ω < ${{\tilde {\lambda }}_{2}}$ будет, если “гироскопическое число”:

${{{{I}_{0}}} \mathord{\left/ {\vphantom {{{{I}_{0}}} {\tilde {I}}}} \right. \kern-0em} {\tilde {I}}} < 0.05$

Таким образом, в случае переноса больших инерционных масс с консоли в пролет между опорами и наоборот, ни первая тенденция, связанная с уменьшением гироскопических моментов и получением увеличившихся собственных частот и гироскопических членов, ни вторая (противоположная), обусловленная бóльшими гироскопическими моментами и меньшими собственными частотами и гироскопическими членами, не является превалирующей, т.е. вкупе предел применимости предлагаемого подхода для роторов без консолей такой же, как для валов с консольным расположением дисков.

В общем можно заключить, что представлен полностью аналитический подход с его возможностями по отысканию собственных частот гироскопической системы с трением. Полученные приближенные зависимости частот от скорости вращения удовлетворительно согласуются с точными. Особенно хорошо определяются критические скорости обратной прецессии (погрешность не превысит 5% пока гироскопическое число меньше 0.09). Все это выгодно использовать, например, в задаче обкатки ротором статора.

Работа выполнена при финансовой поддержке Минобрнауки России в рамках Федеральной целевой программы “Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2014–2020 годы”, Соглашение о предоставлении субсидии № 14.607.21.0191 от 26.09.2017 г., проект RFMEFI60717X0191.

Список литературы

Крестниковский К.В., Никифоров А.Н. Частота обкатки ротором статора в зависимости от зазоров между ними (часть I: статическая сторона задачи) // Приводы и компоненты машин. 2017. № 3–4. С. 12–16.
Nayfeh Ali H. Perturbation Methods. NY: Wiley, 1973. 425 p. = Найфэ А. Методы возмущений. М.: Мир, 1976. 456 с.
Маслов В.П. Асимптотические методы и теория возмущений. М.: Наука, 1988. 312 с.
Moaveni S. Finite Element Analysis: Theory and Application with ANSYS. Pearson Education. 3^rd Edition, 2008. 868 p.
Огородникова О.М. Расчет конструкций в ANSYS. Сборник учебных материалов. Екатеринбург: УГТУ-УПИ, 2009. 454 с.
Шиманский Ю.А. Динамический расчет судовых конструкций. Л.: Судпромгиз, 1963. 444 с.
Заславский Б.В. Краткий курс сопротивления материалов. Учебник для авиационных специальностей вузов. М.: Машиностроение, 1986. 328 с.
Биргер И.А., Мавлютов Р.Р. Сопротивление материалов: Учебное пособие. М.: Наука, 1986. 560 с.
Феодосьев В.И. Сопротивление материалов. М.: Наука, 1970. 544 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал