Известия РАН. Механика твердого тела, 2019, № 3, стр. 136-146

Продольные волны Похгаммера–Кри: аномальная поляризация

А. В. Ильяшенко^*

Московский государственный строительный университет
Москва, Россия

Поступила в редакцию 25.12.2017
После доработки 25.12.2017
Принята к публикации 03.05.2018

DOI: 10.1134/S0572329919030103

Аннотация

Анализируются точные решения волнового уравнения Похгаммера–Кри, описывающего распространение гармонических волн в упругом цилиндрическом стержне. Для продольных аксиально симметричных мод впервые проведен спектральный анализ матрицы дисперсионного уравнения. Получены аналитические выражения для поляризации волн. На поверхности стержня для фундаментальной продольной аксиально симметричной моды определены коэффициенты поляризации соответствующих волн и проведен анализ вариации этих коэффициентов в зависимости от частоты. Обнаружено, что при фазовой скорости фундаментальной аксиально симметричной продольной моды, совпадающей со скоростью поперечной волны, происходит одновременное обращение в нуль всех компонент перемещений на боковой поверхности стержня, что представляется исключительно важным для проектирования акустических волноводов.

Ключевые слова: волны Похгаммера–Кри, поляризация, дисперсия, спектральный анализ

1. Введение. Впервые дисперсионные уравнения, описывающие распространение гармонических волн в цилиндрическом стержне, называемых волнами Похгаммера–Кри, получены в [1–3]. Однако, решения этих уравнений, связывающие фазовую (или групповую) скорость с частотой, оставались практически неизученными вплоть до середины прошлого века, когда в [4–23] с помощью численного анализа дисперсионных уравнений [1–3, 8] были найдены первые ветви дисперсионных кривых. Надо отметить, что в [4–20] исследовались продольные аксиально симметричные моды, тогда как в [21–23] рассматривались также изгибные и крутильные моды.

С помощью асимптотических методов в [4–12] были найдены длинноволновой и коротковолновой пределы для фазовой скорости фундаментальной продольной аксиально симметричной моды. При этом коротковолновой предел (${{c}_{{{\text{1,lim}}}}}$) фазовой скорости при $\omega \to \infty $:

(1.1)

${{c}_{{{\text{1,lim}}}}} = {{c}_{R}}$

совпал со скоростью волны Рэлея (${{c}_{R}}$), а длинноволновой предел дал следующее значение фазовой скорости ${{c}_{{{\text{2,lim}}}}}$:

(1.2)

${{c}_{{{\text{2,lim}}}}} = \sqrt {\frac{E}{\rho }} $

где $E$ – модуль упругости, а $\rho $ – плотность материала стержня. В [4–6] для скорости ${{c}_{{{\text{2,lim}}}}}$ предложено наименование “стержневая” скорость.

Дисперсионные кривые высших мод в терминах безразмерных фазовой частоты и волнового числа с помощью численных методов исследовались в [4–20], причем в [8], по-видимому, впервые были вычислены корни дисперсионного уравнения применительно и построены первые три дисперсионные кривые, отвечающие низшим продольным аксиально симметричным модам.

Помимо собственно дисперсионных кривых в [19] численно исследовалось распределение по сечению стержня амплитуд компонент перемещений для первых трех продольных аксиально симметричных мод.

Одна из интересных особенностей незатухающих высших мод $L(0,m)$, m > 1 соответствующих дисперсионных кривых, появляется при $\gamma \to 0$:

(1.3)

$\mathop {\lim }\limits_{\gamma \to 0} \frac{{\partial \Omega }}{{\partial \gamma }} = 0$

Фактически, условие (1.3) означает наличие в высших модах горизонтальной асимптоты в дисперсионной зависимости $\omega (c)$ при фазовой скорости $c \to \infty $. Здесь обнаруживается связь с незатухающими высшими модами соответствующих дисперсионных кривых волн Лэмба [24], для которых также выполняется соотношение (1.3). Аналогичные эффекты возникают и в случае изгибных волн в балках Тимошенко [25].

2. Основные соотношения. Уравнения движения для изотропного упругого тела в отсутствии массовых сил представимы в виде

(2.1)

$c_{1}^{2}\nabla {\text{div}}{\mathbf{u}} - c_{2}^{2}{\text{rot}}\,{\text{rot}}{\mathbf{u}} = {\mathbf{\ddot {u}}}$

где u – поле перемещений, ${{c}_{1}}$, ${{c}_{2}}$ – скорости продольной и поперечной объемных волн в среде, причем

(2.2)

${{c}_{1}} = \sqrt {\frac{{\lambda + 2\mu }}{\rho }} ,\quad {{c}_{2}} = \sqrt {\frac{\mu }{\rho }} $

В (2.2) $\lambda $, $\mu $ – константы Ламе, $\rho $ – плотность среды.

Далее для векторного поля u применяется представление Гельмгольца

(2.3)

${\mathbf{u}} = \nabla \Phi + {\text{rot}}\Psi $

где $\Phi $ и $\Psi $ соответственно скалярный и векторный потенциалы. В цилиндрических координатах представление Гельмгольца (2.3) для физических компонент вектора перемещений приобретает вид

(2.4)

$\begin{gathered} {{u}_{r}} = \frac{{\partial \Phi }}{{\partial r}} + \frac{1}{r}\frac{{\partial {{\Psi }_{z}}}}{{\partial \theta }} - \frac{{\partial {{\Psi }_{\theta }}}}{{\partial z}} \\ {{u}_{\theta }} = \frac{1}{r}\frac{{\partial \Phi }}{{\partial \theta }} + \frac{{\partial {{\Psi }_{r}}}}{{\partial z}} - \frac{{\partial {{\Psi }_{z}}}}{{\partial r}} \\ {{u}_{z}} = \frac{{\partial \Phi }}{{\partial z}} + \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r{{\Psi }_{\theta }}} \right) - \frac{1}{r}\frac{{\partial {{\Psi }_{r}}}}{{\partial \theta }} \\ \end{gathered} $

причем из условия аксиальной симметрии следует

(2.5)

${{u}_{\theta }} = 0$

Подстановка представления (2.3) в уравнения движения (2.1) дает

(2.6)

$c_{1}^{2}\Delta \Phi = \ddot {\Phi },\quad c_{2}^{2}\Delta \Psi = \ddot {\Psi }$

Для гармонической волны, распространяющейся в направлении оси $z$, потенциалы (2.6) представимы в виде

(2.7)

$\Phi = {{\Phi }_{0}}(x{\text{'}}){{e}^{{i\gamma (z - ct)}}},\quad \Psi = {{\Psi }_{0}}(x{\text{'}}){{e}^{{i\gamma (z - ct)}}}$

где $\gamma $ – волновое число, связанное с фазовой скоростью c и круговой частотой $\omega $ соотношением

(2.8)

$\gamma = \frac{\omega }{c}$

В (2.7) $x{\text{'}}$ – координата в поперечном сечении (${\mathbf{x}}{\text{'}} = {\mathbf{x}} - ({\mathbf{n}} \cdot {\mathbf{x}}){\mathbf{n}}$), ${\mathbf{n}}$ – волновой вектор, $z = {\mathbf{n}} \cdot {\mathbf{x}}$, t – время.

Подстановка представлений (2.7) в уравнения (2.6) дает уравнения Гельмгольца для соответствующих потенциалов

(2.9)

$\Delta {{\Phi }_{0}} + \left( {\frac{{{{c}^{2}}}}{{c_{1}^{2}}} - 1} \right){{\gamma }^{2}}{{\Phi }_{0}} = 0,\quad \Delta {{\Psi }_{0}} + \left( {\frac{{{{c}^{2}}}}{{c_{2}^{2}}} - 1} \right){{\gamma }^{2}}{{\Psi }_{0}} = 0$

Переход в (2.9) к цилиндрическим координатам для скалярного потенциала ${{\Phi }_{0}}$ с учетом аксиальной симметрии потенциала Φ₀:

(2.10)

$\frac{{\partial {{\Phi }_{0}}}}{{\partial \theta }} = 0$

приводит к уравнению Бесселя

(2.11)

$\frac{1}{r}\frac{d}{{dr}}r\frac{d}{{dr}}{{\Phi }_{0}}(r) + \left( {\frac{{{{c}^{2}}}}{{c_{1}^{2}}} - 1} \right){{\gamma }^{2}}{{\Phi }_{0}}(r) = 0$

где c – фазовая скорость волны. Решения уравнения (2.11) выражаются через функции Бесселя первого и второго рода нулевого порядка

(2.12)

${{\Phi }_{0}}(r) = {{C}_{1}}{{J}_{0}}({{q}_{1}}r) + {{C}_{2}}{{Y}_{0}}({{q}_{1}}r)$

где ${{C}_{k}}$, $k = 1,2$ – неизвестные, вообще говоря, комплексные коэффициенты и

(2.13)

$q_{{_{1}}}^{2} = \left( {\frac{{{{c}^{2}}}}{{c_{1}^{2}}} - 1} \right){{\gamma }^{2}}$

Учет аксиальной симметрии компонент потенциала ${{\Psi }_{0}}$ обеспечивается условиями

(2.14)

$\frac{{\partial {{\Psi }_{r}}}}{{\partial \theta }} = \frac{{\partial {{\Psi }_{\theta }}}}{{\partial \theta }} = \frac{{\partial {{\Psi }_{z}}}}{{\partial \theta }} = 0$

Уравнения (2.9), (2.14) дают уравнения Бесселя (для соответствующих физических компонент):

(2.15)

$\begin{gathered} \frac{1}{r}\frac{d}{{dr}}r\frac{d}{{dr}}{{\Psi }_{r}}(r) + \left( {\left( {\frac{{{{c}^{2}}}}{{c_{2}^{2}}} - 1} \right){{\gamma }^{2}} - \frac{1}{{{{r}^{2}}}}} \right){{\Psi }_{r}}(r) = 0 \\ \frac{1}{r}\frac{d}{{dr}}r\frac{d}{{dr}}{{\Psi }_{\theta }}(r) + \left( {\left( {\frac{{{{c}^{2}}}}{{c_{2}^{2}}} - 1} \right){{\gamma }^{2}} - \frac{1}{{{{r}^{2}}}}} \right){{\Psi }_{\theta }}(r) = 0 \\ \frac{1}{r}\frac{d}{{dr}}r\frac{d}{{dr}}{{\Psi }_{z}}(r) + \left( {\frac{{{{c}^{2}}}}{{c_{2}^{2}}} - 1} \right){{\gamma }^{2}}{{\Psi }_{z}}(r) = 0 \\ \end{gathered} $

Решение уравнений (2.15) имеет вид

(2.16)

$\begin{gathered} {{\Psi }_{\theta }}(r) = {{C}_{3}}{{J}_{1}}({{q}_{2}}r) + {{C}_{4}}{{Y}_{1}}({{q}_{2}}r) \\ {{\Psi }_{r}}(r) = {{C}_{5}}{{J}_{1}}({{q}_{2}}r) + {{C}_{6}}{{Y}_{1}}({{q}_{2}}r) \\ {{\Psi }_{z}}(r) = {{C}_{7}}{{J}_{0}}({{q}_{2}}r) + {{C}_{8}}{{Y}_{0}}({{q}_{2}}r) \\ \end{gathered} $

В (2.16) ${{C}_{k}}$, $k = 3,\; \ldots ,\;8$ неизвестные комплексные коэффициенты и

(2.17)

$q_{{_{2}}}^{2} = \left( {\frac{{{{c}^{2}}}}{{c_{2}^{2}}} - 1} \right){{\gamma }^{2}}$

Условие аксиальной симметрии векторного потенциала $\Psi $ накладывает еще одно ограничение [14, 16]:

(2.18)

${{\Psi }_{r}} = {{\Psi }_{z}} = 0$

С учетом (2.4), (2.5), (2.12), (2.16), (2.18), векторное поле, отвечающее распространению продольной аксиально симметричной гармонической незатухающей волны в цилиндрическом стержне, оказывается представимым в виде [19]:

(2.19)

$\begin{gathered} {{u}_{r}} = - \left[ {{{q}_{1}}\left( {{{C}_{1}}{{J}_{1}}({{q}_{1}}r) + {{C}_{2}}{{Y}_{1}}({{q}_{1}}r)} \right) + i\gamma \left( {{{C}_{3}}{{J}_{1}}({{q}_{2}}r) + {{C}_{4}}{{Y}_{1}}({{q}_{2}}r)} \right)} \right]{{e}^{{i\gamma (z - ct)}}} \\ {{u}_{\theta }} = 0 \\ {{u}_{z}} = \left[ {i\gamma \left( {{{C}_{1}}{{J}_{0}}({{q}_{1}}r) + {{C}_{2}}{{Y}_{0}}({{q}_{1}}r)} \right) + {{q}_{2}}\left( {{{C}_{3}}{{J}_{0}}({{q}_{2}}r) + {{C}_{4}}{{Y}_{0}}({{q}_{2}}r)} \right)} \right]{{e}^{{i\gamma (z - ct)}}} \\ \end{gathered} $

С учетом необходимой ограниченности поля перемещений на оси $r = 0$ и неограниченности при $r \to 0$ бесселевых функций второго рода, из (2.19) следует

(2.20)

$\begin{gathered} {{u}_{r}} = - \left[ {{{q}_{1}}{{C}_{1}}{{J}_{1}}({{q}_{1}}r) + i\gamma {{C}_{2}}{{J}_{1}}({{q}_{2}}r)} \right]{{e}^{{i\gamma (z - ct)}}} \\ {{u}_{\theta }} = 0 \\ {{u}_{z}} = \left[ {i\gamma {{C}_{1}}{{J}_{0}}({{q}_{1}}r) + {{q}_{2}}{{C}_{2}}{{J}_{0}}({{q}_{2}}r)} \right]{{e}^{{i\gamma (z - ct)}}} \\ \end{gathered} $

При получении (2.20) из (2.19) константа C₃ обозначена C₂.

Замечание 2.1. Выражения (2.20) показывают, что на оси стержня при r = 0 выполняется естественное условие ${{u}_{r}} = 0$, поскольку ${{J}_{1}}(0) = 0$. В то же время, поскольку ${{J}_{0}}(0)$ = 1, компонента ${{u}_{z}}$ при r = 0 принимает вид

(2.21)

${{u}_{z}} = \left[ {i\gamma {{C}_{1}} + {{q}_{2}}{{C}_{2}}} \right]{{e}^{{i\gamma (z - ct)}}}$

Выражение (2.21) показывает, что для обращения в нуль компоненты ${{u}_{z}}$ при r = 0 необходимо выполнение соотношения

(2.22)

$i\gamma {{C}_{1}} = - {{q}_{2}}{{C}_{2}}$

Далее будет показано, что соотношение (2.22) выполняется, в частности, том случае, когда фазовая скорость волны $c$ совпадает со скоростью ${{c}_{2}}$, а матрица дисперсионного уравнения простая.

3. Дисперсионное уравнение. Условие равенства нулю поверхностных усилий на боковой поверхности цилиндра при $r = R$ представимо в виде

(3.1)

${{\left. {{{{\mathbf{t}}}_{\nu }} \equiv \left( {\lambda ({\text{tr}}\varepsilon )\nu + 2\mu \varepsilon \cdot \nu } \right)} \right|}_{{r = R}}} = 0$

где $\nu $ – вектор единичной внешней нормали к боковой поверхности.

Подстановка поля перемещений (2.20) в условия (3.1) позволяет записать граничные условия (с точностью до экспоненциального множителя ${{e}^{{i\gamma (z - ct)}}}$) в терминах соответствующих бесселевых функций

(3.2)

$\begin{gathered} {{t}_{{rr}}} \equiv \lambda {{I}_{\varepsilon }} + 2\mu {{\varepsilon }_{{rr}}} \\ = - {\kern 1pt} {{\left[ {\lambda (q_{1}^{2}\, + \,{{\gamma }^{2}}){{J}_{0}}({{q}_{1}}r){{C}_{1}}\, + \,\frac{{2\mu }}{r}\left[ {{{q}_{1}}{{C}_{1}}({{q}_{1}}r{{J}_{0}}({{q}_{1}}r)\, - \,{{J}_{1}}({{q}_{1}}r))\, + \,i\gamma {{C}_{2}}({{q}_{2}}r{{J}_{0}}({{q}_{2}}r)\, - \,{{J}_{1}}({{q}_{2}}r))} \right]} \right]}_{{r = R}}}\, = \,0 \\ {{t}_{{rz}}} \equiv 2\mu {{\varepsilon }_{{rz}}} = - \mu {{[i\gamma \left[ {{{q}_{1}}{{C}_{1}}{{J}_{1}}({{q}_{1}}r) + i\gamma {{C}_{2}}{{J}_{1}}({{q}_{2}}r)} \right]\,\, + \,\,[i\gamma {{q}_{1}}{{C}_{1}}{{J}_{1}}({{q}_{1}}r) + q_{2}^{2}{{C}_{2}}{{J}_{1}}({{q}_{2}}r)]]}_{{r = R}}} = 0 \\ \end{gathered} $

Условия (3.2) дают искомое дисперсионное уравнение, записываемое в виде

(3.3)

$\det {\mathbf{A}} = 0$

где A – квадратная матрица второго порядка с (комплексными) коэффициентами

(3.4)

$\begin{gathered} {{A}_{{11}}} = - \left( {(q_{1}^{2} + {{\gamma }^{2}})\frac{{c_{1}^{2}}}{{c_{2}^{2}}} - 2{{\gamma }^{2}}} \right){{J}_{0}}({{q}_{1}}R) + \frac{{2{{q}_{1}}}}{R}{{J}_{1}}({{q}_{1}}R) \\ {{A}_{{12}}} = - \frac{{2i\gamma }}{R}\left( {{{q}_{2}}R{{J}_{0}}({{q}_{2}}R) - {{J}_{1}}({{q}_{2}}R)} \right) \\ {{A}_{{21}}} = - 2i\gamma {{q}_{1}}{{J}_{1}}({{q}_{1}}R) \\ {{A}_{{22}}} = - (q_{2}^{2} - {{\gamma }^{2}}){{J}_{1}}({{q}_{2}}R) \\ \end{gathered} $

При получении (3.4) использовано тождество

(3.5)

$\frac{\lambda }{\mu } = \frac{{c_{1}^{2}}}{{c_{2}^{2}}} - 2$

Двумерные и, вообще говоря, комплексные собственные векторы, отвечающие нулевым собственным числам матрицы (3.3), определяют поляризацию соответствующих волн.

Замечания 3.1. а) Дисперсионное уравнение (3.3) может иметь как действительные, так и мнимые и комплексные корни [13–15]. Действительным корням отвечают распространяющиеся моды, (незатухающие в направлении оси z) с действительной фазовой скоростью, а мнимым и комплексным корням соответствуют нераспространяющиеся моды, затухающие в направлении оси z. Решения, отвечающие нераспространяющимся модам, необходимы для удовлетворения граничных условий на торцах стержня при решении краевой задачи для ограниченного или полуограниченного стержня.

б) Подстановка компонент (3.4) в уравнение (3.3) позволяет представить дисперсионное уравнение в виде

(3.6)

$\begin{gathered} 4{{\gamma }^{2}}{{q}_{1}}{{q}_{2}}{{J}_{0}}({{q}_{2}}R){{J}_{1}}({{q}_{1}}R) - \frac{{2{{q}_{1}}}}{R}(q_{2}^{2} + {{\gamma }^{2}}){{J}_{1}}({{q}_{1}}R){{J}_{1}}({{q}_{2}}R) + \\ + \;(q_{2}^{2} - {{\gamma }^{2}})\left( {(q_{1}^{2} + {{\gamma }^{2}})\frac{{c_{1}^{2}}}{{c_{2}^{2}}} - 2{{\gamma }^{2}}} \right){{J}_{0}}({{q}_{1}}R){{J}_{1}}({{q}_{2}}R) = 0 \\ \end{gathered} $

причем, ввиду (2.13), (2.17), волновое число $\gamma $ входит неявно в качестве аргумента в соответствующие бесселевы функции.

4. Спектральный анализ дисперсионного уравнения (2.3). Спектральный анализ матрицы ${\mathbf{A}}$, определяющей дисперсионное уравнение (3.3), распадается на два случая.

4.1. Матрица ${\mathbf{A}}$ полупростая. Спектральное разложение матрицы A дает

(4.1)

${{\vec {\alpha }}_{1}} \leftrightarrow {{\lambda }_{1}},\quad {{\vec {\alpha }}_{2}} \leftrightarrow {{\lambda }_{2}}$

где ${{\lambda }_{1}}$, ${{\lambda }_{2}}$ собственные числа матрицы A, а ${{\vec {\alpha }}_{1}}$, ${{\vec {\alpha }}_{2}}$ двухкомпонентные собственные векторы, причем

(4.2)

${{\lambda }_{{1,2}}} = s\, \pm d$

где обозначено

(4.3)

$s = \frac{{{{A}_{{11}}} + {{A}_{{22}}}}}{2},\quad d = \sqrt {{{f}^{2}} + {{A}_{{12}}}{{A}_{{21}}}} ,\quad f = \frac{{{{A}_{{11}}} - {{A}_{{22}}}}}{2}$

Коэффициенты ${{A}_{{ij}}}$ в (4.3) определены выражениями (3.4).

Соответствующие (нормированные) собственные векторы имеют вид

(4.4)

${{\vec {\alpha }}_{{1,2}}} = \left( {\begin{array}{*{20}{c}} {\frac{{f \pm d}}{{\sqrt {{{{\left| {{{A}_{{21}}}} \right|}}^{2}} + {{{\left| {f \pm d} \right|}}^{2}}} }}} \\ {\frac{{{{A}_{{21}}}}}{{\sqrt {{{{\left| {{{A}_{{21}}}} \right|}}^{2}} + {{{\left| {f \pm d} \right|}}^{2}}} }}} \end{array}} \right)$

Анализ выражений (4.4) для собственных векторов и выражений (4.2) для собственных чисел, дает

Предложение 4.1. а) Необходимым и достаточным условием полупростоты матрицы A является условие отличия от нуля дискриминанта d, определенного по (4.3).

б) Условие вырождения матрицы A (необходимо простой при однократном вырождении) имеет вид

(4.5)

${{A}_{{11}}}{{A}_{{22}}} = {{A}_{{12}}}{{A}_{{21}}}$

Доказательство. а) Выражение (4.2) показывает, что условие $d \ne 0$ дает необходимое и достаточное условие для того, чтобы $2 \times 2$-матрица была простой (в этом случае ее собственные числа различны) и, как следствие полупростой.

б) В силу (4.2), условие вырождения эквивалентно условию

(4.6)

${{s}^{2}} = {{d}^{2}}$

из (4.6) подстановкой выражений для $s$, $d$ и f из (4.3), получаем требуемое условие (4.5).

Замечание 4.1. Непосредственный анализ показывает, что условие (4.5), вытекающее из (4.2), (4.3), эквивалентно дисперсионному уравнению (3.3).

4.2. Матрица A неполупростая. В этом случае

(4.7)

$d = 0$

и спектральное разложение матрицы A принимает вид

(4.8)

$\left( {\begin{array}{*{20}{c}} {\frac{f}{{\sqrt {{{{\left| {{{A}_{{21}}}} \right|}}^{2}} + {{{\left| f \right|}}^{2}}} }}} \\ {\frac{{{{A}_{{21}}}}}{{\sqrt {{{{\left| {{{A}_{{21}}}} \right|}}^{2}} + {{{\left| f \right|}}^{2}}} }}} \end{array}} \right) \leftrightarrow {{\lambda }_{{1,2}}} = s$

Двукратное вырождение для неполупростой матрицы эквивалентно выполнению условия

(4.9)

$s = 0$

Откуда, принимая во внимание (4.3), следует

Предложение 4.2. а) Необходимым и достаточным условием неполупростоты матрицы ${\mathbf{A}}$ является выполнение условия

(4.10)

${{f}^{2}} = - {{A}_{{12}}}{{A}_{{21}}}$

б) При выполнении (4.10) условие двукратного вырождения неполупростой матрицы ${\mathbf{A}}$ принимает вид

(4.11)

${{A}_{{11}}} = - {{A}_{{22}}}$

Доказательство. а) Как показано, в Предложении 4.1.а для неполупростоты матрицы A необходимо и достаточно выполнение условия (4.7). Но при выполнении этого условия оба собственных вектора, как показывает (4.4), совпадают. Это означает, что матрица становится неполупростой. Далее, подстановка в (4.7) соответствующих выражений из (4.3) дает условие (4.10).

б) В силу (4.2), вырождение матрицы A при выполнении условия (4.7) эквивалентно выполнению условия

(4.12)

$s = 0$

Принимая во внимание (4.3), последнее условие эквивалентно (4.11).

Замечание 4.2. Для случая двукратного вырождения соответствующее дисперсионное уравнение, отвечающее условиям (4.10), (4.11), при использовании (3.4), представимо в виде

(4.13)

${{(q_{2}^{2} - {{\gamma }^{2}})}^{2}}{{\left( {{{J}_{1}}({{q}_{2}}R)} \right)}^{2}} - {{\gamma }^{2}}{{q}_{1}}{{q}_{2}}{{J}_{0}}({{q}_{2}}R){{J}_{1}}({{q}_{1}}R) + \frac{{{{\gamma }^{2}}{{q}_{1}}}}{R}{{J}_{1}}({{q}_{2}}R){{J}_{1}}({{q}_{1}}R) = 0$

5. Поля перемещений. Компоненты корневых собственных векторов (4.4), (4.8), отвечающих нулевым собственным числам, являются коэффициентами ${{C}_{1}}$, ${{C}_{2}}$ в выражениях (2.20) для компонент поля перемещений.

5.1. Матрица Α полупростая. Подстановка в (2.20) компонент корневого собственного вектора (4.4), отвечающего нулевому собственному числу (4.2) при выполнении условия вырождения (4.5), дает

(5.1)

$\begin{gathered} {{u}_{r}} = \frac{{ - \left[ {{{q}_{1}}\left( {f \pm d} \right){{J}_{1}}({{q}_{1}}r) + i\gamma {{A}_{{21}}}{{J}_{1}}({{q}_{2}}r)} \right]}}{{\sqrt {{{{\left| {{{A}_{{21}}}} \right|}}^{2}} + {{{\left| {f \pm d} \right|}}^{2}}} }}{{e}^{{i\gamma (z - ct)}}} \hfill \\ {{u}_{z}} = \frac{{\left[ {i\gamma \left( {f \pm d} \right){{J}_{0}}({{q}_{1}}r) + {{q}_{2}}{{A}_{{21}}}{{J}_{0}}({{q}_{2}}r)} \right]}}{{\sqrt {{{{\left| {{{A}_{{21}}}} \right|}}^{2}} + {{{\left| {f \pm d} \right|}}^{2}}} }}{{e}^{{i\gamma (z - ct)}}} \hfill \\ \end{gathered} $

где f, $d$ определены выражениями (4.3), коэффициенты ${{A}_{{ij}}}$ матрицы A определены по (3.4). В (5.1) и далее нулевая компонента ${{u}_{\theta }}$ отдельно не указывается.

Предложение 5.1. В случае полупростой матрицы A амплитуда компоненты ${{u}_{z}}$ на оси стержня (r = 0) обращается в нуль при $c = {{c}_{2}}$.

Доказательство. Для рассматриваемого случая условие (2.22) принимает вид

(5.2)

$i\gamma \left( {f \pm d} \right) = - {{q}_{2}}{{A}_{{21}}}$

Это условие при учете (4.3) удается преобразовать к эквивалентному виду

(5.3)

$i\gamma {{q}_{2}}\left( {{{A}_{{11}}} - {{A}_{{22}}}} \right) + q_{2}^{2}{{A}_{{21}}} + {{\gamma }^{2}}{{A}_{{12}}} = 0$

Подстановка в (5.3) выражений (3.4) для коэффициентов ${{A}_{{ij}}}$ при $c = {{c}_{2}}$ обеспечивает выполнение условия (5.3).

Замечание 5.1. Для рассматриваемого случая полупростой матрицы A, выражения для перемещений (5.1) применимы для аксиально симметричных мод $L(0,m)$ любого порядка m.

5.2. Матрица A неполупростая. Подстановка в (2.20) компонент корневого собственного вектора (4.8), отвечающего нулевому собственному числу (4.2) при выполнении условий вырождения (4.10), (4.11), дает

(5.4)

$\begin{gathered} {{u}_{r}} = \frac{{ - \left[ {{{q}_{1}}f{{J}_{1}}({{q}_{1}}r) + i\gamma {{A}_{{21}}}{{J}_{1}}({{q}_{2}}r)} \right]}}{{\sqrt {{{{\left| {{{A}_{{21}}}} \right|}}^{2}} + {{{\left| f \right|}}^{2}}} }}{{e}^{{i\gamma (z - ct)}}} \hfill \\ {{u}_{z}} = \frac{{\left[ {i\gamma f{{J}_{0}}({{q}_{1}}r) + {{q}_{2}}{{A}_{{21}}}{{J}_{0}}({{q}_{2}}r)} \right]}}{{\sqrt {{{{\left| {{{A}_{{21}}}} \right|}}^{2}} + {{{\left| f \right|}}^{2}}} }}{{e}^{{i\gamma (z - ct)}}} \hfill \\ \end{gathered} $

Предложение 5.2. В случае неполупростой матрицы A амплитуда компоненты ${{u}_{z}}$ на оси стержня (r = 0) не обращается в нуль при фазовой скорости c, совпадающей со скоростью поперечной волны ${{c}_{2}}$.

Доказательство. Для случая неполупростой матрицы условие (2.22) принимает вид

(5.5)

$i\gamma \,f = - {{q}_{2}}{{A}_{{21}}}$

Это условие при учете (4.3) можно преобразовать к эквивалентному виду

(5.6)

$i\gamma \left( {{{A}_{{11}}} - {{A}_{{22}}}} \right) + 2{{q}_{2}}{{A}_{{21}}} = 0$

Подстановка в (5.6) выражений (3.4) для коэффициентов ${{A}_{{ij}}}$ при $c = {{c}_{2}}$ показывает, что условие (5.5) не выполняется.

Замечание 5.2. Так же, как и для случая полупростой матрицы A, для неполупростой матрицы выражения перемещений (5.4) применимы для аксиально симметричных мод $L(0,m)$ любого порядка m.

5.3. Амплитуды перемещений на боковой поверхности. При определении поляризации волны, особый интерес представляют нормализованные (по модифицированной ${{l}^{1}}$‑норме) амплитуды ${{U}_{r}}$, ${{U}_{z}}$ компонент перемещений (5.1), (5.4) на боковой поверхности стержня

(5.7)

$\begin{gathered} {{U}_{r}} \equiv {{\left. {\frac{{\left| {{{u}_{r}}} \right|}}{{\left| {{{u}_{r}}} \right| + \left| {{{u}_{z}}} \right| + 1}}} \right|}_{{r = R}}} \hfill \\ {{U}_{z}} \equiv {{\left. {\frac{{\left| {{{u}_{z}}} \right|}}{{\left| {{{u}_{r}}} \right| + \left| {{{u}_{z}}} \right| + 1}}} \right|}_{{r = R}}} \hfill \\ \end{gathered} $

Замечание 5.3. Надо отметить, что, вообще говоря, амплитудные значения компонент смещений $\left| {{{u}_{r}}} \right|$ и $\left| {{{u}_{z}}} \right|$ для рассматриваемой установившейся гармонической волны при каком-либо значении радиуса r и, в частности, при r = R, могут одновременно обратиться в нуль (для учета этого введена единица в знаменатель в (5.7)). Таким образом, при некоторых значениях параметров в аксиально симметричных продольных модах гипотетически возможна ситуация, когда одновременно ${{U}_{r}} = {{U}_{z}} = 0$.

6. Амплитуды перемещений для фундаментальной моды. По уравнениям (5.1) для случая полупростой матрицы A и уравнениям (5.4) для неполупростой матрицы с помощью (5.7), определялись амплитуды ${{U}_{r}}$, ${{U}_{z}}$ на боковой поверхности цилиндрического стержня. Амплитуды определялись при различных значениях коэффициента Пуассона в диапазоне $\nu \in [0,\;0.4]$.

Для этих значений коэффициента Пуассона по дисперсионному уравнению (3.3) определены нижние ветви дисперсионных кривых, отвечающие фундаментальной аксиально симметричной моде. Соответствующие дисперсионные кривые приведены на фиг. 1.

Фиг. 1

Кривые на фиг. 1 отвечают различным значениям коэффициента Пуассона (значения коэффициента Пуассона указаны на графике).

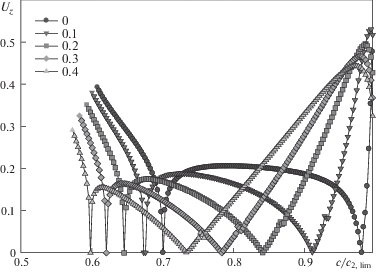
На фиг. 2, 3 приведены графики изменения амплитуд ${{U}_{r}}$, ${{U}_{z}}$ для фундаментальной аксиально симметричной моды в зависимости от изменения относительной фазовой скорости $c{\text{/}}{{c}_{{2,\lim }}}$.

Фиг. 2

Фиг. 3

На фиг. 2, 3 для всех исследованных значений коэффициента Пуассона обращает на себя внимание убывание до нуля обеих амплитуд ${{U}_{r}}$, ${{U}_{z}}$ при вариации фазовой скорости в диапазоне от ${{c}_{{1,\lim }}}$ до ${{c}_{2}}$. Далее, при фазовых скоростях $c > {{c}_{2}}$, компонента ${{U}_{r}}$ возрастает и вновь убывает до нуля уже в окрестности скорости ${{c}_{{2,\lim }}}$.

Замечания 6.1. а) Подстановка фазовой скорости $c = {{c}_{2}}$ в выражения (3.4) показывает, что при этой скорости матрица A является простой с единственным корневым собственным вектором

(6.1)

$\left( {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right) \leftrightarrow \lambda = 0$

Корневой собственный вектор (6.1) соответствует коэффициентам ${{C}_{1}} = 0$, ${{C}_{2}} = 1$ в представлении (2.2). Далее, непосредственный анализ выражений (5.1), (5.7) для случая полупростой матрицы A показывает, что, действительно, при $c = {{c}_{2}}$ на боковой поверхности ${{U}_{r}} = {{U}_{z}} = 0$.

б) Одновременное обращение в нуль амплитуд ${{U}_{r}}$, ${{U}_{z}}$ фундаментальной моды при фазовой скорости, совпадающей со скоростью волны сдвига ${{c}_{2}}$, представляется важным с точки зрения проектирования акустических волноводов: в этом случае соответствующая волна оказывается полностью локализованной внутри стержня. Интересно, что такую волну невозможно обнаружить с помощью поверхностных детекторов, поскольку на поверхности стержня обе компоненты перемещений обращаются в нуль.

7. Выводы. Проведен анализ решений волнового уравнения Похгаммера–Кри, описывающего распространение гармонических волн в упругом цилиндрическом стержне.

Для продольных аксиально симметричных мод впервые проведен спектральный анализ матрицы дисперсионного уравнения. Получены аналитические выражения для поляризации волн.

На поверхности стержня для фундаментальной продольной аксиально симметричной моды определены амплитуды поляризации соответствующих волн и проведен анализ вариации амплитуд в зависимости от фазовой скорости и коэффициента Пуассона.

Обнаружено, что при фазовой скорости фундаментальной продольной аксиально симметричной моды, совпадающей со скоростью поперечной волны, происходит одновременное обращение в нуль всех компонент перемещений на боковой поверхности стержня, – это представляется важным для проектирования акустических волноводов.

Автор благодарит РФФИ (гранты 17-08-00311 и 18-58-41001Узб_т) за частичную финансовую поддержку.

Список литературы

Pochhammer L. Ueber die Fortpflanzungsgeschwindigkeiten kleiner Schwingungen in einem unbegrenzten isotropen Kreiscylinder // J. Reine Angew. Math. 1876. V. 81. S. 324–336.
Chree C. Longitudinal vibrations of a circular bar // Quart. J. Pure Appl. Math. 1886. V. 21. P. 287–298.
Chree C. The equations of an isotropic elastic solid in polar and cylindrical coordinates, their solutions and applications // Trans. Cambridge Philos. Soc. 1889. V. 14. P. 250–309.
Field G.S. Velocity of sound in cylindrical rods // Canadian J. Res. 1931. V. 5. P. 619–624.
Field G.S. Longitudinal waves in cylinders of liquid, in hollow tubes and in solid rods // Canadian J. Res. 1934. V. 11. P. 254–263.
Field G.S. Dispersion of supersonic waves in cylindrical rods // Phys. Rev. 1940. V. 57. P. 1188.
Shear S.K., Focke A.B. The dispersion of supersonic waves in cylindrical rods of polycrystalline silver, nickel, and magnesium // Phys. Rev. 1940. V. 57. P. 532–537.
Bancroft D. The velocity of longitudinal waves in cylindrical bars // Phys. Rev. 1941. V. 59. P. 588–593.
Hudson G.E. Dispersion of elastic waves in solid circular cylinders // Phys. Rev. 1943. V. 63. P. 46–51.
Holden A.H. Longitudinal modes of elastic waves in isotropic cylinders and slabs // Bell System Tech. J. 1951. V. 30. P. 956–969.
Adem J. On the axially-symmetric steady wave propagation in elastic circular rods // Quart. Appl. Math. 1954. V. 12. P. 261–275.
Redwood M., Lamb J. On propagation of high frequency compressional waves in isotropic cylinders // Proc. Phys. Soc. London. 1957. B. 70. P. 136–143.
Mindlin R.D., McNiven H.D. Axially symmetric waves in elastic rods // Trans. ASME. J. Appl. Mech. 1960. V. 27. P. 145–151.
McNiven H.D., Perry D.C. Axially symmetric waves in infinite, elastic rods // J. Acoust. Soc. Amer. 1962. V. 34. P. 433–437.
Onoe M., McNiven H.D., Mindlin R.D. Dispersion of axially symmetric waves in elastic rods // Trans. ASME. J. Appl. Mech. 1962. V. 29. P. 729–734.
Meeker T.R., Meitzler A.H. Guided wave propagation in elongated cylinders and plates // Physical acoustics. Principles and methods. New York: Acad. Press., 1964. V. 1A. P. 111–167.
Kolsky H. Stress waves in solids // J. Sound Vibr. 1964. V. 1. P. 88–110.
Hutchinson J.R., Percival C.M. Higher modes of longitudinal wave propagation in thin rod // J. Acoust. Soc. Amer. 1968. V. 44. P. 1204–1210.
Zemanek J. An experimental and theoretical investigation of elastic wave propagation in a cylinder // J. Acoust. Soc. Amer. 1972. V. 51. P. 265–283.
Thurston R.N. Elastic waves in rods and clad rods // J. Acoust. Soc. Amer. 1978. V. 64. P. 1–37.
Pao Y.-H., Mindlin R.D. Dispersion of flexural waves in an elastic, circular cylinder // Trans. ASME. J. Appl. Mech. 1960. V. 27. P. 513–520.
Valsamos G., Casadei F., Solomos G. A numerical study of wave dispersion curves in cylindrical rods with circular cross-section // Applied and Computational Mechanics. 2013. V. 7. P. 99–114.
Murav’eva O.V., Lenkov S.V., Murashov S.A. Torsional waves excited by electromagnetic–acoustic transducers during guided-wave acoustic inspection of pipelines // Acoustical Physics. 2016. V. 62(1). P. 117–124.
Kuznetsov S.V. Lamb waves in anisotropic plates // Acoustical Physics. 2014. V. 60(1). P. 95–103.
Абрамян А.К., Индейцев Д.А., Постнов В.А. Бегущие и стоячие волны балки Тимошенко // Изв. РАН. МТТ. 2018. № 2. С. 101–109.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал