Известия РАН. Механика твердого тела, 2019, № 4, стр. 94-108
ПОТЕРЯ УСТОЙЧИВОСТИ СТЕРЖНЯ ИЗ СПЛАВА С ПАМЯТЬЮ ФОРМЫ, ВЫЗВАННАЯ ОБРАТНЫМ МАРТЕНСИТНЫМ ПРЕВРАЩЕНИЕМ
С. А. Думанский a, А. А. Мовчан a, *
a Институт прикладной механики РАН
Москва, Россия
* E-mail: movchan47@mail.ru
Поступила в редакцию 25.09.2018
После доработки 25.09.2018
Принята к публикации 18.10.2018
Аннотация
В различных постановках (несвязанной, связанной и дважды связанной) в рамках концепций “Фиксированной нагрузки” и “Варьируемой нагрузки” получены аналитические решения задачи о потере устойчивости шарнирно закрепленного стержня из сплава с памятью формы, материал которого испытывает обратное термоупругое фазовое превращение под действием постоянной сжимающей нагрузки при наличии начальных фазово-структурных деформаций сжатия. Обоснована формулировка концепции “Варьируемой нагрузки”, в рамках которой решение для критической длины не зависит от величины возмущений.
1. Введение. Общие вопросы устойчивости деформируемых твердых тел, испытывающих твердотельные фазовые переходы рассматривались в [1–5]. Экспериментальные данные по устойчивости стержней из сплавов с памятью формы (СПФ) изложены в [6–11], численному анализу критических нагрузок и закритического поведения стержней из СПФ посвящены работы [9, 12–18]. Анализ устойчивости фермы Мизеса на стержнях, испытывающих твердотельные фазовые переходы, проведен в работах [19–21]. Устойчивость композитных стержней с элементами из СПФ исследовалась в [22, 23]. Задачи о потере устойчивости в арках-полосках, лентах и сотовых панелях из СПФ рассматривались в [24–26], круглые пластины из СПФ исследовались на устойчивость в [27]. Экспериментальные исследования в области устойчивости оболочек из СПФ описаны в [28–30]. Задачи устойчивости цилиндрических оболочек из СПФ рассматривались в [30–34]. Потеря устойчивости сферических сегментов и оболочек вращения из СПФ рассматривалась в [35, 36].
В большинстве перечисленных выше работ анализировались явления потери устойчивости при активном изотермическом нагружении возрастающими по модулю сжимающими напряжениями в режиме сверхупругости [6, 9, 12, 13, 28–32], мартенситной неупругости [7, 8, 10, 14–16] или обратного превращения в заневоленном состоянии [17, 18, 24, 25], (в последнем случае потеря устойчивости вызывается возрастающими, так называемыми “реактивными” напряжениями).
В [37] было экспериментально установлено, что причиной потери устойчивости элементов из СПФ могут служить термоупругие фазовые (как прямые, так и обратные) превращения, происходящие под действием сжимающих, в том числе и постоянных, напряжений. Постановке и решению задач такого типа посвящены работы [4, 38–40] для стержней, [41, 42] для прямоугольных, [43–45] для круглых и [46] для кольцевых пластин из СПФ, [47] – для цилиндрических и [48] для оболочек вращения из СПФ.
Причиной такого типа потери устойчивости являются дополнительные фазовые и структурные превращения, вызываемые малыми изменениями напряженно-деформированного состояния при переходе в смежную форму квазистатического равновесия.
Этот эффект может быть качественно правильно описан при решении задачи в однократно связанной постановке [49], учитывающей влияние изменения действующих напряжений и фазово-структурных деформаций на величину параметра фазового состава. Помимо связанной, известна дважды связанная постановка задач термомеханики для СПФ [49], в рамках которой учитывается еще и обратное влияние происходящих фазового и структурного переходов на температурный режим материала – выделение при прямом превращении и поглощение при обратном превращении латентного тепла фазового перехода и диссипативные явления. Необходимо отметить, что большинство известных решений задач устойчивости для элементов из СПФ не учитывало эти эффекты, т.е. получено либо в несвязанной, либо в однократно связанной постановке. В дважды связанной постановке получены лишь решения модельных задач для стойки Шенли на стержнях из СПФ [50] и работающих на изгиб стержней из СПФ при прямом превращении [4].
Решение задачи устойчивости зависит от совокупности тех величин, по отношению к возмущениям которых устойчивость рассматривается. Если учитываются лишь возмущения геометрической формы, а не возмущения нагрузки, то речь идет о концепции фиксированной нагрузки (сокращенно ФН). Если помимо возмущения геометрии учитываются еще и малые вариации нагрузки, то речь идет о концепции варьируемой нагрузки (сокращено ВН). Недостаток концепции ВН, по сравнению с концепцией ФН состоит в том, что в рамках этой концепции критические значения параметров зависят от величины и направления соответствующих возмущений.
В данной работе в рамках различных подходов (ВН и ФН), в том числе – в дважды связанной постановке аналитически решена задача о потере устойчивости стержня из СПФ, при обратном превращении материала, происходящем под действием постоянной сжимающей нагрузки при наличии начальных фазово-структурных деформаций сжатия. Проведено сравнение решений, полученных в несвязанной, однократно связанной и дважды связанной постановках. Обоснована модифицированная формулировка концепции ВН, в рамках которой решение задачи устойчивости становится корректным.
2. Постановка задачи. Задача решается в рамках системы определяющих соотношений модели нелинейного деформирования СПФ при фазовых и структурных превращениях [39, 49], одномерный вариант которой для случая обратного фазового превращения, сопровождающегося, вообще говоря, структурным переходом, имеет вид
(2.1)
$d{{\varepsilon }^{{{\text{ph}}}}}' = {{\varepsilon }^{{{\text{phst}}}}}'dq{\text{/}}q,$ $dq < 0,$ $d{{\varepsilon }^{{{\text{st}}}}} = {{\rho }_{{\text{D}}}}qF'\left( {\left| \sigma \right|} \right)d\sigma ,$ $d\left| \sigma \right| > 0$(2.2)
$q = \frac{1}{2}\left\{ {1 - \cos \left[ {\pi \left( {\frac{{A_{{\text{f}}}^{0} - T}}{{A_{{\text{f}}}^{0} - A_{{\text{s}}}^{0}}} + \frac{{\sigma {{\varepsilon }^{{{\text{phst}}}}}{\text{'}} + \left( {Z(\sigma ) + \sigma {{\varepsilon }_{0}}} \right)q}}{{q\Delta S(A_{{\text{s}}}^{0} - A_{{\text{f}}}^{0})}}} \right)} \right]} \right\}$(2.3)
$Z(\sigma ) = \frac{{\left( {{{E}_{{\text{A}}}} - {{E}_{{\text{M}}}}} \right){{\sigma }^{2}}}}{{2{{E}_{{\text{A}}}}{{E}_{{\text{M}}}}}}$(2.4)
${{k}_{{\text{q}}}}\Delta T = {{C}_{\sigma }}\dot {T} + T\alpha \dot {\sigma } - (\Delta U + {{\varepsilon }^{{{\text{phst}}}}}{\text{'}}\sigma {\text{/}}q + Z(\sigma ) + \sigma {{\varepsilon }_{0}})\dot {q} - {{\rho }_{{\text{D}}}}qF{\kern 1pt} {\text{'}}{\kern 1pt} (\left| \sigma \right|)\sigma \dot {\sigma }$Здесь $\varepsilon $, ${{\varepsilon }^{{\text{e}}}}$, ${{\varepsilon }^{{{\text{phst}}}}}$, ${{\varepsilon }^{{{\text{phst}}}}}'$, ${{\varepsilon }_{0}} > 0$ – осевая компонента полной, упругой и фазово-структурной деформации, девиаторная часть соответствующей компоненты и линейная деформация объемного эффекта фазового превращения (температурная деформация в силу ее малости не учитывается); ${{\rho }_{{\text{D}}}}$ – параметр материала – максимальное значение интенсивности структурной деформации которая может быть достигнута при монотонном нагружении СПФ в режиме мартенситной неупругости (одноосное сжатие), $\sigma $ – осевая компонента напряжения; $q$ – объемная доля мартенситной фазы; ${{E}_{{\text{M}}}}$, ${{E}_{{\text{A}}}}$ – значения модуля Юнга мартенситного и аустенитного фазовых состояний; $A_{{\text{s}}}^{0}$, $A_{{\text{f}}}^{0}$ – температуры начала (нижний индекс ${\text{s}}$) и окончания (нижний индекс ${\text{f}}$) обратного фазового превращения в свободном от напряжений материале, $A_{{\text{s}}}^{\sigma }$ температура начала обратного превращения при наличии напряжений; соотношение (2.4) [49] представляет собой уравнение энергетического баланса, в нем ${{k}_{{\text{q}}}}$, ${{C}_{\sigma }}$, $\alpha $, ΔU, ΔS – коэффициент теплопроводности, теплоемкость единицы объема при постоянном напряжении, коэффициент температурного расширения, объемная плотность латентного тепла фазового перехода, и скачек объемной плотности энтропии при переходе от мартенситного состояния в аустенитное; $F{\kern 1pt} {\text{'}}\left( \sigma \right)$ – производная материальной функции, определяющей диаграмму мартенситной неупругости СПФ при одноосном монотонном сжатии, для которой ниже используется аппроксимация $F(\sigma ) = 1 - \exp [ - {{(\sigma {\text{/}}{{\sigma }_{0}})}^{a}}]$, где ${{\sigma }_{0}}$ и $a$ – параметры материала. Ниже при расчетах используются следующие значения постоянных материала, характерные для никелида титана:
(2.5)
${{E}_{{\text{A}}}} = 84000$ МПа, ${{E}_{{\text{M}}}} = 28000$ МПа, ${{\rho }_{{\text{D}}}} = 0.04,$ $a = 2,$ ${{\varepsilon }_{0}} = 0.001$Шарнирно опертый стержень из СПФ прямоугольного поперечного сечения $b \cdot 2h$ (2h – высота сечения), материал которого находится первоначально в полностью мартенситном фазовом состоянии, нагружен продольной сжимающей силой P, создающей равномерно распределенное по материалу сжимающее напряжение $\sigma $ и обладает равномерно распределенной по объему начальной фазово-структурной сжимающей деформацией ${{\varepsilon }^{0}} = {{\varepsilon }_{0}} + \varepsilon _{0}^{'}$. Здесь $\varepsilon _{0}^{'} < 0$ – девиаторная компонента ${{\varepsilon }^{0}}$. Результат решения задачи устойчивости зависит от расположения точки $({\text{|}}\varepsilon _{0}^{'}{\text{|}},\left| \sigma \right|)$ по отношению к диаграмме мартенситной неупругости при сжатии $\left| \varepsilon \right| = {{\rho }_{{\text{D}}}}F\left( {\left| \sigma \right|} \right)$, т.е. фактически от того, каким образом создана начальная деформация. Если деформация $\varepsilon _{0}^{'}$ была получена путем нагружения стержня, находящегося в мартенситном фазовом состоянии в режиме мартенситной неупругости, то точка $({\text{|}}\varepsilon _{0}^{'}{\text{|}},\left| \sigma \right|)$ находится на указанной диаграмме. В этом случае при малой догрузке $d\left| \sigma \right| > 0$ материал стержня будет испытывать дополнительный структурный переход в соответствии с предпоследней формулой (2.1). Для краткости этот случай далее будет обозначаться как вариант 1. Если же, например, начальная деформация была создана в процессе полного прямого превращения под действием постоянного напряжения $\sigma $, которое сохраняет свое значение и при дальнейшем обратном фазовом переходе, то, согласно экспериментальным данным [51] точка $({\text{|}}\varepsilon _{0}^{'}{\text{|}},\left| \sigma \right|)$ находится ниже вдоль оси $\left| \sigma \right|$ диаграммы мартенситной неупругости. В этом случае при малой догрузке $d\left| \sigma \right| > 0$ дополнительного структурного превращения не будет (вариант 2 задания начальной деформации).
В качестве критерия потери устойчивости используется квазистатический критерий Эйлера, согласно которому под критическими условиями понимаются такие, при которых наряду с невозмущенной прямолинейной существует еще и близкая к ней возмущенная форма квазистатического равновесия. Задача решается в линеаризованной постановке.
3. Описание невозмущенного процесса и возмущенного состояния. Невозмущенный процесс представляет собой равномерный нагрев прямолинейного стержня, находящегося под действием постоянной продольной сжимающей силы через интервал температур обратного мартенситного фазового превращения, в процессе которого ранее сообщенная материалу фазово-структурная деформация ${{\varepsilon }^{0}}$ снимается за счет явления памяти формы (т.е. стержень удлиняется). Действующее в этом процессе сжимающее напряжение не меняется, поэтому структурного превращения не происходит. Интегрируя для этого процесса первое уравнение (2.1) получаем
(3.1)
${{\varepsilon }^{{{\text{phst}}}}} = {{\varepsilon }^{0}}q,\quad {{\varepsilon }^{{{\text{phst}}}}}' = \varepsilon _{0}^{'}q$Здесь и далее все величины без знака вариации относятся к невозмущенному процессу.
Для определенности считается, что форма возмущенного состояния продольных слоев стержня (расположенного горизонтально) является выпуклой вниз, так что для вариации кривизны справедливо неравенство $\delta \kappa = {{\partial }^{2}}\delta w{\text{/}}\partial {{x}^{2}} > 0$, где $\delta w < 0$ – вариация прогиба, поперечная координата отсчитывается от нейтральной плоскости вверх, зона догрузки занимает верхнюю часть сечения, а зона разгрузки – нижнюю.
Для вариации параметра фазового состава q из (2.2) с учетом (2.3) получаем
(3.2)
$\delta q = \lambda (q)\left[ {\frac{{{{\varepsilon }^{0}} + B\sigma + \tau {{\rho }_{{\text{D}}}}F{\kern 1pt} {\text{'}}\left( {\left| \sigma \right|} \right)\sigma }}{{\Delta S}}\delta \sigma - \delta T} \right]$В (3.2) третье слагаемое числителя правой части связано с дополнительным структурным превращением при выпучивании. Это слагаемое равно нулю в зоне разгрузки $\delta \left| \sigma \right| < 0$ и в зоне догрузки при втором варианте задания начальной деформации. В этих случаях τ = 0. При догрузке и первом варианте задания начальной деформации τ = 1.
Считается, что переход к смежной форме квазистатического равновесия происходит достаточно быстро, так, что теплообменом материала стержня с окружающей средой можно пренебречь. В этом случае величина $\delta T$ определяется только процессом поглощения латентного тепла обратного фазового перехода и диссипативными явлениями. Заменяя в (2.4) знак производной по времени на знак вариации, пренебрегая малым слагаемым $T\alpha \delta \sigma $, выражая из полученного соотношения $\delta T$, подставляя результат в (3.2) и решая полученное уравнение относительно $\delta q$, можно получить
(3.3)
$\delta q = \frac{{\lambda (q)\gamma _{1}^{ \pm }(q,\sigma ,{{\varepsilon }^{0}})}}{{\Delta S{{\gamma }_{2}}(q,\sigma ,{{\varepsilon }^{0}})}}\delta \left| \sigma \right|$(3.4)
$\gamma _{1}^{ - } = - {{\varepsilon }^{0}} + B\left| \sigma \right|,\quad \gamma _{1}^{ + } = \gamma _{1}^{ - } + \tau \left( {1 - \frac{{q\Delta S}}{{{{C}_{\sigma }}}}} \right){{\rho }_{{\text{D}}}}F{\kern 1pt} {\text{'}}\left( {\left| \sigma \right|} \right)\left| \sigma \right|$В (3.3) учтено, что $\sigma < 0$. Величина $\gamma _{1}^{ + }$ соответствует наличию дополнительного структурного перехода, а величина $\gamma _{1}^{ - }$ его отсутствию. Для значений постоянных материала, соответствующих никелиду титана, выполняется $\gamma _{1}^{ + } > \gamma _{1}^{ - }$. Соотношение (3.3) соответствует дважды связанной постановке задачи. В случае однократно связанной постановки в (3.3) следует положить ${{\gamma }_{2}} \equiv 1$. Поскольку речь идет об обратном превращении, то пользоваться формулой (3.3) для определения $\delta q$ можно лишь в том случае, когда при этом получается $\delta q < 0$. Если при вычислении по формуле (3.3) получается $\delta q > 0$, то следует считать $\delta q = 0$, т.е. дополнительного фазового превращения при выпучивании не происходит.
Задача устойчивости решается в двух основных постановках. Согласно первой (концепция ФН), учитываются лишь малые возмущения геометрии стержня. Сечение стержня делится на область догрузки, где $\delta \left| \sigma \right| > 0$ и область разгрузки, где $\delta \left| \sigma \right| < 0$, граница между которыми заранее не известна и находится в процессе решения задачи.
Согласно (3.4), в случае, если суммарная начальная деформация является сжимающей: ${{\varepsilon }^{0}} < 0$, то для значений постоянных материала, характерных для никелида титана выполняются неравенства ${{\gamma }_{2}} > 0$, $\gamma _{1}^{ \pm } > 0$, то есть знаки $\delta \left| \sigma \right|$ и $\delta q$ совпадают. Следовательно, в зоне догрузки, согласно (3.3), получается $\delta q > 0$ т.е. дополнительное обратное превращение отсутствует, и в случае первого вида задания начальной деформации будет наблюдаться дополнительный структурный переход (а для второго лишь упругое деформирование). В зоне разгрузки $\delta q < 0$ и наблюдается только дополнительное обратное фазовое превращение.
Ситуация осложняется, если девиаторная компонента заданной неупругой деформации является сжимающей, однако по модулю меньше, чем линейная деформация объемного эффекта реакции фазового перехода, т.е. $\varepsilon _{0}^{'} < 0$, ${\text{|}}\varepsilon _{0}^{'}{\text{|}} < {{\varepsilon }_{0}}$. В этом случае ${{\varepsilon }^{0}} > 0$, неравенство ${{\gamma }_{2}} > 0$ выполняется по-прежнему, однако для малых значений $\left| \sigma \right|$ функции $\gamma _{1}^{ \pm }$ могут быть отрицательными.
В случае второго вида задания начальной деформации для малых значений $\left| \sigma \right|$:
(3.5)
$\left| \sigma \right| < {{\sigma }^{ - }},\quad {{\sigma }^{ - }} = {{\varepsilon }^{0}}{\text{/}}B$Наиболее сложный сценарий дополнительных фазово-структурных переходов имеет место при малых значениях модуля сжимающих напряжений для первого вида задания начальных деформаций. В этом случае начальная деформация, получаемая при нагружении в режиме мартенситной неупругости до напряжения $\sigma $, при котором происходит последующее обратное превращение, жестко связана с величиной этого напряжения уравнением диаграммы мартенситной неупругости ${{\varepsilon }^{0}} = {{\varepsilon }_{0}} - {{\rho }_{{\text{D}}}}F\left( {\left| \sigma \right|} \right)$. При этом условие $\gamma _{1}^{ + } > 0$ эквивалентно $\left| \sigma \right| > {{\sigma }^{ + }}(q)$, а условие $\gamma _{1}^{ - } > 0$ эквивалентно $\left| \sigma \right| > {{\sigma }^{ - }}$, причем ${{\sigma }^{ + }}(q),$ σ– положительные корни уравнений $\gamma _{1}^{ + }(\left| \sigma \right|,q) = 0$ и $\gamma _{1}^{ - }\left( {\left| \sigma \right|} \right) = 0$, которые удовлетворяют условию ${{\sigma }^{ + }}(q) < {{\sigma }^{ - }}$ для любого $q \in \left( {0,1} \right)$, причем с ростом значения $q$ эти корни сближаются. Для величин параметров материала (2.5) значения соответствующих корней достаточно малы: ${{\sigma }^{ + }}(1) \approx 14$ МПа, ${{\sigma }^{ - }} \approx 17$ МПа.
Если $\left| \sigma \right| < {{\sigma }^{ + }}(q)$, то $\gamma _{1}^{ + }(\left| \sigma \right|,q) < 0$, $\gamma _{1}^{ - }\left( {\left| \sigma \right|} \right) < 0$. В зоне догрузки, согласно (3.3), получается δq < 0, т.е. происходит дополнительный обратный фазовый переход. Там же происходит дополнительное структурное превращение. В зоне разгрузки, согласно (3.3) будет δq > 0, т.е. фазовый переход не возможен, так же как и структурный – из-за разгрузки.
Если ${{\sigma }^{ + }}(q) < \left| \sigma \right| < {{\sigma }^{ - }}$, то $\gamma _{1}^{ + }(\left| \sigma \right|,q) > 0$, $\gamma _{1}^{ - }\left( {\left| \sigma \right|} \right) < 0$. В зоне догрузки, согласно (3.3), получается δq > 0, т.е. дополнительного обратного перехода нет. Дополнительный структурный переход происходит из-за догрузки. В зоне разгрузки, согласно (3.3), также получается δq > 0, т.е. дополнительного фазового перехода нет и там. Структурного перехода нет из-за разгрузки.
Если $\left| \sigma \right| > {{\sigma }^{ - }}$, то $\gamma _{1}^{ + }(\left| \sigma \right|,q) > 0$, $\gamma _{1}^{ - }\left( {\left| \sigma \right|} \right) > 0$. В зоне догрузки опять получается δq > 0, т.е. фазового перехода нет, есть только структурный. В зоне разгрузки, согласно (3.3), получается δq < 0, т.е. осуществляется дополнительное обратное превращение без структурного.
Ниже приводятся выражения для вариаций упругих деформаций $\delta \varepsilon _{1}^{{\text{e}}}$, $\delta \varepsilon _{2}^{{\text{e}}}$ соответственно для тех областей, где происходит и не происходит дополнительный фазовый переход, фазовых $\delta {{\varepsilon }^{{{\text{ph}}}}}$ и структурных $\delta {{\varepsilon }^{{{\text{st}}}}}$ деформаций, справедливые в тех областях сечения, где, согласно предшествующему тексту эти вариации отличны от нуля:
(3.6)
$\delta \varepsilon _{1}^{{\text{e}}} = - \frac{{\delta \left| \sigma \right|}}{{E(q)}},$ $\delta \varepsilon _{2}^{{\text{e}}} = - \left( {\frac{{\delta \left| \sigma \right|}}{{E(q)}} + B\left| \sigma \right|\delta q} \right),$ $\delta {{\varepsilon }^{{{\text{ph}}}}} = {{\varepsilon }^{0}}\delta q,$ $\delta {{\varepsilon }^{{{\text{st}}}}} = - {{\rho }_{{\text{D}}}}qF{\kern 1pt} {\text{'}}\left( {\left| \sigma \right|} \right)\delta \left| \sigma \right|$С учетом выражения для $\delta q$ (3.3) выражения для $\delta \varepsilon _{2}^{{\text{e}}}$ и $\delta {{\varepsilon }^{{{\text{ph}}}}}$ принимают вид:
(3.7)
$\delta \varepsilon _{2}^{{\text{e}}} = - \left[ {\frac{1}{{E(q)}} + \frac{{\lambda (q)B\left| \sigma \right|\gamma _{1}^{ \pm }}}{{\Delta S{{\gamma }_{2}}}}} \right]\delta \left| \sigma \right|,$ $\delta {{\varepsilon }^{{{\text{ph}}}}} = \frac{{{{\varepsilon }^{0}}\lambda \left( q \right)B\left| \sigma \right|\gamma _{1}^{ \pm }}}{{\Delta S{{\gamma }_{2}}}}\delta \left| \sigma \right|$Для определения вариации напряжений записывается гипотеза плоских сечений:
(3.8)
$\delta \varepsilon = \delta {{\varepsilon }^{{\text{e}}}} + \delta {{\varepsilon }^{{{\text{ph}}}}} + \delta {{\varepsilon }^{{{\text{st}}}}} = \delta e - z\delta \kappa $(3.9)
$\delta \sigma = \left\{ {\begin{array}{*{20}{c}} {\frac{{{{z}_{0}} - z}}{{{{\psi }_{2}}}}\delta \kappa \quad {\text{при}}\quad z > {{z}_{0}}} \\ {\frac{{{{z}_{0}} - z}}{{{{\psi }_{1}}}}\delta \kappa \quad {\text{при}}\quad z < {{z}_{0}}} \end{array}} \right.$(3.10)
${{\psi }_{2}} = \left\{ \begin{gathered} \frac{1}{{E(q)}} + {{\rho }_{{\text{D}}}}qF{\kern 1pt} {\text{'}}\left( {\left| \sigma \right|} \right) + {{D}_{1}}\quad {\text{при}}\quad \left| \sigma \right| < {{\sigma }^{ + }}(q) \hfill \\ \frac{1}{{E(q)}} + {{\rho }_{{\text{D}}}}qF{\kern 1pt} {\text{'}}\left( {\left| \sigma \right|} \right)\quad {\text{при}}\quad \left| \sigma \right| > {{\sigma }^{ + }}(q) \hfill \\ \end{gathered} \right.,\quad {{D}_{1}} = \frac{{\lambda (q)\gamma _{1}^{ + }\gamma _{1}^{ - }}}{{\Delta S{{\gamma }_{2}}}}$(3.11)
${{\psi }_{1}} = \left\{ \begin{gathered} \frac{1}{{E(q)}}\quad {\text{при}}\quad \left| \sigma \right| < {{\sigma }^{ - }} \hfill \\ \frac{1}{{E(q)}} + {{D}_{2}}\quad {\text{при}}\quad \left| \sigma \right| > {{\sigma }^{ - }} \hfill \\ \end{gathered} \right.,\quad {{D}_{2}} = \frac{{\lambda (q){{{(\gamma _{1}^{ - })}}^{2}}}}{{\Delta S{{\gamma }_{2}}}}$Верхняя строка в (3.9) соответствует зоне догрузки, нижняя – зоне разгрузки. Формула (3.9) справедлива не только для ${{z}_{0}} \in \left[ { - h,h} \right]$. В случае, если ${{z}_{0}} > h$ для всех точек сечения справедливо нижнее выражение правой части (3.9). Если же ${{z}_{0}} < - h$, то для всех точек сечения справедливо верхнее выражение правой части (3.9).
В случае первого вида задания начальной деформации в формулах (3.10), (3.4) следует положить $\tau = 1$. Для второго вида в (3.10) полагается $\gamma _{1}^{ + } = \gamma _{1}^{ - }$.
Для вариации осевой силы $P$ (растягивающая сила считается положительной) в случае прямоугольного поперечного сечения $b \cdot 2h$ путем интегрирования $\delta P = b\int\limits_{ - h}^h {\delta \sigma dz} $ с учетом (3.9) получается
(3.12)
$\frac{{\delta P}}{{\delta \kappa }} = \frac{{b{{h}^{2}}}}{{2{{\psi }_{1}}{{\psi }_{2}}}}[\left( {{{\psi }_{2}} - {{\psi }_{1}}} \right)(\zeta _{0}^{2} + 1) + 2\left( {{{\psi }_{1}} + {{\psi }_{2}}} \right){{\zeta }_{0}}]$ при ${{\zeta }_{0}} \in \left( { - 1,1} \right)$(3.13)
$\frac{{\delta P}}{{\delta \kappa }} = \frac{{2b{{h}^{2}}{{\zeta }_{0}}}}{{{{\psi }_{2}}}}$ при ${{\zeta }_{0}} \leqslant - 1,$ $\frac{{\delta P}}{{\delta \kappa }} = \frac{{2b{{h}^{2}}{{\zeta }_{0}}}}{{{{\psi }_{1}}}}$ при ${{\zeta }_{0}} \geqslant 1$Здесь ${{\zeta }_{0}} = {{z}_{0}}{\text{/}}h$. Для ${{z}_{0}} \in \left( { - h,h} \right)$ ${{\zeta }_{0}}$ – безразмерная координата границы зоны догрузки. Легко видеть, что согласно (3.12), (3.13) при любых соотношениях между величинами ${{\psi }_{1}} > 0$ и ${{\psi }_{2}} > 0$ и любых значениях ζ0 величина $\delta P{\text{/}}\delta \kappa $ является непрерывной и непрерывно дифференцируемой монотонно возрастающей функцией ζ0. Следовательно, существует монотонно возрастающая непрерывно-дифференцируемая обратная функция, позволяющая для любого заданного отношения возмущений внешней нагрузки и кривизны определить единственное значение параметра ζ0. При этом, если значение $\frac{{\delta P}}{{\delta \kappa }}$ принадлежит отрезку
(3.14)
$\left[ { - \frac{{2b{{h}^{2}}}}{{{{\psi }_{2}}}},\frac{{2b{{h}^{2}}}}{{{{\psi }_{1}}}}} \right]$Подставляя в формулу для вариации изгибающего момента в стержне такого же сечения: $\delta M = b{{h}^{2}}\int\limits_{ - 1}^1 {\delta \sigma \zeta d\zeta } $ выражения (3.9) и производя интегрирование, получаем
(3.16)
${{\theta }_{2}} = \frac{{2\left( {{{\psi }_{1}} + {{\psi }_{2}}} \right) - \left( {{{\psi }_{2}} - {{\psi }_{1}}} \right)(\zeta _{0}^{3} - 3{{\zeta }_{0}})}}{{12{{\psi }_{1}}{{\psi }_{2}}}},$ при ${{\zeta }_{0}} \in \left[ {0,1} \right]$Согласно формулам (3.15), величина δM, в случае, если ${{\zeta }_{0}} \notin \left( { - 1,1} \right)$, в отличие от δP не зависит от ζ0. Отсюда, учитывая полученный ранее вывод об однозначной зависимости $\delta P{\text{/}}\delta \kappa $ от ζ0 следует, что в случае, если относительное значение вариации осевой силы $\delta P{\text{/}}\delta \kappa $ не принадлежит интервалу (3.14), то вариация момента не зависит от величины δP. В то же время, внутри интервала ${{\zeta }_{0}} \in \left( { - 1,1} \right)$ вариация момента, согласно (3.15), является монотонной функцией ζ0, а значит, и монотонной функцией $\delta P{\text{/}}\delta \kappa $. Отсюда следует, что вариация момента, как функция $\delta P{\text{/}}\delta \kappa \in \left( { - \infty , + \infty } \right)$, достигает, как своего наибольшего, так и своего наименьшего значения на границах интервала (3.14), причем это наибольшее (наименьшее) значение не зависят от возмущения внешней нагрузки δP.
4. Решение в рамках концепции ФН. В рамках концепции ФН вариация нагрузки должна быть равна нулю. Приравнивая нулю выражение $\delta P{\text{/}}\delta \kappa $ (3.12) можно получить уравнение для определения ζ0:
(4.1)
$\zeta _{0}^{2} + 2\frac{{{{\psi }_{2}} + {{\psi }_{1}}}}{{{{\psi }_{2}} - {{\psi }_{1}}}}{{\zeta }_{0}} + 1 = 0$Решение (4.1), принадлежащий отрезку $\left[ { - 1,1} \right]$, определяется по формуле
(4.2)
${{\zeta }_{0}} = \frac{{\sqrt {{{\psi }_{1}}} - \sqrt {{{\psi }_{2}}} }}{{\sqrt {{{\psi }_{1}}} + \sqrt {{{\psi }_{2}}} }}$Подставляя (4.2) в (3.16) получаем
Записывая линеаризованные уравнения равновесия для возмущенного состояния $\delta M = N\delta w$, где $N = - P$ – сжимающая сила, $\delta w < 0$, $\delta M < 0$, с учетом (3.15) получаем
(4.4)
$\frac{{{{\partial }^{2}}\delta w}}{{\partial {{x}^{2}}}} + {{k}^{2}}\delta w = 0,\quad {{k}^{2}} = \frac{{\left| \sigma \right|}}{{{{h}^{2}}{{\theta }_{2}}}}$Наименьшее собственное значение задачи (4.4) в условиях шарнирного опирания $k = \pi {\text{/}}l$, где $l$ – длина стержня, дает выражение для критической длины:
Подстановка (4.3) в (4.5) дает выражение для критической длины стержня в рамках концепции ФН:
(4.6)
$l(q,\left| \sigma \right|,{{\varepsilon }^{0}}) = \frac{{2\pi h}}{{\sqrt {3\left| \sigma \right|} (\sqrt {{{\psi }_{1}}} + \sqrt {{{\psi }_{2}}} )}}$Согласно (4.6), при фиксированном значении $\left| \sigma \right|$ критическая длина зависит от параметра фазового состава q. Естественно, для определения единственного значения критической длины провести минимизацию l (4.6) по q. Найденное таким образом критическое значение длины стержня не зависит от величины возмущения кривизны стержня $\delta \kappa $.
5. Решение в рамках концепции ВН. В рамках концепции ВН учитываются, как возмущения геометрии стержня (кривизны), так и внешней нагрузки $\delta P$. Формула (4.5) по-прежнему верна, однако в качестве ${{\theta }_{2}}$ в эту формулу необходимо подставлять выражение (3.16). В результате получается:
(5.1)
$l = \frac{{\pi h}}{2}\sqrt {\frac{{({{\psi }_{1}} - {{\psi }_{2}})(\zeta _{0}^{3} - 3{{\zeta }_{0}}) + 2({{\psi }_{1}} + {{\psi }_{2}})}}{{3{{\psi }_{1}}{{\psi }_{2}}\left| \sigma \right|}}} $ при ${{\zeta }_{0}} \in \left[ { - 1,1} \right]$(5.2)
$l = \pi h\frac{1}{{\sqrt {3{{\psi }_{2}}\left| \sigma \right|} }} = {{l}_{2}}(q),$ ${{\zeta }_{0}} < - 1;$ $l = \pi h\frac{1}{{\sqrt {3{{\psi }_{1}}\left| \sigma \right|} }} = {{l}_{1}}(q),$ ${{\zeta }_{0}} > 1$Поскольку значение критических длин (5.1), (5.2) при фиксированных значениях $\left| \sigma \right|$ и ${{\zeta }_{0}}$ зависит от q, для получения окончательного результата опять следует минимизировать l по q.
Согласно (5.1), с учетом монотонной однозначной зависимости (3.12) при заданном значении $\left| \sigma \right|$ критическая длина стержня является монотонной однозначной функцией относительного значения возмущения внешней нагрузки $\delta P{\text{/}}\delta \kappa $ когда величина этого отношения принадлежит интервалу (3.14). Если же данное отношение выходит за пределы этого интервала, то критическая длина от возмущения нагрузки не зависит.
Таким образом, при анализе устойчивости в рамках концепции ВН, в отличие от концепции ФН, результат зависит от величины и направления действующих возмущений (точнее, от знака и величины отношения возмущения нагрузки к возмущению кривизны). Чтобы сделать результат решения задачи устойчивости в рамках концепции ВН однозначным, можно поставить задачу поиска такого значения вариации внешней нагрузки, являющегося бесконечно малой того же порядка, что и возмущение кривизны, при котором критическая длина имеет наименьшее значение из всех значений критической длины, соответствующих различным значениям вариации нагрузки. Именно это наименьшее значение следует считать критическим, поскольку оно соответствует наиболее опасному сочетанию внешних возмущений. В результате для каждого значения $\left| \sigma \right|$ и ${{\varepsilon }^{0}}$, которые далее для краткости в качестве аргументов функций не фигурируют, возникает следующая задача. Необходимо найти минимальное значение функции двух аргументов $l = l\left( {q,{{\zeta }_{0}}} \right)$ (5.1) по обоим аргументам: lmin = = $\mathop {\min }\limits_{q,{{\zeta }_{0}}} l\left( {q,{{\zeta }_{0}}} \right)$, $q \in \left[ {0,1} \right]$, ${{\zeta }_{0}} \in \left( { - \infty , + \infty } \right)$. При этом известно, что для каждого фиксированного значения $q$ функция $l\left( {q,{{\zeta }_{0}}} \right)$ на интервале ${{\zeta }_{0}} \in \left( { - 1,1} \right)$ монотонно зависит от ${{\zeta }_{0}}$, а за пределами этого интервала сохраняет постоянные значения $l\left( {q,{{\zeta }_{0}}} \right) = {{l}_{2}}\left( q \right)$ для ${{\zeta }_{0}} \leqslant - 1$ и $l\left( {q,{{\zeta }_{0}}} \right) = {{l}_{1}}\left( q \right)$ для ${{\zeta }_{0}} \geqslant 1$. Ниже будет доказано, что это минимальное значение функция $l\left( {q,{{\zeta }_{0}}} \right)$ будет достигать либо для ${{\zeta }_{0}} = - 1$, либо для ${{\zeta }_{0}} = 1$.
Пусть точка $({{q}_{{\min }}},\zeta _{0}^{{\min }})$ доставляет функции $l\left( {q,{{\zeta }_{0}}} \right)$ искомое минимальное значение ${{l}_{{\min }}}$. Если $\xi _{0}^{{\min }} \leqslant - 1$, то в силу независимости $l$ от ${{\zeta }_{0}}$ на множестве ${{\zeta }_{0}} \in \left( { - \infty , - 1} \right]$, функция l будет иметь то же минимальное значение в точке $\left( {{{q}_{{\min }}}, - 1} \right)$. Аналогично, если $\zeta _{0}^{{\min }} \geqslant 1$, то же минимальное значение функция $l$ будет достигать в точке $\left( {{{q}_{{\min }}},1} \right)$. Пусть теперь $ - 1 < \zeta _{0}^{{\min }} < 1$. Функция $l\left( {{{q}_{{\min }}},{{\zeta }_{0}}} \right)$ монотонно изменяется на отрезке [–1.1]. Следовательно, на одном из концов этого отрезка ее значение должно быть меньше, чем в точке $({{q}_{{\min }}},\zeta _{0}^{{\min }})$, чего быть не может.
Отсюда следует, что минимальное значение критической длины для любых значений $\delta P{\text{/}}\delta \kappa $ равно либо $\mathop {\min }\limits_q {{l}_{1}}\left( q \right)$, либо $\mathop {\min }\limits_q {{l}_{2}}(q)$ (5.2), т.е. от величины возмущений $\delta \kappa $, $\delta P$ не зависит и соответствует, либо случаю, когда все сечение находится в зоне догрузки, либо, случаю, когда все сечение находится в зоне разгрузки. Таким образом, решение задачи в рамках концепции ВН имеет вид: $l = \min \left[ {\mathop {\min }\limits_q {{l}_{1}}(q),\;\mathop {\min }\limits_q {{l}_{2}}(q)} \right]$.
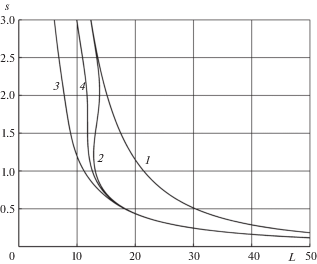
6. Результаты расчетов. Далее будут использованы следующие обозначения для безразмерных переменных: $L = l{\text{/}}h$, $s = \left| \sigma \right|{\text{/}}{{\sigma }_{0}}$. На рис. 1 приведены графики зависимости безразмерной критической длины стержня L от безразмерного параметра нагрузки s получаемые для случая вида 1 задания начальной деформации в рамках концепции ФН. Кривая 1 соответствует упругому решению для мартенситного значения модуля. Кривая 2 соответствует решению несвязанной задачи (т.е. без учета влияния действующих напряжений и накопленных деформаций на процесс фазового перехода), но с учетом дополнительного структурного превращения. Кривая 3 соответствует решению однократно связанной задачи, кривая 4 – решению дважды связанной задачи (в обоих случаях учитываются, как дополнительный структурный, так и дополнительный фазовый переходы). Обращает на себя внимание тот факт, что для малых нагрузок (больших длин) решения в несвязанной, связанной и дважды связанной постановках (с учетом дополнительного структурного превращения) близки между собой. В то же время, для больших нагрузок (малых длин) сближаются решения несвязанной (с учетом структурного перехода) и упругой задач, в то время как критические длины, получаемые в рамках связанной и дважды связанной задач имеют существенно меньшие значения.
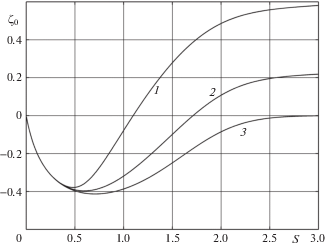
На рис. 2 приведены графики зависимости безразмерной координаты границы между зонами догрузки (над графиками) и разгрузки (под графиками) от безразмерного действующего напряжения, соответствующие решению в рамках концепции ФН, тип 1 задания начальной деформации. Кривая 3 получена при решении задачи в несвязанной постановке (с учетом дополнительного структурного превращения). Кривая 1 соответствует однократно связанной, а кривая 2 – дважды связанной постановкам. Обращает на себя внимание факт немонотонной зависимости ${{\zeta }_{0}}$ от s для всех рассмотренных случаев. При учете только структурного перехода для всех значений s выполняется ${{\zeta }_{0}} < 0$, т.е. большая часть сечения находится в области дополнительного структурного превращения и меньшая в зоне разгрузки. При решении в связанной и дважды связанной постановках та же ситуация имеет место для относительно небольших значений s. Если же s достаточно велико, то зона догрузки в момент потери устойчивости становится меньше половины сечения, а зона дополнительного фазового перехода больше зоны дополнительного структурного перехода.
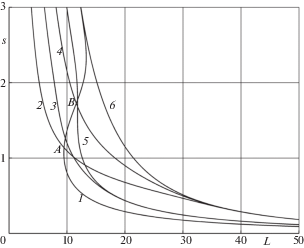
Рисунок 3 соответствует решению задачи в рамках концепции ВН. Линии 1 и 2 (последняя построена в рамках однократно связанной постановки) представляют собой графики зависимости L от s, соответствующие функциям ${{l}_{2}}$ и ${{l}_{1}}$, для решений, при которых по всему сечению происходит, соответственно только дополнительный структурный или только дополнительный фазовый переходы. В соответствии со сформулированной выше концепцией ВН, до точки $A$ пересечения этих линий (если двигаться снизу) решение в рамках однократно связанной постановки дается линией 1, а после точки пересечения $A$ – линией 2. Для контроля на график нанесена линия 3, соответствующая решению в однократно связанной постановке в рамках концепции ФН. Видно, что всем значениям $s$ на этой линии соответствуют величины $L$, большие, чем для полученного решения в рамках концепции ВН. Линии 1 и 4 на рис. 4 соответствуют решению задачи в рамках концепции ВН в дважды связанной постановке. Поскольку решение для повсеместного структурного перехода не зависит от того, в однократно или дважды связанной постановке решается задача, то первая часть решения (до точки пересечения $B$) дает та же линия 1. Решение после точки пересечения $B$ дает линия 4. Линия 5, соответствующая дважды связанному решению в рамках концепции ФН, опять дает значение $L$, большее, чем для концепции ВН. Линия 6, соответствующая упругому решению при мартенситном значении модуля, приведена для контроля.
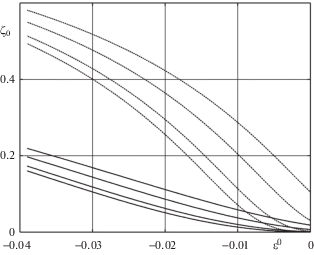
На рис. 4 изображены графики зависимости безразмерной координаты границы между зонами догрузки и разгрузки от заданной начальной деформации для решения задачи устойчивости в рамках концепции ФН при типе 2 задания начальных деформаций, когда дополнительное структурное превращение не возможно. Группа сплошных линий соответствует дважды связанной, а штриховых линий – однократно связанной постановкам. В каждой группе кривые снизу вверх соответствуют значениям безразмерной нагрузки $s = 0.5,\;1,\;2,\;3$. Как видно, в данном случае всегда выполняется ${{\zeta }_{0}} > 0$, т.е. зона разгрузки, а значит и дополнительного фазового перехода превосходит по размерам зону догрузки. Размер зоны дополнительного фазового перехода монотонно растет с ростом начальных деформаций, а при фиксированных начальных деформациях возрастает с ростом нагрузки.
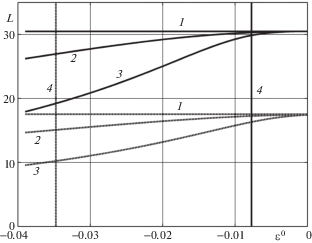
На рис. 5 изображены результаты решения задачи для случая второго типа задания начальных деформаций в рамках концепции ФН. Приведены две совокупности графиков зависимости безразмерной критической длины $L$ от заданной начальной деформации ${{\varepsilon }^{0}}$, соответствующих значениям $s = 0.5$ (сплошные линии) и $s = 1.5$ (штриховые линии). Горизонтальные прямые 1 соответствуют упругому решению для мартенситных значений модуля, которое от начальной деформации не зависит. Линии 3 соответствуют решению в однократно связанной, а линии 2 – в дважды связанной постановках. Вертикальные линии 4 ограничивают сверху возможные в рамках второго типа задания начальных деформаций величины этих деформаций, связанные со значениями s уравнением диаграммы мартенситной неупругости.
Заключение. На примере решения задачи о потере устойчивости стержня из СПФ, вызванной обратным мартенситным превращением под действием постоянной сжимающей нагрузки, сформулирована концепция “Варьируемой нагрузки”, согласно которой критической длиной стержня считается минимальное значение длины, соответствующее различным значениям отношения вариации нагрузки к вариации кривизны, которые считаются бесконечно-малыми величинами одного порядка. Показано, что это критическое значение соответствует либо случаю, когда все сечение стержня находится в зоне дополнительного фазового превращения, либо в зоне дополнительного структурного перехода. Минимальное значение критической нагрузки получается при решении задачи в рамках этой концепции и в однократно связанной постановке.
Работа выполнена в рамках госбюджетной темы, государственная регистрация номер АААА-А19-119012290118-3 при частичной финансовой поддержке РФФИ (грант № 17-01-00216_а).
Список литературы
Еремеев В.А., Зубов Л.М. Об устойчивости равновесия нелинейно-упругих тел, испытывающих фазовые превращения // Изв. АН СССР. МТТ. 1991. № 2. С. 56–65.
Еремеев В.А., Фрейдин А.Б., Шарипова Л.Л. О неединственности и устойчивости в задачах равновесия упругих двухфазных тел // Доклады Академии наук. 2003. Т. 391. № 2. С. 189–193.
Fu Y.B., Freidin A.B. Characterization and stability of two-phase piecewise-homogeneous deformations // Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 2004. V. 460. № 2051. P. 3065–3094.
Мовчан А.А., Думанский С.А. Решение дважды связанной задачи о потере устойчивости стержня из сплава с памятью формы, вызванной прямым термоупругим фазовым превращением // ПМТФ. 2018. Т. 59. № 4. С. 160–168.
Еремеев В.А., Фрейдин А.Б., Шарипова Л.Л. Об устойчивости равновесия двухфазных упругих тел // ПММ. 2007. Т. 71. Вып. 1. С. 66–92.
Rahman M.A., Qiu J., Tani J. Bucling and postbucling characteristics of the superelastic SMA columns // Int. J. Solids and Structure. 2001. V. 38. P. 9253–9265.
Ocel J., DesRoches R., Leon R.T., Hess W.G., Krumme R., Hayes J.R., Sweeney S. Steel beam – column connections using shape memory alloys // J. Structural Eng. 2004. V. 130. № 5. P. 739–740.
Urushiyama Y., Lewinnek D., Qiu J., Tani J. Bucling of shape memory alloy columns // JMSE Int. J. 2003. Ser. A. Solid. Mech. Mater. Eng. 2003. V. 46 (1). P. 60–67.
Rahman M.A., Tani J. Postbucling characteristics of the short superelastic shape memory alloy columns – experiment and quantitative analysis // Int. J. Applied Mechanics and Engineering. 2006. V. 11. № 4. P. 941–955.
Leon T.R., DesRoches R., Ocel J., Hess G. Innovative beam column connection using shape memory alloys // Smart Structure and materials 2001: Smart System for Bridges, Structures, and Highways. Ed. S.C. Liu. Proc. SPIE. 2001. V. 4330. P. 227–237.
Watkins R., Shaw J.B. Shape memory alloy column buckling: an experimental study // In: ICAST 2013 – 24th International Conference on Adaptive Structures and Technologies. 2013. P. 270–282.
Rahman M.A., Qui J., Tani J. Bucling and postbuclimg characteristics of the superelastic SMA columns – numerical simulation // J. Intelligent Material Systems and Structures. 2005. V. 16. P. 691–702.
Rahman M.A., Akanda S.R., Hossain M.A. Effect of cross section geometry on the response of an SMA column // J. Intelligent Material Systems and Structures. 2008. V. 19. P. 243–252.
Richter F., Kastner O., Eggeler G. Finite element simulation of the anty-bucling effect of a shape memory alloy bar // J. Materials Engineering and Performans. 2011. V. 20. P. 719–730.
Сильченко Л.Г. Явление потери устойчивости при мартенситной неупругости // Механика композиционных материалов и конструкций. 2002. Т. 8. № 2. С. 161–169.
Сильченко Л.Г., Сильченко Т.Л. О потере устойчивости элементов из сплавов с памятью формы при структурном превращении с учетом пороговых напряжений // Механика композиционных материалов и конструкций. 2010. Т. 16. № 4. С. 455–467.
Kunavar J., Kozel F., Puksic A., Videnic T. Geometry optimization in buckling of shape memory alloy columns due to constrained recovery // J. Intelligent Material Systems and Structures. 2012. V. 23. P. 65–76.
Сильченко Л.Г. Устойчивость стесненного стержня из сплава с памятью формы при обратном мартенситном фазовом превращении // Механика композиционных материалов и конструкций. 2004. Т. 10. № 4. С. 543–553.
Еремеев В.А. О потере устойчивости упругих систем при наличии мартенситных превращений на примере фермы Мизеса // Вестник Южного научного центра РАН. 2005. Т. 1. № 2. С. 91–93.
Еремеев В.А. О потере устойчивости фермы Мизеса при наличии мартенситных превращений // Известия высших учебных заведений. Северо-Кавказский регион. Серия: Естественные науки. 2006. № 1 (133). С. 35–38.
Pedro A.S., Pacheco M.C.L., Braga A.M.B. Chaos in a shape memory two-bar truss // Int. J. Non-Linear Mechanics. 2002. V. 37. P. 1387–1395.
Lee J.J., Choi S. Thermal buckling and postbuckling analysis of a laminated composite beam with embedded SMA actuators // Composite Structures. 1999. V. 47. P. 695–703.
Kabir M.-Z., Tehrani B.T. Closed-form Solution for Thermal, Mechanical and Thermo-mechanical Buckling and Post-buckling of SMA Composite Beams // Composite Struct. 2017. V. 168. P. 535–548.
Малыгин Г.А. Эйлерова неустойчивость двунаправленного эффекта памяти формы в ленте из никелида титана // ФТТ. 2003. Т. 45. Вып. 12. С. 2233–2237.
Малыгин Г.А., Хусаинов М.А. Анализ устойчивости механического поведения арки – полоски из никелида титана в условиях стесненного эффекта памяти формы // Ж. техн. физики. 2004. Т. 74. Вып. 10. С. 57–63.
Michailidis P.A., Triantafyllidis N., Shaw J.A., Grummon D.S. Superelasticity and stability of a shape memory alloy hexagonal honeycomb under in-plane compression // Int. J. Solids Struct. 2009. V. 46. P. 2724–2738.
Хусаинов М.А. Исследование эффекта осесимметричного выпучивания круглых пластин // Ж. техн. физики. 1997. Т. 67. № 6. С. 118–120.
Nemat-Nasser S., Choi J.Y., Isaacs J.B., Lisher D.W. Experimental observation of high-rate buckling of thin cylindrical shape-memory shells // SPIE Proceedings. V. 5761. Smart structure and materials 2005. Active materials: Behavior and mechanics / Ed. by W.D. Armstrong. P. 347–354.
Tang Z., Li D. Experimental investigation of axial impact bucling response of pseudo-elastic NiTi cylindrical shells // Int. J. Impact Eng. 2012. V. 39. P. 28–41.
Tang Z., Li D. Quasi-static axial bucling behavior of TiNi thin-walled cylindrical shells. Thin-Walled structures. 2012. V. 51. P. 130–138.
Amini M.R., Nemat-Nasser S. Dynamic bucling and recovery of thin cylindrical shells // SPIE Proceedings. V. 5761. Smart structure and materials 2005. Active materials: Behavior and mechanics / Ed. by W.D. Armstrong. P. 450–453.
Nemat-Nasser S., Choi J.Y., Isaacs J.B., Lisher D.W. Quasi-static and dynamic buckling of thin cylindrical shape memory alloy shells // J. Applied Mechanics. 2006. V. 73. № 5. P. 825–833.
Jiang D., Bechle N., Landis C.M., Kyriakides S. Buckling and Recovery of NiTi Tubes Under Axial Compression // Int. J. Solids Struct. 2016. V. 80. P. 52–63.
Jiang D., Landis C.M. and Kyriakides S. Effects of Tension/Compression Asymmetry on the Buckling and Recovery of NiTi Tube under Axial Compression // Int. J. Solids Struct. 2016. V. 100–101. P. 41–53.
Хусаинов М.А., Малухина О.А. Анализ устойчивости сферических сегментов с памятью формы // Тр. 3-го Междунар. семинара “Современные проблемы прочности” им. В.А. Лихачева. 1999 г. Великий Новгород: Изд-во Новгородского ун-та, 1999. Т. 2. С. 185–189.
Шкутин Л.И. Нелинейные деформации и катастрофы тонких тел // Новосибирск: Изд-во СО РАН, 2014. 139 с.
Мовчан А.А., Казарина С.А. Экспериментальное исследование явления потери устойчивости, вызванной термоупругими фазовыми превращениями под действием сжимающих напряжений // Проблемы машиностроения и надежности машин. 2002. № 6. С. 82–89.
Мовчан А.А., Сильченко Л.Г. Устойчивость стержня, претерпевающего прямое или обратное мартенситные превращения под действием сжимающих напряжений // ПМТФ. 2003. Т. 4. № 3. С. 169–178.
Мовчан А.А., Мовчан И.А., Сильченко Л.Г. Влияние структурного превращения и нелинейности процесса деформирования на устойчивость стержня из сплава с памятью формы // Изв. РАН. МТТ. 2010. № 6. С. 137–147.
Nushtaev D.V., Zhavoronok S.I. Dynamics of martensite phase transitions in shape memory beams under buckling and postbuckling conditions // IFAC. 2018. V. 51. № 2. P. 873–878.
Мовчан А.А., Сильченко Л.Г. Аналитическое решение связной задачи об устойчивости пластины из сплава с памятью формы при прямом термоупругом фазовом превращении // ПММ. 2004. Т. 68. Вып. 1. С. 60–72.
Мовчан А.А., Сильченко Л.Г. Аналитическое решение связной задачи об устойчивости пластины из сплава с памятью формы при обратном мартенситном превращении // Изв. РАН. МТТ. № 5. С. 164–178.
Мовчан А.А., Сильченко Л.Г. Устойчивость круглой пластины из сплава с памятью формы при прямом мартенситном превращении // ПММ. 2006. Т. 70. Вып. 5. С. 871–883.
Шкутин Л.И. Анализ плоских фазовых деформаций стержней и пластин // ПМТФ. 2006. Т. 47. № 2. С. 156–164.
Мовчан А.А., Сильченко Л.Г. Потеря устойчивости круглой пластины из сплава с памятью формы, вызванная обратным термоупругим мартенситным превращением // Изв. РАН. МТТ. 2008. № 1. С. 117–130.
Мовчан А.А., Мовчан И.А., Сильченко Л.Г. Устойчивость кольцевой пластины из сплава с памятью формы // ПМТФ. 2011. Т. 52. № 2. С. 144–155.
Sil'chenko L.G., Movchan A.A., Sil’chenko O.L. Stability of Cylindrical Shell Made from Shape-Memory Alloys // Int. Applied Mechanics. 2014. V. 50. Issue 2. P. 171–178.
Шкутин Л.И. Анализ осесимметричных фазовых деформаций в пластинах и оболочках // ПМТФ. 2007. Т. 48. № 2. С. 163–171.
Мовчан А.А., Казарина С.А. Материалы с памятью формы как объект механики деформируемого твердого тела: экспериментальные исследования, определяющие соотношения, решение краевых задач // Физическая мезомеханика. 2012. Т. 15. № 1. С. 105–116.
Думанский С.А., Мовчан А.А. Дважды связная постановка задачи о потере устойчивости вызванной обратным термоупругим фазовым превращением в сплаве с памятью формы // Изв. РАН. МТТ. 2017. № 5. С. 37–48.
Казарина С.А., Мовчан А.А., Сильченко А.Л. Экспериментальное исследование взаимодействия фазовых и структурных деформаций в сплавах с памятью формы // Механика композиционных материалов и конструкций. 2016. Т. 22. № 1. С. 85–98.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела