1. На главную
  2. Электронные версии
  3. Известия РАН. Механика твердого тела
  4. № 4, 2019

Известия РАН. Механика твердого тела, 2019, № 4, стр. 3-7

АППРОКСИМАЦИЯ ВЫРАЖЕНИЙ ДЛЯ СИЛЫ И МОМЕНТА СИЛЫ СУХОГО ТРЕНИЯ

А. А. Загордан a, Е. А. Привалов b, *

a ООО “Авиакомпания Волга-Днепр”
Москва, Россия

b Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия

* E-mail: prival@ipmnet.ru

Поступила в редакцию 06.12.2018
После доработки 06.12.2018
Принята к публикации 19.12.2018

Полный текст (PDF)

Аннотация

Динамика колеса, движущегося по опорной поверхности, в значительной мере определяется трением в области его контакта с поверхностью. Для определения силы и момента силы сухого трения применяется модель, основанная на теории контактных напряжений Герца. При исследовании конкретных механических систем с сухим трением удобно использовать аппроксимации компонент силы трения более простыми выражениями. В данной работе предложено два варианта построения приближенных выражений компонент силы трения c использованием аппроксимации функции в среднем.

Ключевые слова: сухое трение, контактные напряжения, аппроксимация функции в среднем

Рассматривается модель сухого трения, основанная на теории Герца о распределении напряжений в области контакта колеса с опорой [1]. Считается, что область контакта – круг. Силовые характеристики трения задаются проекциями на оси декартовой системы координат $Oxyz$, начало которой находится в центре круга, оси Ox и Oy лежат в плоскости опорной поверхности, ось Ox направлена по скорости центра колеса. Получены выражения для проекций силы сухого трения оси Ox и Oy в виде эллиптических интегралов. Использование других переменных [2] позволяет получить выражения для проекций силы и момента силы сухого трения в элементарных функциях.

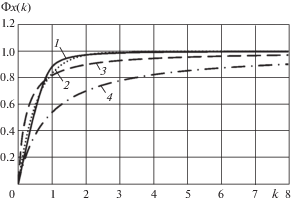
Проекция силы сухого трения на ось Ox с точностью до постоянного множителя определяется функцией Φx(k), изменяющейся в пределах 0–1

(1)
${{\Phi }_{x}}(k) = \left\{ \begin{gathered} \frac{3}{{32}}{\pi }k(4 - {{k}^{2}}),\quad k \leqslant 1 \hfill \\ \frac{3}{{16}}\left[ {k(4 - {{k}^{2}})\arcsin \frac{1}{k} + \left( {k + \frac{2}{k}} \right)\sqrt {{{k}^{2}} - 1} } \right],\quad k \geqslant 1 \hfill \\ \end{gathered} \right.$

Здесь: , $v$ – скорость скольжения колеса, ${\omega }$ – угловая скорость верчения, ${\varepsilon }$ – радиус круга контакта.

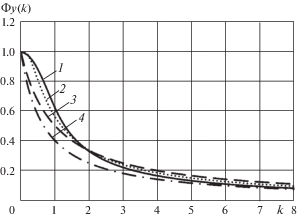
Функция Φy(k), пропорциональная проекции силы сухого трения на ось Oy, также меняется в пределах 0–1

(2)
${{\Phi }_{y}}(k) = \left\{ \begin{gathered} 1 - \frac{1}{2}{{k}^{2}} + \frac{1}{8}{{k}^{4}},\quad k \leqslant 1 \hfill \\ \frac{2}{{\pi }}\left\{ {\left( {1 - \frac{1}{2}{{k}^{2}} + \frac{1}{8}{{k}^{4}}} \right)\arcsin \frac{1}{k} + \left( {\frac{1}{3}\frac{1}{{{{k}^{2}}}} + \frac{5}{{12}} - \frac{1}{8}{{k}^{2}}} \right)\sqrt {{{k}^{2}} - 1} } \right\},\quad k > 1 \hfill \\ \end{gathered} \right.$

Момент силы трения относительно оси Oz с точностью до постоянного множителя задается функцией $0 \leqslant \Phi _{z}^{{}}(k) \leqslant 1$, которая имеет вид

(3)
${{\Phi }_{z}}(k) = \left\{ \begin{gathered} \frac{1}{8}(8 - 8{{k}^{2}} + 3{{k}^{4}}),\quad k \leqslant 1 \hfill \\ \frac{1}{{4{\pi }}}\left[ {(8 - 8{{k}^{2}} + 3{{k}^{4}})\arcsin \frac{1}{k} + 3(2 - {{k}^{2}})\sqrt {{{k}^{2}} - 1} } \right],\quad k > 1 \hfill \\ \end{gathered} \right.$

В [2], [3] предлагается при решении практических задач использовать аппроксимации функций (1–3) дробно-линейными функциями

(4)
${\varphi }(k) = \frac{{{{A}_{0}} + {{A}_{1}}k}}{{1 + Bk}}$
– аппроксимациями Паде [4], [5], имеющими те же значения функции и производной в нуле и предела функции в бесконечности.

1. Рассмотрим иной способ построения дробно-линейных приближений функций (1–3). При этом два коэффициента функции (4) найдем из используемых в [2], [3] условий равенства значений аппроксимирующей и аппроксимируемой функций при k = 0 и при $k \to \infty $. Значение третьего коэффициента определим, применив аппроксимацию функции в среднем [6, 7]. Потребуем, чтобы на некотором выбранном интервале [k1, k2] при этой величине коэффициента достигался минимум интеграла U – среднего квадратического отклонения функции $\Phi (k)$ от ${\varphi }{\kern 1pt} {\kern 1pt} (k)$

(5)
$U = \frac{1}{{{{k}_{2}} - {{k}_{1}}}}\int\limits_{{{k}_{1}}}^{{{k}_{2}}} {{{{[\Phi (k) - {\varphi }(k)]}}^{2}}dk} $

Пределы интегрирования ${{k}_{1}}$ и ${{k}_{2}}$, выбираем, исходя из диапазона значений, в котором меняются скорости скольжения и верчения колеса в рассматриваемой задаче. Поиск минимума функции U осуществляется численно. Результаты вычислений, полученные ниже, приведены для значений ${{k}_{1}} = 0,{{k}_{2}} = 20$.

Определим коэффициенты дробно-линейной функции, аппроксимирующей Φx(k). Функция ${{\Phi }_{x}}(k)$ удовлетворяет условиям

${{\Phi }_{x}}(0) = 0,\quad {{\lim }_{{k \to \infty }}}{{\Phi }_{x}}(k) = 1$
c учетом которых функцию (4) запишем в виде

(6)
${\varphi }_{x}^{{}}(k) = \frac{{{{B}_{x}}k}}{{1 + {{B}_{x}}k}}$

Подставим функции (1) и (6) в (5). Значение коэффициента Bx, при котором интеграл (5) имеет минимум $\min U_{x}^{{}}$ = 0.00215, достигается при величине коэффициента $B_{x}^{*}$ = 4.52.

При построении приближения функции Φy(k) дробно-линейной функцией считаем, что функция (4) удовлетворяет условиям

${\varphi }(0) = 1,$ ${{\lim }_{{k \to \infty }}}{\varphi }_{y}^{{}}(k) = 0,$
которым удовлетворяет функция Φy(k). Аппроксимирующая функция имеет вид

(7)
${\varphi }_{y}^{{}}(k) = \frac{1}{{1 + {{B}_{y}}k}}$

Результат аппроксимации (2) функцией (7): интеграл (5) имеет минимум min${{U}_{y}}$ = = 0.0021 при значении коэффициента $B_{y}^{*}$ = 0.98.

При аппроксимации функции Φz(k) функцией (4) с учетом условий

$\Phi _{z}^{{}}(0) = 1$, ${{\lim }_{{k \to \infty }}}\Phi _{z}^{{}}(k) = 0$
получим функцию вида

(8)
${\varphi }_{z}^{{}}(k) = \frac{1}{{1 + {{B}_{z}}k}}$

Минимум среднего квадратического отклонения функций (3) и (8) $\min {{U}_{z}}$ = 0.0023 достигается при $B_{z}^{*}$ = 1.76.

2. Рассмотрим результаты аппроксимаций в среднем выражений для проекций силы и момента силы сухого трения функциями ϕ(k), содержащими экспоненту. Как и ранее, при формировании среднего квадратического отклонения V аппроксимируемой функции от аппроксимирующей

(9)
$V = \frac{1}{{{{k}_{2}} - {{k}_{1}}}}\int\limits_{{{k}_{1}}}^{{{k}_{2}}} {{{{[\Phi (k) - \phi (k)]}}^{2}}dk} $
значения пределов интегрирования ${{k}_{1}} = 0,$ ${{k}_{2}} = 20$.

Функцию Φx(k) будем аппроксимировать в среднем функцией

${{\phi }_{x}}(k) = 1 - {{e}^{{ - {{b}_{x}}k}}}$

Интеграл (9) имеет минимум $\min {\kern 1pt} {\kern 1pt} {{V}_{x}}$ = 0.0023 при $b_{x}^{*} = 1.792$.

Функцию, аппроксимирующую функции Φy(k), зададим в виде

(10)
${{\phi }_{y}}(k) = 1 - {{e}^{{ - {{b}_{y}}/k}}}$

В результате подстановки в (9) функций (2) и (10), получим функцию, имеющую минимум $\min {{V}_{y}} = 0.00036$ при $b_{y}^{*} = 0.833$.

Для аппроксимации функции ${{\Phi }_{z}}(k)$ выберем функцию

${{\phi }_{z}}(k) = 1 - {{e}^{{ - {{b}_{z}}/k}}}$

Минимум функции (9) $\min V_{z}^{{}} = $ 0.00082 достигается при $b_{z}^{*} = $ 0.477.

3. На рис. 1 представлены: график зависимости Φx(k), график аппроксимации Φx(k) в среднем функцией ϕk(k), график аппроксимации в среднем дробно-линейной функций (6) и график аппроксимации дробно-линейной функцией Паде. Нумерация графиков соответствует порядку их перечисления.

Рис. 1

Графики функций Φy(k), Φz(k) и графики таких же аппроксимаций этих функций представлены на рис. 2 и рис. 3 соответственно и имеют ту же нумерацию, что на рис. 1. Графики дробно-линейных приближений Паде функций Φx(k), Φy(k), Φz(k) построены соответственно для значений коэффициентов

(11)
$B_{x}^{{Pade}} = $ $\frac{3}{8}{\pi } \approx 1.178$, $B_{y}^{{Pade}} = $ $\frac{{15}}{{32}}{\pi } \approx $ $1.473$, $B_{z}^{{Pade}} = $ $\frac{{15}}{{16}}{\pi } \approx $ $2.945$
Рис. 2
Рис. 3

Интеграл (5) при подстановке в него функций 1 и 6, 2 и 7, 3 и 8 и соответствующего значения коэффициента из набора (11) принимает значения

$U_{x}^{{Pade}} = $ $0.017$, $U_{y}^{{Pade}} = $ 0.0045, $U_{z}^{{Pade}} = $ 0.0043.

Проведенное исследование показывает, что аппроксимации в среднем функций (1), (2), (3) дают лучшие приближения, чем аппроксимации дробно-линейными функциями с использованием разложений Паде, но требуют большего объема вычислений.

Авторы благодарят В.Ф. Журавлева за обсуждение постановки задачи.

Работа выполнена по госзаданию № АААА-А17-117021310382-5.

Список литературы

  1. Контенсу П. Связь между трением скольжения и трением верчения и ее учет в теории волчка // Проблемы гироскопии. М.: Мир, 1967. С. 60–77.

  2. Журавлев В.Ф. О модели сухого трения в задаче качения твердых тел // ПММ. 1998. Т. 62. Вып. 5. С. 762–767.

  3. Журавлев В.Ф., Климов Д.М. Теория явления шимми // Изв. РАН. МТТ. 2010. № 3. С. 22–29.

  4. Андронов В.В., Журавлев В.Ф. Сухое трение в задачах механики. М.: Ижевск: Ижевский институт компьютерных исследований. НИЦ “Регулярная и хаотическая динамика”, 2010. 184 с.

  5. Бейкер Дж., Грейвс-Моррис П. Аппроксимации Паде. М.: Мир, 1986. 502 с.

  6. Журавлев В.Ф., Климов Д.М. Прикладные методы в теории колебаний. М.: Наука, 1988. 328 с.

  7. Пискунов Н.С. Дифференциальное и интегральное исчисления. Для втузов. Т. 2. 1976. 576 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал