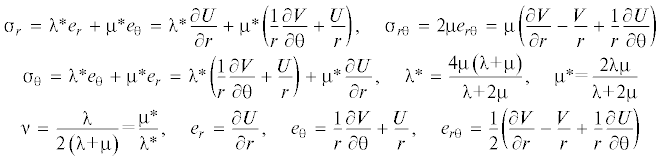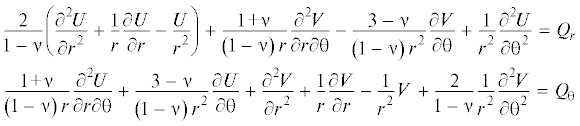Известия РАН. Механика твердого тела, 2019, № 5, стр. 113-130
РЕШЕНИЕ ЗАДАЧИ О НАПРЯЖЕНИЯХ В ОСТРОМ КЛИНОВИДНОМ РЕЖУЩЕМ ИНСТРУМЕНТЕ МЕТОДОМ БЫСТРЫХ РАЗЛОЖЕНИЙ И ПРОБЛЕМА СОГЛАСОВАНИЯ ГРАНИЧНЫХ УСЛОВИЙ
В. В. Горяйнов b, *, М. И. Попов a, А. Д. Чернышов a, **
a Воронежский государственный университет инженерных технологий
Воронеж, Россия
b Воронежский государственный технический университет
Воронеж, Россия
* E-mail: gorvit77@mail.ru
** E-mail: chernyshovad@mail.ru
Поступила в редакцию 08.11.2018
После доработки 20.12.2018
Принята к публикации 28.02.2019
Аннотация
Методом быстрых разложений в аналитическом виде решена упругая задача со смешанными граничными условиями о напряжениях в остром клиновидном режущем инструменте конечных размеров в виде усеченного сектора. К граням клина и его носику приложена нагрузка, быстро убывающая при удалении от носика. На большем радиусе клин жестко закреплен. Полученное решение справедливо для любого угла раствора клина. Если принять внутренний радиус и угол раствора достаточно малыми, то форма предполагаемого резца будет достаточно близкой к реальной. Исследовано влияние угла раствора и внутреннего радиуса клина на величину и месторасположение наибольшего напряжения ${\tilde {\sigma }}$. Найдены критические размеры клина, но при любых его размерах напряжения всюду конечные.
Введение. В [1] приведены случаи нагружения клина неограниченными сосредоточенными силами, в [2] используются граничные условия смешанного типа. Внедрение клина в пластическое полупространство изучалось в монографии [3]. Решения с помощью рядов Тейлора по радиусу получены в [4], нагруженный клин с гладкими гранями рассматривался в [5]. Поле напряжений для антиплоской деформации упругого клина рассмотрено в [6–8]. Плоская деформация клина обсуждается в [9, 10]. Некоторые конкретные результаты получены путем применения преобразований Меллина [6, 9–11] и использования функций комплексного переменного [7, 8, 12]. В работе [11] фигурируют критические углы раствора клина. Частные решения для усеченного кругового сектора приводятся также в [13]. Некоторые исследования посвящены трехмерным задачам для упругого клина [14, 15]. В [14] предложен явный матричный алгоритм решения трехмерной клиновой задачи. В [15] одна из поверхностей клина усилена покрытием типа Винклера. На другой поверхности заданы произвольные граничные условия. В этом случае используются методы нелинейных граничных интегральных уравнений и последовательных приближений.
В данной работе применен новый аналитический метод быстрых разложений [16], позволяющий получить решение задачи с высокой точностью в явном аналитическом виде. Метод быстрых разложений применим для решения задач, связанных с дифференциальными уравнениями в частных производных [17, 18], с интегро-дифференциальными [19] и обыкновенными дифференциальными уравнениями [20]. Рассматриваемая задача особенно усложнена заданием граничных условий смешанного типа.
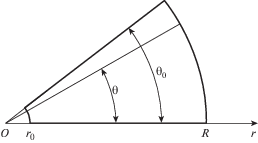
1. Постановка задачи. Все рассмотрения будем проводить в цилиндрической системе координат. В задаче упругости со смешанными граничными условиями на внешней границе резца (рис. 1) при $r = R$ зададим перемещения
(1.1)
${{\left. U \right|}_{{r = R}}} = {{U}_{R}}\left( {\theta } \right),\quad {{\left. V \right|}_{{r = R}}} = {{V}_{R}}\left( {\theta } \right),\quad {\theta } \in \left[ {0,{{{\theta }}_{0}}} \right]$(1.2)
$\begin{gathered} {{\left. {{{{\sigma }}_{{r{\theta }}}}} \right|}_{{{\theta } = 0}}} = {\mu }{{\Phi }_{1}}\left( r \right),\quad {{\left. {{{{\sigma }}_{{\theta }}}} \right|}_{{{\theta } = 0}}} = {\lambda *}{{\Phi }_{3}}\left( r \right),\quad {{\left. {{{{\sigma }}_{{r{\theta }}}}} \right|}_{{{\theta } = {{{\theta }}_{0}}}}} = {\mu }{{\Phi }_{2}}\left( r \right) \\ {{\left. {{{{\sigma }}_{{\theta }}}} \right|}_{{{\theta } = {{{\theta }}_{0}}}}} = {\lambda *}{{\Phi }_{4}}\left( r \right),\quad {{\left. {{{{\left. {{{{\sigma }}_{r}}} \right|}}_{{r = {{r}_{0}}}}} = {\lambda *}{{F}_{1}}\left( {\theta } \right),\quad {{{\sigma }}_{{r{\theta }}}}} \right|}_{{r = {{r}_{0}}}}} = {\mu }{{F}_{2}}\left( {\theta } \right) \\ \end{gathered} $Постоянная ${\lambda *}$ определяется через упругие коэффициенты Ламе ниже в формулах (1.5). Напряжения и деформации по физическому смыслу задачи должны быть ограниченными всюду в области режущего инструмента, бесконечности не допускаются, иначе резец сломается, поэтому кроме приведенных граничных условий добавим условия ограниченности и гладкости
(1.3)
$\left( {U,V} \right) \in \{ {{C}^{{\left( 3 \right)}}}\left( {0 \leqslant {\theta } \leqslant {{{\theta }}_{0}}} \right),{{C}^{{\left( {11} \right)}}}\left( {{{r}_{0}} \leqslant r \leqslant R} \right)\} ,\quad \left| {U,V} \right| < \infty $Необходимость в вычислении производных 11-го порядка по $r$ и 3-го порядка по ${\theta }$ будет показана в процессе построения аналитического решения. Полагаем, что резец выполнен из тонкой упругой пластины и имеет форму усеченного сектора (рис. 1). Запишем уравнения равновесия при плоском напряженном состоянии
(1.4)
$\frac{{\partial {{{\sigma }}_{r}}}}{{\partial r}} + \frac{1}{r}\frac{{\partial {{{\sigma }}_{{r{\theta }}}}}}{{\partial {\theta }}} + \frac{{{{{\sigma }}_{r}} - {{{\sigma }}_{{\theta }}}}}{r} = {\mu }{{Q}_{r}}\left( {r,{\theta }} \right),\quad \frac{{\partial {{{\sigma }}_{{r{\theta }}}}}}{{\partial r}} + \frac{1}{r}\frac{{\partial {{{\sigma }}_{{\theta }}}}}{{\partial {\theta }}} + 2\frac{{{{{\sigma }}_{{r{\theta }}}}}}{r} = {\mu }{{Q}_{{\theta }}}\left( {r,{\theta }} \right)$Здесь ${{Q}_{r}}$, ${{Q}_{{\theta }}}$ – массовые силы, их используем при проведении тестовых примеров. Напряжения выразим через деформации по закону Гука, а деформации через перемещения $U$, $V$ по формулам Коши [21]
Здесь ${\lambda }$, ${\mu }$ – упругие постоянные Ламе, ${\nu }$ – коэффициент Пуассона. Составляющая деформаций ez не равна нулю и при плоском напряженном состоянии находится из уравнения σz = 0, откуда 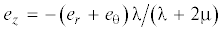 . Если деформации, выраженные через перемещения, подставить в напряжения, а затем
в уравнения равновесия (1.4), то получим систему дифференциальных уравнений в частных
производных второго порядка относительно U, V:
. Если деформации, выраженные через перемещения, подставить в напряжения, а затем
в уравнения равновесия (1.4), то получим систему дифференциальных уравнений в частных
производных второго порядка относительно U, V:
При помощи (1.5) граничные условия (1.2) приводятся к виду
(1.7)
$\begin{gathered} {{\left. {{{{\left. {\left( {\frac{1}{r}\frac{{\partial U}}{{\partial {\theta }}} + \frac{{\partial V}}{{\partial r}} - \frac{V}{r}} \right)} \right|}}_{{{\theta } = 0}}} = {{\Phi }_{1}}\left( r \right),\quad \left[ {\left( {\frac{U}{r} + \frac{1}{r}\frac{{\partial V}}{{\partial {\theta }}}} \right) + {\nu }\frac{{\partial U}}{{\partial r}}} \right]} \right|}_{{{\theta } = 0}}} = {{\Phi }_{3}}\left( r \right) \\ {{\left. {\left( {\frac{1}{r}\frac{{\partial U}}{{\partial {\theta }}} + \frac{{\partial V}}{{\partial r}} - \frac{V}{r}} \right)} \right|}_{{{\theta } = {{{\theta }}_{0}}}}} = {{\Phi }_{2}}\left( r \right){{\left. {\quad \left[ {\left( {\frac{U}{r} + \frac{1}{r}\frac{{\partial V}}{{\partial {\theta }}}} \right) + {\nu }\frac{{\partial U}}{{\partial r}}} \right]} \right|}_{{{\theta } = {{{\theta }}_{0}}}}} = {{\Phi }_{4}}\left( r \right) \\ \end{gathered} $(1.8)
$a)\,{{\left. {\left( {\frac{{\partial U}}{{\partial r}} + {\nu }\left( {\frac{1}{r}\frac{{\partial V}}{{\partial {\theta }}} + \frac{U}{r}} \right)} \right)} \right|}_{{r = {{r}_{0}}}}} = {{F}_{1}}\left( {\theta } \right),\quad b)\,{{\left. {\left( {\frac{1}{r}\frac{{\partial U}}{{\partial {\theta }}} + \frac{{\partial V}}{{\partial r}} - \frac{V}{r}} \right)} \right|}_{{r = {{r}_{0}}}}} = {{F}_{2}}\left( {\theta } \right)$Из условия непрерывности напряжений в угловых точках клина и условия ${{{\sigma }}_{{r{\theta }}}} = {{{\sigma }}_{{{\theta }r}}}$ следует, что граничные условия в (1.7) и (1.8) должны удовлетворять равенствам
(1.9)
${{\Phi }_{1}}\left( {{{r}_{0}}} \right) = {{F}_{2}}\left( 0 \right),\quad {{\Phi }_{2}}\left( {{{r}_{0}}} \right) = {{F}_{2}}\left( {{{{\theta }}_{0}}} \right)$Будем полагать, что сторона резца при θ = 0 свободна от нагрузки
Для ${{\Phi }_{2}}\left( r \right)$, ${{\Phi }_{4}}\left( r \right)$, ${{F}_{1}}\left( {\theta } \right)$, ${{F}_{2}}\left( {\theta } \right)$ выберем одни из простейших зависимостей, удовлетворяющих условиям (1.9)
Постоянные ${{F}_{{03}}}$, ${{\Phi }_{{03}}}$, ${{\Phi }_{{06}}}$ зависят от силы прижатия резца к обрабатываемому образцу и определяются экспериментально, а константы
(1.10)
${{F}_{{01}}},{{F}_{{02}}},{{\Phi }_{{01}}},{{\Phi }_{{02}}},{{\Phi }_{{04}}},{{\Phi }_{{05}}}$2. Построение решения методом быстрых разложений. Для получения решения подобных многомерных линейных задач в аналитическом виде можно применять метод угловых суперпозиций [22], но предлагаемый здесь метод быстрых разложений еще более эффективен вследствие существенной экономии времени и высокой точности при работе на ЭВМ [17–20]. Для нахождения перемещений U и V будем использовать их быстрые разложения по углу ${\theta }$. В первом уравнении (1.6) от U берется частная производная по ${\theta }$ второго порядка, от V – первого порядка. Во втором уравнении (1.6) от U берется частная производная по ${\theta }$ первого порядка, от V – второго порядка. Поэтому удобнее будет использовать следующие быстрые разложения
(2.1)
$\begin{gathered} U = C{{h}_{2}}U = {{M}_{2}} + \sum\limits_{m = 1}^N {{{u}_{m}}\left( r \right)\sin m{\pi }\frac{{\theta }}{{{{{\theta }}_{{\text{0}}}}}}} \\ V = C{{h}_{3}}V = {{M}_{3}} + {{\upsilon }_{0}}\left( r \right) + \sum\limits_{m = 1}^N {{{\upsilon }_{m}}\left( r \right)\cos m{\pi }\frac{{\theta }}{{{{{\theta }}_{{\text{0}}}}}}} \\ \end{gathered} $(2.2)
$\begin{gathered} {{M}_{2}} = {{A}_{1}}\left( {1 - \frac{{\theta }}{{{{{\theta }}_{{\text{0}}}}}}} \right) + {{A}_{2}}\frac{{\theta }}{{{{{\theta }}_{{\text{0}}}}}} + {{A}_{3}}\left( {\frac{{{{{\theta }}^{{\text{2}}}}}}{{\text{2}}} - \frac{{{{{\theta }}^{{\text{3}}}}}}{{{\text{6}}{{{\theta }}_{{\text{0}}}}}} - \frac{{{{{\theta }}_{{\text{0}}}}{\theta }}}{{\text{3}}}} \right) + {{A}_{4}}\left( {\frac{{{{{\theta }}^{{\text{3}}}}}}{{{\text{6}}{{{\theta }}_{{\text{0}}}}}} - \frac{{{{{\theta }}_{{\text{0}}}}{\theta }}}{{\text{6}}}} \right) \\ {{M}_{3}} = {{B}_{1}}\left( {{\theta } - \frac{{{{{\theta }}^{{\text{2}}}}}}{{{\text{2}}{{{\theta }}_{{\text{0}}}}}}} \right) + {{B}_{2}}\frac{{{{{\theta }}^{{\text{2}}}}}}{{{\text{2}}{{{\theta }}_{{\text{0}}}}}} + {{B}_{3}}\left( {\frac{{{{{\theta }}^{{\text{3}}}}}}{{\text{6}}} - \frac{{{{{\theta }}^{{\text{4}}}}}}{{{\text{24}}{{{\theta }}_{{\text{0}}}}}} - \frac{{{{{\theta }}_{{\text{0}}}}{{{\theta }}^{{\text{2}}}}}}{{\text{6}}}} \right) + {{B}_{4}}\left( {\frac{{{{{\theta }}^{{\text{4}}}}}}{{{\text{24}}{{{\theta }}_{{\text{0}}}}}} - \frac{{{{{\theta }}_{{\text{0}}}}{{{\theta }}^{{\text{2}}}}}}{{{\text{12}}}}} \right) \\ \end{gathered} $Специальный вид ${{M}_{2}}$, ${{M}_{3}}$ в (2.2) подобран так, чтобы ряды Фурье в разложениях (2.1) быстро сходились [16] и тогда N в суммах будет небольшим. Это позволяет более точно выполнить условия равновесия (1.6).
В (2.1) и (2.2) неизвестными являются 9 + 2N функций, зависящих только от одной переменной $r$:
(2.3)
${{A}_{1}}(r) \div {{A}_{4}}(r),\quad {{B}_{1}}(r) \div {{B}_{4}}(r),\quad {{u}_{m}}(r),\quad {{\upsilon }_{0}}(r),\quad {{\upsilon }_{m}}(r),\quad m = 1 \div N$Для нахождения коэффициентов синус-разложения для U, заданного в (2.1), (2.2) оператором $C{{h}_{2}}U$, необходимо выполнить следующие действия:
1. В левой и правой частях (2.1) для U положим θ = 0, затем ${\theta } = {{{\theta }}_{0}}$
(2.4)
${{\left. U \right|}_{{{\theta } = 0}}} = {{A}_{1}}\left( r \right),\quad {{\left. U \right|}_{{{\theta = }{{{\theta }}_{0}}}}} = {{A}_{2}}\left( r \right)$2. Левую и правую части (2.1) для U дважды продифференцируем по ${\theta }$ (максимально допустимый порядок дифференцирования рядов Фурье по ${\theta }$ в разложении (2.1) для $U$) и положим θ = 0, затем ${\theta } = {{{\theta }}_{0}}$:
(2.5)
${{\left. {{{{{\partial }^{2}}U} \mathord{\left/ {\vphantom {{{{\partial }^{2}}U} {\partial {{{\theta }}^{2}}}}} \right. \kern-0em} {\partial {{{\theta }}^{2}}}}} \right|}_{{{\theta } = 0}}} = {{A}_{3}}\left( r \right),\quad {{\left. {{{{{\partial }^{2}}U} \mathord{\left/ {\vphantom {{{{\partial }^{2}}U} {\partial {{{\theta }}^{2}}}}} \right. \kern-0em} {\partial {{{\theta }}^{2}}}}} \right|}_{{{\theta = }{{{\theta }}_{0}}}}} = {{A}_{4}}\left( r \right)$3. Левую и правую части (2.1) для U умножим на $\sin {{n{\pi \theta }} \mathord{\left/ {\vphantom {{n{\pi \theta }} {{{{\theta }}_{0}}{\text{,}}}}} \right. \kern-0em} {{{{\theta }}_{0}}{\text{,}}}}n = 1\, \div \,N$ и проинтегрируем по ${\theta } \in \left[ {0,\,{{{\theta }}_{0}}} \right]$:
(2.6)
${{u}_{n}}\left( r \right) = \frac{2}{{{{{\theta }}_{0}}}}\int\limits_0^{{{{\theta }}_{0}}} {\left( {U - {{M}_{2}}} \right)\sin n{\pi }\frac{{\theta }}{{{{{\theta }}_{{\text{0}}}}}}d{\theta }} ,\quad n = 1 \div N$Алгоритм нахождения коэффициентов косинус-разложения для V, заданного в (2.1), (2.2) оператором $C{{h}_{3}}V$, состоит из следующих действий:
1. Левую и правую части (2.1) для V проинтегрируем по ${\theta } \in \left[ {0,\,{{{\theta }}_{0}}} \right]$:
(2.7)
${{\upsilon }_{0}}\left( r \right) = \frac{1}{{{{{\theta }}_{0}}}}\int\limits_0^{{{{\theta }}_{0}}} {\left( {V - {{M}_{3}}} \right)d{\theta }} $2. Левую и правую части (2.1) для V один раз продифференцируем по θ, после чего положим θ = 0, затем ${\theta } = {{{\theta }}_{0}}$:
(2.8)
${{\left. {{{\partial V} \mathord{\left/ {\vphantom {{\partial V} {\partial {\theta }}}} \right. \kern-0em} {\partial {\theta }}}} \right|}_{{{\theta } = 0}}} = {{B}_{1}}\left( r \right),\quad {{\left. {{{\partial V} \mathord{\left/ {\vphantom {{\partial V} {\partial {\theta }}}} \right. \kern-0em} {\partial {\theta }}}} \right|}_{{{\theta = }{{{\theta }}_{0}}}}} = {{B}_{2}}\left( r \right)$3. Левую и правую части (2.1) для $V$ трижды продифференцируем по ${\theta }$ (максимально допустимый порядок дифференцирования рядов Фурье по ${\theta }$ в разложении (2.1) для $V$) и положим θ = 0, затем ${\theta } = {{{\theta }}_{0}}$:
(2.9)
${{\left. {{{{{\partial }^{3}}V} \mathord{\left/ {\vphantom {{{{\partial }^{3}}V} {\partial {{{\theta }}^{3}}}}} \right. \kern-0em} {\partial {{{\theta }}^{3}}}}} \right|}_{{{\theta } = 0}}} = {{B}_{3}}\left( r \right),\quad {{\left. {{{{{\partial }^{3}}V} \mathord{\left/ {\vphantom {{{{\partial }^{3}}V} {\partial {{{\theta }}^{3}}}}} \right. \kern-0em} {\partial {{{\theta }}^{3}}}}} \right|}_{{{\theta = }{{{\theta }}_{0}}}}} = {{B}_{4}}\left( r \right)$4. Левую и правую части (2.1) для $V$ умножим на $\cos {{n{\pi \theta }} \mathord{\left/ {\vphantom {{n{\pi \theta }} {{{{\theta }}_{0}}}}} \right. \kern-0em} {{{{\theta }}_{0}}}}$, $n = 1 \div N$ и проинтегрируем по ${\theta } \in \left[ {0,\,{{{\theta }}_{0}}} \right]$:
(2.10)
${{\upsilon }_{n}}\left( r \right) = \frac{2}{{{{{\theta }}_{0}}}}\int\limits_0^{{{{\theta }}_{0}}} {\left( {V - {{M}_{3}}} \right)\cos n{\pi }\frac{{\theta }}{{{{{\theta }}_{{\text{0}}}}}}d{\theta }} ,\quad n = 1 \div N$При подстановке разложений (2.1) в (1.6) необходимо использовать следующие два правила:
Правило 1. Если f(x) представлена быстрым оператором $C{{h}_{m}}f\left( x \right)$ порядка m, то после подстановки данного разложения в ДУ $n$-го порядка к полученному уравнению после указанной подстановки следует применять оператор $C{{h}_{{m - n}}}$ порядка $\left( {m - n} \right) \geqslant 0$.
Правило 2. Пусть в ДУ некоторые два члена представлены быстрыми разложениями порядков ${{m}_{1}}$ и ${{m}_{2}}$ и от них в данном ДУ вычисляются производные порядков ${{n}_{1}}$, ${{n}_{2}}$ соответственно и пусть $0 \leqslant {{m}_{1}} - {{n}_{1}} < {{m}_{2}} - {{n}_{2}}$. Тогда к данному ДУ следует применить оператор $C{{h}_{{{{m}_{1}} - {{n}_{1}}}}}$, соответственный меньшей разности порядков ${{m}_{1}} - {{n}_{1}}$. Если в ДУ присутствуют более двух членов в форме быстрых разложений, то поступают аналогично, определяя наименьшую разность порядков ${{m}_{j}} - {{n}_{j}} \geqslant 0$.
Для нахождения коэффициентов разложений (2.3) подставим U, V из (2.1) в два уравнения равновесия (1.6), предварительно умноженные на r2 для удобства вычисления интегралов в дальнейших рассмотрениях:
(2.11)
$\begin{gathered} + \;\sum\limits_{m = 1}^N {\left( \begin{gathered} \frac{2}{{1 - {\nu }}}({{r}^{2}}u_{m}^{{''}} + ru_{m}^{'} - {{u}_{m}}) - \\ - \frac{{m{\pi }}}{{{{{\theta }}_{{\text{0}}}}}}\left( {\frac{{1 + {\nu }}}{{\left( {1 - {\nu }} \right)}}r\upsilon _{m}^{'} - \frac{{3 - {\nu }}}{{\left( {1 - {\nu }} \right)}}{{\upsilon }_{m}}} \right) - \frac{{{{{\pi }}^{{\text{2}}}}}}{{{\theta }_{{\text{0}}}^{{\text{2}}}}}{{m}^{2}}{{u}_{m}} \\ \end{gathered} \right)\sin m{\pi }\frac{{\theta }}{{{{{\theta }}_{{\text{0}}}}}}} + \\ + \;\frac{{1 + {\nu }}}{{(1 - {\nu })}}r\left( {B_{1}^{'}\left( {1 - \frac{{\theta }}{{{{{\theta }}_{{\text{0}}}}}}} \right) + B_{2}^{'}\frac{{\theta }}{{{{{\theta }}_{{\text{0}}}}}} + B_{3}^{'}\left( {\frac{{{{{\theta }}^{2}}}}{2} - \frac{{{{{\theta }}^{{\text{3}}}}}}{{{\text{6}}{{{\theta }}_{{\text{0}}}}}} - \frac{1}{3}{{{\theta }}_{{\text{0}}}}{\theta }} \right) + B_{4}^{'}\left( {\frac{{{{{\theta }}^{{\text{3}}}}}}{{{\text{6}}{{{\theta }}_{{\text{0}}}}}} - \frac{{{{{\theta }}_{{\text{0}}}}{\theta }}}{6}} \right)} \right) - \\ \end{gathered} $(2.12)
$\begin{gathered} {{r}^{2}}\upsilon _{0}^{{''}} + r\,\upsilon _{0}^{'} - {{\upsilon }_{0}} + \frac{{1 + {\nu }}}{{\left( {1 - {\nu }} \right)}}r\left( {\frac{{A_{2}^{'} - A_{1}^{'}}}{{{{{\theta }}_{0}}}} + A_{3}^{'}\left( {{\theta } - \frac{{{{{\theta }}^{{\text{2}}}}}}{{{\text{2}}{{{\theta }}_{{\text{0}}}}}} - \frac{1}{3}{{{\theta }}_{{\text{0}}}}} \right) + A_{4}^{'}\left( {\frac{{{{{\theta }}^{{\text{2}}}}}}{{{\text{2}}{{{\theta }}_{{\text{0}}}}}} - \frac{{{{{\theta }}_{{\text{0}}}}}}{6}} \right)} \right) + \\ + \;\frac{{3 - {\nu }}}{{\left( {1 - {\nu }} \right)}}\left( {\frac{{{{A}_{2}} - {{A}_{1}}}}{{{{{\theta }}_{{\text{0}}}}}} + {{A}_{3}}\left( {{\theta } - \frac{{{{{\theta }}^{{\text{2}}}}}}{{{\text{2}}{{{\theta }}_{{\text{0}}}}}} - \frac{1}{3}{{{\theta }}_{{\text{0}}}}} \right) + {{A}_{4}}\left( {\frac{{{{{\theta }}^{{\text{2}}}}}}{{{\text{2}}{{{\theta }}_{{\text{0}}}}}} - \frac{{{{{\theta }}_{{\text{0}}}}}}{6}} \right)} \right) + \\ + \;\left( {{\theta } - \frac{{{{{\theta }}^{{\text{2}}}}}}{{{\text{2}}{{{\theta }}_{{\text{0}}}}}}} \right)({{r}^{2}}B_{1}^{{''}} + rB_{1}^{'} - {{B}_{1}}) + \frac{{{{{\theta }}^{{\text{2}}}}}}{{{\text{2}}{{{\theta }}_{{\text{0}}}}}}({{r}^{2}}B_{2}^{{''}} + rB_{2}^{'} - {{B}_{2}}) + \\ + \;\left( {\frac{{{{{\theta }}^{{\text{3}}}}}}{{\text{6}}} - \frac{{{{{\theta }}^{{\text{4}}}}}}{{{\text{24}}{{{\theta }}_{{\text{0}}}}}} - \frac{{{{{\theta }}_{{\text{0}}}}{{{\theta }}^{2}}}}{6}} \right)({{r}^{2}}B_{3}^{{''}} + rB_{3}^{'} - {{B}_{3}}) + \left( {\frac{{{{{\theta }}^{{\text{4}}}}}}{{{\text{24}}{{{\theta }}_{{\text{0}}}}}} - \frac{{{{{\theta }}_{{\text{0}}}}{{{\theta }}^{2}}}}{{12}}} \right)({{r}^{2}}B_{4}^{{''}} + rB_{4}^{'} - {{B}_{4}}) + \\ \end{gathered} $Левые и правые части уравнений (2.11), (2.12) будем рассматривать как гладкие функции от (r, θ), к которым можно применить оператор быстрых разложений, руководствуясь при этом приведенными выше правилами 1 и 2. В (2.11) была использована вторая старшая производная от синус-рядов Фурье по углу θ с граничной функцией второго порядка M2. Разность порядков 2 – 2 = 0 означает, что по правилу 2 к (2.11) следует применить оператор быстрых синус-разложений нулевого порядка по переменной θ, т.е.:
– положить в (2.11) θ = 0, затем ${\theta } = {{{\theta }}_{0}}$:
(2.13)
$\frac{2}{{1 - {\nu }}}({{r}^{2}}A_{1}^{{''}} + rA_{1}^{'} - {{A}_{1}}) + \frac{{{\text{1 + }}\,{\nu }}}{{\left( {{\text{1}} - {\nu }} \right)}}rB_{1}^{'} - \frac{{3 - {\nu }}}{{\left( {1 - {\nu }} \right)}}{{B}_{1}} + {{A}_{3}} = {{r}^{2}}{{Q}_{r}}\left( {r,0} \right)$(2.14)
$\frac{2}{{1 - {\nu }}}({{r}^{2}}A_{2}^{{''}} + rA_{2}^{'} - {{A}_{2}}) + \frac{{1 + {\nu }}}{{\left( {1 - {\nu }} \right)}}rB_{2}^{'} - \frac{{3 - {\nu }}}{{\left( {1 - {\nu }} \right)}}{{B}_{2}} + {{A}_{4}} = {{r}^{2}}{{Q}_{r}}\left( {r,{{{\theta }}_{0}}} \right)$Это действие соответствует нахождению двух коэффициентов граничной функции M0 нулевого порядка левой и правой частей уравнения (2.11).
Теперь умножим (2.11) на $\sin n{\pi }{{\theta } \mathord{\left/ {\vphantom {{\theta } {{{{\theta }}_{{\text{0}}}}}}} \right. \kern-0em} {{{{\theta }}_{{\text{0}}}}}}$ ($n = 1 \div N$) и проинтегрируем по ${\theta } \in \left[ {0,{{{\theta }}_{0}}} \right]$, что соответствует нахождению коэффициентов Фурье при быстрых разложениях левой и правой частей (2.11) по синусам:
(2.15)
$\begin{gathered} \left. { - \;\frac{{{\theta }_{{\text{0}}}^{{\text{3}}}}}{{{{n}^{3}}{{{\pi }}^{3}}}}({{r}^{2}}A_{3}^{{''}} + rA_{3}^{'} - {{A}_{3}}) + \frac{{{\theta }_{{\text{0}}}^{{\text{3}}}}}{{{{n}^{3}}{{{\pi }}^{3}}}}{{{\left( { - 1} \right)}}^{n}}({{r}^{2}}A_{4}^{{''}} + rA_{4}^{'} - {{A}_{4}})} \right] + \\ + \;\frac{{{{{\theta }}_{{\text{0}}}}}}{{1 - {\nu }}}({{r}^{2}}u_{n}^{{''}} + ru_{n}^{'} - {{u}_{n}}) - \frac{{{{{\pi }}^{2}}}}{{2{{{\theta }}_{0}}}}{{n}^{2}}{{u}_{n}} - \frac{{n{\pi }}}{2}\left( {\frac{{1 + {\nu }}}{{\left( {1 - {\nu }} \right)}}r\upsilon _{n}^{'} - \frac{{3 - \nu }}{{\left( {1 - \nu } \right)}}{{\upsilon }_{n}}} \right) + \\ + \;\frac{{1 + \nu }}{{\left( {1 - \nu } \right)}}r\left( {\frac{{{{\theta }_{0}}}}{{n\pi }}(B_{1}^{'} - {{{\left( { - 1} \right)}}^{n}}B_{2}^{'}) + \frac{{\theta _{0}^{3}}}{{{{n}^{3}}{{\pi }^{3}}}}(B_{4}^{'}{{{\left( { - 1} \right)}}^{n}} - B_{3}^{'})} \right) - \\ - \;\frac{{3 - \nu }}{{\left( {1 - \nu } \right)}}\left( {\frac{{{{\theta }_{0}}}}{{n\pi }}({{B}_{1}} - {{B}_{2}}{{{\left( { - 1} \right)}}^{n}}) + \frac{{\theta _{0}^{3}}}{{{{n}^{3}}{{\pi }^{3}}}}({{B}_{4}}{{{\left( { - 1} \right)}}^{n}} - {{B}_{3}})} \right) + \\ + \;\frac{{{{\theta }_{0}}}}{{n\pi }}({{A}_{3}} - {{A}_{4}}{{\left( { - 1} \right)}^{n}}) = {{r}^{2}}\int\limits_0^{{{\theta }_{0}}} {{{Q}_{r}}\left( {r,\theta } \right)\sin n\pi \frac{\theta }{{{{\theta }_{0}}}}d\theta } ,\quad n = 1 \div N \\ \end{gathered} $Всего в (2.13)–(2.15) имеем $2 + N$ обыкновенных дифференциальных уравнений. Перейдем к рассмотрению уравнения (2.12), которое получено из второго уравнения равновесия (1.6). В данном уравнении была использована вторая производная от косинус-рядов Фурье по θ с граничной функцией третьего порядка M3, т.е. разность порядков (3 – 2 = 1) равна 1. Поэтому левую и правую части (2.12) можно рассматривать как непрерывные функции от ${\theta } \in \left[ {0,{{{\theta }}_{0}}} \right]$, к которым по правилу 2 применим оператор быстрых косинус-разложений первого порядка $C{{h}_{1}}$. Для этого проинтегрируем уравнение (2.12) по ${\theta } \in \left[ {0,{{{\theta }}_{0}}} \right]$, что соответствует нахождению свободного коэффициента Фурье перед суммой ряда по косинусам для левой и правой частей (2.12):
(2.16)
$\begin{gathered} ({{r}^{2}}\upsilon _{0}^{{''}} + r\upsilon _{0}^{'} - {{\upsilon }_{0}}){{\theta }_{0}} + \frac{{1 + \nu }}{{\left( {1 - \nu } \right)}}r(A_{2}^{'} - A_{1}^{'}) + \frac{{3 - \nu }}{{\left( {1 - \nu } \right)}}\left( {{{A}_{2}} - {{A}_{1}}} \right) + \\ + \;\frac{{\theta _{0}^{2}}}{3}({{r}^{2}}B_{1}^{{''}} + rB_{1}^{'} - {{B}_{1}}) + \frac{{\theta _{0}^{2}}}{6}({{r}^{2}}B_{2}^{{''}} + rB_{2}^{'} - {{B}_{2}}) + \frac{2}{{1 - \nu }}\left( {{{B}_{2}} - {{B}_{1}}} \right) - \\ - \;\frac{{\theta _{0}^{4}}}{{45}}({{r}^{2}}B_{3}^{{''}} + rB_{3}^{'} - {{B}_{3}}) - \frac{{7\theta _{0}^{4}}}{{360}}({{r}^{2}}B_{4}^{{''}} + rB_{4}^{'} - {{B}_{4}}) = {{r}^{2}}\int\limits_0^{{{\theta }_{0}}} {{{Q}_{\theta }}\left( {r,\theta } \right)d\theta } \\ \end{gathered} $Теперь надо продифференцировать один раз уравнение (2.12) по ${\theta }$ и после дифференцирования положить θ = 0 и затем ${\theta } = {{{\theta }}_{0}}$:
(2.17)
${{r}^{2}}B_{1}^{{''}} + rB_{1}^{'} - {{B}_{1}} + \frac{{1 + {\nu }}}{{\left( {1 - {\nu }} \right)}}rA_{3}^{'} + \frac{{\left( {3 - {\nu }} \right)}}{{\left( {1 - {\nu }} \right)}}{{A}_{3}} + \frac{2}{{\left( {1 - {\nu }} \right)}}{{B}_{3}} = {{\left. {{{r}^{2}}\frac{\partial }{{\partial {\theta }}}{{Q}_{r}}\left( {r,{\theta }} \right)} \right|}_{{{\theta } = 0}}}$(2.18)
${{r}^{2}}B_{2}^{{''}} + rB_{2}^{'} - {{B}_{2}} + \frac{{1 + {\nu }}}{{\left( {1 - {\nu }} \right)}}rA_{4}^{'} + \frac{{\left( {3 - {\nu }} \right)}}{{\left( {1 - {\nu }} \right)}}{{A}_{4}} + \frac{2}{{\left( {1 - {\nu }} \right)}}{{B}_{4}} = {{\left. {{{r}^{2}}\frac{\partial }{{\partial {\theta }}}{{Q}_{r}}\left( {r,{\theta }} \right)} \right|}_{{{\theta = }{{{\theta }}_{0}}}}}$Для нахождения коэффициентов ряда Фурье разложения (2.12) умножим это уравнение на $\cos n{\pi }{{\theta } \mathord{\left/ {\vphantom {{\theta } {{{{\theta }}_{{\text{0}}}}}}} \right. \kern-0em} {{{{\theta }}_{{\text{0}}}}}}$, где $n = 1 \div N$, и проинтегрируем по ${\theta } \in \left[ {0,{{{\theta }}_{0}}} \right]$:
(2.19)
$\begin{gathered} \frac{{1 + \nu }}{{\left( {1 - \nu } \right)}}r\left( { - A_{3}^{'}\frac{{\theta _{0}^{2}}}{{{{n}^{2}}{{\pi }^{2}}}} + A_{4}^{'}\frac{{\theta _{0}^{2}}}{{{{n}^{2}}{{\pi }^{2}}}}{{{\left( { - 1} \right)}}^{n}}} \right) + \frac{{3 - \nu }}{{\left( {1 - \nu } \right)}}\left( { - {{A}_{3}}\frac{{\theta _{0}^{2}}}{{{{n}^{2}}{{\pi }^{2}}}} + {{A}_{4}}\frac{{\theta _{0}^{2}}}{{{{n}^{2}}{{\pi }^{2}}}}{{{\left( { - 1} \right)}}^{n}}} \right) - \\ - \;\frac{{\theta _{0}^{2}}}{{{{n}^{2}}{{\pi }^{2}}}}({{r}^{2}}B_{1}^{{''}} + rB_{1}^{'} - {{B}_{1}}) + \frac{{\theta _{0}^{2}}}{{{{n}^{2}}{{\pi }^{2}}}}{{\left( { - 1} \right)}^{n}}({{r}^{2}}B_{2}^{{''}} + rB_{2}^{'} - {{B}_{2}}) + \\ + \;\frac{{\theta _{0}^{4}}}{{{{n}^{4}}{{\pi }^{4}}}}({{r}^{2}}B_{3}^{{''}} + rB_{3}^{'} - {{B}_{3}}) - \frac{{\theta _{0}^{4}}}{{{{n}^{4}}{{\pi }^{4}}}}{{\left( { - 1} \right)}^{n}}({{r}^{2}}B_{4}^{{''}} + rB_{4}^{'} - {{B}_{4}}) + \\ + \;\frac{2}{{1 - \nu }}\left( { - {{B}_{3}}\frac{{\theta _{0}^{2}}}{{{{n}^{2}}{{\pi }^{2}}}} + {{B}_{4}}\frac{{\theta _{0}^{2}}}{{{{n}^{2}}{{\pi }^{2}}}}{{{\left( { - 1} \right)}}^{n}} - \frac{{{{\pi }^{2}}{{n}^{2}}{{\upsilon }_{n}}}}{{2{{\theta }_{0}}}}} \right) + \frac{\pi }{2}\frac{{1 + \nu }}{{\left( {1 - \nu } \right)}}rnu_{n}^{'} + \frac{\pi }{2}\frac{{3 - \nu }}{{\left( {1 - \nu } \right)}}n{{u}_{n}} + \\ + \;\frac{{{{\theta }_{0}}}}{2}({{r}^{2}}\upsilon _{n}^{{''}} + r\upsilon _{n}^{'} - {{\upsilon }_{n}}) = {{r}^{2}}\int\limits_0^{{{\theta }_{0}}} {{{Q}_{\theta }}\left( {r,\theta } \right)\sin n\pi \frac{\theta }{{{{\theta }_{0}}}}d\theta } ,\quad n = 1 \div N \\ \end{gathered} $В (2.16)–(2.19) имеем 3 + N уравнений. Еще четыре уравнения получим после подстановки (2.1) в граничные условия (1.7) при θ = 0 и ${\theta } = {{{\theta }}_{0}}$:
(2.20)
${{A}_{1}} + {{B}_{1}} + {\nu }rA_{1}^{'} = r{{\Phi }_{3}}\left( r \right),\quad {{A}_{2}} + {{B}_{2}} + {\nu }rA_{2}^{'} = r{{\Phi }_{4}}\left( r \right)$(2.21)
$\begin{gathered} \frac{{{{A}_{2}} - {{A}_{1}}}}{{{{{\theta }}_{0}}}} - \frac{{{{{\theta }}_{0}}}}{3}{{A}_{3}} - \frac{{{{{\theta }}_{0}}}}{6}{{A}_{4}} + r\upsilon _{0}^{'} - {{\upsilon }_{0}} + \sum\limits_{m = 1}^N {\left( {{{u}_{m}}{\pi }\frac{m}{{{{{\theta }}_{0}}}} + r\upsilon _{m}^{'} - {{\upsilon }_{m}}} \right)} = r{{\Phi }_{1}} \\ \frac{{{{A}_{2}} - {{A}_{1}}}}{{{{{\theta }}_{0}}}} + \frac{{{{{\theta }}_{{\text{0}}}}}}{{\text{6}}}{{A}_{3}} + \frac{{{{{\theta }}_{{\text{0}}}}}}{{\text{3}}}{{A}_{4}} + \sum\limits_{m = 1}^N {{{{\left( { - 1} \right)}}^{m}}\left( {{{u}_{m}}{\pi }\frac{m}{{{{{\theta }}_{{\text{0}}}}}} + r\upsilon _{m}^{'} - {{\upsilon }_{m}}} \right)} + \\ + \;r\upsilon _{0}^{'} - {{\upsilon }_{0}} + \frac{{{{{\theta }}_{{\text{0}}}}}}{{\text{2}}}(r(B_{1}^{'} + B_{2}^{'}) - {{B}_{1}} - {{B}_{2}}) + \frac{{{\theta }_{{\text{0}}}^{{\text{3}}}}}{{{\text{24}}}}({{B}_{3}} + {{B}_{4}} - r(B_{3}^{'} + B_{4}^{'})) = r{{\Phi }_{2}} \\ \end{gathered} $Вся система (2.13)–(2.21) состоит из $9 + 2N$ уравнений относительно такого же количества неизвестных функций, перечисленных в (2.3).
Для данной системы запишем граничные условия, подставляя $U$, $V$ из (2.1) в пока неиспользованные граничные условия (1.1) при $r = R$:
(2.22)
$\begin{gathered} a)\,{{M}_{2}}\left( {R,{\theta }} \right) + \sum\limits_{m = 1}^N {{{u}_{m}}\left( R \right)\sin m{\pi }\frac{{\theta }}{{{{{\theta }}_{{\text{0}}}}}}} = 0, \hfill \\ b)\,{{M}_{3}}\left( {R,{\theta }} \right) + \sum\limits_{m = 1}^N {{{\upsilon }_{m}}\left( R \right)\cos m{\pi }\frac{{\theta }}{{{{{\theta }}_{{\text{0}}}}}}} = 0 \hfill \\ \end{gathered} $Левую часть уравнения (2.22)-а будем рассматривать как функцию, представленную оператором быстрых синус-разложений второго порядка $C{{h}_{2}}$, определенного в (2.1), поэтому и правую часть представим таким же разложением. По определению оператора $C{{h}_{2}}$ в данном уравнении вначале следует положить θ = 0, ${\theta } = {{{\theta }}_{0}}$, затем дважды продифференцировать по ${\theta }$ и снова взять θ = 0, ${\theta } = {{{\theta }}_{0}}$, после чего уравнение (2.22)-а надо умножить на $\sin n{\pi }{{\theta } \mathord{\left/ {\vphantom {{\theta } {{{{\theta }}_{{\text{0}}}}}}} \right. \kern-0em} {{{{\theta }}_{{\text{0}}}}}}$ и проинтегрировать по переменной ${\theta } \in \left[ {0,\,{{{\theta }}_{0}}} \right]$. В результате будем иметь 4 + N граничных условий
(2.23)
${{A}_{1}}\left( R \right) = {{A}_{2}}\left( R \right) = {{A}_{3}}\left( R \right) = {{A}_{4}}\left( R \right) = 0,\quad {{u}_{n}}\left( R \right) = 0,\quad n = 1 \div N$В левой части (2.22)-b ряд Фурье не дифференцировался, поэтому к данному уравнению применим оператор $C{{h}_{3}}$, состоящий из следующих действий. Вначале уравнение (2.22)-$b$ проинтегрируем по ${\theta }$ в пределах $0 \leqslant \theta \leqslant {{\theta }_{0}}$, затем продифференцируем (2.22)-b по переменной ${\theta }$ последовательно один раз и три раза, после чего положим в них θ = 0 и ${\theta } = {{{\theta }}_{0}}$. Теперь умножим уравнение (2.22)-b на $\cos n{\pi }{{\theta } \mathord{\left/ {\vphantom {{\theta } {{{{\theta }}_{{\text{0}}}}}}} \right. \kern-0em} {{{{\theta }}_{{\text{0}}}}}}$ и проинтегрируем по переменной ${\theta } \in \left[ {0,\,{{{\theta }}_{0}}} \right]$. Выполняя указанные действия, получим 5 + N граничных условий:
(2.24)
${{B}_{1}}\left( R \right) = {{B}_{2}}\left( R \right) = {{B}_{3}}\left( R \right) = {{B}_{4}}\left( R \right) = 0,\quad {{\upsilon }_{0}}\left( R \right) = 0,\quad {{\upsilon }_{n}}\left( R \right) = 0,\quad n = 1 \div N$Всего в (2.23)–(2.24) имеем 9 + 2N граничных условий.
Теперь выполним два граничных условия (1.8) при r = r0 на носике резца
(2.25)
$\begin{gathered} {{\left. \begin{gathered} \left( {A_{1}^{'} + \frac{\nu }{{{{r}_{0}}}}\left( {{{A}_{1}} + {{B}_{1}}} \right)} \right)\left( {1 - \frac{\theta }{{{{\theta }_{0}}}}} \right) + \left( {A_{3}^{'} + \frac{\nu }{{{{r}_{0}}}}\left( {{{A}_{3}} + {{B}_{3}}} \right)} \right)\left( {\frac{{{{\theta }^{2}}}}{2} - \frac{{{{\theta }^{3}}}}{{6{{\theta }_{0}}}} - \frac{{{{\theta }_{0}}\theta }}{3}} \right) + \hfill \\ а)\, + \;\left( {A_{2}^{'} + \frac{\nu }{{{{r}_{0}}}}\left( {{{A}_{2}} + {{B}_{2}}} \right)} \right)\frac{\theta }{{{{\theta }_{0}}}} + \left( {A_{4}^{'} + \frac{\nu }{{{{r}_{0}}}}\left( {{{A}_{4}} + {{B}_{4}}} \right)} \right)\left( {\frac{{{{\theta }^{3}}}}{{6{{\theta }_{0}}}} - \frac{{{{\theta }_{0}}\theta }}{6}} \right) + \hfill \\ + \;\sum\limits_{m = 1}^N {\left( {u_{m}^{'} + \frac{\nu }{{{{r}_{0}}}}\left( {{{u}_{m}} - {{\upsilon }_{m}}m\frac{\pi }{{{{\theta }_{0}}}}} \right)} \right)\sin m\pi \frac{\theta }{{{{\theta }_{0}}}} = {{F}_{1}}\left( \theta \right)} \hfill \\ \end{gathered} \right|}_{{r = {{r}_{0}}}}}\, \hfill \\ b)\,{{\left. \begin{gathered} \frac{{{{A}_{2}} - {{A}_{1}}}}{{{{r}_{0}}{{\theta }_{0}}}} + \frac{{{{A}_{3}}}}{{{{r}_{0}}}}\left( {\theta - \frac{{{{\theta }^{2}}}}{{2{{\theta }_{0}}}} - \frac{{{{\theta }_{0}}}}{3}} \right) + \frac{{{{A}_{4}}}}{{{{r}_{0}}}}\left( {\frac{{{{\theta }^{2}}}}{{2{{\theta }_{0}}}} - \frac{{{{\theta }_{0}}}}{6}} \right) + \left( {B_{1}^{'} - \frac{{{{B}_{1}}}}{{{{r}_{0}}}}} \right)\left( {\theta - \frac{{{{\theta }^{2}}}}{{2{{\theta }_{0}}}}} \right) + \hfill \\ + \;\left( {B_{2}^{'} - \frac{{{{B}_{2}}}}{{{{r}_{0}}}}} \right)\frac{{{{\theta }^{2}}}}{{2{{\theta }_{0}}}} + \left( {B_{3}^{'} - \frac{{{{B}_{3}}}}{{{{r}_{0}}}}} \right)\left( {\frac{{{{\theta }^{3}}}}{6} - \frac{{{{\theta }^{4}}}}{{24{{\theta }_{0}}}} - \frac{{{{\theta }_{0}}{{\theta }^{2}}}}{6}} \right) + \hfill \\ + \;\left( {B_{4}^{'} - \frac{{{{B}_{4}}}}{{{{r}_{0}}}}} \right)\left( {\frac{{{{\theta }^{4}}}}{{24{{\theta }_{0}}}} - \frac{{{{\theta }_{0}}{{\theta }^{2}}}}{{12}}} \right) + \upsilon _{0}^{'}\left( r \right) - \frac{{{{\upsilon }_{0}}}}{{{{r}_{0}}}} + \hfill \\ + \;\sum\limits_{m = 1}^N {\left( {{{u}_{m}}\left( r \right)m\frac{\pi }{{{{r}_{0}}{{\theta }_{0}}}} + \upsilon _{m}^{'}\left( r \right) - \frac{{{{\upsilon }_{m}}}}{{{{r}_{0}}}}} \right)\cos m\pi \frac{\theta }{{{{\theta }_{0}}}}} = {{F}_{2}}\left( \theta \right) \hfill \\ \end{gathered} \right|}_{{r = {{r}_{0}}}}} \hfill \\ \end{gathered} $В уравнении (2.25)-a используются функции U и ${{\partial U} \mathord{\left/ {\vphantom {{\partial U} {\partial r}}} \right. \kern-0em} {\partial r}}$, представленные в (2.1) оператором Ch2 по переменной θ. При вычислении ${{\partial U} \mathord{\left/ {\vphantom {{\partial U} {\partial r}}} \right. \kern-0em} {\partial r}}$ производная по переменной r не изменяет порядок оператора Ch2. Функция V в (2.1) записана с помощью Ch3. В уравнении (2.25)-а при вычислении производной по θ порядок оператора понижается на единицу, поэтому производная ${{\partial V} \mathord{\left/ {\vphantom {{\partial V} {\partial {\theta }}}} \right. \kern-0em} {\partial {\theta }}}$, используемая при получении (2.25)-$a$, по правилу 1 выражается через Ch2. Итак, каждое слагаемое в первом уравнении (1.8) записано с помощью Ch2 и потому по правилу 2 ко всему уравнению (2.25)-а надо применить оператор Ch2 второго порядка. Выполняя действия, соответственные оператору Ch2, получим 4 + N уравнений:
(2.26)
${{\left. {\left( {A_{1}^{'} + \frac{\nu }{{{{r}_{0}}}}\left( {{{B}_{1}} + {{A}_{1}}} \right)} \right)} \right|}_{\begin{subarray}{l} r = {{r}_{0}}, \\ {\theta } = 0 \end{subarray} }} = 0,\quad {{\left. {\left( {A_{2}^{'} + \frac{\nu }{{{{r}_{0}}}}\left( {{{B}_{2}} + {{A}_{2}}} \right)} \right)} \right|}_{\begin{subarray}{l} r = {{r}_{0}}, \\ {\theta } = {{{\theta }}_{0}} \end{subarray} }} = {{F}_{{01}}} + {{F}_{{02}}} + {{F}_{{03}}}$Вычислим вторую производную по ${\theta }$ от левой и правой частей (2.25)-а и положим θ = 0, ${\theta } = {{{\theta }}_{0}}$:
(2.27)
$\begin{gathered} {{\left. {\left( {A_{3}^{'} + \frac{\nu }{{{{r}_{0}}}}\left( {{{B}_{3}} + {{A}_{3}}} \right)} \right)} \right|}_{\begin{subarray}{l} r = {{r}_{0}}, \\ {\theta } = 0 \end{subarray} }} = \frac{2}{{{\theta }_{0}^{2}}}{{F}_{{02}}}, \\ {{\left. {\left( {A_{4}^{'} + \frac{\nu }{{{{r}_{0}}}}\left( {{{B}_{4}} + {{A}_{4}}} \right)} \right)} \right|}_{\begin{subarray}{l} r = {{r}_{0}}, \\ {\theta } = {{{\theta }}_{0}} \end{subarray} }} = \frac{2}{{{\theta }_{0}^{2}}}\left( {{{F}_{{01}}} + {{F}_{{02}}} + {{F}_{{03}}}} \right) \\ \end{gathered} $С учетом (2.26), (2.27) уравнение (2.25)-а упрощается. Затем данное уравнение умножим на $\sin n{\pi }{{\theta } \mathord{\left/ {\vphantom {{\theta } {{{{\theta }}_{{\text{0}}}}}}} \right. \kern-0em} {{{{\theta }}_{{\text{0}}}}}}$, $n = 1 \div N$ и проинтегрируем по ${\theta }$:
(2.28)
${{\left. {{{F}_{{01}}}\frac{{2{{{\theta }}_{0}}}}{{{{n}^{3}}{{{\pi }}^{3}}}}{{{\left( { - 1} \right)}}^{n}} - {{F}_{{03}}}\frac{{4{{{\theta }}_{0}}}}{{{{n}^{3}}{{{\pi }}^{3}}}}{{{\left( { - 1} \right)}}^{n}} + \frac{{{{{\theta }}_{0}}}}{2}\left( {u_{n}^{'} + \frac{{\nu }}{{{{r}_{0}}}}\left( {{{u}_{n}} - {{\upsilon }_{n}}n\frac{{\pi }}{{{{{\theta }}_{{\text{0}}}}}}} \right)} \right)} \right|}_{{r = {{r}_{0}}}}} = 0,\quad n = 1 \div N$Всего в (2.26)–(2.28) имеем 4 + N граничных условий при $r = {{r}_{0}}$.
Перейдем к рассмотрению уравнения (2.25)-$b$, где $V,{{\partial V} \mathord{\left/ {\vphantom {{\partial V} {\partial r}}} \right. \kern-0em} {\partial r}}$ выражены оператором $C{{h}_{3}}$. Так как U выражается в (2.1) оператором $C{{h}_{2}}$, то производная ${{\partial U} \mathord{\left/ {\vphantom {{\partial U} {\partial {\theta }}}} \right. \kern-0em} {\partial {\theta }}}$ в (2.25)-b выражается оператором $C{{h}_{1}}$, т.е. из всех операторов в уравнении (2.25)-b наименьший порядок имеет $C{{h}_{1}}$. Поэтому по правилу 2 к уравнению (2.25)-b следует применить оператор $C{{h}_{1}}$:
1. Проинтегрируем левую и правую части (2.25)-b по ${\theta } \in \left[ {0,\,{{{\theta }}_{0}}} \right]$:
(2.29)
${{\left\{ \begin{gathered} \frac{{{{A}_{2}} - {{A}_{1}}}}{{{{r}_{0}}}} + \left( {B_{1}^{'} - \frac{{{{B}_{1}}}}{{{{r}_{0}}}}} \right)\frac{{\theta _{0}^{2}}}{3} + \left( {B_{2}^{'} - \frac{{{{B}_{2}}}}{{{{r}_{0}}}}} \right)\frac{{\theta _{0}^{2}}}{6} - \left( {B_{3}^{'} - \frac{{{{B}_{3}}}}{{{{r}_{0}}}}} \right)\frac{{\theta _{0}^{4}}}{{45}} - \left( {B_{4}^{'} - \frac{{{{B}_{4}}}}{{{{r}_{0}}}}} \right)\frac{{7\theta _{0}^{4}}}{{360}} + \hfill \\ + \;\left( {\upsilon _{0}^{'} - \frac{{{{\upsilon }_{0}}}}{{{{r}_{0}}}}} \right){{\theta }_{0}} = \left( {{{\Phi }_{{01}}} + {{\Phi }_{{02}}}\left( {1 - \frac{{{{r}_{0}}}}{R}} \right) + {{\Phi }_{{03}}}{{{\left( {1 - \frac{{{{r}_{0}}}}{R}} \right)}}^{2}}} \right)\left( {1 - \frac{{{{r}_{0}}}}{R}} \right)\frac{{{{\theta }_{0}}}}{2} \hfill \\ \end{gathered} \right\}}_{{r = {{r}_{0}}}}}$2. Продифференцируем левую и правую части (2.25)-b по θ, после чего положим в нем θ = 0 и затем ${\theta } = {{{\theta }}_{0}}$:
(2.30)
${\theta } = 0 \Rightarrow {{\left. {\left( {\frac{{{{A}_{3}}}}{{{{r}_{0}}}} + B_{1}^{'} - \frac{{{{B}_{1}}}}{{{{r}_{0}}}}} \right)} \right|}_{{r = {{r}_{0}}}}} = \left( {{{\Phi }_{{01}}} + {{\Phi }_{{02}}}\left( {1 - \frac{{{{r}_{0}}}}{R}} \right) + {{\Phi }_{{03}}}{{{\left( {1 - \frac{{{{r}_{0}}}}{R}} \right)}}^{2}}} \right)\left( {1 - \frac{{{{r}_{0}}}}{R}} \right)\frac{1}{{{{{\theta }}_{0}}}}$(2.31)
${\theta } = {{{\theta }}_{0}} \Rightarrow {{\left. {\left( {\frac{{{{A}_{4}}}}{{{{r}_{0}}}} + B_{2}^{'} - \frac{{{{B}_{2}}}}{{{{r}_{0}}}}} \right)} \right|}_{{r = {{r}_{0}}}}} = \left( {{{\Phi }_{{01}}} + {{\Phi }_{{02}}}\left( {1 - \frac{{{{r}_{0}}}}{R}} \right) + {{\Phi }_{{03}}}{{{\left( {1 - \frac{{{{r}_{0}}}}{R}} \right)}}^{2}}} \right)\left( {1 - \frac{{{{r}_{0}}}}{R}} \right)\frac{1}{{{{{\theta }}_{0}}}}$3. Умножим левую и правую части (2.25)-$b$ на $\cos n{\pi }{{\theta } \mathord{\left/ {\vphantom {{\theta } {{{{\theta }}_{{\text{0}}}}}}} \right. \kern-0em} {{{{\theta }}_{{\text{0}}}}}}$, $n = 1{ \div }N$ и проинтегрируем по ${\theta } \in \left[ {0,\,{{{\theta }}_{0}}} \right]$:
При помощи (2.30), (2.31) последнее уравнение упрощается и принимает вид
(2.32)
${{\left. {\frac{{{\theta }_{0}^{4}}}{{{{n}^{4}}{{{\pi }}^{4}}}}\left( {B_{3}^{'} - \frac{{{{B}_{3}}}}{{{{r}_{0}}}} - B_{4}^{'}{{{\left( { - 1} \right)}}^{n}} + \frac{{{{B}_{4}}}}{{{{r}_{0}}}}{{{\left( { - 1} \right)}}^{n}}} \right) + \frac{{{{{\theta }}_{0}}}}{2}\left( {{{u}_{n}}\frac{{n{\pi }}}{{{{r}_{0}}{{{\theta }}_{0}}}} + \upsilon _{n}^{'} - \frac{{{{\upsilon }_{n}}}}{{{{r}_{0}}}}} \right) = 0} \right|}_{{r = {{r}_{0}}}}},\quad n = 1 \div N$В (2.29)–(2.32) имеем 3 + N граничных условий. Всего же в (2.26)–(2.32) получено $7 + 2N$ граничных условий. В общей сложности в (2.23), (2.24), (2.26)–(2.32) записано $16 + 4N$ граничных условий. Задача сведена к решению замкнутой системы $9 + 2N$ дифференциальных уравнений (2.13)–(2.21) относительно такого же количества неизвестных функций – коэффициентов быстрых разложений, перечисленных в (2.3), для которых в (2.23), (2.24), (2.26)–(2.32) имеем $16 + 4N$ граничных условий. Следует обсудить корректность полученной задачи.
Порядок дифференциальной системы (2.13)–(2.21) равен $10 + 4N$. В этом можно убедиться, если составить характеристический определитель системы. Поэтому общее решение будет содержать $10 + 4N$ произвольных постоянных ${{C}_{j}}$, $j = 1 \div 10 + 4N$. При выполнении граничных условий к этим постоянным добавляются еще шесть неизвестных постоянных (1.10) из условий согласования, поэтому всего будет $16 + 4N$ неизвестных постоянных, для нахождения которых имеем столько же согласованных граничных условий (2.23), (2.24), (2.26)–(2.32). Если бы не были выполнены условия согласований, то постоянные (1.10) не фигурировали бы в граничных условиях задачи. Тогда граничных условий было бы больше на шесть, чем количество неизвестных постоянных, и задача не имела бы непрерывного решения, так как была бы переопределенной. Отказавшись от условий согласования, в углах области резца имели бы разрывы, что недопустимо, т.е. для получения гладкого решения необходимо выполнять условия согласования.
3. Повторное применение быстрых разложений. Метод быстрых разложений можно применять последовательно многократно по каждой независимой переменной. При этом будет отделяться одна соответственная переменная. Решение двумерной задачи после двукратного применения метода приведет к замкнутой системе алгебраических уравнений.
Перед повторным применением метода выполним следующие преобразования, которые позволят систему (2.13)–(2.21) привести к существенному упрощению.
1. (3.1)
Из (2.13) и (2.14) выразим ${{A}_{3}}$, ${{A}_{4}}$: ${{A}_{3}} = {{A}_{3}}\left( {{{A}_{1}},{{B}_{1}}} \right),\quad {{A}_{4}} = {{A}_{4}}\left( {{{A}_{2}},{{B}_{2}}} \right)$2. (3.2)
Из (2.17) и (2.18) найдем ${{B}_{3}}$, ${{B}_{4}}$: ${{B}_{3}} = {{B}_{3}}\left( {{{A}_{3}},{{B}_{1}}} \right),\quad {{B}_{4}} = {{B}_{4}}\left( {{{A}_{4}},{{B}_{2}}} \right)$3. (3.3)
Из (2.20) ${{B}_{1}} = {{B}_{1}}\left( {{{A}_{1}}} \right),\quad {{B}_{2}} = {{B}_{2}}\left( {{{A}_{2}}} \right) \Rightarrow {{A}_{3}} = {{A}_{3}}\left( {{{A}_{1}}} \right),\quad {{A}_{4}} = {{A}_{4}}\left( {{{A}_{2}}} \right)$4. Из первого уравнения (2.21) выразим $r\upsilon _{0}^{'} - {{\upsilon }_{0}}$:
(3.4)
$r\upsilon _{0}^{'} - {{\upsilon }_{0}} = r{{\Phi }_{1}} + \frac{{{{A}_{1}} - {{A}_{2}}}}{{{{{\theta }}_{0}}}} + \frac{1}{3}{{{\theta }}_{0}}{{A}_{3}} + \frac{{{{{\theta }}_{0}}}}{6}{{A}_{4}} - \sum\limits_{m = 1}^N {\left( {{\pi }\frac{m}{{{{{\theta }}_{0}}}}{{u}_{m}} + r\upsilon _{m}^{'} - {{\upsilon }_{m}}} \right)} $5. Прямым дифференцированием из (3.4) найдем
(3.5)
$r\upsilon _{0}^{{''}} = r\Phi _{1}^{'} + {{\Phi }_{1}} + \frac{{A_{1}^{'} - A_{2}^{'}}}{{{{{\theta }}_{0}}}} + \frac{1}{3}{{{\theta }}_{0}}A_{3}^{'} + \frac{{{{{\theta }}_{0}}}}{6}A_{4}^{'} - \sum\limits_{m = 1}^N {\left( {{\pi }\frac{m}{{{{{\theta }}_{0}}}}u_{m}^{'} + r\upsilon _{m}^{{''}}} \right)} $6. Из второго уравнения в (2.21) вычтем первое для исключения ${{\upsilon }_{0}}$:
(3.6)
$\begin{gathered} \frac{1}{2}{{{\theta }}_{0}}\left( {{{A}_{3}} + {{A}_{4}}} \right) + \sum\limits_{m = 1}^N {({{{\left( { - 1} \right)}}^{m}} - 1)\left( {{{u}_{m}}{\pi }\frac{m}{{{{{\theta }}_{0}}}} + r\upsilon _{m}^{'} - {{\upsilon }_{m}}} \right)} - \frac{{{\theta }_{0}^{3}}}{{24}}r(B_{3}^{'} + B_{4}^{'}) + \\ + \;\frac{{{{{\theta }}_{0}}}}{2}r(B_{1}^{'} + B_{2}^{'}) - \frac{{{{{\theta }}_{0}}}}{2}\left( {{{B}_{1}} + {{B}_{2}}} \right) + \frac{{{\theta }_{0}^{3}}}{{24}}\left( {{{B}_{3}} + {{B}_{4}}} \right) = r\left( {{{\Phi }_{2}} - {{\Phi }_{1}}} \right) \\ \end{gathered} $7. Зависимости A3, A4 из (3.3), выраженные через A1, A2, подставим в (3.4) и получим ДУ первого порядка относительно ${{\upsilon }_{0}}$:
(3.7)
$\begin{gathered} r\upsilon _{0}^{'} - {{\upsilon }_{0}} = {{A}_{1}}\frac{{3 - {\theta }_{0}^{2}}}{{3{{{\theta }}_{0}}}} - {{A}_{2}}\frac{{6 + {\theta }_{0}^{2}}}{{6{{{\theta }}_{0}}}} - \sum\limits_{m = 1}^N {\left( {{\pi }\frac{m}{{{{{\theta }}_{0}}}}{{u}_{m}} + r\upsilon _{m}^{'} - {{\upsilon }_{m}}} \right)} + r{{\Phi }_{1}} + \\ + \;\frac{{{{{\theta }}_{{\text{0}}}}}}{{\text{3}}}\left( {{{r}^{2}}{{Q}_{r}}\left( {r,0} \right) - {{r}^{2}}A_{1}^{{''}}\left( {{\nu } + 2} \right) - rA_{1}^{'}\left( {2{\nu } + 1} \right) - \frac{{1 + {\nu }}}{{\left( {1 - {\nu }} \right)}}{{r}^{2}}\Phi _{3}^{'} + 2r{{\Phi }_{3}}} \right) + \\ + \;\frac{{{{{\theta }}_{0}}}}{6}\left( {{{r}^{2}}{{Q}_{r}}\left( {r,{{{\theta }}_{0}}} \right) - {{r}^{2}}A_{2}^{{''}}\left( {{\nu } + 2} \right) - rA_{2}^{'}\left( {2{\nu } + 1} \right) - \frac{{1 + {\nu }}}{{\left( {1 - {\nu }} \right)}}{{r}^{2}}\Phi _{4}^{'} + 2r{{\Phi }_{4}}} \right) \\ \end{gathered} $8. Найденные выражения ${{B}_{1}}$, ${{B}_{2}}$, ${{B}_{3}}$, ${{B}_{4}}$, ${{A}_{3}}$, ${{A}_{4}}$ из (3.1)–(3.3) подставим в (3.6) и получим ДУ четвертого порядка относительно A1, A2:
(3.8)
$\begin{gathered} + \;\frac{{(\theta _{0}^{3}\left( {2 - 5\nu } \right) - 12{{\theta }_{0}}\nu )}}{{12\left( {1 - \nu } \right)}}{{r}^{2}}(\Phi _{3}^{'} + \Phi _{4}^{'}) - \\ - \;\frac{{\theta _{0}^{3}}}{{24}}{{r}^{3}}\frac{\partial }{{\partial r}}\left( {{{{\left. {\frac{\partial }{{\partial \theta }}{{Q}_{r}}\left( {r,\theta } \right)} \right|}}_{{\theta = 0}}} + {{{\left. {\frac{\partial }{{\partial \theta }}{{Q}_{r}}\left( {r,\theta } \right)} \right|}}_{{\theta = {{\theta }_{0}}}}}} \right) + \\ + \;\frac{{1 + \nu }}{2}{{r}^{4}}\frac{{{{\partial }^{2}}}}{{\partial {{r}^{2}}}}\left( {{{Q}_{r}}\left( {r,0} \right) + {{Q}_{r}}\left( {r,{{\theta }_{0}}} \right)} \right) + \\ + \;\frac{1}{2}\left( {{{\theta }_{0}} + \left( {5 + \nu } \right)\frac{{\theta _{0}^{3}}}{{24}}} \right){{r}^{2}}\left( {{{Q}_{r}}\left( {r,0} \right) + {{Q}_{r}}\left( {r,{{\theta }_{0}}} \right)} \right) + \\ \end{gathered} $9. Подставляя ${{B}_{1}}$, ${{B}_{2}}$, ${{B}_{3}}$, ${{B}_{4}}$, ${{A}_{3}}$, ${{A}_{4}}$ из (3.1)–(3.3), а также $r\upsilon _{0}^{'} - {{\upsilon }_{0}}$ из (3.4) и $r\upsilon _{0}^{{''}}$ из (3.5) в (2.16), будем иметь ДУ пятого порядка относительно A1, A2:
(3.9)
$\begin{gathered} - \frac{4}{3}\theta _{0}^{2}\left( {\nu + 1} \right){{r}^{2}}(2A_{1}^{{''}} + A_{2}^{{''}}) - \frac{{\theta _{0}^{4}}}{{45}}\left( {30\nu + 28} \right){{r}^{2}}\left( {A_{1}^{{''}} + \frac{7}{8}A_{2}^{{''}}} \right) + \frac{{\theta _{0}^{4}}}{{45}}\left( {{{A}_{1}} + \frac{7}{8}{{A}_{2}}} \right) - \\ - \;\frac{2}{3}\theta _{0}^{2}\left( {\nu + 1} \right)r(2A_{1}^{'} + A_{2}^{'}) - \frac{{\theta _{0}^{4}}}{{45}}r\left( {A_{1}^{'} + \frac{7}{8}A_{2}^{'}} \right) - \frac{{\theta _{0}^{4}}}{{45}}\frac{{2\nu }}{{\left( {1 - \nu } \right)}}{{r}^{5}}\left( {\Phi _{3}^{{\left( 4 \right)}} + \frac{7}{8}\Phi _{4}^{{\left( 4 \right)}}} \right) - \\ - \;\sum\limits_{m = 1}^N {(\pi m(ru_{m}^{'} + {{u}_{m}}) + {{\theta }_{0}}({{r}^{2}}\upsilon _{m}^{{''}} + r\upsilon _{m}^{'} - {{\upsilon }_{m}}))} - \\ - \;\frac{{2\nu \theta _{0}^{4}{{r}^{4}}}}{{5\left( {1 - \nu } \right)}}\left( {\Phi _{3}^{{'''}} + \frac{7}{8}\Phi _{4}^{{'''}}} \right) - \frac{{\nu \theta _{0}^{2}}}{{3\left( {1 - \nu } \right)}}{{r}^{3}}(2\Phi _{3}^{{''}} + \Phi _{4}^{{''}}) - \frac{{\theta _{0}^{4}}}{{45}}\frac{{50\nu - 4}}{{\left( {1 - \nu } \right)}}{{r}^{3}}\left( {\Phi _{3}^{{''}} + \frac{7}{8}\Phi _{4}^{{''}}} \right) + \\ \end{gathered} $Если в (2.15) и (2.19) исключить ${{B}_{1}}$, ${{B}_{2}}$, ${{B}_{3}}$, ${{B}_{4}}$, ${{A}_{3}}$, ${{A}_{4}}$ при помощи (3.1)–(3.3), то полученные $2N$ уравнений совместно с (3.7), (3.8), (3.9) относительно ${{A}_{1}}$, ${{A}_{2}}$, ${{u}_{n}}$, ${{\upsilon }_{0}}$, ${{\upsilon }_{n}}$, $n = 1 \div N$ образуют замкнутую дифференциальную систему. Порядок данной системы равен 10 + 4N. Общее решение совместной системы (2.15), (2.19), (3.7), (3.8), (3.9) содержит кроме 10 + 4N произвольных постоянных еще 6 неизвестных (1.10) из условий согласования, т.е. общее решение данной системы будет содержать всего $\left( {16 + 4N} \right)$ неизвестных постоянных, которые находятся при выполнении такого же количества граничных условий: из (2.23)–(2.24) имеем $\left( {9 + 2N} \right)$ условий, из (2.26)–(2.28) – (4 + + N) условий, из (2.29)–(2.32) – (3 + N) уравнений, всего $\left( {16 + 4N} \right)$ граничных условий.
Рассмотрим решение системы ДУ (2.15), (2.19), (3.7), (3.8), (3.9) относительно ${{A}_{1}}$, ${{A}_{2}}$, ${{u}_{n}}$, ${{\upsilon }_{0}}$, ${{\upsilon }_{n}}$ $n = 1 \div N$.
Для увеличения точности вычислений неизвестные ${{A}_{1}}$, ${{A}_{2}}$ представим быстрыми косинус-разложениями по $r \in \left[ {{{r}_{0}},\,R} \right]$ с оператором $C{{h}_{{11}}}$ одиннадцатого порядка, а неизвестные ${{\upsilon }_{0}}\left( r \right)$ и ${{u}_{n}}\left( r \right)$, ${{\upsilon }_{n}}\left( r \right)$, $n = 1 \div N$ запишем быстрыми синус-разложениями оператором $C{{h}_{8}}$ восьмого порядка
(3.10)
$\begin{gathered} {{A}_{j}}\left( r \right) = M_{{11}}^{{\left( j \right)}}\left( r \right) + a_{0}^{{\left( j \right)}} + \sum\limits_{m = 1}^N {a_{{m + 12}}^{{\left( j \right)}}\cos m{\pi }z} ,\quad z = \frac{{r - {{r}_{0}}}}{{R - {{r}_{0}}}} \in \left[ {0,1} \right],\quad j = 1,2 \\ M_{{11}}^{{\left( j \right)}}\left( r \right) = \sum\limits_{q = 1}^{12} {a_{q}^{{\left( j \right)}}{{Q}_{q}}\left( z \right)} ,\quad {{Q}_{q}}\left( z \right) = \int\limits_0^z {\left( {\int\limits_{}^{} {{{Q}_{{q - 2}}}\left( t \right)dt} } \right)dt} ,\quad Q_{q}^{'}\left( 1 \right) = 0 \\ {{Q}_{1}}\left( z \right) = z - {{{{z}^{2}}} \mathord{\left/ {\vphantom {{{{z}^{2}}} 2}} \right. \kern-0em} 2},\quad {{Q}_{2}}\left( z \right) = {{{{z}^{2}}} \mathord{\left/ {\vphantom {{{{z}^{2}}} 2}} \right. \kern-0em} 2} \\ \end{gathered} $(3.11)
$\begin{gathered} {{u}_{n}}\left( r \right) = M_{8}^{{\left( {{{u}_{n}}} \right)}} + \sum\limits_{m = 1}^N {u_{{m + 10}}^{{\left( n \right)}}\sin m{\pi }z} ,\quad n = 1 \div N,\quad M_{8}^{{\left( {{{u}_{n}}} \right)}}\left( r \right) = \sum\limits_{q = 1}^{10} {u_{q}^{{\left( j \right)}}{{P}_{q}}\left( z \right)} \\ {{P}_{q}}\left( z \right) = \int\limits_0^z {\left( {\int\limits_{}^{} {{{P}_{{q - 2}}}\left( t \right)dt} } \right)dt} ,\quad {{P}_{q}}\left( 1 \right) = 0,\quad {{P}_{1}}\left( z \right) = \left( {1 - z} \right),\quad {{P}_{2}}\left( z \right) = z \\ \end{gathered} $(3.12)
${{\upsilon }_{s}}\left( r \right) = M_{8}^{{\left( {{{\upsilon }_{s}}} \right)}} + \sum\limits_{m = 1}^N {\upsilon _{{m + 10}}^{{\left( s \right)}}\sin m{\pi }z} ,\quad M_{8}^{{\left( {{{\upsilon }_{s}}} \right)}} = \sum\limits_{q = 1}^{10} {\upsilon _{q}^{{\left( s \right)}}{{P}_{q}}\left( z \right)} ,\quad s = 0 \div N$Представление функций ${{u}_{n}}\left( r \right)$, ${{\upsilon }_{0}}\left( r \right)$, ${{\upsilon }_{n}}\left( r \right)$, $j = 1,2$; $n = 1 \div N$ в виде (3.11), (3.12) позволяет вычислять производные от них до восьмого порядка включительно на всем отрезке $r \in \left[ {{{r}_{0}},\,R} \right]$, включая и границу, а выражения (3.10) для ${{A}_{j}}\left( r \right)$ позволяют вычислять производные от них до одиннадцатого порядка включительно на том же отрезке. Таким образом, решение задачи сводится к нахождению $\left( {26 + 2N} \right)$ постоянных $a_{k}^{{\left( j \right)}}$, $k = 0 \div 12 + N$, $j = 1,2$, определяющих ${{A}_{1}}$, ${{A}_{2}}$. Функции ${{u}_{m}}(r)$, ${{\upsilon }_{m}}(r)$, m = $1 \div N$ выражаются через $2N\left( {10 + N} \right)$ постоянных $u_{k}^{{\left( n \right)}}$, $\upsilon _{k}^{{\left( n \right)}}$, $k = 1 \div 10 + N$, n = $1{\kern 1pt} \div {\kern 1pt} N$, функция ${{\upsilon }_{0}}\left( r \right)$ определяется через (10 + N) постоянные $\upsilon _{k}^{{\left( 0 \right)}}$, $k = 1 \div 10 + N$. Дополнительными неизвестными являются еще шесть величин ${{F}_{{01}}}$, ${{F}_{{02}}}$, ${{\Phi }_{{01}}}$, ${{\Phi }_{{02}}}$, ${{\Phi }_{{04}}}$, ${{\Phi }_{{05}}}$. Общее количество неизвестных равно $(42 + 23N + 2{{N}^{2}})$.
При использовании метода быстрых разложений для определения функций ${{A}_{1}}\left( r \right)$, ${{A}_{2}}\left( r \right)$, ${{\upsilon }_{0}}\left( r \right)$, ${{u}_{m}}\left( r \right)$, ${{\upsilon }_{m}}\left( r \right)$, $m = 1 \div N$ составим линейную алгебраическую систему, которую обозначим через $S$, − из $\left( {32 + 2N} \right) + 2N\left( {10 + N} \right) + \left( {10 + N} \right)$ уравнений относительно $\{ a_{k}^{{\left( 1 \right)}},a_{k}^{{\left( 2 \right)}},\,k = 0 \div 12 + N\} + \{ u_{p}^{{\left( n \right)}},\upsilon _{p}^{{\left( n \right)}},p = 1 \div 10 + N,n = 1 \div N\} + \{ \upsilon _{k}^{{\left( 0 \right)}},k = 1 \div 10$ + N} и шести постоянных ${{F}_{{01}}}$, ${{F}_{{02}}}$, ${{\Phi }_{{01}}}$, ${{\Phi }_{{02}}}$, ${{\Phi }_{{04}}}$, ${{\Phi }_{{05}}}$ из условий согласования.
Для получения замкнутой системы $S$ имеем $\left( {16 + 4N} \right)$ уравнений из граничных условий (2.23), (2.24), (2.26)–(2.32), которые дополним следующими равенствами. Быстрые разложения ${{A}_{1}}$, ${{A}_{2}}$ из (3.10) и ${{u}_{n}}$, ${{\upsilon }_{s}}$ из (3.11), (3.12) подставим в ДУ (3.8) четвертого порядка и после данной подстановки к полученному уравнению применим оператор $C{{h}_{7}}$ по переменной $z$, так как разность порядков оператора $C{{h}_{{11}}}$ и ДУ (3.8) $11 - 4 = 7$ равна семи (нечетный порядок). Оператор $C{{h}_{7}}$ предполагает выполнение следующих действий с уравнением (3.8):
• нахождение первой, третьей, пятой и седьмой производных от (3.8) и подстановка в полученные производные значений $z = 0$ и $z = 1$;
• вычисление интеграла от (3.8) в пределах $z \in \left[ {0;\,\,1} \right]$;
• умножение (3.8) на $\cos n\pi z$ ($n = 1 \div N$) и последующее интегрирование полученного выражения в пределах $z \in \left[ {0;\,\,1} \right]$.
В результате этих действий имеем (9 + N) алгебраических уравнений.
Точно такие же преобразования сделаем и с уравнением (3.7), так как разность порядков оператора $C{{h}_{8}}$ для ${{\upsilon }_{0}}$ и ДУ (3.7) 8 – 1 = 7 равна семи (нечетный порядок). В результате получим еще $(9 + N)$ алгебраических уравнений.
Теперь подставим ${{A}_{1}}$, ${{A}_{2}}$ из (3.10) и ${{u}_{m}}$, ${{\upsilon }_{m}}$ из (3.11), (3.12) в ДУ (3.9) и применим к полученному уравнению оператор $C{{h}_{6}}$ по переменной $z$, так как разность порядков оператора $C{{h}_{{11}}}$ и ДУ (3.9) $11 - 5 = 6$ равна шести. Оператор $C{{h}_{6}}$ предполагает выполнение следующих действий с уравнением (3.9):
• нахождение второй, четвертой и шестой производных от (3.9) и подстановка значений z = 0 и z = 1 в полученные производные, а также в уравнение (3.9);
• умножение (3.9) на $\sin n\pi z$ ($n = 1 \div N$) и последующее интегрирование полученного выражения в пределах $z \in \left[ {0;\,\,1} \right]$.
Таким образом, получим (8 + N) уравнений.
После подстановки ${{A}_{1}}$, ${{A}_{2}}$, ${{u}_{m}}$, ${{\upsilon }_{m}}$ из (3.10)–(3.12) в ДУ (2.15) и (2.19) применим к полученным уравнениям оператор $C{{h}_{6}}$ – шестого порядка по переменной z, так как в обоих уравнениях (2.15) и (2.19) минимальная разность порядков оператора $C{{h}_{8}}$ и ДУ (2.15) и (2.19) второго порядка, т.е. $8 - 2 = 6$ равна шести. Выполняя с (2.15) и (2.19) преобразования, аналогичные преобразованиям с уравнением (3.9), будем иметь $2N\left( {8 + N} \right)$ уравнений.
Таким образом, к ранее записанным из граничных условий $\left( {16 + 4N} \right)$ алгебраическим уравнениям добавляются $(26 + 19N + 2{{N}^{2}})$ алгебраических уравнений, полученных из ДУ (2.15), (2.19), (3.7)–(3.9). После решения замкнутой алгебраической системы $S$, состоящей из $(42 + 23N + 2{{N}^{2}})$ уравнений, перемещения U, V находятся по формулам (2.1), затем из (1.5) определяются напряжения ${{{\sigma }}_{r}}$, ${{{\sigma }}_{{\theta }}}$, ${{{\sigma }}_{{r{\theta }}}}$ в аналитическом виде.
4. Полученные результаты и их обсуждение. При изучении свойств поля напряжений в клине наибольший интерес представляет анализ расположения точки с наибольшим значением второго инварианта ${\tilde {\sigma }}$ [23]:
Это можно сделать при помощи использования полученного решения. В качестве материала резца выбрана инструментальная быстрорежущая сталь марки Р18. Она имеет следующие характеристики [24, 25]
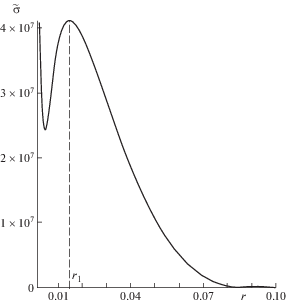
Значения параметров F03, ${{\Phi }_{{03}}}$, ${{\Phi }_{{06}}}$, ${{r}_{0}}$, R, ${{\theta }_{0}}$ подбирались таким образом, чтобы напряжения не превосходили предел текучести, т.е. ${\tilde {\sigma }} \leqslant {{{\sigma }}_{{0,2}}}$. В ходе вычислительных экспериментов выяснилось, что для значений радиуса r0, существует критическое ${{r}_{0}} = r_{0}^{*}$, при котором величина ${\tilde {\sigma }}$ достигает своего наибольшего значения сразу в двух местах клина: на углу с координатами ${{r}_{0}} = r_{0}^{*}$, ${\theta } = {{{\theta }}_{0}}$ и на грани ${\theta } = {{{\theta }}_{0}}$ на небольшом удалении от носика в точке $\left( {{{r}_{1}};\,\,{{{\theta }}_{0}}} \right)$ (рис. 2, θ = θ0 = 5π/180). Значение $r_{0}^{*}$ зависит от угла раствора ${{{\theta }}_{0}}$. Для некоторых углов ${{{\theta }}_{0}}$ в табл. 1 представлены значения критического радиуса закругления носика $r_{0}^{*}$, полученные при
(4.1)
${{\Phi }_{{03}}} = 2 \cdot {{10}^{{ - 5}}},\quad {{\Phi }_{{06}}} = 2 \cdot {{10}^{{ - 5}}},$ ${{F}_{{03}}} = 2 \cdot {{10}^{{ - 5}}},$ $R = {{10}^{{ - 1}}}$ (м)Таблица 1
| ${{{\theta }}_{{\text{0}}}}$ | ${{\pi } \mathord{\left/ {\vphantom {{\pi } {180}}} \right. \kern-0em} {180}}$ | $5{{\pi } \mathord{\left/ {\vphantom {{\pi } {180}}} \right. \kern-0em} {180}}$ | $67{{\pi } \mathord{\left/ {\vphantom {{\pi } {180}}} \right. \kern-0em} {180}}$ | $82{{\pi } \mathord{\left/ {\vphantom {{\pi } {180}}} \right. \kern-0em} {180}}$ | $92{{\pi } \mathord{\left/ {\vphantom {{\pi } {180}}} \right. \kern-0em} {180}}$ |
|---|---|---|---|---|---|
| $r_{0}^{*}$, м | 5.03 × 10–3 | 2.34 × 10–3 | 5.97 × 10–4 | 5.805 × 10–4 | 5.72 × 10–4 |
Из табл. 1 видно, что с увеличением угла раствора ${{{\theta }}_{0}}$ значения $r_{0}^{*}$ уменьшаются и, приближаясь к прямому углу, значения $r_{0}^{*}$ очень малы − сотые доли миллиметра. Величины углов раствора ${{{\theta }}_{0}} = 67{{\pi } \mathord{\left/ {\vphantom {{\pi } {180}}} \right. \kern-0em} {180}}$, ${{{\theta }}_{0}} = 82{{\pi } \mathord{\left/ {\vphantom {{\pi } {180}}} \right. \kern-0em} {180}}$, ${{{\theta }}_{0}} = 92{{\pi } \mathord{\left/ {\vphantom {{\pi } {180}}} \right. \kern-0em} {180}}$ соответствуют углам заточки резца ${\beta }$ [26].
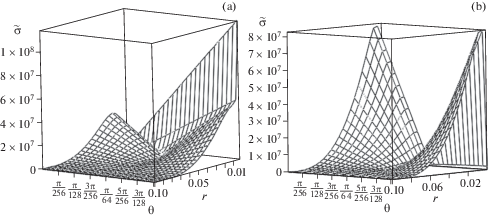
Если ${{r}_{0}} \ne r_{0}^{*}$, то величина ${\tilde {\sigma }}$ достигает своего наибольшего значения только в одной точке: в случае ${{r}_{0}} > r_{0}^{*}$ – на углу с координатами $r = {{r}_{0}}$, ${\theta } = {{{\theta }}_{0}}$ (рис. 3а), а при ${{r}_{0}} < r_{0}^{*}$ − на грани ${\theta } = {{{\theta }}_{0}}$ на небольшом удалении от носика (рис. 3б). Распределения ${\tilde {\sigma }}$, представленные на рис. 3, получены при значениях (4.1), ${{{\theta }}_{0}} = 5{{\pi } \mathord{\left/ {\vphantom {{\pi } {180}}} \right. \kern-0em} {180}}$ и ${{r}_{0}} = 3 \cdot {{10}^{{ - 3}}}$ (м) и ${{r}_{0}}$ = 10–5 (м) соответственно для рис. 3а и рис. 3b.
Изучение влияния размеров клина при ${{r}_{0}} < r_{0}^{*}$ на величину ${\tilde {\sigma }}$ представляет наибольший интерес, так как в [26] описаны случаи, когда “вследствие износа трением на передней поверхности резца образуется лунка, несколько удаленная от носика”. Но в [26] не указано численное значение этого удаления. Будем считать, что лунка на поверхности резца образуется в точке с наибольшим напряжением ${\tilde {\sigma }}$ при $r = {{r}_{1}}$. Из решения данной задачи выяснили, что координаты точки с наибольшим значением ${\tilde {\sigma }}$ при ${{r}_{0}} < r_{0}^{*}$ не постоянны и изменяются в зависимости от угла раствора ${{{\theta }}_{0}}$. С увеличением ${{{\theta }}_{0}}$ точка с наибольшим значением ${\tilde {\sigma }}$ приближается к носику резца. Это отражено в табл. 2, где значения ${{r}_{1}}$ получены при данных (4.1) и ${{r}_{0}} = {{10}^{{ - 6}}}$ (м).
Таблица 2
| ${{{\theta }}_{{\text{0}}}}$ | ${{\pi } \mathord{\left/ {\vphantom {{\pi } {180}}} \right. \kern-0em} {180}}$ | $5{{\pi } \mathord{\left/ {\vphantom {{\pi } {180}}} \right. \kern-0em} {180}}$ | $67{{\pi } \mathord{\left/ {\vphantom {{\pi } {180}}} \right. \kern-0em} {180}}$ | $82{{\pi } \mathord{\left/ {\vphantom {{\pi } {180}}} \right. \kern-0em} {180}}$ | $92{{\pi } \mathord{\left/ {\vphantom {{\pi } {180}}} \right. \kern-0em} {180}}$ |
|---|---|---|---|---|---|
| r1, м | 8.72 × 10–3 | 1.46 × 10–3 | 2.68 × 10–5 | 2.57 × 10–5 | 2.53 × 10–5 |
Заключение. Применение быстрых разложений позволило представить решение в явном аналитическом виде и выявить особенности поля напряжений при ${{r}_{0}} = r_{0}^{*}$. Получено, что наибольшее напряжение ${\tilde {\sigma }}$ достигается в резце в двух точках $(r_{0}^{*};{{{\theta }}_{0}})$ и $({{r}_{1}};{{{\theta }}_{0}})$. Первая точка находится непосредственно на носике, а вторая близко от носика. В случае ${{r}_{0}} \ne r_{0}^{*}$ величина ${\tilde {\sigma }}$ достигает своего наибольшего значения только в одной точке: при ${{r}_{0}} > r_{0}^{*}$ в точке $(r_{0}^{*};{{{\theta }}_{0}})$, а при ${{r}_{0}} < r_{0}^{*}$ в точке $\left( {{{r}_{1}};{{{\theta }}_{0}}} \right)$.
Список литературы
Никифоров С.Н. Теория упругости и пластичности. М.: Госуд. изд-во литер. по строит. и архитек., 1955. 284 с.
Уфлянд Я.С. Смешанная задача теории упругости для клина // Изв. АН СССР. ОТН. Механика и машиностроение. 1959. № 2. С. 156–158.
Быковцев Г.И., Ивлев Д.Д. Теория пластичности. Владивосток: Дальнаука, 1998. 528 с.
Иванов Э.Г. Решение первой основной задачи теории упругости для составного клина с помощью степенных рядов // Матем. моделир. и краевые задачи: труды шестой Всероссийской науч. конф. с междунар. участием. 1–4 июня 2009 г. Ч. 1. Самара: Сам. ГТУ, 2009. С. 113–115.
Чернышов А.Д. О деформировании сплошных сред в клиновидной области с гладкими гранями // ПММ. 1975. Т. 39. С. 1093–1099.
Shahani A.R., Adibnazari S. Analysis of perfectly bonded wedges and bonded wedges with an interfacial crack under antiplane shear loading // Int. J. of Solids and Structures. 2000. V. 37. P. 2639–2650.
Shahani A.R. Analysis of an anisotropic finite wedge under antiplane deformation // J. Elasticity. 1999. V. 56. P. 17–32.
Shahani A.R., Ghadiri M. Analysis of anisotropic sector with a radial crack under anti-plane shear loading // Int. J. Solids and Structures. 2010. V. 47. P. 1030–1039.
Stampouloglou I.H., Theotokoglou E.E. The plane elasticity problem of an isotropic wedge under normal and shear distributed loading – application in the case of a multi-material problem // Int. J. Solids and Structures. 2003. V. 40. P. 5839–5860.
Linkov A., Rybarska-Rusinek L. Plane elasticity problem for a multi-wedge system with a thin wedge // Int. J. of Solids and Structures. 2010. V. 47. P. 3297–3304.
Лурье А.И. Теория упругости. М.: Наука, 1970. 940 с.
Chue C.H., Liu Ch.I. A general solution on stress singularities in an anisotropic wedge // Int. J. Solids and Structures. 2001. V. 38. P. 6889–6906.
Тимошенко С.П., Гудьер Дж. Теория упругости. М.: Наука, 1979. 560 с.
Guo L., Zhang Z.M., Wang W., Wong P.L. An explicit matrix algorithm for solving three-dimensional elastic wedge under surface loads // Int. J. Solids and Structures. 2017. V. 128. P. 231–242.
Александров В.М., Пожарский Д.А. Трехмерные контактные задачи для упругого клина с покрытием // ПММ. 2008. Т. 72. Вып. 1. С. 103–109.
Чернышов А.Д. Метод быстрых разложений для решения нелинейных дифференциальных уравнений // Журнал вычислительной математики и математической физики. Т. 54. № 1. 2014. С. 13–24.
Чернышов А.Д., Горяйнов В.В., Марченко А.Н. Исследование температурных полей в прямоугольной пластине с внутренним источником, зависящим от температуры, при помощи быстрых разложений // Теплофизика и аэромеханика. 2016. Т. 23. № 2. С. 247–256.
Чернышов А.Д., Попов В.М., Горяйнов В.В., Лешонков О.В. Исследование контактного термического сопротивления в конечном цилиндре с внутренним источником методом быстрых разложений и проблема согласования граничных условий // Инженерно-физический журнал. 2017. Т. 90. № 5. С. 1288–1297.
Чернышов А.Д., Горяйнов В.В. Решение одного нелинейного интегро-дифференциального уравнения методом быстрых разложений // Вестник ЧГПУ им. И.Я. Яковлева. Серия: механика предельного состояния. 2012. № 4 (12). С. 105–112.
Чернышов А.Д., Горяйнов В.В., Чернышов О.А. Применение метода быстрых разложений для расчета траекторий космических кораблей // Известия вузов. Авиационная техника. 2015. № 2. С. 41–47.
Демидов С.П. Теория упругости. М.: Высшая школа, 1979. 432 с.
Чернышов А.Д. Метод угловых суперпозиций для краевых задач. Изд-во LAP LAMBERT Academic Publishing, 2012. P. 350.
Ишлинский А.Ю., Ивлев Д.Д. Математическая теория пластичности. М.: Физматлит, 2001. 704 с.
URL: http://metallicheckiy-portal.ru/marki_metallov/sti/R18 (дата обращения 10.08.2016).
URL: http://docs.cntd.ru/document/1200093817 (дата обращения 10.08.2016).
Яковцев А.Д. Работа на строгальных и долбежных станках. М.: Высшая школа, 1971. 264 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела