Известия РАН. Механика твердого тела, 2019, № 5, стр. 27-36

1. Введение. Эластомеры, характеризуются способностью испытывать большие (до сотен процентов) деформации и возвращаться к исходному размеру по снятии нагрузки. Среди других присущих данной группе материалов свойств отметим снижения упругого модуля, наличие упругого гистерезиса и его уменьшение при повторных циклах нагружения (эффект Маллинза) [1–3], анизотропию данного эффекта (снижение модуля и уменьшение упругого гистерезиса более выражено при нагружении по направлениям близким к направлению нагружения первого цикла) [3], а также появляющуюся после нагружения анизотропию прочностных свойств (в первую очередь, трещиностойкости), проявляющуюся в снижении энергии разрушения при растяжении по нормали к первичному растяжению [4]. Указанные свойства наблюдаются для широкого круга эластомеров (натуральный каучук – в большей степени, стирол-бутадиеновые и силоксановые резины и др. – в меньшей степени) и становятся более выраженными при наличии частиц наполнителя, в качестве которого используют частицы с высокой поверхностной энергией – обычно, технический углерод, реже – кремнезем, применяемые для увеличения прочности, жесткости и износостойкости эластомеров.

Для объяснения усиливающего действия наполнителя и остального круга указанных явлений было предложено множество моделей, основанных на том, что в процессе деформирования в эластомерах происходит перестроение структуры [2, 5–22], выражающееся в скольжении полимерных цепочек по частицам наполнителя [5, 7, 9–11, 19], вытягивании их из областей, непосредственно прилегающих к наполнителю [16, 21], разрушении связей между полимерными молекулами и частицами наполнителя и образовании новых [6]. Благодаря данным механизмам предполагается выравнивание длин полимерных цепочек, ориентированных в направлении растяжения, и, как следствие, более равномерное перераспределение напряжений, приводящее к увеличению прочности. При разгрузке обратное перестроение не происходит, или происходит в меньшей степени, что и вызывает гистерезис, остаточные деформации и снижение модуля при повторном нагружении.

Роль скольжения полимерных молекул по частицам технического углерода особенно подчеркивалась Александровым и Лазуркиным [5], Данненбергом [9, 10]. В основе модели Ригби [12] лежит представление о том, что перераспределение длин полимерных цепочек происходит путем дискретных перескоков устойчивых положений контакта макромолекул полимера с частицами технического углерода. Данную идеологию можно рассматривать как более детальное рассмотрение скольжения.

Сходные идеи были заложены в модели Маллинза и Тобина [8], согласно которой эластомер может быть представлен состоящим из жесткой и мягкой фаз, а полимерные цепочки могут переходить из твердой фазы в мягкую в процессе растяжения. Модель получила развитие в работе [13]. В развитие этой идеи Свистковым и соавторами был явно введен трансмиссионный элемент, соответствующий переходу части материала в более мягкую фазу [20, 22].

Согласно модели Маркманна и соавторов [14] при растяжении перестроение структуры выражается в увеличении числа звеньев полимерных цепочек за счет сокращения количества (концентрации) цепочек при сохранении суммарного количества звеньев (баланс масс). В качестве механизмов, реализующих такое перераспределение, предполагался отрыв цепочек от частиц включения. Диани и соавторами [18] изотропная модель [14] была обобщена для учета анизотропии эффекта Маллинза введением предположения о независимости баланса масс по каждому из направлений. Маркманном и соавторами в последующей работе [23] была высказана идея о сохранении интегрального баланса масс по всем направлениям при индивидуальном, зависящем от деформированного состояния, перераспределении числа звеньев и количества цепочек по каждому направлению; однако при математической формулировке идея не была реализована.

Кроме моделей, основанных на концепции перестроения структуры, вероятно начиная с работы [24], большое распространение получили модели в духе теории накопления поврежденности, в основе которых лежит предположение о разрыве цепей (или их отрыве от частиц наполнителя), как причины упругого гистерезиса. Данные модели, обзор которых не входит в цели данной работы, позволяют достаточно хорошо описывать упругий гистерезис и даже его анизотропию, однако вступают в противоречие с рядом других наблюдаемых явлений:

– добавление наполнителя вызывает существенное увеличение не только упругого гистерезиса, но и прочности (для стирол-бутадиеновых резин предельные удлинения возрастают на 30%, а предельные усилия в 16 раз [4]); обрыв большего числа связей, если им обусловлены размягчение и гистерезис, должен был бы приводить к обратному эффекту;

– в эластомерах с наполнителем, проявляющих при первичном растяжении существенно большую жесткость, чем аналогичные ненаполненные эластомеры, при последующих циклах растяжения жесткость снижается до величин, характерных для ненаполненных эластомеров [2], при этом прочность эластомеров с наполнителем остается существенно больше, чем без них [4]; обрыв связей должен был бы приводить к аналогичному снижению прочности;

– отсутствие снижения прочности при повторном растяжении [2];

– снижение трещиностойкости при повторном растяжении в направлении, перпендикулярном первичному, а не в направлении, совпадающим с первичным; накопление повреждений должно было бы приводить к снижению прочности в направлении первичного растяжения;

– при внесении частиц бронзы, образующей с макромолекулами эластомеров весьма прочные контакты, явлений, подобных вызываемым частицами технического углерода, не происходит [12]; в то же время, уменьшение энергии связи полимерных молекул с частицами технического углерода путем предварительного нагрева последних приводит к увеличению прочности (максимального удлинения при разрыве) [9]; данные явления можно объяснить механизмом скольжения, но никак не обрывами связей;

– при набухании эластомеров под воздействием растворителей в случае, если образцы были предварительно подвержены одноосному растяжению наблюдается увеличение величины набухания в направлении предварительного растяжения и уменьшение в других направлениях при некотором уменьшении суммарного увеличения объема [2]; это свидетельствует о том, что изменение структуры в одном направлении происходит за счет противоположного изменения в других направлениях.

Следует однако заметить, что в ряде работ (например, [18]) для описания механизма структурного перестроения используется термин “поврежденность” (“damage”), что приводит к искажению смысла.

В настоящей работе будет рассмотрена модель достаточно общего вида, основанная на концепции деформирования полимерных цепочек, перестроения их структуры в процессе нагружения и не содержащая параметра “поврежденности”. Далее будет осуществлена конкретизация модели, содержащая минимальное количество функций, подлежащих определению. Простейший вариант модели с минимальным количеством параметров будет реализован для случая конечного числа цепочек различной ориентации.

2. Модель. В основе модели лежит традиционное представление о деформировании эластомера как совокупности изменения конфигураций полимерных цепочек, приводящей при отклонении от равновесной конфигурации уменьшению энтропии и, следовательно, к увеличению свободной энергии. Благодаря процессам изменения структуры молекулярных цепочек в процессе деформирования: скольжению их друг относительно друга, распутыванию и – что наиболее существенно – скольжению относительно частиц наполнителя, происходит перераспределение числа звеньев и относительной концентрации полимерных цепочек, ориентированных в различных направлениях, при общем сохранении суммарного числа звеньев (баланс масс).

Выражение для свободной энергии W_j индивидуальной полимерной  j-той цепочки [25, 26] можно записать следующим образом

Здесь T – абсолютная температура; S_j – энтропия j-той цепочки; k – постоянная Больцмана; r_j – расстояние между концами полимерной цепочки; N_j – число звеньев полимерной цепочки; l – длина звена; c – постоянная; ${{\mathcal{L}}^{{ - 1}}}$ – обратная функция Ланжевена, $L(x) = cth(x) - 1{\text{/}}x$. Приближенно обратную функцию Ланжевена можно представить как ${{L}^{{ - 1}}}\left( x \right) \approx 3x + {{x}^{3}}{\text{/}}\left( {1 - x} \right)$. Выражение для силы, возникающей при изменении длины полимерной цепочки получается дифференцированием выражения для свободной энергии по величине r_j

Ненапряженное состояние соответствует среднестатистическому расстоянию между концами полимерной цепочки [25, 26]

Подставляя (2.4) в (2.3) получаем

где ${{{\lambda }}_{j}} = {{r}_{j}}{\text{/}}{{r}_{{0j}}}$ – относительное удлинение цепочки.

Свободная энергия элемента объема и истинные напряжения Коши в системе координат, связанной с главными осями, могут быть представлены как [27]

где интегрирование осуществляется по всем возможным ориентациям; ${{C}_{j}}\left( {\theta } \right)$ – плотность распределения полимерных цепей по объемному углу θ; ${{\Lambda }_{i}}$ – удлинения в системе координат, связанной с главными осями; p – давление; неопределенность которого следует из условия несжимаемости

Величина p для одноосного и двухосного растяжений находится из условия равенства нулю напряжения вдоль оси, вдоль которой нагрузка отсутствует.

Основу предлагаемого подхода составляет предположение, что в процессе деформирования числа звеньев в цепочках ${{N}_{j}}\left( {\theta } \right)$ и концентрации цепочек ${{C}_{j}}\left( {\theta } \right)$ не остаются постоянными, а являются функциями текущих состояний и всей истории деформирования с сохранением общего баланса масс

при этом увеличение длины какой-либо цепочки может происходить как за счет сокращения концентрации цепочек данной пространственной ориентации, так и за счет сокращения концентраций и длин цепочек других пространственных ориентаций. Схематически процесс перераспределения длин полимерных цепочек представлен на рис. 1. Отметим, что возможность уменьшения длин полимерных цепочек, ориентированных в направлениях, отличных от направления растяжения, была заложена в модель [23], являющуюся обобщением модели [14] для анизотропного случая. Так же была высказана идея о сохранении общего баланса масс (2.9) [23], однако в окончательно сформулированной в указанной работе математической модели изменение длин цепочек рассматривалось по отдельности для каждого направления, и вместо условия баланса масс типа ${{C}_{j}}{{N}_{j}} = {\text{const}}$ даже в пределах выделенного направления, была введена функция поврежденности.

Для квазистационарных процессов можно предположить сохранение вида свободной энергии полимерной цепочки и усилия в ней в форме (2.1)–(2.3). Тогда, с учетом того, что ненапряженное состояние соответствует среднестатистическому расстоянию между концами полимерной цепочки (2.4) определяется текущим числом звеньев цепочки, а относительное удлинение должно отсчитываться от начальной равновесной длины цепочки, определяемой начальным числом звеньев, выражение для усилия (2.5) модифицируется следующим образом

где ${\lambda }_{j}^{'}$ – относительное удлинение цепочки относительно исходного состояния, определяемого начальной длиной полимерных цепочек

Учет различия между ${{r}_{{0j}}}$ и $r_{{0j}}^{'}$ в рассматриваемой модели приводит к естественному появлению в ней остаточных деформаций, не рассматриваемых в модели [14].

Для конкретизации модели необходимо задать законы изменения соответствующих величин от истории деформирования, которые в самом общем случае могут рассматриваться как функционалы от удлинений цепочек (или действующих в них усилиях) по всем направлениям

либо

Выбор данных соотношений должен обеспечить описание упругого гистерезиса (эффекта Маллинза) и его анизотропию. Отметим, что наличие остаточных деформаций уже заложено в уравнении (2.10).

3. Конкретизация модели. В целях упрощения вычислений непрерывное распределение направлений полимерных цепочек часто моделируют дискретным. Далее будет использована 7-цепочечная модель [28], представляющая собой суперпозицию 3-цепочечной модели [29], и 4-цепочечной модели [30], направления цепочек в недеформированном состоянии для которой следующие

Интегрирование в (2.6) заменяется суммированием

Здесь ${{{\omega }}_{j}} = 1{\text{/}}7$ – относительные веса, принятые для простоты равными; относительные удлинения цепочек вычисляются через тензор градиента смещения

как где ${{\Lambda }_{1}}$, ${{\Lambda }_{2}}$, ${{\Lambda }_{3}}$ – величины главных удлинений.

Выражения для напряжений Коши в системе координат, связанной с главными осями, преобразуются к виду

Для замыкания системы необходимо конкретизировать вид зависимости (2.13) либо (2.14). В данной работе сознательно выбран достаточно простой вид зависимостей с минимальным числом параметров с целью продемонстрировать возможность скорее качественного, чем количественного непротиворечивого описания достаточно широкого круга явлений.

Параметры C₀ – начальная концентрация цепочек, равная для всех направлений, и N₀ – начальное число звеньев в цепочках, являются традиционными для моделей подобного рода и характеризуют упругий модуль на начальном участке деформирования и предельное удлинение. Дополнительные параметры ${{k}_{C}}$, ${{k}_{{CN}}}$, характеризующие изменение концентрации цепочек и суммарного числа звеньев во всех цепочках по направлению, служат для описания упругого гистерезиса и его анизотропии; $d{\lambda }$ – величина, характеризующая приращение удлинения; ${\lambda }_{j}^{{\max }}$ – максимальное удлинение, достигнутое в j-том направлении. Вид уравнения (3.6) выбран таким образом, что при отсутствии зависимости (3.7) соответствует линейному росту ${{N}_{j}}({\lambda }_{j}^{'})$, т.е. является для этого случая упрощенным аналогом модели [18], в которой баланс масс предполагался сохраняющимся по каждому направлению. Вид уравнения (3.7) выбран для обеспечения возможности “перетекания” звеньев из одной системы ориентации в другую, кроме того, выбранный вид автоматически обеспечивает условие интегрального баланса масс (2.9). Подобно теории пластического течения изменение структурных параметров происходит только при активном нагружении.

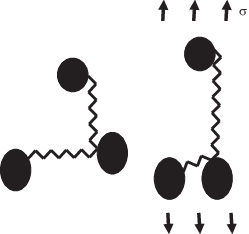
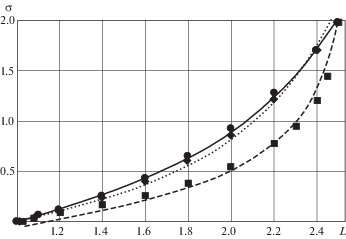
4. Пример расчета. Для проверки работоспособности модели было проведено сравнение с экспериментальными результатами [31], где образцы силикатной резины подвергались одному циклу одноосного растяжения, а затем из них вырезались образцы меньших размеров под различными углами к оси первичного растяжения. Эти образцы затем подвергались растяжению до той же величины номинальных напряжений, что и в первом цикле. На рис. 2 представлены результаты опытов [31] (снятые с графиков и пересчитанные в напряжения Коши) и результаты вычислений согласно используемой модели, со следующими параметрами: ${{C}_{0}} = 0.152$, ${{N}_{0}} = 2.5$, ${{k}_{C}} = 0.42$, k_CN = $5.6 \times {{10}^{{ - 4}}}$; в качестве величины, характеризующей приращение удлинения dλ взята величина приращения удлинения по активному направлению. Круглыми маркерами отмечены экспериментальные точки первичного растяжения, квадратными – разгрузки, ромбами – повторного растяжения в перпендикулярном направлении. Соответствующие расчетные зависимости представлены сплошной, пунктирной и точечной линиями.

Из графика видно, что задание зависимостей (2.13), (2.14) в виде функций, зависящих всего от двух скалярных параметров позволило качественно описать наблюдаемые явления: упругий гестерезис, его анизотропию, наличие остаточных деформаций (параметры C₀ и N₀ служат для описания начального наклона ниспадающей ветви, или ветви повторного нагружения в направлении первичного, и степени отклонения этой ветви от линейного закона с ростом деформаций). Безусловно, введением более сложных зависимостей вместо (3.6), (3.7) можно добиться существенно лучшего согласования с экспериментом, в частности лучшего совпадения величины остаточных деформаций. Отдельно обращает на себя внимание несильный, но выраженный опережающий рост напряжений, даваемых моделью, для повторного цикла образца, растягиваемого по нормали к первичному нагружению. Для данного расчета это может является артефактом реализации модели, вызванным малым числом выделенных направлений (3.1). Однако подобный опережающий, хотя и не сильно выраженный, рост наблюдался для подобных материалов в других экспериментах [32, 33]. На повышение жесткости, до величин больших, чем соответствующих первичному циклу растяжения, для вторичного растяжения под углами, близкими к 90° к первичному растяжению, при больших деформациях прямо указывалось в [23].

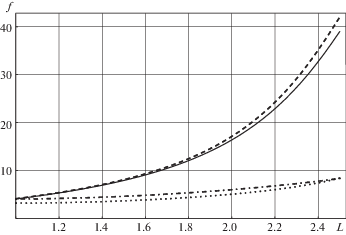
Интересно отметить возможность в рамках рассматриваемого подхода оценить эффект, вызываемый предполагаемыми изменениями структуры не только на упругие, но и на прочностные свойства. Известно, что для большинства эластомеров снижение прочности вдоль направления растяжения наблюдается в наполненных эластомерах и по снятию нагрузки [2, 4, 8]. Естественно предположить, что разрушение начинается с разрыва наиболее напряженных цепей. На рис. 3 представлены зависимости усилия в некоторых цепочках от удлинения: усилия в цепочках, направленных вдоль ${{{v}}_{1}}$ и ${{{v}}_{{4 - 7}}}$ от удлинения ${{\Lambda }_{1}}$ в первом цикле (сплошная и штрих-пунктирная линии) и усилия в цепочках, направленных вдоль ${{{v}}_{2}}$ и ${{{v}}_{{4 - 7}}}$ от удлинения ${{\Lambda }_{2}}$ во втором цикле (пунктирная и точечная линии). Из представленного графика видно, что, максимальные натяжения в цепочках выше для второго цикла. Противоположная тенденция для наклонных цепочек (${{{v}}_{{4 - 7}}}$) компенсирует вклад в суммарные макроскопические напряжения, и приводит к их снижению (по крайней мере, для начальных стадий деформирования) на втором цикле (рис. 2). Увеличение усилий в наиболее напряженных цепочках во втором цикле, согласно модели происходит за счет сокращения их длины в первом.

5. Заключение. Представлена модель эластомеров, основанная на классическом механизме изменения конфигураций полимерных молекул и модификации структуры (скольжения молекул по частицам включения), позволяющая без привлечения понятия “поврежденности” описать характерные черты деформирования: снижение жесткости при повторном растяжении (эффект Маллинза), упругий гистерезис и его анизотропию. Из модели также естественным образом следует появление наведенной прочностной анизотропии – уменьшение прочности при повторном растяжении в направлении, перпендикулярном первичному растяжению.

Основные положения модели следующие:

– упругие модули по каждому направлению пропорциональны количеству молекулярных цепей, ориентированных по данному и близких к нему направлению и уменьшаются с увеличением длин данных цепей (в соответствие с классической теорией упругости эластомеров);

– перераспределение длин полимерных цепей, в первую очередь за счет их скольжения по поверхностям частиц активного наполнителя (технического углерода) приводит к удлинению цепей, расположенных вдоль растяжения;

– количество сегментов всех молекулярных цепей остается постоянным в процессе нагружения (согласно закону сохранения массы); увеличение длин молекулярных цепочек, вытянутых вдоль растяжения, происходит за счет уменьшения количества звеньев в цепочках, расположенных по другим направлениям. Именно это предположение является принципиальным и отличающим рассматриваемую модель от предложенных ранее.

Простейший вариант модели с минимальным количеством параметров реализован для случая конечного числа цепочек различной ориентации.

Работа выполнена при финансовой поддержке Программы Президиума РАН № 27.