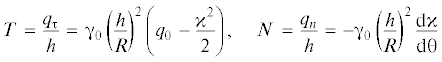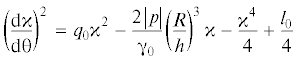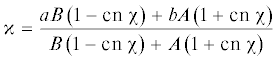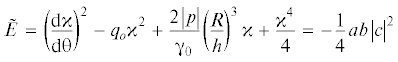Известия РАН. Механика твердого тела, 2019, № 6, стр. 54-67

1. Введение. Круговые оболочки являются основными несущими элементами многих конструкций. Изменение формы оболочки при достижении определенных критических нагрузок ведет к ее разрушению. Поэтому большинство теоретических и экспериментальных исследований нацелено на выяснение условий, при которых оболочка сохранит неизменной свою форму при заранее заданном уровне внешних воздействий. Линейная теория упругости позволяет грубо оценить критические нагрузки, при которых теряются устойчивые формы оболочек, и предсказать число волн, образующихся при этом на их поверхностях [1, 2]. Однако теоретическое описание процессов локализации деформации и образования узоров из вмятин на поверхностях нагруженных оболочек возможно только в рамках нелинейной теории.

К настоящему времени имеются первые экспериментальные работы [3, 4], в которых в условиях внешнего гидростатического сжатия удалось управлять развитием локальных неустойчивостей первоначально круговых металлических оболочек. Экспериментально найдены интервалы давлений, значений геометрических и материальных параметров оболочки, конфигурации внешних и внутренних оправок, при которых удается контролировать течение материала и получать из холоднокатаных труб полые изделия с заданной формой поперечного сечения: круговым, но переменным по длине оболочки, треугольным, квадратным, любым зубчатым. Примеры конкретных изделий приведены на рис. 1: это карданный вал автомобиля и приемный вал, сопрягаемый с карданным валом (a); рулевые колонки мотоциклов с разной формой поперечного сечения в средней части (b). Проведенные исследования открывают возможность создания новых высокоэффективных технологий, которые позволят существенно сократить временные, энергетические и материальные затраты.

Теоретическое описание таких процессов даже на начальной стадии деформирования материала, когда на поверхностях оболочек образуются нелинейно-упругие узоры из локализованных вмятин, является одной из наиболее сложных задач механики. Большинство исследований по изменению формы оболочек тяготеют к численному моделированию процесса без привлечения аналитических методов (см., например, [5–8] и цитируемую там литературу). Наиболее содержательные результаты получены для оболочек из модельного материала типа резины [6]. Однако численный подход не вскрывает в полной мере закономерностей наблюдаемых явлений и не исследует возможностей управления деформированием металлических образцов под давлением. Более эффективным представляется сочетание аналитических и численных методов. Анализ явных решений упрощенных нелинейных моделей дает критерии выбора связей для управления изменениями формы оболочки. При построении моделей следует учитывать только ключевые факторы, определяющие именно те черты поведения системы, которые нас интересуют. В экспериментах при гидростатическом сжатии оболочки на ее поверхности образуются выпуклости и впадины, чередующиеся в окружном направлении. При этом поперечное сечение оболочки остается неизменным на протяженных участках вдоль образующей. Поэтому представление о характере гофрирования оболочки дает задача об изменении формы первоначально кругового тонкого кольца единичной высоты [9, 10]. В такой постановке уравнения, определяющие нелинейно-упругие изгибы кольца, совпадают с уравнениями, характеризующими изменение формы гибкого стержня, ось которого все время лежит в одной плоскости. Напомним результаты теории стержней, полезные для обсуждения задачи об изменении формы оболочки. Известно, что с ростом внешних напряжений одни формы стержней могут переходить в другие. Хотя некоторые формы равновесия стержней неустойчивы, их можно стабилизировать, вводя подходящие подкрепляющие связи [1]. Именно такой подход использовался в [3, 4] для управления изменениями формы оболочки. При быстром сжатии стержня (время нарастания нагрузки меньше времени релаксации деформаций) элементы стержня не успевают переместиться в направлении, нормальном к оси стержня. Раньше, чем прогибы стержня станут заметными, сжимающее усилие может превысить не только первое, но и более высокие критические значения, характерные для разных стационарных состояний стержня. При этом экспериментально наблюдаются конечные состояния нагруженных стержней с высшими формами изгибов. Впервые такая возможность для стержней была описана в рамках линейной теории упругости [11]. На поверхностях гидростатически сжатых оболочек также наблюдают разное число выпуклостей и вмятин в зависимости от соотношения геометрических и материальных параметров оболочки и величины внешнего давления [1, 3, 4]. Задачи об изменении формы гибких стержней и колец при разных точечных нагрузках или контактах колец друг с другом и гладкими поверхностями получили пристальное внимание со стороны исследователей (см. [12–14] и цитированную там литературу). Однако практически важная задача о роли связей в локализации изгибов гидростатически сжатой оболочки на начальной (нелинейно-упругой) стадии ее деформирования, возможности управления процессом изменения формы оболочки до сих пор не изучены.

В [15–17] предложены упрощенные модели, описывающие начальную нелинейно-упругую стадию изменения формы поперечного сечения оболочки в условиях внешнего гидростатического сжатия. С их помощью выполнен качественный анализ роли ограничивающей оболочку полости и внутренних оправок с подходящими сечениями для преобразования круговых оболочек в полые изделия. Показано, что даже при большом различии сечений оболочки и внутренней оправки можно избежать образования жестких ребер на поверхности требуемого изделия, если внешней полостью ограничить амплитуду нежелательных складок на ранних стадиях гофрирования поперечного сечения оболочки [17]. После контакта с внешней полостью дальнейшие изменения формы оболочки с ростом давления сильно замедляются. Поэтому варьируя давление в конечном интервале можно управлять изгибами оболочки в угловых точках ее сечения. Теоретические расчеты показывают, что с ростом давления в вершинах выпуклостей на поверхности оболочки происходит концентрация внутренних напряжений и последующее локальное течение материала так, что в результате получаются изделия в форме правильных многогранников или полых деталей с переменным радиусом (рис. 1, b).

В настоящей работе в рамках упрощенных моделей [15–17] мы изучим начальную нелинейно-упругую стадию получения гидростатическим сжатием из трубных заготовок зубчатых деталей (рис. 1, a). В разделе 2 приведены основные уравнения и их аналитические решения, необходимые для описания изменений формы круговой оболочки. В разделе 3 обсуждаются методы численного моделирования и полученные результаты. Найдены параметры внутренней оправки, необходимой для преобразования первоначально круговой оболочки в зубчатую деталь без жестких складок и ребер на поверхности.

2. Формулировка нелинейно-упругой модели, основные соотношения. Деформирование свободных оболочек. Пусть в недеформированном состоянии срединная линия поперечного сечения оболочки имеет радиус $R$, а при деформировании описывается плоской кривой ${\mathbf{r}}{\text{(}}s{\text{)}} = \left( {x{\text{(}}s{\text{)}},y{\text{(}}s{\text{)}},0} \right)$. Поскольку при изгибах оболочки в главном приближении сохраняются расстояния между точками срединной линии, натуральный параметр кривой s изменяется в интервале $\left[ {0;2\pi R} \right]$. Единичные векторы касательной и нормали к поверхности оболочки имеют вид

Угол ${\Phi (}s{\text{)}}$ между касательной к кривой ${\mathbf{r}}{\text{(}}s{\text{)}}$ и осью $Ox$ связан с кривизной сечения ${\tilde {\kappa }}$: ${\tilde {\kappa }} = - d{\Phi /}ds$.

В подходе Коссера взаимодействие частей поверхности тонкой оболочки осуществляется силами и изгибающими моментами, распределенными по линиям их раздела [10]. Рассмотрим элемент оболочки, заключенный в окружном направлении между радиус-векторами ${\mathbf{r}}\left( {s + {\text{d}}s} \right)$ и r(s). Материал, расположенный при значениях $\tilde {s} \geqslant s$ + ds, оказывает воздействие на выделенный элемент результирующей контактной силой ${\mathbf{q}}(s + {\text{d}}s)$ и изгибающим моментом ${\mathbf{m}}\left( {s + {\text{d}}s} \right) = m\left( {s + {\text{d}}s} \right){\mathbf{k}}$, а материал со стороны $\tilde {s} \leqslant s$ воздействует силой $ - {\mathbf{q}}\left( s \right)$ и моментом $ - {\mathbf{m}}\left( s \right) = - m\left( s \right){\mathbf{k}}$. Здесь единичный вектор ${\mathbf{k}} = \left( {0,~0,~1} \right)$ параллелен оси оболочки. Внешнее давление p < 0 всегда направлено по нормали к поверхности оболочки. Поэтому на рассматриваемый элемент оболочки действует сила $p{\mathbf{n}}{\text{d}}s$. Если оболочка достаточно тонка, то величина изгибающего момента хорошо описывается материальным уравнением Эйлера–Бернулли–Клебша:

Здесь ${\gamma }$ – коэффициент пропорциональности. Приближение (2.2) при условии ${\tilde {\kappa }}~h \ll 1$ (h – толщина оболочки) совпадает с соотношением традиционной геометрически нелинейной теории упругих оболочек [1, 13] и хорошо обосновано в нелинейной теории выпучивания колец [18]. В линейной теории оболочек коэффициент пропорциональности

где E – модуль Юнга, ${\nu }$ – коэффициент Пуассона. Физическую нелинейность материала, в частности, его упруго-пластические свойства, часто учитывают перенормировкой упругих модулей [1]. Далее будем рассматривать ${{{\gamma }}_{0}}$ как феноменологический параметр модели. В приближении (2.2) мы получим точные решения задачи и установим ключевые особенности деформирования оболочек при наличии связей. В результате выявим возможности управления изменением формы оболочки в условиях внешнего гидростатического сжатия.

Уравнения равновесия оболочки имеют вид [10]:

Учитывая, что вектор силы допускает разложение ${\mathbf{q}} = {{q}_{n}}{\mathbf{n}} + {{q}_{\tau }}{\mathbf{\tau }}$, из системы (2.4) выражаем напряжения $T$ сжатия материала вдоль направления ${\mathbf{\tau }}$ и сдвиговые напряжения $N$ вдоль нормали ${\mathbf{n}}$ через кривизну сечения оболочки:

где ${{q}_{0}}$ – постоянная интегрирования. Здесь и далее используются безразмерные переменные: ${\theta } = s{\text{/}}R$ ($0 \leqslant {\theta } \leqslant 2{\pi }$), ${\kappa } = {\tilde {\kappa }}R$

Условия равновесия сводятся к уравнению для расчета кривизны:

где ${{l}_{0}}$ – еще одна постоянная интегрирования. Физически содержательные решения уравнения (2.6) (однозначные, без самопересечения срединной линии и замкнутых петель) получаются только тогда, когда полином четвертой степени в правой части имеет два вещественных корня $a$ и $b$ и два комплексно сопряженных корня $c = {{b}_{1}} + i{{a}_{1}}$ и $c{\text{*}} = {{b}_{1}} - i{{a}_{1}}$. Корни полинома связаны с параметрами уравнения: где $b < a < - b$. Явное решение уравнения (2.6) имеет вид [19]: где ${\chi } = {\theta /}\left( {2g} \right)$, ${{A}^{2}} = {{\left( {a - {{b}_{1}}} \right)}^{2}} + a_{1}^{2}$, ${{B}^{2}} = {{\left( {b - {{b}_{1}}} \right)}^{2}} + a_{1}^{2}$, $g = {{\left( {AB} \right)}^{{ - 1/2}}}$. Модуль эллиптических функций Якоби определяется выражением

Допустимые значения кривизны ${\kappa } \in \left[ {b,a} \right]$, параметр b всегда отрицателен. Точки ${\theta }$, в которых ${\kappa }\left( {\theta } \right) = b\left( p \right)$, соответствуют вершинам наиболее ярко выраженных выпуклостей на поверхности оболочки. В зависимости от давления параметр a может быть как отрицательным, так и положительным. Точки ${\theta }$, в которых ${\kappa }\left( {\theta } \right) = a\left( p \right) < 0$, определяют вершины меньших по амплитуде выпуклостей на поверхности оболочки. Точки, где ${\kappa }\left( {\theta } \right) = a\left( p \right) > 0$, соответствуют дну впадин, которые с ростом давления появляются на поверхности оболочки. Особенно интересен случай a(p) = 0. При таких давлениях на поверхности оболочки формируются плоские грани, и ее сечение приобретает вид правильного многоугольника со скругленными вершинами. Образование плоских граней на поверхностях гидростатически сжатых оболочек наблюдается экспериментально [1]. Традиционная теория оболочек не дает их описания.

Интегрирование уравнения 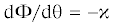определяет угол ${\Phi }\left( {\theta } \right)$ в терминах эллиптических функций и интегралов [15, 16]:

Здесь ${\text{sd}}\left( {x,k} \right) = {\text{sn}}\left( {x,k} \right){\text{/dn}}\left( {x,k} \right)$, и ${\Pi }(x,~{{{\alpha }}^{2}},k)$ – полный эллиптический интеграл третьего рода [19]:

с модулем $k$ и параметром ${{{\alpha }}^{2}} = - {{\left( {A - B} \right)}^{2}}{\text{/}}\left( {4AB} \right) < 0$. Постоянная, появляющаяся при интегрировании, определяет положение луча в плоскости $xOy$, от которого отсчитывается фаза Φ(θ). В формуле (2.8) постоянная интегрирования выбрана так, что ${\Phi }({\theta } = 0)$ = 0, тогда луч совпадает с осью $Ox$ декартовой системы координат и проходит через вершину выпуклости на поверхности свободной оболочки.

По известному углу численное интегрирование первого уравнения (2.1) дает срединную линию сечения оболочки в зависимости от величины внешнего давления. Для свободной оболочки три параметра задачи $a$, $b$, ${{a}_{1}}$ фиксируются дополнительными условиями. Кривизна срединной линии должна быть одинаковой при ${\theta } = 0$, 2π. Это требование приводит к первому ограничению на параметры решения:

где $K(k)$ – полный эллиптический интеграл первого рода [19], параметр $n$ определяет число выпуклостей в сечении оболочки после потери ею устойчивости формы. Чтобы кривая ${\mathbf{r}}({\theta })$ не имела петель, функция ${\Phi }({\theta })$ должна получать приращение 2π при изменении аргумента ${\theta }$ от 0 до 2π. Это условие приводит ко второму ограничению: где ${\Lambda }\left( {{\beta },k} \right)$ – лямбда-функция Хеймана [19], ${\beta } = \arcsin \frac{{2\sqrt {AB} }}{{A + B}}$. Третье ограничение на параметры задачи дает последнее уравнение (2.7).

На начальной (нелинейно-упругой) стадии изменения формы оболочки образование узоров из выпуклостей на ее поверхности обусловлено балансом эффектов нелинейности и дисперсии. Нелинейные взаимодействия приводят к локализации деформаций, а эффекты дисперсии способствуют их расплыванию. Приближение линейной теории соответствует случаю, когда параметры $a$ и $b$ близки друг к другу и кривизне ${\kappa } = - 1$ недеформированного сечения. В [15, 16] показано, что гофрирование оболочки начинается, когда внешнее давление превышает пороговое значение:

Если для для ${{{\gamma }}_{0}}$ использовать выражение (2.3), то давление (2.11) совпадает с критической нагрузкой по линейной теории [1].

В [15, 16] проанализированы возможные равновесные сечения свободной оболочки в зависимости от величины внешнего давления. Каждое из равновесных состояний оболочки существует в определенном интервале давлений. Меньшие давления соответствуют меньшему числу выпуклостей в поперечном сечении оболочки. Нелинейность задачи проявляется в том, что интервалы давлений, в которых возможно существование разных равновесных решений модели, могут перекрываться. Наиболее распространенный подход при анализе изменений формы нагруженных стержней состоит в рассмотрении набора возможных статических конфигураций и изучении с помощью энергетических принципов бифуркаций между ними (см. монографии [1, 10] и ссылки, приведенные там). Для гидростатически сжатой оболочки величина

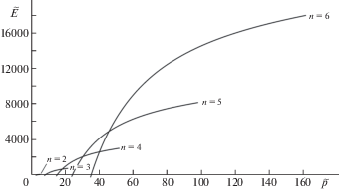
играет роль плотности энергии. Поэтому давление ${{p}_{{\text{c}}}}$, при котором возможен переход между состояниями оболочки с $n$ и n + 1 выпуклостями определяется условием:

Расчеты показывают, что диапазоны давлений, при которых образуются состояния с двумя и тремя выпуклостями на поверхности оболочки, не перекрываются между собой (рис. 2, $\tilde {p} = \left| p \right|{{R}^{3}}{\text{/(}}{{{\gamma }}_{0}}{{h}^{3}}{\text{)}}$). Поэтому переход между такими состояниями затруднен. Переход их состояния n = 3 в состояние n = 4 возможен при относительно небольшом внешнем давлении ${{p}_{{\text{c}}}}$. С ростом давления возможна последовательность переходов между состояниями оболочки с разным числом выпуклостей $n$. При достаточно малой скорости изменения давления оболочка из состояния с n = 3 будет последовательно переходить в состояния $n = 4$,$5$,$6$,… В то же время, при большей скорости изменения давления оболочка после перехода между состояниями n = 3 и n = 4 может сразу перейти в состояние n = 6. Из графиков на рис. 2 следует, что во втором случае полные приращения давления и энергии системы оказываются меньше, чем в первом. Достаточное условие устойчивости стационарного состояния ${\kappa } = {{{\kappa }}_{0}}$ – положительная определенность второй вариации плотности энергии (2.12). Конфигурация ${{{\kappa }}_{0}}$ устойчива, если

Численные расчеты показывают, что это неравенство выполняется во всем диапазоне допустимых давлений для конфигураций с параметром $n = 2,3 \ldots 6$.

Образование при определенных условиях на поверхности круговой оболочки плоских граней указывает на принципиальную возможность создания новых технологий получения методом гидростатического сжатия из трубных заготовок призматических полых изделий. Однако одним только гидростатическим сжатием из круговой оболочки трудно получить изделие с плоскими гранями и заданным многоугольником в сечении. Необходимый результат достигается при вполне определенной величине внешнего давления, которое согласовано со скоростью нагружения оболочки и ее размерами. В работах [3, 4] экспериментально найдены пути преодоления этой трудности. Оказывается, развитием локальных неустойчивостей на поверхности оболочки можно управлять посредством введения подходящих внешних связей.

3. Деформирование оболочки на оправках. Экспериментально управление деформированием оболочки достигалось с помощью двух основных связей: внешней ограничивающей оболочку полости и жесткого стержня с заданным сечением внутри оболочки [3, 4]. Учет связей при теоретическом описании изменения формы оболочки осуществляется через краевые условия для упрощенных моделей. Это дает зависимость параметров $a$, $b$, ${{a}_{1}}$, а вместе с ними кривизны поперечного сечения оболочки, от величины внешнего давления $\left| p \right|$ и числа выпуклостей n на поверхности оболочки. По известной кривизне конечная форма оболочки восстанавливается методами дифференциальной геометрии. Анализ, выполненный в [15, 16], показывает, что совместное использование двух связей открывает широкие возможности для контролирования изменений формы оболочки при ее гидростатическом сжатии. В то же время, внутренняя оправка играет ведущую роль. Конструкция установки и ее геометрические размеры должны быть таковы, чтобы деформируемая оболочка вначале касалась внутреннего стержня, а лишь затем внешней полости.

В экспериментах [3, 4] зубчатые изделия получены из круговых оболочек без использования внешней оправки. Для управления процессом деформирования внутрь оболочки помещался призматический стержень с $n$ чередующимися выпуклостями и углублениями в сечении. Проанализируем эту задачу в рамках упрощенной нелинейной модели.

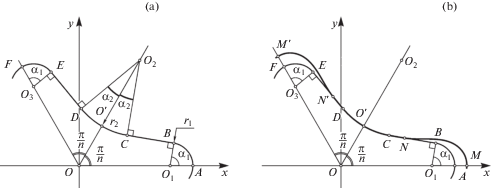
Пусть поперечное сечение призматического стержня имеет вид фигуры определенного порядка симметрии $n$ (рис. 3,a). В плоскости $xOy$, перпендикулярной оси стержня, вершины его выпуклостей опишем дугами окружностей радиуса ${{r}_{1}}$ и ${{r}_{2}}$ (${{O}_{1}}A = {{O}_{1}}B$ = r₁, ${{O}_{2}}C = {{O}_{2}}D = {{r}_{2}}$). Экспериментально установлено [3, 4], что наличие скругленных вершин обеспечивает проскальзывание оболочки вдоль поверхности оправки. В результате стабилизируется равновесное состояние оболочки с $n$ выпуклостями на поверхности. Кроме того, это позволяет избежать образования складок на поверхности оболочки вдоль пологих граней стержня. В упрощенной модели мы не описываем динамику проскальзывания, а обсуждаем только равновесные конфигурации оболочки, которые меняются с ростом давления.

Дуги радиусов ${{r}_{1}}$ и ${{r}_{2}}$ опираются на центральные углы $2{{{\alpha }}_{1}}$ и $2{{{\alpha }}_{2}}$ соответственно (угол $A{{O}_{1}}B = {{{\alpha }}_{1}}$, угол $C{{O}_{2}}O{\kern 1pt} ' = {{{\alpha }}_{2}}$). Вершины углов $2{{{\alpha }}_{1}}$ и $2{{{\alpha }}_{2}}$ удалены на расстояния ${{h}_{1}} = O{{O}_{1}}$ и ${{h}_{2}} = O{{O}_{2}}$ от начала декартовой системы координат. Соседние дуги соединяются прямолинейными отрезками $CB$ и $DE$ длиной ${{l}_{0}}$. В точках соединения отрезки перпендикулярны радиусам соответствующих окружностей. В такой геометрии углы ${{{\alpha }}_{1}}$ и ${{{\alpha }}_{2}}$ связаны между собой: ${{{\alpha }}_{1}} = {{{\alpha }}_{2}} + {\pi /}n$. Благодаря симметрии оправки, достаточно указать параметризацию части $ABCO{\kern 1pt} '$ ее границы:

где угол $\vartheta $ выражается через натуральный параметр $l$ кривой $ABCO{\kern 1pt} '$: $\vartheta = l{\text{/}}{{r}_{1}}$, $0 \leqslant l \leqslant {{\alpha }_{1}}{{r}_{1}}$;

Угол ${\varphi } = {{{\alpha }}_{1}} - {\Delta }l~{\text{/}}{{r}_{2}}$, где ${\Delta }l = l - {{{\alpha }}_{1}}{{r}_{1}} - {{l}_{0}}$, $0 \leqslant {\Delta }l \leqslant {{{\alpha }}_{2}}{{r}_{2}}~$. Натуральный параметр кривой $ABCO'$ меняется в пределах $0 \leqslant l \leqslant {{l}_{0}} + {{{\alpha }}_{1}}{{r}_{1}} + {{{\alpha }}_{2}}{{r}_{2}}$. Параметры ${{h}_{{1,2}}}$, ${{l}_{0}}$, ${{r}_{{1,2}}}$, ${{{\alpha }}_{2}}$ не могут быть произвольными. Из рис. 3,a следуют геометрические связи:

Угол ${{{\alpha }}_{1}} \in \left[ {{\pi /}n,{\pi }} \right]~$ вместе с параметрами ${{{\alpha }}_{2}}$, ${{r}_{{1,2}}}$, ${{l}_{0}}$ выбираются так, чтобы величины ${{h}_{{1,2}}}$ оставались положительными. При численном моделировании форму оправки удобнее менять, варьируя независимые параметры ${{h}_{{1,2}}}$, ${{r}_{{1,2}}}$. Если из оболочки толщиной $h$ необходимо получить зубчатое изделие с одинаковыми радиусами углублений и выпуклостей, то следует выбрать ${{r}_{1}} = {{r}_{0}} - h$, ${{r}_{2}} = {{r}_{0}} + h$. Дно углубления и вершина выпуклости в сечении стержня удалены от центра сечения соответственно на расстояния ${{R}_{h}} = {{h}_{2}} - {{r}_{2}}$, ${{R}_{b}} = {{h}_{1}} + {{r}_{1}}$. Отсюда находим высоту зубца оправки:

где согласно (3.1) параметры ${{l}_{0}}$ и ${{{\alpha }}_{1}}$ суть функции от ${{h}_{1}}$, $~{{h}_{2}}$, $~{{r}_{1}}$, $~{{r}_{2}}$. Меняя значения параметров ${{h}_{{1,2}}}$, ${{r}_{{1,2}}}$ можно смоделировать все оправки, использованные в экспериментах [3, 4] по управлению изменением формы оболочки, включая (при ${{r}_{2}} = 0$, ${{{\alpha }}_{1}} = {\pi /}n$) призматический стержень с сечением в виде правильного многоугольника со скругленными вершинами [17].

Напомним, что для свободной оболочки, натуральный параметр $s$ срединной линии сечения оболочки отсчитывается от точки M $(~{{s}_{M}} = 0$) пересечения кривой ${\mathbf{r}}(s)$ с осью $Ox$ (рис. 3,b). Tочка M совпадает с вершиной выпуклости, которая образуется на поверхности оболочки при ее свободном деформировании. Тогда точке $O{\kern 1pt} '$ первого касания оболочки с внутренней призмой при давлении ${{\tilde {p}}_{{\text{t}}}}$ будет соответствовать параметр ${{s}_{{O{\kern 1pt} '}}} = {\pi }R{\text{/}}n$. Следовательно, ${{\tilde {p}}_{{\text{t}}}}$ является корнем уравнения:

где ${\mathbf{r}}(s)$ – срединная линия свободной оболочки. После касания оболочки с внутренней оправкой уравнения, описывающие форму оболочки, должны быть изменены. Приведем основные уравнения, которые позволят изучить нелинейно-упругое деформирование оболочки вокруг зубчатой оправки.

При $p > {{p}_{{\text{t}}}}$ c ростом давления оболочка прижимается к поверхности зубчатого стержня (участок $NN{\kern 1pt} '$ на рис. 3,b). При этом точки касания оболочки и стержня $N$, $N{\kern 1pt} '$ перемещаются вдоль поверхности оправки. В точке $N$ параметры l и s связаны между собой через длину отрезка $O{\kern 1pt} 'N$:

В силу симметрии задачи достаточно описать равновесные состояния участка $MN$ сечения оболочки при $s \in \left[ {0,{{s}_{N}}} \right]$. На этом участке оболочка свободна, поэтому фаза Φ(s), как и ранее, определяется формулой (2.8). Интегрирование первого уравнения (2.1) дает координаты сечения оболочки для $s \in \left[ {0,{{s}_{N}}} \right]$:

Параметры $a$, $b$, ${{a}_{1}}$, ${{l}_{N}}$ определяются граничными условиями. Требование совпадения касательных к сечению оболочки и оправки в точке N приводит к первому из них:

Второе ограничение на параметры следует из геометрической связи $y({{s}_{N}}) = {{y}_{p}}({{l}_{N}})$ или

Там, где оболочка огибает зубчатый стержень, вдоль направления нормали ${\mathbf{n}}$ внешнее давление скомпенсировано реакцией связи, поэтому в материале оболочки в точке $N$ имеем 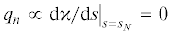. Иными словами, точка $N$ соответствует минимуму кривизны кривой ${\mathbf{r}}\left( s \right)$: ${\kappa (}{{s}_{N}}{\text{)}} = a$. Это приводит к третьему уравнению для расчета параметров задачи:

Как и в случае свободной оболочки, выражение (2.7) связывает параметры ${{a}_{1}}$, $a$, b с величиной внешнего давления. Замкнутая система четырех уравнений (2.7), (3.4)–(3.6) определяет величины $a$, $b$, ${{a}_{1}}$, ${{l}_{N}}$ как функции от давления $\left| p \right|$ и геометрических параметров связи ${{{\mathbf{r}}}_{p}}\left( l \right)$.

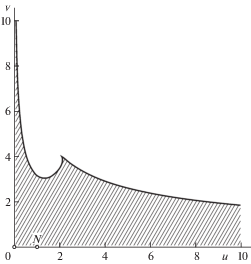
4. Методы численных расчетов и анализ результатов. Для численного моделирования изменений формы свободной оболочки до ее касания со стержнем удобно ввести переменные $u$ и $v$: $a = - u + v$; $b = - u - v$. Параметры $A$, $B$, $b$, ${{k}^{2}}$ также выражаются через $u$, $v$, поэтому уравнения (2.9), (2.10) фиксируют $u$, $v$. По заданным $u$, $v$ и обезразмеренному давлению $\tilde {p} = \left| p \right|{{R}^{3}}{\text{/(}}{{{\gamma }}_{0}}{{h}^{3}}{\text{)}}$ из (2.7) находим параметр ${{a}_{1}}$.

Неравенства $b < 0$, $b < a < - b$, $0 \leqslant {{k}^{2}} \leqslant 1$ выделяют область возможных значений $u$, $v$ в первом квадранте $u,v$-плоскости (на рис. 4 она заштрихована). Форма области качественно не меняется при разных допустимых давлениях. Параметры $u$, $v$ находятся методом Ньютона. Система (2.7), (2.9), (2.10) разрешима при пороговых давлениях (см. уравнение (2.11)) $~\tilde {p} \approx {{\tilde {p}}_{{{\text{lin}}}}} = {{n}^{2}} - 1$, где $n \geqslant 2$, и дает начальные значения параметров $\left( {{{u}_{0}},\;{{v}_{0}}} \right)$ в малой окрестности точки $N = (1,0)$ для итеративного алгоритма. Последовательными приближениями по давлению можно определить все равновесные конфигурации оболочки в промежутке ${{\tilde {p}}_{{\text{t}}}} \geqslant \tilde {p} > {{\tilde {p}}_{{{\text{lin}}}}}$ до момента касания оболочки с внутренней оправкой при давлении ${{\tilde {p}}_{{\text{t}}}}$, которое определяем из уравнения (3.2) численным методом бисекции. Значения параметров ${{u}_{{\text{t}}}}$, ${{v}_{{\text{t}}}}$, соответствующие давлению $\tilde {p} = {{\tilde {p}}_{{\text{t}}}}$, удовлетворяют также уравнениям (3.3)–(3.6) и служат начальными данными итеративного алгоритма для решения системы (2.7), (3.3)–(3.6) и определения формы оболочки в интервале давлений ${{\tilde {p}}_{*}} \geqslant \tilde {p} \geqslant {{\tilde {p}}_{{\text{t}}}}$ после ее касания с оправкой. На конечных этапах деформирования оболочки на ее боковой поверхности вблизи вершин выпуклостей обычно образуются волновые складки из лишнего материала при давлении $\tilde {p} = {{\tilde {p}}_{*}}$.

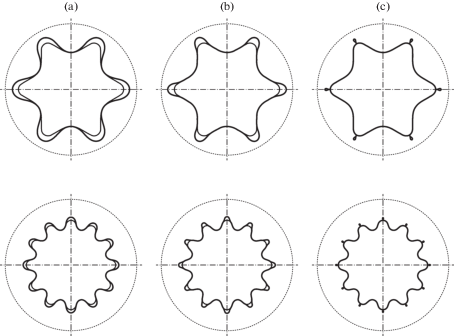
На рис. 5 приведены решения, иллюстрирующие изменения формы сечения оболочки на оправке зубчатого профиля при разных значениях внешнего давления для двух случаев: n = 6, ${{h}_{1}} = 0.7R$, ${{r}_{1}} = 0.1R$, ${{h}_{2}} = 0.823R$, ${{r}_{2}} = 0.26R$ и $n = 12$, ${{h}_{1}} = 0.605R$, ${{r}_{1}} = 0.075R$, ${{h}_{2}} = 0.63R$, ${{r}_{2}} = 0.08R$. Рассматривался наиболее важный случай, когда оболочка вначале касалась углублений жесткого стержня (левые фигуры на рис. 5, $\tilde {p} = 56.01$ и $\tilde {p} = 274.75$ соответственно). Подбором геометрических параметров оболочки и оправки необходимо удовлетворить этому ограничению. Тогда при дальнейшем росте давления оболочка будет огибать зубцы внутренней оправки (центральные фигуры, $\tilde {p} = 556.01$ и $\tilde {p} = 8275$) пока не придет в конечное состояние с образованием складок в вершинах выпуклостей (правые фигуры, $\tilde {p} = 11200$ и $\tilde {p} = 78800$). Если периметры сечений оболочки и внутреннего стержня сильно отличаются, то складки превращаются в жесткие ребра, которые не устраняются даже при дальнейшем росте давления. Давление ${{\tilde {p}}_{*}}$, при котором происходит смыкание свободных участков сечения оболочки в единственной точке (рис. 5, правые фигуры), является для этой задачи предельным. Алгоритм поиска ${{\tilde {p}}_{*}}$ для рассматриваемого случая принципиально не отличается от задачи о предельной конфигурации свободной оболочки [15, 16].

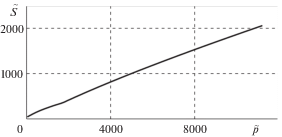
Численные расчеты показывают, что результирующая интенсивность напряжений S = $\sqrt {{{T}^{2}} + {{N}^{2}}} $ (см. (2.5)) достигает максимума в вершинах выпуклостей в точках $M$ и $M{\kern 1pt} '$ на рис. 3, причем исключительно за счет компоненты $T$. На рис. 6 приведена зависимость максимального значения результирующего напряжения $\tilde {S}$ от внешнего давления $\tilde {p}$ для конфигурации рис. 5,а. Здесь $\tilde {N} = {{\left( {R{\text{/}}h} \right)}^{2}}~\left( {N{\text{/}}{{{\gamma }}_{0}}} \right)$, $\tilde {T} = {{\left( {R{\text{/}}h} \right)}^{2}}~\left( {T{\text{/}}{{{\gamma }}_{0}}} \right)$, $\tilde {S} = \sqrt {{{{\tilde {T}}}^{2}} + {{{\tilde {N}}}^{2}}} $.

Из-за наличия внутренней оправки интенсивность напряжений в вершинах выпуклостей в 20–30 раз больше, чем таковая для предельных состояний свободных оболочек. При условии $S \geqslant {{{\sigma }}_{s}}$, где ${{{\sigma }}_{s}}$ – предел текучести материала оболочки, в вершинах выпуклостей начнется пластическое деформирование оболочки. Из геометрических соображений следует, что волновые складки с амплитудой, не превышающей величину порядка ${\zeta }h$, где $h$ – толщина оболочки, $0 < {\zeta } < 3$, не могут образовать заметных ребер. С ростом давления они будут растекаться по поверхности оправки из-за пластического течения материала оболочки. В конечно счете образец сохранит полезную форму зубчатого изделия даже после сброса давления. Сформулированное утверждение соответствует экспериментальным данным по управлению деформированием оболочек из малоуглеродистых сталей [3, 4]. Экспериментально установлено, что зубчатые детали получаются, когда периметр сечения оправки составляет долю ${\eta } = 0.85$ от периметра оболочки.

Для упрощения расчетов мы пренебрегли толщиной оболочки $h$. С учетом толщины радиус срединной линии первоначального сечения оболочки $\bar {R}$ отличается от $R$: $\bar {R} = R + h{\text{/}}2$. Когда периметр сечения оправки составляет долю $0 < {\eta } < 1$ от периметра оболочки, справедливо равенство:

Отсюда получаем связь расчетного радиуса оболочки с параметрами оправки:

Примеры рис. 5 с отношениями ${\eta } = 0.8$ и ${\eta } = 0.84$ для n = 6 и n = 12, соответственно, удовлетворяют этому выражению и хорошо согласуются с экспериментальным значением ${\eta } \approx 0.85$ [3].

5. Заключение. В данной работе интегрируемые нелинейные модели типа Коссера использованы для теоретического описания больших нелинейно-упругих деформаций круговых оболочек. Исследованы возможности производства из трубных заготовок зубчатых изделий при использовании одной только внутренней оправки.

Установлено, что из-за наличия оправки с ростом внешнего давления происходит значительная концентрация внутренних напряжений вблизи вершин выпуклостей на поверхности оболочки (при высоких давлениях они вызывают пластическое течение материала в вершинах детали). Проанализированы условия образования не устранимых с ростом давлении жестких складок на поверхности оболочки. Показана возможность управления гофрированием оболочки вдоль пологих частей ее сечения и подавления нежелательных складок в вершинах зубцов изделия путем согласования геометрических размеров и периметров оболочки и оправки.

Полученные результаты качественно объясняют имеющиеся экспериментальные данные. Сформулированные в работе общие принципы важны для развития новых технологий производства полых изделий из трубных заготовок с минимальными временными, материальными и энергетическими затратами.

Авторы признательны Б.И. Каменецкому за полезные стимулирующие обсуждения.

Работа выполнена в рамках государственного задания Министерства науки и высшего образования России (тема “Квант”, номер г. р. 01201463332 (АААА-А18-118020190095-4)).