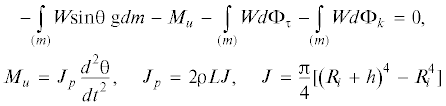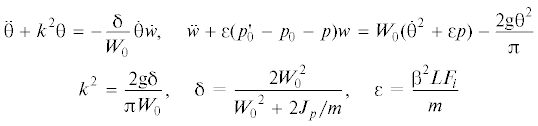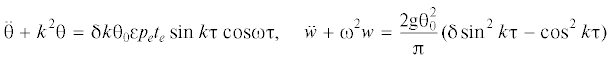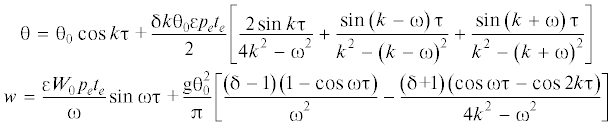1. На главную
  2. Электронные версии
  3. Известия РАН. Механика твердого тела
  4. № 6, 2019

Известия РАН. Механика твердого тела, 2019, № 6, стр. 76-84

ПРОСТРАНСТВЕННЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ ТРУБОПРОВОДА ПРИ ДЕЙСТВИИ ВНУТРЕННЕГО УДАРНОГО ДАВЛЕНИЯ

М. М. Шакирьянов *

Институт механики Уфимского федерального исследовательского центра РАН
Уфа, Россия

* E-mail: shakmar9@mail.ru

Поступила в редакцию 09.01.2019
После доработки 09.01.2019
Принята к публикации 30.01.2019

Полный текст (PDF)

Аннотация

Изучены пространственные нелинейные колебания участка трубопровода, находящегося по концам на опорах. Труба, изогнутая собственным весом и постоянным давлением заключенной в ней жидкости, подвергается гидравлическому удару. Используется модель изгибно-вращательных движений трубопровода. Учитываются силы гравитации и силы инерции Кориолиса, взаимодействие внутреннего давления и изменения кривизны осевой линии трубы. Колебательные движения трубопровода описываются системой двух нелинейных дифференциальных уравнений. Рассматривается первая форма колебаний. Для приближенного анализа динамики деформирования трубопровода вводятся в рассмотрение инерционная и инерционно-упругая стадии по времени. На первой стадии учитываются только давление в жидкости и инерционные силы. Вторая стадия изгибно-вращательных движений трубопровода является продолжением ее инерционной стадии. В конце первой стадии действие ударной нагрузки прекращается. Задача Коши с нулевыми начальными условиями решается также численным методом Рунге–Кутта. Дается сравнение результатов приближенного аналитического и численного решений. Изменения прогиба середины пролета и угла поворота стального трубопровода представлены в зависимости от времени для разных амплитуд динамического давления.

Ключевые слова: трубопровод, внутреннее среднее и ударное давление, пространственные колебания, инерционная и инерционно-упругая стадии деформации

1. Введение. Изучение пространственных колебаний трубопровода имеет практический интерес ввиду их частого возбуждения в трубопроводных системах.

Общие вопросы механики трубопроводов и шлангов рассмотрены в [1] и других изданиях. Статический изгиб и устойчивость трубы при действии внутреннего перепада давления теоретически и экспериментально изучались в [2, 3]. Колебания упругих оболочек, содержащих жидкость и газ, исследованы в [4]. Свободные колебания участка трубопровода и их свойства рассмотрены в [5–7].

Теоретическое и экспериментальное исследование вынужденных и параметрических изгибных колебаний трубы с внутренним потоком жидкости проведено в [8–11]. Влияние внешнего и внутреннего воздействия на изгибные колебания трубы, транспортирующей жидкость со сверхкритической скоростью, изучено в [12–14]. Исследование колебаний трехслойного трубопровода для транспортировки газа приведено в [15]. Нелинейная динамика трубопровода, заполненного сжимаемой средой, рассмотрена в [16, 17]. Сейсмические колебания трубопровода с жидкостью в грунтовой среде исследованы в [18, 19]. В [20–22] изучена нелинейная динамика консольного трубопровода, транспортирующего жидкость.

Пространственные колебания трубопровода в сплошной среде при действии внутреннего давления, изменяющегося по гармоническому закону, рассмотрены в [23–25]. В [26] представлен широкий обзор литературы, посвященной исследованию динамического взаимодействия трубопроводных систем с транспортируемой жидкостью. Упругая реакция трубы на внутреннее ударное давление рассмотрена в [27, 28]. Предложенная в [28] процедура аналитического решения задачи позволяет учитывать реальное изменение ударного давления по времени.

В настоящей работе исследуются пространственные нелинейные колебания участка трубопровода со скользящей опорой при действии внутреннего ударного давления.

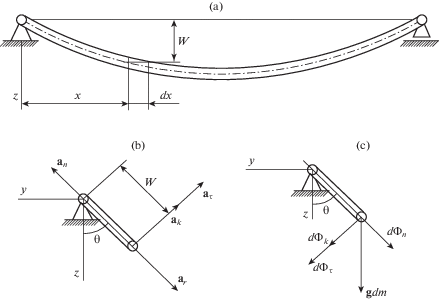
2. Постановка задачи. Рассматриваются пространственные колебания трубопровода и заключенной в нем идеальной несжимаемой жидкости относительно горизонтальной оси, проходящей через опоры, при действии внутреннего ударного давления. Крепления трубы на опорах – шарнирные. Одна из опор является неподвижной, а другая – может свободно смещаться в продольном направлении. Обе опоры допускают свободный поворот трубы вокруг оси. Расчетная схема трубопровода представлена на рис. 1,a. Длина, внутренний радиус, толщина стенки и плотность материала трубы обозначены через L, Ri, h и ρ, плотность заполняющей трубу жидкости – через ρ0. Труба, изогнутая под действием собственного веса и постоянного давления p0 заключенной в ней жидкости, находится в положении, отклоненном от вертикали на небольшой угол θ0. В момент времени t = 0 начинается его изменение без начальной угловой скорости, а также происходит гидравлический удар. В течение характерного времени te внутреннее давление pi в трубе становится равным сумме статической p0 и динамической p составляющих. Форма динамической составляющей давления по времени $t$ может быть разной, но по всей длине трубы устанавливается мгновенно в соответствии с моделью несжимаемой жидкости. Предполагается, что при деформировании ось трубопровода всегда находится в одной плоскости, совершающей повороты на угол θ.

Рис. 1

Поскольку деформации, связанные с выходом оси трубопровода из плоскости изгиба, предполагаются малыми, то в каждый момент времени пространственное движение трубопровода можно рассматривать как совокупность изгибных перемещений в одной плоскости и свободного поворота этой плоскости на угол θ вокруг оси x, проходящей через опоры. На рис. 1, a, b, c изображены прогиб W элемента трубы длиной dx и массой dm = π{ρ0$R_{i}^{2}$ + ρ[(Ri + h)2 – $R_{i}^{2}$]}dx, а также его ускорения и силы, действующие на него. Здесь g, ak, ar, aτ и an – гравитационное, кориолисово, относительное, переносные касательное и нормальное ускорения; gdm – сила тяжести, dΦr, dФτ, dФn и dФk – относительная, касательная, нормальная силы инерции и сила инерции Кориолиса.

Выражения для ускорений выделенного элемента, а также сил, приложенных к нему, приведены в [23]:

(2.1)
$\begin{gathered} {{{\mathbf{a}}}_{r}} = \frac{{{{\partial }^{2}}W}}{{\partial {{t}^{2}}}},\quad {{{\mathbf{a}}}_{\tau }} = W\frac{{{{d}^{2}}\theta }}{{d{{t}^{2}}}},\quad {{{\mathbf{a}}}_{n}} = W{{\left( {\frac{{d\theta }}{{dt}}} \right)}^{2}},\quad {{{\mathbf{a}}}_{k}} = 2\frac{{d\theta }}{{dt}}\frac{{\partial W}}{{\partial t}} \\ d{{\Phi }_{r}} = {{{\mathbf{a}}}_{r}}dm,\quad d{{\Phi }_{\tau }} = {{{\mathbf{a}}}_{\tau }}dm,\quad d{{\Phi }_{n}} = {{{\mathbf{a}}}_{n}}dm,\quad d{{\Phi }_{k}} = {{{\mathbf{a}}}_{k}}dm \\ \end{gathered} $

Дифференциальное уравнение вращательного движения трубопровода относительно оси x имеет вид

(2.2)

Дифференциальное уравнение изгибных колебаний трубы, учитывающее взаимодействие изменения кривизны ее осевой линии и внутреннего давления, сле-дующее [23]

(2.3)
$\frac{{{{\partial }^{2}}W}}{{\partial {{t}^{2}}}}dm = - EJ\frac{{{{\partial }^{4}}W}}{{\partial {{x}^{4}}}}dx - {{F}_{i}}{{p}_{i}}\frac{{{{\partial }^{2}}W}}{{\partial {{x}^{2}}}}dx + {\text{g}}\cos {\theta }dm + d{{\Phi }_{n}},\quad {{F}_{i}} = {\pi }R_{i}^{2}$

Здесь E – модуль Юнга материала трубы.

Функция прогиба трубопровода, удовлетворяющая условиям шарнирного крепления, принимается в виде

(2.4)
$W = \left[ {{{W}_{0}} + w(t)} \right]\sin \beta x,\quad \beta = \frac{\pi }{L}$

Первая часть (2.4) обусловлена действием собственного веса mg трубопровода с жидкостью и постоянного внутреннего давления p0, а вторая – добавочного динамического давления p.

Подставляя выражения (2.1), (2.4) в уравнения (2.2), (2.3) и применяя к последнему процедуру Бубнова–Галеркина, получаем нелинейные дифференциальные уравнения вращательных и изгибных колебаний трубопровода

(2.5)
${\ddot {\theta }}\left[ {\frac{{2{{J}_{p}}}}{m} + {{{\left( {{{W}_{0}} + w} \right)}}^{2}}} \right] + 2\left( {{\dot {\theta }}\dot {w} + \frac{{2{\text{g}}}}{{\pi }}\sin {\theta }} \right)\left( {{{W}_{0}} + w} \right) = 0$
(2.6)
$\ddot {w} + \frac{{{{{\beta }}^{{\text{4}}}}EJL}}{m}\left( {{{W}_{0}} + w} \right) = \frac{{4{\text{g}}}}{{\pi }}\cos {\theta } + \left( {{{W}_{0}} + w} \right){{{\dot {\theta }}}^{2}} + \frac{{{{{\beta }}^{{\text{2}}}}L{{F}_{i}}}}{m}\left( {{{p}_{0}} + p} \right)\left( {{{W}_{0}} + w} \right)$

Здесь и далее точки над буквами обозначают производные по времени t.

Начальные условия

(2.7)
${\theta = }{{{\theta }}_{0}}{\text{,}}\quad {\dot {\theta } = }0,\quad w = \dot {w} = 0,\quad (t = 0)$

Полагая в уравнении (2.6) ${ \theta = }{{{\theta }}_{0}}$, ${\dot {\theta }}(t){\text{ }} \equiv {\text{ }}0$, $w(t) \equiv 0$, $p \equiv 0$, определяем статическую составляющую прогиба середины пролета трубопровода. Имеем

(2.8)
${{W}_{0}} = \frac{{4{\text{g}}mL\cos {{\theta }_{0}}}}{{{{{\pi }}^{3}}({{{\beta }}^{{\text{2}}}}EJ - {{F}_{i}}{{p}_{0}})}}$

Из (2.8) видно, что его решение неограниченно возрастает при значении среднего давления

(2.9)
$p_{0}^{'} = \frac{{{{\pi }^{2}}EJ}}{{{{L}^{2}}{{F}_{i}}}}$

Значение давления (2.9) может быть названо критическим [23].

3. Приближенное аналитическое решение. Для приближенного анализа динамики начального процесса деформирования трубопровода введем в рассмотрение инерционную стадию, переходящую с течением времени в инерционно-упругую стадию свободных колебаний [27, 28]. На обеих стадиях угловое θ и изгибное w перемещения предполагаются малыми. Полагая в системе (2.5), (2.6) sinθ ≈ θ, cosθ ≈ 1 – θ2/2, $w{\text{/}}{{W}_{0}} \ll 1$ и учитывая равенство (2.8), имеем

(3.1)

Далее рассмотрим случай ступенчатого возрастания давления от значения ${{p}_{0}}$ в момент времени t = 0 до постоянной величины ${{p}_{0}} + {{p}_{e}}$ в интервале 0 < t < te и понижения давления до постоянного значения ${{p}_{0}}$ при t ≥ te. Для простоты время ${{t}_{*}}$ инерционной стадии процесса примем равным времени te ударной нагрузки.

На инерционной стадии деформирования учитываются только ударные и инерционные силы. Кроме того, на этой стадии перемещения и скорости остаются малыми. Поэтому из (3.1) имеем

(3.2)
${\ddot {\theta }} = 0,\quad \ddot {w} = {{W}_{0}}{\varepsilon }{{p}_{e}}$

Решение (3.2) с начальными условиями (2.7) следующее

(3.3)
${\theta } = {{{\theta }}_{0}},\quad w = \frac{{{\varepsilon }{{W}_{0}}{{p}_{e}}{{t}^{2}}}}{2}\quad {\text{(0 }} \leqslant t \leqslant {{t}_{e}})$

Из (3.3) видно, что изгибные перемещения и их скорости находятся в прямой зависимости от амплитуды переменной составляющей внутреннего давления в трубе.

На инерционно-упругой стадии деформирования (pe = 0 при t > te) трубопровод совершает свободные изгибно-вращательные движения под действием постоянного внутреннего давления, инерционных, упругих и гравитационных сил. Следовательно, на этой стадии первое уравнение системы (3.1) сохраняет свой вид, а во втором уравнении нужно исключить члены, содержащие p. Начальными условиями для этой системы служат функции и производные из (3.3) при t = te. Вводя время τ = t – te , имеем

(3.4)
${\theta } = {{{\theta }}_{0}},\quad {\dot {\theta }} = {\text{0,}}\quad w = {\varepsilon }{{W}_{0}}{{p}_{e}}t_{e}^{2}{\text{/}}2 \approx 0,\quad \dot {w} = {\varepsilon }{{W}_{0}}{{p}_{e}}{{t}_{e}},\quad {\text{(}}\tau {\text{ = 0)}}$

Важно отметить, что время te воздействия ударных волн в жидкостных и газовых средах имеет порядок 10–4–10–3 с [28]. Поэтому в третьем из условий (3.4) в конце гидравлического удара изгибное перемещение без заметной погрешности можно принять равным нулю.

Рассмотрим лишь колебательные движения трубопровода, когда среднее давление p0 в жидкости меньше критического давления (${{p}_{0}} < p_{0}^{'}$ ). Для решения системы нелинейных уравнений (3.1) при p = 0 воспользуемся методом последовательных приближений. При этом будем определять периодические решения. В первом приближении, пренебрегая нелинейными членами, имеем

(3.5)
${\ddot {\theta }} + {{k}^{2}}{\theta } = 0,\quad \ddot {w} + {{{\omega }}^{2}}w = 0,\quad {{{\omega }}^{2}} = {\varepsilon }(p_{0}^{'} - {{p}_{0}})$

Из (3.5) следует, что в линейном приближении вращательные и изгибные движения трубопровода являются независимыми. Решение (3.5) с учетом начальных условий (3.4) запишется

(3.6)
${\theta = }{{{\theta }}_{0}}\cos k{\tau ,}\quad w = \frac{{{\varepsilon }{{W}_{0}}{{p}_{e}}{{t}_{e}}}}{{\omega }}\sin {\omega \tau }$

Система уравнений второго приближения имеет вид

(3.7)

Периодическое решение задачи Коши (3.4), (3.7) следующее (ω ≠ 0, 2k)

(3.8)

Из сравнения решений (3.6) и (3.8) можно видеть, что в последнем присутствуют решения первого приближения и функции, учитывающие нелинейные члены.

4. Зависимость прогиба и угла поворота от динамического давления. Вычисления проводились для стального трубопровода длиной L = 8.5 м, внутренним радиусом Ri = = 0.06 м, толщиной стенки h = 0.003 м и модулем Юнга E = 2 × 105 МПа. Плотности материала трубы и заполняющей ее жидкости равны ρ = 7800 кг/м3 и ρ0 = 800 кг/м3. Гравитационное ускорение: g = 9.81 м/c2. Начальный угол отклонения плоскости изгиба трубопровода от вертикали: θ0 = 0.1 рад. Среднее внутреннее давление имеет только одно значение p0 = 0.7 МПа. При этом значение амплитуды W0 статической составляющей прогиба средней точки пролета трубы, согласно формуле (2.8), равно 0.0318 м. Приняты два значения амплитуды динамической составляющей ступенчатого внутреннего давления: pe = 2.8, 7.0 МПа. Продолжительность te действия ударной нагрузки принята равной 0.0055 с.

Продолжительность инерционной стадии определяется по приближенной формуле [28] $t_{*}^{{}} = {{L}^{2}}{\text{/}}({{\pi }^{2}}{{R}_{i}}c)$, где скорость волны растяжения–сжатия с = (E/ρ)1/2. Для принятых данных $t_{*}^{{}} \approx 0.024$ с. Поэтому время действия ударного давления меньше, чем продолжительность инерционной стадии (${{t}_{e}} < t_{*}^{{}}$). Это означает, что упругие силы в отрезке 0≤ t ≤ te еще меньше, чем при $t = t_{*}^{{}}$, а точность приближенного решения (3.4) повышается.

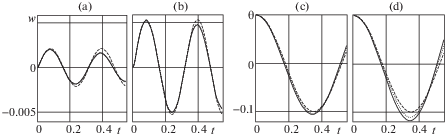
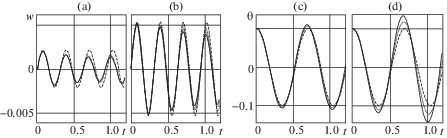
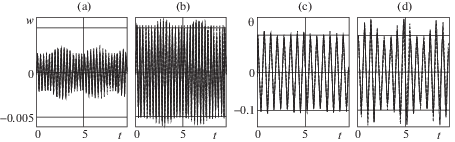
Результаты вычислений приведены в виде графических зависимостей (рис. 2–4) динамической составляющей прогиба w средней точки пролета и угла θ поворота трубопровода от времени t. На каждом из рис. 2–4 слева направо попарно расположены графические зависимости, которые соответствуют указанным выше двум значениям амплитуды pe. Для прогибов w эти зависимости сверху обозначены буквами a, b, а для углов θ поворота – c, d. Переменные на графиках измеряются: время t – в секундах, динамическая составляющая прогиба w – в метрах, угол θ – в радианах. На графиках толстыми и тонкими сплошными линиями нанесены результаты вычислений, полученные численным интегрированием методом Рунге–Кутта соответственно систем уравнений (2.5), (2.6) и (3.1) с начальными условиями (2.7). Штриховыми линиями обозначены зависимости, построенные на основе функций (3.3) и (3.6), а точечными – функций (3.8).

Рис. 2
Рис. 3
Рис. 4

Из числовых расчетов следует, что на инерционной стадии динамического процесса в каждый момент времени значения изгибных перемещений и их скоростей, полученные по формулам (3.3) и методом Рунге–Кутта при одном и том же значении переменной части внутреннего давления, практически совпадают. Таким образом, на инерционной стадии динамики трубопровода вполне пригодно решение (3.3). Вместе с тем следует отметить, что в течение времени удара изгибные перемещения точек трубы остаются очень малыми, а их скорости имеют конечные значения. Это подтверждается также численным решением задачи Коши (2.5)–(2.7). Например, в момент времени te прекращения действия ударной нагрузки имеют место следующие значения: w = 1.14 × 10–4 м и $\dot {w}$ = 0.0414 м/c (pe = 2.8 МПа), w = 2.87 × 10–4 м и $\dot {w}$ = 0.1043 м/c (pe = 7.0 МПа). Поэтому в (3.4) в конце времени удара изгибное перемещение принято равным нулю.

Приведенные на рис. 2–4 графические зависимости построены для трех отрезков времени: 0–0.55 с (рис. 2), 0–1.2 с (рис. 3) и 0–9.5 с (рис. 4). Из графиков a, b рис. 2 видно, что после прекращения действия ударной нагрузки изгибные перемещения трубы растут. Вместе с ними растут и упругие силы. Далее кинетическая энергия, полученная трубой при ударе, в большей мере расходуется на работу возросших упругих сил. В результате скорости изгибных перемещений трубы уменьшаются и с течением времени они становятся равными нулю. Затем из-за действия упругих сил скорости изгибных перемещений изменяют свой знак и процесс повторяется. То есть при принятых значениях параметров изгибные перемещения трубы совершают колебательные движения, которые с течением времени принимают вид биений (графики a, b рис. 3, 4). Можно отметить также зримые расхождения между толстой сплошной и штриховой линиями. При этом сплошные и точечные линии практически сливаются в одну линию. Это свидетельствует, во-первых, о существенных расхождениях решений нелинейной и линейной задач, и, во-вторых, о возможности замены основной системы нелинейных уравнений (2.5), (2.6) приближенной системой уравнений (3.1) и о пригодности аналитического решения (3.8) задачи второго приближения.

Одновременно с изгибными перемещениями происходят вращательные движения трубопровода. В течение всего времени действия ударной нагрузки угол θ поворота плоскости изгиба трубы остается почти равным начальному углу θ0. Из графиков c, d рис. 2 можно видеть, что после окончания действия ударной нагрузки угол поворота трубы, уменьшаясь, сначала становится равным нулю, а затем достигает минимального значения. В линейном приближении абсолютная величина этого значения равна начальному углу θ0 отклонения трубопровода, так как в данном случае вращательные и изгибные движения трубопровода являются независимыми. В нелинейных же приближениях, как видно из графиков c, d рис. 2, с определенных моментов времени наблюдается расхождение штриховых и сплошных линий. При этом тонкая сплошная и точечная линии визуально сливаются и располагаются на незначительном удалении от толстой сплошной линии. Также отчетливо видно, что модули минимумов угла поворота трубы всегда больше начального угла отклонения θ0 . Данный факт имеет такое объяснение. Если сопоставить графики a, b и c, d рис. 2, то можно видеть, что после достижения своих максимумов изгибные перемещения с течением времени уменьшаются и далее принимают отрицательные значения. В результате сумма ${{W}_{0}} + w$ статической и динамической составляющих прогиба средней точки пролета трубы с течением времени уменьшается. Вследствие этого, согласно теореме об изменении момента количества движения механической системы, происходит увеличение модуля угловой скорости трубы, которое приводит к увеличению ее модуля угла поворота. Далее (графики c, d рис. 3, 4) вращательные движения трубы повторяются и также принимают вид биений.

5. Заключение. Таким образом, из результатов вычислений можно сделать следующие краткие выводы.

1. На начальной стадии реакции трубопровода на ударное давление в транспортируемой жидкости можно учитывать только инерционные силы и пользоваться линеаризованными уравнениями движения. В конце времени удара, являющегося началом инерционно-упругой стадии деформирования, изгибные перемещения трубы без заметной погрешности могут быть приняты равными нулю.

2. Скорости изгибных перемещений трубы за время удара достигают конечных значений. Они прямо пропорциональны амплитуде динамической составляющей внутреннего давления. При этом угловая скорость вращательного движения трубопровода может быть принята равной нулю.

3. С ростом амплитуды динамической составляющей внутреннего давления на инерционно-упругой стадии растут также амплитуды изгибных перемещений трубопровода. При этом модули минимумов угла поворота трубы всегда больше ее начального угла отклонения.

4. В рамках принятых в работе допущений для описания пространственных колебаний трубопровода можно использовать приближенную систему нелинейных уравнений.

5. На инерционно-упругой стадии колебаний положение трубы в пространстве с допустимой погрешностью может быть определено также аналитическим решением, полученным методом последовательных приближений. Для принятых входных данных приближенное аналитическое и численное решения находятся в удовлетворительном согласии.

Автор выражает благодарность М.А. Ильгамову за обсуждение работы.

Работа частично поддержана грантами РФФИ №17-41-020400р_а, №18-01-00150_а и средствами государственного бюджета по госзаданию на 2017–2019 годы (№ г.р. 0246-2019-0088).

Список литературы

  1. Светлицкий В.А. Механика трубопроводов и шлангов. М.: Машиностроение, 1982. 280 с.

  2. Ilgamov M.A. Static problems of hydroelasticity. Moscow: Fizmatlit, 1998. 208 p.

  3. Tang D.M., Ilgamov M.A., Dowell E.H. Buckling and post-buckling behavior of a pipe subjected to internal pressure // J. of Appl. Mech. 1995. V. 62. № 3. P. 595–600.

  4. Ильгамов М.А. Колебания упругих оболочек, содержащих жидкость и газ. М.: Наука, 1969. 180 с.

  5. Акуленко Л.Д., Иванов М.И., Коровина Л.И., Нестеров С.В. Свободные колебания участка трубопровода // Изв. РАН. МТТ. 2011. № 1. С. 172–187.

  6. Акуленко Л.Д., Иванов М.И., Коровина Л.И., Нестеров С.В. Основные свойства собственных колебаний протяженного участка трубопровода // Изв. РАН МТТ. 2013. № 4. С. 119–134.

  7. Акуленко Л.Д., Гавриков А.А., Нестеров С.В. Собственные колебания трубопровода на упругом основании, транспортирующего жидкость // Изв. РАН МТТ. 2018. № 1. С. 123–133.

  8. Миронов М.А., Пятаков П.А., Андреев А.А. Вынужденные колебания трубы с потоком жидкости // Акустический журнал. 2010. Т. 56. № 5. С. 684–692.

  9. McDonald R.J., Namchchivaya N. Sri. Pipes conveying pulsating fluid near a 0:1 resonance: global bifurcations // J. of Fluids and Structures . 2005. V. 21. P. 665–687.

  10. Panda L.N., Kar R.C. Nonlinear dynamics of a pipe conveying pulsating fluid with parametric and internal resonances // J. Nonlinear Dynamics. 2007. V. 49. P. 9–30.

  11. Panda L.N., Kar R.C. Nonlinear dynamics of a pipe conveying pulsating fluid with combination, principal parametric and internal resonances // J. of Sound and Vibration. 2008. V. 309. P. 375–406.

  12. Zhang Y.L., Chen L.Q. Internal resonance of pipes conveying fluid in the supercritical regime // J. Nonlinear Dynamics. 2012. V. 67. P. 1505–1514.

  13. Zhang Y.L., Chen L.Q. External and internal resonances of the pipe conveying fluid in the supercritical regime // J. of Sound and Vibration. 2013. V. 332. P. 2318–2337.

  14. Chen L.Q., Zhang Y.L., Zhang G.C., Ding H. Evolution of the double-jumping in pipes conveying fluid flowing at the supercritical speed // International J. of Non-Linear Mechanics. 2014. V. 58. P. 11–21.

  15. Zou G.P., Cheraghi N., Taheri F. Fluid-induced vibration of composite gas pipelines // J. of Solids and Structures. 2005. V. 42. P. 1253–1268.

  16. Modarres-Sadeghi Y., Païdoussis M.P. Nonlinear dynamics of extensible fluid conveying pipes, supported at both ends // J. of Fluids and Structures. 2009. V. 25. P. 535–543.

  17. Bai Y., Xie W., Gao X., Xu W. Dynamic analysis of a cantilevered pipe conveying fluid with density variation // J. of Fluids and Structures. 2018. V. 81. P. 638–655.

  18. Ан Е.В., Рашидов Т.Р. Сейсмодинамика подземных трубопроводов, взаимодействующих с водонасыщенным мелкодисперсным грунтом // Изв. РАН МТТ. 2015. № 3. С. 89–104.

  19. Исраилов М.Ш. Связанные сейсмические колебания трубопровода в бесконечной упругой среде // Изв. РАН МТТ. 2016. № 1. С. 57–66.

  20. Ilgamov M.A., Tang D.M., Dowell E.H. Flutter and forced response of a cantilevered pipe: the influence of internal pressure and nozzle discharge // J. of Fluids and Structures. 1994. V. 8. P. 139–156.

  21. Modarres-Sadeghi Y., Semler C., Wadham-Gagnon M., Paidoussis M.P. Dynamics of cantilevered pipes conveying fluid. Part 3: Three-dimensional dynamics in the presence of an end-mass // J. of Fluids and Structures. 2007. V. 23. P. 589–603.

  22. Łuczko J., Czerwiński A. Nonlinear three-dimensional dynamics of flexible pipes conveying fluids // J. of Fluids and Structures. 2017. V. 70. P. 235–260.

  23. Ганиев Р.Ф., Ильгамов М.А., Хакимов А.Г., Шакирьянов М.М. Пространственные колебания трубопровода в сплошной среде под действием переменного внутреннего давления // Проблемы машиностроения и надежности машин. 2016. № 6. С. 3–13.

  24. Шакирьянов М.М. Пространственные хаотические колебания трубопровода в сплошной среде под действием переменного внутреннего давления // Известия Уфимского научного центра РАН. 2016. № 4. С. 35–47.

  25. Ганиев Р.Ф., Ильгамов М.А., Хакимов А.Г., Шакирьянов М.М. Пространственные непериодические колебания трубопровода под действием переменного внутреннего давления // Проблемы машиностроения и надежности машин. 2017. № 2. С. 3–12.

  26. Li S., Karney B. W., Liu G. FSI research in pipeline systems – A review of the literature // J. of Fluids and Structures. 2015.V. 57. P. 277–297.

  27. Ганиев Р.Ф., Ильгамов М.А. Упругая реакция трубопровода на внутреннее ударное давление // ДАН. 2016. Т. 470. № 2. С. 162–165.

  28. Ильгамов М.А. Динамика трубопровода при действии внутреннего ударного давления // Изв. РАН МТТ. 2017. № 6. С. 83–96.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал