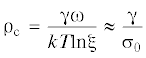Известия РАН. Механика твердого тела, 2020, № 1, стр. 94-101

1. Введение. Вопросы прочности и долговечности материалов играют важную роль в современном материаловедении [1–4]. Одним из многих известных механизмов разрушения кристаллов в высокотемпературной области является вакансионный механизм, которому посвящено значительное число работ [5–9]. В соответствии с ним рост и коагуляция пор осуществляется за счет притока избыточных вакансий, формирующихся в объеме кристалла под воздействием радиации [5], упругих растягивающих напряжений [6–9] или иных процессов. Отметим, что в большинстве работ [5–9] подробно рассмотрены механизмы зарождения и роста, в основном, сферических пор. В них делается допущение, что рост поры ограничен либо диффузионным транспортом вакансий к поверхности сферической поры, либо граничной кинетикой встраивания вакансий в пору, причем последняя практически всегда считается линейно зависящей от концентрации вакансий у поверхности. Однако, при малых нагрузках в состояниях близких к равновесному пора может стать ограненной для минимизации поверхностной энергии [10, 11]. В этом случае, проводя аналогию поры с ограненным кристаллом “пустоты” [5], следует ожидать и появления режимов роста поры, когда граничная кинетика зависит от вакансионного пересыщения более сложным образом. Так, в работе [12] рассмотрен рост ограненной поры по механизму Бартона–Кабреры–Франка (БКФ) – за счет попадания вакансий из объема кристалла на поверхность поры, их дальнейшей диффузии по поверхности и встраиванию в ступени. В работе было показано, что скорость роста поры может зависеть как линейно, так и квадратично от приложенных упругих напряжений. Возможна реализация и других механизмов роста, также нелинейно зависящих от пересыщения. Одним из них является механизм А. Чернова [13], предложенный для описания роста кристалла из раствора, при котором диффузия атомов происходит непосредственно из раствора к ступени на поверхности кристалла. Такой механизм может реализоваться и при росте поры в случае, если поверхностная диффузия и нуклеация островков из вакансий затруднена, например, при адсорбции молекул газа на внутренней поверхности поры.

Настоящая работа продолжает цикл работ [6–9, 12, 15–18], посвященных росту и эволюции кристаллов и пор в одно- и многокомпонентных системах по различным механизмам, и ее основная цель – рассмотреть рост ограненных пор в кристалле из газа вакансий по механизму Чернова, описанному в классической работе [13]. Поскольку именно диффузионный рост пор может быть ключевым фактором, обуславливающим долговечность материала при высоких температурах в режиме малых нагрузок, детальное понимание этого процесса является актуальной задачей физики разрушения.

2. Рост ограненной поры по механизму Чернова. В качестве модели рассмотрим кристалл, содержащий крупные, имеющие радиус десятки микрон и более, поры. В ряде случаев такие поры могут иметь кристаллическую огранку, так как это позволяет минимизировать свободную энергию системы [5, 10]. Предположим, что в объеме кристалла равномерно распределены стоки и источники вакансий ограниченной мощности (дислокации, иные дефекты, либо вакансии, зарождающиеся за счет тепловых флуктуаций). Также сделаем допущение, что размеры граней поры значительно больше характерных расстояний между атомарными ступенями на их поверхности, и при рассмотрении движения отдельной ступени можно считать грань бесконечной и пренебречь влиянием ребер поры на распределение вакансий возле ступеней. Предположим, что кристалл подвергается равномерной механической растягивающей нагрузке ${{\sigma }_{0}}$ по внешней границе. В результате возле источников формируется избыточное количество вакансий, концентрацию ${{C}_{{v}}}~$ которых вдали от поры можно записать в виде [7]:

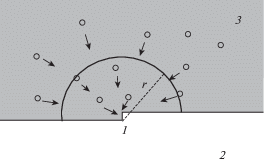
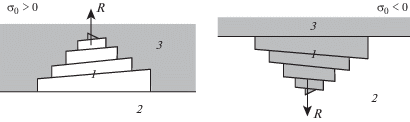
где ${\omega }$ – объем приходящийся на одну вакансию, $k$ – постоянная Больцмана, $T$ – температура, а ${{C}_{{{v}0}}} = С~{\text{exp}}\left( { - {{E}_{{v}}}{\text{/}}kT} \right)$ – равновесная концентрация вакансий у плоской границы при данной температуре, $С~$ – концентрация атомов в кристаллической решетке, ${{E}_{{v}}}$ – энергия активации зарождения вакансий. Величина ${{\sigma }_{0}}$ считается положительной при растягивающей нагрузке.

Схематический вид потока вакансий из объема кристалла к ступени на поверхности ограненной поры представлен на рис. 1, на котором (и далее) введены обозначения: 1 – ступень на поверхности поры, 2 – пора, 3 – кристалл. Вакансии могут диффундировать по кристаллу к ступеням на поверхности ограненной поры. Их встраивание в изломы вызывает движение ступеней по террасе и постепенное увеличение объема поры. Задача очень похожа на рост реального кристалла из раствора по механизму Чернова, однако есть и некоторые отличия. Во-первых, в случае роста кристалла из раствора концентрация вещества в растворе определяется тем, сколько этого вещества поступает в систему; если речь идет о росте поры (кристалла “пустоты”) из газа вакансий, то концентрация вакансий определяется приложенными упругими напряжениями ${{\sigma }_{0}}$ и температурой кристалла [7]. Во-вторых, в классической модели Чернова [13] рассматривается фиксированный диффузионный слой, через который происходит диффузионный перенос массы, и толщина которого зависит от вязкости раствора и скорости его перемешивания, тогда как в настоящей задаче ширина этого слоя зависит от мощности объемных источников вакансий и заранее неизвестна.

Рассмотрим одиночную ступень “пустоты”, двигающуюся по поверхности поры. Будем считать, что скорость ее перемещения достаточно мала, чтобы вокруг нее установилось стационарное распределение вакансий. Также мы считаем, что ступень достаточно плотно покрыта изломами и является непрерывным стоком для вакансий, диффундирующих из объема. Аналогично работе [13] выберем систему координат так, чтобы ось x совпала со ступенью и рассмотрим распределение вакансий вокруг нее. Мы считаем, что распределение имеет радиальную симметрию. Пусть скорость генерации вакансий в единице объема кристалла $Q = {\alpha }\left( {{{C}_{{{v}\infty }}} - {{C}_{{v}}}\left( r \right)} \right)$, где ${\alpha } = {\tau }_{{v}}^{{ - 1}}$ – мощность источников, ${{{\tau }}_{{v}}}$ – среднее время жизни вакансии в кристалле, а ${{C}_{{v}}}\left( r \right)$ – концентрация вакансий на расстоянии $r$ от ступени (см. рис. 1). Введем также по аналогии с [12] величину ${\varphi } = {{C}_{{{v}\infty }}} - {{C}_{{v}}}\left( r \right)$.

Тогда для распределения вакансий вокруг ступени, учитывая непрерывность функции ${\varphi }$, можно записать квазистационарное уравнение диффузии при наличии источников в цилиндрических координатах:

Мы считаем, что на поверхности цилиндра радиусом a (параметр решетки) [13], ограничивающего ступень, поддерживается равновесная концентрация вакансий, так как вакансии эффективно встраиваются в ступень:

Вдали от ступени в объеме кристалла концентрация вакансий равна ${{C}_{{{v}\infty }}}$:

Нетрудно показать, что решением этой краевой задачи будет выражение:

или где $\lambda _{s}^{2} = {{D}_{{v}}}{{{\tau }}_{{v}}}$ – средняя длина свободного пробега вакансии по объему кристалла.

Учитывая (2.2), определим диффузионный поток вакансий к поверхности цилиндра, окружающего ступень:

Считая длину свободного пробега вакансий много большей параметра решетки (${{\lambda }_{s}} \gg a$), и пользуясь разложением функций Макдональда при малом аргументе (${{K}_{1}}(x) \approx \frac{1}{2}{\Gamma }(1){{(x{\text{/}}2)}^{{ - 1}}}$, $~{{K}_{0}}\left( x \right) = \ln \left( {2{\text{/}}{{\gamma }_{e}}x} \right)$, $x \to 0$, ${{{\gamma }}_{e}} = 1.78$ – постоянная Эйлера) преобразуем выражение:

Теперь, зная поток вакансий к ступени, можно записать скорость ее перемещения:

где $1{\text{/}}{{n}_{0}} = {{a}^{2}}$ – площадь, занимаемая одной вакансией. Вводя по аналогии с [7, 12] пересыщение газа вакансий $\xi $ вдали от поры, которое при малой нагрузке ${{\sigma }_{0}}{\omega } \ll kT$ можно записать в виде: ${\xi } = \frac{{{{C}_{{{v}\infty }}}}}{{{{C}_{{{v}0}}}}} - 1 \approx \frac{{{{\sigma }_{0}}{\omega }}}{{kT}}~$, получим окончательное выражение для скорости перемещения ступени по поверхности поры:

Из формулы (2.4) следует, что при сжимающих напряжениях скорость движения ступени отрицательна, поток вакансий направлен от ступени – пора растворяется и уменьшается в размерах. При растягивающих напряжениях, наоборот, поток вакансий направлен к поре, и она растет в размерах. Поскольку, как правило, зарождение и аннигиляция вакансий происходит в основном на дефектах кристаллической решетки, например, дислокациях, то скорость роста поры по рассматриваемому механизму будет зависеть от среднего расстояния ${{\lambda }_{s}} \approx \sqrt[2]{{\rho }}$ между дефектами, где ${\rho }$ – плотность дислокаций.

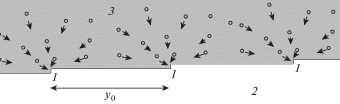
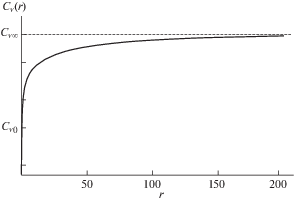
Рассмотрим теперь группу эквидистантных ступеней на вицинальной (рис. 2) грани поры, находящихся на расстоянии ${{y}_{0}}~$ друг от друга. Будем считать, что это расстояние больше длины свободного пробега вакансий (${{y}_{0}} \gg ~{{\lambda }_{s}}$). В противном случае (${{y}_{0}} \ll ~{{\lambda }_{s}}$), поверхность становится непрерывным стоком для вакансий и задача сводится к уже рассмотренным ранее случаям [5]. Отметим, что согласно формуле (2.2), на расстояниях порядка 2–4 ${{\lambda }_{s}}$ от ступени концентрация вакансий уже практически не отличается от ${{C}_{{{v}\infty }}}$ (при условии ${{\lambda }_{s}} \gg a$). Так, на рис. 3 приведен график зависимости ${{C}_{{v}}}\left( r \right)~$ при $a$ = 0.1 нм, ${{\lambda }_{s}} = 100$ нм. Таким образом, при ${{y}_{0}} \geqslant 4{{\lambda }_{s}}$ диффузионные поля соседних ступеней не влияют друг на друга и для нормальной скорости роста поры ${{R}_{{norm}}}$ можно использовать следующую формулу [13]

Если на террасу выходит винтовая дислокация, то, как было показано в [12, 13], может реализоваться механизм спирального роста поры. Отметим, что именно такой механизм, вероятно, ответственен за рост пор при экстремально малых перенапряжениях, так как в этом случае нуклеация островков “пустоты” на поверхности поры невозможна, и только винтовая дислокация может обеспечить бесконечный источник ступеней на поверхности, к которым будут присоединяться поступающие вакансии. Скорость вращения такой спиральной ступени “пустоты” за счет диффузии к ней вакансий можно найти, подставив в полученное в предыдущем разделе выражение (2.5) среднее расстояние между последовательными витками спирали ${{y}_{0}} = 19{{{\rho }}_{{\text{c}}}}$ [19], которое определяется ${{{\rho }}_{{\text{c}}}}~$ – критическим радиусом двумерного зародыша вакансий$~$ [7]. При этом по-прежнему должно сохраняться условие $19{{{\rho }}_{{\text{c}}}} \geqslant 4{{\lambda }_{s}}$:

где ${\gamma }$ – поверхностная энергия. Таким образом, мы получим следующую формулу для нормальной скорости ${{R}_{{sp}}}$ роста поры по спиральному механизму [13]:

Отметим, что при смене знака упругих напряжений поверхность кристалла должна прийти в равновесие – спираль роста сперва полностью растворится, а затем “закрутится” в обратную сторону (см. рис. 4) и стабилизирует свое вращение. В связи с подобной инверсией системы в уравнении (2.4) для скорости перемещения одиночной ступени должен поменяться знак (ступень движется в обратную сторону при том же приложенном упругом напряжении), поэтому удобно записать в выражении (2.6) упругое напряжение с учетом знака “модуль”. В таком виде формула (2.6) справедлива как для режима роста поры (${{\sigma }_{0}} > 0$), так и для режима растворения (${{\sigma }_{0}} < 0$). Отметим, однако, что она применима только в стабилизированном режиме.

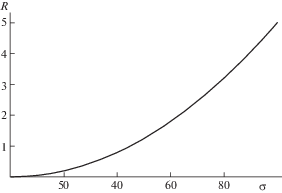
Оценка для зависимости ${{R}_{{sp}}}$(${{\sigma }_{0}})$ (нм/c) по выражению (2.6) представлена на рис. 5. Для оценки приняты: коэффициент диффузии вакансий ${{D}_{v}}\sim {{10}^{{ - 12}}}$ м²/с, объем вакансии ${\omega }\sim {{10}^{{ - 29}}}$ м², поверхностное натяжение ${\gamma }\sim 1$ Дж/м², температура T ~ 800°C, длина свободного пробега вакансий по объему кристалла ${{\lambda }_{s}}$ ∼ 100 нм. Из сравнения рис. 5 и [12] видно, что характерные скорости роста поры по механизму Чернова меньше, чем по механизму БКФ, что обусловлено значительно более эффективной диффузией вакансий по поверхности (БКФ), чем по объему кристалла (Чернов).

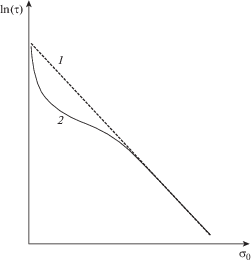
Пользуясь выражением для скорости роста поры (2.6) можно оценить и зависимости долговечности от упругого напряжения, считая, что именно рост пор по механизму Чернова является фактором, лимитирующим разрушение материала. Затем, сравнивая экспериментально полученные зависимости с теоретическими оценками для различных механизмов можно сделать вывод о том, какой именно механизм разрушения играет основную роль для данного материала. Отметим, что для многих материалов характерен изгиб кривой на экспериментальном графике зависимости долговечности ln(τ) от упругого напряжения ${{\sigma }_{0}}$ в области крайне малых упругих напряжений [20], который, насколько известно авторам, не имеет строгого теоретического обоснования. Этот изгиб свидетельствует о том, что при уменьшении напряжения меняется фактор, лимитирующий разрушение. И если при более высоких нагрузках основную роль играют дислокационные и иные механизмы [20], то диффузионное разрастание пор может играть важную роль при малых напряжениях, когда дислокационные процессы подавлены. Спиральный вакансионный рост поры, по аналогии с ростом обычных кристаллов, вероятно, является основным механизмом роста при малых напряжениях, и поскольку зависит от приложенного напряжения нелинейным образом (формула (2.6)), его учет может повлиять на вид зависимости долговечности материала ${\tau }$ от ${{\sigma }_{0}}$. Так, на рис. 6 показана зависимость долговечности кристалла ${\tau }$ от приложенного механического напряжения $~{{\sigma }_{0}}$ при малых ${{\sigma }_{0}}$: 1 – классическая кривая [20] ${\tau } = {{{\tau }}_{0}} \cdot {\text{exp}}\left( {\frac{{{{U}_{0}} - {\beta \sigma }}}{{kT}}} \right)$ без учета возможности спирального роста пор по механизмам БКФ [12] и Чернова, 2 – с учетом спирального роста.

3. Заключение. В работе рассмотрен процесс роста ограненных пор в кристаллических материалах по механизму Чернова под воздействием небольших механических растягивающих нагрузок. Показано, что рост подобных ограненных кристаллов “пустоты” полностью аналогичен классическому росту кристалла из растворов и описывается теми же уравнениями, если в качестве источника “пустоты” рассматривать газ вакансий в кристалле. Найдены уравнения для скорости передвижения отдельных ступеней по террасам кристалла “пустоты”, их групп, а также ступеней, образованных винтовыми дислокациями. Показана связь скорости роста пор, и как следствие, долговечности материала, и величины механических напряжений. Полученные результаты позволяют сделать оценки времени жизни материалов до разрушения по рассматриваемому механизму под воздействием небольших, но постоянных растягивающих нагрузок.

Благодарности. А.В. Редьков благодарит за поддержку данной работы Cовет по грантам Президента РФ (грант № МК-1574.2019.2). А.В. Осипов выполнял свою часть работы в рамках гранта РНФ № 19-72-30004.