Известия РАН. Механика твердого тела, 2020, № 1, стр. 68-76

1. Введение. Вопросу о влиянии размера малой капли на ее поверхностное натяжение посвящено много работ. В [1–4] в рамках метода функционала плотности было впервые показано, что учет только толменовской поправки (пропорциональной кривизне капли) недостаточен для описания этой зависимости, и нужно учитывать следующий вклад в поверхностное натяжение, который пропорционален квадрату кривизны и связан с константой эффективной жесткости поверхностного слоя [4, 5]. Термодинамический анализ в рамках метода разделяющих поверхностей Гиббса для поверхностного натяжения малой капли полярной и неполярной жидкости, образованной на заряженном ядре конденсации, был проведен в работах [6–10]. Этот анализ, как и термодинамический анализ в случае наноразмерных ядер конденсации в [11], был сделан в предположении разделения поверхностных слоев ядро–жидкость и жидкость–пар в капле, при этом поправки по параметру кривизны учитывались только в первом порядке. Как будет видно из дальнейшего нашего рассмотрения, разделение поверхностных слоев ядро–жидкость и жидкость–пар объемной жидкой прослойкой не всегда возможно, а в тех случаях, когда оно возможно, требует мотивированного выбора границы между поверхностными слоями ядро–жидкость и жидкость–пар. Исследование нуклеации на ионах в рамках метода функционала плотности было проведено в [12, 13]. Однако, нам неизвестны работы, в которых бы обсуждалась зависимость поверхностного натяжения малых капель на ядрах молекулярного размера в присутствии или отсутствии электрического поля.

Недавно нами в рамках градиентного метода функционала плотности была исследована роль расклинивающего давления в тонких сферических жидких пленках вокруг наноразмерных ядер конденсации [14, 15]. При достаточно больших размерах ядер можно уже пренебречь зависимостью поверхностного натяжения капли от кривизны и связать все размерные эффекты с расклинивающим давлением. Однако для ядер конденсации молекулярного размера понятие расклинивающего давления теряет смысл, и зависимость поверхностного натяжения капли от ее радиуса может быть существенной. Чтобы ее найти, мы воспользовались в данной работе градиентным методом функционала плотности для молекул пересыщенного пара аргона при разных значениях химического потенциала молекул аргона. Взаимодействие молекул аргона между собой описывалось в рамках модели Карнахана–Старлинга для вклада твердых сфер и приближения среднего поля для молекулярного притяжения [16, 17]. Взаимодействие молекул аргона с незаряженным ядром конденсации задавалось потенциалом Леннард–Джонса. В случае иона дополнительно учитывался дальнодействующий кулоновский потенциал электрических сил в духе работы Китамуры и Онуки [18]. При этом диэлектрические проницаемости пара и жидкости были заданы как известные функции локальной плотности аргона и температуры. В качестве переменной, описывающей размер капли, был выбран радиус эквимолекулярной поверхности капли. Расчеты термодинамически определенного поверхностного натяжения капли были проведены при нескольких размерах ядер конденсации, как меньших, так и больших размера молекулы конденсирующегося вещества. Полученные зависимости поверхностного натяжения капель были сравнены с зависимостью поверхностного натяжения от размера капли без ядра конденсации.

2. Постановка задачи. Рассмотрим открытую систему с пересыщенным однокомпонентным паром при некоторой фиксированной температуре $T$ и химическом потенциале молекул пара ${\mu }$. Поместим в систему сферическое ядро конденсации (или ион) радиуса ${{R}_{i}}$. Считаем поверхность ядра равномерно покрытой образующимся конденсатом, вещество ядра нерастворимым в конденсате, электрический заряд (если он присутствует) равномерно распределенным по поверхности ядра.

Большой термодинамический потенциал системы с каплей, образовавшейся вокруг ядра (конечное состояние системы), может быть представлен суммой вкладов [6, 10, 11]

Здесь ${{\Omega }_{i}}({{R}_{d}})$ – вклад в большой термодинамический потенциал, связанный с присутствием ядра конденсации, окруженного сольватной оболочкой радиуса ${{R}_{d}}$; ${{R}_{{em}}}$ – радиус эквимолекулярной разделяющей поверхности между каплей и паром. Верхний греческий индекс у величины указывает к какой фазе она относится: α – жидкость, β – пар. Двойным греческим верхним индексом будем помечать величины, относящиеся к соответствующим межфазным границам, ${{{\sigma }}^{{{\alpha \beta }}}}$ – термодинамически определенное поверхностное натяжение для эквимолекулярной разделяющей поверхности на границе жидкость–пар. Величина ${{p}_{Т}}\left( r \right)$ – тангенциальная компонента локального тензора давления в присутствии центрального электрического поля, создаваемого зарядом иона, D – индукция этого поля, ${\varepsilon }$ – диэлектрическая проницаемость соответствующей фазы, L – внешний радиус системы, который выбирается достаточно далеко от ядра там, где влияние ядра на плотность вещества в системе практически отсутствует, и плотность окружающего флюида достигает плотности пара в объемной фазе.

В присутствии центрального электрического поля [6, 10, 11]

где ${{p}^{{\alpha }}}$, ${{p}^{{\beta }}}$ – давления в жидкости и паре в отсутствие поля при заданных T и ${\mu }$. Проинтегрировав с учетом (2.2) и выражения для индукции кулоновского поля слагаемые в выражении (2.1), выразим термодинамическое поверхностное натяжение ${{{\sigma }}^{{{\alpha \beta }}}}$ капли как где Z – заряд иона в единицах элементарного заряда $e$.

Найти Ω₂ можно в рамках градиентного метода функционала плотности [14–17]. В соответствии с [14–17], представим ${{\Omega }_{2}}$ как следующий функционал радиального профиля плотности $\rho \left( r \right)$ вещества:

Здесь $r$ – расстояние от центра ядра конденсации, ${{k}_{{\text{B}}}}$ – постоянная Больцмана, η = = ${{{\pi }{{d}^{3}}{\rho }} \mathord{\left/ {\vphantom {{{\pi }{{d}^{3}}{\rho }} 6}} \right. \kern-0em} 6}$ – безразмерная плотность числа молекул конденсирующегося вещества, d – диаметр твердой сферы (далее ${\sigma } \equiv {{\left( {{{\pi } \mathord{\left/ {\vphantom {{\pi } 6}} \right. \kern-0em} 6}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}d$ используется для перехода к безразмерной длине), ${{{\lambda }}_{{th}}} = \hbar \sqrt {{{2{\pi }} \mathord{\left/ {\vphantom {{2{\pi }} {(m{{k}_{{\text{B}}}}T}}} \right. \kern-0em} {(m{{k}_{{\text{B}}}}T}})} $ – тепловая длина де Бройля, $\hbar $ – постоянная Планка, m – масса молекулы конденсирующегося вещества, a – параметр среднего поля, определяемый потенциалом межмолекулярного взаимодействия молекул конденсирующегося вещества, $C = 14{{{\sigma }}^{5}}{{k}_{{\text{B}}}}T$ – параметр, определяемый потенциалом межмолекулярного взаимодействия в конденсате, но не зависящий от параметров ядра конденсации, $w(r)$ – потенциал молекулярного поля ядра конденсации, ε(ρ) = (1 + +  ${{8{\pi }{{{\alpha }}_{m}}{\rho }} \mathord{\left/ {\vphantom {{8{\pi }{{{\alpha }}_{m}}{\rho }} 3}} \right. \kern-0em} 3}){\text{/}}(1 - {{4{\pi }{{{\alpha }}_{m}}{\rho }} \mathord{\left/ {\vphantom {{4{\pi }{{{\alpha }}_{m}}{\rho }} 3}} \right. \kern-0em} 3})$ – диэлектрическая проницаемость как функция локальной плотности конденсата.

В выражении (2.4) возьмем потенциал $w(r)$ как потенциал Леннард–Джонса w(r) = = ${{E}_{{{v}w}}}\{ {{({\sigma /}r)}^{{12}}} - {{({\sigma /}r)}^{6}}\} $. При расчетах энергетический параметр ${{E}_{{{v}w}}}$ для ядра конденсации был выбран ${{E}_{{{v}w}}} = 12a{\text{/}}{{{\sigma }}^{3}}$, т.е. потенциал притяжения молекулы конденсата к ядру приблизительно в 12 раз больше, чем к другой молекуле конденсата. Выбор ${{E}_{{{v}w}}}$ был обусловлен, во-первых, требованием получить при расчете капли, полностью покрывающие поверхность ядра конденсации для обеспечения центральной симметрии. Во-вторых, необходимо иметь выраженную сольватную оболочку вокруг ядра, чтобы при расчете поверхностного натяжения слоя жидкость–газ исключить эффекты, связанные со структурой этой оболочки.

Равновесный профиль плотности ${\rho }(r)$ может быть найден из условия стационарности 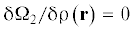для функционала (2.4). С учетом сферической симметрии системы (с центром в центре ядра конденсации), условие стационарности принимает вид нелинейного обыкновенного дифференциального уравнения второго порядка на профиль плотности числа молекул:

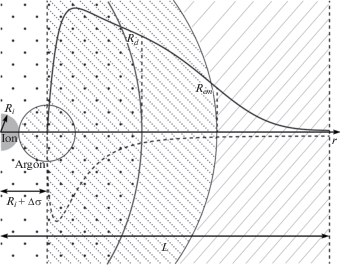
3. Численные результаты. На рис. 1 схематично представлена рассматриваемая система размера $L$ в конечном состоянии, то есть с образовавшейся на ядре конденсации радиально неоднородной по плотности жидкой каплей. Начало координат помещено в центр ядра. Расчеты были проведены для ядер конденсации разных размеров, которые были меньше или больше размера молекулы конденсирующегося вещества. На рис. 1 проиллюстрирован случай, когда радиус ядра ${{R}_{i}} = 0.4{\sigma }$, что меньше радиуса молекулы конденсата $\Delta {\sigma } = 0.6{\sigma }$. Пунктирной кривой изображена характерная зависимость безразмерного потенциала ${{w(r)} \mathord{\left/ {\vphantom {{w(r)} {{{k}_{{\text{B}}}}T}}} \right. \kern-0em} {{{k}_{{\text{B}}}}T}}$ сил молекулярного взаимодействия молекул конденсата с ядром. Сплошная кривая на рис. 1 – это характерный профиль безразмерной локальной плотности пленки ${\eta }(r)$. Радиус ${{R}_{d}}$ задает границу сольватной оболочки вокруг ядра (обозначена крупными точками). Радиус ${{R}_{{em}}}$ определяет положение точками эквимолекулярной поверхности капли, жидкая фаза обозначена мелкими точкам, газовая фаза – косыми линиями.

Решая численно уравнение (2.5) при температуре $T = 90$ K для аргоноподобных молекул, мы нашли профили плотности капель как функции безразмерного радиуса r/σ при нескольких значениях безразмерного сдвига химического потенциала ${{\Delta {\tilde {\mu }} = \left( {{\mu } - {{{\mu }}_{\infty }}} \right)} \mathord{\left/ {\vphantom {{\Delta {\tilde {\mu }} = \left( {{\mu } - {{{\mu }}_{\infty }}} \right)} {{{k}_{{\text{B}}}}T}}} \right. \kern-0em} {{{k}_{{\text{B}}}}T}}$ (${{{\mu }}_{\infty }}$ – значение химического потенциала при равновесии с плоской границей раздела жидкость–пар). При значении химического потенциала ${\mu } > {{{\mu }}_{\infty }}$ (но ниже некоторого порогового значения) уравнение (2.5) имеет два решения, соответствующие стабильной (устойчивому равновесию с паром) и критической (неустойчивому равновесию с паром) каплям. В статье были использованы следующие значения параметров [14–17]: ${{{\pi }{{d}^{3}}} \mathord{\left/ {\vphantom {{{\pi }{{d}^{3}}} 6}} \right. \kern-0em} 6}$ = 16.22 × 10^–30 м³, ${\sigma } = {{({\pi }{{d}^{3}}{\text{/}}6)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}} = 2.53$ × 10^–10 м³, $a = 3.58 \cdot {{10}^{{ - 49}}}$ Дж ⋅ м³, ${{{\mu }}_{\infty }}$ = = ‒1.539 × 10^–20 Дж, ${\eta }_{\infty }^{{\alpha }} = {{{\pi }{{d}^{3}}{{{\rho }}^{{\alpha }}}\left( {{{{\mu }}_{\infty }}} \right)} \mathord{\left/ {\vphantom {{{\pi }{{d}^{3}}{{{\rho }}^{{\alpha }}}\left( {{{{\mu }}_{\infty }}} \right)} 6}} \right. \kern-0em} 6} = 0.408$, ${\eta }_{\infty }^{{\beta }} = {{{\pi }{{d}^{3}}{{{\rho }}^{{\beta }}}\left( {{{{\mu }}_{\infty }}} \right)} \mathord{\left/ {\vphantom {{{\pi }{{d}^{3}}{{{\rho }}^{{\beta }}}\left( {{{{\mu }}_{\infty }}} \right)} 6}} \right. \kern-0em} 6} = 0.00296$, ${\sigma }_{\infty }^{{{\alpha \beta }}}$ = = 0.0119 Н/м, ${{{\alpha }}_{m}} = 6.9$ × 10^–30 м³.

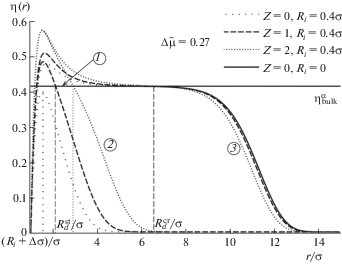
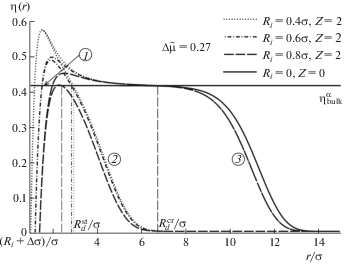
Результаты расчетов профилей при $\Delta {\tilde {\mu }} = 0.27$ в безразмерных величинах ${\eta }$ и ${r \mathord{\left/ {\vphantom {r {\sigma }}} \right. \kern-0em} {\sigma }}$ приведены на рис. 2 и 3. Сплошная кривая показывает профиль плотности капли в отсутствие ядра конденсации. Горизонтальная линия соответствует значению плотности жидкости в объемной фазе при заданном химическом потенциале (кривая 1). Приведены профили плотности для стабильных (кривые 2) и критических капель (кривые 3). На рис. 2 представлен расчет для ядра размера ${{R}_{i}} = 0.4{\sigma }$ при Z = 0 (нейтральное ядро конденсации, профиль изображен точками с длинным пробелом), Z = 1 (однократно заряженный ион, профиль показан штрихами), Z = 2 (двухкратно заряженный ион, профиль показан точками). На рис. 3 показаны профили плотности для капель, образовавшихся на ионах с зарядом Z = 2 при различных размерах ионов: R_i = = $0.4{\sigma }$ (профиль показан точками), ${{R}_{i}} = 0.6{\sigma }$ (профиль показан штрихами с точками), ${{R}_{i}} = 0.8{\sigma }$ (профиль показан длинными штрихами).

Точку пересечения профиля ${\eta }(r)$ с линией плотности жидкой фазы ${{{\eta }}^{{\alpha }}}$ принимаем за радиус сольватной оболочки ${{R}_{d}}$ вокруг ядра. Если капля достаточно рыхлая (на рис. 2 это случай стабильной капли на нейтральном ядре), и профиль плотности не достигает объемной фазы, тогда ${{R}_{d}}$ совпадает с координатой максимума профиля плотности. Радиус ${{R}_{{em}}}$ эквимолекулярной поверхности при заданном химическом потенциале вычислялся по формуле [16]

Подставив полученные численные зависимости ${\rho }(r)$ в выражение (2.4), можно рассчитать разность больших термодинамических потенциалов ${{\Omega }_{2}} - {{\Omega }_{i}}({{R}_{d}})$. Так как в формуле (2.3) стоит разность ${{\Omega }_{2}} - {{\Omega }_{i}}({{R}_{d}})$, то для ее вычисления нужно интегрировать выражение (2.4) от точки ${{R}_{d}}$ до границы системы.

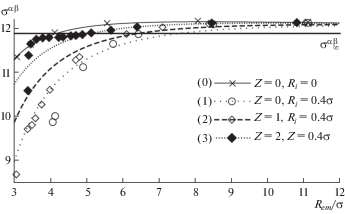
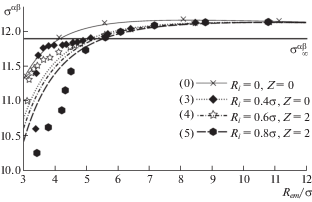
На рис. 4 и рис. 5 приведены результаты расчета поверхностного натяжения по формуле (2.3) для различных значений химического потенциала $\Delta {\tilde {\mu }}$, которым соответствуют значения безразмерного эквимолекулярного радиуса 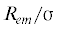для стабильной и критической капель. По оси ординат отложены величины ${\sigma }_{{}}^{{{\alpha \beta }}}$ в единицах 10³ Н/м, по оси абсцисс безразмерный радиус эквимолекулярной поверхности 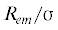. Результаты расчета показаны символами, кривые соответствуют квадратичной по кривизне капли аппроксимации [4]

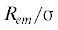где ${{{\delta }}_{\infty }}$ – толменовская длина и ${\kappa }$ – константа эффективной жесткости поверхностного слоя [5]. Сплошная кривая с косыми крестиками показывает зависимость поверхностного натяжения от безразмерного внешнего радиуса капли для случая капли без ядра (${{{\delta }}_{\infty }} = - 0.19{\sigma }$, ${\kappa } = - 1.58{{{\sigma }}^{2}}$). Горизонтальная сплошная линия соответствует значению поверхностного натяжения при плоской границе раздела ${\sigma }_{\infty }^{{{\alpha \beta }}}$. К этому значению все кривые на рис. 4 и 5 стремятся в пределе больших радиусов 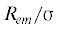, проходя перед этим через максимум. На рис. 4 представлен расчет для иона радиуса ${{R}_{i}} = 0.4{\sigma }$ и различных зарядов: Z = 0 (кружки, кривая с редким пунктиром отвечает формуле (3.2) с ${{{\delta }}_{\infty }} = - 0.25{\sigma }$ и ${\kappa } = - 3.70{{{\sigma }}^{2}}$), Z = 1 (ромбы, кривая со штрихами отвечает формуле (3.2) с ${{{\delta }}_{\infty }} = - 0.23{\sigma }$ и ${\kappa } = - 2.90{{{\sigma }}^{2}}$), Z = 2 (закрашенные ромбы, кривая с частым пунктиром отвечает формуле (3.2) с ${{{\delta }}_{\infty }} = - 0.21{\sigma }$ и ${\kappa } = - 2.12{{{\sigma }}^{2}}$). На рис. 5 приведены результаты для капель, образовавшихся на ионах с зарядом Z = 2 при ${{R}_{i}} = 0.4{\sigma }$ (закрашенные ромбы на пунктирной кривой по формуле (3.2) с ${{{\delta }}_{\infty }} = - 0.21{\sigma }$ и ${\kappa } = - 2.12{{{\sigma }}^{2}}$), ${{R}_{i}} = 0.6{\sigma }$ (звезды на штрих-пунктирной кривой по формуле (3.2) с ${{{\delta }}_{\infty }}$ = = –0.21σ и ${\kappa } = - 2.26{{{\sigma }}^{2}}$), ${{R}_{i}} = 0.8{\sigma }$ (шестиугольники на штриховой кривой по формуле (3.2) с ${{{\delta }}_{\infty }} = - 0.22{\sigma }$ и ${\kappa } = - 2.46{{{\sigma }}^{2}}$). Отметим, что при малых 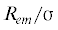на рис. 4 и 5 видно появление немонотонного поведения вычисленных значений поверхностного натяжения. При таких радиусах капель разделение поверхностного слоя капли и сольватной оболочки становится плохо определенным. Поэтому эту область размеров капель мы не будем обсуждать.

4. Выводы. При исключении эффектов, связанных непосредственно с сольватной оболочкой, зависимость поверхностного натяжения от размера капли для капель без ядра и капель на нейтральном и заряженном ядре молекулярного размера демонстрирует похожее поведение. Во всех случаях с уменьшением размера капли поверхностное натяжение сначала растет, проходит через максимум и затем уменьшается. Это поведение вполне описывается формулой (3.2). При этом толменовская длина оказывается приблизительно одинаковой во всех случаях (наибольшее отклонение для нейтрального ядра с ${{R}_{i}} = 0.4{\sigma }$ на рис. 4 связано, по-видимому, с тем, что в этом случае сольватная оболочка слабо выражена). Однако, вклад в поверхностное натяжение, который пропорционален квадрату кривизны и связан с константой эффективной жесткости поверхностного слоя, различается уже существенно. Этот вклад наименьший в случае капли без ядра конденсации, с ростом размера заряженного ядра он возрастает.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (грант 18-53-50015 ЯФ_а).