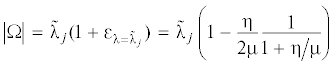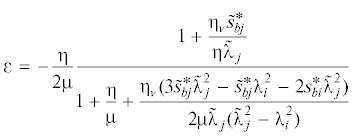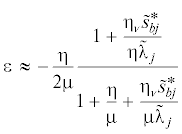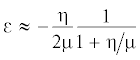Известия РАН. Механика твердого тела, 2020, № 2, стр. 40-58
ЧАСТОТА КОЛЕБАНИЙ ПРИ КАЧЕНИИ С ПРОСКАЛЬЗЫВАНИЕМ РОТОРА СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ ПО СТАТОРУ
А. Н. Никифоров *
Институт машиноведения им. А.А. Благонравова РАН
Москва, Россия
* E-mail: n.andre@mail.ru
Поступила в редакцию 19.03.2019
После доработки 16.05.2019
Принята к публикации 16.05.2019
Аннотация
Предложены математическая модель гибкого ротора с n степенями свободы, обкатывающего податливый статор с проскальзыванием между ними, а также подход к исключению контактных сил для динамического анализа системы. Определяются угловая скорость и амплитуда обратной прецессии ротора матричными методами. Показано, что скорость обкатки не всегда равна произведению скорости вращения на отношение радиуса ротора к радиальному зазору в месте контакта. В случае проскальзывания она зависит от той или иной собственной частоты ротора, опирающегося на статор, а также от коэффициентов конструкционного и контактного трения. Показано также, что фактически трение задает только скорость обкатки, а амплитуда обратной прецессии (прогиб ротора вне места контакта) определяется величиной зазора в контактном месте.
1. Введение. Большая часть проблем в инженерной практике, связанных с вибрацией вала или ротора, возникает вследствие разрушительного влияния на систему статора. Оригинальность данной работы в том, что для определения возникающих при контакте сил нормального давления и сухого/полусухого трения используются гармонические перемещения, скорости и ускорения, т.е. уравнение нормальных колебаний, эквивалентной системы “гибкий ротор – податливый статор”. Рассматривается как система “гибкий ротор – упругие подшипники – фундамент”, кратко называемая исходной роторной, так и система “гибкий ротор – упругие подшипники – жесткий статор – упругие опоры – фундамент”, которая просто называется исходной роторно-статорной. В эквивалентной системе непосредственный контакт между гибким ротором и податливым статором представляется в виде дополнительной линейно упругой связи (пружины) между ними жесткостью kk (контактная жесткость). Причем наряду с динамическими параметрами эквивалентной системы, называемыми параметрами контактной системы, активно используются динамические характеристики исходной системы при отсутствии в ней явного контакта ротора со статором, которые, в свою очередь, называются характеристиками бесконтактной системы.
Прежде исследователи определяли контактные силы либо динамикой податливого ротора, опертого на жесткий статор [1–5], либо жесткостью и демпфированием податливого статора [6–13], нормальная реакция которого в месте контакта имеет линейную [6–8] или нелинейную [9–11] или обобщенную в виде гистерезисной петли характеристику. В последнем случае учитываются как деформация статора, так и ее направление [12, 13], а также пластический эффект [13] на пути “нагрузка–разгрузка”. В некоторых работах [9–12] под ”статорной податливостью” понимается, в том числе перемещение статора на упруго-демпферных опорах.
Предложенные модели с жестким статором не позволяют исследовать влияние перемещений статора как упругого и твердого тела, а также виброударные движения системы на основе обыкновенных дифференциальных уравнений.
Недостатками моделей с заданной упруго-диссипативной характеристикой статора N = 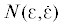 являются эмпирические или теоретические коэффициенты. Например, в широко применяемой
модифицированной модели Герца с вязкой компонентой, с устраненным “прилипанием” и
коэффициентом восстановления, не зависящим от скорости сближения тел $N = {{k}_{k}}{{{\varepsilon }}^{{v}}} + {{d}_{k}}{{{\varepsilon }}^{w}}{\dot {\varepsilon }}$, где ${v} = 3{\text{/}}2$, $w = 1{\text{/}}4$, параметр kk зависит от материалов тел и формы их поверхностей в области контакта, параметр dk определяет значение коэффициента восстановления. В подобных моделях возникает проблема
достоверного получения контактно-динамических характеристик системы, в частности максимальных
ускорений ротора. Отсюда следует уделять отдельное внимание анализу корректности задания
упругой компоненты характеристики статора и добиваться приемлемой точности принятой
модели с помощью подбора параметров вязкой компоненты. Некорректный выбор параметров
компонент может привести к физически неверным результатам, например, к значению коэффициента
восстановления больше единицы.
являются эмпирические или теоретические коэффициенты. Например, в широко применяемой
модифицированной модели Герца с вязкой компонентой, с устраненным “прилипанием” и
коэффициентом восстановления, не зависящим от скорости сближения тел $N = {{k}_{k}}{{{\varepsilon }}^{{v}}} + {{d}_{k}}{{{\varepsilon }}^{w}}{\dot {\varepsilon }}$, где ${v} = 3{\text{/}}2$, $w = 1{\text{/}}4$, параметр kk зависит от материалов тел и формы их поверхностей в области контакта, параметр dk определяет значение коэффициента восстановления. В подобных моделях возникает проблема
достоверного получения контактно-динамических характеристик системы, в частности максимальных
ускорений ротора. Отсюда следует уделять отдельное внимание анализу корректности задания
упругой компоненты характеристики статора и добиваться приемлемой точности принятой
модели с помощью подбора параметров вязкой компоненты. Некорректный выбор параметров
компонент может привести к физически неверным результатам, например, к значению коэффициента
восстановления больше единицы.
2. Моделирование системы “гибкий ротор–податливый статор”. Для исследования динамики ротора, контактирующего со статором, необходимо построить колебательную модель, имеющую две степени свободы или больше, т.е. содержащую, по меньшей мере, несколько инерционных, упругих и демпфирующих элементов.
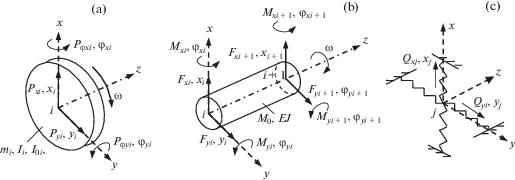
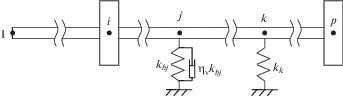
Роторная система или ситуация жесткозакрепленного статора. Любую осесимметричную роторную систему выгодно (поскольку просто, в том числе с точки зрения выполнения достаточно точных расчетов) представлять в виде комбинации трех конечных элементов. Конечные элементы ротора, в том числе их обобщенные силы и перемещения, показаны на рис. 1, где a – жесткий диск, b – балочный элемент, c – линеаризованная “короткая” опора.
a) Жесткий диск с сосредоточенными массой mi, поперечным Ii и полярным I0i моментами инерции. Уравнение двумерного11 движения такого диска, вращающегося с постоянной угловой скоростью ω, в неподвижной системе отсчета и матричной форме [14]:
b) Вращающийся балочный элемент длиной l, радиуса r, с распределенными инерционно-упругими параметрами и внутренним трением гистерезисного типа. Уравнение движения такого балочного элемента в принятой форме [15, 16]:
Любой из элементов матриц этого уравнения является обобщенной силой в узле i, возникающей от единичного(й) ускорения (скорости) или перемещения в этом или i + 1 узле.
В данном общем случае элемент представляет собой балку Тимошенко, т.е. наряду с классическими процессами упругости (подматрицы [k]) и инерции прецессии, включающими поступательные перемещения (подматрицы [mt]) и гироскопическое действие (подматрицы [g]), учитываются инерция вращения (подматрицы [mr], добавляемые к [mt]) и деформация сдвига (s-члены). Если отношение длины элемента к его диаметру получается больше единицы и меньше трех, то допустимо (с точки зрения сохранения высокой точности расчетов) пренебрежение влиянием деформации сдвига (использование балки Релея). Если ${1 \mathord{\left/ {\vphantom {1 {(2r)}}} \right. \kern-0em} {(2r)}} > 3$, то возможно рассмотрение без инерции вращения (т.е. балки Бернулли–Эйлера).
Принято, что балочный элемент обладает диссипацией, которая не зависит от частоты. Напряжение опережает соответствующую деформацию на угол ${\theta }$, который определяется материалом. Петля гистерезиса в плоскости напряжение–деформация повторяет эллипс, площадь которого пропорциональна sinθ и характеризует величину рассеянной энергии, так что $\sin {\theta } = {{{{{\eta }}_{{\text{h}}}}} \mathord{\left/ {\vphantom {{{{{\eta }}_{{\text{h}}}}} {\sqrt {1 + {\eta }_{{\text{h}}}^{2}} }}} \right. \kern-0em} {\sqrt {1 + {\eta }_{{\text{h}}}^{2}} }}$, где ηh – коэффициент гистерезисных потерь в материале балки.
c) Линеаризованная “короткая” опора, характеризующаяся уравнением вида:
В общем подшипник, препятствуя также угловым перемещениям ротора, определяется 16 коэффициентами жесткости и 16 коэффициентами неупругого сопротивления, пропорционального скоростям поперечно-угловых деформаций. Угловые коэффициенты оказываются существенными для жесткого ротора или при высших формах колебаний гибкого ротора. Однако в таких случаях так называемые “длинные” подшипники часто заменяются парой близкорасположенных “коротких” подшипников.
Как правило, заметную роль играют только радиальные коэффициенты:
Существенные побочные коэффициенты жесткости kxy, kyx (относительно главных kxx, kyy) и вязкого демпфирования cxy, cyx (относительно cxx, cyy) характерны для подшипника жидкостного трения. Вместе с тем следует учитывать, что обычно такой подшипник значительно неконсервативен, т.е. его матрица жесткости (демпфирования) значительно асимметрична [17, 18]. Разность побочных коэффициентов жесткости Δkij = kxy – kyx определяет направление действия на ротор “циркуляционной” результирующей, что в случае немалости Δkij по сравнению с главными коэффициентами жесткости приводит к циркуляции (прецессии) ротора, причем при kxy < kyx к обратной, при kxy > kyx к прямой. Последнее непосредственно связано с возникновением явления динамической неустойчивости ротора на подшипниках жидкостного трения (в виде его значительной прямой асинхронной прецессии).
Здесь следует обратить внимание, что подшипник с равными главными коэффициентами жесткости (kxx = kyy) и малыми по сравнению с ними побочными коэффициентами жесткости (kxy ≈ kyx ≈ 0) называется изотропным. Подшипник с равными главными, а также с немалыми и почти одинаковыми побочными коэффициентами жесткости (kxy ≈ kyx ≠ 0) называется ортотропным. Подшипник с неравными главными (kxx ≠ kyy) и близкими к нулю или друг к другу побочными (kxy ≈ kyx ≈ 0 или kxy ≈ kyx ≠ 0) коэффициентами жесткости называется анизотропным, а подшипник со значительными и несовпадающими побочными (kxy ≠ kyx ≠ 0) – неконсервативным.
Также важно отметить, что место непосредственного контакта ротора со статором формально аналогично “короткой” опоре, лишенной вязкого трения, поэтому:
Так как сцепление роторных элементов производится в осевом направлении, переход от местных координат элементов к общим координатам роторной системы тривиален. Он не содержит геометрических преобразований и сводится к простому последовательному нумерованию обобщенных перемещений/сил. Правило составления роторной системы таково, что если два элемента связаны, то перемещения смежных концов должны быть равны, а соответствующие обобщенные силы должны суммироваться. Эта методика, называемая сборкой элементов, так или иначе, обсуждается в любом пособии по матричному структурному анализу.
Конечным результатом является система линейных дифференциальных уравнений с постоянными коэффициентами вида:
(2.1)
${{{\text{[M]}}}_{{2n \cdot 2n}}}{{\{ \ddot {q}\} }_{{2n \cdot 1}}} + {{[C]}_{{2n \cdot 2n}}}{{\{ \dot {q}\} }_{{2n \cdot 1}}} + {{{\text{[K]}}}_{{2n \cdot 2n}}}{{\{ q\} }_{{2n \cdot 1}}} = {{{\text{\{ F\} }}}_{{2n \cdot 1}}}$Число степеней свободы в плоскости n равно 2p, где p – число узлов, а (p – 1) – число балочных элементов. Векторы порядка $n \cdot 1$ образуются из совершающихся в плоскости поступательных и угловых перемещений узлов или из действующих в плоскости на некоторые узлы компонент внешних сил, среди которых могут быть и контактные. Подматрицы размера $n \cdot n$ означают сборку из подматриц или из констант конечных элементов.
Подматрицы инерции [M], гироскопических моментов [G] и жесткости [K] балочных элементов являются ленточными вида:
Инерционная [Md] и гироскопическая [Gd] подматрицы дисков, а также подматрица жесткости подшипников [Kb] диагональные вида ${{[ \ddots ]}_{{n \cdot n}}}$, поэтому их объединение с подматрицами балочных элементов может быть выражено как:
Здесь под каждым двузначным индексом понимается номер строки и номер столбца объединенных матриц, которые определяются тем или иным номером узла, константа Ci равна mi, константа Ci + 1 равна Ii или I0i, константа Cj равна kbj. В качестве примера можно посмотреть на рис. 2, где схематизируется произвольная роторная система и ее p узлов.
Константа Сk, равная kk, добавляется в матрицу жесткости роторной системы ${{[K]}_{{n \cdot n}}}$ = [K] + [Kb], когда k-е или/и другое сечение гибкого ротора контактирует с упругой поверхностью неподвижного статора. Получающаяся матрица жесткости контактной (эквивалентной) роторной системы далее обособляется тильдой ${{[\tilde {K}]}_{{n \cdot n}}} = [K] + [{{K}_{b}}]$ + [Kk], где [Kk] – κ-заполненная диагональная матрица, κ – количество мест контакта.
Так как система осесимметричная, допустима более компактная форма (2.1) за счет объединения матричных уравнений
где ${{[{\text{M}}]}_{{n \cdot n}}} = [M] + [{{M}_{d}}]$, $[{\text{G}}] = [G] + [{{G}_{d}}]$.В результате, определяя перемещения в плоскости xz действительными, а перемещения в плоскости yz мнимыми, т.е. рассматривая векторы комплексных обобщенных координат ${{\{ q\} }_{{n \cdot 1}}} = \{ {{q}_{x}}\} + {\text{i}}\{ {{q}_{y}}\} $ и сил ${{{\text{\{ F\} }}}_{{n \cdot 1}}} = \{ {{F}_{x}}\} + {\text{i}}\{ {{F}_{y}}\} $, будет:
В приведенных уравнениях перемещения элементов считаются малыми (гироскопические моменты и позиционные силы линеаризованы). Хотя теория ограничивается малыми амплитудами (колебаний элементов), она дает удивительно хорошие результаты для больших амплитуд (колебаний ротора в целом). При этом основное правило простое – число используемых балочных элементов должно на единицу превышать номер наивысшей интересующей частоты и формы собственных колебаний ротора. Достаточность малого числа степеней свободы для точного моделирования объясняется слабой зависимостью динамической реакции ротора от его высших форм колебаний.
Роторно-статорная система или ситуация упругозакрепленного статора. Обычно в роторных машинах жесткость статора на отклонение его поперечных сечений от плоскостей, перпендикулярных оси вращения недеформированного ротора, превышает, по меньшей мере, вдвое жесткость ротора на изгиб.
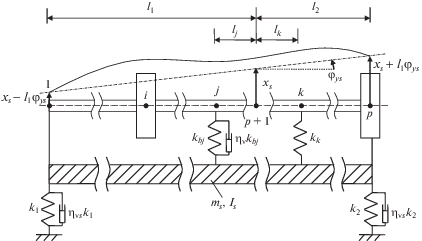
При моделировании практически применяемой осесимметричной статорной подсистемы, т.е. состоящей из сравнительно жесткого и одновременно равножесткого корпуса, а также из нежестких и вместе с тем одинаковой жесткости элементов крепления к фундаменту, подходяще выбрать ее дискретное представление. Другими словами, в виде сосредоточенных в p + 1 узле массы ms и момента инерции относительно поперечных осей Is с линейными связями, в том числе c упруго-демпферными опорами суммарной в плоскости жесткостью ks = k1 + k2 и общим для той же плоскости коэффициентом вязкого демпфирования ηvsks = ηvsk1 + ηvsk2. Произвольная роторно-статорная система и ее p + 1 узлов продемонстрирована на рис. 3.
Пусть координатами центра инерции статора являются xs, ys, φys, φxs, и его поступательные/угловые колебания как отдельного твердого тела на податливых опорах малы, тогда уравнения его движения в поперечных направлениях и вокруг центра инерции (точки p + 1) примут вид:
Очевидно, такой подход обеспечивает наименьшее число необходимых степеней свободы роторно-статорной системы. Системными векторами и матрицами будут:
(2.3)
${{{\eta }}_{{\text{v}}}}{{[{{K}_{b}}]}_{{n + 2 \cdot n + 2}}} = {{{\eta }}_{{\text{v}}}}\left[ {\begin{array}{*{20}{c}} {..}&{}&{}&{}&{} \\ {}&{{{k}_{{bj}}}}&{}&{ - {{k}_{{bj}}}}&{} \\ {}&{}&{..}&{}&{} \\ {}&{ - {{k}_{{bj}}}}&{}&{{{{\text{k}}}_{{2(p + 1) - 1\;2(p + 1) - 1}}}}&{{{{\text{k}}}_{{2(p + 1) - 1\;2(p + 1)}}}} \\ {}&{}&{}&{{{{\text{k}}}_{{2(p + 1)\;2(p + 1) - 1}}}}&{{{{\text{k}}}_{{2(p + 1)\;2(p + 1)}}}} \end{array}} \right]$Причем матрица ${{[{\text{K}}]}_{{n + 2 \cdot n + 2}}}$ отличается от матрицы ${{[{\tilde {K}}]}_{{n + 2 \cdot n + 2}}}$ тем, что в первой kk = 0.
3. Реакция осесимметричной системы “гибкий ротор–податливый статор” на контакт. Уравнения либо вида (2.1) с порядком матриц $2n \cdot 2n$ или $2(n + 2) \cdot 2(n + 2)$, либо вида (2.2) с порядком матриц $n \cdot n$ или $(n + 2) \cdot (n + 2)$ могут быть непосредственно использованы для определения реакции прецессирующего ротора на контактные силы. Пусть правую часть (2.1) или (2.2) образуют только компоненты контактных сил, приложенные к k-й точке исходной системы (рис. 4) и вызывающие регулярную (круговую установившуюся) прецессию:
Математические преобразования будут компактнее, если исходить из (2.2):
где $\{ {{f}_{N}}\} = {{\left\{ {..N..} \right\}}^{{\text{т}}}}$, $\{ {{f}_{T}}\} = {{\left\{ {..Т..} \right\}}^{{\text{т}}}}$, индексы $n \cdot n$ или $n + 2 \cdot n + 2$ опущены.Как видно, это стандартная конечно-элементная формулировка системы “ротор–статор”. Исходный ротор на n подшипниках представлен комбинацией трех конечных элементов (жесткий диск, балочный элемент и линеаризованная вязкоупругая опора) и сосредоточенно нагружен (в k-й точке) силами нормального давления N и сухого трения T = μN.
Однако силовое (граничное) условие в месте контакта неоднозначно. Оно может быть каким угодно – жестким или упругим, линейным или нелинейным, точечным или рассредоточенным по площадке, с сухим или “полусухим” трением. Поэтому существует потребность в физическом преобразовании (методе), который позволял бы априори неизвестные контактные силы исходной системы исключать из рассмотрения.
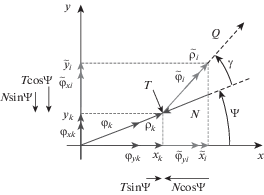
Как следствие, логичным является следующее предложение – рассматривать эквивалентную систему – ротор на n + 1 опорах в виде комбинации тех же конечных элементов, в которой дополнительная опора в k-м узле есть нежесткий шарнир (свободное опирание на податливый статор), при этом разгруженную здесь же на величину результирующей Q тех же самых сил N и T = μN, а также с фазовым сдвигом поперечных перемещений (эквивалентной системы относительно исходной) на угол, равный углу трения, т.е. удовлетворяющий тождеству μ = tanγ (рис. 4). Изображены перемещения k-го узла исходной (темн.) и i-го узла эквивалентной (светл.) системы “гибкий ротор–податливый статор”, контактные силы (нормального давления N и сухого трения T = μN), проекции этих сил, нагружающие исходную систему, и их результирующая (Q), разгружающая эквивалентную систему.
Конечно-элементная формулировка эквивалентной системы “ротор–статор” с возросшей поперечной жесткостью (с бóльшими коэффициентами матрицы жесткости по сравнению с исходной системой), а также с противоположно направленными контактными силами:
Так как движение предполагается круговым, стационарным и обратным, то Ψ = = ‒Ωt и решения имеют вид:
Подстановка этих равенств в вышеприведенные уравнения дает:
Если пренебречь гироскопическим влиянием и трением, то:
(3.2)
$\begin{gathered} ({{\Omega }^{2}}[{\text{M}}] - [{\text{K}}])\{ A\} = \{ {{f}_{N}}\} \\ ([{\tilde {K}}] - {{\Omega }^{2}}[{\text{M}}])\{ \tilde {A}\} = \{ {{f}_{N}}\} \\ \end{gathered} $Исключение правых частей приводит к фундаментальному уравнению безотрывного скольжения ротора по статору (важно обратить внимание, что движение необязательно обратное, вследствие квадрата Ω):
(3.3)
$({{\Omega }^{2}}[{\text{M}}] - [{\text{K}}])\{ A\} = ([{\tilde {K}}] - {{\Omega }^{2}}[{\text{M}}])\{ \tilde {A}\} $Это уравнение линейное, поэтому применим метод суперпозиции мод, т.е. применимы разложение реальных перемещений ротора без опоры {A} и с опорой $\{ \tilde {A}\} $ на статор по собственным формам колебаний свободного от контакта и опертого ротора, а также переход к соответствующим модальным перемещениям:
(3.4)
$\{ A\} = \sum\limits_{v = 1}^s {{{{\{ {\text{u}}\} }}_{{v}}}{{a}_{{v}}}} ,\quad \{ \tilde {A}\} = \sum\limits_{w = 1}^s {{{{\{ {\tilde {u}}\} }}_{w}}{{{\tilde {a}}}_{w}}} $После подстановки (3.4) в матричные уравнения (3.2), преобразования каждого из них к приведенному виду, т.е. умножения слева на [M]–1, а также после левого умножения их на “резонирующую” или характерную форму колебаний $\{ {\text{u}}\} _{i}^{{\text{т}}}$ и $\{ {\tilde {u}}\} _{j}^{{\text{т}}}$ (что представляет собой частотно-избирательный отклик колебательной системы на периодическое внешнее воздействие, который проявляется ростом амплитуды характерных для данной системы колебаний при приближении частоты внешнего воздействия к одной из собственных частот) будет:
Из условия ортогональности собственных форм колебаний (которое можно объяснить как равенство нулю сил инерции i-й (j-й) формы колебаний на перемещениях ${v}$-й (w-й) формы колебаний) следует:
(3.5)
$\begin{gathered} \{ {\text{u}}\} _{i}^{{\text{т}}}{\mathbf{E}}{{\{ {\text{u}}\} }_{{v}}} = 0,\quad \{ {\text{u}}\} _{i}^{{\text{т}}}{\mathbf{D}}{{\{ {\text{u}}\} }_{{v}}} = 0 \\ \{ {\tilde {u}}\} _{j}^{{\text{т}}}{\mathbf{E}}{{\{ {\tilde {u}}\} }_{w}} = 0,\quad \{ {\tilde {u}}\} _{j}^{{\text{т}}}{\mathbf{\tilde {D}}}{{\{ {\tilde {u}}\} }_{w}} = 0 \\ \end{gathered} $Делая замены ${{\{ {\text{u}}\} }_{i}}{{a}_{i}} = {{\{ A\} }_{i}}$ и ${{\{ {\tilde {u}}\} }_{j}}{{\tilde {a}}_{j}} = {{\{ \tilde {A}\} }_{j}}$, можно получить то, что возможна альтернативная запись фундаментального уравнения (3.3):
Вследствие нормирования по матрице масс (приведения к единичной инерционной матрице):
(3.6)
$\begin{gathered} \{ {\text{u}}\} _{i}^{{\text{т}}}{\mathbf{E}}{{\{ {\text{u}}\} }_{i}} = 1,\quad \{ {\text{u}}\} _{i}^{{\text{т}}}{\mathbf{D}}{{\{ {\text{u}}\} }_{i}} = {\lambda }_{i}^{2} \\ \{ {\tilde {u}}\} _{j}^{{\text{т}}}{\mathbf{E}}{{\{ {\tilde {u}}\} }_{j}} = 1,\quad \{ {\tilde {u}}\} _{j}^{{\text{т}}}{\mathbf{\tilde {D}}}{{\{ {\tilde {u}}\} }_{j}} = {\tilde {\lambda }}_{j}^{2} \\ \end{gathered} $В результате существуют отношения:
Приравнивая, получится что:
Умножая справа на {u}i, это равенство можно свести к зависимости модальной амплитуды для j-й роторной формы при опирании на статор от амплитуды модальных перемещений по i-й собственной форме ротора, свободного от контакта:
(3.7)
${{\tilde {a}}_{j}} = \frac{{{{\Omega }^{2}} - \lambda _{i}^{2}}}{{\tilde {\lambda }_{j}^{2} - {{\Omega }^{2}}}}{{\Delta }_{{ji}}}{{a}_{i}}$Амплитуда модальных перемещений по i-й форме свободного ротора ai определяется в задаче бесконтактной динамики соответствующего ротора, поэтому, например, как известно, при его неуравновешенности без учета внешнего трения:
Зная вектор и амплитуду относительных (модальных) перемещений при контакте ротора со статором, можно определить реальные амплитуды (амплитуды реальных перемещений) на каждой “контактной” моде:
Суммируя реальные амплитуды на всех рассмотренных модах, можно найти амплитуды реальных контактных перемещений ротора:
Так как выборка зазора между ротором и статором – результат динамического прогиба бесконтактной системы, то вектор ${{\{ A\} }_{i}} + {{\{ \tilde {A}\} }_{j}}$ – полные реальные перемещения узлов контактной системы. В сущности, суммарные перемещения ${{\{ A\} }_{i}} + {{\{ \tilde {A}\} }_{j}}$ определяют радиусы орбит кругового движения различных сечений ротора при его постоянном контакте со статором, которые показательно соотносить с величиной радиального зазора δ = R – r, где r и R – радиусы поверхностей ротора и статора в месте их контакта.
Так как {fN} > 0, то на основании (3.2) должно быть:
Замены (3.4), умножения слева на [M]–1, а затем на $\{ {\text{u}}\} _{i}^{{\text{т}}}$, $\{ {\tilde {u}}\} _{j}^{{\text{т}}}$, вследствие (3.5), дают:
В результате (3.6) и объединения неравенств:
Отношение (3.7) описывает реакцию невращающейся недемпфированной системы “гибкий ротор–податливый статор” на установившийся контакт, что возможно при выполнении условия существования или устойчивости безотрывного движения ротора по статору (3.8).
В случае зависимости частот и форм собственных колебаний λωi, {uω}i и ${{{\tilde {\lambda }}}_{{{\omega }j}}}$, {ũω}j от скорости вращения (когда учитываются эффекты вращения: гироскопическое действие, внутреннее, внешнее и контактное трение) “гироскопический вклад” и “вклад трения” могут быть проанализированы по отдельности. Это допустимо ввиду пренебрежимо слабого влияния трения на собственные частоты и формы колебаний.
Влияние трения на обкатывание ротором статора. Возвратившись к уравнениям обратного безотрывного движения ротора по статору (3.1) без учета гироскопических моментов, разделяя вещественные и мнимые части, можно получить:
(3.9)
$\begin{array}{*{20}{c}} {({{\Omega }^{2}}[{\text{M}}] - [{\text{K}}])\{ A\} = \{ {{f}_{N}}\} } \\ {\left( {{{{\eta }}_{{\text{h}}}}[K] + {{{\eta }}_{{{\text{h}}b}}}[{{K}_{b}}] + \Omega {{{\eta }}_{{\text{v}}}}[{{K}_{b}}]} \right)\{ A\} = \{ {{f}_{T}}\} } \\ \begin{gathered} ([{\tilde {K}}] - {{\Omega }^{2}}[{\text{M}}])\{ \tilde {A}\} \cos {\gamma } + \\ + \;\left( {{{{\eta }}_{{\text{h}}}}[K] + {{{\eta }}_{{{\text{h}}b}}}[{{K}_{b}}] + {{{\eta }}_{{{\text{h}}k}}}[{{K}_{k}}] + \Omega {{{\eta }}_{{\text{v}}}}[{{K}_{b}}]} \right)\{ \tilde {A}\} \sin {\gamma } = \{ {{f}_{N}}\} \\ \end{gathered} \\ \begin{gathered} - \left( {{{{\eta }}_{{\text{h}}}}[K] + {{{\eta }}_{{{\text{h}}b}}}[{{K}_{b}}] + {{{\eta }}_{{{\text{h}}k}}}[{{K}_{k}}] + \Omega {{{\eta }}_{{\text{v}}}}[{{K}_{b}}]} \right)\{ \tilde {A}\} \cos {\gamma } + \\ + \;([{\tilde {K}}] - {{\Omega }^{2}}[{\text{M}}])\{ \tilde {A}\} \sin {\gamma } = \{ {{f}_{T}}\} \\ \end{gathered} \end{array}$Очевидно и ожидаемо, сила нормального давления {fN} содействует силам упругости [K]{A} исходного ротора, который условно не опирается на статор, а силы трения (ηh[K] + ηhb[Kb] + Ω${{\eta }_{{v}}}$[Kb]){A} противодействуют силе (уравновешивают силу) контактного трения $\{ {{f}_{T}}\} $. Однако результирующая контактных сил {fQ} = 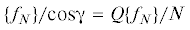 = =
= = 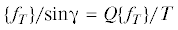 противоположна восстанавливающим силам $[{\tilde {K}}]\{ \tilde {A}\} $ опирающегося (эквивалентного) ротора, т.е. сила Q по отношению к нему является возмущающей.
противоположна восстанавливающим силам $[{\tilde {K}}]\{ \tilde {A}\} $ опирающегося (эквивалентного) ротора, т.е. сила Q по отношению к нему является возмущающей.
Если разложить бесконтактные {A} и контактные $\{ \tilde {A}\} $ реальные перемещения по собственным формам и перейти к модальным перемещениям, т.е. если подставить (3.4) в (3.9), а затем умножить полученные уравнения слева на [M]–1, а также на характерные формы $\{ {\text{u}}\} _{i}^{{\text{т}}}$ и $\{ {\tilde {u}}\} _{j}^{{\text{т}}}$, то:
Собственные векторы динамических матриц ортогональны, поэтому выполняются равенства (3.5), (3.6) и:
Как следствие, система уравнений обкатывания упрощается, в частности до:
Исключение $\{ {{f}_{N}}\} $ и $\{ {{f}_{T}}\} $ дает:
Умножение справа на {u}i приводит к:
Неизвестные амплитудные множители ${{\tilde {a}}_{j}}\cos {\gamma }$ и ${{\tilde {a}}_{j}}\sin {\gamma }$ найдутся из отношений:
Отсюда, вследствие малости произведения ${{{\varepsilon }}_{{\eta }}} \cdot {{{\tilde {\varepsilon }}}_{{\eta }}}$, а также квадратов ${\varepsilon }_{{\eta }}^{{\text{2}}}$ и ${\tilde {\varepsilon }}_{{\eta }}^{{\text{2}}}$, во-первых:
во-вторых:
Очевидно, формула для расчета Ω будет громоздкой, поэтому разумно отыскать упрощенное решение с помощью проверенного подхода [19].
При отсутствии вязкого и гистерезисного демпфирования будет:
С трением будет:
где λ – та или иная круговая собственная частота бесконтактной или контактной недемпфированной/невращающейся системы, Δ – некоторая поправка для λ от трения.Представление как |Ω| = λ(1 + ε), где ε = Δ/λ – малая поправка, и подстановка этого и приближенных выражений
в уравнение четвертой степени раскрывают введенную ε-поправку:Как правило, гистерезисные потери в материалах ротора, подшипников и статора незначительно разнятся ${{{\eta }}_{{\text{h}}}} \approx {{{\eta }}_{{{\text{h}}b}}} \approx {{{\eta }}_{{{\text{h}}k}}} \approx {\eta }$, где η – коэффициент гистерезисных потерь в материалах системы.
В результате:
Как следствие:
При ${{\eta }_{{v}}}$ = 0:
Имеющаяся неоднозначность ${\lambda } = {{{\lambda }}_{i}}$ или ${\lambda } = {{{\tilde {\lambda }}}_{j}}$ устранима, если проанализировать аналитические выражения:
С приближением η к μ значения скорости обкатки Ω по модулю в первом случае неограниченно возрастают, во втором – уменьшаются без разрыва. Физически увеличение трения не может давать увеличение скорости, отсюда λ не может быть равной λi.
Таким образом, ε-добавка к ${{{\tilde {\lambda }}}_{j}}$, определяющая Ω, т.е. угловую скорость обратного безотрывного движения ротора по статору, вследствие трения:
илиПоскольку $\tilde {s}_{{bj}}^{*} = \{ {\tilde {u}}\} _{j}^{{\text{т}}}{{[{\text{M}}]}^{{--{\text{1}}}}}[{{K}_{b}}]{{\{ {\tilde {u}}\} }_{j}}$, то как при малом вязком демпфировании, так и при мягких опорах ротора и/или статора члены с множителем ηv будут близкими к нулю:
Конструкционное демпфирование, в частности рассмотренного гистерезисного и вязкого типа, во многом определяется качеством изготовления деталей и сборки механизма или машины. При этом точность оценки трения зависит от экспериментальной конструкции, измерительного оборудования, а также от так называемого человеческого фактора. Вкупе, ожидаема погрешность, соизмеримая с результатом приближения как по менее (3.10), так и по максимально упрощенной формуле (3.11). И, наоборот, формулы (3.10) и (3.11) удовлетворительно соответствуют действительности.
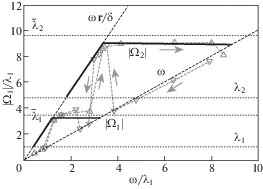
На рис. 5 проиллюстрированы угловые скорости обратной прецессии материализованного ротора, обкатывающего в одном из своих сечений статор, предсказываемые теорией (темными линиями) и наблюдавшиеся в экспериментах при постепенном разгоне-останове (точками, соединенными светлыми линиями со стрелками).
4. Заключение. В отличие от существующих представлений при построении модели “ротор–статор” для определения возникающих при контакте сил нормального давления и сухого/полусухого трения используются не коэффициенты контактной жесткости и контактного демпфирования, а вибрационные перемещения, скорости и ускорения эквивалентной системы, т.е. уравнение ее нормальных колебаний. Тем самым априори неизвестные контактные силы исходной системы исключаются из рассмотрения. Причем под исходной системой понимается n-опорный ротор, загруженный на величину результирующей Q контактных сил, а под эквивалентной – ротор на n+1 опорах с возросшей поперечной жесткостью (с бóльшими по сравнению с n-опорным коэффициентами матрицы жесткости), и разгруженный на такую же величину Q.
Анализ динамических характеристик линеаризованной изотропной системы (возможных частот и амплитуд обратной прецессии ротора при обкатке им статора) выполнен в общем виде на основе балочной модели с учетом гироскопического действия. При этом применяются матричные методы, разложение роторных перемещений по собственным формам колебаний, а также введение малого параметра – малой добавки к собственным частотам – поправки на конструкционное и контактное трение в системе.
Полученные основные теоретические результаты согласуются с известными экспериментальными. Во-первых, условиями устойчивости обкатки являются:
Во-вторых, угловая скорость прецессии ротора при обкатке статора с проскальзыванием между ними близка к ${{{\tilde {\lambda }}}_{j}}$, а именно:
В-третьих, трение, препятствуя прямому скольжению, т.е. делая его неустойчивым режимом контактной ненагруженной (прочими силами неконтактного происхождения) изотропной системы “ротор–статор”, приводит к установлению в ней обратного безотрывного движения. При этом оно слабо влияет на амплитуду прецессии, которой сопровождается обкатка, но задает частоту этой прецессии. Вследствие влияния трения частота обкатывания ротором статора при проскальзывании между ними оказывается всегда несколько ниже той или иной собственной частоты контактной системы. Причем без конструкционного демпфирования контактное трение никак не влияет на частоту обкатки.
Работа выполнена при финансовой поддержке Минобрнауки России в рамках Федеральной целевой программы “Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2014–2020 годы”, Соглашение о предоставлении субсидии № 14.607.21.0191 от 26.09.2017 г., проект RFMEFI60717X0191.
Список литературы
Begg I.C. Friction Induced Rotor Whirl – A Study in Stability // ASME Journal of Engineering for Industry. 1974. V. 96. № 2. P. 450–454.
Позняк Э.Л. Крутильный удар в валопроводе при внезапной и сильной разбалансировке одного из роторов // Машиноведение. 1987. № 5. С. 66–74.
Ахметишен Н.Х., Нагаев Р.Ф. Динамика неуравновешенного ротора с сухим трением в подшипнике // Изв. РАН. МТТ. 1995. № 5. С. 57–63.
Shen X., Jia J., Zhao M. Effect of parameters on the rubbing condition of an unbalanced rotor system with initial permanent deflection // Archive of Applied Mechanics. 2007. V. 77. P. 883–892.
Никифоров А.Н. Об обкатке с проскальзыванием ротора по статору и влияние на ее частоту трения и гироскопических моментов // Справочник. Инженерный журнал. 2018. № 9. С. 21–31.
Grapis O., Tamuzs V., Ohlson N.G., Andersons J. Overcritical high-speed rotor systems, full annular rub and accident // Journal of Sound and Vibration. 2006. V. 290. P. 910–927.
Yu J.J., Goldman P., Bently D.E., Muszynska A. Rotor/Seal Experimental and Analytical Study on Full Annular Rub. // ASME Journal of Engineering for Gas Turbines and Power. 2002. V. 124. № 2. P. 340–350.
Куракин А.Д., Нихамкин М.Ш., Семенов С.В. Динамика неуравновешенного гибкого ротора в анизотропных опорах при контакте со статором // Вестник Пермского национального исследовательского политехнического университета. Механика. 2016. № 4. С. 364–381.
Sawicki J.T., Montilla-Bravo A., Gosiewski Z. Thermomechanical Behavior of Rotor with Rubbing // International Journal of Rotating Machinery. 2003. V. 9. № 1. P. 41–47.
Zhang G.F., Xu W.N., Xu B., Zhang W. Analytical study of nonlinear synchronous full annular rub motion of flexible rotor–stator system and its dynamic stability // Nonlinear Dynamics. 2009. V. 57. P. 579–592.
Lahriri S., Weber H.I., Santos I.F., Hartmann H. Rotor-stator contact dynamics using a non-ideal drive – Theoretical and experimental aspects // Journal of Sound and Vibration. 2012. V. 331. P. 4518–4536.
Костюк А.Г., Шатохин В.Ф., Циммерман С.Д. Численное моделирование нестационарных колебаний после внезапной разбалансировки многоопорного ротора с обкатом неуравновешенного ротора по статору // Авиационно-космическая техника и технология. 2011. № 8 (85). С. 81–93.
Никифоров А.Н., Шохин А.Е. Упругопластическая вязкая модель ударного и безотрывного взаимодействия ротора со статором // Изв. РАН. МТТ. 2016. № 1. С. 67–78.
Крестниковский К.В., Никифоров А.Н., Шохин А.Е. Частота обкатки ротором статора в зависимости от величины зазоров между ними // Справочник. Инженерный журнал. 2018. № 8. С. 24–38.
Zorzi E.S., Nelson H.D. Finite Element Simulation of Rotor-Bearing Systems with Internal Damping // ASME Journal of Engineering for Power. 1977. V. 99. № 1. P. 71–76.
Nelson H.D. A Finite Rotating Shaft Element Using Timoshenko Beam Theory // ASME Journal of Mechanical Design. 1980. V. 102. № 4. P. 793–803.
Леонтьев М.К., Давыдов А.В., Дегтярев С.А. Динамическая устойчивость ротора турбогенератора // Газотурбинные технологии. 2012. № 4 (105). С. 36–40.
Подольский М.Е. Физическая природа и дискуссионные вопросы теории масляных вибраций // Теория механизмов и машин. 2009. Т. 7. № 13. С. 42–59.
Брысин А.Н., Никифоров А.Н. О подходе к определению собственных частот гироскопической системы с трением в общем виде // Изв. РАН. МТТ. 2019. № 3. С. 100–107.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела


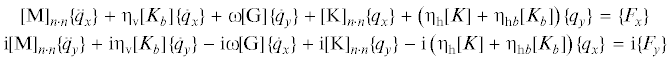
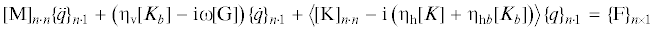
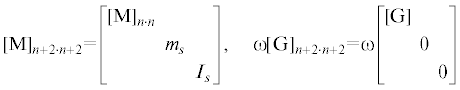

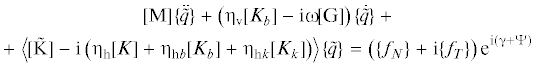
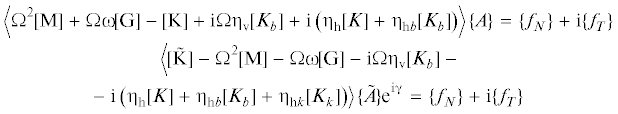
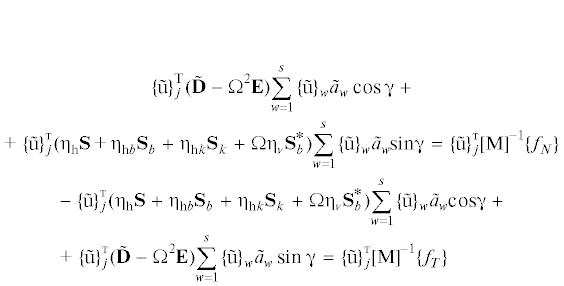
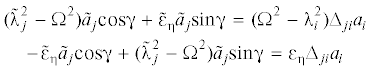
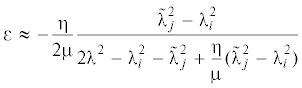
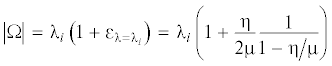 и
и