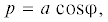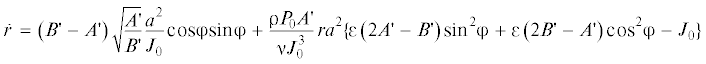Известия РАН. Механика твердого тела, 2020, № 2, стр. 88-95

1. Введение. Спутник или космический корабль в своем движении относительно центра масс подвержен влиянию моментов сил различной природы. На них действуют, например, моменты сил, обусловленные движением некоторых масс внутри тела. Эти движения могут быть связаны с наличием жидкости в полостях, расположенных в теле (например, жидкого топлива или окислителя в баках ракет).

Задачи динамики твердого тела с полостями, содержащими вязкую жидкость, представляют бо́льшие трудности, чем в случае идеальной жидкости. Важный вклад в решение этих задач внесли работы Ф.Л. Черноусько с соавторами [1, 2]. В них рассматриваются движения тела с полостью, заполненной вязкой жидкостью. Получено асимптотическое решение, описывающее эволюцию движения тела, имеющего полость с жидкостью большой вязкости, на большом интервале времени.

В работе А.И. Кобрина [3] методом пограничного слоя исследован начальный участок вращения тела с полостью, содержащей жидкость большой вязкости. Статья [4] посвящена изучению стабилизирующего влияния вязкой жидкости в полости на вращение волчка вокруг заданной оси. В работе [5] исследуются колебания на эллиптической орбите твердого тела со сферической полостью, заполненной вязкой жидкостью, при малых числах Рейнольдса. В статье [6] асимптотическим методом изучается движение по инерции твердого тела со сферической или эллипсоидальной полостью, заполненной вязкой жидкостью. В статьях [7, 8, 10] и книге [9] исследуются быстрые вращательные движения относительно центра масс динамически несимметричного спутника с полостью, целиком заполненной жидкостью большой вязкости, под действием моментов сил гравитации, светового давления и сопротивления среды. В работе [11] проведен численный анализ изменения вектора кинетического момента твердого тела с полостью, заполненной вязкой жидкостью. В [12] представлено численное решение задачи о движении тела с полостью кубической формы, заполненной вязкой жидкостью, вокруг неподвижной точки. В статье [13] представлены аналитические и численные результаты, полученные при исследовании системы, состоящей из твердого тела с полостью, заполненной вязкой жидкостью. В работе [14] предложен подход для моделирования динамики твердого тела с полостью, целиком заполненной жидкостью большой вязкости. Хаотические движения твердого тела и спутника с полостью, заполненной жидкостью, исследуются в статьях [15, 16]. Книга [17] посвящена аналитическим приближенным методам в нелинейной динамике твердого тела с полостями, частично заполненными жидкостью. В [18] рассматриваются некоторые задачи управления вращающимися твердыми телами с полостями, заполненными идеальной или вязкой жидкостью. В статье [19] исследуется оптимальное торможение вращающегося несимметричного тела с полостью, заполненной вязкой жидкостью, в среде с сопротивлением. В [20] получены и исследованы уравнения движения системы n связанных твердых тел с полостями, заполненными вязкой жидкостью.

В основе астрометрических исследований лежит динамическая теория вращения Земли относительно центра масс [21, 22]. В работе [23] отмечается, что с позиций теоретической механики проблема анализа процесса колебаний полюса Земли аналогична задаче исследования движений оси гироскопа под действием возмущающих моментов сил и с учетом вязкоупругих деформаций в квазистатическом приближении.

2. Постановка задачи. Рассмотрим свободное движение в пространстве твердого тела с вязкой жидкостью относительно центра инерции. Здесь O₁y₁y₂y₃ – движущаяся поступательно система координат с началом, связанным с центром инерции системы. Тензор P = (P_ij) задается в виде P_ij = P₀δ_ij, где δ_ij – символ Кронекера, скалярный коэффициент P₀ > 0. Данный вид тензор P имеет в случае сферической полости, для которой согласно [1, 2] значение параметра P₀ = 8πb⁷/525, где b – радиус полости. Через A, B, C обозначим главные центральные моменты инерции системы, через p, q, r – проекции абсолютной угловой скорости ω на главные центральные оси инерции. Уравнения движения запишем в проекциях на главные центральные оси инерции (точка – производная по времени t):

Выражение в правой части (2.1) определяет в асимптотическом приближении момент сил вязкой жидкости в полости тела [1, 2].

Остальные уравнения получаются из (2.1) циклической перестановкой символов A, B, C и p, q, r.

Рассмотрим случай сфероида, т.е. тела, когда главные центральные моменты инерции “замороженного” твердого тела близки друг к другу и представим их в виде:

где 0 < ε $ \ll $ 1 – малый параметр. При ε = 0 уравнения (2.1) описывают движение сферически симметричного тела.

Предположим также, что имеют место оценки:

Тогда, следуя (2.2), (2.3), имеют место выражения:

После перехода к медленному времени τ = εt (далее точка – производная по времени τ) и формальных преобразований системы (2.1) с учетом соотношений (2.2)–(2.4) получим возмущенную систему типа Эйлера вида:

В системе уравнений (2.5) введены возмущения. Здесь r – медленная переменная в медленном времени τ. Система дифференциальных уравнений (2.5) – существенно нелинейная система, в которой частота зависит от медленной переменной r.

В (2.5) введены возмущения:

Момент сил трения вязкой жидкости в полости тела является малым [1, 2, 7, 9, 11].

Решение невозмущенной системы (2.5) при значениях ε = 0, 1/ν = 0 имеет вид:

Здесь $a = \sqrt {p_{0}^{2} + {{{({{{\dot {p}}}_{0}}{\text{/}}w)}}^{2}}} $ – амплитуда (медленная переменная), φ – фаза, w = = $\sqrt {A{\text{'}}B{\text{'}}} {{r}_{0}}{\text{/}}{{J}_{0}}$, $A{\text{'}}B{\text{'}} > 0$ по предположению.

Проведем переход от медленных переменных (p, q, r) к новым стандартным медленным переменным a, r и фазе φ. Используем для этого замену переменных:

Продифференцируем выражения (2.8) в силу возмущенной системы. После ряда преобразований получим систему в стандартной форме:

Разрешим уравнения (2.9) относительно $\dot {a}$ и $\dot {\varphi }$. Получим систему вида:

Подставим (2.8) в третье уравнение (2.5) для переменной r. С учетом стандартных преобразований получим следующую систему уравнений:

Здесь величина $w\left( r \right) = \sqrt {A{\text{'}}B{\text{'}}} r{\text{/}}{{J}_{0}}$ имеет смысл возмущенной частоты преобразованной системы. После усреднения системы (2.11) по фазе φ [24–26] находим:

Здесь введены обозначения:

Систему (2.12) преобразуем к виду:

Здесь введены переменные $x = {{a}^{2}}$, $y = {{r}^{2}} > 0$ и параметр .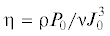

Отметим, что в системе (2.13) x, y – медленные переменные. Разделим первое уравнение (2.13) на второе; получим скалярное уравнение, допускающее элементарное аналитическое интегрирование

Для этого обозначим: $z = x{\text{/}}y$.

Имеем параметры ${\tilde {\alpha }} = 2{\alpha /\gamma }$, 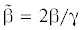и выражение для производной $z{\text{'}} = dz{\text{/}}dy$.

Так как $z = x{\text{/}}y$, то получим линейное уравнение для переменной x:

где $yz{\text{'}} = y\frac{{dz}}{{dy}} = \frac{{dz}}{{d{\theta }}}$; здесь введен аргумент ${\theta } = \ln y$. С учетом введенных ранее обозначений имеет место выражение:

Получим в итоге линейное неоднородное уравнение элементарного вида:

Его решение записывается следующим образом:

Раньше было получено уравнение вида:

Здесь согласно принятому выше обозначению x/y = z.

В результате интегрирования находим первый интеграл:

Подставим выражение (2.19) во второе уравнение системы (2.13), получим следующее уравнение:

Оно допускает разделение переменных y, τ и интегрирование в квадратурах.

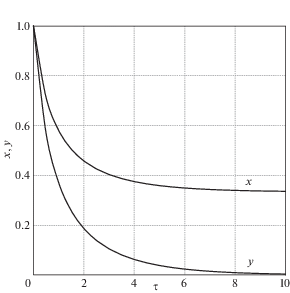
3. Численное интегрирование. Система (2.13) в первом расчетном случае (рис. 1) в силу выбранных значений параметров имеет следующие коэффициенты:

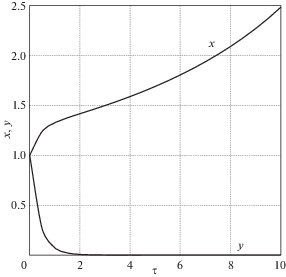
и начальные условия: x(0) = 1, y(0) = 1.

Во втором расчетном случае (рис. 2):

при тех же начальных условиях: x(0) = 1, y(0) = 1.

В обоих случаях y = r² убывает на интервале [0; 10] асимптотически приближаясь к нулю (рис. 1, 2).

В первом случае (рис. 1) x = a² убывает на интервале [0; 10], асимптотически приближаясь к стационарному значению 0.3359. Во втором случае (рис. 2) переменная x возрастает, достигая значения 2.4816 на интервале [0; 10].

Заключение. Исследовано движение близкого к динамически сферическому твердого тела (сфероида) с полостью, целиком заполненной вязкой жидкостью, при малых числах Рейнольдса. Получена уточненная в квадратическом приближении по малому параметру система уравнений движения в стандартной форме. Проанализирована задача Коши для системы, определенной после усреднения. Эволюция движения твердого тела на бесконечном интервале времени описывается решениями, полученными асимптотически, аналитически и численно.

Исследуемая в работе модель представляет определенный естественнонаучный, познавательный интерес для динамики фигуры Земли.

Работа выполнена при частичной финансовой поддержке Российского научного фонда (проект № 16-11-10343).