Известия РАН. Механика твердого тела, 2020, № 2, стр. 64-76

Введение. Элементы современных конструкций трудно представить без различных покрытий или тонких пленок, выполняющих различные функции-усиливающие, антикоррозионные, термобарьерные. Важным этапом исследования является изучение их работоспособности, причем основным механизмом нарушения их функционального назначения является отслоение. Иногда предварительно напряженные покрытия отслаиваются под действием продольных сжимающих сил, происходит выпучивание в области отслоения или коробление.

Классическими работами, которые посвящены данной проблематике, можно считать работы [1–4]. В них вопрос деформирования покрытия в зоне отслоения рассмотрен с различных позиций.

В работе [1] участок отслоения моделировался в виде жестко-защемленной пластины. Результат работы – подробное описание закритического поведения. В работах [2–4] подробно изучалась система покрытие-подложка. В частности, в работе [2] была получена взаимосвязь энергии отслоения пленки с жесткостью подложки. В работе [3] был предложен новый метод для анализа распределения касательных напряжений по границе отслоения пленки от подложки, а также скорости высвобождения энергии. Отслоение в работе [4] моделировалось для балочной модели, а акцент делался на изучение влияния податливости подложки, с ссылками на более раннюю работу [2]. Была определена средняя скорость высвобождения энергии при расслоении системы покрытие-подложка.

В рамках классической теории пластин была представлена работа [5]. В ней решена задача потери устойчивости сжатой в собственной плоскости пластины с некоторой областью отслоения, лежащей на упругой подложке, рассматриваемой как неограниченное упругое основание. Проанализированы альтернативные формулировки граничных условий и условий контакта покрытия с подложкой.

Работа [6] представляет собой значительный вклад в исследование деформирования и устойчивости многослойных пластин. В ней предложена асимптотическая модель для вычисления прогиба и частот свободных колебаний шарнирно-опертой многослойной прямоугольной нанопластины с графеновыми слоями. Многослойная пластина заменена эквивалентной пластиной Тимошенко–Рейсснера. Результатом работы являются явные формулы для расчета прогиба и частот колебаний.

Зачастую, когда пленки достаточно хрупкие, при изгибном отслоении возникают трещины. Так как отслоение подобного типа происходит на плоских или изогнутых подложках, это имеет важное технологическое значение, особенно на последних. В работе [7] проанализирована механика развития подобных отслоений для алмазоподобных углеродных пленок, расположенных на плоских стеклянных подложках и теплозащитного многослойного слоя на изогнутой подложке из жаропрочного сплава. В  статье [8] дан краткий обзор, в котором сформулированы условия развития трещинообразования.

Ряд работ [9–13] посвящен исследованию расслоения полос или пластин с образованием трещины между слоями

В работах [9–11] изучено расслоение полосы по границе раздела упругих свойств. Задача моделировалась двумя изотропными полосами, разделенными полубесконечной трещиной, проходящей по границе раздела упругих свойств. Исследован случай нормального отрыва, рассмотрен случай сдвиговой трещины, а так же построено точное аналитическое решение для частного случая. В статье [12] покрытие и подложка моделировались в виде двух пластин, однако, особое внимание уделялось граничным условиям – они рассматривались как обобщенные упругие связи. Такой тип граничных условий возникает из решения задачи о двухслойной полосе, нагруженной на бесконечности, ослабленной полубесконечной межфазной трещиной. Было получено аналитическое решение этой задачи для частного соотношения упругих констант слоев, а для общего случая произвольных упругих постоянных и толщин слоев – приближенное решение. В работе [13] было получено точное аналитическое решение, а также асимптотические формулы для полей напряжений вблизи вершины трещины (коэффициенты интенсивности напряжений), а также для относительных перемещений граней трещины, удаленных от ее вершины.

В процессе индентирования некоторых слоистых структур, в результате контактного взаимодействия и внедрения индентора в образец в некоторой области, близкой к контактной, происходит частичное разрушение этих связей, образуется ослабленная зона – зона возможного отслоения. Процесс внедрения инденторов различных типов рассмотрен в работах [14, 15], в которых на основе ряда гипотез сформулированы уточненные балочные модели.

За основу настоящей работы была взята [15], в которой помимо рассмотрения некоторых особенностей индентирования слоистых структур было получено трансцендентное уравнение, связывающее основные параметры модели с критической нагрузкой. В результате действия некоторых факторов (нарушение упругих связей в ограниченной приповерхностной зоне и наличия сжимающих напряжений), в некоторой конечной области происходит потеря устойчивости тонкого слоя образца и выпучивание. Моделирование подобного деформирования описано в рамках модели предварительно напряженного балочного покрытия, которое расположено на упругом основании. Изучено влияние ослабления связей на критические нагрузки, что моделируется уменьшением, возможно до нуля, коэффициентов постели в некоторой области. При исследовании такого рода задач наиболее просто исследуется случай, когда оба коэффициента постели равны нулю. Подобный случай был рассмотрен в работе [16].

В работе [16], в рамках традиционных моделей был исследован вопрос об отслоении покрытия от упругого основания – была решена задача потери устойчивости при осевом сжатии бесконечного покрытия, частично покоящегося на упругом основании. При этом покрытие моделировалось балкой модели Бернулли–Эйлера с постоянным коэффициентом постели.

В настоящей работе на основе моделей, предложенных в [15], изучены основные соотношения для определения параметров критических нагрузок, рассмотрен вопрос потери устойчивости, найдена зависимость критической силы от величины коэффициентов постели.

После определения критической нагрузки в зависимости от основных параметров исследовано закритическое поведение покрытия на основе вариационного подхода, примененного к анализу неквадратичного функционала, аналогично исследованиям, представленных в работах [17, 18].

1. Постановка задачи и ее аналитическое решение. В рамках модели, предложенной в [15], рассматривается равновесие упругого бесконечного покрытия, частично лежащего на упругом основании и находящегося в равновесии под действием сжимающей нагрузки ${{{\sigma }}_{0}}$; будем считать, что отслоение произошло на участке [–b, b]. Поставим задачу об определении критической нагрузки и расчете закритического деформирования.

Согласно работе [14], квадратичный функционал потенциальной энергии для неоднородного покрытия имеет следующий вид

где ${{D}_{0}},{{D}_{1}},{{D}_{2}}$ – в общем случае определяются следующими соотношениями: в которых ${{B}_{1}},{{B}_{2}}$ – коэффициенты постели (для изотропного тела ${{B}_{1}} = {{\left( {{\lambda } + 2{\mu }} \right)} \mathord{\left/ {\vphantom {{\left( {{\lambda } + 2{\mu }} \right)} H}} \right. \kern-0em} H}$, ${{B}_{2}} = {{{\mu }H} \mathord{\left/ {\vphantom {{{\mu }H} 3}} \right. \kern-0em} 3}$; в идейном смысле эти два коэффициента постели аналогичны введенным в модели Пастернака [20], ${{B}_{3}},{{B}_{4}}$ – некоторые постоянные, определенные следующим образом B₃ = $\int\limits_H^{h + H} {{{{\sigma }}_{0}}{{{({{x}_{3}} - H)}}^{2}}d{{x}_{3}}} ,$ ${{B}_{4}}\, = \,\int\limits_H^{h + H} {{{{\sigma }}_{0}}d{{x}_{3}}} ,$ а $D = \int\limits_H^{h + H} {({\lambda } + 2{\mu }){{{({{x}_{3}} - H)}}^{2}}d{{x}_{3}}} $ – аналог изгибной жесткости.

В случае постоянных характеристик покрытия и постоянства ${{\sigma }_{0}}$ коэффициенты ${{D}_{0}},{{D}_{1}}$ упрощаются и задаются соотношениями ${{D}_{0}} = {{\left( {{\lambda } + 2{\mu }} \right){{h}^{3}}} \mathord{\left/ {\vphantom {{\left( {{\lambda } + 2{\mu }} \right){{h}^{3}}} 3}} \right. \kern-0em} 3}$, ${{D}_{1}} = {{B}_{2}} - {{{\sigma }}_{0}}h$.

Представим функционал (1.1), предварительно осуществив обезразмеривание Λ, отнеся его к ${{D}_{0}}$, а также учтем симметричность покрытия

где ${{d}_{1}} = {{{{D}_{1}}} \mathord{\left/ {\vphantom {{{{D}_{1}}} {{{D}_{0}}}}} \right. \kern-0em} {{{D}_{0}}}}$, ${{d}_{2}} = {{{{D}_{2}}} \mathord{\left/ {\vphantom {{{{D}_{2}}} {{{D}_{0}}}}} \right. \kern-0em} {{{D}_{0}}}}$.

Представим безразмерные параметры ${{d}_{1}},\;{{d}_{2}}$ через следующие безразмерные величины $k,\;{\eta },\;{{{\eta }}_{0}}$, пропорциональные силе и двум коэффициентам постели соответственно. Тогда

Учитывая, что после отслоения коэффициенты постели на участке [0; 1] равны нулю, функционал энергии можно представить в виде:

Варьирование функционала приводит к следующим уравнениям:

в зоне прилегания

в зоне отслоения

Отметим, что уравнение (1.4) имеет следующие корни характеристического уравнения ${\lambda } = \pm {\alpha } \pm i{\beta },$ где

Традиционным путем аналогично работе [14] строится решение в каждой подобласти и после выполнения условий сопряжения получается трансцендентное уравнение, связывающее основные параметры модели

и позволяющее оценить зависимость $k$ от других параметров задачи. Как правило, такие зависимости анализируются численно. Заметим, что при ${{{\eta }}_{0}} = 0$ (1.7) переходит в соответствующее уравнение работы [15]. Упростим уравнение (1.7), возведя в квадрат обе его части и, разрешая его относительно ${\eta }$, получим: (индексу 1 соответствует верхний знак, индексу 2 – нижний знак). Отметим, что η₁ будет удовлетворять (1.7) в случае, когда $k \in [{\pi },2{\pi }]$. Поскольку целью исследования является поиск наименьшего значения критической силы, то решение η₁ пока не будем рассматривать, а η₂ представим в более удобном виде:

Отметим, что при ${{{\eta }}_{0}} = 0$ из (1.9) следует ${{k}^{2}} = {\eta }\left( {1 + \cos k} \right)$.

Для анализа решений уравнения (1.9) введем в рассмотрение следующую функцию $f({\eta },k)$:

где $a\left( k \right) = {{{{{\sin }}^{2}}k} \mathord{\left/ {\vphantom {{{{{\sin }}^{2}}k} {{{k}^{2}}}}} \right. \kern-0em} {{{k}^{2}}}}$.

Используем функцию (1.10) для анализа решений уравнения (1.9) на отрезке $k \in [0,{\pi }]$. Сразу отметим, что $\mathop {\lim }\limits_{k \to 0} f\left( {{\eta },k} \right) = 1 - {\eta } - \sqrt {1 + {\eta }_{0}^{2}} < 0$, а $f\left( {{\eta },{\pi }} \right) = 2 > 0$, следовательно, в силу непрерывности рассматриваемой функции на отрезке $k \in \left[ {0,{\pi }} \right]$ существует по меньшей мере один корень уравнения (1.9). Для исследования единственности исследуем введенную функцию на монотонность.

Производная функции (1.10) по $k$ имеет вид:

которая будет положительна, если где $a{\text{'}}(k) = 2{{\sin k} \mathord{\left/ {\vphantom {{\sin k} {{{k}^{3}}}}} \right. \kern-0em} {{{k}^{3}}}}(k{\text{cos}}k - {\text{sin}}k)$.

Отметим, что на отрезке $k \in \left[ {0,\pi } \right]$ неравенство (1.12) будет верно, т.к.

Неравенство (1.13) будет выполнено на отрезке $k \in \left[ {0,{{\pi } \mathord{\left/ {\vphantom {{\pi } 2}} \right. \kern-0em} 2}} \right]$, в силу известного неравенства $\sin k > k\cos k$ [19], а на отрезке $k \in \left[ {{{\pi } \mathord{\left/ {\vphantom {{\pi } 2}} \right. \kern-0em} 2},{\pi }} \right]$, в силу $\cos k < 0$ и $\sin k < 0$. Следовательно, всюду на $k \in \left[ {0,{\pi }} \right]$ (1.13) будет выполнено, что обеспечит положительность производной (1.11). Отсюда следует, что функция (1.10) будет монотонно возрастать на отрезке [0, π] и корень уравнения (1.9) на этом отрезке – единственный.

Сузим отрезок для поиска корня и рассмотрим различные ситуации в зависимости от параметров задачи, для чего найдем$f\left( {{\eta },{{\pi } \mathord{\left/ {\vphantom {{\pi } 2}} \right. \kern-0em} 2}} \right) = 1 - {{4{\eta }} \mathord{\left/ {\vphantom {{4{\eta }} {{{{\pi }}^{2}}}}} \right. \kern-0em} {{{{\pi }}^{2}}}}$. Отметим, что это значение не зависит от параметра ${{{\eta }}_{0}}$.

Исходя из этого, рассмотрим два случая – первый из них – ${\eta } > {{{{{\pi }}^{2}}} \mathord{\left/ {\vphantom {{{{{\pi }}^{2}}} 4}} \right. \kern-0em} 4}$. Тогда $f({\eta },{{\pi } \mathord{\left/ {\vphantom {{\pi } 2}} \right. \kern-0em} 2})$ < 0. Это соответствует большим значениям ${\eta }$, т.е. условно-жесткому основанию, тогда $k \in [\pi {\text{/}}2,\pi ]$, соответствующее значение ${{P}_{{{\text{кр}}}}} = {{EJk_{*}^{2}} \mathord{\left/ {\vphantom {{EJk_{*}^{2}} {{{b}^{2}}}}} \right. \kern-0em} {{{b}^{2}}}}$ будет лежать между значениями критических сил для шарнирно-опертой балки ${{P}_{1}}$ и жестко-защемленной P₂ = ${{EJ{{{\pi }}^{2}}} \mathord{\left/ {\vphantom {{EJ{{{\pi }}^{2}}} {{{b}^{2}}}}} \right. \kern-0em} {{{b}^{2}}}}$ длины $2b$.

Для второго случая примем, что ${\eta } < {{{{{\pi }}^{2}}} \mathord{\left/ {\vphantom {{{{{\pi }}^{2}}} 4}} \right. \kern-0em} 4}$, соответственно, $f\left( {{\eta },{{\pi } \mathord{\left/ {\vphantom {{\pi } 2}} \right. \kern-0em} 2}} \right) > 0$. Это соответствует малым значениям ${\eta }$, т.е. условно-мягкому основанию, тогда $k \in \left[ {0,{{\pi } \mathord{\left/ {\vphantom {{\pi } 2}} \right. \kern-0em} 2}} \right]$. Соответствующее значение критической силы для этого случая равно ${{P}_{{{\text{кр}}}}} = {{EJk_{*}^{2}} \mathord{\left/ {\vphantom {{EJk_{*}^{2}} {{{b}^{2}}}}} \right. \kern-0em} {{{b}^{2}}}}$ и будет меньше значения критической силы для шарнирно-опертой балки ${{P}_{2}} = {{EJ{{{\pi }}^{2}}} \mathord{\left/ {\vphantom {{EJ{{{\pi }}^{2}}} {4{{b}^{2}}}}} \right. \kern-0em} {4{{b}^{2}}}}$ длины $2b$.

При малых значениях ${\eta }$ несложно получить приближенную формулу для решения уравнения (1.9). Если в (1.9) разложить тригонометрические функции по формуле Тейлора, сохраняя слагаемые с $k$ до второго порядка включительно, получим асимптотическую формулу для критического значения в случае условно-мягкого основания:

Получим также приближенную формулу для решения (1.9) в случае больших значений параметра ${\eta }$. Введем малый параметр соотношением $k = {\pi } - {\varepsilon }$, причем $\varepsilon > 0$. Разложив (1.9) по формуле Тейлора и, сохраняя параметры с ${\varepsilon }$ до второго порядка включительно, получим

Учитывая положительность ${\varepsilon }$, получим следующее асимптотическое выражение для $k$

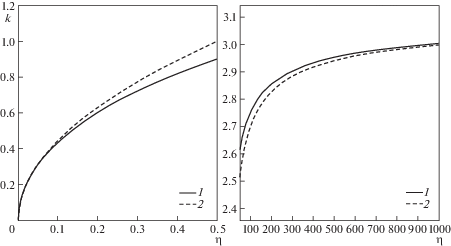
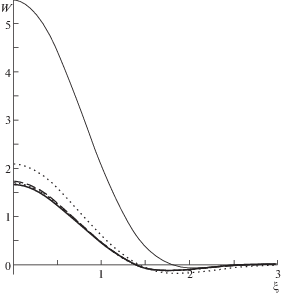
Приняв ${{{\eta }}_{0}} = {{\eta } \mathord{\left/ {\vphantom {{\eta } {100}}} \right. \kern-0em} {100}}$, осуществим сравнение асимптотических приближений с численными решениями (1.9). На рис. 1 левый график соответствует случаю ${\eta } \to 0$, а правый – случаю ${\eta } \to \infty $. Цифрой 1 обозначено решение (1.9), найденное численно, цифрой 2 – асимптотические приближения согласно (1.14) и (1.15), соответственно.

Как видно из графиков, асимптотики (1.14) и (1.15) при параметре ${{{\eta }}_{0}} = {{\eta } \mathord{\left/ {\vphantom {{\eta } {100}}} \right. \kern-0em} {100}}$ дают хорошее приближение и существенно упрощают анализ.

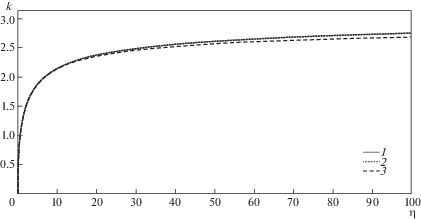
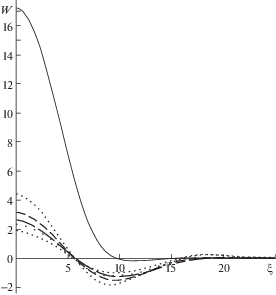
Далее изучим вопрос, как влияет величина ${{{\eta }}_{0}}$ на критическое значение, найденное из (1.9). Ниже представлен рис. 2, на котором изображена исследуемая зависимость при фиксированном параметре ${{{\eta }}_{0}}$. Цифре 1 соответствует ${{{\eta }}_{0}} = 0$, цифре 2 – η₀ = = $\eta {\text{/}}100$, цифре 3 – ${{{\eta }}_{0}} = {{\eta } \mathord{\left/ {\vphantom {{\eta } {10}}} \right. \kern-0em} {10}}$.

Из формулы (1.14) (и из рис. 2) можно заметить, что при увеличении ${{{\eta }}_{0}}$ уменьшается значение критической силы.

Проведем сравнение решения трансцендентного уравнения (1.9) с решениями других известных моделей. В работе [5], из граничных условий упругого шарнира было получено подобное трансцендентное уравнение

где ${{{\gamma }}_{0}}$ – коэффициент отношения величин критических напряжений в случае упругой и жесткой заделки, ${\sigma }_{{{\text{кр}}}}^{{{\text{уз}}}} = {{{\gamma }}_{0}}{\sigma }_{{{\text{кр}}}}^{{{\text{жз}}}}$, ${{{\beta }}_{1}} = (h{{a}^{{ - 1}}})\sqrt[3]{{E{\text{*}}E_{s}^{{* - 1}}}}$, где $h$ – толщина покрытия, $a$ – полудлина участка отслоения, $E{\text{*}} = E{{(1 - {{\upsilon }^{2}})}^{{ - 1}}}$, $E_{s}^{*} = {{E}_{s}}{{(1 - \upsilon _{s}^{2})}^{{ - 1}}}$, $E,\;{{E}_{s}},\;\upsilon ,\;{{\upsilon }_{s}}$ – модули упругости и коэффициенты Пуассона покрытия и подложки, ${{d}_{0}}$ – коэффициент, определяемый из коэффициента пропорциональности между углом наклона в заделке и второй производной от смещения, $d = {{d}_{0}}\sqrt[3]{{{{E{\text{*}}} \mathord{\left/ {\vphantom {{E{\text{*}}} {E_{s}^{*}}}} \right. \kern-0em} {E_{s}^{*}}}}}$, причем ${{d}_{0}} \approx 0.636$ [6]. Для данного расчета выберем значения параметров $h{{a}^{{ - 1}}} = {{10}^{{ - 1}}}$, а отношение $E{\text{*}}E_{s}^{{* - 1}}$ будем изменять от 1 до 100.

В работе [16] было представлено следующее трансцендентное уравнение, которое запишем с учетом наших обозначений

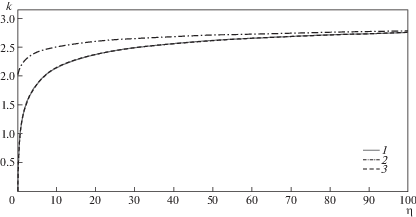
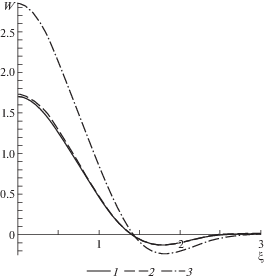
Отметим также, что (1.16) и (1.17) учитывают влияние только одного коэффициента постели в отличие от (1.9), поэтому в (1.9) положим ${{{\eta }}_{0}} = 0$. На рис. 3 цифрой 1 обозначено (1.9), цифрой 2 – (1.17), цифрой 3 – (1.16).

Как видно, наименьшее решение (1.9) достаточно хорошо совпадает с наименьшим решением, полученным из анализа (1.17).

2. Упрощенная балочная модель. Отметим возможность упрощения исходной задачи путем сведения к краевой задаче для конечной балки с модифицированными граничными условиями при ${\xi } = \pm 1$.

Оценим функционал ${{{\Lambda }}_{{11}}}$ из (1.3), заменив ${{w}_{1}}$ некоторой убывающей на $\left[ {1,\infty } \right)$ функцией вида ${{w}_{1}} = ({{c}_{1}} + ({{c}_{1}}{\gamma } + {{c}_{2}})\left( {{\xi } - 1} \right)){{e}^{{ - {\gamma }\left( {{\xi } - 1} \right)}}}$, где ${{w}_{1}}\left( 1 \right) = {{c}_{1}},\,\,{{w'}_{1}}\,\left( 1 \right) = {{c}_{2}}$, а ${\gamma }$ – пока произвольный положительный параметр.

Получим представление для ${{{\Lambda }}_{{11}}}$ в виде квадратичной формы

причем коэффициенты ${{a}_{{11}}},\;{{a}_{{22}}},\;{{a}_{{12}}}$ при ${\gamma } = {\alpha }$ ($\alpha $ из (1.6)) определяются следующим образом: где ${\gamma } = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}\sqrt {2{\eta } - {{k}^{2}} + {\eta }_{0}^{2}} $.

Путем варьирования функционала в (1.3) получим уравнение равновесия со следующими модифицированными граничными условиями

Общим симметричным решением уравнения в (2.2) будет функция w₁ = ${{С}_{1}}{\text{cos}}(k{\xi })$ + C₂. Условие существования нетривиального решения краевой задачи (2.2) приводит к следующему трансцендентному уравнению:

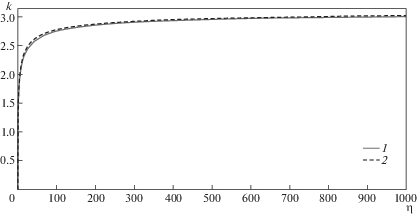
Сравним структуру зависимости критического значения параметра, полученного из точного трансцендентного уравнения (1.9) с решением трансцендентного уравнения (2.3), полученным для упрощенной модели. Ниже на рис. 4 представлены полученные результаты. Здесь цифрой 1 обозначена зависимость, отвечающая (1.9), цифрой 2 – зависимость, отвечающая уравнению (2.3) ( в расчетах принято ${{{\eta }}_{0}} = {{\eta } \mathord{\left/ {\vphantom {{\eta } {100}}} \right. \kern-0em} {100}}$).

Из сравнительного анализа этих зависимостей видно, что они практически совпадают, что свидетельствует о том, что при анализе подобных задач можно рассматривать модель конечной балки с модифицированными граничными условиями (2.2).

3. Закритическое поведение. Для полного исследования задачи остается исследовать вопрос о закритическом поведении покрытия. Для этого необходимо исходить из нелинейной модели покрытия. Используем для такого исследования вариационный подход.

Неквадратичный функционал (сохранены слагаемые до четвертого порядка включительно), согласно идеям работ [16, 17], будет иметь вид

Для исследования минимального значения функционала (3.1) будем использовать метод Ритца. Для этого представим ${{w}_{1}}$ в виде линейной комбинации координатных функций ${{\varphi }_{k}}$

где $N$ – некоторое число, определяющее количество координатных функций.

Координатные функции выберем следующим образом, чтобы они убывали на $[0,\infty ]$:

где параметр ${\chi }$ – пока некоторый произвольный положительный параметр, n = = $1,2...N.$

Введем ${{k}_{1}} = {\delta }k$, где k определяется по (1.10), ${\delta }$ – коэффициент закритичности. Находя минимальное значение функционала для различного числа координатных функций, получим нелинейную систему N уравнений относительно неизвестных параметров, которая решалась численно методом Ньютона. В качестве начального приближения для системы N уравнений будем выбирать решение системы для N – 1 уравнений, дополнив его нулевым значением нового коэффициента.

Приведем некоторые результаты расчетов. Рассмотрим случай ${\eta } = 10,$ ${{{\eta }}_{0}} = \,{{\eta } \mathord{\left/ {\vphantom {{\eta } {100}}} \right. \kern-0em} {100}},$ ${\delta } = 1.01$.

Ниже приведена таблица № 1, которая показывает изменение значений функционала с увеличением числа координатных функций, если принять параметр χ = 1.

Из таблицы 1 видно монотонное убывание функционала энергии, а также стабилизация первых параметров ${{C}_{k}}$. Вместе с тем отметим, что осуществление расчетов при $N > 10$ приводило к немонотонному изменению функционала.

На рис. 5 показана сходимость формы прогиба к некоторой функции с ростом числа координатных функций. Из рис. 5 видно, что уже при шести координатных функциях форма прогиба отличается от других форм, с большим числом координатных функций, не более чем на 1%.

Покажем изменение формы прогиба для другого набора значений параметров ${\eta }$ = 0.1, ${{{\eta }}_{0}} = \,{{\eta } \mathord{\left/ {\vphantom {{\eta } {100}}} \right. \kern-0em} {100}}$. Параметр ${\chi }$ выберем равным ${\alpha }$ из (1.6) для увеличения скорости сходимости. Обратим внимание, тогда из (1.6) следует, что $2{\eta } + {\eta }_{0}^{2} > {{k}^{2}}$. Это дает ограничение для выбора параметра закритичности в случае малых значений параметра ${\eta }$. Для расчета выберем ${\delta } = 1.01$, при больших значениях ${\delta }$ это приводит к нарушению этого неравенства в силу $2{\eta } + {\eta }_{0}^{2} < {{k}^{2}}$ и, соответственно, все ненулевые решения переходят в комплексную плоскость и являются посторонними. Результаты расчетов представим в таблице № 2 и на рис. 6.

На рис. 6 показана сходимость формы прогиба к некоторой функции с ростом числа координатных функций.

Как видно из рис. 6, для малых значений параметра ${\eta }$ форма прогиба имеет волнообразный характер.

Для дальнейшего исследования ограничимся шестью координатными функциями. Покажем, как изменяется форма закритического поведения для различных фиксированных значений параметра ${{{\eta }}_{0}}$. Зафиксируем ${{{\eta }}_{0}} = {1 \mathord{\left/ {\vphantom {1 {1000}}} \right. \kern-0em} {1000}}{\eta },{{\,1} \mathord{\left/ {\vphantom {{\,1} {100}}} \right. \kern-0em} {100}}{\eta },\,\,{1 \mathord{\left/ {\vphantom {1 {10}}} \right. \kern-0em} {10}}{\eta }$, что соответствует обозначениям 1–3 на рис. 7. Формы прогибов построены для следующих значений параметров ${\eta } = 10$, ${\delta } = 1.01$, χ = 1.

Таким образом, можно отметить, что при увеличении параметра ${{{\eta }}_{0}}$ амплитуда закритической формы увеличивается.

Заключение. Была рассмотрена модель отслоения покрытия под действием сжимающей нагрузки, учитывающая два коэффициента постели, аналогично модели Пастернака. Были установлены соотношения для параметра критической силы, построена упрощенная модель, позволяющая сводить задачу для бесконечного покрытия к исследованию задачи устойчивости для конечной балки с модифицированными граничными условиями. Произведен анализ закритического поведения, построена вычислительная схема на основе метода Ритца, проведено исследование сходимости процесса в зависимости от числа координатных функций.

Работа выполнена при поддержке РНФ, проект № 18-11-00069.