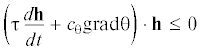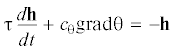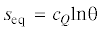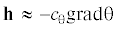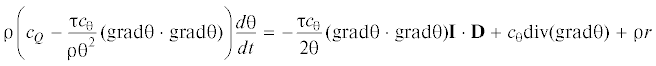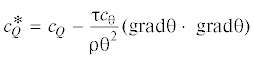Известия РАН. Механика твердого тела, 2020, № 4, стр. 152-157

ТЕРМОДИНАМИКА УПРУГОГО МАТЕРИАЛА С РЕЛАКСИРУЮЩИМ ПОТОКОМ ТЕПЛА

Л. А. Комар^a, *, А. Л. Свистков^a, **

^a Институт механики сплошных сред Уральского отделения РАН Филиал федерального государственного бюджетного учреждения науки Пермского федерального исследовательского центра Уральского отделения РАН
Пермь, Россия

^* E-mail: komar@icmm.ru
^** E-mail: svistkov@icmm.ru

Поступила в редакцию 31.01.2020
После доработки 03.03.2020
Принята к публикации 04.04.2020

DOI: 10.31857/S0572329920040066

Полный текст (PDF)

Аннотация

Для получения уравнения теплопроводности использованы первое и второе начало термодинамики и следствия из них, которые получаются из требования независимости законов от выбора инерциальной системы отсчета. Для записи второго начала термодинамики использовано неравенство Клаузиуса–Дюгема. В работе осуществлен вывод уравнения теплопроводности из законов термодинамики для упругих материалов с релаксирующим потоком тепла. Сформулированы определяющие уравнения для среды, работающей в условиях конечных деформаций. Показано, что тензор напряжений Коши в упругом материале зависит от градиента теплового потока. Рассмотрен приближенный вариант использования нелинейного уравнения теплопроводности в материалах с очень малым временем релаксации теплового потока. Это процессы, в которых релаксирующий поток тепла быстро становится близким к потоку, определяемому законом Фурье. Но при этом рассматривается состояние, в котором градиент температуры имеет большое значение и нельзя пренебрегать в уравнении теплопроводности квадратом модуля вектора теплового потока. В этом случае целесообразно говорить об использовании понятия “неравновесная теплоемкость” материала, которая зависит от градиента температуры.

Ключевые слова: законы термодинамики, уравнение теплопроводности, релаксирующий поток тепла, конечные деформации

1. Введение. Можно выделить три наиболее известные научные школы термодинамики сплошной среды. Между ними нет принципиальных различий. Но есть отличие в формулировке исходных посылок, в используемой терминологии, в круге решаемых с их помощью задач. Первой, получившей наибольшее распространение, является школа линейной термодинамики. Особенностью этой школы является то, что в ней используются понятия термодинамических сил, термодинамических потоков и соотношений Онзагера. Второе начало термодинамики формулируется в виде условия на производство энтропии.

Однако не все явления в реальном мире можно описать с помощью линейной термодинамики. Иногда требуется более общая теория. Такой теорией может быть расширенная необратимая термодинамика. В частности, это касается представлений о том, что поток тепла не может измениться мгновенно при изменении состояния тела. Вместо закона Фурье, в котором тепловой поток пропорционален градиенту температуры, нужно использовать релаксационное уравнение для потока тепла. Такое уравнение предложил Каттанео [1]. Скорость изменения во времени потока тепла состоит из двух слагаемых. Одно слагаемое пропорционально потоку тепла, второе пропорционально градиенту температуры. В перечисленных выше случаях коэффициенты пропорциональности должны быть отрицательными. Использование релаксационного уравнения Каттанео приводит к новым результатам, принципиально отличающимся от результатов, полученных с использованием закона Фурье. В решении задач появляются тепловые волны и возможна передача тепла из холодных областей в горячие. В отличие от классического уравнения теплопроводности, дающего бесконечную скорость распространения тепла, в модели с релаксирующим потоком скорость распространения тепла будет конечной. Обзор соответствующих работ можно посмотреть в публикациях [2, 3].

Третью школу термодинамики обычно используют специалисты, работающие с деформируемыми средами в области конечных деформаций. В ней первое начало сформулировано для произвольно выбранного объема пространства с учетом кинетической энергии движения материальных точек. Второе начало задается в виде неравенства Клаузиуса–Дюгема. Термины “термодинамические силы” и “термодинамические потоки” при выводе определяющих уравнений не применяются. Важную роль играет требование объективности, в том числе и требование независимости формулировки начал термодинамики от выбора инерциальной системы отсчета. В данной работе использован такой подход для получения определяющих уравнений термомеханики упругих материалов с учетом релаксирующего потока тепла.

2. Первое и второе начала термодинамики, требование объективности и следствия из них. В качестве первой исходной посылки для получения определяющих уравнений использовалась формулировка первого начала термодинамики для деформируемого континуума

$\frac{d}{{dt}}\mathop \smallint \limits_V^{} \left( {{\rho }e + \frac{1}{2}{\rho }{\mathbf{v}} \cdot {\mathbf{v}}} \right)dV = \mathop \smallint \limits_V^{} {\rho }rdV + \mathop \smallint \limits_S^{} {\mathbf{f}} \cdot {\mathbf{v}}dS - \mathop \smallint \limits_S^{} {\mathbf{n}} \cdot {\mathbf{h}}dS$

где V, S, n – произвольно выделенный объем среды, ограничивающая его поверхность и внешняя нормаль, t – текущий момент времени, e – массовая плотность внутренней энергии, ρ – плотность массы континуума, r – массовая плотность источника тепла, f – плотность поверхностной силы, v – скорости точек континуума, h – тепловой поток.

Первое начало термодинамики должно выполняться в любой инерциальной системе отсчета. Добавление произвольной постоянной скорости для всех моментов времени и всех точек континуума не должно отразиться на математической формулировке первого начала термодинамики. Справедливо это должно быть как для любой среды со сложным механическим поведением, так и для смеси континуумов. Это позволяет получать необходимые следствия [4–7]. В рассматриваемом случае инвариантность к выбору системы инерциальной системы отсчета представляет собой условие

(2.1)

$\frac{d}{{dt}}\mathop \smallint \limits_V^{} \left( {{\rho }e + \frac{1}{2}{\rho }({\mathbf{v}} + {{{\mathbf{v}}}_{0}}) \cdot ({\mathbf{v}} + {{{\mathbf{v}}}_{0}})} \right)dV = \mathop \smallint \limits_V^{} {\rho }rdV + \mathop \smallint \limits_S^{} {\mathbf{f}} \cdot ({\mathbf{v}} + {{{\mathbf{v}}}_{0}})~dS - \mathop \smallint \limits_S^{} {\mathbf{n}} \cdot {\mathbf{h}}dS~$

где v₀ – произвольная постоянная скорость, неизменная для всех моментов времени и одна и та же для всех точек континуума. Выполняться оно должно при любом выборе вектора v₀. Равенство (2.1) можно переписать в виде

(2.2)

$\left( {\frac{d}{{dt}}\mathop \smallint \limits_V^{} \frac{1}{2}{\rho }dV} \right)~{{{\mathbf{v}}}_{0}} \cdot {{{\mathbf{v}}}_{0}} + \left( {\frac{d}{{dt}}\mathop \smallint \limits_V^{} {\rho }~{\mathbf{v}}dV - \mathop \smallint \limits_S^{} {\mathbf{f}}dS} \right) \cdot {{{\mathbf{v}}}_{0}}~$

$ + \left( {\frac{d}{{dt}}\mathop \smallint \limits_V^{} \left( {{\rho \;}e + \frac{1}{2}{\rho \;}{\mathbf{v}} \cdot {\mathbf{v}}} \right)~dV - \mathop \smallint \limits_V^{} {\rho }rdV - \mathop \smallint \limits_S^{} {\mathbf{f}} \cdot {\mathbf{v}}~dS + \mathop \smallint \limits_S^{} {\mathbf{n}} \cdot {\mathbf{h}}~dS} \right) = 0~~~~~~$

Требование выполнения условия (2.2) при произвольном векторе v₀ позволяет получать полезные следствия. Первое из них представляет собой закон сохранения массы

$\frac{{\partial ~{\rho }}}{{\partial ~t}} + {\text{div}}({\rho }{\mathbf{v}}) = 0$

Второе следствие – уравнение движения

${\rho }{\mathbf{w}} = {\text{div}}{\mathbf{T}}~$

где w – ускорение, T – тензор напряжений Коши. Третье следствие дает более простую формулировку первого начала термодинамики, в которую не входит кинетическая энергия

(2.3)

${\rho }\frac{{de}}{{dt}} = {\mathbf{T}} \cdot {\mathbf{D}} - {\text{div}}{\mathbf{h}} + {\rho }r~$

где D – тензор скоростей деформации. Точка между тензорами T и D означает скалярное умножение векторов девятимерного векторного пространства, которое образует множество тензоров второго ранга. Эта запись используется во многих публикациях (например, в справочной монографии [8]).

Второе начало термодинамики для деформируемого континуума формулируется в виде неравенства Клаузиуса–Дюгема

(2.4)

$\frac{d}{{dt}}\mathop \smallint \limits_V^{} {\rho }sdV \geqslant \mathop \smallint \limits_V^{} \frac{{{\rho }r}}{{\theta }}~dV - \mathop \smallint \limits_S^{} \frac{{{\mathbf{n}} \cdot {\mathbf{h}}}}{{\theta }}dS$

где s – массовая плотность энтропии, θ – температура. Из условий (2.3) и (2.4) получается важное термодинамическое неравенство, которое должно автоматически удовлетворяться

(2.5)

${\mathbf{T}} \cdot {\mathbf{D}} - {\rho }\frac{{df}}{{dt}} - {\rho }s\frac{{d{\theta }}}{{dt}} - \frac{{{\text{grad}}~{\theta } \cdot {\mathbf{h}}}}{{\theta }} \geqslant 0$

где $f = e - {\theta \;}s$ – массовая плотность свободной энергии материала. Нас интересуют упругие изотропные среды. Рассмотрим модель такого континуума с релаксирующим потоком тепла.

3. Термодинамические свойства упругого материала. В большинстве используемых для практических приложений моделях изотропных упругих сред полагается, что плотности свободной энергии и плотность энтропии являются функциями только температуры и кратностей удлинений. Тензор напряжений Коши зависит только от температуры, от кратностей удлинений и собственных векторов левого тензора растяжений. Но в таких моделях невозможно удовлетворить неравенство (2.5) если тепловой поток релаксирует во времени, а не мгновенно меняет свое значение по закону Фика. Выход указан в работах [9–11]. Предложено ввести в выражение массовой плотности свободной энергии еще одно дополнительное слагаемое, которое зависит от неравновесного параметра – вектора теплового потока. Осуществить это можно следующим образом. Запишем плотность свободной энергии в виде

(3.1)

$f = {{f}_{{{\text{eq}}}}}({\theta },{{{\lambda }}_{i}}) + {\tau }~({\mathbf{h}} \cdot {\mathbf{h}}){\text{/}}2{\rho \theta }{{c}_{{\theta }}}~$

где f_eq – равновесная часть массовой плотности свободной энергии, λ_i – кратности удлинений материала (i = 1, 2, 3), τ и c_θ – константы материала, имеющие положительные значения. Нетрудно проверить, что термодинамическое неравенство примет простой вид при следующих условиях. Тензор напряжений Коши целесообразно вычислять по формуле

(3.2)

${\mathbf{T}} = \frac{{{\tau \;}({\mathbf{h}} \cdot {\mathbf{h}})}}{{2{\theta }{{c}_{{\theta }}}}}{\mathbf{I}}\,{\text{ + }}\,{\rho }\mathop \sum \limits_{i = 1}^3 {{{\lambda }}_{i}}\frac{{\partial {{f}_{{{\text{eq}}}}}}}{{\partial {{{\lambda }}_{i}}}}{{{\mathbf{n}}}_{i}} \otimes {{{\mathbf{n}}}_{i}}~$

где I – единичный тензор, n_i – ортонормированная тройка собственных векторов левого тензора растяжений (i = 1, 2, 3). Для массовой плотности энтропии следует использовать связь с массовой плотностью свободной энергии с помощью выражения

(3.3)

$s = - \frac{{\partial f}}{{\partial {\theta }}} = {{s}_{{{\text{eq}}}}} + \frac{{{\tau }({\mathbf{h}} \cdot {\mathbf{h}})}}{{2{\rho }{{{\theta }}^{2}}{{c}_{{\theta }}}}}$

в котором равновесная составляющая массовой плотности энтропии определена равенством

(3.4)

${{s}_{{{\text{eq}}}}} = - \frac{{\partial {{f}_{{{\text{eq}}}}}}}{{\partial {\theta }}}~$

Воспользовавшись формулами

(3.5)

$\frac{{d{{\lambda }_{i}}}}{{dt}} = {{{\lambda }}_{i}}{{{\mathbf{n}}}_{i}} \otimes {{{\mathbf{n}}}_{i}} \cdot {\mathbf{D}},\quad \frac{d}{{dt}}\left( {~\frac{1}{{\rho }}~} \right) = \frac{1}{{\rho }}~{\mathbf{I}}\, \cdot \,{\mathbf{D}}~$

нетрудно убедиться, что термодинамическое неравенство (2.5) принимает вид

(3.6)

Из него следует, что поток тепла должен быть задан таким выражением, которое автоматически приведет к выполнению условия (3.6). Только в этом случае будет выполняться второе начало термодинамики в виде неравенства Клаузиуса–Дюгема.

4. Уравнение теплопроводности. Условие (3.6) окажется справедливым если подставить в него математическое выражение для потока тепла, предложенного Каттанео

(4.1)

Рассмотрим, какой вид при этом примет уравнение теплопроводности. Получить его можно, воспользовавшись законом сохранения энергии, записанным в виде равенства (2.3). При этом необходимо выразить массовую плотность свободной энергии через массовую плотность свободной энергии $e = f + {\theta \;}s$

${\rho }\frac{{d(f + {\theta }s)}}{{dt}} = {\mathbf{T}} \cdot {\mathbf{D}} - {\text{div}}{\mathbf{h}} + {\rho }r$

и раскрыть производную по времени, воспользовавшись выражениями (3.1)–(3.5). В результате получим равенство

(4.2)

${\rho \theta }\frac{{d{{s}_{{{\text{eq}}}}}}}{{dt}} - \frac{{{\tau }({\mathbf{h}} \cdot {\mathbf{h}})}}{{{{с}_{{\theta }}}{{{\theta }}^{2}}}}\frac{{d{\theta }}}{{dt}} + \frac{{{\tau }({\mathbf{h}} \cdot {\mathbf{h}})}}{{2{{с}_{{\theta }}}{\theta }}}~{\mathbf{I}} \cdot {\mathbf{D}} + \frac{{\tau }}{{2{{с}_{{\theta }}}{\theta }}}\frac{{d({\mathbf{h}} \cdot {\mathbf{h}})}}{{dt}} = - {\text{div}}{\mathbf{h}}\; + \;{\rho }r~$

Оно и является искомым уравнением теплопроводности.

5. Частный случай уравнения теплопроводности при малом отличии релаксационного потока тепла от потока, заданного законом Фурье. Рассмотрим модель материала, у которого равновесная энтропия рассматриваемого континуума имеет следующий вид:

где c_Q – удельная теплоемкость. В этом случае равенство (4.2) примет форму

(5.1)

${\rho }{{c}_{Q}}\frac{{d{\theta }}}{{dt}} - \frac{{{\tau }({\mathbf{h}} \cdot {\mathbf{h}})}}{{{{с}_{{\theta }}}{{{\theta }}^{2}}}}\frac{{d{\theta }}}{{dt}} + \frac{{{\tau }({\mathbf{h}} \cdot {\mathbf{h}})}}{{2{{с}_{{\theta }}}{\theta }}}~{\mathbf{I}} \cdot {\mathbf{D}} + \frac{{\tau }}{{{{с}_{{\theta }}}{\theta }}}~{\mathbf{h}} \cdot \frac{{d{\mathbf{h}}}}{{dt}} = - {\text{div}}\;{\mathbf{h}}\; + \;{\rho }r$

Имеется много работ, в которых исследуются решения задач в линейном приближении. В этом приближении скалярное умножение векторов h ⋅ h полагается величиной второго порядка малости и ее исключают из рассмотрения. При таком подходе остается только расшифровать слагаемое div h в правой части равенства (5.1) с учетом процесса релаксации теплового потока.

С нашей точки зрения наиболее интересным является другое приближение, в котором нельзя пренебречь скалярной величиной τ(h ⋅ h). Закон релаксации теплового потока Каттанео (4.1) можно записать в более удобном виде

Параметр τ определяет характерное время релаксации теплового потока. Этот параметр может быть настолько малым, что можно полагать следующее. Тепловой поток мгновенно приходит к состоянию, в котором с хорошей точностью выполняется закон Фурье

При этом значение вектора h может быть большим. Возникает интересная для практических приложений ситуация, когда производной по времени от теплового потока можно пренебречь, но выражение τ(h ⋅ h) заметно отличается от нулевого значения при больших значениях величины теплового потока h. Уравнение теплопроводности в таком приближении записывается в виде равенства

В дальнейшем исследовании можно вести понятие “удельной теплоемкости континуума в неравновесном состоянии”. Обозначим ее символом $с_{Q}^{{\text{*}}}$

Новое приближение в уравнение теплопроводности приведет к следующему. Скорость изменения температуры может происходить значительно быстрее в точках материала, чем это предсказывает классическое уравнение теплопроводности. Такое явление будет иметь место в случае, когда градиент температуры в точках среды имеет большое значение. На практике такие ситуации возможны при облучении поверхности материала короткими импульсами высокой энергии. Например, это может быть ионно-плазменная обработка поверхности полимера. На границе материала на очень коротком интервале времени повышается температура. Но тепло не успевает в этот короткий интервал времени рассеяться. В результате на малом расстоянии от границы образца, измеряемым десятками нанометров, будет высокий градиент температуры и произойдет существенное повышение температуры материала, которая быстро рассеется в последующие моменты времени. При этом около поверхности образца, согласно формуле для напряжений Коши (3.2), будут действовать значительные всесторонние растягивающие напряжения, которые после уменьшения градиента температуры станут намного ниже. Поверхность изменит свое физическое состояние. В реальности, это приведет к тому, что полимер разрушится на границе образца и вместо него появится углеродный слой. После этого произойдет усадка углеродного слоя при выравнивании температуры и уменьшении всесторонних растягивающих напряжений.

6. Заключение. В работе получены определяющие уравнения упругой среды с релаксирующим потоком тепла, работающей в условиях конечных деформаций. Установлено, что тензор напряжений Коши должен зависеть от теплового потока. Выведено уравнение теплопроводности. Рассмотрен вариант приближенного использования уравнения теплопроводности, когда с хорошей точностью удовлетворяется закон Фурье при высоких скоростях релаксации теплового потока, но в уравнении теплопроводности нельзя пренебречь квадратом модуля градиента температуры.

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 19-08-00725.

Список литературы

Cattaneo C. Sulla conduzione del calore // Atti del seminario matematico e fisico dell’Universita di Modena e Reggio Emilia. 1948. V. 3. P. 83–101.
Joseph D.D., Preziosi L. Heat waves // Rev. Mod. Phys. 1989. V. 61. № 1. P. 41–73.
Joseph D.D., Preziosi L. Addendum to the paper “Heat waves” // Rev. Mod. Phys. 1990. V. 62. № 2. P. 375–391.
Green A.E., Rivlin R.S. On Cauchy’s equations of motion // Zeitschrift für angewandte Mathematik und Physik ZAMP. 1964. V. 15. № 3. P. 290–292.
Green A.E., Rivlin R.S. Multipolar continuum mechanics // Arch. Ration. Mech. Anal. 1964. V. 17. № 2. P. 113–147.
Green A.E., Naghdi P.M. A. general theory of an elastic-plastic continuum // Arch. Ration. Mech. Anal. 1965. V. 18. № 4. P. 251–281.
Green A.E., Naghdi P.M. A dynamical theory of interacting continua // International Journal of Engineering Science. 1965. V. 3. № 2. P. 231–241.
Bechtel S., Lowe R.L. Fundamentals of continuum mechanics with applications to mechanical, thermomechanical, and smart materials. Elsevier Science. 2014. 340 p.
Coleman B.D., Fabrizio M., Owen D.R. On the thermodynamics of second sound in dielectric crystals // Arch. Ration. Mech. Anal. 1982. V. 80. № 2. P. 135–158.
Coleman B.D., Hrusa W.J., Owen D.R. Stability of equilibrium for a nonlinear hyperbolic system describing heat propagation by second sound in solids // Arch. Ration. Mech. Anal. 1986. V. 94. P. 267–289.
Barletta A., Zanchini E. Hyperbolic heat conduction and local equilibrium: a second law analysis // Int. J. Heat Mass Transf. 1997. V. 40. № 5. P. 1007–1016.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал