Известия РАН. Механика твердого тела, 2020, № 6, стр. 125-133

1. Введение. Изучение спектральных свойств динамических краевых задач для упругих неоднородных волноводов и связанных с ними резонансных эффектов всегда было в фокусе научных интересов Иосифа Израилевича Воровича [1, 2]. Он неоднократно указывал на особенно интересный случай их возникновения и проявления в волноводных структурах с локальными неоднородностями, когда наряду со сплошным спектром, дающим бегущие волны, у соответствующих краевых задач появляются точки дискретного спектра (комплексные резонансные частоты рассеяния). Хорошо известно, что в случае тел конечных размеров с идеально-упругими свойствами весь бесконечный набор точек спектра (резонансных частот) лежит на вещественной оси. Если же такой объект встроен в упругий волновод или контактирует с ним, то за счет оттока энергии, уносимой на бесконечность бегущими волнами, его колебания демпфируются и резонансные частоты перестают быть вещественными, то есть точки дискретного спектра смещаются с вещественной оси в комплексную плоскость частоты.

В 1970–1980-е годы на семинарах кафедры теории упругости Ростовского госуниверситета под руководством И.И. Воровича нередко возникали дискуссии о возможности формирования смешанного спектра для различных типов волноводных структур и локальных препятствий. При этом активный интерес и горячее обсуждение неизменно вызывал вопрос возможности выхода какой-либо точки дискретного спектра на вещественную ось и, если да, то при каких условиях. Настоящая работа посвящена исследованию таких резонансных эффектов для препятствий в виде горизонтальной трещины в свободном упругом слое. Задачи в такой постановке возникают при моделировании процесса зондирования ультразвуковыми бегущими волнами тонкостенных конструкций из слоистых композитных материалов с целью обнаружения возможных внутренних расслоений. Волоконно-армированные композиты (углепластики) все шире используются в конструкциях ответственного назначения (аэрокосмические изделия, трубопроводы, машиностроение, химическая индустрия и др.), чем определяется высокая актуальность данного класса задач.

Предварительно дается краткий исторический обзор от первых исследований 1980–1990-х годов, во многом начатых непосредственно под влиянием идей И.И. Воровича, до недавних экспериментально-теоретических результатов прикладного характера (раздел 2). Затем, в разделе 3, дается краткое описание используемых математических моделей и их экспериментальной верификации. Приводятся примеры численного анализа и экспериментальных измерений средствами лазерной интерферометрии для образцов с искусственным расслоением. Обсуждаются особенности формирования ловушечных мод в волноводах с горизонтальной трещиной и демонстрируется возможность использования выявленных резонансных эффектов для неразрушающего экспресс-определения размера и глубины залегания расслоений.

2. История вопроса. Очевидно, что появление вещественных точек спектра и связанных с ними бесконечных резонансов при вынужденных колебаниях (или незатухающих свободных гармонических колебаний после снятия нагрузки) возможно только при отсутствии демпфирования, вызванного переносом энергии из зоны резонансных колебаний на бесконечность бегущими волнами, связанными с непрерывным спектром, которые также возникают на данной резонансной частоте. Отсутствие оттока волновой энергии приводит к ее локализации вблизи резонирующего объекта, поэтому собственные решения, соответствующие таким вещественным точкам спектра получили название “ловушечные моды” (trapping mode [3, 4]).

Механизм возможного блокирования оттока энергии из ближней зоны препятствия в упругом волноводе первоначально был не ясен. Но он стал понятнее, когда в ходе анализа траекторий переноса осредненной за период колебаний волновой энергии были обнаружены вихревые зоны, в которых энергия циркулирует по замкнутым траекториям, локализуясь в ограниченных областях [5]. Вихри энергии возникают из-за интерференции как бегущих волн, распространяющихся в дальней от источника или препятствия зоне без экспоненциального затухания, так и неоднородных волн с комплексными волновыми числами, проявляющихся только в ближней зоне. Вклад последних приводит к тому, что вихревые зоны, меняющиеся в зависимости от частоты, размера и формы препятствия, при определенных условиях могут полностью перекрывать поперечное сечение волновода, препятствуя оттоку энергии на бесконечность и устраняя тем самым фактор демпфирования. Численные примеры такой полной локализации волновой энергии вблизи некоторого объекта (локальной неоднородности) были первоначально получены для случая круглого штампа, вибрирующего на упругом слое [6], и дифракции бегущих волн на передней кромке жесткой поверхностной накладки [7]. Очевидно, аналогичный механизм блокирования оттока волновой энергии имеет место и при локальном резонансе неоднородных волн в полубесконечном упругом слое [8] (краевом резонансе [9]).

Тем не менее, в случае дифракции упругих волн на трещине возможность появления вещественных точек спектра (частот бесконечного резонанса) долгое время вызывала сомнения из-за отсутствия у нее массы, в то время как в возникновении резонансных колебаний некоторого локального объекта в упругом волноводе важную роль играет его инерционность [10]. Действительно, численный анализ показывает, что все точки дискретного спектра задачи дифракции объемных волн на планарных трещинах различной формы, расположенных в безграничном упругом пространстве, лежат в комплексной плоскости [11–13]. Варьирование формой трещины меняет положение точек спектра в комплексной плоскости, но без их выхода на вещественную ось [13]. С физической точки зрения, здесь нет бесконечного набора неоднородных волн, возникающих вблизи препятствия в случае волновода, поэтому трудно представить, за счет чего мог бы быть заблокирован отток энергии, переносимой на бесконечность рассеянными объемными волнами. А вот в случае трещины в упругом слое [14] дифракция набегающих волн приводит к появлению бесконечного набора неоднородных нормальных мод, то есть возникают те же условия для блокирования оттока энергии и формирования ловушечных мод, что и при дифракции на поверхностной накладке [7] или на препятствиях других типов, например, на жестких включениях [15] или поверхностных выемках [16].

Траектории движения точек спектра в комплексной плоскости частоты, получающиеся при изменении полуширины a горизонтальной полосовой трещины в свободном упругом слое (рис. 14 работы [14]), показывают, что в этом случае резонансные полюса регулярно подходят к вещественной оси, поочередно касаются ее, становясь вещественными, и снова уходят в нижнюю полуплоскость до следующего возвращения на ось при бóльших значениях a. На рис. 15 той же работы приводится пространственный график собственных колебаний, соответствующий спектральной точке, вышедшей на вещественную ось, который подтверждает резкую локализацию волнового процесса в окрестности трещины на данной резонансной частоте, то есть возникновение ловушечной моды. Линии тока энергии, построенные для этой частоты, показывают, что локализация волнового процесса действительно происходит в виде вихрей энергии, заполняющих все пространство вокруг трещины. Аналогичная картина поочередного выхода комплексных точек спектра на вещественную ось и формирования ловушечных мод наблюдается и при варьировании параметрами препятствий других типов, например, расстоянием между двумя горизонтальными трещинами [15] или шириной и глубиной поверхностной выемки [16].

После численного обнаружения ловушечных мод для препятствий в виде горизонтальных трещин, следующим естественным шагом стало экспериментальное подтверждение теоретически предсказанного резонансного эффекта. Оно было проведено совместно с немецкими коллегами, располагающими требуемым оборудованием (лазерный интерферометр, аппаратура для обработки сигналов и др.) [17]. Измерения, проведенные на двухслойных алюминиевых образцах с искусственным полосовым расслоением, моделирующим горизонтальную трещину, были нацелены на подтверждение резонансного захвата волновой энергии на частотах, совпадающих с теоретически предсказанными значениями точек дискретного спектра ω_{n, с} (индекс с указывает здесь и далее на то, что эти точки лежат в комплексной плоскости, в то время как ω_n = Reω_{n, c} – их вещественная часть). Эти точки совпадают с полюсами частотного спектра вектора смещений u(x, ω) = (u, ${v}$, w), который рассматривается как аналитическая вектор-функция круговой частоты ω = 2πf (f – частота). Они расположены в нижней полуплоскости Imω ≤ 0, причем для каждого полюса ω_{n, c} = ω_n – iδ_n (ω_n > 0, δ_n > 0) имеется симметричный относительно мнимой оси парный полюс ${{{\tilde {\omega }}}_{{n,c}}}$ = – ω_n – iδ_n.

В эксперименте измеряется не частотный спектр u(x, ω), а нестационарные смещения u(x, t), связанные со спектром обратным преобразованием Фурье в частотной области:

Резонансные полюса дают вклад в u(x, t) в виде суммы вычетов, причем вклад каждой пары ω_{n, c} и ${{{\tilde {\omega }}}_{{n,c}}}$ можно записать в следующем виде:

где w_n(x) = 2Resu(x, ω)${{|}_{{\omega = {{\omega }_{{n,c}}}}}}$ – вычет в полюсе ω_{n, c}.

Вектор-функции u_n описывают затухающие гармонические колебания с круговой частотой ω_n и логарифмическим декрементом затухания d_n = 2πδ_n/ω_n. Вклад вещественных полюсов (δ_n = 0) дает установившиеся (незатухающие) гармонические колебания, а полюсов, близких к вещественной оси (d_n $ \ll $ 1) – медленно затухающие гармоники, длящиеся сравнительно долгое время после снятия возбуждающей их нагрузки. Фактически u_n(x, t) – это собственные решения рассматриваемой задачи дифракции, соответствующие точкам дискретного спектра ω_{n, c}. Для вещественных и близких к вещественной оси точек спектра пространственные формы собственных колебаний, описываемые функциями w_n(x), демонстрируют резкую локализацию колебаний в окрестности препятствия, характерную для ловушечных мод.

На практике собственные колебания, регистрируемые даже на теоретически вещественной резонансной частоте ω_{n, c}, не могут длиться неограниченное время, так как реальные материалы обладают внутренним поглощением, дающим ненулевой декремент затухания колебаний (d_n > 0) и, как следствие, ненулевую мнимую часть соответствующей точки спектра (δ_n > 0). Тем не менее, экспериментальная регистрация таких пролонгированных колебаний на частоте, совпадающей с вещественной или близкой к вещественной оси точкой спектра интегрального уравнения, к которому сводится рассматриваемая задача дифракции на трещине [14, 17], представляется вполне достаточной для подтверждения существования ловушечных мод, теоретически предсказанных для трещин в идеально-упругих волноводах. Чувствительность резонансных частот к размерам и расположению трещины в упругом слое, а также хорошее совпадение расчетных и экспериментальных значений резонансных частот рассеяния позволяют использовать эту информацию для решения обратной задачи определения характеристик внутреннего расслоения по результатам ультразвукового зондирования образца.

3. Резонансная идентификация трещин. Частотный спектр u(x, ω), входящий в представления (2.1) и (2.2), описывается решением двумерной краевой задачи об установившихся гармонических колебаниях ue^–iωt упругого слоя толщины H с горизонтальной полосовой трещиной полуширины a, расположенной на глубине d. В декартовых координатах x = (x, z) полоса занимает область |x| < ∞, –H ≤ z ≤ 0 (сечение трехмерного слоя плоскостью y = 0). Трещина моделируется бесконечно тонким разрезом вдоль отрезка |x| < a, z = –d со свободными от напряжений не контактирующими между собой берегами. Верхняя и нижняя границы полосы z = 0 и z = –H также свободны от напряжений за исключением ограниченной области Ω, к которой приложена поверхностная нагрузка q, моделирующая действие пьезоактуатора, расположенного на некотором удалении от трещины. Актуатор возбуждает поле падающих на трещину волн u₀, которое описывается решением задачи для полосы без трещины. Общее волновое поле u складывается из поля падающих и рассеянных трещиной волн: u = u₀ + u_sc. Явное представление u₀ может быть получено в виде свертки матрицы Грина упругой полосы k(x, z) с заданной нагрузкой q:

Рассеянное трещиной поле u_sc выражается через неизвестный скачок смещения берегов трещины v(x) = $\mathop {\lim }\limits_{{\varepsilon } \to 0} $[u(x, z – ε) – u(x, z + ε)], |x| < a, который определяется из интегрального уравнения Винера–Хопфа с гиперсингулярным матричным ядром l(x):

где τ₀(x) – напряжения, вызываемые набегающими волнами u₀(x) на горизонтальной площадке.

Искомые частоты резонансного рассеяния ω_{n, c} совпадают с точками дискретного спектра интегрального оператора (3.2). Для их определения скачок v(x) ищется в виде разложения по ортогональным полиномам с весом, учитывающим корневое поведение решения при x → ±a. Неизвестные коэффициенты разложения c_j определяются по схеме Галеркина, в рамках которой уравнение (3.2) сводится к линейной алгебраической системе

относительно вектора неизвестных коэффициентов c = (c₁, c₂, …, c_N). Использовался также альтернативный метод сведения к алгебраической системе с помощью применения теории вычетов к представлению ядра интегрального уравнения в виде контурного интеграла обратного преобразования Фурье. В обоих случаях искомые точки спектра ω_{n, c} аппроксимируются корнями характеристического уравнения системы (3.3):

Более детальное описание общей схемы решения рассматриваемой задачи, а также разработанных алгоритмов вывода матрицы Грина k(x) и ядра l(x), в том числе и в случае пакета анизотропных слоев, моделирующих слоистую композитную пластину, можно найти в работах [14, 15, 17] и цитируемых в них статьях.

Экспериментальные измерения проводились на образцах из двух склеенных алюминиевых пластин с областью искусственной непроклейки, дающей расслоение. С учетом ненулевой толщины клеевой прослойки h такой образец моделировался также трехслойным пакетом слоев с прямоугольной полостью |x| < a, |z – d| < h/2 вместо бесконечно тонкой трещины. Поэтому, наряду с полуаналитическим подходом (3.2)–(3.4), для решения задачи в трехслойной постановке использовался метод конечных элементов (МКЭ), который применялся для конечного участка волновода, содержащего трещину, со специальными граничными условиями на боковых торцах, моделирующими отток волновой энергии на бесконечность (поглощающие идеально согласованные слои – PML [18]).

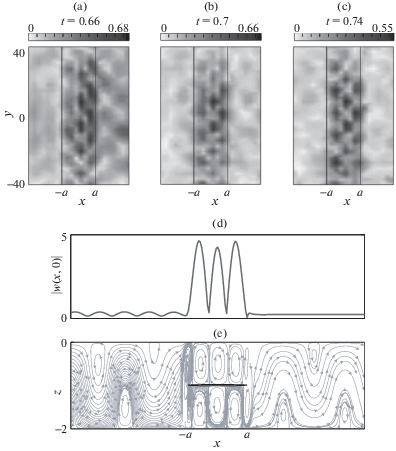
Ловушечные моды, формирующиеся на резонансных частотах, характеризуются резким ростом амплитуды колебаний поверхности образца над трещиной. Причем рост наблюдается не во всей области, а отдельными устойчивыми во времени пятнами, которые регистрируются средствами лазерной интерферометрии (рис. 1, a–c; координаты по горизонтальным осям даны в миллиметрах, время указано в миллисекундах) [17, 19]. Пятна пиковых смещений (вертикальная компонента скорости колебаний поверхности образца z = 0) появляются над вихрями энергии, формирующимися между поверхностью и трещиной (рис. 1, d, e). Амплитуды вертикальных смещений поверхности |w(x, 0)| (рис. 1, d), и линии тока энергии (рис. 1, e) построены здесь на основе решения интегрального уравнения (3.2) для следующих входных параметров: H = 2 мм, a = 10 мм, d = 1 мм, скорость поперечных волн c_s = 3120 м/с, коэффициент Пуассона ν = 0.33,  f = f₃ = 63.3 кГц. Пики резонансных смещений указывают на значительную концентрацию волновой энергии, захваченной ловушечной модой и аккумулируемой в вихрях энергии.

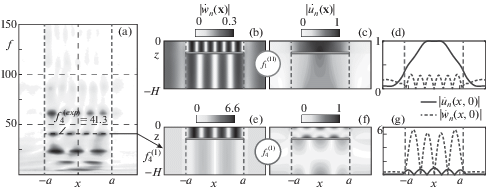
На рис. 2 показан пример сопоставления экспериментальных и расчетных данных для случая нецентральной (d = H/4) трещины полуширины a. Экспериментальные результаты получены для образца, изготовленного из двух алюминиевых пластин толщиной h₁ = 0.5 мм и h₂ = 1.5 мм, склеенных двусторонней клеевой лентой толщины h = 0.05 мм с отсутствием соединения на участке шириной 2a = 22.7 мм. Расчеты, проведенные для данного образца как в рамках полуаналитической модели (3.2)–(3.4), так и с помощью МКЭ-PML, дают близкие значения резонансных частот. Рисунок 2, a – частотная развертка (в кГц) данных интерферометрии вдоль отрезка –20 < x < 20 мм (B-скан), правее, на подрисунках (b), (c) и (e), (f), показаны амплитуды компонент векторов собственных колебаний u_n = (u_n, w_n) на резонансных частотах $f_{1}^{{(II)}} = 93.7 - 1.4i$ и $f_{4}^{{(I)}} = 41.9 - 0.4i$ (кГц) соответственно, а на рис. 2, d и 2, g – их вид на поверхности z = 0 (расчетная схема МКЭ-PML). На B-скане собственные частоты проявляются горизонтальными полосами небольших пятен, указывающих на резонансные пики вертикальных смещений над трещиной. Их число увеличивается с ростом частоты и равно номеру n резонансной частоты f_n. По виду собственных форм выделяется два типа резонансной локализации: с доминированием вертикальной компоненты w_n или горизонтальной – u_n. На рис. 2, a различимы шесть резонансных частот f_n первого типа; частоты второго типа с доминированием касательной компоненты u_n (рис. 2, b–d) на этом рисунке не проявляются, так как в экспериментах использовался лазерный виброметр, измеряющий только вертикальную компоненту w_n.

Набор пятен резонансных смещений позволяет обнаружить наличие расслоения и оценить его размер. Однако оборудование лазерной интерферометрии слишком дорого и громоздко для использования вне лабораторных условий. На практике мониторинг состояния конструкций ответственного назначения обычно ведется на основе данных, собираемых сетью активных и пассивных пьезосенсоров, генерирующих и регистрирующих поверхностные волны, рассеиваемые зарождающимися и развивающимися в процессе эксплуатации внутренними дефектами [20, 21]. Частотный анализ позволяет выделить из этих данных значения частот резонансного рассеяния ω_n = = 2πf_n, поэтому практически важной является задача определения размера и глубины залегания расслоения по этим значениям.

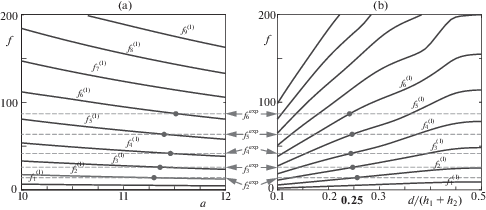
Хорошее совпадение расчетных значений ω_n с данными экспериментальных измерений позволяет решать такие задачи, опираясь на разработанные математические и компьютерные модели [22]. Так на рис. 3, a приводятся расчетные зависимости резонансных частот $f_{n}^{{({\text{I}})}}$ от полуширины a нецентральной трещины, расположенной на глубине d/(h₁ + h₂) = 0.25. Их значения монотонно убывают с ростом a; горизонтальными пунктирными прямыми показаны экспериментальные значения резонансных частот первого типа для моделируемого образца. Абсциссы точек их пересечения, отмеченные темными кружками, очевидно, должны соответствовать его реальному размеру. Действительно, их осредненное значение $\tilde {a}$ = 11.4 мм хорошо согласуется с полушириной расслоения a = 11.35 мм.

Аналогично на рис. 3, b точки пересечения экспериментальных значений с кривыми зависимости f_n от глубины d при фиксированной ширине 2a = 22.8 мм при осреднении дают глубину расслоения $\tilde {d}$/(h₁+ h₂) = 0.249, что близко к реальному значению 0.25.

4. Заключение. На основе решения задачи дифракции бегущих волн на горизонтальной трещине и определения значений резонансных частот рассеяния разработан и экспериментально проверен резонансный метод оценки размера и глубины расположения внутреннего расслоения слоистого материала на основе данных ультразвукового зондирования бегущими волнами.

Работа выполнена в рамках проекта № 0685-2020-0017 государственного задания Минобрнауки России.