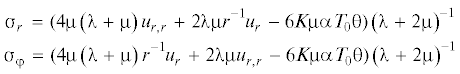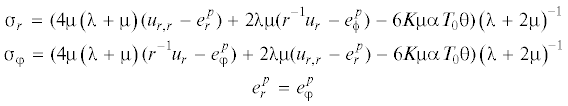1. На главную
  2. Электронные версии
  3. Известия РАН. Механика твердого тела
  4. № 6, 2020

Известия РАН. Механика твердого тела, 2020, № 6, стр. 40-49

КУСОЧНО-ЛИНЕЙНЫЕ ПЛАСТИЧЕСКИЕ ПОТЕНЦИАЛЫ КАК СРЕДСТВО РАСЧЕТОВ ПЛОСКИХ НЕУСТАНОВИВШИХСЯ ТЕМПЕРАТУРНЫХ НАПРЯЖЕНИЙ

А. А. Буренин a, А. В. Ткачева a, *

a Институт машиноведения и металлургии ДВО РАН
Комсомольск-на-Амуре, Россия

* E-mail: 4nansi4@mail.ru

Поступила в редакцию 18.07.2020
После доработки 23.07.2020
Принята к публикации 01.08.2020

Полный текст (PDF)

Аннотация

Строится численно-аналитическое решение одномерной задачи теории температурных напряжений об эволюции плоских напряженных состояний в условиях нагрева и последующего остывания круглой пластины, изготовленной из упругопластического материала. Пластина подвергается нагреву так, что растет пропорционально времени уровень колоколообразного распределения температуры до задаваемого максимального значения. После этого источник нагрева отводится и далее остывание происходит в естественных условиях. Показано, что при следовании условиям кусочно-линейных пластических потенциалов в любой рассчитываемый момент времени процесса деформирования интегрированием уравнения равновесия устанавливаются зависимости, связывающие обратимые и необратимые деформации и напряжения с распределением температуры. Предел текучести полагается квадратично зависимым от температуры; упругие модули, удельная теплоемкость и коэффициент теплового расширения считаются постоянными. Установлено, что рассматриваемая задача в рамках пластического потенциала Треска–Сен-Венана решения не имеет, но разрешается в рамках пластического потенциала Ишлинского–Ивлева.

Ключевые слова: упругость, пластичность, температурные напряжения, пластическое течение, разгрузка, обратное пластическое течение

Введение. Заметный прогресс в развитии теории пластического течения в прошлом веке во многом определялся использованием кусочно-линейных пластических потенциалов [1–4]. Именно с помощью кусочно-линейных класических условий пластического течения максимальных касательных напряжений (условия Треска–Сен-Венана) и максимальных приведенных напряжений (условие Ишлинского–Ивлева) удалось получить решения задач теории [5–9], важных как для развития фундаментальной теории, так и для ее многочисленных приложений.

При решении конкретных и проблемных задач теории пластического течения используется, главным образом, условие пластичности Треска–Сен-Венана. Также кусочно-линейное условие пластического течения Ишлинского–Ивлева в подобном использовании наблюдается значительно реже. Возможно потому, что в сравнении с условием Треска–Сен-Венана (максимальных касательных напряжений) и Мизеса (максимальной интенсивности или максимальных октаэдрических напряжений) оно не обладает столь прозрачным механическим смыслом. Записано оно было значительно позже [10] первых двух, ставших уже к тому времени общепризнанными. В широкую исследовательскую и расчетную практику условие максимальных приведенных напряжений было введено А.Ю. Ишлинским [11] и Д.Д. Ивлевым [1, 12]. После этого оно заслуженно становится [1, 4] третьим после условий Треска–Сен-Венана и Мизеса классическим условием пластического течения, составившим вместе с ними основание теории идеальной пластичности [3, 4, 6, 13].

Условие пластичности максимальных приведенных напряжений успешно использовалось при разрешении разных задач необратимого деформирования [6, 14–16], включая и задачи теории неустановившихся температурных напряжений [17–19]. При этом установлено [18], что имеются задачи, которые при зависимости предела текучести от температуры не имеют решения в условиях пластичности Треска–Сен-Венана, но в то же время благополучно разрешаются в условиях Ишлинского–Ивлева. Здесь рассмотрим отмечающуюся этим же свойством задачу неустановившихся температурных напряжений о численно-аналитическом расчете эволюции плоских напряженных состояний при нагреве и последующем остывании круглой пластины.

Необходимо отметить, что благодаря постоянному и требовательному вниманию со стороны технологической практики, теория термопластичности [20–22] и, в частности, теория температурных напряжений [23–28] остаются уверенно развиваемыми направлениями исследований.

1. Основные соотношения теории неустановившихся температурных напряжений запишем в виде:

(1.1)
$\begin{gathered} {\mathbf{e}} = {{{\mathbf{e}}}^{{\mathbf{e}}}} + {{{\mathbf{e}}}^{{\mathbf{p}}}} = \frac{1}{2}(\nabla {\mathbf{u}} + {{\nabla }^{T}}{\mathbf{u}}) \\ \sigma = (\lambda tr{{{\mathbf{e}}}^{{\mathbf{e}}}} - 3\alpha {{T}_{0}}K\theta ){\mathbf{I}} + 2\mu {{{\mathbf{e}}}^{{\mathbf{e}}}} \\ d{{{\mathbf{e}}}^{{\mathbf{p}}}} = d\varphi \frac{{\partial f\left( {\sigma ,k} \right)}}{{\partial \sigma }};\quad f\left( {\sigma ,k} \right) = 0;\quad d\varphi > 0 \\ \frac{{\partial \theta }}{{\partial t}} = a\Delta \theta - w\left( {t,{\mathbf{z}}} \right);\quad \theta = \frac{{T - {{T}_{0}}}}{{{{T}_{0}}}} \\ \end{gathered} $

В (1.1) t – время, z – радиус вектор места, занимаемого расматриваемой точкой деформируемого тела; u – вектор перемещения; ee, ep – обратимая и необратимая составляющие тензора полных деформаций e; $\sigma $ – тензор напряжений; I – единичный тензор второго ранга; $f\left( {\sigma ,k} \right) = 0$ – уравнение поверхности нагружения (текучести); T, T0 – текущая температура и температура свободного состояния тела; $w\left( {t,{\mathbf{z}}} \right)$ – скалярная функция, задающая интенсивность источников тепла в теле. Упругие модули Ламе ${\lambda }$ и ${\mu }$, модуль всестороннего сжатия $K = {\lambda } + \frac{2}{3}{\mu }$, коэффициент линейного расширения α далее будем считать постоянными, от температуры независимыми. Только предел текучести k полагаем изменяющимся с изменением температуры и такую зависимость принимаем в форме

(1.2)
$k = {{k}_{0}}{{\tau }^{2}};\quad \tau = {{T}_{0}}{{\left( {{{T}_{p}} - {{T}_{0}}} \right)}^{{ - 1}}}\theta $
${{T}_{p}}$ – температура плавления материала неизотермически деформируемого тела, ${{k}_{0}}$ – предел текучести материала при комнатной температуре ${{T}_{0}}$.

Далее массовыми силами и силами инерции пренебрегаем, поэтому уравнение равновесия запишется в форме

(1.3)
$\nabla \sigma = 0$

Записанные соотношения для своей замкнутости требуют указания условия пластического течения. Здесь будем использовать классические кусочно-линейные условия

(1.4)
$\max \left| {{{{\sigma }}_{i}} - {{{\sigma }}_{j}}} \right| = 2k$
(1.5)
$\max \left| {{{\sigma }_{i}} - \sigma } \right| = \frac{4}{3}k;\quad \sigma = \frac{1}{3}\left( {{{\sigma }_{1}} + {{\sigma }_{2}} + {{\sigma }_{3}}} \right)$

Первое из соотношений называется условием максимальных касательных напряжений Треска–Сен-Венана, второе – условием максимальных приведенных Ишлинского–Ивлева.

2. Температурная задача. Рассмотрим круглую пластинку радиуса R, край которой закреплен. В цилиндрической системе координат r, φ, z последнее означает, что

(2.1)
${{u}_{r}}\left( {0,t} \right) = 0;\quad {{u}_{r}}\left( {R,t} \right) = 0$
где ur – компонента вектора перемещений.

Нагрев пластины осуществляется источником, сообщающим пластине колоколообразное распределение температуры с растущим ее максимумом в центре пластины. Это позволяет задать источник в виде

(2.2)
$\omega \left( {t,r} \right) = \beta t{{e}^{{ - \gamma {{r}^{{2n}}}}}}$

Уравнение теплопроводности (последнее равенство в (1.1)) теперь в цилиндрической системе координат перепишем в форме

(2.3)
$\frac{{\partial {\theta }}}{{\partial t}} = a(r{\theta }{{,}_{r}}){{,}_{r}} + \,{\beta }t{{e}^{{ - \gamma {{r}^{{2n}}}}}} - {\chi \theta }$

Коэффициент теплоотдачи χ от пластины в окружающую среду будем считать постоянным. Если пренебречь теплоотводом от кромки r = R пластины, то начальными и граничными условиями для (2.3) будут

(2.4)
${\theta }\left( {r,0} \right) = 0;\quad {\theta }{{,}_{r}}(R,t) = 0$

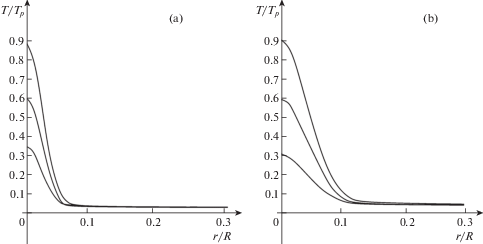
Температурная задача (2.3) и (2.4) разрешается до той поры, пока температура в центре пластины не достигнет своего задаваемого максимального значения $T = {{T}_{*}}$. Следовательно, после того как $\theta = {{T}^{{ - 1}}}{{T}_{*}} - 1$ предпоследнее слагаемое правой части из уравнения теплопроводности (2.3) исключается. Рис. 1 иллюстрирует решение температурной задачи до момента отвода источника тепла. Графически указано распределение температуры в ее росте со временем до максимальной (верхний график) при следующих значениях постоянной задачи: $a = 77.1$ × 10–6 м2/с; $\chi = 7.6$ Вт/(м2 ⋅ °С); $\beta = 20$ с–2; $\gamma = 880$ см–2 (рис. 1, а); $\gamma = 220$ см–2(рис. 1, b); ${{T}_{p}} = 660$°С, ${{T}_{0}} = 20$°С.

Рис. 1

3. Начальное термоупругое деформирование происходит в согласии с уравнением равновесия (1.3), которое в рассмотренном случае запишется в виде

(3.1)
${{{\sigma }}_{{r,r}}} + {{r}^{{ - 1}}}\left( {{{{\sigma }}_{r}} - {{{\sigma }}_{\varphi }}} \right) = 0$

Напряжения ${{{\sigma }}_{{rr}}} = {{{\sigma }}_{r}}$, ${{{\sigma }}_{{\varphi \varphi }}} = {{{\sigma }}_{\varphi }}$, ${{{\sigma }}_{{zz}}} = {{{\sigma }}_{z}} = 0$ в рассматриваемом случае являются главными напряжениями. Исходя из соотношений Дюамеля–Неймана (1.1) и исключая с их помощью uz,z, найдем

(3.2)

Подстановка (3.2) в (3.1) и интегрирование результата приводит к зависимостям

(3.3)
${{u}_{r}} = 1.5K{{r}^{{ - 1}}}{{\left( {\lambda + \mu } \right)}^{{ - 1}}}\alpha {{T}_{0}}\int\limits_0^r {\rho \theta \left( \rho \right)d\rho } + 0.5r{{C}_{1}}\left( t \right) + {{r}^{{ - 1}}}{{C}_{2}}\left( t \right)$
(3.4)
$\begin{gathered} {{\sigma }_{r}} = - 3K\mu {{r}^{{ - 2}}}{{\left( {\lambda + \mu } \right)}^{{ - 1}}}\alpha {{T}_{0}}\int\limits_0^r {\rho \theta \left( \rho \right)d\rho } + 3K\mu {{\left( {\lambda + 2\mu } \right)}^{{ - 1}}}{{C}_{1}}\left( t \right) - 2\mu {{r}^{{ - 2}}}{{C}_{2}}\left( t \right) \\ {{\sigma }_{\varphi }} = 3K\mu {{r}^{{ - 2}}}{{\left( {\lambda + \mu } \right)}^{{ - 1}}}\alpha {{T}_{0}}\int\limits_0^r {\rho \theta \left( \rho \right)d\rho } - 3K\mu {{\left( {\lambda + \mu } \right)}^{{ - 1}}}\alpha {{T}_{0}}\theta + \\ \, + 3K\mu {{\left( {\lambda + 2\mu } \right)}^{{ - 1}}}{{C}_{1}}\left( t \right) + 2\mu {{r}^{{ - 2}}}{{C}_{2}}\left( t \right) \\ \end{gathered} $

Выполняя граничные условия (2.1), найдем

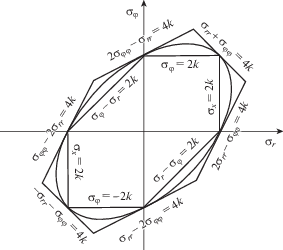
${{C}_{1}} = - 3K{{R}^{{ - 2}}}{{\left( {\lambda + \mu } \right)}^{{ - 1}}}\alpha {{T}_{0}}\int\limits_0^R {\rho \theta \left( \rho \right)d\rho } ;\quad {{C}_{2}} = 0$

4. Пластическое течение. С ростом температуры растут и напряжения. Наступает момент времени $t = {{t}_{1}} > 0$ когда напряжения, рассчитываемые согласно (3.4), удовлетворяют условиям пластического течения (1.4) или (1.5). Расчеты показывают, что в момент времени t = t1 напряжения ${{\sigma }_{r}}$ и σφ одинаковы и равны ${{\sigma }_{r}} = {{\sigma }_{\varphi }} = - 2k$. Одновременно выполняются условие Треска–Сен-Венана и условие Ишлинского–Ивлева (см. рис. 2). Только условие максимальных касательных напряжений выполняется в соответствии ребру призмы Треска (условие полной пластичности), а условие максимальных приведенных напряжений в соответствии грани призмы Ивлева. На рис. 2 указано пересечение призмы Треска (внутренний шестиугольник) и призмы Ивлева (внешний шестиугольник) с координатной плоскостью ${{\sigma }_{z}} = 0$.

Рис.2

Если принять, что осуществляется состояние полной пластичности [1, 4, 5] в соответствии напряжений ребру призмы Треска, то согласно уравнению равновесия (3.1) имеем ${{\sigma }_{{r,r}}} = 0$. Выполнить условие ${{\sigma }_{r}} = {\text{const}}$ невозможно, поскольку k и ${{\sigma }_{r}}$ уже задаются распределением по r температуры. Следовательно, невозможно в таком случае получить решение задачи теории из-за того, что она оказывается переопределенной вследствие зависимости предела текучести от температуры.

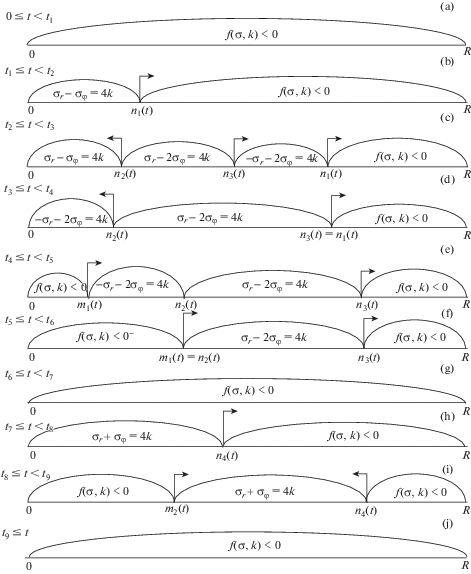
Остается считать, что начавшееся пластическое течение соответствует грани ${{\sigma }_{r}} + {{\sigma }_{\varphi }}$ = = –4k призмы Ивлева (рис. 2). Следовательно, в момент времени t = t1 в центре пластины зарождается и продвигается далее по пластине упругопластическая граница $r = {{n}_{1}}(t)$, оставляя за собой область пластического течения (рис. 3) $0 \leqslant r \leqslant {{n}_{1}}(t)$. В этой области

(4.1)
Рис. 3

Подстановка (4.1) в уравнение равновесия (3.1) и последующее интегрирование результата приводит к зависимостям

(4.2)
$\begin{gathered} {{u}_{r}} = 2{{\left( {\mu r} \right)}^{{ - 1}}}\int\limits_0^r {\rho k(\rho )d\rho } + 0.5r{{C}_{3}}\left( t \right) + {{r}^{{ - 1}}}{{C}_{4}}\left( t \right) \\ {{\sigma }_{r}} = - 4{{r}^{{ - 2}}}\int\limits_0^r {\rho k(\rho )d\rho } - 2{{r}^{{ - 2}}}\mu {{C}_{4}}\left( t \right) \\ e_{r}^{p} = 4({{\left( {3\mu } \right)}^{{ - 1}}} + {{\left( {6K} \right)}^{{ - 1}}})k - \alpha {{Т}_{0}}\theta + 0.5{{C}_{3}}\left( t \right) \\ \end{gathered} $

В рассматриваемый момент времени постоянные C3(t) и C4(t) вместе с новыми значениями C1(t) и C2(t) и положением упругопластической границы $r = {{n}_{1}}\left( t \right)$ определяются при выполнении граничных условий (2.1), условия пластичности и условий на граничной линии $r = {{n}_{1}}\left( t \right)$

(4.3)
${{\left. {[{{u}_{r}}]} \right|}_{{{{n}_{1}}(t)}}} = 0;\quad {{\left. {[{{\sigma }_{r}}]} \right|}_{{{{n}_{1}}(t)}}} = 0$

Квадратными скобками в (4.3) обозначен разрыв переменной на продвигающейся линии $r = {{n}_{1}}(t)$. На рис. 3 представлена последовательная схема возникновения и исчезновения разных областей пластического течения. При продолжающемся нагреве находится момент времени $t = {{t}_{2}} > {{t}_{1}}$, когда на некоторой внутренней линии пластической области наряду с условием ${{{\sigma }}_{r}} + {{{\sigma }}_{\varphi }} = - 4k$, выполняется еще условие ${{{\sigma }}_{r}} - 2{{{\sigma }}_{\varphi }}$ = = 4k, то есть условия ребра призмы Ивлева. Однако в отличие от [19], пластическое течение в этих условиях оказывается неосуществимым. Действительно, на данном ребре ${{{\sigma }}_{r}} = - 4k{\text{/}}3$, ${{{\sigma }}_{\varphi }} = - 8k{\text{/}}3$ и согласно (3.1) $\partial k\left( r \right){\text{/}}\partial r - k = 0$. Разрешая это дифференциальное уравнение получим распределение k(r), которое уже задано распределением по пластине температуры $k = k(T(r))$. Это противоречие приводит к переопределенности задачи. Выход из такой ситуации состоит в том, что в момент времени t = t2 в рассчитываемой линии области пластического течения возникают две линии $r = {{n}_{2}}(t)$ и $r = {{n}_{3}}(t)$, делящие область течения на три части (рис. 3) и продвигающиеся в разные стороны (направление движения указано стрелками). В двух таких частях $0 \leqslant r \leqslant {{n}_{2}}\left( t \right)$ и ${{n}_{3}}(t) \leqslant r \leqslant {{n}_{1}}(t)$ пластическое течение продолжается в соответствии грани ${{{\sigma }}_{r}} + {{{\sigma }}_{\varphi }}$ = –4k, а в области ${{n}_{2}}\left( t \right) \leqslant r \leqslant {{n}_{3}}\left( t \right)$ оно соответствует соседней грани призмы Ивлева. При записи аналога (4.1) для последней области следует учитывать, что наряду с формирующимися деформациями $e_{r}^{p}\left( {r,t} \right)$ и $e_{\varphi }^{p}\left( {r,t} \right)$ в ней присутствуют необратимые деформации pr(t) и ${{p}_{\varphi }}\left( r \right)$, накопленные при пластическом течении в условиях прежней грани поверхности нагружения. Они вычисляются из (4.2) моментом прихода на линию с координатой r разделяющей линии $r = {{n}_{2}}\left( t \right)$ или $r = {{n}_{3}}\left( t \right)$.

(4.4)
$\begin{gathered} \frac{{{{\partial }^{2}}{{u}_{r}}}}{{\partial {{r}^{2}}}} + \frac{1}{r}\frac{{\partial {{u}_{r}}}}{{\partial r}} - \frac{1}{{4{{r}^{2}}}}{{u}_{r}} = \frac{{3\alpha {{T}_{0}}K}}{{2\left( {{\lambda } + {\mu }} \right)}}{{\theta }_{{,r}}} + \frac{{3\alpha {{T}_{0}}K}}{{4\left( {{\lambda } + {\mu }} \right)r}}\theta + \frac{1}{{3K}}{{k}_{{,r}}} + \\ \, + \frac{{{\lambda } + {\mu }}}{{2{\mu }Kr}}k + \left( {{{p}_{{r,r}}} + \frac{1}{{2r}}{{p}_{r}}} \right) + \frac{1}{2}\left( {{{p}_{{\varphi ,r}}} + \frac{1}{{2r}}{{p}_{\varphi }}} \right) \\ \end{gathered} $

После интегрирования (4.4) получим

$\begin{gathered} {{u}_{r}} = \frac{1}{{\sqrt r }}\int\limits_{{{n}_{2}}(t)}^r {\left( {{{p}_{r}}\left( \rho \right) + 0.5{{p}_{\varphi }}\left( \rho \right)} \right)\sqrt \rho d\rho } + \frac{{\sqrt r \left( {3\lambda + 5\mu } \right)}}{{3\mu K}}\int\limits_{{{n}_{2}}(t)}^r {\frac{{k(\rho )}}{{\sqrt \rho }}d\rho } - \\ \, - \frac{{\left( {3\lambda + 5\mu } \right)}}{{3\mu K\sqrt r }}\int\limits_{{{n}_{2}}(t)}^r {k(\rho )\sqrt \rho d\rho } + \frac{3}{{2\sqrt r }}\alpha {{T}_{0}}\int\limits_{{{n}_{2}}(t)}^r {\sqrt \rho \theta \left( \rho \right)d\rho } + \frac{{\sqrt r \left( {3\lambda + 5\mu } \right)}}{{12\mu K}}{{C}_{5}}\left( t \right) - \frac{{{{C}_{6}}\left( t \right)}}{{\sqrt r }} \\ \end{gathered} $
(4.5)
$e_{r}^{p} = - \frac{1}{2}e_{\varphi }^{p} = \frac{1}{2}{{p}_{\varphi }} - \frac{1}{{2\sqrt {{{r}^{3}}} }}\int\limits_{{{n}_{2}}(t)}^r {\left( {{{p}_{r}}\left( \rho \right) + 0.5{{p}_{\varphi }}\left( \rho \right)} \right)\sqrt \rho d\rho } + \frac{{3\left( {\lambda + \mu } \right)}}{{\mu K}}k + \frac{{\alpha {{T}_{0}}}}{2}\theta + $
$\begin{gathered} \, - \frac{{\lambda + \mu }}{{2\mu K\sqrt r }}\int\limits_{{{n}_{2}}(t)}^r {\frac{{k(\rho )}}{{\sqrt \rho }}d\rho } + \frac{{\left( {3\lambda + 5\mu } \right)}}{{6\mu K\sqrt {{{r}^{3}}} }}\int\limits_{{{n}_{2}}(t)}^r {k(\rho )\sqrt \rho d\rho } + \frac{{\left( {\lambda + \mu } \right)}}{{8\mu K\sqrt r }}{{C}_{5}}\left( t \right) + \frac{{{{C}_{6}}\left( t \right)}}{{2\sqrt {{{r}^{3}}} }} \\ {{\sigma }_{r}} = - \frac{2}{{\sqrt r }}\int\limits_{{{n}_{2}}(t)}^r {k(\rho )\sqrt \rho d\rho } + \frac{{{{C}_{5}}\left( t \right)}}{{\sqrt r }} \\ \end{gathered} $

Значение функций ${{C}_{1}}\left( t \right),...,{{C}_{5}}\left( t \right),{{C}_{6}}\left( t \right)$ вместе с положениями разделяющих деформируемую область линий приходится пересчитывать на каждом временном шаге. Для этого решим систему алгебраических уравнений, составленную из граничных условий (2.1) условий пластического течения и непрерывности перемещения ur и напряжения ${{\sigma }_{r}}$ (аналог (4.3)) на разделяющих линиях.

Расчетом установлено, что линия $r = {{n}_{3}}(t)$ продвигается быстрее окружности $r = {{n}_{1}}(t)$; наступает момент времени $t = {{t}_{3}} > {{t}_{2}}$, когда ${{n}_{3}}\left( {{{t}_{3}}} \right) = {{n}_{1}}\left( {{{t}_{3}}} \right)$ (рис. 3, d) и пластическая область исчезает.

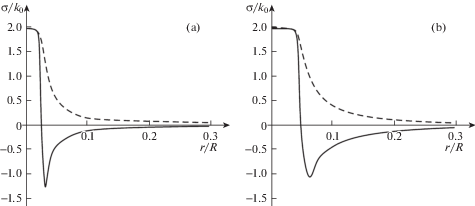
Распределение напряжений в момент отвода источника тепла, то есть в момент времени, когда распределение температуры задается верхней зависимостью на рис. 1, указано на рис. 4 при $\lambda = 192.3{{k}_{0}}$, $\mu = 128.2{{k}_{0}}$, ${{k}_{0}} = 210$ МПа, $\alpha = 23.4$ × 10–6 (°С)–1, $\gamma = 880$ см–2 (рис. 4а); $\gamma = 220$ см–2 (рис. 4, b).

Рис. 4.

5. Остывание и разгрузка. Сразу за моментом t = t4 отвода источника нагрева в центре пластины зарождается область обратимого деформирования $0 \leqslant r \leqslant {{m}_{1}}\left( t \right)$ с продвигающейся разгружающей упругопластической границей $r = {{m}_{1}}\left( t \right)$ (рис. 3, е). Продвижение этой линии приводит к исчезновению сначала пластической, области ${{m}_{1}}(t) \leqslant r \leqslant {{n}_{2}}(t)$ (рис. 3, f), а потом после t = t6 и области ${{n}_{2}}\left( t \right) \leqslant r \leqslant {{n}_{3}}\left( t \right)$ (рис. 3, g). С момента времени t = t3 пластина деформируется обратимо. Следует учитывать, что данное термоупругое деформирование происходит, в отличие от (3.3) и (3.4), в условиях присутствующих, со временем не изменяющихся пластических деформаций ${{p}_{r}}\left( r \right)$ и ${{p}_{\varphi }}\left( r \right)$.

В условиях достаточно высокой степени нагрева при остывании пластины необходимо возникает повторное (обратное) пластическое течение. Начинается оно в момент времени t = t7, когда в центре пластины выполняется условие пластического течения ${{\sigma }_{r}} + {{\sigma }_{\varphi }} = 4k$, соответствующее противоположной грани призмы Ивлева в сравнении с активным процессом деформирования (рис. 2). В области повторного пластического течения $0 \leqslant r \leqslant {{n}_{4}}\left( t \right)$ (рис. 3h) после интегрирования уравнения равновесия в перемещениях получим

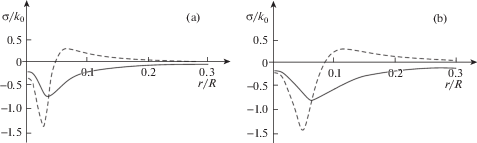
$\begin{gathered} {{u}_{r}} = - 2{{\left( {\mu r} \right)}^{{ - 1}}}\int\limits_0^r {\rho k(\rho )d\rho } + r\int\limits_0^r {{{\rho }^{{ - 1}}}\left( {{{p}_{r}}(\rho ) - {{p}_{\varphi }}(\rho )} \right)d\rho } + 0.5r{{C}_{3}}\left( t \right) + {{r}^{{ - 1}}}{{C}_{4}}\left( t \right) \\ {{\sigma }_{r}} = 4{{r}^{{ - 2}}}\int\limits_0^r {\rho k(\rho )d\rho } - 2{{r}^{{ - 2}}}\mu {{C}_{4}}\left( t \right) \\ e_{r}^{p} = - 4({{\left( {3\mu } \right)}^{{ - 1}}} + {{\left( {6K} \right)}^{{ - 1}}})k - \alpha {{Т}_{0}}\theta - \int\limits_0^r {{{\rho }^{{ - 1}}}\left( {{{P}_{r}}(\rho ) - {{P}_{\varphi }}(\rho )} \right)d\rho } - {{P}_{\varphi }} + 0.5{{C}_{3}}\left( t \right) \\ \end{gathered} $

В момент времени t = t8 в центре пластины возникает разгружающая упругопластическая граница $r = {{m}_{2}}\left( t \right)$, а упругопластическая граница $r = {{n}_{4}}\left( t \right)$ начинает двигаться в обратную сторону. Продвигаясь по пластине (рис. 3, i), он и при $t = {{t}_{9}} > {{t}_{8}}$ встречаются. Далее пластина, вплоть до полного ее остывания деформируется обратимо, формируя окончательное поле остаточных напряжений (рис. 5, а) $\gamma = 880$ см–2, b) $\gamma = 220$ см–2.

Рис. 5.

Таким образом, кусочно-линейное условие пластичности Ишлинского–Ивлева обеспечивает расчет одномерного поля температурных напряжений в круглой пластине в его эволюции от начала нагрева до полного последующего остывания без обращения к приближенным численным методам расчетов. Расчеты проводятся последовательными шагами по времени с использованием конечных зависимостей деформаций и напряжений от распределения в рассчитываемый момент времени температуры по пластине без дискретизации расчетных областей. Впервые обнаружены особенности в расчетах, связанные с выполнением условий пластического течения, соответствующих ребру призмы Ивлева. Указан способ дальнейших расчетов посредством мгновенного перехода с грани призмы на соседнею грань, минуя грань поверхности пластического течения. Установленные особенности окажутся полезными при использовании данного условия пластического течения в задачах более сложной геометрии и более сложного термомеханического воздействия.

Работа выполнена при поддержке государственного задания ХФИЦ ДВО РАН.

Список литературы

  1. Ивлев Д.Д. Теория идеальной пластичности. М.: Наука, 1966. 252 с.

  2. Ивлев Д.Д., Быковцев Г.И. Теория упрочняющегося пластического тела. М.: Наука, 1971. 232 с.

  3. Клюшников В.Д. Математическая теория пластичности. М.: Изд-во МГУ, 1979. 208 с.

  4. Ивлев Д.Д., Ершов Л.В. Метод возмущений в теории упруго-пластического тела. — М.: Наука, 1978. 208 с.

  5. Соколовский В.В. Теория пластичности. М.: Высш. школа, 1969. 608 с.

  6. Быковцев Г.И., Ивлев Д.Д. Теория пластичности. Владивосток: Дальнаука, 1998. 528 с.

  7. Ерхов М.И. Теория идеальной пластичности тел и конструкций. М.: Наука, 1978. 352 с.

  8. Аннин Б.Д., Черепанов Г.Б. Упругопластическая задача. Новосибирск: Наука, 1983. 240 с.

  9. Галин Л.А. Упругопластические задачи. М.: Наука, 1984. 232 с.

  10. Schmidt R. Uber den Zusammenhang von Spannunqen und Iormanderunqen im Verfestigsgebiet // Ingender Arihiv. 1932. V. 3. № 3. P. 215–235.

  11. Ишлинский А.Ю. Гипотеза прочности формоизменения // Ученые записки МГУ. 1940. № 46. С. 104–114.

  12. Ivlev D.D. On the. development of a theory of ideal plasticity // Journal of Applied Mathematics and Mechanics. 1958. V. 22. № 6. P. 1221–1230.

  13. Хилл Р. Математическая теория пластичности. М.: Мир. 1956. 407 с.

  14. Zhao D. W., Xie Y.-J. Liu X.-H., Wang G.-D. Three-Dimensional Analysis of Rolling by Twin Shear Stress Yield Criterion // J. of Iron and Steel Research Int. 2006. V. 13. № 6. P. 21–26.

  15. Cai Q., Pang M., Zhang Y.-Q., Liw X. Elastic-plastic stress distribution of rotating annuar disc based on twin-shear stress yorld criterion criterion // Zhejiang Daxue Xuebao (Gongxue Ban) / J of Zhejiang University (Eng. Scince). 2008. V. 42. № 9. P. 1540–1544.

  16. Zhu X., Pang M., Zhang Y. Estimation of burst pressure of pipeline using twin-shear yield criterion // Chinese J. of Appl. Mech. 2011. V. 28. № 2. P. 135–138.

  17. Дац Е.П., Мурашкин Е.В., Ткачева А.В., Щербатюк Г.А. Температурные напряжения в упругопластической трубе в зависимости от выбора условия пластичности // Изв. РАН. МТТ. 2018. № 1. С. 32–43.

  18. Буренин А.А., Каинг М., Ткачева А.В. К расчету плоских напряженных состояний в теории неустановившихся температурных напряжений в упругопластических телах // ДВМЖ. Т. 18. № 1. С. 1–8.

  19. Буренин А.А., Матвеенко В.П., Ткачева А.В. Температурные напряжения в процессе сборки двухслойного вала способом горячей посадки // Ученые записки КнАГТУ. 2018. № 3 (35). С. 31–41.

  20. Шевченко Ю.Н. Термопластичность при переменных нагружениях. Киев: Наукова думка. 1970. 288 с.

  21. Пэжина П., Савчук А. Проблемы термопластичности// Проблемы теории пластичности и ползучести. М.: Мир. 1979. С. 94–202.

  22. Шевченко Ю.Н., Стеблянко П.А., Петров А.Д. Численные методы в нестационарных задачах теории термопластичности // Пробл. выч. мех. и прочн. конструкций. 2014. № 22. С. 250–264.

  23. Gamer U. A cocise treament of the shrink fit withelostic plastic hab // Int. J. Solids/ Struct. 1992. V. 29. P. 2463–2469.

  24. Mack W. Thermal assembly of an elastic-plastic hub and a solid shaft // Arch. Appl. Mech. 1993. V. 63. P. 42–50.

  25. Kovacs A. Residual Stresses in Thermally Looded Shrink Fits // Periodica Polytechnica: Mech. Eng. 1996. V. 40. № 2. P. 103–112.

  26. Александров С.Е., Ломакин Е.В., Дзенг Й.-Р. Решение термоупругопластической задачи для тонкого диска из пластически сжимаемого материала, подверженного термическому нагружению // ДАН. 2012. Т. 443. № 3. С. 310–312.

  27. Antonio N. Contact separation and failure analysis thermo-elastoplastic shrink-fit assembly // Appl. Math. 2013. V. 37. P. 2352–2364.

  28. Буренин А.А., Ткачева А.В., Щербатюк Г.А. К расчету неустоявшихся температурных напряжений в упругопластических телах // Вычисл. мех. спл. сред. 2017. Т. 10. № 3. С. 245–259.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал