Известия РАН. Механика твердого тела, 2020, № 6, стр. 14-23
О ПОТЕРЕ УСТОЙЧИВОСТИ БЫСТРОВРАЩАЮЩЕГОСЯ ПОЛИМЕТАЛЛИЧЕСКОГО ДИСКА
Ю. В. Немировский a, b, *, С. В. Тихонов c, **
a Институт теоретической и прикладной механики им. С.А. Христиановича СО РАН
Новосибирск, Россия
b Новосибирский государственный технический университет
Новосибирск, Россия
c Чувашский государственный университет им. И.Н. Ульянова
Чебоксары, Россия
* E-mail: nemiryury@mail.ru
** E-mail: strangcheb@mail.ru
Поступила в редакцию 11.08.2020
После доработки 19.08.2020
Принята к публикации 25.08.2020
Аннотация
В работе рассматриваются слоистые по толщине металлические быстровращающиеся диски. Закон деформирования каждого слоя диска принят в виде аппроксимации полиномом второго порядка. Для вращающихся тонких биметаллических дисков приведены основные соотношения для исследования критических деформированных состояний, возникающих вследствие малых технологических отклонений изготовления полотна либо контурных форм.
1. Введение. В настоящее время проектирование любых элементов конструкций, как правило, производится с целями снижения стоимости их производства, веса, эксплуатационных характеристик. Одним из путей достижения поставленных целей является использование в процессе их изготовления многослойных конструкций.
Важнейшими составляющими таких объектов инженерного моделирования, как паровые и газовые турбины, маховики, электрические насосы, работающих в условиях тяжелых нагрузок являются быстровращающиеся сплошные и кольцевые круговые диски [13]. В отечественной и зарубежной литературе существует достаточно много исследований посвященных определению напряженно-деформированного состояния быстровращающихся дисков при различных условиях пластичности [1–7]. Ивлевым Д.Д. впервые в работе [8] рассмотрена задача о механизме потери устойчивости быстровращающегося упругопластического однородного сплошного диска постоянной толщины, методом малого параметра [17] найдены критические значения радиуса пластической зоны и критической относительной скорости вращения. Дальнейшие исследования потери устойчивости плоских однородных, физически-неоднородных, радиально-составных, ступенчатых быстровращающихся дисков методом малого параметра были продолжены в работах [9–12]. Для гибридных слоистых тонких дисков с защитными и упрочняющими слоями такая задача, по-видимому, не рассматривалась и ее решение предлагается в данной статье.
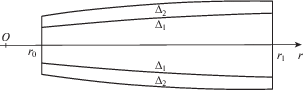
2. Постановка задачи. Рассмотрим двухслойный плоский кольцевой диск с защитными или упрочняющимися поверхностными слоями с симметричной относительно срединной поверхности структурой расположения материалов (рис. 1). Напряженное состояние будем считать двухмерным и кусочно-равномерно распределенным по толщине диска. Задачу будем рассматривать в цилиндрической системе координат r, φ, z. Будем полагать внешний радиус диска гораздо больше максимальной общей толщины диска $2\left( {{{\Delta }_{k}}(r,\varphi ) + {{\Delta }_{2}}(r,\varphi )} \right)$, где $2{{\Delta }_{k}}(r,\varphi ),$ $2{{\Delta }_{m}}(r,\varphi )$ – толщины первого (внутреннего) и второго (внешнего) слоя диска.
Будем считать, что массовый расход материала при определенной технологии изготовления остается заданным и равным M. Если положить, что массы первого и второго слоя равны Mk и Mm соответственно, тогда получим
(2.1)
${{M}_{k}} = 2{{\rho }_{k}}\int\limits_0^{2\pi } {\left( {\int\limits_{{{r}_{0}}}^{{{r}_{1}}} {r{{\Delta }_{k}}(r,\varphi )} dr} \right)d\varphi } ,\quad {{M}_{m}} = 2{{\rho }_{m}}\int\limits_0^{2\pi } {\left( {\int\limits_{{{r}_{0}}}^{{{r}_{1}}} {r{{\Delta }_{m}}(r,\varphi )} dr} \right)d\varphi } $Толщины каждого из слоев диска представим в виде
(2.2)
${{\Delta }_{1}} = {{\Delta }_{{10}}}(r) + {{\Delta }_{{11}}}(r,\varphi ){{\delta }_{1}},\quad {{\Delta }_{2}} = {{\Delta }_{{20}}}(r) + {{\Delta }_{{21}}}(r,\varphi ){{\delta }_{2}}$(2.3)
${{\Delta }_{{11}}}(r,\varphi ) = {{\psi }_{{11}}}(r){{z}_{{11}}}(\varphi ),\quad {{\Delta }_{{21}}}(r,\varphi ) = {{\psi }_{{21}}}(r){{z}_{{21}}}(\varphi )$(2.4)
${{r}_{0}}(\varphi ) = {{r}_{{00}}}\left( {1 + {{\delta }_{3}}\cos \varphi } \right),\quad {{r}_{1}}(\varphi ) = {{r}_{{10}}}\left( {1 + {{\delta }_{4}}\cos \varphi } \right)$Из указанных предположений можно получить
(2.5)
$M = {{M}_{{0m}}} + {{M}_{{1m}}}{{\delta }_{1}} + {{M}_{{2m}}}{{\delta }_{2}} + {{M}_{{3m}}}{{\delta }_{3}} + {{M}_{{4m}}}{{\delta }_{4}}$В дальнейшем, не меняя обозначения будем записывать необходимые уравнения используя соответствующие единые обезразмеривающие параметры длины, напряжения, плотности для некоторого исходного проекта. Тогда ненулевыми будут следующие компоненты тензора деформаций
(2.6)
${{\varepsilon }_{r}} = \frac{{\partial u}}{{\partial r}},\quad {{\varepsilon }_{\varphi }} = \frac{1}{r}\frac{{\partial \upsilon }}{{\partial \varphi }} + \frac{u}{r},\quad {{\gamma }_{{r\varphi }}} = \frac{1}{r}\frac{{\partial u}}{{\partial \varphi }} + r\frac{\partial }{{\partial r}}\left( {\frac{\upsilon }{r}} \right) = 2{{\varepsilon }_{{r\varphi }}}$Уравнения совместности деформаций будут иметь вид
(2.7)
$2\frac{\partial }{{\partial r}}\left( {r\frac{{\partial {{\varepsilon }_{{r\varphi }}}}}{{\partial \varphi }}} \right) = \frac{{{{\partial }^{2}}{{\varepsilon }_{r}}}}{{\partial {{\varphi }^{2}}}} - r\frac{{\partial {{\varepsilon }_{r}}}}{{\partial r}} + r\frac{{{{\partial }^{2}}\left( {r{{\varepsilon }_{\varphi }}} \right)}}{{\partial {{r}^{2}}}}$Усилия в радиальных сечениях диска можно определить из соотношений
(2.8)
$\begin{gathered} {{N}_{r}} = 2\left( {{{\sigma }_{{{{r}_{1}}}}}{{\Delta }_{1}}(r) + {{\sigma }_{{{{r}_{2}}}}}{{\Delta }_{2}}(r)} \right)r,\quad {{N}_{\varphi }} = 2\left( {{{\sigma }_{{{{\varphi }_{1}}}}}{{\Delta }_{1}}(r) + {{\sigma }_{{{{\varphi }_{2}}}}}{{\Delta }_{2}}(r)} \right)r \\ {{N}_{{r\varphi }}} = 2\left( {{{\sigma }_{{r{{\varphi }_{1}}}}}{{\Delta }_{1}}(r) + {{\sigma }_{{r{{\varphi }_{2}}}}}{{\Delta }_{2}}(r)} \right)r \\ \end{gathered} $При этом они должны удовлетворять для рассматриваемых дисков уравнениям равновесия
(2.9)
$\frac{{\partial {{N}_{r}}}}{{\partial r}} + \frac{{{{N}_{r}} - {{N}_{\varphi }}}}{r} + \frac{1}{r}\frac{{\partial {{N}_{{r\varphi }}}}}{{\partial \varphi }} + {{\Psi }_{z}} = 0,\quad \frac{{\partial {{N}_{{r\varphi }}}}}{{\partial r}} + \frac{1}{r}\frac{{\partial {{N}_{\varphi }}}}{{\partial \varphi }} + \frac{{2{{N}_{{r\varphi }}}}}{r} = 0$Для каждого из материалов k-го слоя примем справедливыми соотношения
где ${{\sigma }_{{ik}}}$, ${{\varepsilon }_{{ik}}}$ – интенсивность напряжений и деформаций соответственно в k-м слое диска, Ak, Bk – коэффициенты, которые могут быть определены для данного материала слоя диска на основе физических экспериментов.Интенсивности напряжений и деформаций ${{\sigma }_{{ik}}}$, ${{\varepsilon }_{{ik}}}$ определяются из соотношений
(2.12)
${{\sigma }_{{ik}}} = \sqrt {\sigma _{{^{{rk}}}}^{2} + \sigma _{{\varphi k}}^{2} - {{\sigma }_{{rk}}}{{\sigma }_{{\varphi k}}} + 3\sigma _{{r\varphi k}}^{2}} ,\quad {{\varepsilon }_{{ik}}} = \frac{2}{3}\sqrt {\varepsilon _{{rk}}^{2} + \varepsilon _{{\varphi k}}^{2} - {{\varepsilon }_{{rk}}}{{\varepsilon }_{{\varphi k}}} + 6\varepsilon _{{r\varphi k}}^{2}} $Если имеется реальная диаграмма растяжения соответствующих материалов, то коэффициенты (2.11) могут быть получены методом наименьших квадратов, в противном случае для определения коэффициентов Ak, Bk могут быть использованы простейшие предположения [14, 15]
(2.13)
${{\left. {\frac{{d{{\sigma }_{{ik}}}}}{{d{{\varepsilon }_{{ik}}}}}} \right|}_{{{{\varepsilon }_{{ik}}} = 0}}} = {{E}_{k}},\quad {{\left. {\frac{{d{{\sigma }_{{ik}}}}}{{d{{\varepsilon }_{{ik}}}}}} \right|}_{{{{\varepsilon }_{{ik}}} = \varepsilon {\kern 1pt} *}}} = 0,\quad {{\sigma }_{{ik}}}(\varepsilon _{k}^{*}) = \sigma _{k}^{*}$Из соотношений (2.13) можно получить
(2.14)
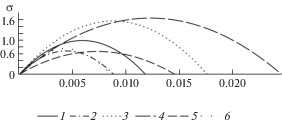
${{A}_{k}} = {{E}_{k}},\quad {{B}_{k}} = - \frac{{E_{k}^{2}}}{{4\sigma _{k}^{*}}},\quad \varepsilon _{k}^{*} = \frac{{2\sigma _{k}^{*}}}{{{{E}_{k}}}}$Результаты расчета коэффициентов Ak, Bk для различных марок сталей [16] по соотношениям (2.14) приведены в табл. 1 и на рис. 2, где на рисунке цифрами 1, 2, 3, 4, 5, 6 обозначены материалы слоя соответствующие номерам образцов табл. 1. Все величины, имеющие размерность напряжения и плотности отнесены к пределу прочности σ* и плотности ρ соответственно стали марки 40Г.
Таблица 1
| Номер образца | Материал слоя | E | Σ* | $\varepsilon _{*}^{ + }$ | Ak | Bk | ρ |
|---|---|---|---|---|---|---|---|
| 1 | 40Г | 338.98 | 1 | 0.006 | 338.98 | –28 727 | 1 |
| 2 | 15Г | 315.25 | 0.69 | 0.0044 | 315.25 | –35 754 | 1 |
| 3 | ЭП-202 | 355.93 | 1.27 | 0.0071 | 355.93 | –24 915 | 1.011 |
| 4 | ЭП-33 | 271.19 | 1.66 | 0.0123 | 271.19 | –11 068 | 1.017 |
| 5 | титан | 186.44 | 0.67 | 0.0072 | 186.44 | –12 818 | 0.58 |
| 6 | никель | 355.93 | 0.76 | 0.0042 | 355.93 | –41 525 | 1.14 |
3. Метод и построение решения. При использовании аппроксимирующих зависимостей (2.11) для пар материалов с номерами k, m ($k \ne m$) выражения для усилий в рассматриваемых двухслойных дисках можно записать в форме
(3.1)
${{N}_{r}} = {{\Phi }_{{km}}} \cdot \left( {{{\varepsilon }_{r}} + \frac{1}{2}{{\varepsilon }_{\varphi }}} \right),\quad {{N}_{\varphi }} = {{\Phi }_{{km}}} \cdot \left( {{{\varepsilon }_{\varphi }} + \frac{1}{2}{{\varepsilon }_{r}}} \right),\quad {{N}_{{r\varphi }}} = {{\Phi }_{{km}}} \cdot {{\varepsilon }_{{r\varphi }}}$(3.2)
${{\Phi }_{{km}}} = \left( {{{A}_{k}} + {{B}_{k}}{{\varepsilon }_{i}}} \right){{\Delta }_{{1k}}} + \left( {{{A}_{m}} + {{B}_{m}}{{\varepsilon }_{i}}} \right){{\Delta }_{{2m}}},\quad \left( {k,m = 1,2,\,\,m \ne k} \right)$Подставим соотношения для усилий (3.1) в уравнение равновесия (2.9), в результате получим
(3.3)
$\frac{{\partial {{\Phi }_{{km}}}}}{{\partial r}}\left( {{{\varepsilon }_{r}} + \frac{1}{2}{{\varepsilon }_{\varphi }}} \right) + {{\Phi }_{{km}}}\left( {\frac{{\partial {{\varepsilon }_{r}}}}{{\partial r}} + \frac{1}{2}\frac{{\partial {{\varepsilon }_{\varphi }}}}{{\partial r}} + \frac{{{{\varepsilon }_{r}} - {{\varepsilon }_{\varphi }}}}{{2r}} + \frac{1}{r}\frac{{\partial {{\varepsilon }_{{r\varphi }}}}}{{\partial \varphi }}} \right) + \frac{1}{r}\frac{{\partial {{\Phi }_{{km}}}}}{{\partial \varphi }}{{\varepsilon }_{{r\varphi }}} + {{\Psi }_{z}} = 0$(3.4)
$\frac{{\partial {{\Phi }_{{km}}}}}{{\partial r}}{{\varepsilon }_{{r\varphi }}} + \frac{{\partial {{\Phi }_{{km}}}}}{{\partial \varphi }}\left( {\frac{{{{\varepsilon }_{\varphi }}}}{r} + \frac{{{{\varepsilon }_{r}}}}{{2r}}} \right) + {{\Phi }_{{km}}}\left( {\frac{1}{r}\frac{{\partial {{\varepsilon }_{\varphi }}}}{{\partial \varphi }} + \frac{1}{{2r}}\frac{{\partial {{\varepsilon }_{r}}}}{{\partial \varphi }} + \frac{{\partial {{\varepsilon }_{{r\varphi }}}}}{{\partial r}} + \frac{{2{{\varepsilon }_{{r\varphi }}}}}{r}} \right) = 0$Уравнения (2.7), (3.3), (3.4) образуют систему дифференциальных уравнений в частных производных относительно неизвестных функций ${{\varepsilon }_{r}}$, ${{\varepsilon }_{\varphi }}$, ${{\varepsilon }_{{r\varphi }}}$.
Граничные условия на осях закрепления с валом и наружных контурах формируются в виде традиционных кинематических условиях (например, жесткое соединение с деформируемым валом и распределенных погонных нагрузок).
Кроме того, должны быть сформулированы дополнительные формальные ограничения по условиям эксплуатации и заданные возможные изменения контуров и модифицированных границ поверхности.
В общих чертах такие громоздкие выражения мы приводить не будем, их необходимо рассматривать при решении конкретных задач.
4. Анализ результатов и примеры. В качестве примера рассмотрим двухслойный диск в случае осесимметрической задачи. В этом случае все величины и условия на границах r0 и r1 не зависят от φ. Тогда, очевидно, $u = u(r)$, $\upsilon = 0$.
Идеальный двухслойный диск имеет постоянные толщины $\Delta _{k}^{0}$ и $\Delta _{m}^{0}$. Массы расходуемых материалов слоев
(4.1)
$M_{k}^{0} = 4\pi {{\rho }_{k}}(r_{1}^{2} - r_{0}^{2})\Delta _{k}^{0} = {\text{const,}}\quad M_{m}^{0} = 4\pi {{\rho }_{m}}(r_{1}^{2} - r_{0}^{2})\Delta _{m}^{0} = {\text{const}}$Пусть некачественное изготовление реализуется вследствие некачественного профилирования слоев.
Тогда затрачиваемые массы материалов слоев будут равны
(4.2)
${{M}_{k}} = 4\pi {{\rho }_{k}}\int\limits_{{{r}_{0}}}^{{{r}_{1}}} {{{\Psi }_{k}}(r)rdr} = M_{k}^{0},\quad {{M}_{m}} = 4\pi {{\rho }_{m}}\int\limits_{{{r}_{0}}}^{{{r}_{1}}} {\left( {{{\Psi }_{m}}(r) - {{\Psi }_{k}}(r)} \right)rdr} = M_{m}^{0}$Усилия в диске определяются через напряжения по формулам
(4.3)
$\begin{gathered} {{N}_{r}} = 2\pi r\left( {{{\sigma }_{{rk}}}(r){{\Delta }_{k}}(r) + {{\sigma }_{{rm}}}(r){{\Delta }_{m}}(r)} \right) \\ {{N}_{\varphi }} = 2\pi r\left( {{{\sigma }_{{\varphi k}}}(r){{\Delta }_{k}}(r) + {{\sigma }_{{\varphi m}}}(r){{\Delta }_{m}}(r)} \right),\quad {{N}_{{r\varphi }}} = 0 \\ \end{gathered} $Связь деформаций ${{\varepsilon }_{r}}$, ${{\varepsilon }_{\varphi }}$ с радиальным перемещением u(r)
Условие совместности деформаций
Материал считаем несжимаемым, тогда
Тогда из (4.5) получаем
(4.7)
$r\frac{{d{{\varepsilon }_{\varphi }}}}{{dr}} = - {{\varepsilon }_{\varphi }},\quad \frac{{d{{\varepsilon }_{\varphi }}}}{{{{\varepsilon }_{\varphi }}}} = - rdr,\quad {{\varepsilon }_{\varphi }} = \frac{C}{{{{r}^{2}}}}$Квадрат интенсивности деформаций
(4.8)
$\varepsilon _{i}^{2} = \frac{4}{9}(\varepsilon _{\varphi }^{2} - {{\varepsilon }_{\varphi }}{{\varepsilon }_{r}} + \varepsilon _{r}^{2}) = {{\beta }^{2}}\varepsilon _{\varphi }^{2},\quad {{\varepsilon }_{i}} = \beta {{\varepsilon }_{\varphi }}$Из (4.8) получим
В этом случае для напряжений в слоях получаем выражения
(4.10)
${{\sigma }_{{rk}}} = - \frac{2}{3}\beta \left( {{{A}_{k}} + \beta {{B}_{k}}{{\varepsilon }_{\varphi }}} \right){{\varepsilon }_{\varphi }},\quad {{\sigma }_{{rm}}} = - \frac{2}{3}\beta \left( {{{A}_{m}} + \beta {{B}_{m}}{{\varepsilon }_{\varphi }}} \right){{\varepsilon }_{\varphi }}$(4.11)
${{\sigma }_{{\varphi k}}} = \frac{2}{3}\beta \left( {{{A}_{k}} + \beta {{B}_{k}}{{\varepsilon }_{\varphi }}} \right){{\varepsilon }_{\varphi }},\quad {{\sigma }_{{\varphi m}}} = \frac{2}{3}\beta \left( {{{A}_{m}} + \beta {{B}_{m}}{{\varepsilon }_{\varphi }}} \right){{\varepsilon }_{\varphi }}$Усилия ${{N}_{r}}$, ${{N}_{\varphi }}$ будут равны
(4.12)
$\begin{gathered} {{N}_{r}} = - \frac{4}{3}\pi r\beta \left( {\left( {{{A}_{k}} + \beta {{B}_{k}}{{\varepsilon }_{\varphi }}} \right)\int\limits_0^{{{\Psi }_{k}}(r)} {dz} + \left( {{{A}_{m}} + \beta {{B}_{m}}{{\varepsilon }_{\varphi }}} \right)\int\limits_{{{\Psi }_{k}}(r)}^{{{\Psi }_{m}}(r)} {dz} } \right){{\varepsilon }_{\varphi }} = \\ \, = - \frac{4}{3}\pi r\beta \left( {\left( {{{A}_{k}} + \beta {{B}_{k}}{{\varepsilon }_{\varphi }}} \right){{\Psi }_{k}}(r) + \left( {{{A}_{m}} + \beta {{B}_{m}}{{\varepsilon }_{\varphi }}} \right)\left( {{{\Psi }_{m}}(r) - {{\Psi }_{k}}(r)} \right)} \right){{\varepsilon }_{\varphi }} \\ {{N}_{\varphi }} = \frac{4}{3}\pi r\beta \left( {\left( {{{A}_{k}} + \beta {{B}_{k}}{{\varepsilon }_{\varphi }}} \right){{\Psi }_{k}}(r) + \left( {{{A}_{m}} + \beta {{B}_{m}}{{\varepsilon }_{\varphi }}} \right)\left( {{{\Psi }_{m}}(r) - {{\Psi }_{k}}(r)} \right)} \right){{\varepsilon }_{\varphi }} \\ \end{gathered} $Таким образом получим равенство
Уравнения равновесия примут вид
откуда получим(4.14)
${{N}_{r}} = {{С}_{1}}{{e}^{{ - \int {\frac{2}{r}dr} }}} + \int {( - M{{\Omega }^{2}}r){{e}^{{\int {\frac{2}{r}dr} }}}dr = \frac{{{{C}_{1}}}}{{{{r}^{2}}}} - } \frac{1}{4}M{{\Omega }^{2}}{{r}^{4}}$Граничное условие для уравнения (4.14) можно взять в виде
Тогда (4.14) примет вид
(4.16)
${{N}_{r}} = \frac{1}{4}{{\Omega }^{2}}\left( {\frac{{r_{1}^{2}}}{{{{r}^{2}}}}(4k + Mr_{1}^{4}) - M{{r}^{4}}} \right)$Решая совместно уравнения (4.12), (4.16) получим
(4.17)
$\varepsilon _{\varphi }^{2} + 2{{\lambda }_{1}}(r){{\varepsilon }_{\varphi }} + {{\lambda }_{2}}(r) = 0$Уравнение (4.17) имеет решение
(4.18)
${{\varepsilon }_{\varphi }} = - {{\lambda }_{1}}(r) \pm \sqrt {\lambda _{1}^{2}(r) - {{\lambda }_{2}}(r)} $При выборе знака в (4.18) следует учитывать, что ${{\varepsilon }_{\varphi }} > 0$. Физические параметры диска должны быть таковыми, чтобы выполнялось условие для всех ${{r}_{0}} \leqslant r \leqslant {{r}_{1}}$ и Ω > 0 условие $\lambda _{1}^{2}(r) - {{\lambda }_{2}}(r) > 0$.
Критические значения r* и угловой скорости Ω при котором диск теряет устойчивость будем искать из решения системы уравнений
(4.19)
$\frac{{d{{\varepsilon }_{\varphi }}}}{{dr}} = 0,\quad \frac{{{{d}^{2}}{{\varepsilon }_{\varphi }}}}{{d{{r}^{2}}}} = 0,\quad {{r}_{0}} \leqslant r{\kern 1pt} * \leqslant {{r}_{1}}$Положим для границ каждого из слоев
(4.20)
${{\Psi }_{k}}(r) = \Delta _{k}^{0} + {{\delta }_{1}}{{\Psi }_{{1k}}}(r),\quad {{\Psi }_{m}}(r) = \Delta _{m}^{0} + {{\delta }_{1}}{{\Psi }_{{1m}}}(r)$Из предположения постоянства масс для идеального диска и диска границы слоев, которого заданы уравнениями (4.20), имеем выражения которым должны удовлетворять функции ${{\Psi }_{{1k}}}(r)$, ${{\Psi }_{{1m}}}(r)$
(4.21)
$\int\limits_{{{r}_{0}}}^{{{r}_{1}}} {r{{\Psi }_{{1k}}}(r)} dr = 0,\quad \int\limits_{{{r}_{0}}}^{{{r}_{1}}} {r{{\Psi }_{{1m}}}(r)} dr = 0$Положим
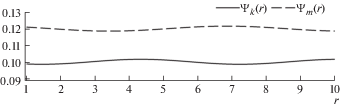
где значения ${{\psi }_{k}},\,{{\psi }_{m}}$ подобраны таким образом, чтобы удовлетворялись соотношения (4.21).Если принять значения физических параметров диска равными
(4.23)
${{r}_{0}} = 1,\quad {{r}_{1}} = 10,\quad \Delta _{k}^{0} = 0.1,\quad \Delta _{m}^{0} = 0.12,\quad {{\delta }_{1}} = {{\delta }_{2}} = 0.001$Результаты расчета критических значений r* и угловой скорости Ω* по соотношениям (4.19) при заданных материалах слоя и параметрах (4.23) приведены в табл. 2.
Таблица 2
| № | Материал k-го слоя | Материал m-го слоя | ψk | ψm | δ1 | δ2 | r* | Ω* | $u({{r}_{1}})$ |
|---|---|---|---|---|---|---|---|---|---|
| 1 | никель | титан | –1.09 | –0.92 | 0.001 | 0.001 | 6.09 | 0.00033 | 0.077 |
| 2 | титан | никель | –1.09 | –0.92 | 0.001 | 0.001 | 3.32 | 0.00018 | 0.107 |
| 3 | никель | титан | –1.09 | –0.92 | 0.0015 | 0.001 | 6.13 | 0.00039 | 0.077 |
| 4 | титан | никель | –1.09 | -0.92 | 0.0015 | 0.001 | 3.40 | 0.00022 | 0.107 |
| 5 | никель | титан | –1.09 | –0.92 | 0.001 | 0.0015 | 6.05 | 0.00036 | 0.077 |
| 6 | титан | никель | –1.09 | –0.92 | 0.001 | 0.0015 | 3.24 | 0.00019 | 0.107 |
| 7 | 15Г | 40Г | –1.09 | –0.92 | 0.001 | 0.001 | 6.09 | 0.00035 | 0.080 |
| 8 | 40Г | 15Г | –1.09 | –0.92 | 0.001 | 0.001 | 3.32 | 0.00011 | 0.097 |
| 9 | 15Г | 40Г | –1.09 | –0.92 | 0.0015 | 0.001 | 6.13 | 0.00040 | 0.080 |
| 10 | 40Г | 15Г | –1.09 | –0.92 | 0.0015 | 0.001 | 3.40 | 0.00013 | 0.098 |
| 11 | 15Г | 40Г | –1.09 | –0.92 | 0.0015 | 0.001 | 6.05 | 0.00038 | 0.080 |
| 12 | 40Г | 15Г | –1.09 | –0.92 | 0.0015 | 0.001 | 3.24 | 0.00011 | 0.098 |
| 13 | 15Г | титан | –1.09 | –0.92 | 0.001 | 0.001 | 6.09 | 0.00035 | 0.0793 |
| 14 | титан | 15Г | –1.09 | –0.92 | 0.001 | 0.001 | 3.32 | 0.00017 | 0.109 |
| 15 | 15Г | титан | –1.09 | –0.92 | 0.001 | 0.0015 | 6.05 | 0.00037 | 0.079 |
| 16 | титан | 15Г | –1.09 | –0.92 | 0.001 | 0.0015 | 3.23 | 0.00018 | 0.110 |
| 17 | 15Г | титан | –1.09 | –0.92 | 0.0015 | 0.001 | 6.13 | 0.00040 | 0.079 |
| 18 | титан | 15Г | –1.09 | –0.92 | 0.0015 | 0.001 | 3.40 | 0.00021 | 0.110 |
| 19 | 15Г | ЭП-202 | –1.09 | –0.92 | 0.001 | 0.001 | 6.09 | 0.00053 | 0.083 |
| 20 | ЭП-202 | 15Г | –1.09 | –0.92 | 0.001 | 0.001 | 3.32 | 0.00020 | 0.134 |
| 21 | 15Г | ЭП-202 | –1.09 | –0.92 | 0.0015 | 0.001 | 6.13 | 0.00062 | 0.083 |
| 22 | ЭП-202 | 15Г | –1.09 | –0.92 | 0.0015 | 0.001 | 3.40 | 0.00024 | 0.134 |
| 23 | 15Г | ЭП-202 | –1.09 | –0.92 | 0.001 | 0.0015 | 6.05 | 0.00057 | 0.083 |
| 24 | ЭП-202 | 15Г | –1.09 | –0.92 | 0.001 | 0.0015 | 3.24 | 0.00020 | 0.134 |
| 25 | ЭП-33 | ЭП-202 | –1.09 | –0.92 | 0.001 | 0.001 | 3.32 | 0.00016 | 0.197 |
| 26 | ЭП-202 | ЭП-33 | –1.09 | –0.92 | 0.001 | 0.001 | 6.09 | 0.00046 | 0.157 |
| 27 | ЭП-33 | ЭП-202 | –1.09 | –0.92 | 0.0015 | 0.001 | 3.40 | 0.00020 | 0.198 |
| 28 | ЭП-202 | ЭП-33 | –1.09 | –0.92 | 0.0015 | 0.001 | 6.13 | 0.00054 | 0.157 |
| 29 | ЭП-33 | ЭП-202 | –1.09 | –0.92 | 0.001 | 0.0015 | 3.24 | 0.00017 | 0.198 |
| 30 | ЭП-202 | ЭП-33 | –1.09 | –0.92 | 0.001 | 0.0015 | 6.05 | 0.00050 | 0.157 |
| 31 | ЭП-33 | ЭП-202 | 2.05 | 1.89 | 0.001 | 0.001 | 6.64 | 0.00062 | 0.196 |
| 32 | ЭП-202 | ЭП-33 | 2.05 | 1.89 | 0.001 | 0.001 | 5.16 | 0.00032 | 0.158 |
| 33 | ЭП-33 | ЭП-202 | 2.05 | 1.89 | 0.0015 | 0.001 | 3.57 | 0.00028 | 0.196 |
| 34 | ЭП-202 | ЭП-33 | 2.05 | 1.89 | 0.0015 | 0.001 | 2.14 | 0.00007 | 0.158 |
| 35 | ЭП-33 | ЭП-202 | 2.05 | 1.89 | 0.001 | 0.0015 | 1.01 | 0.00002 | 0.196 |
| 36 | ЭП-202 | ЭП-33 | 2.05 | 1.89 | 0.001 | 0.0015 | 2.38 | 0.00008 | 0.158 |
| 37 | никель | титан | 2.05 | 1.89 | 0.001 | 0.001 | 2.25 | 0.00005 | 0.077 |
| 38 | титан | никель | 2.05 | 1.89 | 0.001 | 0.001 | 3.70 | 0.00028 | 0.106 |
| 39 | никель | титан | 2.05 | 1.89 | 0.0015 | 0.001 | 2.14 | 0.00005 | 0.077 |
| 40 | титан | никель | 2.05 | 1.89 | 0.0015 | 0.001 | 3.57 | 0.00031 | 0.106 |
| 41 | никель | титан | 2.05 | 1.89 | 0.001 | 0.0015 | 5.40 | 0.00026 | 0.077 |
| 42 | титан | никель | 2.05 | 1.89 | 0.001 | 0.0015 | 1.01 | 0.00002 | 0.105 |
| 43 | 15Г | титан | 2.05 | 1.89 | 0.001 | 0.001 | 5.16 | 0.00024 | 0.080 |
| 44 | титан | 15Г | 2.05 | 1.89 | 0.001 | 0.001 | 3.70 | 0.00027 | 0.108 |
| 45 | 15Г | титан | 2.05 | 1.89 | 0.0015 | 0.001 | 2.14 | 0.00005 | 0.080 |
| 46 | титан | 15Г | 2.05 | 1.89 | 0.0015 | 0.001 | 3.57 | 0.00030 | 0.109 |
| 47 | 15Г | титан | 2.05 | 1.89 | 0.001 | 0.0015 | 5.40 | 0.00028 | 0.080 |
| 48 | титан | 15Г | 2.05 | 1.89 | 0.001 | 0.0015 | 1.01 | 0.00002 | 0.108 |
| 49 | ЭП-202 | никель | 2.05 | 1.89 | 0.001 | 0.001 | 6.64 | 0.00031 | 0.149 |
| 50 | ЭП-202 | титан | 2.05 | 1.89 | 0.001 | 0.001 | 6.64 | 0.00079 | 0.130 |
| 51 | ЭП-202 | ЭП-33 | 3.92 | 4.09 | 0.001 | 0.001 | 1.14 | 0.00003 | 0.157 |
| 52 | ЭП-33 | ЭП-202 | 3.92 | 4.09 | 0.001 | 0.001 | 1.88 | 0.00012 | 0.197 |
| 53 | никель | титан | 3.92 | 4.09 | 0.001 | 0.001 | 1.14 | 0.00002 | 0.077 |
| 54 | титан | никель | 3.92 | 4.09 | 0.001 | 0.001 | 1.88 | 0.00013 | 0.107 |
| 55 | 15Г | 40Г | 3.92 | 4.09 | 0.001 | 0.001 | 1.14 | 0.00002 | 0.080 |
| 56 | 40Г | 15Г | 3.92 | 4.09 | 0.001 | 0.001 | 1.88 | 0.00008 | 0.098 |
| 57 | ЭП-202 | никель | 3.92 | 4.09 | 0.001 | 0.001 | 1.88 | 0.00015 | 0.131 |
| 58 | никель | ЭП-202 | 3.92 | 4.09 | 0.001 | 0.001 | 1.14 | 0.00003 | 0.081 |
5. Заключение. В данной работе для вращающихся тонких биметаллических дисков приведены основные соотношения для исследования критических деформированных состояний, возникающих вследствие малых технологических отклонений изготовления полотна либо контурных форм. Для осесимметричных состояний проведены детальные расчеты влияния структуры материалов, степени и формы технологических вариаций отклонений от заданного идеального проекта на уровень критических скоростей вращения диска и перемещения внешних контуров. Сравнительный анализ проведенных расчетов показывает возможность широкого диапазона улучшения эксплуатационных качеств при создании направленных несущественных технологических отклонений.
Благодарности. Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 19-01-00038.
Список литературы
Соколовский В.В. Теория пластичности. М.: Высшая школа, 1969. 608 с.
Calladine C.R. Plasticity for Engineers: Theory and Applications. Woodhead Publishing, 2000. 328 p.
Durban D., Birman V. Elasto-plastic analysis of an anisotropic rotating disc //Acta Mechanica. 1983. V. 49. P. 1–10
Szuwalski K. Decohesive carrying capacity in perfect and asymptotically perfect plasticity (asurvey) // Mech. Teor. Stos. 1990. № 28. P. 243–253.
Александров С.Е., Ломакин Е.В., Дзенг Й.Р. Влияние зависимости условия текучести от среднего напряжения на распределение напряжений во вращающемся диске // Доклады академии наук. 2010. Т. 435. № 5. С. 610–612.
Артемов М.А., Якубенко А.П. Математическое моделирование механического поведения вращающегося диска // Вестник ВГУ. Серия: Физика, Математика. 2014. № 1. С. 30–38.
Alexandrova N.N., Артемов М.А., Барановский Е.С., Шашкин А.И. О Напряженном и деформированном состоянии вращающегося диска // Актуальные пробл. прикл. матем., информ. и механики сб. трудов Международной научной конференции. 2019. С. 1006–1011.
Ершов Л.В., Ивлев Д.Д. О потери устойчивости вращающихся дисков // Известия АН СССР. Отд. техн. наук. 1958. № 1. С. 124–125.
Lila D.M., Martynyuk A.A. Stability loss of rotating elastoplastic discs of the specific form // Applied Mathematics. 2011. № 2. P. 579–585.
Лила Д.М. Механизм потери устойчивости вращающегося составного плоского кругового диска // Матем. методы и физ.-механ. поля. 2012. Т. 55. № 3. С. 111–120.
Лила Д.М. О неустойчивости вращающегося упругопластического составного плоского кольцевого диска // Матем. методы и физ.-механ. поля. 2013. Т. 56. № 3. С. 81–94.
Лила Д.М. Второе приближение по малому параметру к решению задачи об упругопластической неустойчивости вращающегося диска // Доклады НАН Украины. 2018. № 5. С. 36–43.
Alexandrova N. Exact deformation analysis of a solid rotating elastic-perfectly plastic disk // Int. Journal of Mech. Science. 2014. V. 60. P. 55–60.
Немировский Ю.В., Тихонов С.В. Предельное состояние бетонных и железобетонных стержней при сложном и продольно-поперечном изгибе // Вестник ПНИПУ. Механика. 2020. № 1. С. 60–73.
Немировский Ю.В. Допредельное деформирование гибридных армированных бетонных конструкций // Вестник ЧГПУ им. И.Я. Яковлева. Сер.: Мех. пред. сост. 2018. № 3 (37). С. 26–37
Марочник сталей и сплавов. 2-е изд. доп. и испр. / А.С. Зубченко, М.М. Колосков, Ю.В. Каширский и др. Под общ. ред. А.С. Зубченко. М.: Маш., 2003. 784 с.
Ивлев Д.Д., Ершов Л.В. Метод возмущений в теории упругопластического тела. М.: Наука, 1978. 208 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела