Известия РАН. Механика твердого тела, 2020, № 6, стр. 149-156

Введение. Д.Д. Ивлев являлся убежденным пропагандистом [1, 2] гиперболического характера пространственной математической модели идеальной пластичности с условием Мизеса. Психологическим препятствием для исследования модельной системы пространственных уравнений в частных производных для шести компонент напряжений являлось наличие только пяти уравнений, из которых одно конечное условие пластичности Мизеса являлось нелинейным алгебраическим уравнением второго порядка. Незамкнутость пространственной задачи идеальной пластичности модели Мизеса удалось разрешить Максимовой Л.А. [3], Вервейко Н.Д. и Купцову А.В. [4, 5] при личном участии Д.Д. Ивлева. В первом случае [3] удалось подобрать вид решения задачи в тригонометрическом виде, во втором [4] случае условие пластичности Мизеса было аппроксимировано двумя линейными уравнениями. Результаты этих работ привели к выводу, что пространственная задача теории пластичности при условии Мизеса обладает характеристическими плоскостями скольжения, ориентированными под углом 45 градусов к направлениям главных напряжений.

В представленной работе показано, что в квазистатическом приближении пространственных динамических задач пластическая модель Мизеса применима к описанию напряженно-деформированного состояния в окрестности передних пространственных кромок трещин отрыва и сдвига.

1. Квазистатическое предельное напряжение отрыва в вершине пространственной трещины отрыва. Для описания динамического поведения материала в окрестности передней кромки пространственной трещины рассмотрим систему уравнений для упруговязкопластического материала модели Бингама с условием пластичности Мизеса. В размерном виде в подвижной системе координат, связанной с поверхностью разрыва скоростей и напряжений, система уравнений движения и реологических соотношений представляется в виде [6]

Здесь: ${{u}_{i}},\;{{{v}}_{i}}\;{{e}_{i}}\;{{\varepsilon }_{i}}$ – компоненты векторов перемещения, скорости перемещения, деформации и скорости деформации соответственно; $\rho $ – плотность материала; $\lambda ,\;\mu $ – упругие параметры Ламе; $K$ – предел пластичности; $\eta $ – коэффициент вязкости; $t$ – время; $\frac{{\delta f}}{{\delta t}}$ – локальная производная по времени t от функции f, заданной на подвижной поверхности ${{\Sigma }_{l}}\;\left( {l = 1,2} \right)$; $\sigma _{{ij}}^{'} = {{\sigma }_{{ij}}} - \frac{1}{3}{{\sigma }_{{kk}}}{{\delta }_{{ij}}}$ – девиаторные компоненты тензора напряжений ${{\sigma }_{{ij}}}$; x_i – декартовы координаты; $i = 1,2,3,$ $j = 1,2,3,$ $k = 1,2,3$.

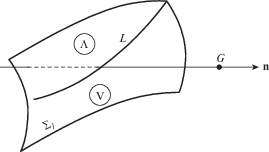
На рис. 1 изображена поверхность разрыва ${{\Sigma }_{l}}\,\left( {l = 1,2} \right)$ скоростей и напряжений и передняя кромка L трещины, распространяющихся со скоростью $G$ упругих волн. Передняя кромка трещины продольного сдвига принадлежит поверхности Σ₁ продольных волн, бегущих со скоростью ${{c}_{1}} = \sqrt {{{\left( {\lambda + 2\mu } \right)} \mathord{\left/ {\vphantom {{\left( {\lambda + 2\mu } \right)} \rho }} \right. \kern-0em} \rho }} $, а передняя кромка трещин отрыва и антиплоского сдвига принадлежит поверхности Σ₂ сдвиговых волн, бегущих со скоростью ${{c}_{2}} = \sqrt {{\mu \mathord{\left/ {\vphantom {\mu \rho }} \right. \kern-0em} \rho }} $ [6].

Рис. 1

Выберем следующие характерные параметры явления вблизи кромки трещины: $K = {\eta \mathord{\left/ {\vphantom {\eta T}} \right. \kern-0em} T}$ – напряжение; $L = GT$ – длина; $T$ – время; $G$ – скорость; $T = {L \mathord{\left/ {\vphantom {L G}} \right. \kern-0em} G} = {\eta \mathord{\left/ {\vphantom {\eta K}} \right. \kern-0em} K}$.

В безразмерном виде система (1.1), в которой для безразмерных величин оставлены прежние обозначения, примет вид

Выбранная динамическая модель поведения материала вблизи кромки трещины определяется двумя характерными числами:

Характерное число R₁ является отношением динамического напряжения $\rho {{G}^{2}}$ к статическому пределу пластичности K. Характеристическое число ${{R}_{2}}$ определяет отношение вязких напряжений η/T к статическому пределу пластичности K, что эквивалентно отношению кинетической энергии единицы объема к работе силы предела пластичности на единице длины. Статическое поведение материала характеризуется числами ${{R}_{3}} = {L \mathord{\left/ {\vphantom {L K}} \right. \kern-0em} K}$ и ${{R}_{4}} = {\mu \mathord{\left/ {\vphantom {\mu K}} \right. \kern-0em} K}$.

В работе [6] показано, что предлагаемая модель упруговязкопластического поведения материала вблизи передней кромки трещины допускает распространение поверхностей Σ_l, при переходе через которые возникают разрывы скоростей и напряжений. Возможно также наличие на этих поверхностях линий L, при переходе через которые также имеют место разрывы скоростей ($\mathop {\mathbf{v}}\limits^ \wedge - \mathop {\mathbf{v}}\limits^ \vee = {{\left. {\left[ {\mathbf{v}} \right]} \right|}_{L}}$) и напряжений (рис. 1). Знаки $ \wedge $ и $ \vee $ используются для обозначения значения функций за Σ_l в точках выше (знак $ \wedge $) или ниже (знак $ \vee $) линии L на поверхности Σ_l.

Наличие разрывов нормальной и касательной скоростей на линии $L$, принадлежащей волновой поверхности Σ_l, и их отождествление с передними кромками трещин продольного сдвига, отрыва и поперечного сдвига приводит к следующим заключениям:

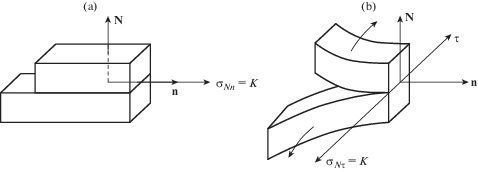
1. Передняя кромка $L$ трещины продольного сдвига вдоль нормали n (рис. 2, a) принадлежит поверхности Σ₁ волны продольного разрыва скорости, распространяющейся со скоростью ${{c}_{1}} = \sqrt {{{\left( {\lambda + 2\mu } \right)} \mathord{\left/ {\vphantom {{\left( {\lambda + 2\mu } \right)} \rho }} \right. \kern-0em} \rho }} $. Условием существования такой кромки трещины продольного сдвига является превышение предела пластичности в окрестности кромки и отличие от нуля скорости пластической деформации

Рис. 2

2. Передняя кромка $L$ трещины поперечного (антипродольного) сдвига принадлежит поверхности Σ₂ сдвиговой волны, распространяющейся со скоростью сдвиговых волн ${{c}_{2}} = \sqrt {{\mu \mathord{\left/ {\vphantom {\mu \rho }} \right. \kern-0em} \rho }} $. Условием существования такой кромки трещины антипродольного сдвига совпадают с условиями существования трещины продольного сдвига (1.3).

3. Передняя кромка $L$ трещины отрыва принадлежит поверхности Σ₂ сдвиговых волн, распространяющихся со скоростью ${{c}_{2}} = \sqrt {{\mu \mathord{\left/ {\vphantom {\mu \rho }} \right. \kern-0em} \rho }} $. Условие существования таких кромок трещин отрыва состоит в достижении предельного напряжения ${{\sigma }_{{N0}}}$ отрыва по направлению нормали к локальной поверхности отрыва N. Предельное условие существования подвижной передней кромки трещины отрыва ${{\sigma }_{N}} = {{\sigma }_{{N0}}}$ может быть приближенно заменено условием достижения пластического квазистатического состояния материала $\sigma _{{ij}}^{'}\sigma _{{ij}}^{'} = 2{{K}^{2}}$ для случая $\rho {{G}^{2}} < K$, то есть ${{R}_{1}} = {{\rho {{G}^{2}}} \mathord{\left/ {\vphantom {{\rho {{G}^{2}}} K}} \right. \kern-0em} K} < 1$.

2. Предельное напряжение отрыва вблизи вершины трещины отрыва. Как следует из уравнений (1.2) квазистатическое пластическое поведение материала в окрестности кромки трещины определяется малостью величин ${{R}_{1}} = {{\rho {{G}^{2}}} \mathord{\left/ {\vphantom {{\rho {{G}^{2}}} K}} \right. \kern-0em} K}$ и ${{R}_{2}} = {\eta \mathord{\left/ {\vphantom {\eta {KT}}} \right. \kern-0em} {KT}}$. Для случая ${{R}_{l}} < 1,$ $l = 1,2$ возможен учет величин ${{R}_{1}}$ и ${{R}_{2}}$ с помощью метода возмущений

Рассмотрим уравнения нулевого и первого приближений. В нулевом приближении имеем

В первом приближении получим

Нулевое приближение в разложении напряжений, скоростей и деформаций (в виде рядов по степеням относительной кинетической энергии ${{R}_{1}}$ и относительной вязкости ${{R}_{2}}$) играет важную роль в оценке вида пластического состояния в вершине трещины и выбора критерия пластического состояния. В случае передних кромок трещин продольного и поперечного сдвигов физически оправданными представляются условия достижения предельных значений касательными напряжениями ${{\sigma }_{{Nn}}} = K,$ ${{\sigma }_{{N\tau }}} = K$, которые в инвариантной форме представлены соотношением (1.3). Предельные касательные напряжения ${{\sigma }_{{Nn}}}$ и ${{\sigma }_{{N\tau }}}$ в плоскости продольного и поперечного сдвигов в вершине трещины показаны на рис. 2,a и рис. 2,b соответственно.

В работе [8] приведены эксперименты с трещинами скольжения, при которых поверхность трещин имеет зеркальный вид, что соответствует деформации сдвига.

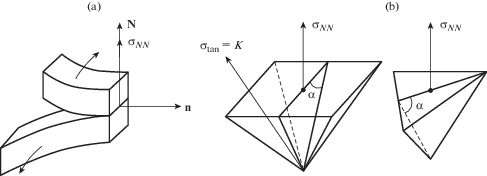
В случае передней кромки трещины отрыва механический отрыв происходит по плоскости с главным нормальным напряжением σ_NN при достижении предельного значения напряжения на отрыв ${{\sigma }_{{NN}}} = \sigma _{{\lim }}^{0}$. В нулевом приближении система (2.1) трехмерных уравнений идеальной пластичности является замкнутой системой уравнений гиперболического типа [1–4] с характеристическими плоскостями, составляющими углы $\alpha = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$ с направлениями главных напряжений.

На рис. 3,a помещено изображение предельного нормального напряжения σ_NN отрыва в вершине трещины отрыва. На рис. 3,b представлено изображение предельно малого допустимого микроэлемента со скольжением вдоль боковых граней с углом $\alpha = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$.

Рис. 3

В наблюдениях на электронном микроскопе [9] в наномасштабе отмечается образование микрообъектов атомов со скольжением по некоторым граням. В динамических экспериментах на отрыв [8] поверхность трещин имеет матовый оттенок в отраженном свете, что можно связать с образованием “вершин” элементов образовавшихся в результате скольжения конечных элементов пирамидальной формы по боковым граням при разрушении отрывом. В [8] отмечен факт изменения вида предельного деформирования в вершине бегущей трещины: от разрушения сдвигом до разрушения отрывам, это соответствует тому, что след поверхности трещины имеет либо зеркальный, либо матовый вид на отдельных участках поверхности трещины.

Конечно-элементное представление микрообъемов материала (в области вершины трещины отрыва) в форме правильных трех, четырех и многогранных пирамид (рис. 3) с углами наклона граней в 45 градусов к плоскости отрыва в рамках квазистатической модели деформирования (при ${{R}_{1}} = {{R}_{2}} = 0$) идеально пластического материала модели Мизеса в отсутствии каких-либо граничных условий [8] приводит к утверждению, что в квазистатическом приближении предельное напряжение σ_N отрыва совпадает с величиной касательного напряжения K при скольжении по боковым граням. Действительно, так как ${{\sigma }_{{\tan }}}\sum\limits_{i = 1}^m {{{S}_{m}}\cos 45^\circ } = {{\sigma }_{N}}{{S}_{{bas}}}$ (здесь S_m – площадь боковой грани, m – количество боковых граней, S_bas – площадь основания правильной пирамиды), а $\sum\limits_{i = 1}^m {{{S}_{m}}{\text{cos}}45^\circ } $ = S_bas, то отсюда следует, что σ_N = K.

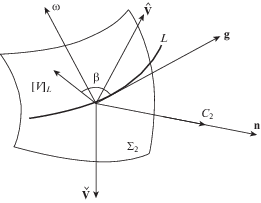
3. Трансформация трещины “отрыва-сдвига” в трещину отрыва или поперечного сдвига. Динамический подход к рассмотрению движения передней кромки трещины отрыва [7] или поперечного сдвига допускает наличие передних кромок трещин с разрывом скоростей перемещения частиц среды под углом $\beta $ к линии $L$ кромки трещины. На рис. 4 представлено схематическое изображение передней кромки $L$ трещины “отрыва с поперечным сдвигом”, на которой имеет место разрыв скачка скорости ${{\left[ v \right]}_{L}}$ в проекции на саму линию L и ортогональное направление.

Рис. 4

В зависимости от вида интенсивности напряженного состояния перед поверхностью ${{\Sigma }_{2}}$, такая передняя кромка разрыва скорости ${{\left[ v \right]}_{L}}$ может в процессе движения реализоваться как трещина отрыва или трещина поперечного сдвига за счет различного переноса интенсивностей ${{\left[ v \right]}_{{L\gamma }}}$ и ${{\left[ v \right]}_{{L\omega }}}$(продольной вдоль линии L и ортогональной к L проекций ${{\left[ v \right]}_{L}}$). Условиями существования таких передних кромок трещин “сдвига–отрыва” являются: 1) достижение пластического состояния на кромке $\sigma _{{ij}}^{'}\sigma _{{ij}}^{'} > 2{{K}^{2}}$, 2) наличие отличного от нуля скачка скорости на кромке L (${{\left[ v \right]}_{{L\tau }}} > 0$ и ${{\left[ v \right]}_{{LN}}} > 0$), 3) реализация пластического сдвига $[\varepsilon _{{N\tau }}^{p}] \ne 0$ и пластического отрыва $[\varepsilon _{{NN}}^{p}] \ne 0$.

Уравнение переноса интенсивности передней кромки трещины “сдвига–отрыва” (рис. 4) имеет вид [6] в проекциях на направления поперечного сдвига $\gamma $ и отрыва $\omega $.

Далее считаем, что индекс $\theta $ принимает два значения $\theta = \gamma ,\omega $, приписываемые проекциям величин на направления $\gamma $ и $\omega $.

Здесь символ “+” приписан значениям величин перед поверхностью Σ_i.

Нелинейная правая часть уравнений переноса упрощается для случая сильно напряженного материала впереди кромки трещины

Уравнения (3.1) с правой частью (3.3) имеют точные решения

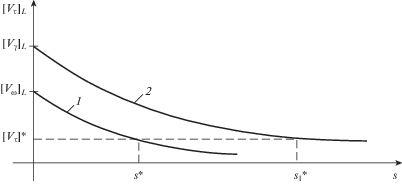
На рис. 5 приведен график затухания интенсивности развертывающейся трещины “сдвига–отрыва” в ходе ее распространения. В предложенном приближении скорости пластического деформирования (3.3), интенсивности сдвига и отрыва передней кромки трещины “сдвига–отрыва” затухают по одному и тому же закону (3.4). Величина ${{\left[ {{{{v}}_{\tau }}} \right]}_{L}}$ с меньшим начальным значением $\left[ {{{{v}}_{\tau }}} \right]_{L}^{0}$ раньше достигает своего предельного значения $\left[ {{{{v}}_{\tau }}} \right]{\kern 1pt} *$ $\left( {\rho {{c}_{2}}\left[ {{{{v}}_{\tau }}} \right]{\kern 1pt} * = {{\sigma }_{{n\tau }}} = K} \right)$ при $s = s{\kern 1pt} *$, так что дальше при s > s* будет распространяться передняя кромка трещины одного типа (символ “*” приписан величинам, соответствующим предельному напряженному состоянию в окрестности вершины трещины в момент ее остановки, то есть в статическом состоянии, s – путь, пройденный вершиной трещины). На рис. 5 раньше затухает отрыв на передней кромке (кривая 1), а при $s \in [s{\kern 1pt} *,s_{1}^{*}]$ будет распространяться передняя кромка трещины поперечного сдвига (кривая 2).

Рис. 5

Заключение. Проведенный анализ динамического деформирования упруговязкопластического материала в окрестности вершины трещины показывает:

1. В случае квазистатического в окрестности вершины трещины отрыва предельные напряжения отрыва и сдвига совпадают (${{\sigma }_{N}} = K$).

2. В случае  динамического распространения (со скоростью c₂ сдвиговых волн) вершины трещины с поперечным сдвигом и отрывом на ней, имеет место вырождение вершины трещины в трещину только поперечного сдвига или только в трещину отрыва.