Известия РАН. Механика твердого тела, 2021, № 1, стр. 6-16

МОДИФИЦИРОВАННАЯ ТЕОРИЯ ПЛАСТИЧНОСТИ ДЛЯ МОНОТОННЫХ И ЦИКЛИЧЕСКИХ ПРОЦЕССОВ ДЕФОРМИРОВАНИЯ

Д. Р. Абашев^a, В. С. Бондарь^a, *

^a Московский политехнический университет
Москва, Россия

Поступила в редакцию 01.11.2018
После доработки 08.10.2019
Принята к публикации 05.12.2019

DOI: 10.31857/S0572329921010025

Аннотация

На основе анализа результатов экспериментальных исследований образцов из нержавеющей стали 12Х18Н10Т при жестком (контролируемые деформации) процессе деформирования, включающем в себя последовательности монотонных и циклических режимов нагружения, выявлены некоторые особенности и различия процессов изотропного и анизотропного упрочнений при монотонных и циклических нагружениях. Для описания этих особенностей в рамках теории пластичности в пространстве тензора пластических деформаций вводится критерий смены направления пластического деформирования и поверхность памяти, позволившие разделить процессы монотонного и циклического деформирования. Для описания переходных процессов формулируются эволюционные уравнения для параметров изотропного и анизотропного упрочнений. Сравниваются расчетные и экспериментальные изменения напряженно-деформированных состояний по процессу монотонных и циклических нагружений.

Ключевые слова: монотонные и циклические нагружения, теория пластичности, поверхность памяти, базовый эксперимент, метод идентификации

Введение. Нестационарные и несимметричные процессы циклического деформирования состоят из последовательности монотонных и циклических режимов нагружения. Математическое моделирование таких процессов в условиях жесткого (контролируемые деформации) нагружения и особенно мягкого (контролируемые напряжения) нагружения представляют собой весьма сложную задачу. К тому же при реализации таких режимов возникают трудно описываемые процессы посадки и вышагивания (ratcheting) петли гистерезиса. Что же касается оценки и прогнозирования ресурса в условиях нестационарных и несимметричных циклических нагружений, то в этих случаях накопление повреждений необходимо определять по всему процессу деформирования, учитывая, что накопление повреждений существенно нелинейно.

Математическое моделирование процессов деформирования и накопления повреждений при циклических нагружениях строится, в основном, на вариантах теорий пластичности, относящихся к классу теорий пластического течения при комбинированном (изотропном и анизотропном) упрочнении, обзор и анализ которых содержатся в работах [1–12]. В настоящей работе математическое моделирование процессов деформирования и накопления повреждений базируется на варианте теории пластичности [1, 9], который, как показано в работе [10], является наиболее адекватным вариантом описания процессов деформирования и разрушения при циклических нагружениях по сравнению с моделями Коротких [2] и Шабоша [6–8].

Для выявления особенностей деформирования при нестационарном и несимметричном циклическом нагружении рассматривается жесткое нагружение в условиях растяжения-сжатия образцов из нержавеющей стали 12Х18Н10Т, которое представляет собой последовательность пяти этапов: циклическое, монотонное, циклическое, монотонное, циклическое вплоть до разрушения. Анализ переходных процессов от циклического к монотонному и от монотонного к циклическому показывает необходимость разделения процессов монотонного и циклического деформирования. Для этого в пространстве пластических деформаций вводится критерий смены направления пластического деформирования и поверхность памяти, разделяющая циклические и монотонные процессы деформирования. Далее в уравнения теории пластичности вводятся уравнения эволюции параметров изотропного и анизотропного упрочнений для монотонных и циклических режимов нагружения.

Разделение процессов монотонного и циклического деформирования имеет место и в модели Коротких [2–4], но только для описания эволюции изотропного упрочнения. Поверхность памяти в этой модели строится в пространстве девиатора микронапряжений с определением в процессе деформирования максимального значения интенсивности микронапряжений. В работах [2, 11] для описания эволюции анизотропного упрочнения в пространстве девиатора пластических деформаций вводится поверхность памяти с определением в процессе деформирования интенсивности максимальной амплитуды пластической деформации. Далее в работе [12] для описания эволюции анизотропного упрочнения используется такая же поверхность памяти, как и ранее для изотропного упрочнения. Все эти подходы [2, 11, 12] обладают одним существенным недостатком – достигнутый размер поверхности памяти имеет возможность в конце цикла и уменьшиться и увеличиться и это приводит к тому, что в конце каждого цикла возможно как монотонное, так и циклическое нагружение. К томе же согласно эволюционному уравнению для максимальной интенсивности микронапряжений при циклическом нагружении эта величина всегда уменьшается, хотя она должна оставаться постоянной на стабилизированном цикле. В заключение следует также сказать, что достаточного обоснования рассматриваемых подходов [2, 11, 12] в литературе нет.

С учетом выявленных особенностей монотонных и циклических нагружений для уточненных уравнений модифицированной теории пластичности определен базовый эксперимент и сформулирован метод идентификации материальных функций. Получены материальные функции нержавеющей стали 12Х18Н10Т при комнатной температуре. Приводится сравнение результатов расчетных и экспериментальных исследований нержавеющей стали 12Х18Н10Т при жестком нагружении, состоящем из последовательности монотонных и циклических режимов нагружения. Анализируется кинетика напряженно-деформированного состояния, рассматриваются изменения размаха и среднего напряжения цикла в процессе этапов циклических нагружений.

1. Основные уравнения теории пластичности. Рассматривается весьма простой вариант теории пластичности [9, 10], являющийся частичным вариантом теории неупругости [1]. Вариант теории пластичности относится к классу одноповерхностных теорий течения при комбинированном упрочнении. Область применимости варианта теории пластичности ограничивается малыми деформациями начально изотропных металлов при температурах, когда нет фазовых превращений, и скоростях деформаций, когда динамическими и реологическими эффектами можно пренебречь.

Далее приводится сводка основных уравнений варианта теории пластичности.

(1.1)

$\dot {\varepsilon } = \dot {\varepsilon }_{{}}^{{\mathbf{e}}} + \dot {\varepsilon }_{{}}^{{\mathbf{p}}}$

(1.2)

${{\dot {\varepsilon }}^{{\mathbf{e}}}} = \frac{{1 + \nu }}{E}\dot {\sigma } - \frac{\nu }{E}{\text{tr}}\left( {\dot {\sigma }} \right){\mathbf{I}}$

(1.3)

$f\left( \sigma \right) = \frac{3}{2}\left( {{\mathbf{s}} - {\mathbf{a}}} \right):\left( {{\mathbf{s}} - {\mathbf{a}}} \right) - {{C}^{2}} = 0$

(1.4)

$\dot {C} = {{q}_{\varepsilon }}\dot {\varepsilon }_{{u{\kern 1pt} *}}^{p},\quad \dot {\varepsilon }_{{u{\kern 1pt} *}}^{p} = {{\left( {\frac{2}{3}\dot {\varepsilon }_{{}}^{{\mathbf{p}}}:\dot {\varepsilon }_{{}}^{{\mathbf{p}}}} \right)}^{{\frac{1}{2}}}}$

(1.5)

${\mathbf{\dot {a}}} = \sum\limits_{m = 1}^M {{\mathbf{\dot {a}}}_{{}}^{{\left( {\mathbf{m}} \right)}}} $

(1.6)

${\mathbf{\dot {a}}}_{{}}^{{\left( {\mathbf{1}} \right)}} = \frac{2}{3}{{g}^{{\left( 1 \right)}}}\dot {\varepsilon }_{{}}^{{\mathbf{p}}} + g_{a}^{{\left( 1 \right)}}{\mathbf{a}}_{{}}^{{\left( {\mathbf{1}} \right)}}\dot {\varepsilon }_{{u{\kern 1pt} *}}^{p}$

(1.7)

${\mathbf{\dot {a}}}_{{}}^{{\left( {\mathbf{2}} \right)}} = \frac{2}{3}{{g}^{{\left( 2 \right)}}}\dot {\varepsilon }_{{}}^{{\mathbf{p}}} + g_{a}^{{\left( 2 \right)}}{\mathbf{a}}_{{}}^{{\left( {\mathbf{2}} \right)}}\dot {\varepsilon }_{{u{\kern 1pt} *}}^{p}$

(1.8)

${\mathbf{\dot {a}}}_{{}}^{{\left( {\mathbf{m}} \right)}} = \frac{2}{3}{{g}^{{\left( m \right)}}}\dot {\varepsilon }_{{}}^{{\mathbf{p}}}\quad \left( {m = 3,...,M} \right)$

(1.9)

${\mathbf{\dot {\varepsilon }}}_{{}}^{{\mathbf{p}}} = \frac{{\partial f}}{{\partial \sigma }}\lambda = \frac{3}{2}\frac{{{\mathbf{s}}{\kern 1pt} *}}{{\sigma _{u}^{*}}}\dot {\varepsilon }_{{u{\kern 1pt} *}}^{p},\quad {\mathbf{s}}{\kern 1pt} * = {\mathbf{s}} - {\mathbf{a}},\quad \sigma _{u}^{*} = {{\left( {\frac{3}{2}{\mathbf{s}}{\kern 1pt} *:{\mathbf{s}}{\kern 1pt} *} \right)}^{{\frac{1}{2}}}}$

(1.10)

$\dot {\varepsilon }_{{u{\kern 1pt} {\kern 1pt} *}}^{p} = \frac{1}{{{{E}_{*}}}}\frac{3}{2}\frac{{{\mathbf{s}}{\kern 1pt} *:{\mathbf{\dot {\sigma }}}}}{{\sigma _{и}^{*}}},\quad {{E}_{*}} = {{q}_{\varepsilon }}\sum\limits_{m = 1}^M {{{g}^{{\left( m \right)}}}} + \sum\limits_{m = 1}^2 {g_{a}^{{\left( m \right)}}} a_{u}^{{\left( m \right){\kern 1pt} *}},\quad a_{u}^{{\left( m \right){\kern 1pt} *}} = \frac{3}{2}\frac{{{\mathbf{s}}{\kern 1pt} *:{\mathbf{a}}_{{}}^{{\left( {\mathbf{m}} \right)}}}}{{\sigma _{u}^{*}}}$

(1.11)

$\dot {\varepsilon }_{{и{\kern 1pt} *}}^{p} = \frac{1}{{{{E}_{*}} + 3G}}3G\frac{{{\mathbf{s}}{\kern 1pt} *:{\mathbf{\dot {\varepsilon }}}}}{{\sigma _{и}^{*}}},\quad G = \frac{E}{{2\left( {1 + \nu } \right)}}$

(1.12)

$\begin{gathered} \sigma _{u}^{*} < C \cup \dot {\varepsilon }_{{u{\kern 1pt} *}}^{p} \leqslant 0\; - \;{\text{упругость}} \\ \sigma _{u}^{*} = C \cap \dot {\varepsilon }_{{u{\kern 1pt} *}}^{p} > 0\; - \;{\text{упругопластичность}} \\ \end{gathered} $

(1.13)

$\dot {\omega } = \alpha {{\omega }^{{\frac{{\alpha - 1}}{\alpha }}}}\frac{{{\mathbf{a}}_{{}}^{{\left( {\mathbf{2}} \right)}}:\dot {\varepsilon }_{{}}^{{\mathbf{p}}}}}{{{{W}_{a}}}},\quad \alpha = {{(\sigma _{a}^{{\left( 2 \right)}}{\text{/}}a_{u}^{{\left( 2 \right)}})}^{{{{n}_{\alpha }}}}},\quad a_{u}^{{\left( 2 \right)}} = {{\left( {\frac{3}{2}{\mathbf{a}}_{{}}^{{\left( {\mathbf{2}} \right)}}:{\mathbf{a}}_{{}}^{{\left( {\mathbf{2}} \right)}}} \right)}^{{\frac{1}{2}}}}$

Здесь $\dot {\varepsilon },\dot {\varepsilon }_{{}}^{{\mathbf{e}}},\dot {\varepsilon }_{{}}^{{\mathbf{p}}}$ – тензоры скоростей полной, упругой и пластической деформаций; $\sigma ,{\mathbf{s}},{\mathbf{s}}{\kern 1pt} *,$ a – тензор напряжений, девиаторы напряжений, активных напряжений и микронапряжений; $\varepsilon _{{u{\kern 1pt} *}}^{p}$ – накопленная пластическая деформация; $\omega $ – поврежденность; E, ν – модуль Юнга, коэффициент Пуассона; $C$ – радиус (размер) поверхности нагружения; ${{{\mathbf{a}}}^{{({\mathbf{1}})}}},{{{\mathbf{a}}}^{{({\mathbf{2}})}}},{{{\mathbf{a}}}^{{({\mathbf{m}})}}}$ – микронапряжения (девиатор смещения центра поверхности нагружения) первого, второго и третьего типов; ${{q}_{\varepsilon }},\,\,\,{{g}^{{\left( m \right)}}},\,\,g_{a}^{{\left( m \right)}}$ – определяющие функции, связь которых с материальными будет приведена ниже.

2. Эксперимент. В статье рассматриваются результаты экспериментальных исследований образцов нержавеющей стали 12Х18Н10Т. Химический состав и механические свойства стали представлены в табл. 1.

Таблица 1

C	Si	Mn	Ni	S	P	Cr	Cu	Ti	Fe
<0.12	<0.8	<2	9–11	<0.02	<0.035	17–19	<0.3	0.4–1	~67
Модуль Юнга (ГПа)		Коэффициент Пуассона		Предел текучести (МПа)		Предел прочности (МПа)		Относительное удлинение при разрыве (%)
198		0.28		196		510		40

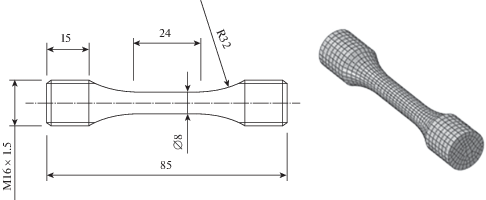
Испытания проведены на универсальной испытательной машине Zwick Z100. Геометрия и размеры испытанных образцов соответствуют требованиям стандарта ASTM E606. Диаметр рабочей части образца 8 мм, длина 24 мм, радиусы перехода от рабочей к захватной части 32 мм (рис. 1). Деформация в процессе испытания измерялась и контролировалась по навесному экстензометру с измерительной базой 10 мм.

Рис. 1

3. Монотонное и циклическое нагружения нержавеющей стали 12Х18Н10Т. Рассматриваются результаты экспериментальных исследований нержавеющей стали 12Х18Н10Т при одноосном жестком нагружении, включающем в себя этапы монотонных и циклических нагружений. Эксперимент состоит из 5-ти этапов нагружения:

– 1 этап включает в себя циклическое нагружение с частотой 0.2 Гц при $\varepsilon _{m}^{{\left( 1 \right)}} = 0,$ $\Delta {{\varepsilon }^{{\left( 1 \right)}}} = 0.016$ и ${{N}^{{\left( 1 \right)}}} = 20$ циклов;

– 2 этап включает в себя монотонное растяжение до ${{\varepsilon }^{{\left( 2 \right)}}} = 0.05$;

– 3 этап включает в себя циклическое нагружение с частотой 0.4 Гц при $\varepsilon _{m}^{{\left( 3 \right)}} = 0.05,$ $\Delta {{\varepsilon }^{{\left( 3 \right)}}} = 0.012$ и ${{N}^{{\left( 3 \right)}}} = 200$ циклов;

– 4 этап включает в себя монотонное растяжение до ${{\varepsilon }^{{\left( 4 \right)}}} = 0.1$;

– 5 этап включает в себя циклическое нагружение с частотой 0.4 Гц при $\varepsilon _{m}^{{\left( 5 \right)}} = 0.1$, $\Delta {{\varepsilon }^{{(5)}}}$ = 0.012 и ${{N}^{{\left( 5 \right)}}} = {{N}_{f}}$ циклов до разрушения.

Здесь $\varepsilon _{m}^{{\left( i \right)}}\,$ – средняя деформация цикла; $\Delta {{\varepsilon }^{{\left( i \right)}}}$ – размах деформации цикла; ε⁽ⁱ⁾ – достигаемая деформация при монотонном нагружении; N⁽ⁱ⁾ – число циклов.

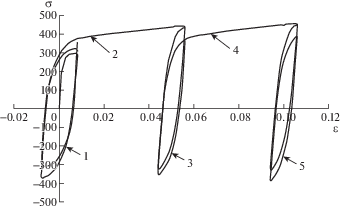
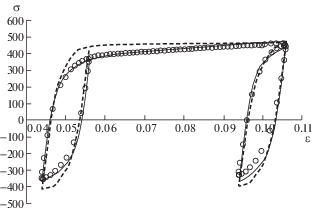
На рис. 2 приведена экспериментальная диаграмма σ(ε) (σ [МПа]) деформирования стали 12Х18Н10Т, включающая все пять этапов нагружения. На циклических диаграммах первого, третьего и пятого этапов показаны петли для первого и последнего циклов. Далее анализируются полученные экспериментальные результаты.

Рис. 2

Циклическое деформирование на первом этапе показывает, что сталь 12Х18Н10Т на начальной стадии циклически упрочняется с последующим замедлением процесса циклического упрочнения до незначительного ($d{{C}_{p}}{\text{/}}d\varepsilon _{{u * }}^{p} \approx 1$ МПа) и сталь становится практически циклически стабильной.

На третьем и пятом этапах циклического деформирования имеет место посадка петли гистерезиса. Причем процессы посадки на этих этапах идентичны – как будто и не было предварительной истории деформирования. Таким образом модуль E_a, входящий в эволюционное уравнение для микронапряжений первого типа и обеспечивающий процесс посадки петли, должен иметь одинаковое начальное значение ${{E}_{a}} = {{E}_{{a0}}}$. Т.е. на этапах монотонного нагружения после циклических нагружений, на которых происходит падение E_a практически до нуля, должен происходить быстрый возврат модуля E_a к своему начальному значению ${{E}_{{a0}}}$.

На втором и четвертом этапах монотонных нагружений упрочнение является одинаковым и постоянным. Упрочнение здесь определяется модулем ${{E}_{{a0}}}$ и в меньшей степени некоторым модулем монотонного изотропного упрочнения.

Таким образом поведение модуля E_a, характеризующего анизотропное упрочнение, и, соответственно, поведение параметров изотропного упрочнения существенно зависит от режима процесса деформирования – циклического или монотонного.

Для разделения процессов монотонного и циклического деформирования в пространстве тензора пластических деформаций $\varepsilon _{{}}^{{\mathbf{p}}}$ вводится поверхность памяти, ограничивающая область циклического деформирования. Поверхность определяется положением ее центра ξ и ее радиусом (размером) ${{C}_{\varepsilon }}$. Для вычисления центра и размера поверхности вводится два тензора пластических деформаций $\varepsilon _{{}}^{{{\mathbf{p}}\left( {\mathbf{1}} \right)}}$ и $\varepsilon _{{}}^{{{\mathbf{p}}\left( {\mathbf{2}} \right)}}$, определяющие границы поверхности. В начале деформирования эти переменные равны нулю. Определение смещения и размера поверхности памяти происходит в момент смены направления пластического деформирования. В качестве критерия смены направления принимается следующее условие:

$\dot {\varepsilon }_{{\left( {{\mathbf{t}} - {\mathbf{0}}} \right)}}^{{\mathbf{p}}}:\dot {\varepsilon }_{{\left( {\mathbf{t}} \right)}}^{{\mathbf{p}}} < 0$

где $\dot {\varepsilon }_{{\left( {\mathbf{t}} \right)}}^{{\mathbf{p}}}$ – тензор скоростей пластической деформации в текущей момент времени; $\dot {\varepsilon }_{{\left( {{\mathbf{t}} - {\mathbf{0}}} \right)}}^{{\mathbf{p}}}$ – тензор скоростей пластической деформации в предшествующий момент времени.

В этот момент изменение границ, центра и размера поверхности нагружения описывается на основе следующих соотношений:

$\varepsilon _{{}}^{{{\mathbf{p}}\left( {\mathbf{2}} \right)}} = \varepsilon _{{}}^{{{\mathbf{p}}\left( {\mathbf{1}} \right)}},\quad \varepsilon _{{}}^{{{\mathbf{p}}\left( {\mathbf{1}} \right)}} = \varepsilon _{{}}^{{\mathbf{p}}},\quad \xi = \frac{{\varepsilon _{{}}^{{{\mathbf{p}}\left( {\mathbf{1}} \right)}} + \varepsilon _{{}}^{{{\mathbf{p}}\left( {\mathbf{2}} \right)}}}}{2},\quad {{C}_{\varepsilon }} = {{\left[ {\frac{2}{3}\left( {\frac{{\varepsilon _{{}}^{{{\mathbf{p}}\left( {\mathbf{1}} \right)}} - \varepsilon _{{}}^{{{\mathbf{p}}\left( {\mathbf{2}} \right)}}}}{2}} \right):\left( {\frac{{\varepsilon _{{}}^{{{\mathbf{p}}\left( {\mathbf{1}} \right)}} - \varepsilon _{{}}^{{{\mathbf{p}}\left( {\mathbf{2}} \right)}}}}{2}} \right)} \right]}^{{\frac{1}{2}}}}$

Тогда условием циклического деформирования является деформирование в пределах поверхности памяти

${{\left[ {\frac{2}{3}(\varepsilon _{{}}^{{\mathbf{p}}} - \xi ):(\varepsilon _{{}}^{{\mathbf{p}}} - \xi )} \right]}^{{\frac{1}{2}}}} \leqslant {{C}_{\varepsilon }}$

Вне поверхности памяти деформирование является монотонным.

На основании, изложенных выше, особенностей монотонных и циклических нагружений для модуля E_a и определяющих функций для микронапряжений формулируются следующие уравнения:

${{g}^{{\left( 1 \right)}}} = {{E}_{a}},\quad {{g}^{{\left( 2 \right)}}} = {{\beta }^{{\left( 2 \right)}}}\sigma _{a}^{{\left( 2 \right)}},\quad g_{a}^{{\left( 2 \right)}} = - {{\beta }^{{\left( 2 \right)}}}$

${{g}^{{\left( m \right)}}} = \left\{ {\begin{array}{*{20}{l}} {{{\beta }^{{\left( m \right)}}}\sigma _{a}^{{\left( m \right)}}} \\ {0,\,\,{\text{если}}\,\,a_{u}^{{\left( m \right)}} \geqslant \sigma _{a}^{{\left( m \right)}} \cap {\mathbf{a}}_{{}}^{{\left( {\mathbf{m}} \right)}}:{\mathbf{s}}{\kern 1pt} * > 0,} \end{array}} \right.\quad a_{u}^{{\left( m \right)}} = {{\left( {\frac{3}{2}{\mathbf{a}}_{{}}^{{\left( {\mathbf{m}} \right)}}{\mathbf{a}}_{{}}^{{\left( {\mathbf{m}} \right)}}} \right)}^{{\frac{1}{2}}}}\quad \left( {m = 3,...,M} \right)$

${{\dot {E}}_{a}} = \left\{ {\begin{array}{*{20}{l}} { - {{K}_{E}}{{{\left( {\frac{{{{E}_{a}}}}{{{{E}_{{a0}}}}}} \right)}}^{{{{n}_{E}}}}}\dot {\varepsilon }_{{u{\kern 1pt} *}}^{p}\quad {\text{при}}\;{\text{циклическом}}\;{\text{нагружении}}} \\ {{{M}_{E}}\left( {\frac{{{{E}_{{a0}}} - {{E}_{a}}}}{{{{E}_{{a0}}}}}} \right)\dot {\varepsilon }_{{u{\kern 1pt} *}}^{p}\quad {\text{при}}\;{\text{монотонном}}\;{\text{нагружении}}} \end{array}} \right.$

$g_{a}^{{\left( 1 \right)}} = \left\{ {\begin{array}{*{20}{l}} {\frac{1}{{{{E}_{a}}}}\frac{{d{{E}_{a}}}}{{d\varepsilon _{{u{\kern 1pt} *}}^{p}}}\quad {\text{при}}\;{\text{циклическом}}\;{\text{нагружении}}} \\ {0\quad {\text{при}}\,\,{\text{монотонном}}\,\,{\text{нагружении}}} \end{array}} \right.$

Итак, для описания микронапряжений надо определить следующие материальные функции:

${{E}_{{a0}}},\sigma _{a}^{{(m)}},{{\beta }^{{(m)}}}$ – модули анизотропного упрочнения;

${{K}_{E}},\,\,{{n}_{E}},\,\,{{M}_{E}}$ – параметры анизотропного упрочнения при циклическом и монотонном деформировании.

Для определения этих материальных функций используются результаты эксперимента на рис. 2.

Модуль анизотропного упрочнения ${{E}_{{a0}}}$ определяется по формуле

${{E}_{{a0}}} = \frac{{\sigma _{m}^{{\left( 3 \right)}}}}{{\varepsilon _{m}^{{p\left( 3 \right)}}}}\,$

где $\sigma _{m}^{{\left( 3 \right)}}$ – среднее напряжение на первом цикле третьего этапа; $\varepsilon _{m}^{{p\left( 3 \right)}}$ – средняя пластическая деформация на первом цикле третьего этапа.

Модули анизотропного упрочнения $\sigma _{a}^{{\left( m \right)}}$ и ${{\beta }^{{\left( m \right)}}}$ определяются из обработки циклической диаграммы последнего полуцикла первого этапа по методике описанной в работах [1, 9].

Параметры анизотропного упрочнения ${{K}_{E}}$ и ${{n}_{E}}$ определяются на основе результатов посадки петли гистерезиса на третьем и пятом этапах. Для этого строится зависимость в координатах

${{Y}_{E}} = \ln \left[ {\frac{{{{\sigma }_{m}}\left( {N - 1} \right) - {{\sigma }_{m}}\left( N \right)}}{{2\Delta {{\varepsilon }^{p}}\varepsilon _{m}^{p}}}} \right],\quad {{X}_{E}} = \ln \left[ {\frac{{{{\sigma }_{m}}\left( N \right)}}{{\varepsilon _{m}^{p}{{E}_{{a0}}}}}} \right]$

где N – номер цикла; ${{\sigma }_{m}}\left( N \right)$ – среднее напряжение N-го цикла; $\Delta {{\varepsilon }^{p}}$ – размах пластической деформации; $\varepsilon _{m}^{p}$ – средняя пластическая деформация. Полученная зависимость аппроксимируется линейной функцией

${{Y}_{E}} = {{a}_{E}}{{X}_{E}} + {{b}_{E}},\quad {{K}_{E}} = \exp \left( {{{b}_{E}}} \right),\quad {{n}_{E}} = {{a}_{E}}$

Параметр анизотропного упрочнения ${{M}_{E}}$ при монотонном нагружении определяется из соображения восстановления параметра E_a с 0 до значения ${{E}_{{a0}}}$ при изменении пластической деформации при монотонном нагружении за $\varepsilon _{{st}}^{p}$. Тогда параметр ${{M}_{E}}$ будет определяться по формуле

${{M}_{E}} = \frac{{{{E}_{{a0}}}}}{{\varepsilon _{{st}}^{p}}}$

Определив микронапряжения по всему процессу от первого до пятого этапа нагружения, можно определить поведение размера (радиуса) поверхности нагружения, т.е. изменение изотропного упрочнения в переходных процессах от циклического к монотонному и от монотонного к циклическому деформированию.

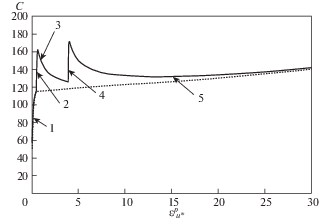
На рис. 3 приведено изменение размера поверхности нагружения (функционала $C$ [МПа]) по всему процессу деформирования от первого до пятого этапа нагружения. Пунктиром на рис. 3 показана функция изотропного упрочнения $C = {{C}_{p}}(\varepsilon _{{u{\kern 1pt} *}}^{p})$ при циклическом нагружении.

Рис. 3

Анализ результатов, приведенных на рис. 3, показывает, что при переходе от циклического деформирования к монотонному (этапы два и четыре) происходит увеличение интенсивности изотропного упрочнения, а при переходе от монотонного к циклическому (этапы три и пять) происходит медленное уменьшение изотропного упрочнения и оно стремится к изотропному $C = {{C}_{p}}(\varepsilon _{{u{\kern 1pt} *}}^{p})$ при циклическом деформировании.

На основании, изложенных выше, особенностей изменения изотропного упрочнения при циклических и монотонных нагружениях для определяющей функции изотропного упрочнения принимается следующая зависимость:

${{q}_{\varepsilon }} = \left\{ {\begin{array}{*{20}{l}} {\left[ {\frac{{d{{C}_{p}}}}{{d\varepsilon _{{u{\kern 1pt} *}}^{p}}} - {{K}_{C}}{{{\left( {\frac{{C - {{C}_{p}}}}{{{{C}_{p}}}}} \right)}}^{{{{n}_{C}}}}}} \right]\quad {\text{при}}\,\,{\text{циклическом}}\,\,{\text{нагружении}}} \\ {\left[ {\frac{{d{{C}_{p}}}}{{d\varepsilon _{{u{\kern 1pt} *}}^{p}}} + {{M}_{C}}} \right]\quad {\text{при}}\,\,{\text{монотонном}}\,\,{\text{нагружении}}} \end{array}} \right.$

Итак, для описания изотропного упрочнения надо определить следующие материальные функции:

${{C}_{p}}(\varepsilon _{{u{\kern 1pt} *}}^{p})$ – функция изотропного упрочнения при циклическом нагружении;

${{K}_{C}},\,\,{{n}_{C}},\,\,{{M}_{C}}$ – модули изотропного упрочнения при циклическом и монотонном нагружении.

Для определения этих материальных функций используются результаты эксперимента на рис. 3.

Функция изотропного упрочнения при циклическом нагружении ${{C}_{p}}(\varepsilon _{{u{\kern 1pt} *}}^{p})$ определяется на основе изменения размера поверхности на первом, третьем и пятом этапах – пунктирная кривая на рис. 3.

Параметры изотропного упрочнения K_C и n_C при циклическом нагружении определяются на основе результатов уменьшения размера поверхности нагружения на третьем и пятом этапах нагружения. Для этого строится зависимость в координатах

${{Y}_{C}} = \ln \left[ {\frac{{d\left( {{{C}_{p}} - C} \right)}}{{d\varepsilon _{{u{\kern 1pt} *}}^{p}}}} \right],\quad {{X}_{C}} = \ln \left[ {\frac{{\left( {C - {{C}_{p}}} \right)}}{{{{C}_{p}}}}} \right]$

Полученная зависимость аппроксимируется линейной функцией

$Y = {{a}_{C}}{{X}_{C}} + {{b}_{C}},\quad {{K}_{C}} = \exp \left( {{{b}_{C}}} \right),\quad {{n}_{C}} = {{a}_{C}}$

Параметр изотропного упрочнения M_C при монотонном нагружении определяется по наклону кривой деформирования на втором и четвертом этапах по формуле

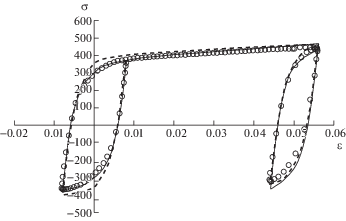
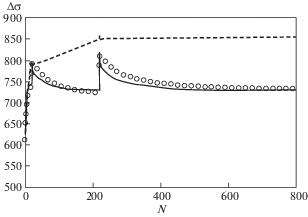
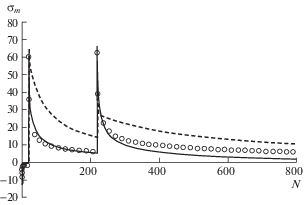
${{M}_{C}} = \frac{{d\sigma }}{{d{{\varepsilon }^{p}}}} - {{E}_{{a0}}} - \frac{{d{{C}_{p}}}}{{d{{\varepsilon }^{p}}}}$

4. Верификация модифицированной теории пластичности. С целью верификации модифицированной теории пластичности и проверки адекватности аппроксимаций материальных функций проводится расчет кинетики напряженно-деформированного состояния нержавеющей стали 12Х18Н10Т при жестком циклическом и монотонном нагружении по программе (пять этапов) изложенной во втором разделе. Для расчетов использовались материальные функции, полученные на основе экспериментальных данных на рис. 2. Сравнения расчетных (сплошные кривые) и экспериментальных (светлые кружки) результатов приведены на рис. 4–7 . Пунктирными кривыми приведены результаты расчетов на основе варианта [10]. На рис. 4 показана циклическая диаграмма 20-го цикла (последнего) первого этапа, монотонное нагружение на втором этапе и первый цикл третьего этапа. На рис. 5 показана циклическая диаграмма 200-го цикла (последнего) третьего этапа, монотонное нагружение на четвертом этапе и первый цикл пятого этапа. Изменения размаха напряжения и среднего напряжения циклов на первом, третьем и пятом этапах нагружения приведены на рис. 6, 7 . Все напряжения и размах напряжений на рис. 4–7 измеряются в МПа.

Рис. 4

Рис. 5

Рис. 6

Рис. 7

Наблюдается значительное улучшение описания кинетики напряженно-деформированного состояния на основе предложенного здесь варианта по сравнению с предыдущим [10]. Что же касается изменений размаха и среднего напряжения циклов, то предложенный вариант достаточно адекватно описывает и эти довольно сложные процессы.

Заключение. На основе анализа результатов экспериментальных исследований нержавеющей стали установлено, что изотропное и анизотропное упрочнения существенно различны при монотонном и циклическом деформировании. Также имеют место переходные процессы упрочнения при смене процессов монотонного и циклического, циклического и монотонного деформирования.

С учетом выявленных особенностей монотонных и циклических нагружений, уточнены уравнения модифицированной теории пластичности. Определен базовый эксперимент, сформулирован метод идентификации материальных функций и получены материальные функции нержавеющей стали 12Х18Н10Т при комнатной температуре.

Проведено сравнение результатов расчетных и экспериментальных исследований нержавеющей стали 12Х18Н10Т при жестком нагружении, состоящем из последовательности монотонных и циклических режимов нагружения. Анализировалась кинетика напряженно-деформированного состояния, рассматривались изменения размаха и среднего напряжения цикла в процессе циклических нагружений. Получено надежное соответствие расчетных и экспериментальных результатов.

Достаточно адекватное описание теорией процессов изменения кинетики, размаха и среднего напряжения цикла при жестком нагружении позволяет предположить возможность более адекватного описания и процессов мягкого нагружения особенно при нестационарных несимметричных режимах нагружения.

Список литературы

Bondar V.S. Inelasticity. Variants of the theory. New York: Begell House, 2013. 194 p.
Волков И.А., Коротких Ю.Г. Уравнения состояния вязкоупругопластических сред с повреждениями. М.: ФИЗМАТЛИТ, 2008. 424 с.
Митенков Ф.М., Волков И.А., Игумнов Л.А., Каплиенко А.В., Коротких Ю.Г., Панов В.А. Прикладная теория пластичности. М.: Физматлит, 2015. 282 с.
Волков И.А., Игумнов Л.А., Коротких Ю.Г. Прикладная теория вязкопластичности: Новгород: Изд-во Нижегород. гос. ун-та, 2015. 317 с.
Капустин С.А., Чурилов Ю.А., Горохов В.А. Моделирование нелинейного деформирования и разрушения конструкций в условиях многофакторных воздействий на основе МКЭ. Н. Новгород: Изд-во ННГУ, 2015. 347 с.
Бессон Ж. [и др]. Нелинейная механика материалов. Санкт-Петербург: Изд-во политехн. ун-та, 2010. 397 с.
Chaboche J.-L. A review of some plasticity and viscoplasticity constitutive theories // Int. J. of Plasticity. 2008. V. 24. P. 1642–1692.
Chaboche J.-L., Kanouté P., Azzouz F. Cyclic inelastic constitutive equations and their impact on the fatigue life predictions // Int. J. of Plasticity. 2012. V. 35. P. 44–66.
Bondar V.S., Danshin V.V., Vu L.D., Duc N.D. Constitutive modeling of cyclic plasticity deformation and low-high-cycle fatigue of stainless steel 304 in uniaxial stress state // Mechanics of advanced materials and structures. 2018. V. 25. № 12. P. 1009–1017.
Бондарь В.С., Абашев Д.Р., Петров В.К. Сравнительный анализ вариантов теорий пластичности при циклических нагружениях // Вестник Пермского национального исследовательского политехнического университета. Механика. 2017. № 2. С. 23–44.
Коротких Ю.Г. Описание процессов накопления повреждений материала при неизотермическом вязкопластическом деформировании // Проблемы прочности. 1985. № 1. С. 18–23.
Волков И.А., Игумнов Л.А., Тарасов И.С. и др. Моделирование усталостной долговечности поликристаллических конструкционных сплавов при блочном несимметричном малоцикловом нагружении // Проблемы прочности и пластичности. 2018. № 1. С. 15–30.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал