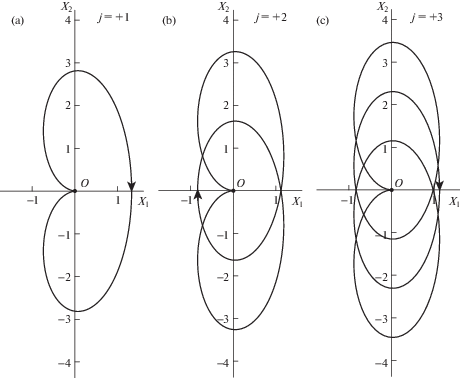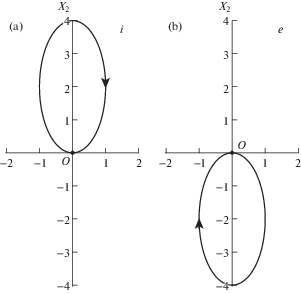Известия РАН. Механика твердого тела, 2021, № 1, стр. 106-118

1. Введение. В связи со 120-летием выхода последнего (третьего) тома книги А. Пуанкаре “Новые методы небесной механики” [1] здесь рассматриваются следующие методы, возникшие за последние 120 лет.

1. Метод нормальной формы, позволяющий изучать регулярные возмущения вблизи стационарного решения [2, гл. I], вблизи периодического решения [2, гл. II], [3–5], вблизи инвариантного тора [2, гл. II] и вблизи семейств таких решений [2, гл. VII, VIII], а также – бифуркации периодических решений и инвариантных торов.

2. Метод укороченных систем, полученных с помощью многогранников Ньютона, позволяющий изучать сингулярные возмущения. Теорию и три приложения см. в [6, гл. IV]. Другие приложения: уравнение Белецкого о колебаниях спутника [7], задачи о периодических облетах Луны и планет [8].

3. Метод порождающих семейств периодических решений (регулярных и сингулярных). Порождающие семейства – это пределы семейств периодических решений при стремлении к нулю возмущающих параметров. Решения порождающих семейств состоят из определенных частей решений предельной задачи. Если предельная задача интегрируема, то порождающие семейства находятся аналитически. Приложения: ограниченная задача трех тел, где предельная задача – это задача двух тел и порождающие семейства однопараметрические [2, гл. III–V], [9–11]; задача Хилла, где предельная задача – это промежуточная задача Хенона и каждое порождающее семейство состоит из одного решения [12, 13].

4. Метод обобщенных задач, допускающих тела с отрицательными массами [14]. В таких задачах имеются единые полные семейства периодических решений, что облегчает их вычисление. Пример: задача Хилла [14].

5. Вычисление сети семейств периодических решений как “скелета” части фазового пространства. О пользе таких “скелетов” писал еще Пуанкаре [1]. Примеры: задача Хилла [14] и отчасти ограниченная задача трех тел [11, 15–20].

Имеется еще много работ по этим методам. Здесь приведены итоговые. В разработке и применении этих пяти методов принимали участие автор и его сотрудники. Эти методы рассматриваются ниже в указанной последовательности в разделах 2–6. Предварительная версия этой работы – препринт [21], который соответствовал секционному докладу автора на I секции XII съезда по механике (Уфа, 2019).

2. Резонансная нормальная форма. 2.1. Автономная система. Рассмотрим автономную систему Гамильтона

с n степенями свободы в окрестности неподвижной точки

Если функция Гамильтона $\gamma (\xi ,\eta )$ аналитична в этой точке, то она разлагается в степенной ряд

где ${\mathbf{p}} = ({{p}_{1}}, \ldots ,{{p}_{n}})$, ${\mathbf{q}} = ({{q}_{1}}, \ldots ,{{q}_{n}}) \in {{\mathbb{Z}}^{n}}$, ${\mathbf{p}},{\mathbf{q}} \geqslant 0$, ${{\xi }^{{\mathbf{p}}}} = \xi _{1}^{{{{p}_{1}}}}\xi _{2}^{{{{p}_{2}}}}...{\kern 1pt} {\kern 1pt} \xi _{n}^{{{{p}_{n}}}}$. Поскольку точка (2.2) неподвижная, то разложение (2.3) начинается с квадратичных членов. Им соответствует линейная часть системы (2.1). Собственные числа ее матрицы $A$ разбиваются на пары

Пусть $\lambda = ({{\lambda }_{1}}, \ldots ,{{\lambda }_{n}})$. Канонические замены координат

сохраняют гамильтоновость системы.

Теорема 1 ([22, § 12]). Существует каноническое формальное преобразование (2.4), приводящее гамильтониан (2.3) к нормальной форме

где ряд $g({\mathbf{x}},{\mathbf{y}})$ содержит только резонансные члены с а квадратичная часть ${{g}_{2}}({\mathbf{x}},{\mathbf{y}})$ имеет свою нормальную форму (так что матрица линейной части системы является гамильтоновым аналогом жордановой нормальной формы). Здесь $\left\langle {{\mathbf{p}},\lambda } \right\rangle = {{p}_{1}}{{\lambda }_{1}} + + {{p}_{n}}{{\lambda }_{n}}$ – скалярное произведение.

Если $\lambda \ne 0$, то нормальная форма (2.5) эквивалентна системе с меньшим числом степеней свободы и дополнительными параметрами. При нормализующем преобразовании (2.4) сохраняются малые параметры и линейные автоморфизмы

Локальные, т.е. проходящие через точку ${\mathbf{x}} = {\mathbf{y}} = 0$, семейства периодических решений системы

соответствующей гамильтониану (2.5), удовлетворяют системе уравнений где a – свободный параметр. Им соответствуют локальные семейства периодических решений исходной системы (2.1).

Для вещественной исходной системы (2.1) коэффициенты g_pq комплексной нормальной формы (2.5) удовлетворяют специальным соотношениям вещественности, и при стандартной канонической линейной замене координат $({\mathbf{x}},{\mathbf{y}}) \to ({\mathbf{X}},{\mathbf{Y}})$ система с гамильтонианом (2.5) переходит в вещественную систему. Имеется несколько способов вычисления коэффициентов g_pq нормальной формы (2.5). Наиболее простой описан в книге [23] Журавлёва, Петрова, Шундерюка. Резонансная нормальная форма автономной системы Гамильтона вблизи стационарного решения, учитывающая только собственные числа матрицы A ее линейной части и без ограничений на эту матрицу A, была введена в [22, § 12]. Позже была введена слегка более простая сверхрезонансная нормальная форма, которая учитывала жордановы клетки нормальной формы матрицы A [24]. Но эти дополнительные упрощения не позволяли дополнительно понизить число степеней свободы.

Теория резонансной нормальной формы вблизи стационарного решения подробно изложена в гл. I книги [2].

2.2. Периодическая система. Пусть $\mu = ({{\mu }_{1}}, \ldots ,{{\mu }_{s}})$ – малые параметры. Посредством формальной канонической периодической замены координат $\xi ,\eta ,t \to {\mathbf{x}},{\mathbf{y}},\tau $ периодическая по t функция Гамильтона $\gamma (\xi ,\eta ,t,\mu )$ с n степенями свободы вблизи нулевого решения $\xi = \eta = 0$, $\mu = 0$ приводится к нормальной форме

где ${\mathbf{p}},{\mathbf{q}} \in {{\mathbb{Z}}^{n}}$, ${\mathbf{r}} \in {{\mathbb{Z}}^{s}}$, $m \in \mathbb{Z}$, ${\mathbf{p}},{\mathbf{q}},{\mathbf{r}} \geqslant 0$ и

Дополнительное каноническое преобразование

преобразует нормальную форму $g({\mathbf{x}},{\mathbf{y}},\tau ,\mu )$ в приведенную нормальную форму, не зависящую от времени [3, 4], где ${\mathbf{p}},{\mathbf{q}} \in {{\mathbb{Z}}^{n}}$, ${\mathbf{r}} \in {{\mathbb{Z}}^{s}}$, ${\mathbf{p}},{\mathbf{q}},{\mathbf{r}} \geqslant 0$ и

Для $\mu = 0$ разложение ряда h в (2.6) начинается с членов порядка 3. Локальные семейства периодических решений исходной системы соответствуют локальным семействам неподвижных точек системы с приведенной нормальной формой функции Гамильтона (2.6). Эти неподвижные точки ${\mathbf{u}},\;{\mathbf{v}},\;\mu $ удовлетворяют системе уравнений

которая не имеет линейной части при μ = 0.

В гл. II книги [2] изложена аналогичная теория резонансной нормальной формы автономной системы Гамильтона вблизи периодического решения. См. также [3–5].

Нормальная форма вблизи инвариантного тора и вблизи семейства периодических решений изложена в [25, Part II]; [2, гл. VII, VIII]. Нормальная форма полезна при исследовании устойчивости [26], бифуркаций, интегрируемости [27, 28] и асимптотического поведения решений.

3. Метод укороченных систем. Если уравнение (или система уравнений) содержит линейную часть и не содержит членов с отрицательным показателем степени, то в качестве первого приближения можно взять его линейную часть, а его нелинейную часть рассматривать как возмущение. Но если уравнение не имеет линейной части или содержит члены с отрицательными показателями степени, то возникает вопрос: что же считать его первым приближением? Ответ на него дает метод укороченных уравнений, позволяющий выписать несколько первых приближений и для каждого указать область в пространстве переменных и параметров, где оно доминирует.

3.1. Укороченная функция Гамильтона. Пусть векторы ${\mathbf{x}} = ({{x}_{1}}, \ldots ,{{x}_{n}})$, ${\mathbf{y}} = ({{y}_{1}}, \ldots ,{{y}_{n}})$ и $\mu = ({{\mu }_{1}}, \ldots ,{{\mu }_{s}})$ суть канонические переменные и малые параметры соответственно. Пусть функция Гамильтона разлагается в степенной ряд

где ${\mathbf{p}} = ({{p}_{1}}, \ldots ,{{p}_{n}})$, ${{{\mathbf{x}}}^{{\mathbf{p}}}} = x_{1}^{{{{p}_{1}}}}....\,x_{n}^{{{{p}_{n}}}}$ и ${{h}_{{{\mathbf{pqr}}}}}$ – постоянные коэффициенты.

Каждому слагаемому ряда (3.1) поставим в соответствие его векторный показатель степени $Q = ({\mathbf{p}},{\mathbf{q}},{\mathbf{r}}) \in {{\mathbb{R}}^{{2n + s}}}$. Множество S всех точек Q с ${{h}_{Q}} \ne 0$ в сумме (3.1) называется носителем ${\mathbf{S}} = {\mathbf{S}}(h)$ суммы (3.1). Выпуклая оболочка $\Gamma ({\mathbf{S}}) = \Gamma (h)$ носителя S называется многогранником Ньютона суммы (3.1). Его граница состоит из вершин $\Gamma _{j}^{{(0)}}$, ребер $\Gamma _{j}^{{(1)}}$ и граней $\Gamma _{j}^{{(d)}}$ размерностей d: $1 < d \leqslant 2n + s - 1$. Пересечение ${\mathbf{S}} \cap \Gamma _{j}^{{(d)}} = {\mathbf{S}}_{j}^{{(d)}}$ называется граничным подмножеством множества S. Каждой обобщенной грани $\Gamma _{j}^{{(d)}}$ (включая вершины и ребра) соответствуют:

– нормальный конус

в пространстве $\{ P\} = \mathbb{R}_{*}^{{2n + s}}$, сопряженном к пространству ${{\mathbb{R}}^{{2n + s}}}$;

– укороченная сумма

Она является первым приближением к сумме (2.6), когда

вдоль ${\mathbf{U}}_{j}^{{(d)}}$. Таким образом с помощью укороченных функций Гамильтона мы можем найти приближенные задачи.

3.2. Ограниченная задача трех тел. Пусть два тела P₁ и P₂ с массами $1 - \mu $ и μ соответственно вращаются вокруг их общего центра масс с периодом 2π. Плоская круговая ограниченная задача трех тел состоит в исследовании плоского движения тела P₃ бесконечно малой массы под действием ньютонова притяжения тел P₁ и P₂. Во вращающейся (синодической) системе координат задача описывается системой Гамильтона с двумя степенями свободы и одним параметром $\mu $ [29]. Функция Гамильтона имеет вид [2]

Здесь тело ${{{\mathbf{P}}}_{1}} = \{ {\mathbf{x}},{\mathbf{y}}:{{x}_{1}} = {{x}_{2}} = 0\} $ и тело ${{{\mathbf{P}}}_{2}} = \{ {\mathbf{x}},{\mathbf{y}}:{{x}_{1}} = 1,{{x}_{2}} = 0\} ,$ где ${\mathbf{x}} = ({{x}_{1}},{{x}_{2}})$, ${\mathbf{y}} = ({{y}_{1}},{{y}_{2}})$. Рассмотрим малые значения отношения масс μ ≥ 0. Для μ = 0 задача становится задачей двух тел P₁ и P₃. Но здесь нужно удалить из фазового пространства точки, соответствующие столкновениям тел ${{{\mathbf{P}}}_{2}}$ и ${{{\mathbf{P}}}_{3}}$. Точки столкновения расщепляют решения задачи двух тел P₁ и ${{{\mathbf{P}}}_{3}}$ на части. Для малых μ > 0 вблизи тела ${{{\mathbf{P}}}_{2}}$ имеется сингулярное возмущение случая μ = 0.

Для того чтобы найти все первые приближения ограниченной задачи трех тел, нужно вблизи тела ${{{\mathbf{P}}}_{2}}$ ввести локальные координаты

и разложить функцию Гамильтона в степенной ряд по этим координатам. После разложения $1{\text{/}}\sqrt {{{{({{\xi }_{1}} + 1)}}^{2}} + \xi _{2}^{2}} $ в ряд Маклорена функция Гамильтона (3.2) примет вид где f – сходящийся степенной ряд, не содержащий членов порядка меньше трех. Положим

Множество ${\mathbf{S}}$ этих точек $(p,q,r)$ состоит из точек

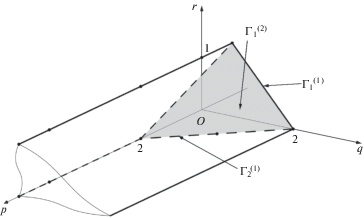
где $k = 3,4,5, \ldots $ Выпуклая оболочка множества S – это многогранник $\Gamma \subset {{\mathbb{R}}^{3}}$. Поверхность $\partial \Gamma $ многогранника Γ состоит из граней $\Gamma _{j}^{{(2)}}$, ребер $\Gamma _{j}^{{(1)}}$ и вершин $\Gamma _{j}^{{(0)}}$. Каждому такому элементу $\Gamma _{j}^{{(d)}}$ соответствует укороченный гамильтониан $\hat {h}_{j}^{{(d)}}$, являющийся суммой тех членов ряда (3.3), точки которых $(p,q,r)$ принадлежат $\Gamma _{j}^{{(d)}}$. Укороченные функции Гамильтона $\hat {h}_{j}^{{(d)}}$ – это различные первые приближения функции (3.3), справедливые в различных областях пространства $({{\xi }_{1}},{{\xi }_{2}},{{\eta }_{1}},{{\eta }_{2}},\mu )$. Рис. 1 изображает многогранник Γ для ряда (3.3) в координатах $p,\;q,\;r$, являющийся полубесконечной трехгранной призмой с косым основанием. Он имеет четыре грани и шесть ребер. Рассмотрим их.

Грань $\Gamma _{1}^{{(2)}}$, являющаяся косым основанием призмы Γ, содержит вершины

Ей соответствует укороченная функция Гамильтона

Она описывает задачу Хилла [30], которая является неинтегрируемой. Степенное преобразование

приводит соответствующую систему Гамильтона к системе Гамильтона с функцией Гамильтона вида (3.4), где ${{\xi }_{i}},{{\eta }_{i}},\mu $ надо заменить на $\mathop {\tilde {\xi }}\nolimits_i ,\mathop {\tilde {\eta }}\nolimits_i ,1$ соответственно.

Грань $\Gamma _{2}^{{(2)}}$ содержит точки

Ей соответствует укороченная функция Гамильтона $\hat {h}_{2}^{{(2)}}$, которая получается из функции h при μ = 0. Она описывает задачу двух тел ${{{\mathbf{P}}}_{1}}$ и ${{{\mathbf{P}}}_{3}}$, которая является интегрируемой.

Рассмотрим ребра. Из шести ребер одно несобственное. Оно проходит через точку (0, 2, 0) параллельно вектору (1, 0, 0). На трех ребрах q = 0, т.е. для них укороченные функции Гамильтона не зависят от ${{\eta }_{1}},{{\eta }_{2}}$, и у решений соответствующих укороченных систем Гамильтона ${{\xi }_{1}},{{\xi }_{2}} = {\text{const}}$, что неинтересно. Остаются два ребра.

Ребро $\Gamma _{1}^{{(1)}}$. Оно содержит точки (0, 2, 0) и (–1, 0, 1) множества ${\mathbf{S}}$. Соответствующая укороченная функция Гамильтона есть

Она описывает задачу двух тел ${{{\mathbf{P}}}_{2}}$ и ${{{\mathbf{P}}}_{3}}$. Степенное преобразование (3.5) переводит ее в систему Гамильтона с функцией Гамильтона вида (3.6), где ${{\xi }_{i}},\;{{\eta }_{i}},\;\mu $ заменены на ${{\tilde {\xi }}_{i}},\;{{\tilde {\eta }}_{i}},\;1$ соответственно.

Ребро $\Gamma _{2}^{{(1)}}$ содержит точки (2, 2, 0) (1, 1, 0) (0, 2, 0) множества ${\mathbf{S}}$. Ему соответствует укороченная функция Гамильтона (3.4) с μ = 0. Она описывает промежуточную задачу (между задачей Хилла и задачей двух тел ${{{\mathbf{P}}}_{1}}$ и ${{{\mathbf{P}}}_{3}}$), которая является интегрируемой. Это первое приближение ввел Хенон [31].

Итак, очень близко к телу ${{{\mathbf{P}}}_{2}}$ первым приближением исходной ограниченной задачи с функцией Гамильтона (3.3) является задача двух тел ${{{\mathbf{P}}}_{2}}$ и ${{{\mathbf{P}}}_{3}}$ с гамильтонианом (3.6), просто близко – задача Хилла с гамильтонианом (3.4), подальше от тела ${{{\mathbf{P}}}_{2}}$ – промежуточная задача, а вдали от тела ${{{\mathbf{P}}}_{2}}$ – задача двух тел ${{{\mathbf{P}}}_{1}}$ и ${{{\mathbf{P}}}_{3}}$. Вблизи тела ${{{\mathbf{P}}}_{2}}$ периодические решения ограниченной задачи являются возмущениями как периодических решений всех указанных четырех первых приближений, так и результатов склейки гиперболических орбит задачи двух тел ${{{\mathbf{P}}}_{2}}$, ${{{\mathbf{P}}}_{3}}$ с решениями-отрезками либо задачи двух тел ${{{\mathbf{P}}}_{1}}$, P₃, либо промежуточной задачи. В [32–36] периодические решения промежуточной задачи были использованы как порождающие для отыскания периодических квазиспутниковых орбит ограниченной задачи.

3.3. Укороченные системы. Рассмотрим теперь совокупность полиномов

Каждому ${{f}_{j}}({\mathbf{x}},{\mathbf{y}},\mu )$ соответствуют свой носитель ${{{\mathbf{S}}}_{j}} \subset {{\mathbb{R}}^{{2n + s}}}$и все сопутствующие объекты: многогранник Ньютона ${{\Gamma }_{j}}$, его обобщенные грани $\Gamma _{{j{{k}_{j}}}}^{{({{d}_{j}})}}$, их нормальные конусы ${\mathbf{U}}_{{j{{k}_{j}}}}^{{({{d}_{j}})}}$, граничные множества ${\mathbf{S}}_{{j{{k}_{j}}}}^{{({{d}_{j}})}}$, укороченные многочлены $\hat {f}_{{j{{k}_{j}}}}^{{({{d}_{j}})}}$. Кроме того, каждому непустому пересечению

соответствует совокупность укорочений которая является первым приближением совокупности (3.7), при вблизи пересечения (3.8) и называется укорочением совокупности (3.7).

Рассмотрим теперь систему уравнений

соответствующую совокупности (3.7). Системе (3.10) соответствуют все объекты, указанные для совокупности (3.7), а также укороченные системы уравнений каждая из которых соответствует одной совокупности укорочений (3.9). Каждая укороченная система (3.11) является первым приближением полной системы (3.10).

3.4. Периодические решения периодической системы Гамильтона. Как было показано в подразделе 2.2, поиск локальных семейств периодических решений периодической системы Гамильтона сводится к поиску локальных семейств неподвижных точек ${\mathbf{u}},\;{\mathbf{v}},\;\mu $ системы с приведенной нормальной формой (2.6) функции Гамильтона, т.е. точек-решений системы (2.7).

Чтобы решить эту систему, надо рассмотреть укороченные системы и найти их решения, которые дадут первые приближения к решениям системы (2.7). Пример таких вычислений см. в [4]. Вообще говоря, одному периодическому решению исходной системы соответствуют несколько неподвижных точек ${\mathbf{u}},\;{\mathbf{v}},\;\mu $ – решений системы (2.7).

Другие приложения этого метода: уравнение Белецкого колебаний спутника [7] и задача о периодических облетах планет с близким подходом к Земле [8].

4. Порождающие семейства периодических решений. Как только появились электронные вычислительные машины, на них стали вычислять семейства периодических решений ограниченной задачи трех тел для разных случаев: Солнце–Юпитер $(\mu \approx {{10}^{{ - 3}}})$, Земля–Луна $(\mu \approx {{10}^{{ - 2}}})$ и т. д. Оказалось, что эти семейства весьма похожи, а их периодические решения напоминают решения задачи двух тел. В 1968 г. Хенон [37] сообразил, что надо рассматривать пределы этих семейств при μ → 0.

4.1. Метод. Пусть функция Гамильтона $H(\mu )$ аналитически зависит от малых параметров $\mu = ({{\mu }_{1}}, \ldots ,{{\mu }_{s}})$ и соответствующая система Гамильтона имеет семейства периодических решений ${{\mathcal{F}}_{j}}(\mu )$. Некоторые из этих семейств могут иметь пределы ${{\mathcal{F}}_{j}}(0)$ при $\mu \to 0$. Семейства ${{\mathcal{F}}_{j}}(0)$ называются порождающими. Их решения образованы частями решений предельной системы Гамильтона с μ = 0.

Если эта предельная система интегрируема, то порождающие семейства можно описать аналитически. Этот подход предложил Хенон [37]. Он был использован для задачи Хилла и для ограниченной задачи трех тел [2, гл. III–V], [9, 10].

4.2. Задача Хилла. Ее функция Гамильтона имеет вид

Соответствующая система

описывает движение Луны (P₃) с нулевой массой под действием притяжения Солнца (P₁), расположенного в бесконечности, и Земли (P₂) с массой 1, расположенной в начале координат. Функция Гамильтона (4.1) аналитична в

Делаем каноническое преобразование координат

и получаем систему Гамильтона где

Положим $\varepsilon = \sqrt {2{\text{|}}H{\text{|}}} $ и $H \to - \infty $. Тогда в пределе получаем систему (4.2) с

Это промежуточная задача [31]. Для h₀ система (4.2) линейна и, следовательно, интегрируема. В силу однородности гамильтониана h₀ достаточно рассматривать ее при ${{h}_{0}} = 1{\text{/}}2$. Она имеет одно регулярное периодическое решение

Если орбита $({{X}_{1}}(t),{{X}_{2}}(t))$ решения задачи Хенона проходит через точку

то тело ${{{\mathbf{P}}}_{3}}$ сталкивается с телом ${{{\mathbf{P}}}_{2}}$ и решение не может быть продолжено через столкновение. Поэтому точка (4.3) делит решение на независимые части. Хенон [31] нашел все решения-отрезки, которые начинаются и заканчиваются такими столкновениями. Они образуют счетное множество двух типов. Решения-отрезки первого типа обозначаются символом ±j, $j \in \mathbb{N}$, и их орбиты являются эпициклоидами. Для $j = + 1$, +2, +3 они показаны на рис. 2. Орбиты решений-отрезков с отрицательными значениями j им симметричны относительно оси X₂.

Решения-отрезки второго типа обозначаются буквами $i$ и $e$, их орбиты являются эллипсами, проходящими через точку (4.3). Они показаны на рис. 3.

Теорема 2 ([12]). Последовательность решений-отрезков, не содержащая подряд двух одинаковых решений-отрезков второго типа, является порождающим решением для задачи Хилла.

Здесь порождающее семейство периодических решений состоит из одного решения. Все известные семейства периодических решений задачи Хилла включают хотя бы одно порождающее решение.

В ограниченной задаче трех тел имеется счетное множество однопараметрических порождающих семейств [37]. Некоторые из них устроены довольно сложно [9, 10, 16, 18–20].

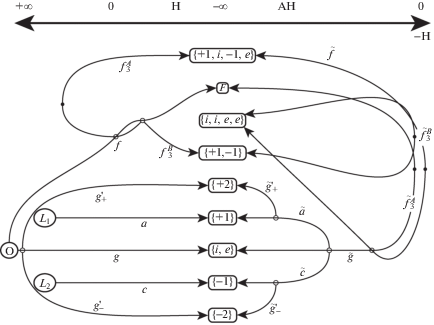
5. Обобщенные задачи. Обычно в небесной механике рассматриваются тела с неотрицательными массами. Но Батхин [14] предложил рассматривать задачи, где некоторые массы отрицательны. В задаче Хилла с массой тела ${{{\mathbf{P}}}_{2}}$ равной –1 (названной задачей анти-Хилла), семейства периодических решений являются продолжениями семейств периодических решений обычной задачи Хилла. Поэтому вычисление семейств периодических решений удобнее делать сразу для обеих задач: Хилла и анти-Хилла. Этот подход дает новые семейства периодических решений для обычной задачи Хилла.

Рис. 4 показывает диаграмму связей между этими семействами задач Хилла (левая часть) и анти-Хилла (правая часть). Центральный столбец дает порождающие решения этих семейств.

6. Скелеты. В некоторых частях фазового пространства системы Гамильтона имеется много семейств периодических решений, и они образуют “скелет” этой части фазового пространства. Поэтому вычисление таких семейств очень полезно для исследования структуры фазового пространства. Батхин [38] заметил, что в системе с конечной группой симметрий большинство таких семейств состоит из периодических решений, которые инвариантны относительно всех симметрий этой группы.

В разных задачах имеется много вычисленных семейств периодических решений, но их количество пока недостаточно, чтобы образовать скелет. Недавние результаты в этом направлении для ограниченной задачи трех тел см. в [11, 15–20, 39–41]. По задаче Хилла см. в [12–14, 31, 42–47].

7. Заключение. Все 5 методов являются новыми не только в небесной механике, но и в гамильтониановой механике. При этом методы 1 и 2 являются новыми в нелинейном анализе, а классический анализ можно рассматривать как квазилинейный, ибо в нем все уравнения имеют линейные части. Пример применения существенно нелинейного анализа – это задача о пограничном слое на игле [48].

Автор благодарит А.Б. Батхина и Э.П. Казанджана за помощь в подготовке этой статьи.