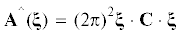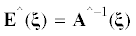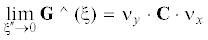Известия РАН. Механика твердого тела, 2021, № 1, стр. 44-49

КРУГОВЫЕ ДИСЛОКАЦИИ В АНИЗОТРОПНОЙ СРЕДЕ: УДЕЛЬНАЯ ЭНЕРГИЯ И ПОЛЯ НАПРЯЖЕНИЙ

С. В. Кузнецов^{a, b, c, *}

^a Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия

^b Московский государственный технический университет им. Баумана
Москва, Россия

^c Московский государственный строительный университет
Москва, Россия

^* E-mail: kuzn-sergey@yandex.ru

Поступила в редакцию 05.04.2019
После доработки 15.08.2019
Принята к публикации 21.09.2020

DOI: 10.31857/S0572329921010074

Полный текст (PDF)

Аннотация

Построен псевдодифференциальный оператор, описывающий поле напряжений в анизотропной среде, вызванное дислокацией с переменным вектором Бюргерса.

В предположении ${\mathbf{b}} \in {{H}_{{1/2}}}(\Pi ,{{R}^{3}})$ впервые получены аналитические выражения для энергии круговых дислокаций с переменным вектором Бюргерса, находящихся в упругой среде с анизотропией общего вида. Обнаружено, что в изотропной среде энергия образования краевой дислокации и дислокации скольжения определяется только равномерной нормой вектора Бюргерса.

Ключевые слова: дислокация, вектор Бюргерса, анизотропия, энергия

1. Введение. Энергия образования изолированной дислокации позволяет судить о многих свойствах кристаллов, с точки зрения механики разрушения наиболее важные из которых связанны с пластичностью и трещиностойкостью. Последнее обусловлено тем, что по современным представлениям краевая дислокация является предшественником трещины. В анизотропных кристаллах энергия дислокации среди прочих параметров может зависеть от ориентации дислокации (ориентации плоскости, в которой расположена дислокация) и ориентации вектора Бюргерса, характеризующего тип дислокации. Так в случае, если вектор Бюргерса лежит в плоскости дислокации говорят о дислокации скольжения, связанной с пластической работой материала, при векторе Бюргерса перпендикулярном плоскости дислокации речь идет о краевой дислокации. Естественно, что минимальные значения энергии отвечают наиболее вероятным расположениям дислокаций и, тем самым, определяют направления линий скольжения в кристаллах и направления, по которым должны развиваться будущие трещины. Кроме того, это позволяет оценить соотношение между пластическими и хрупкими свойствами кристалла.

Наиболее простой и в то же время естественный способ теоретического исследования энергии образования дислокации состоит в описании упругого поля перемещений, индуцированного дислокацией, в виде потенциала двойного слоя

(1.1)

${\mathbf{u}}({\mathbf{x}}) = \int\limits_\Omega {{\mathbf{b}}({\mathbf{y}}{\kern 1pt} ') \cdot {\mathbf{T}}(\nu ,{{\partial }_{y}}} ){\mathbf{E}}({\mathbf{x}} - {\mathbf{y}}{\kern 1pt} ')dy{\kern 1pt} '$

где ${\mathbf{u}}$ – поле перемещений, $\Omega $ – (плоская) область, занятая дислокацией, ${\mathbf{b}}$ – вектор Бюргерса, ${\mathbf{T}}$ – оператор поверхностных напряжений на плоскости $\Pi \supset \Omega $ с вектором единичной нормали $\nu $, E – фундаментальное решение уравнений равновесия. Затем по (1.1) вычисляются напряжения на плоскости Π, после чего оказывается возможным определить и энергию дислокации, как работу поверхностных напряжений на соответствующем скачке смещений, создаваемым вектором Бюргерса:

(1.2)

$W = 1{\text{/}}2\int\limits_\Omega {{\mathbf{t}} \cdot {\mathbf{b}}dx{\kern 1pt} '} $

где t – поверхностные напряжения на плоскости Π.

Этот подход применялся в исследованиях [1–3], где определялась энергия образования дислокации, размещенной в изотропной среде, и в [4], где найдена энергия дислокации, находящейся в плоскости изотропии трансверсально изотропной среды. В [5] аналогичный подход в сочетании с интегральным преобразованием Фурье позволил обойти трудности, связанные с отсутствием аналитических формул для фундаментальных решений при произвольной анизотропии.

Замечание 1.1. В [1–5] при описании дислокаций предполагалось, что вектор Бюргерса постоянен в Ω, – это в сочетании с теоремой Пича–Колера [6], позволяло ограничиться изучением энергии, произведенной дислокационной петлей (контуром, ограничивающим область Ω). В этом случае энергия образования дислокации оказывается бесконечной, и для получения конечных значений энергии приходиться выделять некоторую тороидальную окрестность петли. Метод выделения тороидальных окрестностей для получения конечных значений энергии дислокационных петель применялся в [7]. Надо отметить принципиальное различие между задачами теории трещин и дислокаций: если в теории трещин, в силу предположений о характере поля скачков смещений на берегах трещины, поле напряжений интегрируемо, то в теории дислокаций положение более сложное: для дислокаций с постоянным вектором Бюргерса поле напряжений имеет неинтегрируемую особенность в окрестности дислокационной границы, это вносит отмеченные выше затруднения в подсчете энергии краевой дислокации. Конечные значения энергии дислокаций могут быть получены и в предположении, что вектор Бюргерса непостоянен в Ω. Строго говоря, для конечных значений энергии требуется, чтобы ${\mathbf{b}} \in {{H}_{{1/2}}}(\Pi ,{{R}^{3}})$, при ${\text{supp}}\,{\mathbf{B}} \subset \Omega $, где supp обозначает носитель распределения (функции), а H_1/2 – функциональное пространство Хермандера, определенное как множество распределений, преобразование Фурье которых интегрируемо в квадрате с весом $k(\xi {\kern 1pt} ') = {{(1 + {{\left| {\xi {\kern 1pt} '} \right|}^{2}})}^{{1/2}}}$.

В настоящей работе методом, основанном на анализе символов, построен псевдодифференциальный оператор, описывающий поле напряжений в анизотропной среде, вызванное дислокацией с переменным вектором Бюргерса.

В предположении ${\mathbf{b}} \in {{H}_{{1/2}}}(\Pi ,{{R}^{3}})$ получены аналитические формулы для энергии круговой дислокации в среде с анизотропией общего вида. Кроме того, приведена аналитическая формула, дающая значения энергии круговой дислокации, находящейся в изотропной среде.

2. Основные соотношения. Рассматривается однородная анизотропная упругая среда, уравнения равновесия которой записываются в виде

(2.1)

$A({{\partial }_{{\mathbf{x}}}})u = - {\text{di}}{{{\text{v}}}_{{\text{x}}}}C \cdot \cdot {{\nabla }_{{\mathbf{x}}}}u = {\mathbf{0}}$

где ${\mathbf{u}}$ – вектор перемещений, ${\mathbf{A}}$ – матричный дифференциальный оператор уравнений равновесия, ${\mathbf{C}}$ – четырехвалентный тензор упругости. Предполагается, что тензор ${\mathbf{C}}$ строго эллиптичен

(2.2)

${\mathbf{s}} \cdot \cdot {\mathbf{C}} \cdot \cdot {\mathbf{s}} > {\mathbf{0}},\quad {\mathbf{s}} = {\mathbf{a}} \otimes {\mathbf{b}},\quad {\mathbf{a}},{\mathbf{b}} \in {{R}^{3}},\quad {\mathbf{a}},{\mathbf{b}} \ne {\mathbf{0}}$

Предполагается также, что исследуемая среда гиперупругая, в силу чего тензор ${\mathbf{C}}$ симметричен, как оператор, действующий в шестимерном пространстве симметричных тензоров второго ранга: ${{C}^{{ijmn}}} = {{C}^{{mnij}}}$.

Применяя интегральное преобразование Фурье

${{f}^{ \wedge }}(\xi ) = \int\limits_{{{R}^{3}}}^{} {f({\mathbf{x}})\exp ( - 2\pi i{\mathbf{x}} \cdot \xi )dx,\quad f \in {{L}^{2}}({{R}^{3}})} $

к уравнению (2.1), получим символ оператора A

(2.3)

причем условие (2.2) обеспечивает эллиптичность символа A^{^}. По символу (2.3) легко вычисляется преобразованное по Фурье фундаментальное решение

(2.4)

Замечание 2.1. В общем случае анизотропии обратить по Фурье выражение (2.4) удается только численно. Однако, как показано ниже, при построении основного п.д.о., необходимого для вычисления энергии, оказывается возможным ограничиться символом ${{{\mathbf{E}}}^{ \wedge }}(\xi )$.

Напряжения на плоскости, несущей дислокацию, определяются по (1.1) c помощью следующего п.д.о:

(2.5)

${\mathbf{t}}({\mathbf{x}}{\kern 1pt} ') = - \mathop {\lim }\limits_{{\mathbf{x}} \to {\mathbf{x}}{\kern 1pt} '} {\mathbf{T}}(\nu ,{{\partial }_{{\mathbf{x}}}})\int\limits_\Omega {{\mathbf{b}}({\mathbf{y}}{\kern 1pt} ') \cdot {\mathbf{T}}(\nu ,{{\partial }_{y}}){\mathbf{E}}} ({\mathbf{x}} - {\mathbf{y}}{\kern 1pt} ')dy{\kern 1pt} '{\mathbf{x}}{\kern 1pt} ' \in \Pi $

Предел в правой части (2.5) вычисляется по некасательным направлениям к Π. При этом в области $\Omega $ непосредственный переход к пределу под знаком интеграла оказывается невозможным из-за слишком большой особенности ядра

(2.6)

${\mathbf{G}}({\mathbf{x}} - {\mathbf{y}}) = - {\mathbf{T}}({{\nu }_{y}},{{\partial }_{y}}){\mathbf{E}}({\mathbf{x}} - {\mathbf{y}}){{{\mathbf{T}}}^{t}}({{\nu }_{x}},{{\partial }_{x}})$

Можно показать [7], что ядро ${\mathbf{G}}$ имеет неинтегрируемую особенность r^–3 при r → 0.

Интегральное преобразование Фурье, примененное к (2.6) дает соответствующую амплитуду в виде

(2.7)

${{{\mathbf{G}}}^{ \wedge }}(\xi ) = {{(2\pi )}^{2}}{{\nu }_{y}} \cdot {\mathbf{C}} \cdot \cdot \xi \otimes {{{\mathbf{E}}}^{ \wedge }}(\xi ) \otimes \xi \cdot \cdot {\mathbf{C}} \cdot {{\nu }_{x}}$

где для главного символа оператора поверхностных напряжений использовано представление ${{{\mathbf{T}}}^{ \wedge }}(\nu ,\xi ) = 2\pi i\nu \cdot {\mathbf{C}} \cdot \xi $.

Замечание 2.2. Непосредственно из (2.7) следует, что амплитуда G^ положительно однородна по ξ степени 0.

3. Сужение G^ на плоскость Π. В терминах обратного интегрального преобразования Фурье сужение G^ на плоскость Π, соответствующее формуле (2.5), может быть записано в виде

(3.1)

${{{\mathbf{G}}}^{\sim }}(\xi {\kern 1pt} ') = \mathop {\lim }\limits_{x'' \to 0} \int\limits_{ - \infty }^\infty {{{{\mathbf{G}}}^{ \wedge }}(\xi )\exp (2\pi ix{\kern 1pt} ''\xi {\kern 1pt} '')d\xi {\kern 1pt} '',\quad \xi {\kern 1pt} ' = {{{\Pr }}_{\Pi }}\xi ,\quad \xi {\kern 1pt} '' = {{{\Pr }}_{\nu }}\xi } $

где знак “~” обозначает преобразование Фурье по переменным лежащим в плоскости Π, а $x{\kern 1pt} '{\kern 1pt} '$ – проекция вектора x на направление $\nu $. Надо признать, что пользоваться формулой (3.1) также неудобно, как и (2.5), поскольку для вычисления предела в правой части (3.1) необходимо многократно при различных значениях $x{\kern 1pt} '{\kern 1pt} '$ вычислять несобственный интеграл (3.1).

Для перехода к пределу непосредственно под интегралом, введем в рассмотрение постоянный тензор

(3.2)

Выделяя из амплитуды (2.7) постоянный тензор (3.2), получим асимптотическую оценку

(3.3)

$({{{\mathbf{G}}}^{ \wedge }}(\xi ) - {{\nu }_{y}} \cdot {\mathbf{C}} \cdot {{\nu }_{x}}) = O({{\left| {\xi {\kern 1pt} ''} \right|}^{{ - 1}}}),\quad \left| {\xi {\kern 1pt} '{\kern 1pt} '} \right| \to \infty $

Оценка (3.3) показывает, что после выделения постоянного тензора (3.2) несобственный интеграл в (3.1) при $x{\kern 1pt} '{\kern 1pt} ' = 0$ все еще расходится. Однако, анализ выражения в левой части (3.3) показывает, что компоненты, для которых эта оценка достигается нечетны по $\xi {\kern 1pt} '{\kern 1pt} '$. Это позволяет получить следующую регулярную формулу для вычисления несобственного интеграла (3.1) при $x{\kern 1pt} '{\kern 1pt} ' = 0$:

(3.4)

${{{\mathbf{G}}}^{\sim }}(\xi {\kern 1pt} ') = \int\limits_{ - \infty }^\infty {\{ 1{\text{/}}2[{{{\mathbf{G}}}^{ \wedge }}(\xi ) + {{{\mathbf{G}}}^{ \wedge }}( - \xi )] - {{\nu }_{y}} \cdot {\mathbf{C}} \cdot {{\nu }_{x}}\} } d\xi {\kern 1pt} '{\kern 1pt} '$

Замечания 3.1. а) Методами [7, 8] можно показать, что амплитуда G^~ положительно однородна по $\xi {\kern 1pt} '$ степени 1 и при ${{\nu }_{y}} = {{\nu }_{x}}$ дает символ, строго эллиптичный при любых $\xi {\kern 1pt} ' \ne 0$.

б) Из предыдущего замечания следует, что вычисление ${{{\mathbf{G}}}^{\sim }}$ по формуле (3.4) можно проводить лишь для значений $\xi {\kern 1pt} '$, лежащих на окружности единичного радиуса, поскольку

(3.5)

${{{\mathbf{G}}}^{\sim }}(\xi {\kern 1pt} ') = \left| {\xi {\kern 1pt} '} \right|{\mathbf{G}}_{0}^{\sim }(\varphi ),\quad \varphi = \arcsin \left( {{{\xi }_{2}}{\text{/}}\left| {\xi {\kern 1pt} '} \right|} \right)$

Надо отметить, что зависимость символа ${\mathbf{G}}_{0}^{\sim }$ только от окружной координаты аналогична зависимости положительно однородного символа фундаментального решения уравнений статики ${{{\mathbf{E}}}^{ \wedge }}(\xi )$, представимого в виде ${{\left| \xi \right|}^{{ - 2}}}{\mathbf{E}}_{0}^{\sim }(\varphi ,\theta )$, только от двух сферических координат φ, θ. Это позволяет свести определение символа ${{{\mathbf{E}}}^{ \wedge }}(\xi )$ к определению значений ${\mathbf{E}}_{0}^{\sim }(\varphi ,\theta )$ на сфере единичного радиуса [7].

4. Формула для энергии. Используя (3.4), преобразованные по Фурье напряжения на плоскости Π представим в виде

(4.1)

${{{\mathbf{t}}}^{\sim }}(\xi {\kern 1pt} ') = {{{\mathbf{b}}}^{\sim }}(\xi {\kern 1pt} ') \cdot {{{\mathbf{G}}}^{\sim }}(\xi {\kern 1pt} ')$

Теперь, применяя равенство Парсеваля к выражению для энергии (1.2) и используя (4.1), найдем

(4.2)

$W = 1{\text{/}}2\int\limits_\Pi {{{{\mathbf{b}}}^{\sim }}} (\xi {\kern 1pt} ') \cdot \overline {{{{\mathbf{G}}}^{\sim }}(\xi {\kern 1pt} ') \cdot {{{\mathbf{b}}}^{\sim }}(\xi {\kern 1pt} ')} d\xi {\kern 1pt} '$

В силу (3.5) выражение (4.2) принимает конечные значения, если ${\mathbf{b}} \in {{H}_{{1/2}}}(\Pi ,{{R}^{3}})$.

Замечания 4.1. а) Для любой измеримой области $\Omega \subset \Pi $ характеристическая функция ${{\chi }_{\Omega }} \notin {{H}_{{1/2}}}(\Pi )$. Этот факт немедленно вытекает из рассмотрения выражения преобразованной по Фурье характеристической функции какой-либо простой области, погруженной в заданную, для которой преобразование Фурье удается вычислить явно. Например, для окружности единичного радиуса имеем [9]: 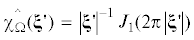, что приводит к асимптотической оценке

(4.3)

${\text{|}}\chi _{\Omega }^{ \wedge }(\xi {\kern 1pt} '){\text{|}} = O({{\left| {\xi {\kern 1pt} '} \right|}^{{ - 3/2}}}),\quad \left| {\xi {\kern 1pt} '} \right| \to \infty $

Из (4.3) в свою очередь следует, что норма такой функции не ограничена в H_1/2. Но для дислокаций с постоянным вектором Бюргерса имеем ${\mathbf{b}}({\mathbf{x}}{\kern 1pt} ') = {\mathbf{b}}{{\chi }_{\Omega }}({\mathbf{x}}{\kern 1pt} '),$ ${\mathbf{x}}{\kern 1pt} ' \in \Pi $.

Таким образом при любой анизотропии упругой среды, в том случае если вектор Бюргерса постоянен в (плоской) области, занятой дислокацией, ее энергия, определяемая по (4.2) при учете (3.5), оказывается неограниченной.

б) Рассмотрим круговые дислокации с переменным вектором Бюргерса:

(4.4)

${\mathbf{b}}({\mathbf{x}}{\kern 1pt} ') = \left\{ \begin{gathered} {{{\mathbf{b}}}_{0}}{{(1 - {{\left| {{\mathbf{x}}{\kern 1pt} '} \right|}^{2}})}^{\delta }},\quad \left| {{\mathbf{x}}{\kern 1pt} '} \right| \leqslant 1,\quad 0 < \delta \hfill \\ 0,\quad \left| {{\mathbf{x}}{\kern 1pt} '} \right| > 1 \hfill \\ \end{gathered} \right.$

где b₀ – постоянный вектор. Преобразование Фурье представления (4.4) дает [8]:

(4.5)

${{{\mathbf{b}}}^{\sim }}(\xi {\kern 1pt} ') = {{{\mathbf{b}}}_{0}}{{\pi }^{{ - \delta }}}\Gamma (\delta + 1){{\left| {\xi {\kern 1pt} '} \right|}^{{ - \delta - 1}}}{{J}_{{\delta + 1}}}(2\pi \left| {\xi {\kern 1pt} '} \right|)$

Имея ввиду асимптотические оценки бесселевых функций

${{J}_{\alpha }} = O({{r}^{\alpha }}),\quad r \to 0,\quad {{J}_{\alpha }} = O({{r}^{{ - 1/2}}}),\quad r \to \infty ,\quad \mathop {\forall \alpha }\limits_{\alpha \geqslant 0} $

При из (4.2), (4.5) по аналогии с п. а) немедленно получаем

При любой анизотропии упругой среды, энергия круговых дислокаций с вектором Бюргерса, определенным формулой (4.4), конечна.

Подстановка выражения (4.5) в формулу для энергии (4.2) при учете (3.5) дает

(4.6)

$W = 1{\text{/}}2{{\pi }^{{ - 2\delta }}}{{\Gamma }^{2}}(\delta + 1)\int\limits_0^\infty {{{r}^{{ - 2\delta - 1}}}} J_{{\delta + 1}}^{2}(2\pi r)dr\int\limits_0^{2\pi } {{{{\mathbf{b}}}_{0}}} \cdot {\mathbf{G}}_{0}^{\sim }(\varphi ) \cdot {{{\mathbf{b}}}_{0}}d\varphi $

В формуле (4.6) упругие свойства среды и тип дислокации входят лишь в последний интеграл, так что при оценке влияния анизотропии упругих свойств на энергию образования круговой дислокации (4.4) оказывается возможным ограничиться анализом значений интеграла на единичной окружности.

5. Дислокация в изотропной среде. Рассматривается изотропная однородная упругая среда, тензор упругости которой имеет вид

(5.1)

${{C}^{{ijkl}}} = \lambda {{\delta }^{{ij}}}{{\delta }^{{kl}}} + \mu ({{\delta }^{{ik}}}{{\delta }^{{jl}}} + {{\delta }^{{il}}}{{\delta }^{{jk}}})$

где λ, μ – константы Ламе, δ_ij – символ Кронекера. Для этой среды непосредственное использование выражений (2.3), (2.4) дает

(5.2)

${{{\mathbf{E}}}^{ \wedge }}(\xi ) = {{(2\pi )}^{{ - 2}}}{{\left[ {\mu (\lambda + 2\mu )} \right]}^{{ - 1}}}[(\lambda + 2\mu ){{\left| \xi \right|}^{{ - 2}}}{\mathbf{I}} - (\lambda + \mu ){{\left| \xi \right|}^{{ - 4}}}\xi \otimes \xi ]$

где I – единичная диагональная матрица. Подставляя выражения (5.1), (5.2) в формулу (2.7) для главного символа G^{^} (при ${{\nu }_{x}} = {{\nu }_{y}}$), получим

(5.3)

$\begin{gathered} {{{\mathbf{G}}}^{ \wedge }}(\xi ) = \frac{1}{{\lambda + 2\mu }}\left[ {{{{(\lambda + \mu )}}^{2}}\nu \otimes \nu + \tfrac{{\mu (\lambda + \mu )}}{{{{{\left| \xi \right|}}^{2}}}}(\xi \cdot \nu )\,(\xi \otimes \nu + \nu \otimes \xi ) + } \right. \\ \left. {\, + \tfrac{{\mu (\lambda + 2\mu )}}{{{{{\left| \xi \right|}}^{2}}}}\xi \otimes \xi - \tfrac{{\mu (\lambda + \mu )}}{{{{{\left| \xi \right|}}^{4}}}}{{{(\xi \cdot \nu )}}^{2}}\xi \otimes \xi } \right] \\ \end{gathered} $

Далее, используя для символа (5.3) регуляризацию (3.4), будем иметь

(5.4)

${{G}^{\sim }}(\xi ') = \frac{{\mu \left| {\xi {\kern 1pt} '} \right|}}{{2(\lambda + 2\mu )}}\left[ {(\lambda + 2\mu )I + \lambda \left( {\frac{{\xi {\kern 1pt} '\; \otimes \xi {\kern 1pt} '}}{{{{{\left| {\xi {\kern 1pt} '} \right|}}^{2}}}} + \nu \otimes \nu } \right)} \right]$

Выражение (5.4) с точностью до множителя $\left| {\xi {\kern 1pt} '} \right|$ совпадает с символом оператора теории трещин для изотропной среды [7, 10].

Имея ввиду замечание 4.1.б), из (5.4) получим формулу для интеграла по единичной окружности в формуле (4.6):

(5.5)

$\int\limits_0^{2\pi } {{{{\mathbf{b}}}_{0}} \cdot {\mathbf{G}}_{0}^{\sim }(\varphi ) \cdot {{{\mathbf{b}}}_{0}}\,d\varphi } = 2\pi \frac{{\mu (\lambda + \mu )}}{{\lambda + 2\mu }}{{\left| {{{{\mathbf{b}}}_{0}}} \right|}^{2}}$

Выражение (5.5) показывает, что в изотропной среде энергия рассматриваемой круговой дислокации не зависит от ее типа. Таким образом, в изотропной среде появление краевых дислокаций и дислокаций скольжения с точки зрения энергии равновероятно.

6. Заключение. Построен псевдодифференциальный оператор, описывающий поле напряжений в анизотропной среде, вызванное дислокацией с произвольным вектором Бюргерса.

В предположении ${\mathbf{b}} \in {{H}_{{1/2}}}(\Pi ,{{R}^{3}})$ получены аналитические формулы для энергии круговой дислокации с переменным вектором Бюргерса, находящейся в анизотропной среде с анизотропией общего вида.

Получены аналитические выражения, дающие значения энергии круговой дислокации, находящейся в изотропной среде. Показано, что в изотропной среде энергия рассматриваемой круговой дислокации с переменным вектором Бюргерса ${\mathbf{b}} \in {{H}_{{1/2}}}(\Pi ,{{R}^{3}})$ не зависит от типа дислокации.

Работа выполнена при финансовой поддержке гранта РНФ 19-19-00616.

Список литературы

Mechanics of Generalized Continua (editor Kroner E.). Proceedings of the IUTAM-Symposium. Springer; 2014. ISBN-13:978-3662302590.
Collected Works of J. D. Eshelby: The Mechanics of Defects and Inhomogeneities. Springer; 2006 edition. ISBN-10:140204416X.
Nabarro F.R.N. The mathematical theory of stationary dislocations // Adv. Phys. 1952. V. 1. № 3. P. 269–394.
Chou Y.T., Eshelby J.D. The energy and line tension of a dislocation in a hexagonal crystal // J. Mech. Phys. Solids. 1962. V. 10. № 1. P. 27–34.
Kuznetsov S.V. On the operator of the theory of cracks // Comptes Rendus de l’Académie des Sciences. Série II, Mécanique, Physique, Chimie, Astronomie. 1996. V. 323. Iss. 7. P. 427–432.
Peach M.O., Koehler J.S. The forces exerted in dislocations and the stress field produced by them // Phys. Rev. Ser. 2. 1950. V. 80. P. 436–439.
Kuznetsov S.V. Fundamental and singular solutions of Lamé equations for media with arbitrary elastic anisotropy // Quart. Appl. Math. 2005. V. 63. P. 455–467.
Ilyashenko A.V., Kuznetsov S.V. 3D Green’s function for equations of harmonic vibrations // Arch. Appl. Mech. 2017. V.87. P. 159–165. https://doi.org/10.1007/s00419-016-1184-y
Stein E. Real Analysis: Measure Theory, Integration, and Hilbert Spaces. Princeton University Press, 2005. ISBN-13:978-0691113869.
Willis J.R. A penny-shaped crack on an interface // Quart. J. Mech. Appl. Math. 1972. V. 25. № 3. P. 367–385.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал