Известия РАН. Механика твердого тела, 2021, № 2, стр. 63-71
О ПРОБИВАНИИ СЛОИСТЫХ СТРУКТУР ТВЕРДЫМ СФЕРИЧЕСКИМ ТЕЛОМ
Н. В. Баничук a, С. Ю. Иванова a, *, К. Ю. Осипенко a
a Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия
* E-mail: syuivanova@yandex.ru
Поступила в редакцию 05.03.2020
После доработки 12.04.2020
Принята к публикации 20.04.2020
Аннотация
Экспериментально исследовано пробивание по нормали сферическим жестким ударником пакета из нескольких пластин, обладающих различными прочностными свойствами. Изучено влияние на процесс пробивания наличия дополнительных свободных поверхностей (расслоения) и порядка расположения пластин с различными прочностными свойствами в пробиваемом пакете.
1. Введение. Исследование процессов проникания в деформируемую среду жестких тел, движения тел в среде и процессов пробивания различных преград являются актуальной проблемой, представляющей как теоретический, так и практический интерес. С использованием в технике новых материалов и их различных комбинаций становится важным проведение исследований движения твердых тел в неоднородных, в том числе слоистых средах. Данной проблематике посвящено значительное число научных публикаций. Некоторые задачи оптимизации однородных покрытий и слоистых конструкций, подверженных внедрению в них жестких ударников (в случае нормального удара), были изучены в [1–5]. При этом на основе использования принципа максимума Понтрягина решались дискретные задачи оптимизации слоистых пластин, состоящих из нескольких слоев из различных материалов. Было установлено, что оптимальное решение характеризуется кусочно-постоянным распределением материальных свойств. В монографиях [6, 7] отражены исследования по анализу и проектированию слоистых конструкций, оптимизации покрытий, подверженных удару, оптимизации слоистых механических систем, включая проблемы проникания ударников в сплошные среды. В книге [8] исследовались задачи оптимизации формы жестких ударников, проникающих в пластические, бетонные и некоторые композитные среды. Третий раздел этой книги посвящен оптимизации многослойных покрытий. В монографии [9] представлены важные теоретические результаты и данные численного моделирования по проблеме динамического контактного взаимодействия жестких тел и деформируемых сред. Экспериментальные и теоретические результаты по проблеме проникания в слоистые материалы содержатся в работах [10–12]. В статье [12] представлены результаты экспериментальных исследований проникания сферических и конических твердых тел в среду, составленную из слоев пластилина разной прочности (выдержанных при различной температуре). Работы [13, 14] посвящены отысканию оптимальной структуры слоистой защитной плиты, формируемой из заданного конечного набора материалов с известными прочностными и инерционными характеристиками. Поиск решения осуществлялся численно на основе применения эволюционного метода отыскания нелокального экстремума (генетического алгоритма). Также данные вопросы освещены в книге [15].
Целью настоящего исследования является экспериментальное изучение процесса пробивания слоистых преград из упругопластического материала жесткими ударниками. Исследуется пробивание по нормали сферическим жестким телом пакета из нескольких пластин, обладающих различными прочностными свойствами. Изучается влияние на процесс пробивания наличия дополнительных свободных поверхностей (пробивание разнесенных пластин) и порядка расположения пластин с различными прочностными свойствами в пробиваемом пакете.
2. Исследование влияния свободных поверхностей на процесс пробивания слоистых пластин жестким ударником. Пробивание пакета из двух или трех пластин осуществлялось стальным сферическим ударником, имеющим диаметр d = 0.01 м и массу m = = 0.004 кг. Пластины толщиной H = 0.02 м, изготовленные из однородного и изотропного упругопластического материала (формованного пластилина), устанавливались и жестко закреплялись перпендикулярно направлению движения ударника, который разгонялся пневматической пушкой. Давление в камере пушки выставлялось таким образом, чтобы скорость вылета ударника составляла приблизительно 250 м/с. Скорость ударника на вылете из ствола пушки принималась за скорость входа в пластину ${{{v}}_{0}}$, сопротивлением воздуха движению тела можно было пренебречь в силу небольших размеров экспериментальной установки. Скорости входа ${{{v}}_{0}}$ и выхода из пластины ${{{v}}_{f}}$ измерялись с помощью хронографов. Во всех экспериментах пластинам присваивались номера 1, 2 или 3, считая по направлению движения тела. Целью данного исследования было изучение влияния свободных поверхностей на изменение скорости ударника при пробивании пакета из пластин, разнесенных на расстояние h = 0.02 м. Для экспериментов использовались пластины, выдержанные при комнатной температуре, которая измерялась лабораторным термометром, и пластины, выдержанные в термостате при заданной температуре не менее 24 часов. Температуры первой, второй и третьей пробиваемых пластин обозначались через ${{t}_{1}}$, ${{t}_{2}}$ и ${{t}_{3}}$, соответственно.
Для выявления влияния свободных поверхностей на защитные свойства слоистой преграды была проведена серия экспериментов, в которых отдельные слои имели одинаковую температуру, то есть обладали одинаковыми прочностными свойствами. Результаты проведенных экспериментов с пластинами, имеющими одинаковые температуры, приведены в табл. 1.
Таблица 1
| Номер экспери-мента (i) | Кол-во слоев в пакете | ${{t}_{1}} = {{t}_{2}}$, °С | ${{{v}}_{0}}$, м/с | ${{{v}}_{f}}$, м/с | ${{\delta }_{i}} = \frac{{{{{v}}_{0}} - {{{v}}_{f}}}}{{{{{v}}_{0}}}}$ | Δ = ${{\delta }_{{n + 1}}} - {{\delta }_{n}}$ |
|---|---|---|---|---|---|---|
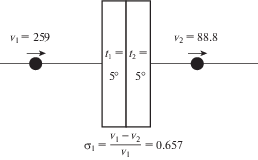
| 1, совмещ. | 2 | 5 | 259 | 88.8 | 0.657 | –0.056 |
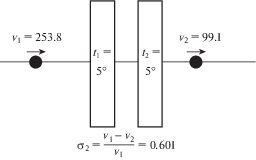
| 2, разнес. | 2 | 5 | 253.8 | 99.1 | 0.601 | |
| 3, совмещ. | 2 | 24.8 | 256.1 | 179.9 | 0.277 | 0.033 |
| 4, разнес. | 2 | 24.8 | 252 | 173.7 | 0.31 | |
| 5, совмещ. | 3 | 25 | 250.4 | 152.2 | 0.392 | 0.07 |
| 6, разнес. | 3 | 25 | 255.9 | 137.5 | 0.462 |
На рис. 1 и 2 , соответствующих экспериментам 1 и 2, схематично показано, как изменялась скорость ударника (м/с) при пробивании двух пластин при одинаковой температуре ${{t}_{1}} = {{t}_{2}} = 5$°C. Видно, что совмещенные пластины представляют собой более эффективную защиту при пробивании сферическим ударником. В рассмотренном примере появление двух дополнительных свободных поверхностей (рис. 2 ) приводит к ослаблению пакета в целом, т.е. ${{\delta }_{2}} < {{\delta }_{1}}$.
Эксперименты 3 и 4 по пробиванию двух пластин с одинаковой температурой были проведены также для случая, когда ${{t}_{1}} = {{t}_{2}} = 24.8$°C. В этом случае прочностные свойства пластилина были существенно снижены, а плотность (инерционная характеристика) оставалась практически неизменной. В результате экспериментов было установлено, что появление двух свободных поверхностей при рассматриваемой повышенной температуре (эксперимент 4) улучшают защитные свойства пакета в целом, и в этом случае ${{\delta }_{4}} > {{\delta }_{3}}$.
В случае пробивания пакета из трех одинаковых пластин, имеющих температуры ${{t}_{1}} = {{t}_{2}} = {{t}_{3}} = 25$°C (эксперименты 5 и 6), эффект влияния четырех свободных поверхностей (эксперимент 6) усиливался примерно в два раза по сравнению с эффектом от двух свободных поверхностей (эксперимент 4). Вводя обозначения ${{\Delta }_{{43}}} = {{\delta }_{4}} - {{\delta }_{3}}$ и ${{\Delta }_{{65}}}$ = δ6 – δ5, видим, что ${{\Delta }_{{65}}} = 0.07 > 0.033 = {{\Delta }_{{43}}}$.
На рис. 3,a,b представлены фотографические изображения входного (15-1) и выходного (15-2) отверстий в случае пробивания пластины при t = 5°C. На рис. 4,a,b , соответственно, показаны входное (13-1) и выходное (13-2) отверстия при температуре пробиваемой пластины t = 24°C. Из снимков видно, что размер каверны, образовавшейся после пробивания пластины сферическим ударником при t = 24°C, существенно больше, чем при t = 5°C. Канал, образовавшийся в холодной пластине, сужается по ходу движения шарика, и его остаточный диаметр становится меньше диаметра тела за счет упругого сжатия. Более мягкая пластина при t = 24°C имеет широкий канал (большего диаметра, чем диаметр тела) и более выраженные “выбросы” материала на входе и выходе из каверны. Это можно объяснить проявлением свойств пластичности при повышении температуры пластины.
Анализируя результаты описанной серии экспериментов, можно сделать вывод, что пакет из двух охлажденных пластин при t = 5°C, как совмещенных, так и разнесенных, лучше гасит скорость ударника, чем пакет из двух или трех более мягких пластин при t = 25°C. Однако, если условия эксплуатации таковы, что прочностные свойства используемых материалов слоев пакета могут изменяться (например, при нагреве или охлаждении), то разнесение или совмещение слоев пакета может дать дополнительный защитный эффект при его пробивании.
Возможное объяснение выявленных экспериментально закономерностей может быть основано на том факте, что ударное воздействие тела на свободную поверхность приводит к локальному возрастанию силы сопротивления непосредственно вблизи этой поверхности. Для затупленных тел [16, 17] сила сопротивления на некотором небольшом участке входа тела в среду (удара) пропорциональна скорости тела и не зависит от его прочностных свойств. В случае разнесенных пластин возникает повторный удар на поверхности второй пластины. Однако, так как скорость тела после прохождения твердого слоя может быть существенно меньше, чем в том случае, когда слой мягкий, второй удар будет более слабым и слабее сможет влиять на последующее прохождение телом второй пластины. Если оба слоя прочные (холодные), то возрастание силы сопротивления в момент второго удара будет незначительным, а если слои мягкие (теплые), то возрастание силы сопротивления будет почти как в первом слое, и это приведет к усилению защитных свойств пакета. При выходе тела из пластины сопротивление среды ослабевает за счет деформирования свободной поверхности (происходит ослабление защитных свойств пакета) [18]. В теплых слоях ударное воздействие может быть сильнее, чем ослабляющее влияние на выходе, что и приводит к усилению сопротивления пакета при разнесении мягких пластин. В холодных прочных слоях, наоборот, ослабление силы сопротивления на выходе оказывается более существенным, чем слабый рост сопротивления при втором ударе. Для более точного прогнозирования влияния разнесения пластин на скорость выхода ударника ниже в параграфе 3 предложена математическая модель, учитывающая как усиливающее ударное воздействие, так и ослабляющее влияние свободных поверхностей на выходе.
Были проведены также эксперименты 7–10, когда пробиваемые пластины имели различные температуры, а, следовательно, различные прочностные характеристики. Результаты этих экспериментов приведены в табл. 2.
Таблица 2
| Номер экспери-мента (i) | Кол-во слоев в пакете | ${{t}_{1}}$; ${{t}_{2}}$, °C | ${{{v}}_{0}}$, м/с | ${{{v}}_{f}}$, м/с | ${{\delta }_{i}} = \frac{{{{{v}}_{0}} - {{{v}}_{f}}}}{{{{{v}}_{0}}}}$ | Δ = ${{\delta }_{{n + 1}}} - {{\delta }_{n}}$ |
|---|---|---|---|---|---|---|
| 7, совм. | 2 | 24; 5 | 255.5 | 132.5 | 0.481 | –0.039 |
| 8, разнес. | 2 | 24; 5 | 257.2 | 143.4 | 0.442 | |
| 9, совм. | 2 | 5; 24 | 250.1 | 141.7 | 0.433 | –0.025 |
| 10, разнес. | 2 | 5; 24 | 255.2 | 151 | 0.408 |
Разнесение пластин в эксперименте 10 так же, как и в эксперименте 8, приводило к ослаблению защитных свойств пакета. Это позволяет сделать вывод, что в рассмотренном диапазоне температур расслоение пакета, то есть появление в пакете пластин дополнительно одной холодной и одной теплой свободной поверхности (независимо от их расположения) приводит только к ослаблению защитных свойств.
Сравнивая измеренные скорости ударника на выходе из пакета пластин, можно видеть, что расположение более холодных (обладающих большими прочностными свойствами) слоев в конце пакета (эксперименты 7 и 8) более эффективно снижает скорость тел на выходе, чем их альтернативное расположение (эксперименты 9 и 10). Это подтверждает справедливость известного [8, 15] двучленного соотношения для силы сопротивления $D$ упругопластической среды, действующей на движущееся в ней тело: $D = {{A}_{0}} + {{A}_{2}}{{{v}}^{2}}$. Здесь ${v}$ – скорость движения тела в среде, зависящая от его положения, а коэффициенты ${{A}_{0}}$ и ${{A}_{2}}$ – интегральные характеристики, описывающие прочностные и инерционные свойства среды при движении в ней жесткого тела заданной формы. По мере пробивания пакета пластин скорость тела снижается, и больший вклад в силу сопротивления вносят прочностные свойства.
3. Моделирование процесса пробивания слоистой преграды. Рассматривается пробивание жестким сферическим ударником массы $m$ и радиуса $R$ упругопластического слоя толщиной $H$ с дозвуковой скоростью. Материал преграды имеет плотность $\rho $, модуль упругости E, динамический предел текучести ${{\tau }_{d}}$ и считается несжимаемым. Движение ударника происходит по нормали к поверхности плиты вдоль оси $Ox$ (x – координата фронтальной точки ударника, точка x = 0 соответствует моменту касания ударником плиты, точку $x = H + R$ будем считать точкой выхода тела из преграды). В точке x = 0 скорость тела имеет заданное значение ${{{v}}_{0}}$. Сила сопротивления среды движению ударника определяется выражением
Введем безразмерные переменные $s = x{\text{/}}2R$, $l = \eta {\text{/}}2R$ и разделим процесс пробивания плиты на четыре этапа.
Первый этап (от s = 0 до s = s1) соответствует прониканию ударника от момента касания да момента, когда край области контакта перемещается по поверхности полупространства со скоростью распространения продольных волн a. Нормальное давление на этом этапе и значение s = s1 определяются формулами [16, 17]
Второй этап внедрения ударника (от s = s1 до s = 1/2) соответствует процессу погружения тела в среду на половину диаметра. Будем считать, что на этом участке происходит переход к режиму квазистационарного обтекания, когда скорость расширения границы контакта меняется от $d{{r}_{c}}{\text{/}}dt = a$ до $d{{r}_{c}}{\text{/}}dt = 0$ (rc – радиус границы контакта сферы и среды). Нормальное давление на поверхности тела будем аппроксимировать следующим образом:
Третий этап внедрения ударника соответствует его движению от момента погружения на половину диаметра (s = 1/2) до остановки тела или момента пробивания преграды ($s = H{\text{/}}2R + 1{\text{/}}2$). Считаем, что на этом участке шар обтекается квазистационарно. По аналогии с методом сферического приближения [8, 18–23] давление в каждой точке поверхности контакта отождествим с давлением на внутреннюю поверхность сферического слоя несжимаемой упругопластической среды толщины $b - R$ и внутреннего радиуса $R$, расширяющегося со скоростью ${{{v}}_{n}}$. Через b обозначено расстояние по нормали от данной точки поверхности контакта до тыльной поверхности пробиваемой преграды (радиус внешней поверхности сферического слоя). При $l > 0.5$ взаимодействие с преградой отсутствует.
Выражение для давления на внутренней поверхности расширяющегося сферического слоя из несжимаемой упругопластической среды определяется формулой [18]:
На четвертом этапе (${{1{\text{/}}2 + H} \mathord{\left/ {\vphantom {{1{\text{/}}2 + H} {2R}}} \right. \kern-0em} {2R}} < s$) ударник движется по инерции до момента касания с новой преградой.
Сила сопротивления D для шара, пробивающего преграду, определяется следующей трехчленной формулой в виде суммы инерционного, вязкостного и прочностного слагаемых:
Коэффициенты в этой формуле меняются при движении ударника сквозь преграду из-за влияния свободной поверхности.
Запишем уравнение движения ударника на каждом из участков пробивания
На отрезке $0 < s < {{s}_{1}}$ данное уравнение можно проинтегрировать аналитически. Имеем
Учитывая, что ${{s}_{1}} = 1{\text{/}}2 - {a \mathord{\left/ {\vphantom {a {(2\sqrt {{v}_{1}^{2} + {{a}^{2}}} )}}} \right. \kern-0em} {(2\sqrt {{v}_{1}^{2} + {{a}^{2}}} )}}$, получим нелинейное уравнение для определения значения скорости ${{{v}}_{1}} = {v}\left( {{{s}_{1}}} \right)$:
4. Некоторые замечания и выводы. В работе представлены результаты экспериментов по пробиванию жесткими сферическими ударниками пакета из разнесенных или совмещенных пластин, обладающих различными прочностными свойствами. Варьирование прочностных свойств достигалось за счет нагревания или охлаждения используемого материала (формованного пластилина). Установлено, что пакет из двух охлажденных пластин, как совмещенных, так и разнесенных, лучше гасит скорость ударника, чем пакет из двух или трех более мягких нагретых пластин. Однако две разнесенные нагретые пластины лучше гасят скорость ударника, чем эти же пластины, но совмещенные. Для охлажденных (более прочных) пластин эффект был обратный. Поэтому можно сделать вывод, что если условия эксплуатации таковы, что прочностные свойства используемых материалов слоев пакета могут изменяться (например, при нагреве или охлаждении), то разнесение или совмещение слоев пакета может дать дополнительный защитный эффект при его пробивании. Сравнивая измеренные скорости ударника на выходе из пакета пластин, можно видеть, что расположение слоев, обладающих большими прочностными свойствами, в конце пакета более эффективно снижает скорость тел на выходе, чем их альтернативное расположение. Это подтверждает справедливость двучленного соотношения для силы сопротивления упругопластической среды, в котором есть прочностное и инерционное слагаемое, пропорциональное квадрату скорости ударника. По мере пробивания пакета пластин скорость тела снижается, и больший вклад в силу сопротивления вносят прочностные свойства.
В работе предложен также метод оценивания скорости ударника при пробивании отдельного слоя, основанный на поэтапном учете силы сопротивления среды на различных участках движения ударника. В случае упругопластической среды для упрощения вычислений можно в выражениях для силы сопротивления пренебречь вязкостью и ограничиться только инерционным и прочностным слагаемыми.
Работа выполнена по теме Госзадания (номер госрегистрации АААА-А20-120011690132-4).
Список литературы
Аптуков В.Н. Оптимальная структура неоднородной пластины с непрерывным распределением свойств по толщине // Изв. АН СССР. МТТ. 1985. № 3. С. 149–152.
Аптуков В.Н., Поздеев А.А. Некоторые минимаксные задачи технологии и прочности конструкций // Изв. АН СССР. Техн. кибернетика. 1982. № 1. С. 47–55.
Аптуков В.Н., Петрухин Г.И., Поздеев А.А. Оптимальное торможение твердого тела неоднородной пластиной при ударе по нормали // Изв. АН СССР. МТТ. 1985. № 1. С. 165–170.
Аптуков В.Н., Белоусов В.Л., Каниболотский М.А. Оптимизация структуры слоистой плиты при проникании жесткого ударника // Механика композит. материалов. 1986. № 2. С. 252–257.
Аптуков В.Н., Мурзакаев А.В., Фонарев А.В. Прикладная теория проникания. М.: Наука, 1992. 105 с.
Каниболотский М.А., Уржумцев Ю.С. Оптимальное проектирование слоистых конструкций. Новосибирск: Наука, 1989. 176 с.
Алехин В.В., Уржумцев Ю.С. Оптимизация слоистых систем. Якутск: ЯФ изд-ва СО РАН, 2002. 177 с.
Ben-Dor G., Dubinsky A., Elperin T. Applied high-speed plate penetration dynamics. Solid Mechanics and its Applications. V. 132. Dordrecht: Springer, 2006. 364 p.
Баженов В.Г., Котов В.Л. Математическое моделирование нестандартных процессов удара и проникания осесимметричных тел и задачи идентификации свойств грунтовых сред. М.: Физматлит, 2011. 208 с.
Бивин Ю.К. Проникание твердых тел в сыпучие и слоистые среды // Изв. РАН. МТТ. 2008. № 1. С. 154–160.
Бивин Ю.К. Пробивание, проникание, рикошет. Saarbrücken: Lap Lambert, 2012. 235 p.
Бивин Ю.К. Проникание твердого тела в слоистую преграду // Изв. РАН. МТТ. 2019. № 3. С. 64–68.
Баничук Н.В., Иванова С.Ю., Макеев Е.В. Проникание жестких ударников в слоистые пластины и некоторые задачи глобальной многоцелевой структурной оптимизации // Проблемы прочности и пластичности. 2012. Вып. 74. С. 124–133.
Баничук Н.В., Иванова С.Ю. Игровой подход к решению задачи оптимизации формы ударника и структуры слоистой среды при высокоскоростном пробивании // Проблемы прочности и пластичности. 2016. Вып. 78. № 4. С. 426–435.
Баничук Н.В., Иванова С.Ю. Оптимизация: контактные задачи и высокоскоростное проникание. М.: Физматлит, 2016. 176 с.
Симонов И.В. Динамическая задача о вдавливании осесимметричного штампа в упругое полупространство // Изв. АН СССР. МТТ. 1967. № 2. С. 163–165.
Бивин Ю.К., Осипенко К.Ю. Измерения электромагнитного излучения в динамических процессах с твердыми телами. Препринт ИПМех РАН № 830. Москва, 2007. 32 с.
Фомин В.М., Гулидов А.И., Сапожников Г.А. и др. Высокоскоростное взаимодействие тел. Новосибирск: Изд-во СО РАН, 1999. 600 с.
Warren T.L., Hanchak S.J., Kevin L. Penetration of 6061-T6511 aluminum targets by ogive-nosed VAR 4340 steel projectiles at oblique angles: experiments and Simulations // International Journal of Impact Engineering. 2001. V. 25. P. 993–1022.
Masri R., Durban D. Deep penetration analysis with dynamic cylindrical cavitation fields // International Journal of Impact Engineering. 2009. V. 36. P. 830–841.
Котов В.Л., Линник Е.Ю., Макарова А.А., Тарасова А.А. Анализ приближенных решений задачи о расширении сферической полости в грунтовой среде // Проблемы прочности и пластичности: Межвуз. сб. Нижегород. ун-т. 2011. Вып. 73. С. 58–63.
Линник Е.Ю., Котов В.Л., Тарасова А.А., Гоник Е.Г. Решение задачи о расширении сферической полости в грунтовой среде в предположении несжимаемости за фронтом ударной волны // Проблемы прочности и пластичности: Межвуз. сб. Нижегород. ун-т. 2012. Вып. 74. С. 49–58.
Котов В.Л., Линник Е.Ю., Тарасова А.А. Определение параметров квадратичной модели локального взаимодействия при внедрении сферического ударника в мягкий грунт // Проблемы прочности и пластичности. 2013. Вып. 75. № 1. С. 47–55.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела