Известия РАН. Механика твердого тела, 2021, № 2, стр. 124-132
ЗАДАЧА ОПТИМИЗАЦИИ ДВИЖЕНИЯ УПРУГОГО СЛЕДЯЩЕГО МАНИПУЛЯТОРА
Г. А. Геворкян *
Институт механики НАН
Ереван, Армения
* E-mail: hrgevorkian@mail.ru
Поступила в редакцию 05.02.2020
После доработки 08.02.2020
Принята к публикации 12.02.2020
Аннотация
Актуальные задачи моделирования механизмов с упругими звеньями предполагают усовершенствование существующих формализмов и алгоритмов динамического анализа, синтеза и оптимального управления рассматриваемого класса систем. В то же время, современные исследования в указанной области главным образом ориентированы на повышение быстродействия расчетных алгоритмов без причинения ущерба точности вычислительного процесса. Если упругие многозвенные динамические системы, не включающие в себя замкнутых кинематических цепей, могут быть исчерпывающим образом исследованы на основе стратегии без обращения матрицы масс (обобщенный метод Ньютона–Эйлера), то упругие механизмы с замкнутыми кинематическими цепями подлежат исследованию с использованием стратегии обращения матрицы масс. К последнему классу принадлежат задачи на нахождение условного минимума функционала действия по Остроградскому при наличии голономных (геометрических) дополнительных связей. Здесь предстоит ознакомиться с задачей оптимизации движения упругого трехзвенного следящего манипулятора, заключающейся в минимизации функции отклонения исполнительного органа от наперед заданной окружной траектории. Эта задача также сводится к нахождению условного минимума функционала действия по Остроградскому при наличии голономной дополнительной связи.
Введение. В предлагаемой статье представлены итоги численного решения задачи точного воспроизведения упругим манипулятором заданной траектории движения исполнительного органа. В качестве воспроизводимой траектории движения выступает окружная траектория, а в роли следящей динамической системы – трехзвенный манипулятор с упруго-деформируемым звеном [1].
В указанной постановке задача оптимизации движения следящего манипулятора сводится к нахождению условного экстремума (минимума) функционала действия по Остроградскому при наличии дополнительной склерономной связи [2]. В качестве критерия оптимизации движения манипулятора используется условие тождественности функций положений исполнительного органа с учетом и без учета упругого отклонения [1].
Численное решение задачи осуществляется на основе стратегии, использующей процедуру обращения матрицы масс, в силу разработанного модифицированного метода Лагранжа, нашедшего успешное применение в процессе динамического анализа сложного класса упругих многозвенных систем с замкнутыми кинематическими цепями [3–18].
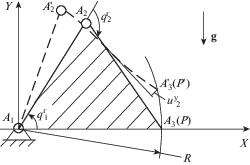
1. Моделирование движения упругого следящего манипулятора. Рассматривается трехзвенный манипулятор (рис. 1), состоящий из неподвижной и недеформируемой опорной стойки C0, абсолютно жесткого звена C1 и линейно-упругого звена C2. В предположении идеальности связей между звеньями (кинематических пар Ai, $i = 1,\,\,2$), упругий манипулятор помещается в потенциальное поле силы тяжести.
Когда звено C2 предполагается абсолютно жестким, исполнительный орган ${{A}_{3}}$ в точности описывает дугу окружности ${{A}_{3}}A_{3}^{'}$ (рис. 1) при движении манипулятора по законам, удовлетворяющим условию: ${{A}_{1}}{{A}_{3}} = R = {\text{сonst}}$. Очевидно, что это условие обеспечивается в том случае, если замкнутый контур ${{A}_{1}}{{A}_{2}}{{A}_{3}}{{A}_{1}}$ сохраняется неизменным на протяжении всего интервала действия следящего манипулятора.
Когда же звено C2 принимается упругим, точное воспроизведение желаемой траектории путем несложного выбора законов движения не представляется возможным. В самом деле, вследствие наличия упругих деформаций второго звена, проблема соблюдения постоянства кривизны траектории точки ${{A}_{3}}$ сводится к задаче минимизации функции отклонения исполнительного органа ${{A}_{3}}$ от заданной окружной траектории. А это означает, что воспроизводимая траектория выражает не что иное, как дополнительную геометрическую связь, налагаемую на движение упругого трехзвенного манипулятора [1].
2. Задача нахождения абсолютного минимума функционала действия. При отсутствии дополнительной связи, налагаемой на движение исполнительного органа манипулятора, первая задача динамики трехзвенного манипулятора с упругим выходным звеном сводится к нахождению абсолютного экстремума (минимума) функционала действия по Остроградскому:
(2.1)
$S = \int\limits_{{{t}_{1}}}^{{{t}_{2}}} {\left[ {(T - П) + \sum\limits_{i = 1}^{n = 2} {Q_{i}^{r}q_{i}^{r}} } \right]dt} $В развернутом виде условие минимума функционала (2.1) сводится к системе нелинейных дифференциальных уравнений второго порядка [2]:
(2.2)
$\left[ {\begin{array}{*{20}{c}} {{{M}_{{rr}}}}&{{{M}_{{re}}}} \\ {{{M}_{{er}}}}&{{{M}_{{ee}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{{\vec {\ddot {q}}}}^{r}}} \\ {{{{\ddot {q}}}^{e}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{{{\vec {C}}}^{r}}} \\ {{{C}^{e}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\vec {Q}} \\ 0 \end{array}} \right]$Система нелинейных дифференциальных уравнений (2.2) предполагает численное решение путем их линеаризации относительно обобщенных координат $q_{i}^{r}$, i = 1, 2, их скоростей $\dot {q}_{i}^{r}$, i = 1, 2, а также варьируемых параметров $\vec {q}_{i}^{е}$, i = 1, 2 и их скоростей $\vec {\dot {q}}_{i}^{е}$, i = 1, 2 [3–12].
3. Задача нахождения условного минимума функционала действия. При наличии дополнительной связи, налагаемой на движение исполнительного органа манипулятора, первая задача динамики трехзвенного манипулятора с упругим выходным звеном сводится к нахождению условного экстремума (минимума) функционала действия по Остроградскому, а именно – к нахождению минимума функционала (2.1) с учетом условия
(3.1)
$\begin{array}{*{20}{c}} \begin{gathered} \text{[}{{L}_{1}}{\text{cos}}q_{1}^{r} + {{L}_{2}}{\text{cos}}(q_{1}^{r} + q_{2}^{r}) - u_{2}^{y}\sin (q_{1}^{r} + q_{2}^{r})]{}^{2} + \\ + \;[{{L}_{1}}{\text{sin}}q_{1}^{r} + {{L}_{2}}{\text{sin}}(q_{1}^{r} + q_{2}^{r}) + u_{2}^{y}{\text{cos}}(q_{1}^{r} + q_{2}^{r})]{}^{2} = R{}^{2} \\ \end{gathered} \\ {\left| {{{L}_{1}} - {{L}_{2}}} \right| \leqslant R \leqslant \left| {{{L}_{1}} + {{L}_{2}}} \right|} \end{array}$В таком случае, система алгебро-дифференциальных уравнений движения упругого следящего манипулятора, объединяющих (2.2) и (3.1), принимает вид [2]:
(3.2)
$\left[ {\begin{array}{*{20}{c}} {{{M}_{{rr}}}}&{{{M}_{{re}}}}&{{{M}_{{r\lambda }}}} \\ {{{M}_{{er}}}}&{{{M}_{{ee}}}}&{{{M}_{{е\lambda }}}} \\ {{{M}_{{\lambda r}}}}&{{{M}_{{\lambda e}}}}&{{{M}_{{\lambda \lambda }}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{{\vec {\ddot {q}}}}^{r}}} \\ {{{{\ddot {q}}}^{e}}} \\ \lambda \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{{{\vec {C}}}^{r}}} \\ {{{C}^{e}}} \\ {{{C}^{\lambda }}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\vec {Q}} \\ 0 \\ 0 \end{array}} \right]$Критерий оптимизации. Отождествление функций положений исполнительного органа P трехзвенного манипулятора с учетом и без учета упругого отклонения (см. рис. 1) выступает необходимым и достаточным признаком минимизации начального упругого отклонения следящего манипулятора, причем минимизация этого отклонения при отсутствии сил сопротивления подчиняется зависимости, близкой к линейной.
Доказательство. Рассмотрим функции отклонений исполнительного органа следящего манипулятора (см. рис. 1) с учетом и без учета начального упругого отклонения:
(3.3)
$\begin{array}{*{20}{c}} {{{x}_{{P'}}} = {{L}_{1}}{\text{сos}}q_{1}^{r} + {{L}_{2}}{\text{сos}}(q_{1}^{r} + q_{2}^{r}) - u_{2}^{y}{\text{sin}}(q_{1}^{r} + q_{2}^{r})} \\ {{{y}_{{P'}}} = {{L}_{1}}{\text{sin}}q_{1}^{r} + {{L}_{2}}{\text{sin}}(q_{1}^{r} + q_{2}^{r}) + u_{2}^{y}{\text{cos}}(q_{1}^{r} + q_{2}^{r})} \end{array}$(3.4)
$\begin{array}{*{20}{c}} {{{x}_{P}} = R{\text{cos}}\omega t} \\ {{{y}_{P}} = R{\text{sin}}\omega t} \end{array}$После приравнивания функций отклонений в системах равенств (3.3) и (3.4), их возведения в квадрат и последующего почленного сложения образуется уравнение дополнительной связи (3.1). Можно показать, что тригонометрическое уравнение (3.1) в результате двойного дифференцирования и последующих упрощений приводится к следующему эквивалентному дифференциальному уравнению дополнительной связи:
Следовательно, при соответствующих ненулевых начальных условиях (например, при положительном начальном отклонении и отрицательной скорости) упругая следящая система, изображенная на рис. 1 и подчиненная условию (3.5), будет стремиться к обнулению этого отклонения при отсутствии демпфирования, следуя линейной зависимости.
Что и требовалось доказать.
4. Численная реализация задачи при отсутствии дополнительной связи. Процесс численной реализации сформулированной задачи предполагается произвести в два этапа с применением явной схемы численного интегрирования Ньюмарка [16]. Первый этап усматривает моделирование движения трехзвенного манипулятора при отсутствии дополнительной геометрической связи (3.1) на основании системы дифференциальных уравнений (2.2), тогда как второй этап подразумевает решение задачи в полной постановке, т.е. принимая во внимание дополнительную связь (3.1), в силу системы алгебро-дифференциальных уравнений (3.2).
Положим длины звеньев ${{C}_{1}}$ и ${{C}_{2}}$ изображенного на рис. 1 следящего манипулятора равными радиусу описываемой окружности, т.е. $R = {{L}_{1}} = {{L}_{2}} = 0.35$ м, вследствие чего замкнутый контур ${{A}_{1}}{{A}_{2}}{{A}_{3}}{{A}_{1}}$ отождествляется с правильным треугольником. Поперечные сечения звеньев принимаются круглыми радиусов ${{r}_{1}} = 6.0 \times {{10}^{{ - 3}}}$ м и ${{r}_{2}} = 3.0$ × 10–3 м, массы звеньев – равными ${{m}_{1}} = 0.309$ кг и ${{m}_{2}} = 0.0772$ кг, а модуль Юнга второго звена – ${{E}_{2}} = 200$ ГПа.
Исследуемый манипулятор функционирует в интервале $t \in [0,T]$, где $T = 0.7$ с, согласно следующим законам движения:
(4.1)
$\begin{array}{*{20}{c}} {\omega \equiv \dot {q}_{1}^{r}(t) \equiv 10} \\ {\dot {q}_{2}^{r}(t) \equiv 0} \end{array}$Ограничиваясь рассмотрением одной изгибной степени свободы звена C2, т.е. ${{N}_{2}} = N_{2}^{y}$ = 1, задаются начальные условия в обобщенных координатах и скоростях: $q_{1}^{r}{\text{(0)}} = \pi {\text{/}}3$ рад, $q_{2}^{r}{\text{(0)}} = - 2\pi {\text{/}}3$ рад и $\dot {q}_{1}^{r}{\text{(0)}} = 10$ рад/с, $\dot {q}_{2}^{r}(0) = 0$. На первом этапе тестирования задачи начальные условия для упругого перемещения и скорости будут полагаться нулевыми: $u_{2}^{y}(P,0) = \dot {u}_{2}^{y}(P,0)$ = 0. Шаг численного интегрирования полагается равным $\Delta t = {{10}^{{ - 5}}}$ с.
На рис. 2, а представлен график зависимости упругого перемещения (м) концевой точки звена ${{C}_{2}}$ (исполнительного органа P) во времени (с) [16]; на рис. 2, b, c предлагаются графики функций обобщенных сил (Н ⋅ м), действующих в кинематических парах ${{A}_{1}}$ и ${{A}_{2}}$.
Для оценки отклонения исполнительного органа $P$ следящего манипулятора от заданной окружной траектории вследствие деформирования звена C2 предусматривается функция ошибки Er, которая в проекциях на оси неподвижной системы координат OXY определяется следующими равенствами [16]:
(4.2)
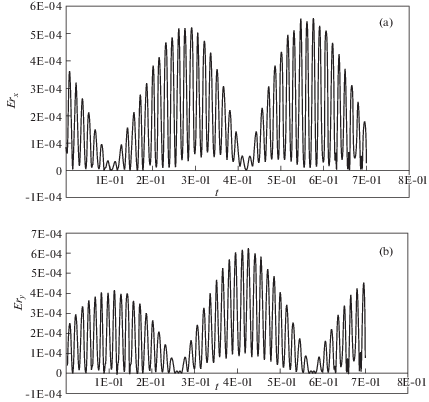
$\begin{gathered} E{{r}_{X}} = {\text{|}}{{P}_{X}} - P_{X}^{'}{\text{|}} = {\text{|}}R{\text{cos}}\omega t - [{{L}_{1}}\cos (q_{1}^{r}) + {{L}_{2}}\cos (q_{1}^{r} + q_{2}^{r}) - u_{2}^{y}\cos (q_{1}^{r} + q_{2}^{r})]{\text{|}} \hfill \\ E{{r}_{Y}} = {\text{|}}{{P}_{Y}} - P_{Y}^{'}{\text{|}} = {\text{|}}R\sin \omega t - [{{L}_{1}}\sin (q_{1}^{r}) + {{L}_{2}}\sin (q_{1}^{r} + q_{2}^{r}) + u_{2}^{y}\cos (q_{1}^{r} + q_{2}^{r})]{\text{|}} \hfill \\ \end{gathered} $Графики первого теста функции отклонения (функции ошибки, м) исполнительного органа P от окружной траектории в проекциях на оси неподвижной системы координат XOY представлены на рис. 3, a, b [16].
5. Численная реализация задачи при наличии дополнительной связи. Вторичный тест моделирования движения упругого следящего манипулятора проводится с учетом дополнительной геометрической связи (3.1) путем численного решения системы алгебро-дифференциальных уравнений (3.2).
При аналогичных начальных условиях в обобщенных координатах и обобщенных скоростях начальные условия в упругом перемещении и в скорости упругого перемещения принимаются следующими (размерность перемещения – м, размерность скорости – м/с):
(5.1)
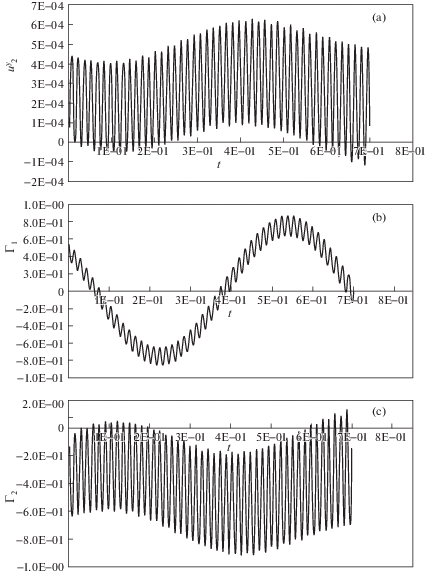
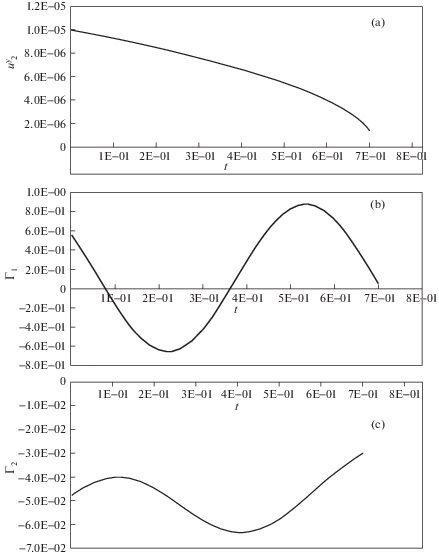
$\begin{array}{*{20}{c}} {u_{2}^{y}(P,0) = {{{10}}^{{ - 5}}}} \\ {\dot {u}_{2}^{y}(P,0) = - 7 \times {{{10}}^{{ - 6}}}} \end{array}$Принимая шаг численного интегрирования равным $\Delta t = {{10}^{{ - 4}}}$ с, осуществляется тест численной реализации задачи минимизации упругого отклонения исполнительного органа от заданной окружной траектории следящего манипулятора (см. рис. 1). Результаты тестирования задачи приводятся на рис. 4, a, b, c [16]. Как видно из рис. 4, а, вблизи значения $u_{2}^{y}(P,0) = 0$ имеет место искажение численного решения, что объясняется наличием особенности в этой точке.
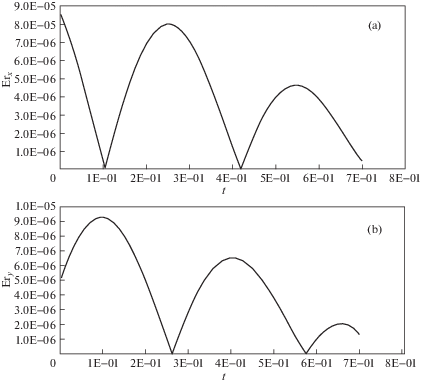
Графики второго теста функции отклонения (функции ошибки, м) исполнительного органа P от окружной траектории в проекциях на оси неподвижной системы координат XOY представлены на рис. 5, а и 5, b [16].
6. Заключение. В представленной статье проведено моделирование следящего трехзвенного манипулятора с упругим звеном на основе численного решения задачи нахождения условного минимума функционала действия по Остроградскому. По итогам минимизации начального упругого отклонения исполнительного органа следящего манипулятора от наперед заданной окружной траектории можно утверждать о хороших предпосылках приложения методов, алгоритмов и программного обеспечения динамического анализа упругих многозвенных систем к решению задач оптимального управления.
Список литературы
Pascal M., Gagarina T. A pseudo-rigid model for the dynamical simulation of flexible mechanisms // Multibody System Dynamics. 1999. V. 3. P. 303–331.
Gofron M., Shabana A.A. Control structure interaction in the nonlinear analysis of flexible mecha-nical systems // International Journal of Nonlinear Dynamics. 1993. V. 4. P. 183–206.
Luh J.Y.S., Walker M.W., Paul R. On-line computational scheme for mechanical manipulators // Trans. ASME. Journal of Dynamic Systems, Measurement and Control. 1980. V. 74. P. 251–269.
Featherstone R. The calculation of robot dynamics using articulated-body inertias // International Journal of Robotics Research. 1983. V. 2. № 1. P. 13–30.
Dombre E., Khalil W. Modélisation et commande des robots. Edition Hermès, 1988. 448 p.
Dombre E., Khalil W. Modélisation, identification et commande des robots. Edition Hermès, 1999. 480 p.
Verlinden O. Simulation du comportement dynamique de systèmes multicorps flexibles comportant des membrures de forme complexe: Doctoral Thesis of the Polytechnic Faculty of Mons. 1994. 222 p.
Fisette P., Samin J.-C. Symbolic generation of large multibody system dynamic equations using a new semi-explicite Newton-Euler recursive scheme // Archive of Applied Mechanics. 1996. V. 66. P. 187–199.
Boyer F., Coiffet P. Generalization of Newton-Euler model for flexible manipulators // Internatio-nal Journal of Robotic Systems. 1996. V. 13. № 1. P. 11–24.
Boyer F., Coiffet P. Symbolic modeling of a flexible manipulator via assembling of its generalized Newton-Euler model // International Journal Mechanism and Machine Theory. 1996. V. 31. № 1. P. 45–56.
Boyer F., Khalil W. An efficient calculation of flexible manipulators inverse dynamics // International Journal of Robotics Research. 1998. V. 17. № 3. P. 282–293.
Саркисян Ю.Л., Степанян К.Г., Азуз Н., Геворкян Г.А. Динамический анализ упругих манипуляторов обобщенным методом Ньютона–Эйлера // Известия НАН РА и ГИУА. Сер. Т.Н. – 2004. Т. 57. № 1. С. 3–10.
Саркисян Ю.Л., Степанян К.Г., Геворкян Г.А. Динамический анализ упругих древовидных механических систем без внешних связей // Известия НАН РА и ГИУА. Сер. Т.Н. 2006. Т. 59. № 1. С. 3–9.
Геворкян Г.А. Динамический анализ упругих древовидных механических систем в присутствии внешних голономных связей // Information Technologies and Management. Encyclopedia-Armenica. 2004. № 4. С. 36–43.
Геворкян Г.А. Динамическое моделирование механизмов с упругими звеньями переменной длины // Вестник ГИУА. Серия: Механика, машиноведение, машиностроение. 2014. Выпуск 17. № 2. С. 34–41.
Геворкян Г.А. Приложение обобщенного метода Ньютона–Эйлера к задачам оптимального управления упругих механизмов // Известия НАН РА и ГИУА. Сер. ТН. 2010. Т. 63. № 2. С. 133–138.
Геворкян Г.А. Об одной разновидности динамического анализа манипуляторов посредством обращения их матрицы масс // Мат. V межд. конф. “Актуальные проблемы механики сплошной среды”, окт. 02–07, 2017, Цахкадзор, Армения. С. 61–62.
Геворкян Г.А. Динамическое моделирование механизма шарнирного четырехзвенника с упругим шатуном // Труды VIII международной конференции “Проблемы динамики взаимодействия деформируемых сред”, сентябрь 22–26, 2014, Горис-Степанакерт. Ереван.: Чартарагет, 2014. С. 143–147.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела