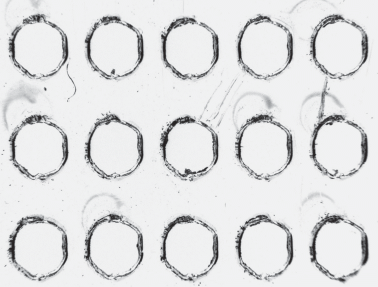Известия РАН. Механика твердого тела, 2021, № 3, стр. 7-12

1. Введение. Сверхрешетки представляют собой двоякопериодические системы неоднородностей (отверстий, пор, микротрещин, включений и т.д.). Характерный размер неоднородностей варьируется от нанометров (наномасштаб) до сотен нанометров (мезомасштаб). Размеры промежутков между неоднородностями при этом, как правило, сравнимы с размерами неоднородностей.

Сверхрешетки возникают и в природе, естественным путем, и в технологических процессах. Ярким примером являются фотонные кристаллы (ФК) – материалы, коэффициент преломления которого меняется периодически в пространственных направлениях [1, 2]. В качестве примеров естественного происхождения можно представить некоторые разновидности опалов (неорганические ФК) и чешуйки на крыльях бабочек-парусников (органические ФК). При этом существуют технологии, позволяющие создавать ФК искусственным путем, например, протравливанием системы полостей в прозрачном материале. Другими примерами могут быть цеолиты (сверхрешетки естественного и искусственного типа) [3–5] и пористый кремний (сверхрешетки искусственного типа) [6].

Сверхрешетки обладают уникальными свойствами – например, фотонные кристаллы могут действовать как фильтр для заданных частот. Свойства сверхрешеток обуславливаются их внутренней структурой. При разрушении ее они исчезают полностью или частично. Кроме того, свойства могут зависеть от периодов двоякопериодической структуры сверхрешетки, а значит и от деформации структуры, которая может возникать из-за внешних и внутренних нагрузок.

Соответственно, корректная оценка напряженно-деформированного состояния имеет существенное значение. Особенно важен расчет эффективных упругих характеристик сверхрешетки, с учетом анизотропии структуры.

Характерные особенности механического поведения сверхрешеток описываются в рамках плоской задачи теории упругости о плоскости, ослабленной двоякопериодической системой отверстий. В работах [7, 8] с помощью аналитических расчетов получены эффективные модули упругости для перфорированных пластин, содержащих квадратные решетки круглых отверстий. Отношение промежутка между отверстиями к радиусу отверстий меняется от 0.1 до 10. Построены зависимости эффективных модулей от ориентации растягивающей силы. В работе [9] представлены результаты испытаний на растяжение перфорированных пластин, радиус отверстий 1 мм, промежуток между отверстиями 1 мм. Решетки в пластинах сделаны под различными углами, от 0 до 45°. Экспериментально полученные величины эффективных модулей подтвердили аналитические оценки, выведенные в работе [7].

В данной работе рассмотрены аналитические оценки эффективных модулей для прямоугольных решеток (т.е. наименьшая ячейка которых имеет взаимно перпендикулярные стороны, и длины сторон не равны). Проведены испытания на растяжение пластин с решетками, радиус отверстий которых 1 мм, с промежутками между отверстиями 2 мм вдоль одной оси и 1 мм вдоль перпендикулярной. Ориентация решеток меняется от 0° до 90°. Получены экспериментальные значения эффективных модулей, проведено их сравнение с аналитическими оценками.

2. Аналитический расчет эффективных модулей упругости. Аналитическая оценка зависимости эффективного модуля от ориентации решетки рассчитывалась с помощью метода мультипольных разложений, представленного в [7]. Метод заключается в том, что в плоской задаче упругости поле напряжений в материале вокруг круглого отверстия можно представить как линейную комбинацию сингулярных решений (ряд мультиполей):

где g(t) – аналитическая функция смещений, g_n – коэффициенты при членах ряда мультиполей, t – комплексная локальная координата точки на контуре отверстия.

Эффективные модули упругости определяются через обратную матрицу к матрице эффективных податливостей. В свою очередь, эффективные податливости S_ijkl определяются через соотношение

Здесь $\tilde {\varepsilon }$ – эффективная деформация, вызванная эффективным напряжением $\tilde {\sigma }$.

В работе [7] получены следующие выражения эффективных податливостей:

Здесь E, ν – упругие характеристики матрицы решётки, $S = \operatorname{Im} \left( {{{{\bar {\omega }}}_{I}}{{\omega }_{{II}}}} \right)$ – площадь основного параллелограмма решетки.

Получив коэффициенты разложения ряда для элементарных эффективных нагрузок в решетке, – всестороннее растяжение ($g_{n}^{\sigma }$), чистый сдвиг ($g_{n}^{s}$) и диагональный сдвиг ($g_{n}^{\tau }$), – рассчитываются эффективные податливости решетки, а отсюда матрицa упругих модулей.

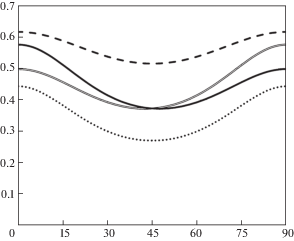
На рис. 1 представлены зависимости эффективных модулей упругости по отношению к модулю упругости материала. Сплошная и двойная линии соответствуют эффективным модулям решетки с промежутками 2 и 1 мм (т.е. с периодами 4 и 3 мм), для каждой из осей. Пунктирная линия соответствуeт эффективным модулям квадратной решетки с промежутками 1 мм, штриховая – 2 мм, эти линии даны для сравнения.

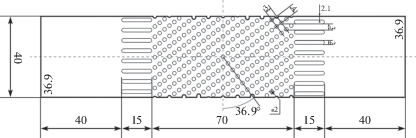
3. Проведение экспериментов. Изготовлено 8 серий по 4 образца (всего 32 образца) из полиэтилена, размером 180 × 40 × 0.65 мм. В первой серии образцы сплошные, в остальных создана область, содержащая решетку отверстий (один из образцов в качестве примера представлен на рис. 2). Периоды решеток 3 и 4 мм, радиус отверстий 1 мм, таким образом, промежутки между отверстиями 1 и 2 мм по каждой из осей. Решетки созданы с помощью лазерной резки.

Образцы были подвержены растяжению с нагрузкой до 340 Н для сплошных образцов и до 230 Н для остальных.

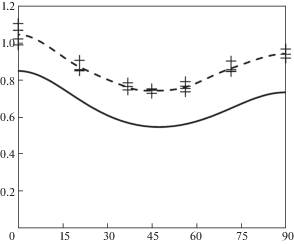
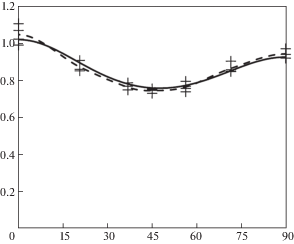
4. Результаты экспериментов. Полученные значения эффективных модулей (ГПа) представлены на рис. 3. Расчетные данные представлены сплошной линией, данные экспериментов – маркерами “+”. Штриховая линия соответствует интерполированным усредненным экспериментальным данным.

Обратим внимание, что полученная усредненная экспериментальная кривая по форме достаточно близка к теоретической кривой, но она расположена выше приблизительно на 20%. Подробное изучение образцов показало, что в процессе изготовления образцов при прожигании отверстий края отверстий оплавляются (отверстия решетки образца под увеличением представлены на рис. 4). Наплыв приводит к уменьшению отверстий в среднем на 10% от запланированных размеров. Кроме того, происходит утолщение образца в окрестностях краев отверстий максимально до ≈20%.

Математическая модель скорректирована с учетом обнаруженных эффектов. Прежде всего, в модели радиус отверстий уменьшен до 0.9 мм, соответственно, промежутки между отверстиями увеличены до 1.2 и 2.2 мм.

Так как модель основана на плоской задаче теории упругости, утолщение образца в окрестностях отверстий будем рассматривать как увеличение жесткости материала. Поскольку модель предполагает однородность среды, увеличение жесткости в модели необходимо заменить модуль Юнга на эффективный. Размер жестких колец наплыва вокруг отверстий сравним с размерами промежутков между отверстиями, что позволяет предположить, что эффективный модуль по отношению к реальному будет близок к усредненной величине толщин образца по отношению к проектной толщине. Таким образом, эффективный модуль увеличен на 10%. Экспериментальные данные и скорректированная теоретическая кривая представлены на рис. 5.

5. Заключение. Спроектирован и изготовлен ряд образцов в виде пластин, содержащих двоякопериодические решетки с периодами 3 и 4 мм (с промежутками 1 и 2 мм между отверстиями радиусом 1 мм). Решетки имеют различные ориентации от 0° до 90°. Проведены испытания образцов на растяжение, получены их эффективные модули упругости.

Проведенное сравнение полученных экспериментальных и теоретических (с учетом коррекции) результатов показало хорошее совпадение (отклонение до 3%).

Можно заключить, что представленная численная модель может быть использована для расчета эффективных упругих коэффициентов двоякопериодических систем круглых отверстий с неравными периодами.