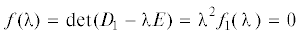Известия РАН. Механика твердого тела, 2021, № 4, стр. 44-51

ОБ УСТОЙЧИВОСТИ ОДНОГО ПЕРМАНЕНТНОГО ВРАЩЕНИЯ В ОКРЕСТНОСТИ РАВЕНСТВА АППЕЛЬРОТА

М. А. Новиков^*

Институт динамики систем и теории управления им. В.М. Матросова СО РАН
Иркутск, Россия

Поступила в редакцию 27.01.2020
После доработки 03.02.2020
Принята к публикации 12.02.2020

DOI: 10.31857/S0572329921030090

Аннотация

В механических автономных консервативных системах, допускающих частный интеграл, иногда имеются стационарные движения, существующие как с частным интегралом, так и без него. Рассматривается система, в которой при выполнении равенства Аппельрота существует интеграл Гесса и выделено стационарное движение, имеющее место и без равенства Аппельрота. В статье вторым методом Ляпунова проведено исследование устойчивости такого стационарного движения. Установлено, что граница области достаточных условий устойчивости не совпадает с границей области необходимых условий устойчивости.

Ключевые слова: стационарное движение, общий интеграл, частный интеграл, связка интегралов, устойчивость движения

1. Введение. Более полное изучение свойств механических автономных консервативных систем можно осуществить при нахождении наибольшего числа первых интегралов. В задаче о движении твердого тела вокруг неподвижной точки [1, 2] кроме трех известных общих интегралов: полной энергии, кинетического момента и Пуассона, в [2] приведены случаи существования частных интегралов. Одним из них является интеграл Гесса, существующий только при выполнении равенства Аппельрота [2].

В консервативных системах важной характеристикой считается существование стационарных движений, которые отыскиваются методом Рауса–Ляпунова [3, 11]: составлением связки из первых интегралов. Иногда найденные по полной связке известных первых интегралов стационарные движения совпадают с такими же стационарными движениями, составленными для неполной связки без учета какого-либо первого интеграла. Особое значение имеет игнорирование частного интеграла.

Хотя этот вопрос недостаточно изучен, он представляет интерес исследования устойчивости по Ляпунову [12–16] найденных стационарных движений и устойчивости в окрестности этого интеграла, когда не существует частный интеграл.

2. Постановка задачи. Рассматривается нелинейная механическая автономная консервативная система [1, 2], описываемая дифференциальными уравнениями:

(2.1)

$\begin{gathered} ОA\dot {p} = (B - C)qr + {{z}_{0}}{{{{\gamma }}}_{{\text{2}}}},\quad {{{\dot {\gamma }}}_{1}} = r{{{{\gamma }}}_{2}} - q{{{{\gamma }}}_{3}} \\ B\dot {q} = (C - A)rp - {{z}_{0}}{{{{\gamma }}}_{3}} + {{x}_{0}}{{{{\gamma }}}_{1}},\quad {{{\dot {\gamma }}}_{2}} = p{{{{\gamma }}}_{3}} - r{{{{\gamma }}}_{1}} \\ C\dot {r} = (A - B)rq - {{x}_{0}}{{{{\gamma }}}_{2}},\quad {{{\dot {\gamma }}}_{3}} = q{{{{\gamma }}}_{1}} - p{{{{\gamma }}}_{2}} \\ \end{gathered} $

где ${{x}_{0}} \ne 0 \ne {{z}_{0}}$; $A$, $B$, $C$ – моменты инерции твердого тела относительно главных осей Ox, Oy, Oz; $p$, $q$, $r$ – проекции мгновенной угловой скорости на подвижные, связанные с телом оси; ${{x}_{0}}$, ${{z}_{0}}$ – координаты центра масс в подвижных осях; ${{{{\gamma }}}_{1}}$, ${{{{\gamma }}}_{2}}$, ${{{{\gamma }}}_{3}}$ – проекции ортов подвижных осей на неподвижную вертикальную ось OZ.

Для системы (2.1) известны три первых общих интеграла [2]:

${{V}_{0}} = A{{p}^{2}} + B{{q}^{2}} + C{{r}^{2}} + 2({{x}_{0}}{{{{\gamma }}}_{1}} + {{z}_{0}}{{{{\gamma }}}_{3}}) = {\text{const}}$

${{V}_{1}} = Ap{{{{\gamma }}}_{1}} + Bq{{{{\gamma }}}_{2}} + Cr{{{{\gamma }}}_{3}} = {\text{const}}$

${{V}_{2}} = {{\gamma }}_{1}^{2} + {{\gamma }}_{2}^{2} + {{\gamma }}_{3}^{2} = 1$

При выполнении равенства Аппельрота [2]:

(2.2)

$AC(x_{0}^{2} + z_{0}^{2}) = B(Ax_{0}^{2} + Cz_{0}^{2})$

система (2.1) допускает частный линейный интеграл Гесса, заданный в аналитическом виде

(2.3)

${{V}_{3}} = A{{x}_{0}}p + C{{z}_{0}}r = 0$

В статье [16] приведены некоторые стационарные движения системы (2.1). Одним из них является перманентное вращение:

$\begin{gathered} {{p}_{0}} = \frac{{ - {{z}_{0}}}}{{\sqrt[4]{{{{A}^{2}}x_{0}^{2} + {{C}^{2}}z_{0}^{2}}}}}\sqrt {\frac{{C(Ax_{0}^{2} + Cz_{0}^{2})}}{{A(A - C){{x}_{0}}{{z}_{0}}}}} ;\quad {{q}_{0}} = 0 \\ {{r}_{0}} = \frac{{{{x}_{0}}}}{{\sqrt[4]{{{{A}^{2}}x_{0}^{2} + {{C}^{2}}z_{0}^{2}}}}}\sqrt {\frac{{A(Ax_{0}^{2} + Cz_{0}^{2})}}{{C(A - C){{x}_{0}}{{z}_{0}}}}} \\ \end{gathered} $

(2.4)

$\begin{gathered} {{{{\gamma }}}_{{{\text{10}}}}} = \frac{{ - C{{z}_{0}}}}{{\sqrt {{{A}^{2}}x_{0}^{2} + {{C}^{2}}z_{0}^{2}} }},\quad {{{{\gamma }}}_{{20}}} = 0 \\ {{{{\gamma }}}_{{30}}} = \frac{{A{{x}_{0}}}}{{\sqrt {{{A}^{2}}x_{0}^{2} + {{C}^{2}}z_{0}^{2}} }},\quad A > C,\quad {{x}_{0}}{{z}_{0}} > 0 \\ \end{gathered} $

Отметим сразу, что для системы (2.1) стационарное движение (2.4) может существовать и без участия интеграла (2.3), что соответствует невыполнению равенства (2.2).

Ставится цель исследования вторым методом Ляпунова устойчивости перманентного вращения (2.4) в малой окрестности соотношения (2.2), когда не выполняется равенство Аппельрота. Это выражается условием

(2.5)

$B = \frac{{AC(x_{0}^{2} + z_{0}^{2})}}{{Ax_{0}^{2} + Cz_{0}^{2}}} + b$

при достаточно малых отличных от нуля вещественных величинах b. Здесь предварительно не оговаривается знак b.

3. Необходимые условия устойчивости. Получаемые достаточные условия следует в дальнейшем сопоставлять с необходимыми условиями устойчивости стационарного движения (2.4). Для этого введем отклонения:

$\begin{gathered} {{x}_{1}} = {\text{p}} - {{{\text{p}}}_{0}},\quad {{x}_{2}} = {\text{q,}}\quad {{x}_{3}} = {\text{r}} - {{{\text{r}}}_{{\text{0}}}} \\ {{x}_{4}} = {{{{\gamma }}}_{{\text{1}}}} - {{{{\gamma }}}_{{{\text{10}}}}},\quad {{x}_{5}} = {{{{\gamma }}}_{2}},\quad {{x}_{6}} = {{{{\gamma }}}_{3}} - {{{{\gamma }}}_{{30}}} \\ \end{gathered} $

Матрица линейной правой части системы обыкновенных дифференциальных уравнений возмущенного движения будет следующей

$D = \left( {\begin{array}{*{20}{c}} {\text{0}}&{\frac{{{\text{(B}} - {\text{C)}}{{{\text{r}}}_{{\text{0}}}}}}{{\text{A}}}}&{\text{0}}&{\text{0}}&{\frac{{{{{\text{z}}}_{{\text{0}}}}}}{{\text{A}}}}&{\text{0}} \\ {\frac{{{\text{(C}} - {\text{A)}}{{{\text{r}}}_{{\text{0}}}}}}{{\text{B}}}}&{\text{0}}&{\frac{{{\text{(C}} - {\text{A)}}{{{\text{p}}}_{{\text{0}}}}}}{{\text{B}}}}&{\frac{{ - {{{\text{z}}}_{{\text{0}}}}}}{{\text{B}}}}&{\text{0}}&{\frac{{{{{\text{x}}}_{{\text{0}}}}}}{{\text{B}}}} \\ {\text{0}}&{\frac{{{\text{(A}} - {\text{B)}}{{{\text{p}}}_{{\text{0}}}}}}{{\text{C}}}}&{\text{0}}&{\text{0}}&{\frac{{ - {{{\text{x}}}_{{\text{0}}}}}}{{\text{C}}}}&{\text{0}} \\ {\text{0}}&{ - {{{{\gamma }}}_{{{\text{30}}}}}}&{\text{0}}&{\text{0}}&{{{{\text{r}}}_{{\text{0}}}}}&{\text{0}} \\ {{{{{\gamma }}}_{{{\text{30}}}}}}&{\text{0}}&{ - {{{{\gamma }}}_{{{\text{10}}}}}}&{ - {{{\text{r}}}_{{\text{0}}}}}&{\text{0}}&{{{{\text{p}}}_{{\text{0}}}}} \\ {\text{0}}&{{{{{\gamma }}}_{{{\text{10}}}}}}&{\text{0}}&{\text{0}}&{ - {{{\text{p}}}_{{\text{0}}}}}&{\text{0}} \end{array}} \right)$

Получение необходимых условий устойчивости опирается на характеристическое уравнение матрицы ${{D}_{1}}$ [12–15], которое имеет вид

(3.1)

${{f}_{1}}({{\lambda }}) = {{{{\lambda }}}^{4}} + {{a}_{4}}{{{{\lambda }}}^{2}} + {{a}_{2}}$

где

${{a}_{4}} = \frac{{{{F}_{4}}}}{{ABC(A - C){{x}_{0}}{{z}_{0}}\sqrt {{{A}^{2}}x_{0}^{2} + {{C}^{2}}z_{0}^{2}} }},\quad {{a}_{2}} = \frac{{{{F}_{2}}}}{{{{A}^{2}}B{{C}^{2}}(A - C)x_{0}^{2}z_{0}^{2}({{A}^{2}}x_{0}^{2} + {{C}^{2}}z_{0}^{2})}}$

$\begin{gathered} {{F}_{4}} = {{A}^{2}}\left[ {AB + (A - C)(B - C)} \right]x_{0}^{4} + AC\left[ {B + 2(A - C)} \right]x_{0}^{2}z_{0}^{2} + \\ + \;{{C}^{2}}\left[ {BC + (A - C)(A - B)} \right]z_{0}^{4} \\ \end{gathered} $

${{F}_{2}} = (Ax_{0}^{2} + Cz_{0}^{2})[A(B - C)x_{0}^{2} - C(A - B)z_{0}^{2}]\varphi (A,C,{{x}_{0}},{{z}_{0}})$

$\varphi (A,C,{{x}_{0}},{{z}_{0}}) = {{A}^{3}}x_{0}^{4} - 4AC(A - C)x_{0}^{2}z_{0}^{2} - {{C}^{3}}z_{0}^{4}$

Вычисления определителей матриц, подстановки, замены переменных и факторизация символьных выражений были проведены на персональном компьютере системой аналитических вычислений “Mathematica”.

Многочлены F₄, F₂ выделены отдельно, чтобы освободиться от выражений с знаменателями.

Нельзя исключать из анализа нулевые корни уравнения (3.1). Вместе с тем из вида матрицы D₁ не допускается возможность возникновения всех нулевых корней уравнения (3.1). Тогда для отсутствия отличных от нуля вещественных корней уравнения ${{f}_{1}}(\lambda ) = 0$ необходимо и достаточно выполнения одного из условий:

(3.2)

${\text{I}}{\text{.}}\quad {{a}_{2}} > 0,\quad {{a}_{4}} > 0$

(3.3)

${\text{II}}.\quad {{a}_{2}} > 0,\quad {{a}_{4}} \leqslant 0,\quad a_{4}^{2} < 4{{a}_{2}}$

(3.4)

${\text{III}}{\text{.}}\quad {{a}_{2}} > 0,\quad {{a}_{4}} = 0$

Отдельно для существования дополнительных нулевых корней вводится случай

(3.5)

${\text{IV}}.\quad {{a}_{2}} = 0;\quad {{a}_{4}} > 0$

Проверка перечисленных условий осуществляется вычислением знаков выражений ${{F}_{2}}$, ${{F}_{4}}$.

При подстановке (2.5) в выражения ${{F}_{2}}$, ${{F}_{2}}$, $a_{4}^{2} - 4{{a}_{2}}$ запишем

$\begin{gathered} {{F}_{4}} = b{{a}_{{41}}} + {{a}_{{40}}},\quad {{F}_{2}} = b(Ax_{0}^{2} + Cz_{0}^{2})\varphi (A,C,{{x}_{0}},{{z}_{0}}) \\ a_{4}^{2} - 4{{a}_{2}} = \frac{{{{a}_{{02}}}{{b}^{2}} + {{a}_{{01}}}b + {{a}_{{00}}}}}{{A{{B}^{2}}C(Ax_{0}^{2} + Cz_{0}^{2})x_{0}^{2}z_{0}^{2}}} \\ \end{gathered} $

где

${{a}_{{41}}} = (Ax_{0}^{2} + Cz_{0}^{2})[A(2A - C)x_{0}^{2} - C(A - 2C)z_{0}^{2}]$

${{a}_{{40}}} = AC[{{A}^{2}}x_{0}^{4} + 2({{A}^{2}} - AC + {{C}^{2}})x_{0}^{2}z_{0}^{2} + {{C}^{2}}z_{0}^{4}] > 0$

${{a}_{{02}}} = (Ax_{0}^{2} + Cz_{0}^{2})\,\,[AC\,{{(x_{0}^{2} + z_{0}^{2})}^{2}} - 12\,{{(A - C)}^{2}}\,x_{0}^{2}z_{0}^{2}]$${{a}_{{01}}} = 2{{(Ax_{0}^{2} + Cz_{0}^{2})}^{2}}[{{A}^{2}}Cx_{0}^{4} + (A + C)( - 6{{A}^{2}} + 13AC + A{{C}^{2}})x_{0}^{2} + A{{C}^{2}}z_{0}^{4}]$

${{a}_{{00}}} = AC[{{(Ax_{0}^{2} + Cz_{0}^{2})}^{4}} - 12{{(A - C)}^{2}}({{A}^{2}}x_{0}^{2} + {{C}^{2}}z_{0}^{2})(x_{0}^{2} + z_{0}^{2})x_{0}^{2}z_{0}^{2}]$

Кроме того запишем необходимые условия существования твердого тела [1]:

$A + B > C,\quad A + C > B,\quad B + C > A$

Здесь первое неравенство выполняется тождественно ввиду $A > C$. Из второго неравенства следует ограничение

(3.6)

$b < \frac{{{{A}^{2}}x_{0}^{2} + {{C}^{2}}z_{0}^{2}}}{{Ax_{0}^{2} + Cz_{0}^{2}}}$

Последнее неравенство сводится к

(3.7)

$b > \frac{{A(A - 2C)x_{0}^{2} - {{C}^{2}}z_{0}^{2}}}{{Ax_{0}^{2} + Cz_{0}^{2}}}$

Очевидно, в правой части (3.7) возможен любой знак выражения.

4. Достаточные условия устойчивости. Наиболее эффективным способом получения достаточных условий устойчивости является второй метод Лянунова [12]. Построение знакоопределенных функций Ляпунова будем выполнять методом Четаева [13] – составлением связок из первых интегралов возмущенного движения.

Общие интегралы возмущенного движения запишутся:

${{V}_{{01}}} = Ax_{1}^{2} + Bx_{2}^{2} + Cx_{3}^{2} + 2(A{{p}_{0}}{{x}_{1}} + C{{r}_{0}}{{x}_{3}} + {{x}_{0}}{{x}_{4}} + {{z}_{0}}{{x}_{6}}) = {\text{const}}$

${{V}_{{11}}} = A{{x}_{1}}{{x}_{4}} + B{{x}_{2}}{{x}_{5}} + C{{x}_{3}}{{x}_{6}} + A{\text{(}}{{{{\gamma }}}_{{10}}}{{x}_{1}} + {{p}_{0}}{{x}_{4}}) + C({{{{\gamma }}}_{{30}}}{{x}_{3}} + {{r}_{0}}{{x}_{6}}) = {\text{const}}$

${{V}_{{21}}} = x_{4}^{2} + x_{5}^{2} + x_{6}^{2} + 2({{{{\gamma }}}_{{10}}}{{x}_{4}} + {{{{\gamma }}}_{{30}}}{{x}_{6}}) = 0$

Равенство Аппельрота и частный интеграл Гесса здесь могут не выполняться, и поэтому не учитываются. При анализе связки интегралов значительно проще и эффективнее предварительное исключение интегралов с фиксированными константами (в данном случае интеграл Пуассона). Для этого из интеграла ${{V}_{{21}}} = 0$ запишем решение

${{x}_{6}} = - {{{{\gamma }}}_{{30}}} + {{{{\gamma }}}_{{30}}}\sqrt {1 - \frac{{(x_{4}^{2} + x_{5}^{2} + 2{{{{\gamma }}}_{{10}}}{{x}_{4}})}}{{{{\gamma }}_{{30}}^{2}}}} $

Для анализа многочленов нужно освободиться от иррациональности разложением подкоренного выражения в ряд Маклорена

${{x}_{6}} = - {{{{\gamma }}}_{{30}}}\left( {\frac{k}{2} + \frac{{{{k}^{2}}}}{8} + \frac{{{{k}^{3}}}}{{16}} + \cdots } \right),\quad k = \frac{{(x_{4}^{2} + x_{5}^{2} + 2{{{{\gamma }}}_{{10}}}{{x}_{4}})}}{{{{\gamma }}_{{30}}^{2}}}$

Из оставшихся интегралов с подставленной переменной ${{x}_{6}}$ составим связку

(4.1)

$K(x,\alpha ) = {{{{\alpha }}}_{0}}{{V}_{{01}}} + {{{{\alpha }}}_{1}}{{V}_{{11}}}$

Чтобы не вводить дробные множители полагаем

${{{{\alpha }}}_{0}} = \sqrt {AC(A - C){{x}_{0}}{{z}_{0}}} ;\quad {{{{\alpha }}}_{1}} = 2\sqrt {Ax_{0}^{2} + Cz_{0}^{2}} \sqrt[4]{{{{A}^{2}}x_{0}^{2} + {{C}^{2}}z_{0}^{2}}}$

Квадратичная часть составленной связки интегралов будет представлена квадратичной формой от оставшихся пяти переменных ${{K}^{{(2)}}}(x) = x{\text{'}}Mx$, $x \in {{R}^{5}}$ с матрицей

$M = \left( {\begin{array}{*{20}{c}} {{{m}_{{11}}}}&0&0&{{{m}_{{14}}}}&0 \\ 0&{{{m}_{{22}}}}&0&0&{{{m}_{{25}}}} \\ 0&0&{{{m}_{{33}}}}&{{{m}_{{34}}}}&0 \\ {{{m}_{{14}}}}&0&{{{m}_{{34}}}}&{{{m}_{{44}}}}&0 \\ 0&{{{m}_{{25}}}}&0&0&{{{m}_{{55}}}} \end{array}} \right)$

где

${{m}_{{11}}} = \sqrt {{{A}^{3}}C(A - C){{x}_{0}}{{z}_{0}}} ,\,\,\,\,{{m}_{{14}}} = A\sqrt {Ax_{0}^{2} + Cz_{0}^{2}} \sqrt[4]{{{{A}^{2}}x_{0}^{2} + {{C}^{2}}z_{0}^{2}}}$

${{m}_{{22}}} = B\sqrt {AC(A - C){{x}_{0}}{{z}_{0}}} ,\quad {{m}_{{25}}} = B\sqrt {Ax_{0}^{2} + Cz_{0}^{2}} \sqrt[4]{{{{A}^{2}}x_{0}^{2} + {{C}^{2}}z_{0}^{2}}}$

${{m}_{{33}}} = \sqrt {A{{C}^{3}}(A - C){{x}_{0}}{{z}_{0}}} ,\quad {{m}_{{34}}} = \frac{{{{C}^{2}}z}}{{A{{x}_{0}}}}\sqrt {Ax_{0}^{2} + Cz_{0}^{2}} \sqrt[4]{{{{A}^{2}}x_{0}^{2} + {{C}^{2}}z_{0}^{2}}}$

${{m}_{{44}}} = (x_{0}^{2} + z_{0}^{2})\sqrt {\frac{{C(Ax_{0}^{2} + Cz_{0}^{2})}}{{{{A}^{3}}(A - C)x_{0}^{5}{{z}_{0}}}}} ,\quad {{m}_{{55}}} = (x_{0}^{2} + z_{0}^{2})\sqrt {\frac{{AC(Ax_{0}^{2} + Cz_{0}^{2})}}{{(A - C){{x}_{0}}{{z}_{0}}}}} $

На главной диагонали матрицы M находятся только положительные элементы. Согласно [17] по критерию Сильвестра для положительной определенности K⁽²⁾(x) необходимо и достаточно положительности всех главных миноров матрицы M. Для краткости обозначим их как $J({{i}_{1}},{{i}_{2}},\; \cdots ,\;{{i}_{s}})$, состоящие из ${{i}_{1}},{{i}_{2}}, \cdots ,{{i}_{s}}$, ($s \geqslant 1$) строк и столбцов. Тогда для миноров матрицы M можно составить тождества: $J(1,2,3,4) = {{m}_{{22}}}J(1,3,4)$, $J(1,2,3,4,5)$ = $J(1,3,4)J(2,5)$.

Проведенные вычисления получают:

$J(1) = {{m}_{{11}}} > 0,\quad J(1,2) = {{m}_{{11}}}{{m}_{{22}}} > 0,\quad J(1,2,3) = {{m}_{{11}}}{{m}_{{22}}}{{m}_{{33}}} > 0$

$J(1,\;3,\;4) = - \sqrt {\frac{{{{C}^{3}}{{{(A - C)}}^{3}}({{A}^{2}}x_{0}^{2} + {{C}^{2}}z_{0}^{2}){{z}_{0}}}}{{Ax_{0}^{3}}}} ({{A}^{3}}x_{0}^{4} - {{C}^{3}}z_{0}^{4})$

$J(2,\;5) = B\sqrt {{{A}^{2}}x_{0}^{2} + {{C}^{2}}z_{0}^{2}} [AC(x_{0}^{2} + z_{0}^{2}) - B(Ax_{0}^{2} + Cz_{0}^{2})]$

Окончательно для положительной определенности ${{K}^{{(2)}}}(x)$ необходимо и достаточно положительности $J(1,\;3,\;4) > 0$, $J(2,\;5) > 0$, что выражается:

(4.2)

$B < \frac{{AC(x_{0}^{2} + z_{0}^{2})}}{{Ax_{0}^{2} + Cz_{0}^{2}}}$

(4.3)

${{A}^{3}}x_{0}^{4} < {{C}^{3}}z_{0}^{4}$

Таким образом, при условиях (4.2), (4.3) и $b < 0$ перманентное вращение (2.4) устойчиво по теореме Ляпунова об устойчивости [12].

Легко показать, что при выполнении (4.2), (4.3) и $b < 0$ имеет место ${{a}_{2}} > 0$, ${{a}_{4}} > 0$. Действительно, для значений ${{A}^{3}}x_{0}^{4} < {{C}^{3}}z_{0}^{4}$ запишем $\varphi (A,C,{{x}_{0}},{{z}_{0}}) = ({{A}^{3}}x_{0}^{4} - {{C}^{3}}z_{0}^{4})$ – $4AC(A - C)x_{0}^{2}z_{0}^{2}$, и полученное выражение будет отрицательным как сумма двух отрицательных величин. Для значений $z_{0}^{2} > \sqrt {{{A}^{3}}{\text{/}}{{C}^{3}}} x_{0}^{2}$ имеет место F₄ > A{B[A² + C² + + ${{(A - C)}^{2}} + (A - C)\sqrt {AC} ]$ + ${{(A - C)}^{2}}\sqrt {AC} \} x_{0}^{4} > 0$ как сумма всех положительных слагаемых. Можно отметить, условия (4.2) и (4.3) при b < 0 относятся к ситуации (3.2).

5. О необходимых условиях устойчивости для $b > 0$. Установленные ранее достаточные условия устойчивости перманентного вращения (2.4) получены на основе второго метода Ляпунова только для значений b < 0. Возможно достаточные условия устойчивости при $b > 0$ тоже существуют. Только их искать следует другим способом, в частности, используя известные теоремы Г.В. Каменкова [14, 15]. Предварительно следует проверить возможность существования необходимых условий устойчивости. Из неравенств (3.6), (3.7) составим:

$\max \left[ {0;\frac{{A(A - 2C)x_{0}^{2} - {{C}^{2}}z_{0}^{2}}}{{Ax_{0}^{2} + Cz_{0}^{2}}}} \right] < b < \frac{{{{A}^{2}}x_{0}^{2} + {{C}^{2}}z_{0}^{2}}}{{Ax_{0}^{2} + Cz_{0}^{2}}}$

${{A}^{3}}x_{0}^{4} - 4AC(A - C)x_{0}^{2}z_{0}^{2} - {{C}^{3}}z_{0}^{4} > 0$

относящиеся к необходимым условиям существования твердого тела. Легко показать, что тогда будет обеспечено выполнение ${{F}_{2}} > 0$, что эквивалентно ${{a}_{2}} > 0$. Далее при имеющихся здесь ограничениях $x_{0}^{2} > \frac{C}{{{{A}^{2}}}}[2(A - C) + \sqrt {4{{A}^{2}} - 7AC + 4{{C}^{2}}} ]z_{0}^{2}$ установим знак коэффициента a₄₁ > $\frac{{C(Ax_{0}^{2} + Cz_{0}^{2})}}{A}[3{{A}^{2}}$ – 4AC + 2C² + $(2A - C)\sqrt {4{{A}^{2}} - 7AC + 4{{C}^{2}}} ]z_{0}^{4}$. Как легко видеть, он получен положительным как сумма положительно определенной квадратичной формы рациональной части выражения и положительного иррационального слагаемого в квадратной скобке. Так как функция ${{F}_{4}}$ по переменной $b$ возрастает и ${{a}_{{40}}} > 0$, то при положительных $b$ и условиях (3.6), (3.7) многочлен ${{F}_{4}}$ всюду принимает положительные значения, соответственно, ${{a}_{4}} > 0$.

Вместе с тем рассмотрим знак выражения ${{F}_{4}}$ при $\varphi (A,C,{{x}_{0}},{{z}_{0}}) = 0$. Из последнего равенства выразим $x_{0}^{2} = \frac{C}{{{{A}^{2}}}}[2(A - C) + \sqrt {4{{A}^{2}} - 7AC + 4{{C}^{2}}} ]z_{0}^{2}$ и подставим в ${{F}_{4}}$, которое примет вид

(5.1)

$\begin{gathered} \frac{{{{C}^{2}}}}{{{{A}^{2}}}}\{ B[(A - C)(17{{A}^{2}} - 23AC + 10{{C}^{2}}) + 2{{C}^{3}} + \\ + \;(A - C)(9A - 4C)\sqrt {4{{A}^{2}} - 7AC + 4{{C}^{2}}} ] + \\ + \;{{(A - C)}^{2}}[(5{{A}^{2}} - 11AC + 8{{C}^{2}}) + 2(A - 2C)\sqrt {4{{A}^{2}} - 7AC + 4{{C}^{2}}} ]\} z_{0}^{4} \\ \end{gathered} $

Для рассматриваемых соотношений моментов инерции $A > C$ коэффициент при величине B положительный как сумма трех положительных слагаемых: положительно определенной квадратичной формы рациональной части, положительного слагаемого и положительной иррациональной части. Первое слагаемое в последней квадратной скобке представляет положительно определенную квадратичную форму рациональной части. Иррациональная часть содержит знакопеременное выражение при $A > C$. Можно проверить, что (5A² – 11AC + 8C²)² – 4(A – 2C)²$(4{{A}^{2}} - 7AC + 4{{C}^{2}})$ = 9A²(A – C)² > 0. Тогда выражение во второй квадратной скобке (5.1) принимает знак рациональной части, т.е. положительно.

Таким образом, в этом случае имеем ${{F}_{4}} > 0$, откуда следует ${{a}_{4}} > 0$.

Следовательно, при $b > 0$ возможны только случаи (3.2) и (3.5) необходимых условий устойчивости.

Обращение в нуль выражения (5.1) возможно только при ${{z}_{0}} = 0$, из чего непосредственно следует ${{x}_{0}} = 0$, что не допустимо для стационарного движения (2.4).

Установление достаточных условий устойчивости описанным в [14, 15] способом для символьных выражений оказалось невозможным ввиду недостатка имеющихся вычислительных ресурсов (оперативной памяти и быстродействия), и их исследование здесь не проведено. Осуществление в символьном виде линейного ортогонального, затем нелинейного нормализующего преобразований переменных, классификация элементарных делителей матрицы ${{D}_{1}}$ и последующий анализ подсистемы с критическими переменными представляется неразрешимой задачей, даже в настоящее время. В численном виде такая задача решается без затруднений.

6. Заключение. Составленные в статье достаточные условия устойчивости перманентного вращения (2.4) установлены только для отрицательных отклонений $\left( {B - \frac{{AC(x_{0}^{2} + z_{0}^{2})}}{{Ax_{0}^{2} + Cz_{0}^{2}}}} \right)$. Эти условия относятся к случаю существования наименьшего числа нулевых корней характеристического уравнения для линейной правой части системы дифференциальных уравнений возмущенного движения (2.1), когда ${{a}_{2}} > 0$, ${{a}_{4}} > 0$. Ввиду $AC(A - C)x_{0}^{2}z_{0}^{2} \ne 0$ достаточные условия устойчивости яляются только частью необходимых, не достигая границы области устойчивости, устанавливаемой необходимыми условиями.

Для положительных отклонений $\left( {B - \frac{{AC(x_{0}^{2} + z_{0}^{2})}}{{Ax_{0}^{2} + Cz_{0}^{2}}}} \right)$, хотя и не удалось получить достаточные условия устойчивости (2.5), составлены только необходимые условия, возможные при ${{a}_{2}} \geqslant 0$, ${{a}_{4}} > 0$. Случаи существования необходимых условий устойчивости (3.3) и (3.4) здесь оказались не существующими.

Подробное изложение выкладок показало, что устойчивость перманентного вращения (2.4) существует как при положительных, так и отрицательных значениях ${{x}_{0}}$, ${{z}_{0}}$.

Следует отметить, что устойчивость перманентного вращения (2.4) при несуществовании частного интеграла Гесса системы (2.1) достигается на членах второго порядка.

Работа выполнена при поддержке РФФИ (проект № 19-08-00746).

Список литературы

Аппель П. Теоретическая механика. Т. 2. М.: ГИФМЛ, 1960. 487 с.
Голубев В.В. Лекции по интегрированию уравнений движения тяжелого твердого тела около неподвижной точки. М.: Регулярная и хаотическая динамика, 2002. 287 с.
Routh E.J. A treatise on the stability of a given state of motion, particulary steadly motion. L.: McMillan, 1877. 108 p.
Routh E.J. The advanced part of a treatiseon the dynamics of a system of rigid bodies. L.: McMillan, 1884. 343 p.
Ляпунов А.М. О постоянных винтовых движениях твердого тела в жидкости // Собрание сочинений. Т. 1. М.: Изд -во АН СССР, 1954. С. 276–319.
Кузьмин П.А. Стационарные движения твердого тела и их устойчивость в центральном поле тяготения // Труды межвузовской конференции по прикладной теории устойчивости движений и аналитической механике. Казань, 1964. С. 93–98.
Иртегов В.Д. Стационарные движения уравновешенного твердого тела и их устойчивость в центральном поле сил тяготения // Труды казанского авиационного института. Казань, 1964. Вып. 83. С. 3–15.
Карапетян А.В., Румянцев В.В. Устойчивость консервативных и дисспативных систем // Итоги науки и техники. Общая механика. Т. 6. М.: ВИНИТИ, 1983. С. 1–132.
Карапетян А.В., Рубановский В.Н. Об устойчивости консервативных и дисспативных механических систем // Прикладная математика и механика. 1986. Т. 50. Вып. 1. С. 43–49.
Карапетян А.В., Рубановский В.Н. О модификации теоремы Рауса об устойчивости стационарных движений систем с первыми интегралами // Сборник научно-методических статей по теоретической механике. М.: Высшая школа, 1986. Вып. 17. С. 91–99.
Карапетян А.В. Устойчивость стационарных движений. М.: Эдиториал, 1998. 165 с.
Ляпунов А.М. Общая задача об устойчивости движения // Собрание сочинений. Т. 2. М.-Л.: Изд-во АН СССР, 1956. С. 7–263.
Четаев Н.Г. Устойчивость движения. Работы по аналитической механике. М.: Изд-во АН СССР, 1962. 535 с.
Каменков Г.В. Устойчивость движения, колебания, аэродинамика.Т. 1. М.: Наука, 1971. 255 с.
Каменков Г.В. Устойчивость и колебания нелинейных систем. Т. 2. М.: Наука, 1972. 213 с.
Новиков М.А. О стационарных движениях твердого тела при существовании частного интеграла Гесса // Известия РАН. Механика твердого тела. 2018. № 3. С. 28–37.
Гантмахер Ф.Р. Теория матриц. М.: Наука, 1967. 576 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал