Известия РАН. Механика твердого тела, 2021, № 6, стр. 33-44
СЕЙСМИЧЕСКИЕ БАРЬЕРЫ ДЛЯ ЗАЩИТЫ ОТ ПОВЕРХНОСТНЫХ И ГОЛОВНЫХ ВОЛН: МНОЖЕСТВЕННЫЕ РАССЕИВАТЕЛИ И МЕТАМАТЕРИАЛЫ
Н. Ф. Морозов a, b, В. А. Братов a, b, c, *, С. В. Кузнецов d, e, f
a Институт проблем машиноведения РАН
Санкт Петербург, Россия
b СПб государственный университет
Санкт Петербург, Россия
c СПб политехнический университет Петра Великого
Санкт Петербург, Россия
d Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия
e Московский государственный технический университет им. Баумана
Москва, Россия
f Московский государственный строительный университет
Москва, Россия
* E-mail: vladimir@bratov.com
Поступила в редакцию 11.03.2021
После доработки 18.03.2021
Принята к публикации 29.03.2021
Аннотация
Рассматриваются перспективные виды сейсмических барьеров, применяемых для защиты зданий и сооружений от воздействия поверхностных акустических волн Рэлея, Рэлея–Лэмба, Лява, а так же головных SP-волн. Барьеры построены на основе множественных рассеивающих элементов и метаматериалов. Приводится сравнение с традиционными типами гомогенных сейсмических барьеров, выполненных из упругих конструкционных материалов.
1. Введение. Сейсмические барьеры предназначены для защиты зданий и сооружений от сейсмических поверхностных волн различной этиологии, включая волны Рэлея, волны Рэлея–Лэмба (волны, распространяющиеся в слоистом полупространстве), волны Лява, а так же головные SP-волны. Последние представляют собой весьма опасный тип сейсмических волн, возникающих при короткофокусных землетрясениях и подземных взрывах [1–5]. В настоящей работе рассматриваются вертикальные сейсмические барьеры имеющие в своем составе как специальные рассеивающие элементы, так и метаматериалы, обладающие повышенной диссипацией волновой энергии.
Ниже дается обзор основных типов сейсмических волн, для защиты от которых требуются вертикальные сейсмические барьеры.
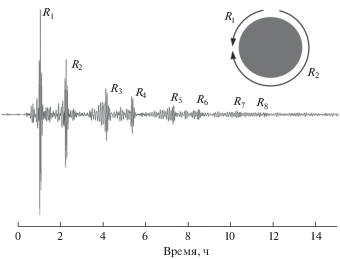
1.1. Рэлеевские волны. Рэлеевские волны являются наиболее распространенным и хорошо изученным типом поверхностных волн, возникающих в гомогенном упругом полупространстве. Эти волны характеризуются (i) скоростью распространения, независящей от частоты (отсутствие дисперсии); (ii) экспоненциальным затуханием амплитуд перемещений по глубине и локализацией энергии волны в относительно узком поверхностном слое, что позволяет этим волнам распространяться на значительно большие расстояния, по сравнению с объемными волнами [6, 7]; и (iii) соотношением между компонентами перемещений, при котором вертикальная компонента волны примерно в полтора раза больше горизонтальной [7]. Последнее обстоятельство делает этот тип волн особенно опасными для протяженных сооружений. Особенности, связанные с локализацией энергии этих волн в приповерхностном слое земной коры, приводят к тому, что рэлеевские волны могут огибать земной шар несколько раз, см. рис. 1, где приведена сейсмограмма прихода рэлеевских волн, обогнувших восемь раз земной шар [8].
Рис. 1.
Сейсмограмма прихода рэлеевской волны на станцию CMB, Berkeley Digital Seismic Network (BDSN), время наблюдения ∼14 ч [8]
В недавнем прошлом модель гомогенного полупространства широко применялась для исследования волновых процессов при землетрясениях и подземных взрывах; см. [9], где отмечается, что рэлеевские волны могут возникать и при глубокофокусных землетрясениях. Кроме того, эти волны генерируются движущимся рельсовым и автомобильным транспортом [10, 11]. В настоящее время в геофизических и геотехнических приложениях модель гомогенного полупространства заменяют на модели слоистых или функционально градиентных полупространств, в которых рассматривают распространение дисперсионных волн Рэлея–Лэмба [12].
1.2. Волны Рэлея–Лэмба. Следующий тип сейсмических волн – волны Рэлея–Лэмба, распространяющиеся в слоистом полупространстве. Отличительной чертой таких волн является дисперсия, т.е. зависимость скорости от частоты, если рассматриваются гармонические волны Рэлея–Лэмба, рис. 2.
Рис. 2.
Дисперсионные кривые для волн Рэлея–Лэмба в многослойном полупространстве: горизонтальная ось – фазовая скорость; вертикальная ось – круговая частота
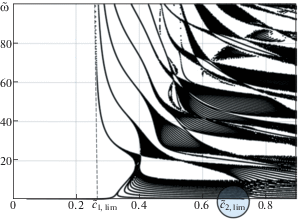
Несмотря на весьма сложную дисперсионную картину, приведенную на рис. 2, с точки зрения сейсмических воздействий на сооружения от землетрясений, значительный интерес представляет так называемая вторая предельная фазовая скорость, определяемая, как соответствующий предел
где c-фазовая скорость, а $\omega $ – круговая частота. В слоистых системах для определения скорости ${{с}_{{2,\lim }}}$ применяют либо различные низкочастотные асимптотические методы [13–15], либо используют непосредственное вычисление по предельной формуле (1.1).1.3. Волны Лява. Также, как и волны Рэлея–Лэмба, волны Лява представляют собой дисперсионные волны, распространяющиеся в системе упругое полупространство и контактирующий с ним упругий слой (или несколько слоев). Волны Лява имеют горизонтальную поперечную поляризацию и экспоненциально затухают с глубиной.
С точки зрения сейсмологии, волны Лява в основном представляют интерес в связи с микросейсмами малой амплитуды, генерируемыми волнами в океане [19, 20]. В то же время, при сильных землетрясениях амплитуды волн Лява не достигают значений, характерных для объемных S-волн и волн Рэлея–Лэмба [21, 22]. Тем не менее, вертикальные сейсмические барьеры могут применяться и для защиты от волн Лява [23, 24].
1.4. Головные SP-волны. Головные SP-волны распространяются параллельно свободной поверхности полупространства со скоростью P-волны, и возникают на некотором расстоянии ${{d}_{{ST}}}$ от эпицентра короткофокусного землетрясения или подземного взрыва, рис. 3. Это расстояние зависит от глубины источника h и физических свойств среды [25–27], причем
(1.2)
${{d}_{{ST}}} = h \cdot {\text{tg}}\left( {\arcsin \left( {\frac{{{{c}_{S}}}}{{{{c}_{P}}}}} \right)} \right)$Рис. 3.
Схемы возникновения головных волн: а) полупространство; b) часть сферической поверхности; S1 и S2 – поперечные волны, расходящиеся от гипоцентра землетрясения или подземного взрыва, SP2 – (истинная) головная волна; на рис. 2,б волна SP1 – квазиголовная
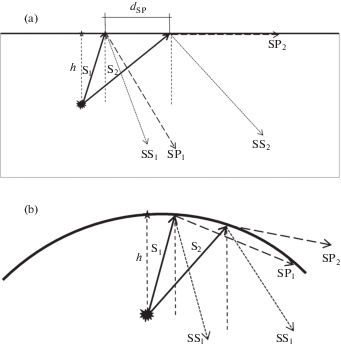
На рис. 3 волна S1 падает на свободную поверхность, образуя отраженные волны: перечную (SS1) и продольную (SP1), аналогичным образом, волна S2 падает на свободную поверхность, образуя отраженные волны (SS2) и продольную (SP2), последняя движется параллельно свободной поверхности, образуя головную волну. Угол, под которым падает волна S2, называется критическим углом, он определяется следующим выражением [27]:
Поскольку головные или квазиголовные волны могут переносить значительную энергию, приводящую к катастрофическим разрушениям [1, 2], для защиты от этих волн требуются вертикальные сейсмические барьеры, аналогичные применяемым для защиты от волн Рэлея–Лэмба.
1.5. Частотные диапазоны. Для проектирования систем сейсмической защиты от рассматриваемых типов сейсмических волн, необходимы примерные оценки частотного диапазона, в котором локализована значительная доля сейсмической энергии.
По оценкам [28–31]в случае землетрясений естественной природы наиболее опасными для большинства зданий и сооружений, включая объекты атомной энергетики, являются частоты 2÷33 Гц с энергетическими пиками в районе 5÷7 Гц и 30÷33 Гц, рис. 4.
Рис. 4.
Амплитудный спектр Фурье (FAS), станция Gebze-Arçelik, афтершок землетрясения Düzce (Турция) 11.11.1999 г. [29]
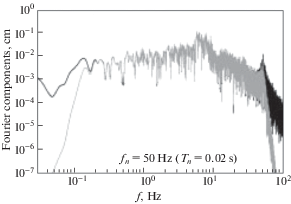
Землетрясения искусственного происхождения, вызванные подземными взрывами, отличаются, как правило, более высокими частотами [32, 33]. Например, по данным [32] на близких расстояниях от эпицентра регистрируются частоты вплоть до 250 Гц, ограниченные разрешающей способностью акселерометров, с увеличением расстояния, высокие частоты затухают, отдельные всплески обнаруживаются на частотах до 40 Гц, а максимум амплитуд регистрируется на частоте ∼25 Гц.
1.6. Скорости распространения сейсмических волн в верхних отделах земной коры. Для выбора геометрических и физических параметров сейсмических барьеров помимо частоты сейсмических волн требуется знание скоростей распространения объемных и рэлеевских волн. По многочисленным экспериментальным исследованиям [34–36], скорости распространения сейсмических волн в верхних отделах земной коры имеют следующие значения, см. табл. 1.
Таблица 1.
Скорости распространения объемных волн в породах земной коры
| Породы | Скорость P-волны, м/с | Скорость S-волны, м/с |
|---|---|---|
| Флювиальные | 1400 | 200 |
| Аллювиальные | 1500 | 250 |
| Морены | 2000 | 700 |
| Корневые породы | 4000 | 2500 |
Скорость распространения рэлеевской волны может быть определена либо как корень уравнения Рэлея, либо по одной из приближенных формул [37, 38], при этом коэффициент Пуассона $\nu $ определяется по соответствующим скоростям объемных волн:
1.7. Математические модели для исследования вертикальных барьеров. Обычно для моделирования сейсмических барьеров используют либо плоские конечноэлементные модели, связанные с численным решением внешней задачи Лэмба, в которой удается получить необходимую рэлеевскую волну, рис. 5,а, [23, 39, 40]; либо рассматривают решение более сложной внутренней задачи Лэмба, в которой наряду с рэлеевской волной удается смоделировать распространение головной SP-волны, см. рис. 5,b [27].
Ввиду более высоких требований к вычислительным ресурсам, значительно реже применяют пространственные модели для решения задачи Лэмба с барьером, см. [41]. В случае, когда необходим учет упругой анизотропии полуплоскости или полупространства, для решения задач Лэмба могут применяться методы граничных интегральных уравнений с построением соответствующих фундаментальных решений [42–44].
1.8. Уравнения состояния для описания динамического деформирования гранулированных метаматериалов. Для описания поведения гранулированных метаматериалов при действии динамических нагрузок, обычно применяют уравнения бимодульной теории упругости при деформировании в упругой зоне [45–47]
(1.5)
$\sigma = {{\nabla }_{\varepsilon }}\Psi ({{I}_{\varepsilon }},I{{I}_{\varepsilon }},II{{I}_{\varepsilon }})$(1.6)
$\Psi ({{I}_{\varepsilon }},II_{\varepsilon }^{\sim }) \equiv \alpha I_{\varepsilon }^{2} + \beta II_{\varepsilon }^{\sim } + \gamma {{I}_{\varepsilon }}\sqrt {II_{\varepsilon }^{\sim }} $В случае, когда девиаторные составляющие тензора напряжений достигают поверхности пластичности, применяют уравнения пластического течения, причем наряду с моделями Мора–Кулона и Дракера–Прагера используют модели критического состояния, например кэм-клей-модели [49–51], см. также [52] по метаматериалам, обладающим свойствами фононных кристаллов. С точки зрения сейсмической защиты от рассматриваемых поверхностных волн значительный интерес представляют метаповерхности [53].
2. Расчетные модели. К сожалению, для большинства задач волновой механики отсутствует возможность получения точных аналитических решений уравнений, описывающих поведение системы. Точные аналитические решения известны только для узкого круга задач с предельно простой геометрией (см. например, [54] для практически исчерпывающего списка доступных решений). Такие решения, как правило, не применимы для анализа реальных задач, но могут применяться для валидации и оценки точности разработанных численных моделей. В большинстве случаев поставленную задачу можно решать только численно с использованием приближенных методов решения получаемых систем дифференциальных уравнений (см. напр. [55]).
С использованием численного метода будем решать задачу о взаимодействии набегающей динамической волны в упругой полуплоскости с включением, представляющим вертикальный сейсмический барьер (см. рис. 5). Будем оценивать эффективность того или иного типа сейсмических барьеров (рис. 6,b и 6,c) по уменьшению амплитуд перемещений и ускорений в точках поверхности за сейсмическим барьером по сравнению с решением аналогичной задачи для полуплоскости без сейсмического барьера (рис. 6,a).
Рис. 6.
(а) Упругое полупространство без защитного барьера, (b) упругое полупространство с защитным барьером и (c) упругое полупространство с барьером с метаструктурами

Будут рассмотрены различные комбинации упругих свойств сейсмического барьера и расположенных на барьере метаструктур и различные геометрии метаструктур.
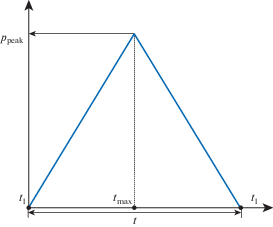
2.1 Модельная задача о распространении упругой волны в упругой полуплоскости. Поставленную задачу будем решать численно, с использованием метода конечных элементов. Решения будут получены с использованием коммерческого пакета ANSYS [57]. На первом этапе решим задачу о распространении волны в упругом полупространстве (рис 6,a). Волна возбуждается при помощи возмущения, приложенного на поверхности, на некотором расстоянии от точки, в которой будем производить измерение возникающих амплитуд перемещений и ускорений. Профиль зависимости интенсивности действующей силы от времени представлен на рис. 7.
На поверхности, на некотором расстоянии от точки приложения силы, получим зависимости перемещений и ускорений по обеим осям от времени. Для данной простой задачи решение возможно получить аналитически, вычислив свертку решения для δ‑функции по времени и пространству и силы, приложенной на поверхности (рис. 7). Такая задача обычно называется двумерной внешней задачей Лэмба и ее аналитическое решение известно (см. например, [58]). Для валидации получаемого численного решения, сравним получаемые зависимости для перемещений с вычисленными аналитически. На рис. 8 представлен получаемый временной профиль перемещения для вертикальной координаты, вычисленный численно, в сравнении с аналитическим точным решением. Как видно из представленных графиков, численное решение достаточно хорошо повторяет точное аналитическое решение. Таким образом, можно сделать вывод о применимости и достаточной точности полученного численного решения для решения исследуемого класса задач.
Рис. 8.
Временной профиль перемещения для вертикальной координаты. Сравнение численного (серая линия) и точного аналитического решения (черная линия)
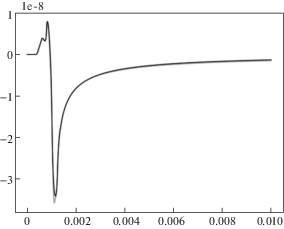
Далее, получим максимальные (по времени) амплитуды перемещений и ускорений по обоим направлениям. Далее данные величины будут использоваться для нормализации при определении защитного коэффициента различных типов барьеров и защитных метаструктур. Для использованных параметров воздействия (длительность 450 микросекунд, максимальная амплитуда 1000 Н) и свойств среды, принятых равным типичным для грунта (Модуль Юнга, E = 10 МПа, коэффициент Пуассона Nu = 0.35, плотность 2000 кг/м3) полученные максимальные значения амплитуды перемещений и ускорений по двум направлениям представлены в табл. 2.
Таблица 2.
Скорости распространения объемных волн в породах земной коры
| Максимальное значение ускорения по горизонтальной оси | 72.3 м/с2 |
| Минимальное значение ускорения по горизонтальной оси | –43.9 м/с2 |
| Максимальное значение ускорения по вертикальной оси | 110.7 м/с2 |
| Минимальное значение ускорения по вертикальной оси | –104.7 м/с2 |
| Максимальное значение перемещения по горизонтальной оси | 4.70E-07 м |
| Минимальное значение перемещения по горизонтальной оси | –1.40E-07 м |
| Максимальное значение перемещения по вертикальной оси | 1.20E-07 м |
| Минимальное значение перемещения по вертикальной оси | –7.50E-07 м |
Далее будем использовать данные амплитуды для нормализации и определения коэффициента защиты для различных типов барьеров.
Кроме того, исследуем зависимость максимальной амплитуды возникающих перемещений и ускорений от расстояния от точки приложения нагрузки. Такие оценки возможно провести как аналитически, с использованием точного решения, так и с использованием разработанной численной конечноэлементной модели. На рис. 9 представлена зависимость максимальной амплитуды возникающих горизонтальных перемещений в условиях решаемой задачи.
Рис. 9.
Зависимость максимальной амплитуды возникающих на поверхности полуплоскости горизонтальных перемещений от расстояния от точки приложения нагрузки. Сравнение численного (серая линия) и точного аналитического решения (черная линия)
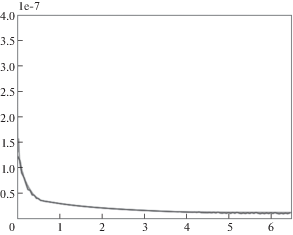
Как видно из данных представленных на рис. 9, численное решение хорошо повторяет точное аналитическое решение, что еще раз свидетельствует о применимости разработанной модели для анализа решаемого класса задач. Кроме того, полученные зависимости максимальных амплитуд перемещений и ускорений далее будут применяться для анализа так называемых “зон тени” – областей за защитными барьерами, в которых обеспечивается значительное уменьшение перемещений и ускорений, вызванных набегающими волнами сейсмической природы. Линейный размер “зоны тени”, обеспечиваемый тем или иным типом барьера, наряду с коэффициентом защиты, является одной из важнейших характеристик защитного сейсмического барьера.
Также на основе анализа зависимостей максимальных амплитуд перемещений и ускорений от расстояния от точки приложения нагрузки, можно провести оценку размеров области, вблизи точки приложения нагрузки, в которой важно влияние объемных волн.
2.2. Более жесткий и менее жесткий барьер. Далее аналогичная задача решалась для защитных сейсмических барьеров (рис. 6,b) выполненных из гораздо более жесткого (1 случай – модуль Юнга больше в 10 раз, плотность больше в 5 раз. 2 случай – модуль Юнга больше в 100 раз, плотность больше в 50 раз.) и гораздо менее жесткого (1 случай – модуль Юнга меньше в 10 раз, плотность меньше в 5 раз. 2 случай – модуль Юнга меньше в 100 раз, плотность меньше в 50 раз.) материалов. Для случая 1 типичные коэффициенты защиты барьеров (отношение максимального значения перемещения/ускорения в случае отсутствия барьера к аналогичному значению при использовании барьера) для выбранного случая составляют 1.5–3.0 для ускорений и примерно столько же для перемещений. В случае 2 типичные коэффициенты защиты барьеров для выбранного случая составляют 10–25 для ускорений и 1.5–3.0 для перемещений.
2.3. Барьеры с метаструктурами. Далее задача решалась для защитных сейсмических барьеров с интегрированными метаструктурами (рис. 6,с). Были рассмотрены различные комбинации упругих свойств барьеров и метаструктур. Кроме того, исследовано влияние количества и размера компонентов метаструктур на обеспечиваемые коэффициенты защиты.
Как показали проведенные расчеты, в некоторых случаях использование метаструктур, интегрированных в защитный сейсмический барьер позволяет значительно увеличить коэффициент защиты. В частности, для некоторых случаев (например, более мягкий (по отношению к среде) барьер с более жесткими (по отношению к среде) метаструктурами), коэффициенты снижения магнитуд могут достигать 30. Иными словами, при такой конфигурации нагрузки и защитного барьера, перемещения и ускорения в защищаемой области умещаются в 30 раз. В то же время, некоторые комбинации свойств барьера и защитных метаструктур не увеличивают коэффициент защиты по сравнению с барьером без метаструктур, либо даже немного уменьшают его. Можно сделать вывод о том, что для конкретных случаев свойств материала среды, возможных свойств и размеров защитного барьера и метаструктур необходимо проводить дополнительный анализ с целью выявления наиболее эффективных комбинаций защитного барьера для конкретного случая возможных воздействий сейсмической природы.
3. Выводы. Проведенными теоретическими и численными исследованиями установлено, что в рамках рассмотренных упругих моделей с помощью вертикальных сейсмических барьеров в виде метаструктур, удается значительно снизить магнитудные значения колебаний в защищаемой зоне, по сравнению с моногенными барьерами прямоугольной формы, причем уровень снижения колебаний в зонах тени за барьером оказывается существенно большим.
Кроме того, проведенные исследования указывают на существенное увеличение протяженности зоны тени, – это открывает перспективы применения метаструктурных сейсмических барьеров для защиты протяженных объектов, например, взлетных полос аэродромов, мостов, акведуков и т.п.
Благодарность. Работа выполнена при финансовой поддержке Российского научного фонда, грант 20-49-08002.
Список литературы
Cerveny V. Seismic Ray Theory. Cambridge: Cambridge University Press, 2001.
Smith P.D., Hetherington, J.G. Blast and Ballistic Loading of Structures. Oxford: Butterworth-Heinemann, 1994.
Nagy N., Mohamed M., Boot J.C. Nonlinear numerical modelling for the effects of surface explosions on buried reinforced concrete structures // Geomech. Eng. 2010. V. 2. P. 1–18.
Ibrahim Y.E., Nabil M. Finite element analysis of pile foundations under surface blast loads // Proceedings of the 13th International Conference on Damage Assessment of Structures. Lecture Notes in Mechanical Engineering / Ed. by Wahab M. Singapore: Springer, 2020.
Helmberger D.V., Malone S.D. Modeling local earthquakes as shear dislocations in a layered half-space // J. Geophys. Res. 1975. V. 80. P. 4881–4888.
Ben-Menahem A., Singh S.J. Seismic Waves and Sources. 2nd edition. N.Y.: Dover Publications, 2000.
Aki K., Richards P.G. Quantitative Seismology. 2nd edition. University Science Books, 2009.
Aki K. Earthquake mechanism // Tectonophys. 1972. V. 13. P. 423–446.
Kanamori H., Anderson D.L. Theoretical basis of some empirical relations in seismology // Bull. Seismol. Soc. Am. 1975. V. 65. P. 1073–1095.
Yang Y.B., Hung H.H., Chang D.W. Train-induced wave propagation in layered soils using finite/infinite element simulation // Soil Dyn. Earthquake Eng. V. 23. Iss. 4. P. 263–278.
Gunn D., Williams G., Kessler H., Thorpe S. Rayleigh wave propagation assessment for transport corridors // Proceedings of the Institution of Civil Engineers – Transport. 2015. V. 168. № 6. P. 487–498.
Kuznetsov S.V. Abnormal dispersion of flexural Lamb waves in functionally graded plates // Z. Angew. Math. Phys. 2019. V. 70. Iss. 89. P. 1–8.
Kaplunov J.D., Nolde E.V. Long-wave vibrations of a nearly incompressible isotropic plate with fixed faces // Quart. J. Mech. Appl. Math. 2002. V. 55. P. 345–356.
Zakharov D.D., Castaings M., Singh D. Numerical and asymptotic approach for evaluating complex wavenumbers of guided modes in viscoelastic plates // J. Acoust. Soc. Am. 2011. V. 130. P. 764–771.
Kuznetsov S.V. Cauchy formalism for Lamb waves in functionally graded plates // J. Vibr. Contr. 2019. V. 25. № 6. P. 1227–1232.
Mallah M., Philippe L., Khater A. Numerical computations of elastic wave propagation in anisotropic thin films deposited on substrates // Comp. Mater. Sci. 1999. V. 15. P. 411–421.
Djeran-Maigre I. et al. Solitary SH waves in two-layered traction-free plates // Comptes Rendus. Mech. 2008. V. 336. № 1–2. P. 102–107. https://doi.org/10.1016/j.crme.2007.11.001
Kuznetsov S.V. Love waves in stratified monoclinic media // Quart. Appl. Math. 2004. V. 62. P. 749–766.
Saito T. Love-wave excitation due to the interaction between a propagating ocean wave and the sea-bottom topography // Geophys. J. Int. 2010. V. 182. P. 1515–1523.
Gualtieri L., Camargo J.S., Pascale S., Pons F.M.E., Ekstrom G. The persistent signature of tropical cyclones in ambient seismic noise // Earth Planet Sci. Lett. 2018. V. 484. P. 287–294.
Ilyashenko A., Kuznetsov S. SH waves in anisotropic (monoclinic) media // Z. Angew. Math. Phys. 2018. V. 69. № 17. P. 1–8. https://doi.org/10.1007/s00033-018-0916-y
Ekstrom G., Tromp J., Larson E.W.F. Measurements and global models of surface wave propagation // J. Geophys. Res. 1997. V. 102. P. 8137–8157.
Dudchenko A.V. et al. Vertical wave barriers for vibration reduction // Arch. Appl. Mech. 2021. V. 91 P. 257–276. https://doi.org/10.1007/s00419-020-01768-2
Kuznetsov S. Seismic waves and seismic barriers // Acoust. Phys. 2011. V. 57. № 3. P. 420–426.
Kausel E., Manolis G. Wave Motion in Earthquake Engineering. Southampton, UK: WIT Press. 1999.
Angelsky O.V., Zenkova C.Y., Hanson S.G., Zheng J. Extraordinary manifestation of evanescent wave in biomedical application // Front. Phys. 2020. V. 8. P. 159. https://doi.org/10.3389/fphy.2020.00159
Kuznetsov S.V., Terentjeva E.O. Planar internal Lamb problem: Waves in the epicentral zone of a vertical power source // Acoust. Phys. 2015. V. 61. P. 356–367.
Ambraseys N.N., Douglas J., Smit P., Sarma S.K. Equations for the estimation of strong ground motions from shallow crustal earthquakes using data from Europe and the Middle East: horizontal peak ground acceleration and spectral acceleration // Bull. Earthquake Eng. 2005. V. 3. № 1. P. 1–35.
Akkar S., Kale O., Yenier E., Bommer J.J. The high-frequency limit of usable response spectral ordinates from filtered analogue and digital strong-motion accelerograms // Earthquake Eng. Struct. Dyn. 2011. V. 40. № 12. P. 1387–1401.
Takewaki I. Frequency-domain analysis of earthquake input energy to structure–pile systems // Eng. Struct. 2005. V. 27. № 4. P. 549–563.
Takewaki I. Response spectrum method for nonlinear surface ground analysis // Int. J. Adv. Struct. Eng. 2004. V. 7. № 6. P. 503–514.
Li X., Li Z., Wang E., Liang Y., Niu Y., Li Q. Spectra, energy, and fractal characteristics of blast waves // J. Geophys. Eng. 2017. V. 15. № 1. P. 81–92.
Bahadori M., Amnieh H.B., Khajezadeh A. A new geometrical-statistical algorithm for predicting two-dimensional distribution of rock fragments caused by blasting // Int. J. Rock Mech. Mining Sci. 2016. V. 86. P. 55–64.
Uyanik O. Estimation of the porosity of clay soils using seismic P- and S-wave velocities // J. Appl. Geophys. 2019. V. 170. № 103832. P. 1–8.
Recommended Provisions for Seismic Regulations for New Buildings and Other Structures. Part 1. Provisions (FEMA 450-2), 2003 Edition. Building Seismic Safety Council. Washington, D.C.: National Institute of Building Sciences, 2004.
International Handbook of Earthquake and Engineering Seismology. Part B / Ed. by Lee W.H.K., Hiroo Kanamori H., Jennings P.C., Kisslinger C.N.Y.: Academic Press, 2003.
Pham ChiVinh, Malischewsky P.G. An approach for obtaining approximate formulas for the Rayleigh wave velocity // Wave Motion. 2007. V. 44. P. 549–562.
Mozhaev V.G. Approximate analytical expressions for the velocity of Rayleigh waves in isotropic media and on the basal plane in high symmetry crystals // Sov. Phys. Acoust. 1991. V. 37. P. 186–189.
Bratov V.A. et al. Homogeneous horizontal and vertical seismic barriers: mathematical foundations and dimensional analysis // Mat. Phys. Mech. 2020. V. 44. № 1. P. 61–65. https://doi.org/10.18720/MPM.4412020_7
Kravtsov A.V. et al. Finite element models in Lamb’s problem // Mech. Solids. 2011. V. 46. P. 952–959. https://doi.org/10.3103/S002565441106015X
Pecker A. Seismic analyses and design of foundation soil structure interaction // Perspectives on European Earthquake Engineering and Seismology. Geotechnical, Geological and Earthquake Engineering / Ed. by Ansal A. V. 39. Springer, 2015.
Kausel E. Lamb’s problem at its simplest // Proc. Roy. Soc. Ser. A. London. 2012. V. 469. № RSPA-20120462. P. 1–44.
Kuznetsov S.V. Fundamental and singular solutions of Lamé equations for media with arbitrary elastic anisotropy // Quart. Appl. Math. 2005. V. 63. P. 455–467. https://doi.org/10.1090/S0033-569X-05-00969-X
Sánchez-Sesma F., Iturrarán-Viveros U. The classic Garvin’s problem revisited // Bull. Seism. Soc. Am. 2006. V. 96 (4A). P. 1344–1351.
Maslov V.P., Mosolov P.P. General theory of the solutions of the equations of motion of an elastic medium of different moduli // J. Appl. Math. Mech. 1985. V. 49. P. 322–336.
Maslov V.P., Antsiferova M.M. Shock waves in a granular medium // Phys. Earth. Planet. Inter. 1988. V. 50 № 1. P. 8–15.
Gavrilov S.N., Herman G.C. Wave propagation in a semi-infinite heteromodular elastic bar subjected to a harmonic loading // J. Sound Vibr. 2012. V. 331. № 20. P. 4464–4480.
Molinari A., Daraio Ch. Stationary shocks in periodic highly nonlinear granular chains // Phys. Rev. E 2009. V. 80. № 056602. P. 1–15.
Goldstein R.V. et al. The modified Cam-Clay (MCC) model: cyclic kinematic deviatoric loading // Arch. Appl. Mech. 2016. V. 86. P. 2021–2031. https://doi.org/10.1007/s00419-016-1169-x
Kuznetsov S.V., Maigre H. Granular metamaterials for seismic protection. Hyperelastic and hypoelastic models // J. Phys.: Conf. Ser. 2019. V. 1425. № 012184. P. 1–6. https://doi.org/10.1088/1742-6596/1425/1/012184
Nedderman R.M. Statics and Kinematics of Granular Materials. Cambridge: Cambridge Univ. Press, 2005.
Witarto W. et al. Three-dimensional periodic materials as seismic base isolator for nuclear infrastructure // AIP Advances. 2019. V. 9. № 045014. P. 1–8.
Wootton P.T., Kaplunov J., Colquitt D.J. An asymptotic hyperbolic–elliptic model for flexural-seismic metasurfaces // Proc. R. Soc. A. 2019 V. 475. P.20190079. https://doi.org/10.1098/rspa.2019.0079
Kausel E. Fundamental Solutions in Elastodynamics. Cambridge: Cambridge Univ. Press, 2005. https://doi.org/10.1017/CBO9780511546112
Bratov V. Incubation time fracture criterion for FEM simulations // Acta Mech. Sinica. 2011. V. 27. № 4. P. 541–549. https://doi.org/10.1007/s10409-011-0484-2
Kazarinov N., Bratov V., Petrov Y. Modelling dynamic propagation of a crack at quasistatic loading // Dokl. Phys. 2014. V. 59. № 2. P. 99–102. https://doi.org/10.1134/S1028335814020116
ANSYS User’s Guide, Release 2020 R1. ANSYS Inc., 2020. Pennsylvania, USA.
Eringen A.C., Suhubi E.S. Elastodynamics. V. 2. Linear Theory. New York: Academic Press, 1975.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела