1. На главную
  2. Электронные версии
  3. Известия РАН. Механика твердого тела
  4. № 1, 2022

Известия РАН. Механика твердого тела, 2022, № 1, стр. 77-88

О ДИНАМИКЕ РАЗГРУЗКИ ЦИЛИНДРИЧЕСКОГО УПРУГОВЯЗКОПЛАСТИЧЕСКОГО СЛОЯ ПРИ АЗИМУТАЛЬНОМ СДВИГЕ

А. А. Буренин a, *, Е. А. Герасименко b, **, Л. В. Ковтанюк b, ***, Г. М. Севастьянов a, ****

a Хабаровский федеральный исследовательский центр ДВО РАН
Хабаровск, Россия

b Институт автоматики и процессов управления ДВО РАН
Владивосток, Россия

* E-mail: burenin@iacp.dvo.ru
** E-mail: gerasimenko@iacp.dvo.ru
*** E-mail: lk@iacp.dvo.ru
**** E-mail: akela.86@mail.ru

Поступила в редакцию 10.03.2021
После доработки 18.04.2021
Принята к публикации 26.04.2021

Полный текст (PDF)

Аннотация

Рассмотрена задача о деформировании упруговязкопластического материала в зазоре между соосными цилиндрическими поверхностями ротационного вискозиметра. Нагружение материала происходит за счет медленного поворота внешней стенки вискозиметра, на этом этапе принимается условие прилипания материала к стенкам. При некотором критическом угле поворота происходит проскальзывание материала, которое вызывает распространение в слое ударной волны разгрузки. При распространении волны происходит ее взаимодействие с упруго-пластической границей и отражение от стенок вискозиметра. Динамика разгрузки исследуется с помощью лучевого метода построения прифронтовых разложений.

Ключевые слова: упругость, вязкопластичность, вискозиметрия, большие деформации, лучевой метод, волна разгрузки

1. Введение. Среди задач, решаемых средствами механики деформируемых тел, выделяются такие, в которых изучаются некоторые пороговые события. Такие события часто оказываются катастрофическими и вызывают разрушения в искусственных и природных структурах. Примеры подобных событий – явление бифуркации равновесных состояний, потеря устойчивости в элементах конструкций (прощелкивание оболочек) [1, 2], в горных породах [3]; образование трещин хрупкого разрушения [4], сход лавин [5] и др. Здесь рассмотрим краевую задачу теории больших упруговязкопластических деформаций о мгновенном изменении в медленном процессе вискозиметрического деформирования, которое вызвано срывом и проскальзыванием материала. Упруговязкопластическое деформирование материала в вискозиметре является, таким образом, докритическим процессом, а динамическая разгрузка, следующая за моментом срыва, процессом закритическим. При этом на обоих этапах деформированное состояние представляет собой азимутальный сдвиг. Учитывая, что обратимые и необратимые деформации, приобретенные в процессе нагружения, взаимосвязаны и не могут быть заданы произвольно, задача о динамической разгрузке требует решения также и задачи активного нагружения [6–8]. Задачи азимутального сдвига для различных моделей сред при квазистатическом и ударно-волновом деформировании имеют долгую историю и разнообразные приложения, в том числе в биомеханике [9–17].

2. Модельные соотношения упруговязкопластического материала. Для описания движения среды примем модель больших упругопластических деформаций [18, 19], в которой обратимая и необратимая составляющие полных деформаций задаются дифференциальными уравнениями их изменения (переноса). Тогда в переменных Эйлера основные кинематические соотношения имеют вид:

${\frac{{D{\mathbf{e}}}}{{Dt}} = {\mathbf{\varepsilon }} - {{{\mathbf{\varepsilon }}}^{{\mathbf{p}}}} - \frac{{\text{1}}}{{\text{2}}}(({\mathbf{\varepsilon }} - {{{\mathbf{\varepsilon }}}^{{\mathbf{p}}}} + {\mathbf{z}}) \cdot {\mathbf{e}} + {\mathbf{e}} \cdot ({\mathbf{\varepsilon }} - {{{\mathbf{\varepsilon }}}^{{\mathbf{p}}}} - {\mathbf{z}})){\text{,}}}\quad \frac{{D{\mathbf{p}}}}{{Dt}} = {{{\mathbf{\varepsilon }}}^{{\mathbf{p}}}} - {\mathbf{p}} \cdot {{{\mathbf{\varepsilon }}}^{{\mathbf{p}}}} - {{{\mathbf{\varepsilon }}}^{{\mathbf{p}}}} \cdot {\mathbf{p}}$
$\begin{gathered} {\frac{{D{\mathbf{n}}}}{{Dt}} = \frac{{d{\mathbf{n}}}}{{dt}} - {\mathbf{r}} \cdot {\mathbf{n}} - {\mathbf{n}} \cdot {{{\mathbf{r}}}^{T}}{\text{,}}\quad {\mathbf{\varepsilon }} = \frac{{\text{1}}}{{\text{2}}}(\nabla {\mathbf{v}} + {{\nabla }^{T}}{\mathbf{v}}){\text{,}}\quad {\mathbf{\omega }} = \frac{{\text{1}}}{{\text{2}}}(\nabla {\mathbf{v}} - {{\nabla }^{T}}{\mathbf{v}})} \\ \,{\mathbf{v}} = \frac{{d{\mathbf{u}}}}{{dt}} = \frac{{\partial {\mathbf{u}}}}{{\partial t}} + {\mathbf{v}}\nabla {\mathbf{u}}{\text{,}}\quad {\mathbf{r}} = {\mathbf{\omega }} + {\mathbf{z}} \\ \end{gathered} $
(2.1)
${{\mathbf{z}} = {{A}^{{ - {\text{1}}}}}\{ {{B}^{{\text{2}}}}\left( {{\mathbf{\varepsilon }} \cdot {\mathbf{e}} - {\mathbf{e}} \cdot {\mathbf{\varepsilon }}} \right) + B({\mathbf{\varepsilon }} \cdot {{{\mathbf{e}}}^{{\text{2}}}} - {{{\mathbf{e}}}^{{\text{2}}}} \cdot {\mathbf{\varepsilon }}) + {\mathbf{e}} \cdot {\mathbf{\varepsilon }} \cdot {{{\mathbf{e}}}^{{\text{2}}}} - {{{\mathbf{e}}}^{{\text{2}}}} \cdot {\mathbf{\varepsilon }} \cdot {\mathbf{e}}\} }$
$\begin{gathered} {A = {\text{8}} - {\text{8}}{{E}_{{\text{1}}}} + {\text{3}}E_{{\text{1}}}^{{\text{2}}} - {{E}_{{\text{2}}}} - \frac{{E_{{\text{1}}}^{{\text{3}}}}}{{\text{3}}} + \frac{{{{E}_{{\text{3}}}}}}{{\text{3}}}{\text{,}}\quad B = {\text{2}} - {{E}_{{\text{1}}}}{\text{,}}}\quad {{E}_{{\text{1}}}} = {\text{tr}}\left( {\mathbf{e}} \right) \\ \quad {{E}_{{\text{2}}}} = {\mathbf{e}} \cdot \cdot \,{\mathbf{e}}{\text{,}}\quad {{E}_{{\text{3}}}} = {{{\mathbf{e}}}^{{\text{2}}}} \cdot \cdot \,{\mathbf{e}} \\ \end{gathered} $
${{\mathbf{d}} = \frac{1}{2}(\nabla {\mathbf{u}} + {{\nabla }^{T}}{\mathbf{u}} - {{\nabla }^{T}}{\mathbf{u}} \cdot \nabla {\mathbf{u}}) = {\mathbf{e}} + {\mathbf{p}} - \frac{{\text{1}}}{{\text{2}}}{\mathbf{e}} \cdot {\mathbf{e}} - {\mathbf{e}} \cdot {\mathbf{p}} - {\mathbf{p}} \cdot {\mathbf{e}} + {\mathbf{e}} \cdot {\mathbf{p}} \cdot {\mathbf{e}}}$

Здесь u, v – векторы перемещений и скорости; ${\mathbf{d}}$ – тензор полных деформаций Альманси; ${\mathbf{e}}$, ${\mathbf{p}}$ – тензоры обратимых и необратимых деформаций соответственно; ${\mathbf{\varepsilon }}$, ${{{\mathbf{\varepsilon }}}^{{\mathbf{p}}}}$ – тензоры скоростей полных и необратимых деформаций; ${\mathbf{\omega }}$ – тензор вихря скорости; $D{\text{/}}Dt$ – объективная производная по времени, записанная для произвольного тензора ${\mathbf{n}}$, которая переходит в производную Яуманна [19], когда нелинейная часть ${\mathbf{z}}$ тензора вращений ${\mathbf{r}}$ равна нулю. Согласно (2.1) при разгрузке (${{{\mathbf{\varepsilon }}}^{{\mathbf{p}}}} = 0$) компоненты тензора необратимых деформаций изменяются также как при жестком перемещении тела. Всюду далее принято условие несжимаемости с целью сосредоточиться на процессах, в которых достигаются значительные деформации сдвига при сравнительно малых изменениях объема. В этом случае аналог формулы Мурнагана, определяющей связь напряжений с обратимыми деформациями, принимает вид [19]:

(2.2)
$\begin{gathered} {{\mathbf{\sigma }} = - {{p}_{{\text{1}}}}{\mathbf{I}} + \frac{{\partial W}}{{\partial {\mathbf{d}}}}\left( {{\mathbf{I}} - {\text{2}}{\mathbf{d}}} \right){\text{,}}\quad {\mathbf{p}} \equiv {\text{0}}} \\ {\mathbf{\sigma }} = - {{p}_{{\text{2}}}}{\mathbf{I}} + \frac{{\partial W}}{{\partial {\mathbf{e}}}}\left( {{\mathbf{I}} - {\mathbf{e}}} \right),\quad {\mathbf{p}} \ne {\text{0}} \\ \end{gathered} $

В (2.2) ${\mathbf{\sigma }}$ – тензор напряжений Эйлера–Коши; ${{{p}_{{\text{1}}}}}$ и ${{{p}_{{\text{2}}}}}$ – функции добавочного гидростатического давления, I – единичный тензор второго ранга, W = W(J1, J2) – упругий потенциал, который для несжимаемой среды может быть представлен в виде [19, 20]:

(2.3)
${W = - {\text{2}}\mu {{J}_{{\text{1}}}} - \mu {{J}_{{\text{2}}}} + bJ_{{\text{1}}}^{{\text{2}}} + \left( {b - \mu } \right){{J}_{{\text{1}}}}{{J}_{{\text{2}}}} - \chi J_{{\text{1}}}^{{\text{3}}} + \cdots }$
${{J}_{k}} = \left\{ {\begin{array}{*{20}{c}} {{{L}_{k}},\quad {\mathbf{p}} \equiv {\text{0}}} \\ {{{I}_{k}},\quad {\mathbf{p}} \ne {\text{0}}} \end{array},\quad k = {\text{1}}{\text{.2}}} \right.$
${{{L}_{{\text{1}}}} = \operatorname{tr} \left( {\mathbf{d}} \right),\quad {{L}_{{\text{2}}}} = {\mathbf{d}} \cdot \cdot \,{\mathbf{d}},\quad {{I}_{{\text{1}}}} = \operatorname{tr} \left( {\mathbf{e}} \right) - \frac{{\text{1}}}{{\text{2}}}{\mathbf{e}} \cdot \cdot \,{\mathbf{e}},\quad {{I}_{{\text{2}}}} = {\mathbf{e}} \cdot \cdot \,{\mathbf{e}} - {{{\mathbf{e}}}^{{\text{2}}}} \cdot \cdot \,{\mathbf{e}} + \frac{{\text{1}}}{{\text{4}}}{{{\mathbf{e}}}^{{\text{2}}}} \cdot \cdot \,{{{\mathbf{e}}}^{{\text{2}}}}}$

Здесь $\mu $, $b$ и $\chi $ – упругие модули среды. Инварианты ${{{I}_{{\text{1}}}}}$ и ${{{I}_{{\text{2}}}}}$ тензора обратимых деформаций выбраны так, чтобы осуществлялся предельный переход в (2.3) от второй зависимости к первой при стремлении к нулю пластических деформаций. Будем считать, что необратимые деформации начинают накапливаться в материале, когда напряжения достигают поверхности нагружения (текучести) ${f({\mathbf{\sigma }}{\text{,}}{{{\mathbf{\varepsilon }}}^{{\mathbf{p}}}},k) = {\text{0}}}$. В качестве поверхности нагружения принимаем условие пластичности Треска с учетом вязкого сопротивления пластическому течению [21]:

(2.4)
${f({{\sigma }_{i}}{\text{,}}\varepsilon _{k}^{p}{\text{,}}k) = \max \left| {{{\sigma }_{i}} - {{\sigma }_{j}}} \right| - {\text{2}}k - {\text{2}}\eta \max \left| {\varepsilon _{k}^{p}} \right|}$

В (2.4) ${{{\sigma }_{i}}}$ и ${\varepsilon _{k}^{p}}$ – главные значения тензоров напряжений и скоростей пластических деформаций, $k$ – предел текучести, $\eta $ – коэффициент вязкости. Скорости необратимых деформаций связаны с напряжениями ассоциированным законом пластического течения

(2.5)
${{{{\mathbf{\varepsilon }}}^{{\mathbf{p}}}} = {{\lambda }}\frac{{\partial f}}{{\partial {\mathbf{\sigma }}}}{\text{,}}\quad {{\lambda }} > {\text{0}}}$

Для того чтобы получить замкнутую систему уравнений и в области упругого деформирования, и в области пластического течения достаточно дополнить предыдущие соотношения уравнением движения или уравнением равновесия

(2.6)
${\nabla \cdot {\mathbf{\sigma }} = {{\rho }}\frac{{d{\mathbf{v}}}}{{dt}}}$
(2.7)
${\nabla \cdot {\mathbf{\sigma }} = {\mathbf{0}}}$

Пренебречь силами инерции в (2.6) так, чтобы иметь (2.7), удается не всегда. Если это оказывается возможно, то говорят о квазистатическом приближении в решении задачи.

3. Постановка задачи. Квазистатическое деформирование. Пусть материал, свойства которого описаны выше, заполняет кольцевой зазор между жесткими цилиндрическими поверхностями с неограниченными образующими. Радиус внутреннего цилиндра обозначим ${{{r}_{{\text{0}}}}}$, а внешнего $R$. Внешний цилиндр поворачивается вокруг своей оси с задаваемым напряжением сдвига, тогда как внутренний остается неподвижным. Полагаем, что при значениях напряжения сдвига не превышающих некоторого заданного порогового значения ${\left| {{{\sigma }_{{r\varphi }}}} \right| \leqslant {{\sigma }_{{\text{0}}}}}$ (${{\sigma }_{{\text{0}}}} = {\text{const}}$) на стенках цилиндров выполняются условия прилипания:

(3.1)
${{\mathbf{u}}\left( {{{r}_{0}},t} \right) = {\mathbf{v}}\left( {{{r}_{0}}{\text{,}}t} \right) = {\text{0,}}\quad {{\sigma }_{{r\varphi }}}\left( {R{\text{,}}t} \right) = \alpha t,\quad \alpha = {\text{const}}}$

Будем считать, что ${{\sigma }_{{\text{0}}}} > k$. Предварительные деформации отсутствуют. Траекториями точек среды будут концентрические окружности, а все искомые функции в цилиндрической системе координат ${\left( {r{\text{,}}\varphi {\text{,}}z} \right)}$ зависят от двух переменных: расстояния от общей оси цилиндров $r$ и времени $t$. Согласно (2.1) кинематика среды в этом случае определяется зависимостями

${{{u}_{r}} = r\left( {{\text{1}} - \cos \psi } \right){\text{,}}\quad {{u}_{\varphi }} = r\sin \psi }$
(3.2)
${{{d}_{{rr}}} = - \frac{{{{r}^{{\text{2}}}}}}{{\text{2}}}{{{\left( {\frac{{\partial \psi }}{{\partial r}}} \right)}}^{2}}{\text{,}}\quad {{d}_{{r\varphi }}} = \frac{r}{{\text{2}}}\frac{{\partial \psi }}{{\partial r}}{\text{,}}\quad {{{v}}_{\varphi }} = r\omega = r\frac{{\partial \psi }}{{\partial t}}}$
${{{\varepsilon }_{{r\varphi }}} = \frac{r}{{\text{2}}}\frac{{{{\partial }^{{\text{2}}}}\psi }}{{\partial r\partial t}}{\text{,}}\quad {{\omega }_{{r\varphi }}} = - \frac{{\partial \psi }}{{\partial t}} - \frac{r}{{\text{2}}}\frac{{{{\partial }^{{\text{2}}}}\psi }}{{\partial r\partial t}}{\text{,}}\quad {{r}_{{r\varphi }}} = - \frac{{\partial \psi }}{{\partial t}} + \frac{{{\text{2}}{{\varepsilon }_{{r\varphi }}}\left( {{\text{1}} - {{e}_{{\varphi \varphi }}}} \right)}}{{{{e}_{{rr}}} + {{e}_{{\varphi \varphi }}} - {\text{2}}}}}$
где ${\psi = \psi \left( {r{\text{,}}t} \right)}$ – центральный угол закручивания точек среды, ${\omega = {{{v}}_{\varphi }}{\text{/}}r}$ – угловая скорость.

До выхода напряжений на поверхность нагружения деформирование является обратимым. Согласно (2.2) компоненты тензора напряжений в этом случае определяются зависимостями:

(3.3)
$\begin{gathered} {{{\sigma }_{{rr}}} = {{\sigma }_{{zz}}} = - \left( {p + {\text{2}}\mu } \right) - \frac{{\left( {b + \mu } \right){{r}^{2}}}}{{\text{2}}}{{{\left( {\frac{{\partial \psi }}{{\partial r}}} \right)}}^{2}} = - s\left( {r{\text{,}}t} \right)} \\ {{\sigma }_{{\varphi \varphi }}} = - s\left( {r{\text{,}}t} \right) + \mu {{\left( {r\frac{{\partial \psi }}{{\partial r}}} \right)}^{{\text{2}}}}{\text{,}}\quad {{\sigma }_{{r\varphi }}} = \mu r\frac{{\partial \psi }}{{\partial r}} \\ \end{gathered} $

Обратимые деформации полагаем малыми, поэтому в (3.3) выписаны только старшие нелинейные слагаемые деформаций. В областях, где присутствуют необратимые деформации, напряжения определяются согласно второй зависимости в (2.2):

(3.4)
$\begin{gathered} {{{\sigma }_{{rr}}} = - p - {\text{2}}\mu + {\text{2}}\left( {b + \mu } \right){{e}_{{rr}}} + {\text{2}}b{{e}_{{\varphi \varphi }}} + \mu e_{{r\varphi }}^{{\text{2}}}} \\ {{\sigma }_{{\varphi \varphi }}} = - p - {\text{2}}\mu + {\text{2}}\left( {b + \mu } \right){{e}_{{\varphi \varphi }}} + {\text{2}}b{{e}_{{rr}}} + \mu e_{{r\varphi }}^{{\text{2}}} \\ {{{\sigma }_{{zz}}} = - p - {\text{2}}\mu + {\text{2}}b\left( {{{e}_{{rr}}} + {{e}_{{\varphi \varphi }}}} \right) - {\text{2}}\mu e_{{r\varphi }}^{{\text{2}}}{\text{,}}}\quad {{\sigma }_{{r\varphi }}} = {\text{2}}\mu {{e}_{{r\varphi }}}{\text{,}}\quad \frac{{{{\sigma }_{{rr}}} - {{\sigma }_{{\varphi \varphi }}}}}{{{{\sigma }_{{r\varphi }}}}} = \frac{{{{e}_{{rr}}} - {{e}_{{\varphi \varphi }}}}}{{{{e}_{{r\varphi }}}}} \\ \end{gathered} $

Компоненты тензоров не выписанные в (3.2)–(3.4) равны нулю. Задавая изменение крутящего момента достаточно медленным, можно рассчитывать процесс деформирования в рамках квазистатического приближения. В этом случае интегрируя уравнения равновесия, следующие из (2.7) и (3.3),

(3.5)
${\frac{{\partial {{\sigma }_{{rr}}}}}{{\partial r}} + \frac{{{{\sigma }_{{rr}}} - {{\sigma }_{{\varphi \varphi }}}}}{r} = {\text{0,}}\quad \frac{{\partial {{\sigma }_{{r\varphi }}}}}{{\partial r}} + {\text{2}}\frac{{{{\sigma }_{{r\varphi }}}}}{r} = {\text{0}}}$
с учетом граничных условий (3.1) запишем решение справедливое в промежуток времени, когда материал испытывает только упругую деформацию

${\psi = \frac{{c\left( t \right)}}{{{\text{2}}\mu }}\left( {\frac{{\text{1}}}{{r_{0}^{2}}} - \frac{{\text{1}}}{{{{r}^{{\text{2}}}}}}} \right){\text{,}}\quad \omega = \frac{{\alpha {{R}^{2}}}}{{{\text{2}}\mu }}\left( {\frac{{\text{1}}}{{r_{0}^{2}}} - \frac{{\text{1}}}{{{{r}^{{\text{2}}}}}}} \right){\text{,}}\quad c\left( t \right) = \alpha {{R}^{2}}t}$
(3.6)
$\begin{gathered} {{{\sigma }_{{r\varphi }}} = \frac{{c\left( t \right)}}{{{{r}^{{\text{2}}}}}}{\text{,}}\quad {{\sigma }_{{rr}}} = {{\sigma }_{{zz}}} = \frac{{c{{{\left( t \right)}}^{2}}}}{{{\text{4}}\mu }}\left( {\frac{{\text{1}}}{{r_{{\text{0}}}^{{\text{4}}}}} - \frac{{\text{1}}}{{{{r}^{{\text{4}}}}}}} \right) + \sigma _{{rr}}^{{\text{0}}}} \\ {{{\sigma }_{{\varphi \varphi }}} = \frac{{c{{{\left( t \right)}}^{{\text{2}}}}}}{{{\text{4}}\mu }}\left( {\frac{{\text{1}}}{{r_{{\text{0}}}^{{\text{4}}}}} + \frac{{\text{3}}}{{{{r}^{{\text{4}}}}}}} \right) + \sigma _{{rr}}^{{\text{0}}}{\text{,}}\quad \sigma _{{rr}}^{{\text{0}}} = {{\sigma }_{{rr}}}\left( {{{r}_{0}},t} \right)} \\ \end{gathered} $
${{{e}_{{r\varphi }}} = {{d}_{{r\varphi }}} = \frac{{c(t)}}{{{\text{2}}\mu {{r}^{{\text{2}}}}}}{\text{,}}\quad {{e}_{{rr}}} = - \frac{{\text{3}}}{{\text{2}}}e_{{r\varphi }}^{{\text{2}}}{\text{,}}\quad {{e}_{{\varphi \varphi }}} = \frac{{e_{{r\varphi }}^{{\text{2}}}}}{{\text{2}}}}$

Решение (3.6) справедливо до момента времени $t = {{t}_{0}}$, когда на поверхности $r = {{r}_{0}}$ выполнится условие пластичности ${{{\sigma }_{{r\varphi }}}\left( {{{r}_{{\text{0}}}},{{t}_{{\text{0}}}}} \right) = k}$, ${{t}_{0}} = kr_{0}^{2}{\text{/}}\alpha {{R}^{2}}$. С этого момента в рассматриваемом слое ${V{\text{:}}\;{{r}_{{\text{0}}}} \leqslant r \leqslant R}$ присутствуют две области: область вязкопластического течения ${{{V}^{{\left( P \right)}}}{\text{:}}\;{{r}_{{\text{0}}}} \leqslant r \leqslant m\left( t \right)}$ и область обратимого (упругого) деформирования ${{{V}^{{\left( E \right)}}}{\text{:}}\;m\left( t \right) \leqslant r \leqslant R}$; $r = m\left( t \right)$ – уравнение движущейся упругопластической границы. Здесь и далее верхними индексами “$E$” и “$P$” в круглых скобках будем обозначать величины в областях ${{V}^{{\left( E \right)}}}$ и ${{V}^{{\left( P \right)}}}$ соответственно. Будем полагать, что напряженное состояние достаточно близко к состоянию чистого азимутального сдвига, пренебрегая эффектами второго порядка. Тогда, исходя из (2.4) условие пластического течения записывается в виде:

(3.7)
${f({{\sigma }_{{r\varphi }}}{\text{,}}\varepsilon _{{r\varphi }}^{p}) = \sigma _{{r\varphi }}^{{\text{2}}} - {{{(k + \eta \left| {\varepsilon _{{r\varphi }}^{p}} \right|)}}^{{\text{2}}}} = {\text{0}}}$
а в силу ассоциированного закона пластического течения (2.5) из условия (3.7) следует

(3.8)
${{{\sigma }_{{r\varphi }}} = k + \eta \varepsilon _{{r\varphi }}^{p}{\text{,}}\quad \lambda = \frac{{\varepsilon _{{r\varphi }}^{p}}}{{k + \eta \varepsilon _{{r\varphi }}^{p}}}}$

Параметры напряженно-деформированного состояния находим интегрированием уравнений равновесия в областях ${{V}^{{\left( E \right)}}}$ и ${{V}^{{\left( P \right)}}}$, а неизвестные функции интегрирования определяются из (3.1) и условия непрерывности перемещения, скорости и напряжения на упругопластической границе $r = m\left( t \right)$. Таким образом, в области вязкопластического течения ${{V}^{{\left( P \right)}}}$ получим

${{{\psi }^{{\left( P \right)}}} = \frac{{c\left( t \right)}}{{{\text{2}}\mu }}\left( {\frac{{\text{1}}}{{r_{0}^{2}}} - \frac{{\text{1}}}{{{{r}^{{\text{2}}}}}}} \right) + \frac{1}{{2\eta }}\left\{ {\alpha {{R}^{2}}{{t}^{2}}\left( {\frac{{\text{1}}}{{r_{0}^{2}}} - \frac{{\text{1}}}{{{{r}^{{\text{2}}}}}}} \right) + 4kt{\kern 1pt} {\text{ln}}\frac{{{{r}_{0}}}}{r} + \frac{{{{k}^{2}}({{r}^{2}} - r_{0}^{2})}}{{\alpha {{R}^{2}}}}} \right\}}$
(3.9)
${{{\omega }^{{\left( P \right)}}} = \frac{{\alpha {{R}^{2}}}}{{{\text{2}}\mu }}\left( {\frac{{\text{1}}}{{r_{0}^{2}}} - \frac{{\text{1}}}{{{{r}^{{\text{2}}}}}}} \right) + \frac{1}{\eta }\left\{ {\alpha {{R}^{2}}t\left( {\frac{{\text{1}}}{{r_{0}^{2}}} - \frac{{\text{1}}}{{{{r}^{{\text{2}}}}}}} \right) + 2k{\kern 1pt} {\text{ln}}\frac{{{{r}_{0}}}}{r}} \right\}}$
${{{p}_{{r\varphi }}} = \frac{1}{\eta }\left( {\frac{{\alpha {{R}^{{\text{2}}}}{{t}^{2}}}}{{2{{r}^{2}}}} - kt + \frac{{{{k}^{2}}{{r}^{2}}}}{{2\alpha {{R}^{2}}}}} \right){\text{,}}\quad }{{e}_{{r\varphi }}} = \frac{{\alpha {{R}^{{\text{2}}}}t}}{{2\mu {{r}^{2}}}}$
а в области упругого деформирования ${{V}^{{\left( E \right)}}}$

(3.10)
$\begin{gathered} {{{\psi }^{{\left( E \right)}}} = \frac{{c\left( t \right)}}{{{\text{2}}\mu }}\left( {\frac{{\text{1}}}{{r_{0}^{2}}} - \frac{{\text{1}}}{{{{r}^{{\text{2}}}}}}} \right) + \frac{1}{{2\eta }}\left\{ {\alpha {{R}^{2}}{{t}^{2}}\left( {\frac{{\text{1}}}{{r_{0}^{2}}} - \frac{{\text{1}}}{{m{{{\left( t \right)}}^{{\text{2}}}}}}} \right) + 4kt{\kern 1pt} {\text{ln}}\frac{{{{r}_{0}}}}{{m\left( t \right)}} + \frac{{{{k}^{2}}(m{{{\left( t \right)}}^{2}} - r_{0}^{2})}}{{\alpha {{R}^{2}}}}} \right\}} \\ {{{\omega }^{{\left( E \right)}}} = \frac{{\alpha {{R}^{2}}}}{{{\text{2}}\mu }}\left( {\frac{{\text{1}}}{{r_{0}^{2}}} - \frac{{\text{1}}}{{{{r}^{{\text{2}}}}}}} \right) + \frac{1}{\eta }\left\{ {\alpha {{R}^{2}}t\left( {\frac{{\text{1}}}{{r_{0}^{2}}} - \frac{{\text{1}}}{{m{{{\left( t \right)}}^{{\text{2}}}}}}} \right) + 2k{\kern 1pt} {\text{ln}}\frac{{{{r}_{0}}}}{{m\left( t \right)}}} \right\}} \\ \end{gathered} $

Напряжения в слое, как и ранее, определяются согласно (3.5). Положение упругопластической границы находим из условия равенства на ней нулю скорости пластических деформаций $\varepsilon _{{r\varphi }}^{p}$

(3.11)
${m\left( t \right) = R\sqrt {\frac{{\alpha t}}{k}} {\text{,}}\quad \varepsilon _{{r\varphi }}^{p} = \frac{{\alpha {{R}^{2}}t}}{{\eta {{r}^{2}}}}} - \frac{k}{\eta }$

Согласно (1.1), (3.7) и (3.8) диагональные компоненты обратимых ${{{e}_{{rr}}}}$, ${{{e}_{{\varphi \varphi }}}}$ и необратимых ${{{p}_{{rr}}}}$, ${{{p}_{{\varphi \varphi }}}}$ деформаций, являющиеся малыми более высокого порядка по сравнению с недиагональными, находятся численно из следующей системы уравнений:

(3.12)
$\begin{gathered} {\frac{{\partial {{p}_{{r\varphi }}}}}{{\partial t}} = \varepsilon _{{r\varphi }}^{p}{\text{,}}\quad \frac{{\partial {{p}_{{\varphi \varphi }}}}}{{\partial t}} = - \varepsilon _{{r\varphi }}^{p}\frac{{{{p}_{{\varphi \varphi }}} - e_{{r\varphi }}^{{\text{2}}}}}{{{{e}_{{r\varphi }}}}} + \frac{{{\text{4}}{{\varepsilon }_{{r\varphi }}}{{p}_{{r\varphi }}}}}{{{\text{2}} + e_{{r\varphi }}^{{\text{2}}}}}\left( {{\text{1}} + {{p}_{{\varphi \varphi }}} - \frac{{\text{1}}}{{\text{2}}}e_{{r\varphi }}^{{\text{2}}} - {\text{2}}{{e}_{{r\varphi }}}{{p}_{{r\varphi }}}} \right)} \\ {{{e}_{{rr}}} = {{p}_{{\varphi \varphi }}} - \frac{{{\text{3}}e_{{r\varphi }}^{{\text{2}}}}}{{\text{2}}} - {\text{2}}{{e}_{{r\varphi }}}{{p}_{{r\varphi }}}{\text{,}}\quad {{p}_{{rr}}} + {{p}_{{\varphi \varphi }}} = - {\text{2}}p_{{r\varphi }}^{{\text{2}}}{\text{,}}\quad {{e}_{{rr}}} + {{e}_{{\varphi \varphi }}} = - e_{{r\varphi }}^{{\text{2}}}} \\ \end{gathered} $

Затем, исходя из (3.4) и (3.6) определяется функция добавочного гидростатического давления.

4. Динамика разгрузки. В момент времени t = ts = ${{{\sigma }_{{\text{0}}}}r_{0}^{2}{\text{/}}\alpha }{{R}^{2}}$ напряжение трения покоя ${\left| {{{\sigma }_{{r\varphi }}}} \right|}$ на поверхности ${r = {{r}_{{\text{0}}}}}$ достигнет предельного значения ${{{\sigma }_{{\text{0}}}}}$ и материал в окрестности этой поверхности начинает проскальзывать. С этого момента условие прилипания на ${r = {{r}_{{\text{0}}}}}$ необходимо заменить каким-либо условием контактного трения. В качестве такового примем условие постоянства касательного напряжения на ${{{r}_{{\text{0}}}}}$, полагая при этом, что последнее в момент ${{t}_{s}}$ меняется скачком, так что

(4.1)
${\left| {{{\sigma }_{{r\varphi }}}\left( {{{r}_{{\text{0}}}}{\text{,}}t} \right)} \right| = {{\sigma }_{s}}\quad {\text{при}}\quad t \geqslant {{t}_{s}};\quad {{\sigma }_{s}} = \operatorname{const} {\text{,}}\quad {{\sigma }_{s}} < k}$

Мгновенное падение напряжения ниже предела текучести приводит к формированию волны разгрузки Σ1, положение которой в пространстве описывается уравнением ${r = {{r}_{{\text{1}}}}\left( t \right) = {{r}_{{\text{0}}}} + \int\limits_{{{t}_{s}}}^t {G\left( \xi \right)d\xi } }$. Под ударной волной понимаем поверхность сильного разрыва, т.е. такую поверхность на которой перемещения непрерывны, а скорости перемещений и напряжения испытывают конечный разрыв. Поверхность сильного разрыва [22] можно интерпретировать как предельный слой толщины $\Delta h$ (${\Delta h \to {\text{0}}}$), в котором скорости и напряжения изменяются от значений ${{v}_{i}^{ + }}$, ${\sigma _{{ij}}^{ + }}$ до значений ${{v}_{i}^{ - }}$, ${\sigma _{{ij}}^{ - }}$ оставаясь внутри слоя монотонными и непрерывными. На поверхностях слабого разрыва, которые также будут встречаться в дальнейшем, напряжения и скорости перемещений остаются непрерывными, а вот их некоторые частные производные претерпевают разрыв.

В [22] показано, что в упруговязкопластической среде существуют два типа волн: продольные и поперечные, скорости которых совпадают со скоростями одноименных волн в упругой среде. Пластические деформации в упруговязкопластической среде остаются непрерывными и при переходе через поверхность разрыва [22]. В силу принятого ранее предположения о малости обратимых деформаций в нашем случае скорость волны разгрузки Σ1 постоянна ${G = \sqrt {\mu {\text{/}}\rho } }$ ($\rho $ – плотность среды). Поскольку рассматриваемый процесс разгрузки является существенно нестационарным, пренебречь правой частью в (2.6) нельзя. Динамическое поведение материала за ударной волной разгрузки подчиняется уравнениям движения:

(4.2)
${\frac{{\partial {{\sigma }_{{r\varphi }}}}}{{\partial r}} + {\text{2}}\frac{{{{\sigma }_{{r\varphi }}}}}{r} = \rho r\ddot {\psi }{\text{,}}\quad \frac{{\partial {{\sigma }_{{rr}}}}}{{\partial r}} + \frac{{{{\sigma }_{{rr}}} - {{\sigma }_{{\varphi \varphi }}}}}{r} = - \rho r\dot {\psi },\quad }\dot {\psi } = \frac{{\partial \psi }}{{\partial t}},\quad \ddot {\psi } = \frac{{{{\partial }^{2}}\psi }}{{\partial {{t}^{2}}}}$

Таким образом, с момента t = ts область решения задачи разделяется на три, в которых напряжения и деформации определяются по-разному. В области разгрузки V(1): ${{{r}_{{\text{0}}}} \leqslant r \leqslant {{r}_{{\text{1}}}}\left( t \right)}$ – интегрированием уравнений движения (4.2), в области продолжающегося вязкопластического течения ${{{V}^{{\left( P \right)}}}{\text{:}}\;{{r}_{{\text{1}}}}\left( t \right) \leqslant r \leqslant m\left( t \right)}$ и области обратимого деформирования ${{{V}^{{\left( E \right)}}}{\text{:}}\;m\left( t \right) \leqslant r \leqslant R}$ будем считать справедливым решение квазистатической задачи.

Первое уравнение в (4.2) является основным и может быть решено независимо от второго, а затем по найденному решению из второго уравнения находится добавочное гидростатическое давление ${p\left( {r,t} \right)}$. Согласно уравнению переноса для тензора необратимых деформаций (2.1) в процессе разгрузки ($\varepsilon _{{ij}}^{p} = 0$) его компоненты ${{p}_{{ij}}}$ изменяются как при жестком перемещении тела. Из (3.9) и (3.12) следует, что компонента тензора пластических деформаций ${{{p}_{{r\varphi }}}}$ перестает изменяться со временем в тех точках области ${{V}^{{\left( P \right)}}}$ через которые прошел волновой фронт и в области ${{V}^{{\left( {\text{1}} \right)}}}$ является только функцией координаты ${{{p}_{{r\varphi }}}\left( r \right)}$. Учитывая это обстоятельство, уравнение движения в области разгрузки принимает вид:

(4.3)
${{{\psi }_{{,rr}}} + \frac{{\text{3}}}{r}{{\psi }_{{,r}}} - \frac{{\ddot {\psi }}}{{{{G}^{{\text{2}}}}}} = \frac{{\text{2}}}{\eta }\left( {\frac{{\alpha {{R}^{2}}{{\tau }_{{\text{1}}}}\left( r \right)}}{{G{{r}^{{\text{3}}}}}} - \frac{k}{{Gr}} - \frac{{{\text{2}}k{{\tau }_{{\text{1}}}}\left( r \right)}}{{{{r}^{{\text{2}}}}}} + \frac{{2{{k}^{{\text{2}}}}}}{{\alpha {{R}^{2}}}}} \right)}$
где ${{\psi }_{{,r}}} = \partial \psi {\text{/}}\partial r$, ${{\psi }_{{,rr}}} = {{\partial }^{2}}\psi {\text{/}}\partial {{r}^{2}}$, ${{{\tau }_{{\text{1}}}}\left( r \right) = {{t}_{s}} + \left( {r - {{r}_{0}}} \right)}{\text{/}}G$ – время прихода волны ${{{\Sigma }_{{\text{1}}}}}$ в точку с координатой $r$. Граничными условиями для (4.3) будут условие трения (4.1) на граничной поверхности ${r = {{r}_{{\text{0}}}}}$ и условие непрерывности перемещений на фронте волны разгрузки $r = {{r}_{{\text{1}}}}\left( t \right)$

(4.4)
${{{{\left. {\left[ \psi \right]} \right|}}_{{{{\Sigma }_{1}}}}}}\,{{\left. { = ({{\psi }^{ + }} - {{\psi }^{ - }})} \right|}_{{r = {{r}_{1}}(t)}}} = 0$

Квадратными скобками в (4.4) и далее обозначается скачок функции на поверхности разрывов, ψ+ = ψ+(r1(t), t) – значение функции ψ(r, t) непосредственно перед поверхностью разрывов, а ψ– = ψ–(r1(t), t) – непосредственно за поверхностью разрывов.

Волны разгрузки рассматривались также в [23, 24], где были получены точные решения краевых задач теории больших деформаций о динамической разгрузке в плоском тяжелом слое, находящемся на наклонной плоскости и подвергнутом нагружению на свободной поверхности, с последующим мгновенным снятием нагрузки [23] или срывом материала с наклонной плоскости [24].

В нашем случае уравнение (4.3) не может быть проинтегрировано точно, его приближенное решение строим лучевым методом, заключающимся в представлении решения в окрестности волнового фронта в виде ряда Тейлора. Практика применения лучевых разложений в решении волновых задач достаточно обширна [25]. Здесь воспользуемся вариантом метода, предложенным в [26], где приближенное решение строилось в форме степенного ряда по времени в окрестности момента прихода волны в данную точку пространства. Так для угловой скорости $\omega \left( {r,t} \right)$ в области ${{V}^{{\left( {\text{1}} \right)}}}$ запишем:

(4.5)
$\begin{gathered} \omega \left( {r,t} \right) = {{\left. {{{\omega }^{ - }}} \right|}_{{t = {{\tau }_{1}}}}} + {{\left. {{{{\dot {\omega }}}^{ - }}} \right|}_{{t = {{\tau }_{1}}}}}\left( {t - {{\tau }_{1}}} \right) + \frac{1}{2}{{\left. {{{{\ddot {\omega }}}^{ - }}} \right|}_{{t = {{\tau }_{1}}}}}{{\left( {t - {{\tau }_{1}}} \right)}^{2}} + \cdots = \\ \, = {{\left. {({{\omega }^{ + }} - \left[ \omega \right])} \right|}_{{t = {{\tau }_{1}}}}} + {{\left. {({{{\dot {\omega }}}^{ + }} - \left[ {\dot {\omega }} \right])} \right|}_{{t = {{\tau }_{1}}}}}\left( {t - {{\tau }_{1}}} \right) + \frac{1}{2} {{\left. {({{{\ddot {\omega }}}^{ + }} - \left[ {\ddot {\omega }} \right])} \right|}_{{t = {{\tau }_{1}}}}}{{\left( {t - {{\tau }_{1}}} \right)}^{2}} + \cdots \\ \end{gathered} $

Аналогично можно записать лучевые ряды для функций напряжения и угла закрутки, причем эти величины также выражаются через скачки угловой скорости и ее производных ${[{{\partial }^{{n - 1}}}\omega {\text{/}}\partial {{t}^{{n - 1}}}]}$ ${\left( { n = {\text{1,2,}} \ldots } \right)}$. Далее будем опускать индекс “+” для величин перед поверхностью разрыва. Обычно асимптотические ряды типа (4.5) ограничивают несколькими первыми членами. В данной работе сохраним линейные по времени слагаемые для напряжений и скорости и квадратичные для перемещений.

С целью вычисления разрыва функции на ударной волне и разрывов ее производных $n$-го порядка необходимо продифференцировать первое уравнение в (4.2) n – 1 раз по времени, записать результат с каждой стороны от волновой поверхности и вычислить их разность привлекая геометрические и кинематические условия совместности [21, 27, 28]. Таким образом, рекуррентно получим систему линейных неоднородных дифференциальных уравнений первого порядка:

(4.6)
$\begin{gathered} {\frac{{\delta {{\chi }_{1}}}}{{\delta t}} + \frac{{{\text{3}}G}}{{{\text{2}}{{r}_{{\text{1}}}}}}{{\chi }_{1}} = \frac{{2G}}{\eta }\left( {\frac{{\alpha {{R}^{2}}t}}{{r_{1}^{2}}} - k} \right)} \\ \frac{{\delta {{\zeta }_{1}}}}{{\delta t}} + \frac{{{\text{3}}G}}{{{\text{2}}{{r}_{{\text{1}}}}}}{{\zeta }_{1}} = \frac{{2k{{G}^{2}}}}{{\eta r_{1}^{2}}} - \frac{{\alpha G{{R}^{2}}}}{{\eta r_{1}^{3}}} - \frac{{3{{A}_{1}}{{G}^{2}}}}{{8r_{1}^{{7{\text{/}}2}}}} \\ \end{gathered} $

В которой ${{\chi }_{1}} = {{\left. {\left[ \omega \right]} \right|}_{{{{\Sigma }_{1}}}}}$, ${{\zeta }_{1}} = {{\left. {\left[ {\dot {\omega }} \right]} \right|}_{{{{\Sigma }_{1}}}}}$; ${\delta {\text{/}}\delta t}$ – дельта-производная по времени от функции, заданной на движущейся поверхности [27]. После интегрирования (4.6) в области V(1) получим:

${{{\chi }_{{\text{1}}}}\left( t \right) = \frac{{{{A}_{1}}}}{{r_{{\text{1}}}^{{{\text{3/2}}}}}} - \frac{{{\text{2}}k}}{{{\text{3}}\eta }} + \frac{{{\text{4}}\alpha {{R}^{2}}}}{{\eta G{{r}_{1}}}}\left( {1 - \frac{{Gt}}{{2{{r}_{1}}}}} \right){\text{,}}\quad {{\zeta }_{{\text{1}}}}\left( t \right) = \frac{{{{B}_{1}}}}{{r_{{\text{1}}}^{{{\text{3/2}}}}}} + \frac{{{\text{3}}{{A}_{1}}G}}{{{\text{8}}r_{{\text{1}}}^{{{\text{5/2}}}}}} + \frac{{{\text{4}}kG}}{{\eta {{r}_{{\text{1}}}}}} + \frac{{{\text{2}}\alpha {{R}^{2}}}}{{\eta r_{{\text{1}}}^{{\text{2}}}}}}$
${{{\psi }^{{\left( {\text{1}} \right)}}}\left( {r{\text{,}}t} \right) = {{\psi }^{{\left( P \right)}}}\left( {r,{{\tau }_{{\text{1}}}}} \right) + {{{\left. {({{\omega }^{{\left( P \right)}}} - {{\chi }_{{\text{1}}}})} \right|}}_{{t = {{\tau }_{1}}}}}\left( {t - {{\tau }_{{\text{1}}}}} \right) + \frac{{\text{1}}}{{\text{2}}}{{{\left. {({{{\dot {\omega }}}^{{\left( P \right)}}} - {{\zeta }_{{\text{1}}}})} \right|}}_{{t = {{\tau }_{1}}}}}{{{\left( {t - {{\tau }_{{\text{1}}}}} \right)}}^{{\text{2}}}} + \cdots }$
(4.7)
${\begin{array}{*{20}{l}} \begin{gathered} \sigma _{{r\varphi }}^{{\left( {\text{1}} \right)}}\left( {r,t} \right) = \frac{{\alpha {{R}^{2}}{{\tau }_{{\text{1}}}}}}{{{{r}^{{\text{2}}}}}} + \frac{{\mu r{{\chi }_{1}}\left( {{{\tau }_{{\text{1}}}}} \right)}}{G} + \\ \, + \left\{ {\frac{{\alpha {{R}^{2}}}}{{{{r}^{{\text{2}}}}}} + \frac{{\mu r}}{G}\left( {\frac{{{\text{3}}G}}{{{\text{2}}r}}{{\chi }_{1}}\left( {{{\tau }_{{\text{1}}}}} \right) + {{\zeta }_{1}}\left( {{{\tau }_{{\text{1}}}}} \right) - \frac{G}{{\eta r}}\left( {k - \frac{{\alpha {{R}^{2}}{{\tau }_{{\text{1}}}}}}{{{{r}^{{\text{2}}}}}}} \right)} \right)} \right\}\left( {t - {{\tau }_{{\text{1}}}}} \right) + \cdots \\ \end{gathered} \end{array}}$
${{{A}_{1}} = \frac{{\sqrt {{{r}_{{\text{0}}}}} G\left( {{{\sigma }_{s}} - {{\sigma }_{{\text{0}}}}} \right)}}{\mu } + \frac{{{\text{2}}r_{{\text{0}}}^{{{\text{3/2}}}}}}{\eta }\left( {\frac{k}{{\text{3}}} + {{\sigma }_{{\text{0}}}} - \frac{{{\text{2}}\alpha {{R}^{2}}}}{{G{{r}_{{\text{0}}}}}}} \right)}$
${{B}_{1}} = \frac{{15{{G}^{2}}({{\sigma }_{0}} - {{\sigma }_{s}})}}{{8\mu \sqrt {{{r}_{0}}} }} - \frac{{\sqrt {{{r}_{0}}} G(13k + 7{{\sigma }_{0}})}}{{4\eta }} - \frac{{\alpha G{{R}^{2}}}}{{\mu r_{0}^{{3/2}}}} - \frac{{\alpha {{R}^{2}}}}{{2\eta \sqrt {{{r}_{0}}} }}$

Верхний индекс “(1)” означает, что вычисленные величины относятся к области V(1). Аналогичным образом можно при необходимости вычислить и следующие члены лучевого ряда. Принципиальных трудностей в этом нет, лишь возрастает объем вычислений.

В момент времени волна разгрузки достигнет упругопластической границы:

(4.8)
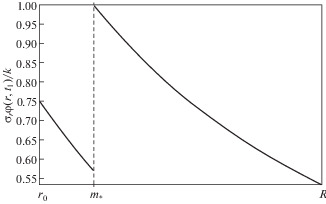
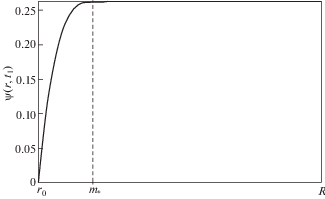
${{{t}_{1}} = {{t}_{s}} + \frac{{\text{1}}}{{{\text{2}}{{G}^{{\text{2}}}}}}\left( {\frac{{\alpha {{R}^{2}}}}{k} - {\text{2}}{{r}_{{\text{0}}}}G + \sqrt {\frac{{{\text{4}}\alpha {{R}^{2}}G}}{k}\left( {G{{t}_{s}} - {{r}_{{\text{0}}}}} \right) + \frac{{{{\alpha }^{{\text{2}}}}{{R}^{4}}}}{{{{k}^{{\text{2}}}}}}} } \right)}$

Распределение по слою касательного напряжения ${{{\sigma }_{{r\varphi }}}\left( {r{\text{,}}t} \right)}$ и угла закручивания ${\psi \left( {r{\text{,}}t} \right)}$, представлены на риc. 1–2 в момент столкновения с упругопластической границей. Расчет проводился при следующих значениях постоянных: ρ0 = 2.7 × 103 кг/м3, μ = 24.5 ГПа, η = 1.25 ГПа ⋅ с, σ0 = 67.56 МПа, σ = 42.225 МПа, $R{\text{/}}{{r}_{0}} = 1.5$, Па/с.

Начиная с момента $t = {{t}_{{\text{1}}}}$, область с накопленными необратимыми деформациями больше не увеличивается и ограничена поверхностями ${r = {{r}_{{\text{0}}}}}$ и ${r = m_{*}^{{}} = R\sqrt {\alpha {{t}_{1}}{\text{/}}k} }$. В результате отражения ${{{\Sigma }_{{\text{1}}}}}$ от упругопластической $r = m_{*}^{{}}$ начинают движение поверхности разрывов с противоположно направленными скоростями: Σ2: r = r2(t) = ${m_{*}^{{}} - G(t - {{t}_{1}})}$ и ${{{\Sigma }_{{\text{3}}}}{\text{:}}\;r = {{r}_{{\text{3}}}}\left( t \right) = m_{*}^{{}} + G\left( {t - {{t}_{1}}} \right)}$ к граничным поверхностям ${r = {{r}_{{\text{0}}}}}$ и ${r = R}$ соответственно. В области ${{{V}^{{\left( {\text{2}} \right)}}}{\text{:}}\;{{r}_{{\text{2}}}}\left( t \right) \leqslant r \leqslant m_{*}^{{}}}$ движение среды подчиняется уравнению (4.3), а в области ${{{V}^{{\left( {\text{3}} \right)}}}{\text{:}}\;m_{*}^{{}} \leqslant r \leqslant }{{r}_{{\text{3}}}}\left( t \right)$ уравнение движения принимает вид:

(4.9)
${{{\psi }_{{,rr}}} + \frac{{\text{3}}}{r}{{\psi }_{{,r}}} - \frac{{\ddot {\psi }}}{{{{G}^{{\text{2}}}}}} = {\text{0}}}$

Краевыми условиями для уравнений (4.3) и (4.9) являются условие непрерывности перемещений на поверхностях r = r2(t) и r = r3(t), а также условие совпадения перемещений и напряжений на упругопластической границе r = ${{m}_{*}}$. Последнее обеспечивает нам гладкость решения в области r2(t) ≤ r ≤ r3(t) в каждый момент времени, следующий за t1

(4.10)
${{{{\left. {\left[ \psi \right]} \right|}}_{{{{\Sigma }_{2}}}}} = {\text{0,}}\quad {{{\left. {\left[ \psi \right]} \right|}}_{{{{\Sigma }_{3}}}}} = {\text{0,}}\quad {{{\left. {{{\psi }^{{\left( {\text{2}} \right)}}}} \right|}}_{{{{m}_{*}}}}} = {{{\left. {{{\psi }^{{\left( {\text{3}} \right)}}}} \right|}}_{{{{m}_{*}}}}}{\text{, }}\quad }{{\left. {\sigma _{{r\varphi }}^{{\left( {\text{2}} \right)}}} \right|}_{{{{m}_{*}}}}} = {{\left. {\sigma _{{r\varphi }}^{{\left( {\text{3}} \right)}}} \right|}_{{{{m}_{*}}}}}$

Как и раньше, индекс в круглых скобках принимает значение номера той волны, к зоне влияния которой эта величина относится. Решение для искомой функции ω(r, t) за волнами ${{\Sigma }_{{\text{2}}}}$ и ${{\Sigma }_{{\text{3}}}}$ представим лучевыми рядами аналогичными (4.5)

(4.11)
${{{\omega }^{{\left( {\text{2}} \right)}}} = {{{\left. {({{\omega }^{{\left( {\text{1}} \right)}}} - {{\chi }_{{\text{2}}}})} \right|}}_{{{{\tau }_{{\text{2}}}}}}} + {{{\left. {({{{\dot {\omega }}}^{{\left( {\text{1}} \right)}}} - {{\zeta }_{{\text{2}}}})} \right|}}_{{{{\tau }_{{\text{2}}}}}}}\left( {t - {{\tau }_{{\text{2}}}}} \right) + \cdots }$
(4.12)
${{{\omega }^{{\left( {\text{3}} \right)}}} = {{{\left. {({{\omega }^{{\left( E \right)}}} - {{\chi }_{{\text{3}}}})} \right|}}_{{{{\tau }_{{\text{3}}}}}}} + {{{\left. {({{{\dot {\omega }}}^{{\left( E \right)}}} - {{\zeta }_{{\text{3}}}})} \right|}}_{{{{\tau }_{{\text{3}}}}}}}\left( {t - {{\tau }_{{\text{3}}}}} \right) + \cdots }$
$\begin{gathered} {{{\chi }_{i}} = {{{\left. {\left[ \omega \right]} \right|}}_{{{{\Sigma }_{i}}}}},\quad {{\zeta }_{i}} = {{{\left. {\left[ {\dot {\omega }} \right]} \right|}}_{{{{\Sigma }_{i}}}}},\quad i = 1,2,\quad {{\tau }_{{\text{2}}}} = {{t}_{1}} + (m_{*}^{{}} - r){\text{/}}G} \\ {{\tau }_{{\text{3}}}} = {{t}_{1}} + (r - m_{*}^{{}}){\text{/}}G \\ \end{gathered} $

Дифференциальные уравнения для коэффициентов лучевых рядов получаем, применив к уравнению движения алгоритм описанный выше. После интегрирования, подстановки результата в лучевые ряды и сравнения с граничными условиями, оказалось, что на волне ${{\Sigma }_{{\text{2}}}}$ скорость и ускорение остаются непрерывными, т.е. ${{\chi }_{{\text{2}}}} = {{\zeta }_{{\text{2}}}} = {\text{0}}$, а ${{\Sigma }_{{\text{3}}}}$ является ударной волной. Разрывы производных более высокого порядка в области ${{V}^{{{\text{(2)}}}}}$ можно отследить, если продолжить лучевой ряд (4.11) с требуемой степенью точности. Таким образом, в рамках принятого линейного по времени приближения для скорости и напряжения, решение в области ${{r}_{{\text{0}}}} \leqslant r \leqslant m_{*}^{{}}$ по-прежнему определяется соотношениями (4.7), а в области ${{V}^{{\left( {\text{3}} \right)}}}$ имеем:

${{{\psi }^{{\left( {\text{3}} \right)}}}\left( {r,t} \right) = {{\psi }^{{\left( E \right)}}}\left( {r,{{\tau }_{{\text{3}}}}} \right) + {{{\left. {({{\omega }^{{\left( E \right)}}} - {{\chi }_{{\text{3}}}})} \right|}}_{{{{\tau }_{{\text{3}}}}}}}\left( {t - {{\tau }_{{\text{3}}}}} \right) + \frac{{\text{1}}}{{\text{2}}}{{{\left. {({{{\dot {\omega }}}^{{\left( E \right)}}} - {{\zeta }_{{\text{3}}}})} \right|}}_{{{{\tau }_{{\text{3}}}}}}}{{{\left( {t - {{\tau }_{{\text{3}}}}} \right)}}^{{\text{2}}}} + \cdots }$
(4.13)
$\begin{gathered} {\sigma _{{r\varphi }}^{{\left( {\text{3}} \right)}}\left( {r{\text{,}}t} \right) = \frac{{\alpha {{R}^{2}}{{\tau }_{3}}}}{{{{r}^{2}}}} + \frac{{\mu {{A}_{3}}}}{{G\sqrt r }} + \left( {\frac{{\alpha {{R}^{2}}}}{{{{r}^{2}}}} + \frac{{15\mu {{A}_{3}}}}{{8{{r}^{{3{\text{/}}2}}}}} + \frac{{\mu {{B}_{3}}}}{{G\sqrt r }}} \right)\left( {t - {{\tau }_{{\text{3}}}}} \right) + \cdots } \\ {{{\chi }_{{\text{3}}}} = \frac{{{{A}_{3}}}}{{r_{{\text{3}}}^{{{\text{3/2}}}}}}{\text{,}}\quad {{\zeta }_{{\text{3}}}} = \frac{{{{B}_{3}}}}{{r_{{\text{3}}}^{{{\text{3/2}}}}}} + \frac{{{\text{3}}G{{A}_{3}}}}{{{\text{8}}r_{{\text{3}}}^{{{\text{5/2}}}}}}} \\ \end{gathered} $
${{A}_{3}} = {{A}_{1}} - \frac{{8km_{*}^{{3{\text{/}}2}}}}{{3\eta }} + \frac{{4\alpha {{R}^{2}}\sqrt {m_{*}^{{}}} }}{{\eta G}},\quad {{{B}_{3}} = }{{B}_{1}} + \frac{{5kG\sqrt {m_{*}^{{}}} }}{\eta } + \frac{{\alpha {{R}^{2}}}}{{2\eta \sqrt {m_{*}^{{}}} }}$

Следующее изменение волновой картины произойдет в момент времени t2 = t1 + + $(R - {{m}_{*}}){\text{/}}G$, когда волна ${{\Sigma }_{{\text{3}}}}$ отразится от внешнего цилиндра ${r = R}$, дав начало новой поверхности разрыва ${{{\Sigma }_{{\text{4}}}}{\text{:}}\;r = {{r}_{{\text{4}}}}\left( t \right) = R - G\left( {t - {{t}_{2}}} \right)}$. Движение среды в области V(4) : ${{{r}_{{\text{4}}}}(t) \leqslant r \leqslant R}$ подчиняется уравнению движения (4.9), краевыми условиями для которого служат условие прилипания на ${r = R}$ (3.1) и условие непрерывности перемещений на фронте волны ${{\Sigma }_{{\text{4}}}}$. Таким образом, в области ${{V}^{{\left( {\text{4}} \right)}}}$ имеем:

${{{\psi }^{{\left( {\text{4}} \right)}}}\left( {r{\text{,}}t} \right) = {{\psi }^{{\left( 3 \right)}}}\left( {r,{{\tau }_{{\text{4}}}}} \right) + {{{\left. {({{\omega }^{{\left( 3 \right)}}} - {{\chi }_{{\text{4}}}})} \right|}}_{{{{\tau }_{{\text{4}}}}}}}\left( {t - {{\tau }_{{\text{4}}}}} \right) + \frac{{\text{1}}}{{\text{2}}}{{{\left. {({{{\dot {\omega }}}^{{\left( 3 \right)}}} - {{\zeta }_{{\text{4}}}})} \right|}}_{{{{\tau }_{4}}}}}{{{\left( {t - {{\tau }_{{\text{4}}}}} \right)}}^{{\text{2}}}} + \cdots }$
(4.14)
${\sigma _{{r\varphi }}^{{\left( {\text{4}} \right)}}\left( {r{\text{,}}t} \right) = \sigma _{{r\varphi }}^{{\left( {\text{3}} \right)}}\left( {r{\text{,}}{{\tau }_{{\text{4}}}}} \right) - \frac{{\mu {{A}_{4}}}}{{G\sqrt r }} + \left( {\dot {\sigma }_{{r\varphi }}^{{\left( {\text{3}} \right)}}\left( {r{\text{,}}{{\tau }_{{\text{4}}}}} \right) + \frac{{15\mu {{A}_{4}}}}{{8{{r}^{{3/2}}}}} - \frac{{\mu {{B}_{4}}}}{{G\sqrt r }}} \right)\left( {t - {{\tau }_{{\text{4}}}}} \right) + \cdots }$
$\begin{gathered} {{{\chi }_{{\text{4}}}} = \frac{{{{A}_{4}}}}{{r_{{\text{4}}}^{{{\text{3/2}}}}}}{\text{,}}\quad {{\zeta }_{{\text{4}}}} = \frac{{{{B}_{4}}}}{{r_{{\text{4}}}^{{{\text{3/2}}}}}} - \frac{{{\text{3}}G{{A}_{4}}}}{{{\text{8}}r_{{\text{4}}}^{{{\text{5/2}}}}}}{\text{,}}}\quad {{A}_{4}} = {{A}_{3}},\quad {{{B}_{4}}}\, = {{B}_{3}} + \frac{{15G{{A}_{3}}}}{{4R}} \\ {{\tau }_{4}} = {{t}_{2}} + \left( {R - r} \right){\text{/}}G \\ \end{gathered} $

Поверхность $r = {{r}_{{\text{4}}}}\left( t \right)$ является сходящейся ударной волной. Следует отметить, что по мере ее продвижения к внутренней границе возможно появление новой пластической области вследствие нарастающей интенсивности разрыва за счет увеличения кривизны волнового фронта. На этом этапе аналитическое исследование считаем законченным, расчет дальнейшего деформирования при необходимости целесообразно вести численно, используя аналитическое решение для аппроксимации решения в узлах прифронтовой области.

5. Заключение. Рассмотренная задача отличается сменой скоростных режимов деформирования: от низкоскоростного (квазистатического) на этапе накопления необратимых деформаций до динамического на этапе разгрузки, распространяющейся в виде слабой ударной волны. Если на первом этапе удается получить точное решение краевой задачи, то на втором этапе для построения приближенного аналитического решения за фронтом волны разгрузки применяется метод лучевых рядов. Таким же способом выполнен расчет отражения первоначальной волны разгрузки от упругопластической границы и граничной поверхности. Существенное упрощение в решение задачи вносят предположение о малости обратимых деформаций и одномерный характер деформирования. В этом случае скорости волн оказываются постоянными, а лучи (ортогональные траектории точек волновой поверхности) прямыми линиями. В случае конечных деформаций скорость и положение волнового фронта будут зависеть от состояния перед волной и интенсивности разрывов на волне. Кроме того, усложняется волновая картина, т.к. в среде с предварительными деформациями распространяются сразу две сдвиговые ударные волны: плоскополяризованная волна и волна круговой поляризации.

Тем не менее, результаты настоящей работы могут быть полезны при постановках нестационарных задач теории больших деформаций, но с более сложными краевыми условиями, а также при использовании полученных приближенных решений в численных конечно-разностных расчетах в прифронтовых узлах на сетке вдоль луча.

Рис. 1.

Распределение касательного напряжения в момент времени $t = {{t}_{{\text{1}}}}$.

Рис. 2.

Распределение угла поворота в момент времени $t = {{t}_{{\text{1}}}}$.

Список литературы

  1. Феодосьев В.И. Избранные задачи и вопросы по сопротивлению материалов. М.: Гостехиздат, 1953. 376 с.

  2. Тимошенко С.П. Устойчивость упругих систем. М. – Л.: Гостехиздат, 1946. 532 с.

  3. Спорыхин А.Н., Шашкин А.И. Устойчивость равновесия пространственных тел и задачи механики горных пород. М.: Физматлит, 2004. 231 с.

  4. Черепанов Г.П., Ершов Л.В. Механика разрушения. М.: Машиностроение, 1977. 224 с.

  5. Chernyshov A.D. On conditions of snow avalanching and landslides // Mech. Solids. 2013. V. 48. P. 348–355. https://doi.org/10.3103/S0025654413030114

  6. Burenin A.A., Kovtanyuk L.V., Polonik M.V. The formation of a one-dimensional residual stress field in the neighbourhood of a cylindrical defect in the continuity of an elastoplastic medium // J. Appl. Math. Mech. 2003. V. 67. № 2. P. 283–292. https://doi.org/10.1016/S0021-8928(03)90014-1

  7. Burenin A.A., Kovtanyuk L.V., Lushpei A.V. The transient retardation of a rectilinear viscoplastic flow when the loading stresses are abruptly removed // J. Appl. Math. Mech. 2009. V. 73. № 4. P. 478–482. https://doi.org/10.1016/j.jappmathmech.2009.08.001

  8. Burenin A.A., Kovtanyuk L.V., Kulaeva D.V. Interaction of a one-dimensional unloading wave with an elastoplastic boundary in an elastoviscoplastic medium // J. Appl. Mech. Tech. Phys. 2012. V. 53. P. 90–97. https://doi.org/10.1134/S0021894412010129

  9. Rivlin R.S. Large elastic deformations of isotropic materials. VI. Further results in the theory of torsion, shear and flexure // Phil. Trans. Roy. Soc. London Ser. A. 1949. V. 242. № 845. P. 173–195. https://doi.org/10.1098/rsta.1949.0009

  10. Jiang X., Ogden R.W. On azimuthal shear of a circular cylindrical tube of compressible elastic material // Q. J. Mech. Appl.Math. 1998. V. 51. № 1. P. 143–158. https://doi.org/10.1093/qjmam/51.1.143

  11. Ogden R.W. Stress softening and residual strain in the azimutal shear of a pseudo-elastic circular cylindrical tube // Int. J. Nonlin. Mech. 2001. V. 36. № 3. P. 477–487. https://doi.org/10.1016/S0020-7462(00)00080-9

  12. Horgan C.O., Saccomandi G. Pure azimuthal shear of isotropic, incompressible hyperelastic materials with limiting chain extensibility // Int. J. Nonlin. Mech. 2001. V. 36. № 3. P. 465–475. https://doi.org/10.1016/S0020-7462(00)00048-2

  13. Carroll M.M. Azimuthal shear in compressible finite elasticity // J. Elasticity. 2007. V. 88. № 2. P. 141–149. https://doi.org/10.1007/s10659-007-9123-3

  14. Kassianidis F., Ogden R.W., Merodio J., Pence T.J. Azimutal shear of a transversely isotropic elastic solid // Math. Mech. Solids. 2009. V. 13. № 8. P. 690–724. https://doi.org/10.1177/1081286507079830

  15. O’Callaghan L., O’Reilly O.M., Zhornitskaya L. On azimuthal shear waves in a transversely iso- tropic viscoelastic mixture: Application to diffuse axonal injury // Math. Mech. Solids. 2011. V. 16. № 6. P. 625–636. https://doi.org/10.1177/1081286510387855

  16. Burenin A.A., Kovtanyuk L.V., Ustinova A.S. Viscosimetric flow of an incompressible elastoviscoplastic material under the presence of a lubricant on the boundary surfaces // J. Appl. Ind. Math. 2012. V. 6. P. 431–442. https://doi.org/10.1134/S1990478912040047

  17. Begun A.S., Burenin A.A., Kovtanyuk L.V. Flow of an elastoviscoplastic material between rotating cylindrical surfaces with nonrigid cohesion // J. Appl. Mech. Tech. Phys. 2015. V. 56. P. 293–303. https://doi.org/10.1134/S0021894415020157

  18. Буренин А.А., Быковцев Г.И., Ковтанюк Л.В. Об одной простой модели для упругопластической среды при конечных деформациях // ДАН. 1996. Т. 347. № 2. С. 199–201.

  19. Буренин А.А., Ковтанюк Л.В. Большие необратимые деформации и упругое последействие. Владивосток: Дальнаука, 2013. 321 с.

  20. Лурье А.И. Нелинейная теория упругости. М.: Наука, 1980. 512 с.

  21. Быковцев Г.И., Ивлев Д.Д. Теория пластичности. Владивосток: Дальнаука, 1998. 528 с.

  22. Быковцев Г.И., Вервейко Н.Д. О распространении волн в упруго-вязко-пластической среде // Инженерный журнал. МТТ. 1966. № 4. С. 111–123.

  23. Burenin A.A., Kovtanyuk L.V., Kulaeva D.V. Interaction of a one-dimensional unloading wave with an elastoplastic boundary in an elastoviscoplastic medium // J. Appl. Mech. Tech. Phys. 2012. V. 53. P. 90–97. https://doi.org/10.1134/S0021894412010129

  24. Kovtanyuk L.V., Rusanov M.M. On collision of an unloading wave with advancing elastoplastic boundary in a flat heavy layer // J. Appl. Ind. Math. 2015. V. 9. P. 519–526. https://doi.org/10.1134/S1990478915040080

  25. Rossikhin Y.A., Shitikova M.V. Ray Method for Solving Dynamic Problems Connected With Propagation of Wave Surfaces of Strong and Weak Discontinuities // Appl. Mech. Rev. 1995. V. 48. № 1. P. 1–39. https://doi.org/10.1115/1.3005096

  26. Achenbach J.D., Reddy D.P. Note on wave propagation in linearly viscoelastic media // ZAMP. 1967. V. 18. P. 141–144. https://doi.org/10.1007/BF01593905

  27. Томас Т. Пластическое течение и разрушение в твердых телах. М.: Мир, 1964. 308 с.

  28. Гринфельд М.А. Методы механики сплошных сред в теории фазовых превращений. М.: Наука, 1990. 312 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал