Известия РАН. Механика твердого тела, 2022, № 1, стр. 133-144

1. Введение. Аэродинамический маятник, т.е. маятниковая система, движущаяся в потоке сопротивляющейся среды и взаимодействующая с ним, представляет собой весьма интересный объект. Он может рассматриваться как компонент различных технических систем, в частности, ветроэнергетических установок различных типов (например, ветротурбины Дарье с прямыми лопастями [1]), систем дозаправки летательных аппаратов в воздухе [2], элементов управления в летательных аппаратах и т.д. В последнее время активно рассматриваются различные варианты ветроэнергетических систем, рабочим элементом которых является упругая конструкция, совершающая колебания в результате взаимодействия с потоком среды [3–5], и исследование динамики упруго закрепленного аэродинамического маятника может оказаться полезным для анализа особенностей поведения таких систем.

При описании движения маятника в потоке среды необходимо, вообще говоря, учитывать нестационарность аэродинамического воздействия. Интегрирование уравнений Навье–Стокса с учетом движения твердого тела позволяет дать подробное описание движения среды и аэродинамических сил. Однако, оно требует достаточно значительных вычислительных ресурсов и времени и практически не позволяет проводить параметрический анализ системы. Поэтому активно используются различные упрощенные феноменологические модели.

Одной из наиболее часто применяемых моделей такого типа является квазистатический подход [6]. С его помощью исследовались разные аспекты поведения различных механических систем, включающих тела, взаимодействующие с сопротивляющейся средой [7, 8], в том числе, однозвенных аэродинамических маятников без пружины в креплении [9–11]. Были рассмотрены локальные и нелокальные бифуркации, возникающие в соответствующей динамической системе, а также изучены периодические режимы, существующие в ней. В [12] на основе квазистатического подхода проанализирована динамика двухзвенного аэродинамического маятника в упругом закреплении и показано, что этот подход обеспечивает качественное (а в ряде случаев и количественное) согласие с экспериментами.

Чтобы описать нестационарные эффекты более точно, чем это позволяет квазистатический подход, были предложены другие феноменологические модели. Среди них выделяется группа моделей, основанных на использовании дополнительных переменных, характеризующих нестационарное взаимодействие тела с потоком (такие модели используются, например, в [13–15]). В работах [16, 17] для учета внутренней динамики потока среды предложен подход подобного типа, основанный на введении дополнительной “скрытой” обобщенной координаты (“присоединенного осциллятора”), интегральным образом характеризующей состояние потока вблизи тела. В [18] модель присоединенного осциллятора была использована для анализа поведения аэродинамического маятника без пружины в креплении, и было показано, в частности, что в случае достаточно малой длины державки тривиальное положение равновесия теряет устойчивость при увеличении момента инерции маятника.

В данной статье анализируются положения равновесия и предельные циклы, возникающие в динамике упруго закрепленного аэродинамического маятника в случае, когда пружина крепления имеет кубическую нелинейность.

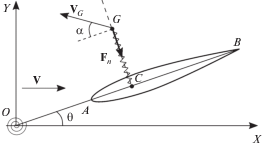
2. Постановка задачи. Рассмотрим механическую систему, представляющую собой однозвенный аэродинамический маятник в упругом закреплении (рис. 1). Этот маятник состоит из тонкого крыла с симметричным профилем и твердого стержня – державки. Державка находится в плоскости симметрии крыла. Ось вращения $O$ вертикальна и также принадлежит плоскости симметрии крыла. В шарнире $O$ установлена спиральная пружина с кубической нелинейностью.

Вся система помещена в стационарный горизонтальный поток среды, скорость которого на бесконечности постоянна и равна $V$. Будем считать также, что пружина крепления не напряжена, когда державка маятника ориентирована вдоль набегающего потока.

Введем в горизонтальной плоскости неподвижную систему координат $OXY$, ось абсцисс которой направим вдоль вектора ${\mathbf{V}}$. Положение маятника будем характеризовать углом $\theta $ между державкой и осью $OX$.

Для учета нестационарности аэродинамического воздействия потока на маятник воспользуемся моделью [18], в которой внутренняя динамика потока описывается с помощью присоединенного осциллятора $CG$, прикрепленного к хорде крыла в статическом центре давления $C$ ($OC = l$), причем точка $G$ может перемещаться вдоль нормали к хорде. Обозначим расстояние $CG$ через $\eta $. Будем считать, что аэродинамическая сила приложена в точке $G$, ее составляющая, направленная вдоль хорды профиля (тангенциальная сила), пренебрежимо мала, а нормальная к хорде составляющая имеет следующую структуру:

Здесь $\rho $ – плотность среды, $S$ – характерная площадь крыла, ${{C}_{n}}$ – безразмерный коэффициент нормальной силы, ${{V}_{G}}$ – воздушная скорость точки $G$, $\alpha $ – угол между вектором ${{{\mathbf{V}}}_{G}}$ и хордой $AB$ (эффективный угол атаки). Из кинематических соображений следует, что

Уравнения движения системы “маятник + осциллятор” можно записать в следующем виде:

Здесь $m$ – масса осциллятора, $k$ и $h$ – его коэффициенты жесткости и демпфирования, $J$ – момент инерции маятника относительно оси вращения, $\kappa $ и ${{\kappa }_{3}}$ – коэффициенты, характеризующие жесткость пружины крепления, $\delta $ – коэффициент демпфирования этой пружины.

Обезразмерим уравнения, выбрав в качестве безразмерного времени величину $\tau = tV{\text{/}}b$ (где $b$ – длина хорды крыла) и введя следующие безразмерные переменные и параметры:

Далее для упрощения записи будем обозначать производную по безразмерному времени точкой и опускать черту над безразмерными величинами.

Вообще говоря, коэффициент нормальной силы представляет собой достаточно сложную $2\pi $-периодическую функцию угла атаки (нечетную в случае крыла с симметричным профилем). Однако из многочисленных экспериментов известно, что при малых углах атаки эта зависимость с хорошей точностью является линейной: ${{C}_{n}} = C_{n}^{\alpha }\alpha $. В дальнейшем ограничимся рассмотрением таких движений маятника, при которых угол атаки остается малым. Отметим, что для крыльев $C_{n}^{\alpha } > 0$.

Тогда уравнения (2.1) примут вид:

Исследуем поведение траекторий системы (2.2).

3. Положения равновесия и их устойчивость. Пусть $\left( {{{\theta }_{s}},{{\eta }_{s}}} \right)$ – неподвижная точка системы (2.2). Тогда величины ${{\theta }_{s}}$ и ${{\eta }_{s}}$ удовлетворяют следующим уравнениям:

Очевидно, что система (3.1) имеет тривиальное равновесие ${{\theta }_{s}} = 0$, ${{\eta }_{s}} = 0$. При этом маятник находится во флюгерном положении.

Если $lC_{n}^{\alpha } + \kappa > 0$ (это условие выполнено, в частности, если $l > 0$, т.е. центр давления расположен “ниже по потоку”, чем точка подвеса), то других неподвижных точек у системы нет, поскольку величины $C_{n}^{\alpha }$ и $\kappa $ положительны. Если же $lC_{n}^{\alpha } + \kappa < 0$, то имеются еще два симметричных “косых” равновесия:

Поскольку наше рассмотрение ограничено областью малых углов атаки, будем считать, что параметры системы таковы, что величины ${{\theta }_{{s1,2}}}$ малы (когда они являются действительными числами). В частности, такая ситуация имеет место, когда параметр ${{\kappa }_{3}}$ велик: ${{\kappa }_{3}} \gg 1$.

Вначале рассмотрим тривиальное равновесие. Система (2.2), линеаризованная в окрестности этого равновесия, имеет следующий вид:

Запишем характеристический полином системы (3.2):

Очевидно, что тривиальное равновесие статически неустойчиво при $lC_{n}^{\alpha } + \kappa < 0$. Если же $lC_{n}^{\alpha } + \kappa > 0$, то все коэффициенты полинома (3.3) положительны. Поэтому достаточные условия асимптотической устойчивости тривиального равновесия в этом случае сводятся к условию положительности третьего минора матрицы Гурвица для (3.3), которое можно представить в следующем виде:

где

Результаты идентификации параметров осциллятора [18] показывают, что для них выполнены следующие неравенства:

Пусть $l > 0$. Нетрудно видеть, что, с учетом (3.6), при этом ${{B}_{0}} > 0$. Кроме того, можно путем несложных выкладок показать, что ${{B}_{1}} > 0$ при ${{B}_{2}} > 0$. Таким образом, ${{B}_{2}} > 0$ оказывается достаточным условием асимптотической устойчивости при $l > 0$. Оно, очевидно, выполнено при любых длинах державки, если коэффициент $\delta $ достаточно велик: $\delta > {{{{{(C_{n}^{\alpha })}}^{3}}} \mathord{\left/ {\vphantom {{{{{(C_{n}^{\alpha })}}^{3}}} {4{{k}^{2}}}}} \right. \kern-0em} {4{{k}^{2}}}}$.

Соответственно, неравенство

является необходимым условием неустойчивости в области $l > 0$. Если коэффициент демпфирования мал, так что $\delta < {{(C_{n}^{\alpha })}^{{\text{3}}}}{\text{/}}4{{k}^{2}}$, то существует интервал $l \in \left( {{{l}_{1}},{{l}_{2}}} \right)$, ${{l}_{{1,2}}} > 0$, в котором ${{B}_{2}} < 0$:

Для каждого $l$ из указанного интервала существует ровно одно положительное значение ${{J}_{*}}$ момента инерции, при котором третий минор матрицы Гурвица обращается в нуль (происходит бифуркация Андронова–Хопфа). При меньших величинах момента инерции положение равновесия асимптотически устойчиво, а при больших – неустойчиво. Таким образом, в случае, когда длина державки маятника удовлетворяет неравенствам ${{l}_{1}} < l < {{l}_{2}}$, увеличение момента инерции маятника приводит к дестабилизации “флюгерного” положения равновесия. Этот эффект был описан в работе [18] для маятника без пружины в креплении. Заметим, что границы этого интервала по l не зависят от параметров, характеризующих жесткость пружины.

Найдем величину $J_{*}^{{}}$ и частоту $\omega _{*}^{{}}$ предельного цикла, рождающегося в результате соответствующей бифуркации. Для этого подставим в (3.3) $\lambda = i\omega _{*}^{{}}$ ($\omega _{*}^{{}} \ne 0$) и после несложных преобразований получим:

С учетом (3.6) и (3.7) первое уравнение (3.9) имеет единственное положительное решение.

Очевидно, что при $l \to {{l}_{1}} + 0$ и $l \to {{l}_{2}} - 0$ имеем $\omega _{*}^{{}} \to 0$, соответственно, $J_{*}^{{}} \to \infty $.

Любопытно, что получаемая из (3.9) величина $\omega _{*}^{{}}$ не зависит от жесткости пружины крепления. При этом, как нетрудно показать, $\omega _{*}^{{}}$ убывает с ростом коэффициента демпфирования $\delta $.

Отметим также, что критическое значение момента инерции растет с увеличением коэффициента жесткости пружины крепления.

С учетом (3.5) нетрудно видеть, что левая часть (3.4) представляет собой полином 6 степени относительно $l$, причем в силу (3.6) все его коэффициенты, за исключением коэффициентов при $l$ и ${{l}^{2}}$, положительны. Значит, по теореме Декарта, этот полином имеет не более 2 действительных корней. Кроме того, при малых значениях момента инерции положительны все коэффициенты полинома, так что при этом асимптотическая устойчивость имеет место при всех положительных $l$.

Теперь обратимся к случаю $l < 0$. Заметим, что при этом все коэффициенты в первом уравнении (3.9) положительны, следовательно, действительных решений нет. Соответственно, в области отрицательных $l$ корни характеристического полинома не могут пересекать мнимую ось в точках, отличных от начала координат. Нулевой корень существует только при $l = - {\kappa \mathord{\left/ {\vphantom {\kappa {C_{n}^{\alpha }}}} \right. \kern-0em} {C_{n}^{\alpha }}}$. Следовательно, при $ - {\kappa \mathord{\left/ {\vphantom {\kappa {C_{n}^{\alpha }}}} \right. \kern-0em} {C_{n}^{\alpha }}} < l < 0$ имеет место асимптотическая устойчивость.

При $l = - \kappa {\text{/}}C_{n}^{\alpha }$ в системе происходит бифуркация типа “вилка”, и тривиальное решение становится неустойчивым при $l < - {\kappa \mathord{\left/ {\vphantom {\kappa {C_{n}^{\alpha }}}} \right. \kern-0em} {C_{n}^{\alpha }}}$. Нетрудно показать, что рождающиеся при этом “косые” равновесия асимптотически устойчивы при $l$, близких к бифуркационному значению.

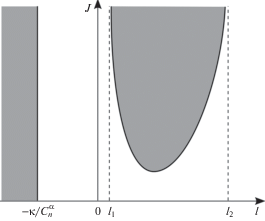
С учетом вышесказанного, границы области асимптотической устойчивости тривиального равновесия на плоскости параметров J, $l$ имеют вид, качественно изображенный на рис. 2 (области неустойчивости показаны серым цветом).

Будем предполагать, что $\left| {{{\theta }_{{s1,2}}}} \right| = \mu = 1$ Характеристический полином системы, линеаризованной в окрестности косого равновесия, имеет следующую структуру:

Видно, что нулевой корень у (3.10) также существует только при $l = - {\kappa \mathord{\left/ {\vphantom {\kappa {C_{n}^{\alpha }}}} \right. \kern-0em} {C_{n}^{\alpha }}}$. В то же время, косые равновесия существуют и отличны от нуля только при $l < - {\kappa \mathord{\left/ {\vphantom {\kappa {C_{n}^{\alpha }}}} \right. \kern-0em} {C_{n}^{\alpha }}}$.

Пусть 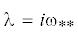(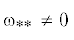). Нетрудно показать, что ${{\omega }_{{**}}}$ является корнем биквадратного уравнения, коэффициенты которого с точностью до $O({{\mu }^{2}})$ совпадают с коэффициентами биквадратного уравнения на $\omega _{*}^{{}}$ (3.8). При $l < 0$ все эти коэффициенты, как было отмечено выше, положительны. Значит, чисто мнимые корни у (3.9) отсутствуют.

Таким образом, корни характеристического полинома (3.10) не пересекают мнимую ось при $l < - {\kappa \mathord{\left/ {\vphantom {\kappa {C_{n}^{\alpha }}}} \right. \kern-0em} {C_{n}^{\alpha }}}$, следовательно, “косые” равновесия остаются асимптотически устойчивыми при всех значениях параметров, при которых они существуют, а углы ${{\theta }_{{s1,2}}}$ достаточно малы.

4. Периодические решения. В соответствии с вышесказанным, в случае, когда $l \in ({{l}_{1}},{{l}_{2}})$, а момент инерции маятника достаточно велик, тривиальное равновесие неустойчиво, других равновесий нет, и в системе существует цикл, родившийся в результате бифуркации Андронова–Хопфа. Исследуем этот цикл, считая, что ${{\kappa }_{3}} \gg 1$. Это означает, что в пружине присутствует значительное упрочнение. Такая ситуация имеет место для некоторых пружин в области небольших деформаций. Введем малый параметр: $\varepsilon = \sqrt {\kappa _{3}^{{ - 1}}} \ll 1$. Тогда амплитуда колебаний будет мала в достаточно широком диапазоне значений остальных параметров, и сделанные выше предположения относительно ${{C}_{n}}$ будут справедливы.

Для оценки параметров цикла воспользуемся методом гармонического баланса. Будем искать периодические решения вида

Подставив (4.1) в систему (2.2), в первом приближении по малому параметру получим:

Нетрудно показать, что ${{\omega }_{0}}$ равно ${{\omega }_{*}}$. Таким образом, частота цикла, существующего при произвольном (но достаточно большом, чтобы имела место неустойчивость тривиального равновесия) значении момента инерции маятника, с точностью до малого параметра совпадает с частотой цикла, рождающегося при бифуркации Андронова–Хопфа:

Здесь ${{q}_{1}} = hlC_{n}^{\alpha }(l(h + C_{n}^{\alpha }) - m) + \delta ({{(h + C_{n}^{\alpha })}^{2}} - 2km)$.

Соответственно, частота цикла достаточно слабо зависит как от коэффициентов, характеризующих жесткость пружины крепления, так и от момента инерции маятника. Этот эффект представляется любопытным.

Для коэффициентов ${{\theta }_{{11}}}$, ${{\eta }_{{11}}}$, ${{\eta }_{{21}}}$, характеризующих амплитуды колебаний маятника и присоединенного осциллятора, из (4.2) получаем следующие формулы:

где $\Delta = {{(h + C_{n}^{\alpha })}^{2}}\omega _{*}^{2} + {{(k - m\omega _{*}^{2})}^{2}}$.

Из (3.9) ясно, что, как и следовало ожидать, величина ${{\theta }_{{11}}}$ убывает с увеличением коэффициента жесткости $\kappa $.

В силу громоздкости выражения для первой ляпуновской величины вопрос о том, является ли цикл притягивающим, не удается разрешить аналитически. Тем не менее, заметим, что, как следует из (4.4), цикл указанного вида существует только при $J > J_{*}^{{}}$, т.е. в области, где тривиальное равновесие неустойчиво. Это косвенно свидетельствует о том, что он является притягивающим, а бифуркация Андронова–Хопфа – суперкритической.

Необходимо отметить, что в отсутствие демпфирования $\mathop {\lim }\limits_{l \to 0} \omega _{*}^{{}} = \infty $ и $\mathop {\lim }\limits_{l \to 0} J_{*}^{{}} = 0$. Соответственно, величина ${{\theta }_{{11}}}$ стремится к бесконечности при $l \to 0$, и предложенная аппроксимация в этой ситуации оказывается неприменимой.

5. Численное моделирование. Проведем численное исследование поведения системы при разных значениях параметров. Примем для параметров присоединенного осциллятора такие же значения, что и в [18]: $m = 1.5$, $k = 3$, $h = 8$. Пусть ${{\kappa }_{3}} = 100$. Для коэффициента нормальной силы примем $C_{n}^{\alpha } = 5.5$ (это соответствует стандартному профилю NACA 0012 [19]). Будем считать также, что коэффициент демпфирования достаточно мал: $\delta < {{{{{(C_{n}^{\alpha })}}^{3}}} \mathord{\left/ {\vphantom {{{{{(C_{n}^{\alpha })}}^{3}}} {4{{k}^{2}}}}} \right. \kern-0em} {4{{k}^{2}}}}$, так что величины ${{l}_{{1,2}}}$ в формулах (3.8) являются вещественными. Для численного интегрирования будем использовать стандартный метод Рунге–Кутты 4 порядка.

Вначале рассмотрим ситуацию, когда в системе существует три положения равновесия: $l < - {\kappa \mathord{\left/ {\vphantom {\kappa {C_{n}^{\alpha }}}} \right. \kern-0em} {C_{n}^{\alpha }}}$. Численное интегрирование показывает, что в достаточно широком диапазоне параметров и начальных условий притягивающие циклы не наблюдаются, и траектории системы стремятся к одному из “косых” равновесий. Области притяжения этих равновесий в пространстве начальных условий в проекции на плоскость ${{\eta }_{0}} = 0$, ${{\dot {\eta }}_{0}} = 0$ при разных значениях параметров $l$ и $J$ представлены на рис. 3 (расчеты проводились при $\kappa = 1$, $\delta = 0.1$). Белым цветом отмечены такие начальные условия ${{\theta }_{0}}$, ${{\dot {\theta }}_{0}}$, что вышедшие из них траектории стремятся к положению равновесия $\theta \equiv {{\theta }_{{s1}}} > 0$, ${{\eta }_{{s1}}} \equiv - {{C_{n}^{\alpha }{{\theta }_{{s1}}}} \mathord{\left/ {\vphantom {{C_{n}^{\alpha }{{\theta }_{{s1}}}} k}} \right. \kern-0em} k} < 0$; траектории, выходящие из начальных условий, отмеченных серым цветом, стремятся ко второму “косому” положению равновесия ($\theta \equiv {{\theta }_{{s2}}} < 0$, ${{\eta }_{{s2}}} \equiv - C_{n}^{\alpha }{{\theta }_{{s2}}}$/k > 0). На рис. 3, a–d приведены результаты для $l = - 0.2$, а на рис. 3, e‒h – для $l = - 0.5$. Параметр $J$ принимает значения 0.1 (рис. 3 a, e), 1 (рис. 3 b, f), 5 (рис. 3, c, g) и 10 (рис. 3, d, h).

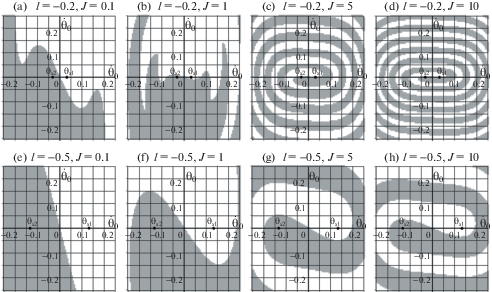
Указанные проекции областей притяжения имеют спиралевидную структуру, причем ширина “рукавов” спиралей и их средний угол закрутки уменьшаются с ростом момента инерции и увеличиваются с ростом $l$.

При $ - {\kappa \mathord{\left/ {\vphantom {\kappa {C_{n}^{\alpha }}}} \right. \kern-0em} {C_{n}^{\alpha }}} < l < {{l}_{1}}$, как было отмечено выше, существует только тривиальное равновесие, и оно асимптотически устойчиво. Численное моделирование показывает, что в достаточно широком диапазоне начальных условий и значений параметров других притягивающих инвариантных многообразий не наблюдается.

При ${{l}_{1}} < l < {{l}_{2}}$ в системе при достаточно больших значениях момента инерции существует цикл. Численное моделирование показывает, что он является притягивающим, а соответствующие колебания с достаточно хорошей точностью являются одночастотными в широком диапазоне значений параметров $l$ и $J$. Это проиллюстрировано на рис. 4, на котором представлены проекции фазовых траекторий на конфигурационную плоскость и плоскость ($\theta ,\dot {\theta }$) при $\kappa = 1$ и разных комбинациях значений параметров $l$, $J$ и $\delta $.

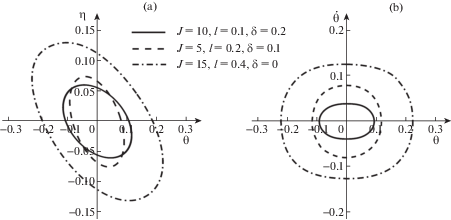
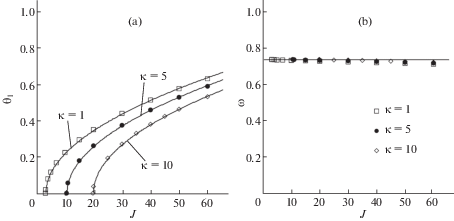
На рис. 5 показаны амплитуды ${{\theta }_{1}}$ и частоты колебаний в зависимости от момента инерции при разных значениях коэффициента жесткости $\kappa $ пружины (квадраты – $\kappa = 1$, круги – $\kappa = 5$, ромбы – $\kappa = 10$), полученные численным интегрированием системы (2.2). Расчеты проводились при $\delta = 0.1$, $l = 0.2$. Сплошные линии соответствуют аппроксимационным формулам (4.3)–(4.4). Видно, что в достаточно широком диапазоне значений параметров частота цикла мало отличается от величины ${{\omega }_{*}}$ и, таким образом, практически не зависит ни от $J$, ни от $\kappa $. Отличие становится заметным, когда амплитуда $\theta $ оказывается большой.

На рис. 6 проиллюстрировано влияние длины державки на амплитуду (рис. 6, а и 6, c) и частоту (рис. 6, b и 6, d) колебаний маятника в случае $\kappa = 1$ при различных значениях момента инерции и коэффициента демпфирования. Рис. 6а, 6b соответствуют значению $\delta = 0$, а рис. 6c и 6d – $\delta = 0.1$. Сплошными линиями вновь обозначены зависимости (4.3)–(4.4), а квадратами – частоты и амплитуды, полученные в результате численного интегрирования системы (2.2) при разных значениях параметров $l$ и J (белые квадраты: $J = 10$; черные квадраты: $J = 5$).

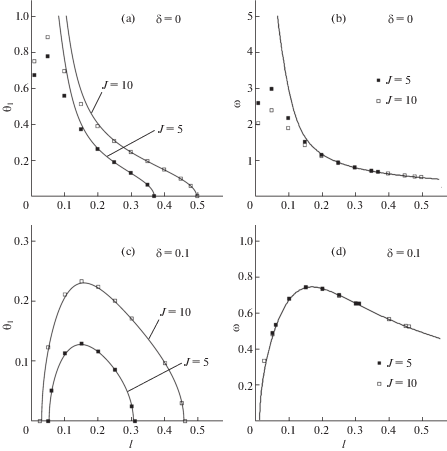
Видно, что аппроксимационные формулы достаточно хорошо согласуются с “точным” численным решением, если амплитуда колебаний маятника невелика (менее 0.3 рад). В частности, при $\delta = 0.1$ аппроксимация при рассмотренных значениях J оказывается достаточно эффективной во всей области существования цикла. Зависимость частоты цикла от момента инерции проявляется только при большой амплитуде цикла.

Впрочем, необходимо отметить, что при больших $\theta $ предложенный подход должен быть модифицирован, поскольку в этом случае необходимо учитывать нелинейность зависимости коэффициента нормальной силы от угла атаки.

6. Заключение. Рассмотрена динамика упруго закрепленного аэродинамического маятника. Для описания нестационарного аэродинамического воздействия используется модель присоединенного осциллятора.

Найден диапазон длин державки, в котором при достаточно больших значениях момента инерции маятника положение равновесия “вдоль потока” является неустойчивым, и существует предельный цикл. Получены аппроксимационные формулы для амплитуды и частоты этого цикла.

Проведено численное моделирование, показано, что предложенные формулы достаточно хорошо согласуются с результатами численного интегрирования уравнений движения в широком диапазоне значений параметров системы.

Исследование выполнено при поддержке Междисциплинарной научно-образовательной школы Московского университета “Фундаментальные и прикладные исследования космоса”.