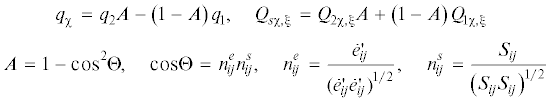Известия РАН. Механика твердого тела, 2022, № 1, стр. 103-121
ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ УСТАЛОСТНОЙ ДОЛГОВЕЧНОСТИ КОНСТРУКЦИОННЫХ СТАЛЕЙ ПРИ ОДНОЧАСТОТНОМ И ДВУХЧАСТОТНОМ НАГРУЖЕНИИ
И. А. Волков a, *, Л. А. Игумнов a, **, Д. Н. Шишулин a, ***, Е. В. Боев a, ****
a Национальный исследовательский Нижегородский государственный университет
им. Н.И. Лобачевского
Н. Новгород, Россия
* E-mail: pmptmvgavt@yandex.ru
** E-mail: igumnov@mech.unn.ru
*** E-mail: shishulindn@gmail.ru
**** E-mail: e.boev87@mail.ru
Поступила в редакцию 30.04.2021
После доработки 03.08.2021
Принята к публикации 24.09.2021
- EDN: UIMDVF
- DOI: 10.31857/S0572329922010111
Аннотация
В настоящей работе проведены исследования упругопластического поведения и ресурсных характеристик для широко использующихся в промышленности конструкционных материалов при усталостном одночастотном и двухчастотном нагружении. Развита математическая модель механики поврежденной среды, позволяющая моделировать упругопластическое поведение и определять ресурсные характеристики для конструкционных материалов при усталостном нагружении. Рассматриваются процессы малоцикловой и многоцикловой усталости. Модель базируется на совместном интегрировании уравнений, описывающих кинетику напряженно-деформированного состояния и процессов накопления повреждений. Замыкающим соотношением является критерий прочности, выполнение которого соответствует образованию макротрещины.
Уравнения пластичности основываются на основных положениях теории течения. В основе соотношений, моделирующих накопление повреждений лежит энергетический подход к определению ресурсных характеристик. Кинетика накопления усталостных повреждений основана на введении скалярного параметра поврежденности конструкционного материала и единой энергетической форме представления механизма деградации в условиях малоциклового и многоциклового нагружения. По предложенной математической модели механики поврежденной среды проведены численные исследования процессов кинетики напряженно-деформированного состояния и разрушения поликристаллических материалов – сталей 20 и 08Х18Н12Т в условиях одночастотного и двухчастотного усталостного нагружения. Результаты оценки достоверности показали, что развитая модель с высокой степенью точности описывает процессы малоцикловой и многоцикловой усталости.
1. Введение. Экспериментальные исследования усталости конструкционных материалов (поликристаллических металлов и их сплавов) позволяют сделать вывод, что усталость условно можно разделить как минимум на три области (рис. 1), характеризующиеся особенностями протекающих процессов накопления повреждений – область малоцикловой усталости обозначена цифрой 1, область многоцикловой усталости обозначена цифрой 2 и область гигацикловой усталости обозначена цифрой 3 [1–4].
Основной характерной особенностью малоцикловой усталости (МЦУ) является наличие в процессе нагружения макроскопических пластических деформаций во всем рассматриваемом объеме конструкционного материала. Данную область циклического нагружения в условиях одноосного нагружения лабораторных образцов (растяжения–сжатия) условно ограничивают числом циклов до образования макротрещины равным 104. Данный деградационный механизм характерен для зон с конструктивными концентраторами напряжений, такие как корень сварного шва, переходы с малыми радиусами скругления и т.п. с номинальными напряжениями в сечении конструктивного элемента ~0.5÷0.8 от предела текучести ${{{{\sigma }}}_{T}}$ и превышающим предел текучести в самом концентраторе. Для малоцикловой усталости характерны проявления эффектов упрочнения и разупрочнения материала, вызванные изменениями микроструктуры и фазового состава. При малоцикловой усталости кинетика образования и роста микродефектов зависит от истории нагружения конструкционного материала и его циклических свойств [5–7].
Характерной особенность многоцикловой усталости (МнЦУ) является наличие в процессе циклического нагружения микроскопических пластических деформаций при уровнях интенсивности действующих напряжений меньших чем предел текучести и больше, чем предел выносливости ${{{{\sigma }}}_{R}}$ на заданной базе числа циклов нагружения для конструкционного материала. Область многоциклового нагружения условно ограничивается числом циклов до образования макротрещины при одноосном нагружении лабораторных образцов (растяжении–сжатии) в диапазоне от 105 до 107. При многоцикловой усталости материала накопление повреждений происходит за счет процессов на микро- и мезоуровнях вследствие микроскопической пластической деформации, реализующейся за счет пластического деформирования отдельных разнесенных зерен и их конгломератов по объему конструкционного материала [3, 4].
Гигацикловая усталость конструкционных материалов возникает при воздействии нагрузок не превосходящих предела выносливости ${{{{\sigma }}}_{R}}$. Накопление повреждений при гигацикловой усталости описывается физическими моделями развития микротрещин и микропор в районе точечных дефектов и включений в поликристаллическом материале [4]. Особенностью разрушения при гигацикловой усталости является превалирующее влияние на ресурсные характеристики конструкционных материалов стадии зарождения усталостных микротрещин, так как процессы накопления повреждений ассоциируются с дефектами различной физической природы. Качественным отличием гигацикловой усталости от МЦУ и МнЦУ является то, что зарождение дефектов и дальнейшее развитие поврежденности происходит в локальных объемах материала. В связи с этим возникает существенная проблема при решении задачи оценки ресурсных характеристик при гигацикловой усталости – необходимость формирования критериев перехода от эволюционного развития точечных и неравномерно распределенных дефектов к макроскопическому разрушению [3].
В [5–12] на базе основных положений механики поврежденной среды развита математическая модель, описывающая процессы кинетики напряженно-деформированного состояния и накопления повреждений в поликристаллических металлах и их сплавах при нерегулярном термосиловом нагружении. В [13, 16] для оценки ресурсных характеристик при многоцикловой усталости приведен энергетический критерий и его экспериментальное обоснование.
Особое место при расчетах ресурсных характеристик машин и аппаратов новой техники, а также при продлении ресурса действующих инженерных объектов занимают виды нагружения в условиях которых реализуется суммарное воздействие от низкочастотных и высокочастотных нагрузок. Данный вид нагружения существенно влияет на пластические и ресурсные характеристики конструкционного материала. Достаточно большое количество работ, связанных с исследованиями процессов двухчастотного нагружения, посвящено разработке аналитических зависимостей для расчетной оценки ресурсных характеристик, однако они в основном основаны на критериальных подходах и не учитывают всей истории нагружения при эксплуатационном воздействии [13–16]. Необходимо отметить, что накопление повреждений при воздействии двухчастотного нагружения является существенно нелинейным процессом и определяющим образом зависит от кинетики напряженно-деформированного состояния и температуры нагружения. Анализ имеющихся экспериментальных данных при двухчастотном нагружении свидетельствует о существенном снижении циклической прочности по сравнению с одночастотным нагружением [14–17].
Таким образом, анализ экспериментальных и теоретических работ позволяет сделать вывод, что требуется научно-обоснованный подход к оценке ресурсных характеристик конструкционных материалов в условиях действия двух и более нагрузок, отличающихся по частоте и амплитуде воздействия. Подход должен основываться на физически обоснованных закономерностях, связывающих упругопластическое поведение материалов и ресурсные характеристики.
Один из подходов, позволяющих устранить данный недостаток, базируется на исследовании неупругих циклических деформаций как при раздельном, так и при двухчастотном нагружениях. Это особенно важно в связи с тем, что в ряде публикаций однозначно была показана взаимосвязь процессов неупругого деформирования и усталостного повреждения металлов [2, 13, 15, 16, 18].
Используемая в настоящей работе математическая модель механики поврежденной среды МПС [5–8] позволяет численно моделировать процессы кинетики напряженно-деформированного состояния при малоцикловой и многоцикловой усталости. Проверка достоверности полученных расчетных данных определялась из сравнения численных данных с результатами экспериментальных исследований.
2. Определяющие соотношения математической модели механики поврежденной среды. Основные гипотезы и положения для рассматриваемой математической модели МПС заключаются в том, что: рассматривается начально изотропный материал; рассматривается только анизотропия, связанная с процессами пластического деформирования; процесс поврежденности материала носит изотропный характер; тензоры деформаций ${{е}_{{ij}}}$ и их скоростей ${{\dot {е}}_{{ij}}}$ являются суммой упругих $е_{{ij}}^{е}$, $\dot {е}_{{ij}}^{е}$ и пластических компонент $е_{{ij}}^{р}$, $\dot {е}_{{ij}}^{р}$; поверхность пластического нагружения описывается уравнением Мизеса; процессы деформирования характеризуются малыми деформациями; рассматривается только упругое изменение элементарного объема материала (пластическая несжимаемость); вводится скалярная мера поврежденности конструкционного материала $\omega $, изменяющийся в диапазоне ${{{{\omega }}}_{o}} \leqslant {{\omega }} \leqslant {{{{\omega }}}_{f}}$; учитывается влияние поврежденности материала на процессы деформирования через тензор эффективных напряжений.
Математическая модель МПС состоит из соотношений, описывающих упругопластическое поведение конструкционного материала, уравнений накопления повреждений и критерия прочности поврежденного материала.
2.1. Определяющие соотношения пластичности. Принимается, что при упругом поведении материала девиаторная и шаровая составляющие тензоров напряжений и деформаций, а также их скоростей связаны обобщенным законом Гука:
Поверхность пластического нагружения описывается в виде:
В пространстве пластических деформаций вводится поверхность “памяти”:
(2.1)
${{a}_{e}} = (e_{{ij}}^{p} - {{{{\xi }}}_{{ij}}})(e_{{ij}}^{p} - {{{{\xi }}}_{{ij}}}) - a_{{e{\text{max}}}}^{2} = 0$При численном моделировании кинетики напряженно-деформированного состояния при пластическом деформировании необходимо максимально точно описывать процессы упрочнения и разупрочнения конструкционных материалов, так как данные механизмы играют определяющую роль в точности оценок ресурсных характеристик. При усталостном нагружении реализуется конкуренция процессов упрочнения и разупрочнения вызванных в материале механизмами изменения фазового состава, микроструктурного состояния, изменением плотности дислокаций, а также влияние изменения температуры [19]. Физические механизмы, протекающие в поликристаллических металлах и сплавах, влияющие на процессы упрочнения и разупрочнения, зависят от действующей температуры, вида траектории деформирования, длины пути пластического деформирования, действующих амплитуд интенсивности пластической деформации и степени стабилизации процесса деформирования.
Для учета эффектов упрочнения и разупрочнения, проявляющихся вследствие протекания различных физических механизмов в поликристаллических металлах и их сплавах [20, 21], изменение радиуса поверхности пластического нагружения принимается в виде суммы скоростей изменений радиуса поверхности пластического нагружения при пластическом деформировании:
(2.2)
${{\dot {C}}_{{pl}}}\left( {{{\chi }},T} \right) = \left[ {\sum\limits_{i = 1}^n {q_{{{\chi }}}^{{(i)}}f_{m}^{{(i)}}\left( {{{a}_{e}}} \right) + \sum\limits_{j = 1}^m {{{a}_{j}}(Q_{s}^{{(j)}} - C_{{pl}}^{{(j)}})f_{c}^{{(j)}}\left( {{{a}_{e}}} \right)} } } \right]{{\dot {\chi }}} + \left[ {\sum\limits_{l = 1}^k {q_{T}^{{(l)}}} } \right]\dot {T}$Зависимость (2.2) описывает изотропное упрочнение (разупрочнение) при монотонном пластическом деформировании (первый член в скобке при ${{\dot {\chi }}}$), циклическом деформировании (второй член в скобке при ${{\dot {\chi }}}$) и от скорости изменения температуры $\dot {T}$.
Экспериментальное определение параметров, входящих в зависимость (2.2), описывающих изменение радиуса поверхности пластического нагружения должно проводиться на основании опытов в которых возможно выделение физических механизмов процессов упрочнения либо разупрочнения, таких как фазовые превращения, изменение микроструктуры и плотности дислокаций, и определения их вклада, также данные процессы можно исследовать с получением их количественных характеристик с использованием дополнительных средств неразрушающего контроля (акустический, вихретоковый и др. [22–24]).
При пластическом деформировании конструкционного материала изменение фазового состава материала приводит либо только к эффекту упрочнения либо разупрочнения, а при изменении микроструктурного состояния и дислокационной картины, может возникать как эффект упрочнения, так и эффект разупрочнения конструкционного материала в зависимости от вида текущей траектории деформирования, причем проявление эффекта существенно зависит от степени стабилизации процесса деформирования в пространстве пластических деформаций. Результаты экспериментальных исследований в работах [13, 15, 16] показывают, что двухчастотное нагружение в отличие от одночастотного приводит к разупрочнению исследуемых материалов, а также в процессе нагружения отсутствует стабилизация петли пластического гистерезиса, что сопровождается постоянным изменением центра ${{{{\xi }}}_{{ij}}}$ в уравнении (2.1), описывающего поверхность “памяти” ${{a}_{e}}$ в пространстве пластических деформаций. Таким образом, в диапазоне температур $Т$, при которых можно пренебречь эффектами отжига и конкретизируя параметры в зависимости (2.2) изотропное упрочнение (разупрочнение) можно записать как:
(2.3)
${{\dot {C}}_{{pl}}} = {{q}_{{{\chi }}}}{{{{\dot {\chi }}}}_{m}} + {{a}_{c}}\left( {{{Q}_{{s{{\chi }}}}} - {{С}_{{pl}}}} \right){{{{\dot {\chi }}}}_{c}} + {{a}_{{{\xi }}}}\left( {{{Q}_{{s{{\xi }}}}} - {{С}_{{pl}}}} \right){{{{\dot {\chi }}}}_{{{\xi }}}} + {{q}_{T}}\dot {T}$(2.5)
${{\dot {\chi }}} = {{\left( {\frac{2}{3}\dot {e}_{{ij}}^{p}\dot {e}_{{ij}}^{p}} \right)}^{{1/2}}},\quad {{\chi }} = \int\limits_0^t {{{\dot {\chi }}}dt} ,\quad ~{{{{\dot {\chi }}}}_{{{\xi }}}} = {{\left( {\frac{2}{3}{{{{{\dot {\xi }}}}}_{{ij}}}{{{{{\dot {\xi }}}}}_{{ij}}}} \right)}^{{1/2}}},\quad {{{{\chi }}}_{{{\xi }}}} = \int\limits_0^t {{{{{{\dot {\chi }}}}}_{{{\xi }}}}dt} $(2.6)
${{{{\dot {\chi }}}}_{m}} = \left\{ {\begin{array}{*{20}{c}} {0,~{{a}_{e}} < 0 \vee e_{{ij}}^{p}\dot {e}_{{ij}}^{p} \leqslant 0} \\ {{{\dot {\chi }}},~{{a}_{e}} = 0 \wedge e_{{ij}}^{p}\dot {e}_{{ij}}^{p} \geqslant 0} \end{array}} \right.,\quad {{{{\dot {\chi }}}}_{c}} = \left\{ {\begin{array}{*{20}{c}} {{{\dot {\chi }}},~{{a}_{e}} < 0 \vee e_{{ij}}^{p}\dot {e}_{{ij}}^{p} \leqslant 0} \\ {0,~{{a}_{e}} = 0 \wedge e_{{ij}}^{p}\dot {e}_{{ij}}^{p} \geqslant 0} \end{array}} \right.$В зависимостях (2.3)–(2.7) введены следующие обозначения: $C_{{pl}}^{0}$ – радиус поверхности пластического нагружения для конструкционного материала в исходном состоянии, ${{q}_{1}}$, ${{q}_{2}}$, ${{q}_{T}}$ – модули монотонного изотропного упрочнения (разупрочнения) при монотонных нагружениях по лучевым путям, при изломе траектории деформирования на 90° и изменении температуры; ${{Q}_{{1{{\chi }},1{{\xi }}}}}$, ${{Q}_{{2{{\chi }},2{{\xi }}}}}$ – модули циклического изотропного упрочнения (разупрочнения), при пропорциональном нагружении и при изломе траектории деформирования на 90° соответственно; ${{a}_{{c,\xi }}}$ – постоянные, определяющие скорость процесса стабилизации формы петли гистерезиса при циклическом нагружении материала; ${{Q}_{{s{{\chi }},s{{\xi }}}}}$ – стационарные значения радиуса поверхности текучести в зависимости от ${{a}_{{e{\text{max}}}}}$ и температуры $T$; ${{{{\dot {\chi }}}}_{m}}$ – скорость изменения длины траектории пластического деформирования материала на монотонных участках; ${{{{\dot {\chi }}}}_{c}}$ – скорость изменения длины траектории пластического деформирования материала на участках стабилизированного циклического деформирования без смещения центра поверхности ${{a}_{e}}$; ${{{{\dot {\chi }}}}_{{{\xi }}}}$ – скорость изменения длины траектории пластического деформирования материала на участках циклического деформирования со смещением центра поверхности ${{a}_{e}}$ (нестабилизированные участки траектории циклического деформирования).
Первый член уравнения (2.3) описывает изотропное упрочнение в результате монотонного пластического деформирования, второй член – циклическое упрочнение (разупрочнение) материала на стабилизированных участках циклического деформирования, третий член – циклическое разупрочнение (разупрочнение) материала при нестабилизированном циклическом деформировании, четвертый – изменение радиуса поверхности пластического нагружения при изменении температуры. Уравнение (2.4) описывает локальную анизотропию пластического упрочнения в зависимости от параметра непропорциональности нагружения $A$.
Эволюция тензора микронапряжений ${{\rho }_{{ij}}}$ принимается в виде:
(2.8)
${{{{\dot {\rho }}}}_{{ij}}} = f\left( {{\chi }} \right)({{\dot {\rho }}}_{{ij}}^{m} + {{\dot {\rho }}}_{{ij}}^{p} + {{\dot {\rho }}}_{{ij}}^{r}),\quad {{{{\rho }}}_{{ij}}} = \int\limits_0^t {{{{{{\dot {\rho }}}}}_{{ij}}}dt} $В формуле (2.8) первый член, указанный в скобках описывает эволюцию ${{{{\rho }}}_{{ij}}}$, связанного с образованием и эволюцией микропластических деформаций; второй – с образованием макроскопических пластических деформаций; третий – при односторонне накапливаемых пластических деформациях ${{{{\xi }}}_{{ij}}}$.
Зависимость (2.8) позволяет описывать основные эффекты анизотропии, вызванной неупругим деформированием при знакопеременном нагружении, а также эффекты, возникающие при реализации жестких (“посадка” петли гистерезиса) и мягких режимов нагружения (“вышагивание” петли гистерезиса).
Функция $f\left( {{\chi }} \right)$ описывает изменение ${{{{\rho }}}_{{ij}}}$ в случае зависимости параметров $g_{1}^{{m,p,r}}$, $g_{2}^{{m,p,r}}$ от длины пути пластического деформирования ${{\chi }}$ при монотонном, циклическом стабилизированном и нестабилизированном деформировании и связанная с физическими механизмами протекающими в процессе пластического нагружения, изменяющими фазовый состав конструкционного материала, дислокационная плотность и др.
Тензор скоростей пластических $\dot {e}_{{ij}}^{р}$ деформаций определяется на основе ассоциированного с поверхностью активного нагружения закона течения:
Влияние накопленной поврежденности учитывается через эффективные значения гидростатической и девиаторной части тензора напряжений. Эффективные значения компонент тензора напряжений определяются через эффективные значения модулей упругости [7] с учетом влияния на них величины накопленной поврежденности ${{\omega }}$:
2.2. Уравнения накопления повреждений при малоцикловой и многоцикловой усталости. Уравнения накопления повреждений базируются на связи величины поврежденности с макроскопическими параметрами, которые могут быть экспериментально определены. Наиболее физически обоснованным и апробированным является энергетический подход [7, 8, 10, 18] при определении ресурсных характеристик поликристаллических тел. Новожиловым В.В. установлена зависимость рассеянной энергии, затраченной на образование дефектов при малоцикловом нагружении, с работой тензора микронапряжений ${{{{\rho }}}_{{ij}}}$ на пластических деформациях $e_{{ij}}^{p}$
Ресурсные характеристики при МнЦУ определяются с использованием подхода [13], основанного на энергетическом критерии, который записывается следующим выражением:
(2.9)
$\mathop \sum \limits_{i = 1}^{{{N}_{p}}} \left[ {\Delta {{W}_{i}} - \Delta {{W}_{R}}{{{\left( {\frac{{\Delta {{W}_{i}}}}{{\Delta {{W}_{R}}}}} \right)}}^{\alpha }}} \right] = \Delta {{W}_{о}} = {\text{const}}$Рассмотрим выражение (2.9) для одного цикла нагружения в следующем виде:
(2.10)
$\Delta {{W}_{о}} = \Delta {{W}_{i}} - \Delta {{W}_{R}}{{\left( {\frac{{\Delta {{W}_{i}}}}{{\Delta {{W}_{R}}}}} \right)}^{{{\alpha }}}} = \Delta {{W}_{i}} - \Delta {{W}_{H}}$В работе [11] Коротких Ю.Г. конкретизировал соотношение (2.10) на случай регулярного циклического нагружения в виде:
(2.11)
$\Delta W_{е}^{{оп}} = \Delta W_{е}^{{}}\left[ {1 - f\left( {{\gamma }} \right)} \right],\quad {{\gamma }} = {{{{{{\sigma }}}_{u}}} \mathord{\left/ {\vphantom {{{{{{\sigma }}}_{u}}} {{{\sigma }}_{u}^{R}}}} \right. \kern-0em} {{{\sigma }}_{u}^{R}}}$На основе (2.9) и (2.11), выражение для опасной энергии за один цикл нагружения представим в следующем виде:
Функция $f\left( {{\gamma }} \right)$, учитывает относительную величину неопасной энергии в полной рассеянной энергии, затраченной на пластическое деформирование и зависящая от параметра ${{\gamma }}$, характеризующего относительный уровень действующих максимальных напряжений в цикле нагружения.
(2.12)
$\begin{gathered} {{\gamma }} = \frac{{{{\tilde {\sigma }}}_{u}^{*}}}{{{{{{{\tilde {\sigma }}}}}_{{hcf}}}}},\quad {{\tilde {\sigma }}}_{u}^{*} = {{[({{\sigma }}_{{ij}}^{'} - {{\rho }}_{{ij}}^{r})({{\sigma }}_{{ij}}^{'} - {{\rho }}_{{ij}}^{r})]}^{{1/2}}} \\ {{{{{\tilde {\sigma }}}}}_{{hcf}}} = \sqrt {\frac{2}{3}} {{{{\sigma }}}_{{hcf}}} + \int\limits_0^t {\dot {C}_{{pl}}^{c}dt,\quad } \dot {C}_{{pl}}^{c} = {{a}_{c}}\left( {{{Q}_{{s{{\chi }}}}} - {{C}_{{pl}}}} \right){{{{{\dot {\chi }}}}}_{c}} + {{a}_{{{\xi }}}}\left( {{{Q}_{{s{{\xi }}}}} - {{C}_{{pl}}}} \right){{{{{\dot {\chi }}}}}_{{{\xi }}}} + {{q}_{T}}\dot {T} \\ \end{gathered} $В выражении (2.12) ${{\tilde {\sigma }}}_{u}^{*}$ – нормированная интенсивность девиатора тензора напряжений; ${{{{\tilde {\sigma }}}}_{{hcf}}}$ – значение интенсивности напряжений при котором происходит переход от механизма МЦУ к МнЦУ с учетом процессов упрочнения (разупрочнения) конструкционного материала (точка перегиба на полной кривой усталости), ${{{{\sigma }}}_{{hcf}}}$ – константа материала.
Для определения ресурсных характеристик поликристаллических металлов и их сплавов при деградации материала по механизмам МЦУ и МнЦУ в качестве энергии повреждения, принимается соотношение:
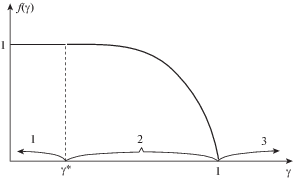
Функция $f\left( {{\gamma }} \right)$ зависит от параметра ${{\gamma }} = {{{{\sigma }}}_{u}}{\text{/}}{{C}_{p}}$, характеризующего относительный уровень действующих напряжений в цикле нагружения:
На рис. 2 приведено графическое представление функции $f\left( {{\gamma }} \right)$ (1 – область гигацикловой усталости, 2 – область многоцикловой усталости, 3 – область малоцикловой усталости).
В задачах оценки ресурсных характеристик необходимо учитывать влияние многоосности нагружения, наличие которой существенным образом снижает ресурс за счет как увеличения действующих компонент тензора деформаций и напряжений при пропорциональном нагружении так и за счет вращения главных площадок тензоров напряжений и деформаций при непропорциональном нагружении.
Многочисленные исследования влияния многоосности нагружения при различных видах напряженных состояний таких как двухосное растяжение–сжатие, трехосное растяжение и др. позволяют сделать вывод, что на ресурс оказывает существенное влияние “объемность” напряженного состояния ${{\beta }} = {{{\sigma }} \mathord{\left/ {\vphantom {{{\sigma }} {{{{{\sigma }}}_{u}}}}} \right. \kern-0em} {{{{{\sigma }}}_{u}}}}$, где σ – гидростатическая компонента тензора напряжений, ${{{{\sigma }}}_{u}}$ – интенсивность тензора напряжений.
Учет влияния “объемности” напряженного состояния на скорость роста поврежденности $\dot {\omega }$ производится за счет введения в уравнение скорости накопления повреждения функции ${{f}_{1}}({{\beta }})$, которая увеличивает скорость накопления повреждений ${{\dot {\omega }}}$ при нагружениях с ${{\beta }} \to + \infty $ и уменьшает скорость при ${{\beta }} \to - \infty $. При нагружениях с ${{\beta }} \to - \infty $ в некоторых поликристаллических металлах и сплавах возможно частичное уменьшение накопленной поврежденности (эффект “залечивания”). При нагружениях с ${{\beta }} = 0$ (чистый сдвиг) функция ${{f}_{1}}({{\beta }}) = 1$.
В условиях непропорционального нагружения, при котором направляющие тензора напряжений и деформаций не соосны реализуемая траектория деформирования существенным образом влияет на кинетику напряженно-деформированного состояния и на ресурсные характеристики конструкционного материала.
Учитывая рассмотренные эффекты, влияющие на ресурсные характеристики, уравнение для скорости накопления усталостных повреждений в условиях малоциклового и многоциклового нагружения можно представить в виде:
(2.13)
${{{{\dot {\omega }}}}_{p}} = {{f}_{1}}\left( {{\beta }} \right){{f}_{2}}\left( {{{{{\omega }}}_{P}}} \right){{f}_{3}}\left( {{{W}_{p}}} \right){{\dot {W}}_{p}}$В (2.13) введены следующие обозначения для функций:
${{f}_{1}}\left( {{\beta }} \right)$ – учет влияния “объемности” напряженного состояния;
${{f}_{2}}\left( {{{{{\omega }}}_{p}}} \right)$ – учет влияния накопленного уровня поврежденности на скорость накопления повреждений;
${{f}_{3}}\left( {{{W}_{p}}} \right)$ – учет текущего относительного уровня рассеянной энергии, идущей на образование микродефектов.
Принимается, что кинетика накопления повреждений состоит из двух последовательных стадий – зарождения микродефектов и их слияния. Данные стадии разграничиваются значением величины рассеянной энергии $W_{p}^{a}$. Образование макродефекта происходит при достижении величины рассеянной энергии значения $W_{p}^{f}$.
2.3. Критерий прочности поврежденного материала. В качестве критерия прочности поврежденного материала принимается достижение накопленной поврежденности ${{\omega }}$ критического значения ${{{{\omega }}}_{f}} \leqslant 1$.
3. Численные результаты. В работе [25] приведены результаты экспериментальных исследований циклического неупругого деформирования и закономерностей усталостного разрушения при действии одночастотного и двухчастотного нагружения для сталей 20 и 08Х18Н12Т. Исследования усталостного разрушения проводили на испытательной машине МИР-СТ при симметричном и несимметричном нагружении в условиях одноосного растяжения–сжатия лабораторных образцов.
Испытывались цилиндрические гладкие образцы широко использующихся конструкционных сталей: углеродистой стали 20 в состоянии поставки и стали аустенитного класса 08Х18Н12Т(1) – в состоянии поставки и 08Х18Н12Т(2) – после эксплуатационной наработки.
Каждый из указанных конструкционных материалов испытывали при следующих режимах нагружения: циклическое нагружение с частотой 34 Гц при симметричном цикле; циклическое нагружение с частотой 34 Гц с асимметрией в цикле, среднее напряжение ${{{{\sigma }}}_{m}} = 50\;{\text{МПа}}$; циклическое нагружение с частотой 0.082 Гц с асимметрией в цикле, среднее напряжение ${{{{\sigma }}}_{m}} = 50\;{\text{МПа}}$; циклическое нагружение реализуемое за счет изменения среднего напряжения в цикле ${{{{\sigma }}}_{m}}$ в пределах от 0 до 100 МПа с частотой 0.082 Гц при циклическом нагружении с частотой 34 Гц (двухчастотное нагружение).
Результатом экспериментальных исследований явились кривые усталости для сталей 20 и 08Х18Н12Т при указанных режимах нагружения.
В таблицах 1–3 для исследуемых сталей приведены физико-механические характеристики и материальные параметры МПС.
Таблица 1.
Физико-механические характеристики и параметры модели МПС конструкционных сталей
| Характеристики | Материал | ||
|---|---|---|---|
| 08Х18Н12Т(1) | 08Х18Н12Т(2) | Сталь 20 | |
| K (МПа) | 166 667 | 166 667 | 166 667 |
| G (МПа) | 76 923 | 76 923 | 76 923 |
| $С_{{pl}}^{о}$ (МПа) | 85 | 90 | 82 |
| $g_{1}^{m}$, (МПа) | 400 000 | 400 000 | 200 000 |
| $g_{2}^{m}$ | 5600 | 5600 | 2000 |
| $g_{1}^{p}$, (МПа) | 24 090 | 24 090 | 19 000 |
| $g_{2}^{p}$ | 289 | 289 | 224 |
| $g_{1}^{r}$ (МПа) | 4000 | 4000 | 1200 |
| $g_{2}^{r}$ | 0 | 0 | 0 |
| ${{a}_{{{\xi }}}}$ | 5 | 5 | 6 |
| $W_{a}^{{}}\,({\text{МДж/}}{{{\text{м}}}^{3}})$ | 0 | 0 | 0 |
| $W_{р}^{f}\,({\text{МДж/}}{{{\text{м}}}^{3}})$ | 2900 | 2884 | 13980 |
| ${{{{\sigma }}}_{{hcf}}}$, МПа | 220 | 240 | 280 |
| ${{{{\gamma }}}_{*}}$ | 0.8182 | 0.8400 | 0.7473 |
| $n$ | 1.55 | 3.1 | 1.05 |
Таблица 2.
Значение модуля монотонного изотропного упрочнения ${{q}_{1}}$ (МПа) от длины траектории пластического деформирования ${{{{\chi }}}_{{{\text{mon}}}}}$ для среднеуглеродистой стали 20 (${{q}_{2}} = 0$)
| ${{\chi }}$ | 0 | 0.0006 | 0.0012 | 0.0024 | 0.0042 | 0.006 | 0.0102 | 0.0132 | 0.015 |
| ${{q}_{1}}$, МПа | 0 | 0 | –11 709 | –11 170 | –10 360 | 3200 | 280 | 120 | 0 |
Таблица 3.
Значение модуля циклического изотропного упрочнения ${{Q}_{{1{{\xi }}}}}$ (МПа) от длины траектории пластического деформирования ${{a}_{{e{\text{max}}}}}$ 08Х18Н12Т (1) (${{Q}_{{2{{\xi }}}}} = 0$ для всех рассмотренных сталей)
| Сталь 08Х18Н12Т(1) | |||||||
|---|---|---|---|---|---|---|---|
| ${{a}_{{e{\text{max}}}}}$ | 0 | 0.00015 | 0.000162 | 0.000165 | 0.000192 | 0.000248 | 0.000350 |
| ${{Q}_{{1{{\xi }}}}}$, МПа | 25 | 30 | 39 | 54 | 78 | 84 | 85 |
| Сталь 08Х18Н12Т(1) | |||||||
| ${{a}_{{e{\text{max}}}}}$ | 0 | 0.00024 | 0.000266 | 0.000284 | 0.000331 | 0.00035 | 0.0004 |
| ${{Q}_{{1{{\xi }}}}}$, МПа | 25 | 32 | 43 | 61 | 77 | 82 | 90 |
| Сталь 20 | |||||||
| ${{a}_{{e{\text{max}}}}}$ | 0 | 0.0004 | 0.000451 | 0.000508 | 0.000591 | 0.00075 | 0.0001 |
| ${{Q}_{{1{{\xi }}}}}$, МПа | 30 | 52 | 55 | 65 | 70 | 74 | 78 |
Значение модуля монотонного изотропного упрочнения ${{q}_{1}}$ и ${{q}_{2}}$ от длины траектории пластического деформирования ${{\chi }}$ для сталей аустенитного класса 08Х18Н12Т(1) и 08Х18Н12Т(2) приняты равными нулю.
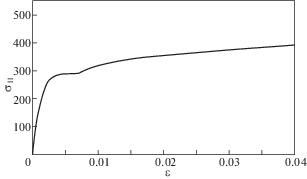
На рис. 3–4 приведены расчетные кривые одноосного растяжения для сталей 2008Х18Н12Т(1), 08Х18Н12Т(2) и стали 20.
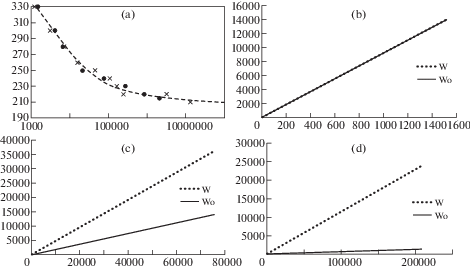
На рис. 5–7 приведено сравнение результатов расчетных и экспериментальных кривых усталости для сталей 08Х18Н12Т(1), 08Х18Н12Т(2), стали 20 соответственно, а также приведены расчетные кривые полной рассеянной энергии $W$, затраченной на пластическое деформирование и “опасной” части полной энергии ${{W}_{o}}$, коррелирующей с энергией, затраченной на образование микродефектов в зависимости от числа циклов нагружения. На рис. 5,а, 6,a и 7,а представлены зависимости амплитуды напряжения от числа циклов, пунктирными линиями отмечены осредненные опытные данные, черными маркерами – результаты расчетов по предложенной модели МПС, а черными крестиками – экспериментальные точки. Из сравнения экспериментальных и расчетных кривых усталости (рис. 5,а, 6,a и 7,а) видно, что расчеты по модели МПС качественно и количественно совпадают с опытными данными. Численные данные по зависимостям рассеянной энергии от числа циклов (рис. 5,b – ${{\sigma }}_{{11}}^{a} = 300\;{\text{МПа}}$, 5,с – ${{\sigma }}_{{11}}^{a} = 200\;{\text{МПа}}$, 5,d – ${{\sigma }}_{{11}}^{a} = 190\;{\text{МПа}}$, 6,b – ${{\sigma }}_{{11}}^{a} = 300\;{\text{МПа}}$, 6,с – ${{\sigma }}_{{11}}^{a} = 230\;{\text{МПа}}$, 6,d – ${{\sigma }}_{{11}}^{a} = 215\;{\text{МПа}}$, 7,b – ${{\sigma }}_{{11}}^{a} = 330\;{\text{МПа}}$, 7,с – ${{\sigma }}_{{11}}^{a} = 240\;{\text{МПа}}$, 7,d – ${{\sigma }}_{{11}}^{a} = 215\;{\text{МПа}}$) показывают, что в области МЦУ кривые полной рассеянной энергии $W\left( N \right)$ и ее “опасной части” ${{W}_{o}}\left( N \right)$ совпадают, но по мере уменьшения амплитуды нагружения данные кривые расходятся и тем больше, чем меньше амплитуда нагружения. Данный эффект связан с тем, что у “неопасной” части рассеянной полной энергии ${{W}_{н}}$ наблюдается незначительная амплитудная зависимость только в области МЦУ, тогда как при МнЦУ амплитудная зависимость ${{W}_{н}}$ вносит значительный вклад в полную рассеянную [13, 16].
На рис. 8–10 приведены результаты сравнения расчетных и экспериментальных кривых усталости при двухчастотном нагружении для сталей 08Х18Н12Т(1), 08Х18Н12Т(2) и стали 20 в циклах высокой частоты. На рис. 11–13 приведены результаты сравнения расчетных и экспериментальных кривых усталости при двухчастотном нагружении для сталей 08Х18Н12Т(1), 08Х18Н12Т(2) и стали 20 в циклах низкой частоты. Здесь пунктирными линиями отмечены расчетные данные при одночастотном нагружении, сплошной черной линией отмечены расчетные данные при двухчастотном нагружении, а черными маркерами – экспериментальные результаты при двухчастотном нагружении. Из представленных рисунков видно, что расчетные значения по математической модели МПС качественно и количественно совпадают с экспериментальными результатами.
Рис. 8.
Кривая усталости для стали 08Х18Н12Т(1) при двухчастотном нагружении в циклах высокой частоты.
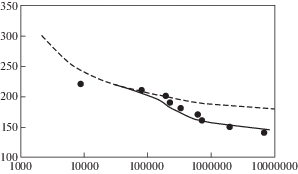
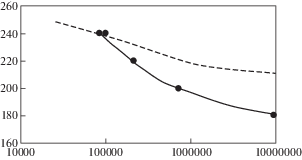
Рис. 9.
Кривая усталости для стали 08Х18Н12Т(2) при двухчастотном нагружении в циклах высокой частоты.

Рис. 11.
Кривая усталости для стали 08Х18Н12Т(1) при двухчастотном нагружении в циклах низкой частоты.

Рис. 12.
Кривая усталости для стали 08Х18Н12Т(2) при двухчастотном нагружении в циклах низкой частоты.

На рис. 14–16 приведено сравнение расчетных стабилизированных петель гистерезиса для одночастотного (пунктирная линия) и двухчастотного нагружения (сплошная линия), из которого виден эффект роста размаха циклической пластической деформации при двухчастотной форме цикла в сравнении с одночастотным нагружением при эквивалентной величине амплитуды напряжений, что связано со снижением сопротивления деформированию материалов (для лучшей визуализации петли нормированы к началу координатной сетки).
Рис. 14.
Сравнение петель пластического гистерезиса при одночастотном и двухчастотном нагружении для стали 08Х18Н12Т(1).
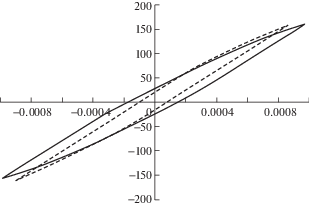
Рис. 15.
Сравнение петель пластического гистерезиса при одночастотном и двухчастотном нагружении для стали 08Х18Н12Т(2).

Рис. 16.
Сравнение петель пластического гистерезиса при одночастотном и двухчастотном нагружении для стали 20.

4. Заключение. Развита математическая модель МПС, описывающая процессы деформирования и накопления повреждений при усталостном нагружении, основанная на энергетическом подходе и единой форме представления процесса накопления повреждений при малоцикловой и многоцикловой усталости. Для математической модели определены параметры и скалярные функции, входящие в определяющие соотношения математической модели МПС. В рамках оценки достоверности развитой математической модели механики поврежденной среды проведены численные исследования процессов усталостного разрушения конструкционных материалов – сталей 20 и 08Х18Н12Т в условиях одночастотного и двухчастотного нагружения. Результаты оценки достоверности показали, что развитая модель с высокой степенью точности описывает процессы малоцикловой и многоцикловой усталости.
Благодарности. Численные исследования стали 08Х18Н12Т выполнены при финансовой поддержке Министерства науки и высшего образования Российской Федерации (проект 0729-2020-0054). Численные исследования стали 20 выполнены при финансовой поддержке Российского фонда фундаментальных исследований (грант № 20-08-00450).
Список литературы
Коллинз Дж. Повреждение материалов в конструкциях. Анализ. Предсказание. Предотвращение. М.: Мир, 1984. 624 с.
Трощенко В.Т. Деформирование и разрушение металлов при многоцикловом нагружении. Киев: Наук. думка, 1981. 343 с.
Банников М.В., Оборин В.А., Наймарк О.Б. Исследование стадийности разрушения титановых сплавов в режиме много- и гигацикловой усталости на основе морфологии поверхности разрушения // Вестник ПНИПУ. Механика. 2015. № 3. С. 15–24. https://doi.org/10.15593/perm.mech/2015.3.02
Терентьев В.Ф. Механизм зарождения усталостных трещин в высокопрочных сталях при гигацикловой усталости // XIII Internation Colloquium “Mechanical fatigue of metals”. Plenar papers. Ternopil, Ukraine: TDTU, 2006. С. 135–140.
Волков И.А., Коротких Ю.Г. Уравнения состояния вязкоупругопластических сред с повреждениями. М.: Физматлит, 2008. 424 с.
Волков И.А., Игумнов Л.А. Введение в континуальную механику поврежденной среды. М.: Физматлит, 2017. 304 с
Волков И.А., Игумнов Л.А., Тарасов И.С., Шишулин Д.Н., Пичков С.Н., Маркова М.Т. Моделирование пластического деформирования поликристаллических конструкционных сплавов при блочных несимметричных режимах мягкого малоциклового нагружения // Проблемы прочности и пластичности. 2019. Т. 81. № 1. С. 63–76. https://doi.org/10.32326/1814-9146-2019-81-1-63-76
Волков И.А., Игумнов Л.А., Коротких Ю.Г., Казаков Д.А., Емельянов А.А., Тарасов И.С., Гусева М.А. Программная реализация процессов вязкопластического деформирования и накопления повреждений в конструкционных сплавах при термомеханическом нагружении // Проблемы прочности и пластичности. 2016. Т. 78. № 2. С. 188–207. https://doi.org/10.32326/1814-9146-2016-78-2-188-207
Chaboche J.-L., Kanouté P., Azzouz F. Cyclic inelastic constitutive equations and their impact on the fatigue life predictions // Int. J. Plasticity. 2012. V. 35. P. 44–66. https://doi.org/10.1016/j.ijplas.2012.01.010
Волков И.А., Коротких Ю.Г. Моделирование процессов усталостной долговечности материалов и конструкций при малоцикловом нагружении // Изв. РАН. МТТ. 2014. № 3. С. 66–78.
Большухин М.А., Зверев Д.Л., Кайдалов В.Б., Коротких Ю.Г. Оценка долговечности конструкционных материалов при совместных процессах малоцикловой и многоцикловой усталости // Проблемы прочности и пластичности. 2010. Т. 72. С. 28–35. https://doi.org/10.32326/1814-9146-2010-72-1-29-35
Бондарь В.С., Даншин В.В., Кондратенко А.А. Вариант теории термовязкопластичности // Вестник ПНИПУ. Механика. 2016. № 1. С. 39–56. https://doi.org/10.15593/perm.mech/2016.1.03
Трощенко В.Т. Рассеянное усталостное повреждение металлов и сплавов. Сообщение 3. Деформационные энергетические критерии // Проблемы прочности. 2006. № 1. С. 5–31.
Гаденин М.М. Исследование повреждаемости и долговечности конструкций при одно- и двухчастотных режимах нагружения на основе деформационных и энергетических подходов // Заводская лаборатория. Диагностика материалов. 2017. № 83 (6). С. 44–51.
Гаденин М.М. Влияние формы цикла нагружения на сопротивление циклическому деформированию и разрушению конструкционных материалов // Вестник научно-технического развития. 2010. № 9 (37). С. 15–19.
Хамаза Л.А., Коваленко В.А. Сопротивление металлов усталостному разрушению и деформированию при двухчастотном нагружении. Сообщение 2. Методика оценки циклической долговечности при двухчастотном нагружении // Проблемы прочности. 1989. № 10. С. 13–18.
Порошин В.Б., Дружинин П.С., Шахова С.А. Методика оценки долговечности лопатки газовой турбины в условиях неупругого деформирования при двухчастотном нагружении // II Международная научно-техническая конференция “Пром–Инжиниринг”. Челябинск: Издательский центр ЮУрГУ, 2016 С. 36–43.
Бондарь В.С., Даншин В.В., Алхимов Д.А. Анализ циклического деформирования и мало-многоцикловой усталости в условиях одноосного напряженного состояния // Вестник ПНИПУ. Механика. 2016. № 4. С. 52–71. https://doi.org/10.15593/perm.mech/2016.4.04
Мовчан Б.А., Фирстов С.А., Луговской Ю.Ф. Структура, прочность и сопротивление усталости микрокристаллических и микрослойных материалов. Киев: Наукова думка, 2016. 170 с.
Гольдштейн М.И., Литвинов В.С., Бронфин Б.М. Металлофизика высокопрочных сплавов. М.: Металлургия, 1986. 312 с.
Пиккеринг Ф.Б. Физическое металловедение и разработка сталей. М.: Металлургия, 1982. 184 с.
Хлыбов А.А., Углов А.Л. Исследование накопления усталостных повреждений в образцах из стали 08Х18Н10Т при малоцикловой усталости // Изв. высших учебных заведений. Черная металлургия. 2016. Т. 59. № 3. С. 185–190. https://doi.org/10.17073/0368-0797-2016-3-185-190
Углов А.Л., Ерофеев В.И., Смирнов А.Н. Акустический контроль оборудования при изготовлении и эксплуатации / Отв. ред. Ф.М. Митенков. М.: Наука, 2009. 280 с.
Муравьев В.В., Зуев Л.Б., Комаров К.Л. Скорость звука и структура сталей и сплавов. Новосибирск: Наука, 1996. 183 с.
Хамаза Л.А., Коваленко В.А. Сопротивление металлов усталостному разрушению и деформированию при двухчастотном нагружении. Сообщение 1. Методика и результаты исследования усталости и неупругости металлов при двухчастотном циклическом нагружении // Проблемы прочности. 1989. № 10. С. 7–13.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела