Известия РАН. Механика твердого тела, 2022, № 2, стр. 50-60
О ВОЛНОВЫХ ПРОЦЕССАХ В ВЯЗКОУПРУГИХ ТОПОГРАФИЧЕСКИХ ВОЛНОВОДАХ
А. О. Ватульян a, b, *, Л. И. Паринова a, **
a Южный федеральный университет
Ростов-на-Дону, Россия
b Южный математический институт-филиал ВНЦ РАН
Владикавказ, Россия
* E-mail: aovatulyan@sfedu.ru
** E-mail: lparinova@sfedu.ru
Поступила в редакцию 28.09.2021
После доработки 05.10.2021
Принята к публикации 07.10.2021
- EDN: GCVYTN
- DOI: 10.31857/S0572329922020192
Аннотация
Исследованы собственные колебания ортотропного вязкоупругого волновода. Сформулирована постановка задачи для упругого волновода в операторной форме, для перехода к вязкоупругому случаю использована концепция комплексных модулей. Выполнена слабая постановка задачи, на основе которой сформулирован вариационный принцип, аналогичный принципу Гамильтона–Остроградского. Из упрощенного функционала, построенного на базе гипотез типа Кирхгофа для клинообразных волноводов, сформирован подход к построению дисперсионного множества на основе метода Ритца.
Проведены вычислительные эксперименты для топографических волноводов с поперечным сечением в виде трапеции, треугольника и прямоугольника. Построены графики дисперсионных зависимостей, проведено сравнение с упругим случаем.
1. Введение. Изучение особенностей формирования локализованных акустических волн, распространяющихся в клиновидных протяженных структурах, началось в 70-х годах прошлого века. Первый интерес к особенностям формирования волновых полей в клиновидных бесконечных волноводах из изотропных упругих материалов был продиктован возможными применениями низкоскоростных волн в акустоэлектронике. Отметим, что аналитическое исследование волн в топографических волноводах, к которым относятся клиновидные волноводы, невозможно для произвольных углов раскрыва и для решения задач в таких областях потребовались некоторые упрощения, учитывающие малость угла раскрыва или прямой численный анализ краевых задач теории упругости с параметром, характеризующим скорость клиновой волны. Так, в работах [1–3] в результате серии расчетов, выполненных на основе метода конечных элементов, установлено, что волна, бегущая в бесконечном клиновидном волноводе с произвольным углом раскрыва, локализуется вдоль ребра пространственного клина. Также было показано, что в такой структуре отсутствует дисперсия. В дальнейшем клиновые волны были исследованы на основе изучения задач на собственные значения, которые решались с помощью разложений по полиномам Лагерра [4, 5]. Последующие исследования в этой области были связаны с использованием геометро-акустического подхода [6, 7] и моделей пластин переменной жесткости [7], использовавшихся в случае малых углов раскрыва. Можно отметить также работу [8], в которой на основе теории пластин переменной жесткости дано обобщение задач о волнах в клиновых волноводах с малым углом раскрыва на материалы с кубическим типом анизотропии.
В монографии [6] изучались различные топографические волноводы, в частности, представляющие собой выступ на поверхности упругого тела, использовалась геометро-акустическая теория, при помощи которой приближенно найдены скорости распространения клиновых волн.
Отметим работу [9], в которой в рамках строгой постановки динамической теории упругости исследована задача о волнах в клиновидном волноводе с углом раскрыва 90°. Задача решена с помощью метода суперпозиции и сведена к нахождению нетривиального решения системы интегральных уравнений Фредгольма второго рода с непрерывными ядрами.
Общей теории волноводов с различными свойствами посвящены монографии [10, 11]. Особенности структуры дисперсионных множеств средствами спектральной теории операторов исследовались при решении задачи о колебаниях анизотропного поперечно-неоднородного волновода [10]. В монографии [11] изучались особенности волновых процессов в нерегулярных волноводах, причем дисперсионные множества исследовались на основе решений Сен-Венана для цилиндрических тел с произвольным поперечным сечением.
В [12] проанализированы волновые процессы в топографических волноводах из ортотропных материалов, для бесконечного клинообразного волновода были найдены оценки для скоростей первых двух антисимметричных мод и осуществлено сравнение с изотропным случаем, проанализированным в рамках геометро-акустической теории, представленной в [6, 7]. В работах [13–16] для топографических волноводов с поперечным сечением в виде треугольника и трапеции с малым углом раскрыва и закрепленной одной гранью на основе гипотез типа Кирхгофа и Тимошенко построен упрощенный лагранжиан, стационарное значение которого находилось методом Ритца. Этот подход позволил осуществлять построение точек дисперсионного множества и изучать влияние геометрии поперечного сечения на его структуру.
Отметим также работы [17, 18], посвященные доказательству существования клиновых волн для антисимметричных и симметричных колебаний бесконечного клинового волновода с различными углами раскрыва.
Исследования волновых процессов для клиновидных структур с эффектом затухания стали изучаться относительно недавно. Учет затухания в волноводах различной структуры обычно опирался на модели линейной вязкоупругости и концепцию комплексных модулей [19, 20]. Так, например, в [21] проанализированы ультразвуковые волновые процессы в осесимметричном цилиндрическом волноводе из вязкоупругого материала.
Колебания предварительно напряженного вязкоупругого волновода в линеаризованной инкрементальной форме изучены в [22], где использован расширенный полуаналитический КЭ-метод.
В настоящей работе основное внимание уделено исследованию фактора затухания волн в топографических волноводах с треугольным и трапециевидным поперечным сечением на основе принципа соответствия в линейной вязкоупругости и использования концепции комплексных модулей. Выяснено влияние реологии материала и геометрии на структуру дисперсионного множества, оценено влияние безразмерного параметра, характеризующего вязкоупругие свойства на вещественную и мнимую компоненту дисперсионного множества.
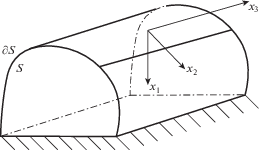
2. Постановка задачи. Рассмотрим защемленный на части границы топографический волновод V = $S \times {{R}_{1}}$ с произвольным поперечным сечением S, ограниченным кусочно-гладкой кривой ∂S. Для исследования особенностей распространения волн в протяженной структуре свяжем с топографическим волноводом декартову систему координат с осью Ox3, ортогональной сечению S (рис. 1). Будем считать, что ∂S = ∂S1 ∪ ∂S2, граница ∂S1 защемлена, а граница ∂S2 свободна от нагрузок.
Сформулируем постановку задачи сначала для упругого ортотропного волновода, причем будем считать, что оси упругой симметрии совпадают с осями координат.
Уравнения движения имеют вид:
где ρ – плотность материала, σmn – компоненты тензора напряжений, um – компоненты вектора смещений.Обобщенный закон Гука для модели упругого тела имеет вид:
Решение задачи ищем в виде волн, бегущих вдоль оси Ox3 волновода:
${{u}_{m}}({{x}_{1}},{{x}_{2}},{{x}_{3}},t) = {{U}_{m}}({{x}_{1}},{{x}_{2}})\exp \left( {i\left( {\gamma {{x}_{3}} - \omega t} \right)} \right),$ где m = 1÷3, ${{U}_{m}}({{x}_{1}},{{x}_{2}})$, – амплитуды вектора смещений, зависящие от координат x1 и x2, γ – волновое число, ω – частота колебаний.
После отделения экспоненциального множителя получим формулировку задачи в виде операторного пучка, который содержит два спектральных параметра γ и ω.
Далее для сокращения записи учитываем правило перехода от четырехиндексных к двухиндексным объектам, которое состоит в следующем Cmnkl заменяется на Cij, где mn заменяется на m, если $m = n$, mn заменяется на $q = 6 - m - n$, если $m \ne n$.
Уравнения движения представимы в операторной форме:
(2.1)
$A(\gamma ,\omega ){\mathbf{U}} = 0,\quad A(\gamma ,\omega ) = {{{\mathbf{A}}}_{{\mathbf{0}}}} + \gamma {{{\mathbf{A}}}_{{\mathbf{1}}}} + {{\gamma }^{2}}{{{\mathbf{A}}}_{{\mathbf{2}}}} + {{\omega }^{2}}\rho {\mathbf{I}}$Граничные условия в операторном виде для вектор-функции ${{U}_{j}} = {{U}_{j}}({{x}_{1}},{{x}_{2}})$ на поверхности волновода ∂S = ∂S1 ∪ ∂S2 представимы в виде:
(2.2)
${{\left. {\mathbf{U}} \right|}_{{\partial {{S}_{1}}}}} = 0,\quad B(\gamma ){{\left. {\mathbf{U}} \right|}_{{\partial {{S}_{2}}}}} = 0,\quad B(\gamma ) = {{{\mathbf{B}}}_{{\mathbf{0}}}} + \gamma {{{\mathbf{B}}}_{{\mathbf{1}}}}$Важной компонентой исследования задачи в упругом случае является изучение дисперсионного множества задачи, которое имеет вид $D(\gamma ,\omega ) = 0$. Оно состоит из пар $(\gamma ,\omega )$, при которых краевая задача (2.1), (2.2) имеет ненулевое решение.
Нетрудно описать некоторые его свойства. В случае, когда $\gamma = 0$, что соответствует стоячим волнам и определяет частоты запирания для волновода, задача (2.1), (2.2) примет вид:
(2.3)
$({{{\mathbf{A}}}_{{\mathbf{0}}}} + \rho {{\omega }^{2}}{\mathbf{I}}){{{\mathbf{U}}}^{{{\mathbf{(0)}}}}} = 0$Эта задача определяет резонансные свойства упругой среды, занимающей область S и, как известно, имеет счетное число компонент, которые обозначены через $\omega _{k}^{2}$, k = 1, 2, … В силу аналитичности компонент дисперсионного множества [10] из этих точек выходят ветви дисперсионного множества, которые могут быть определены лишь численно. В силу структуры операторов A0 и B0 задача (2.3) расщепляется на две подзадачи. Первая подзадача, когда ${{{\mathbf{U}}}^{{{\mathbf{(0)}}}}} = (U_{1}^{{(0)}}({{x}_{1}},{{x}_{2}}),U_{2}^{{(0)}}({{x}_{1}},{{x}_{2}}),0)$ – есть задача о плоских колебаниях области S, и вторая подзадача, когда ${{{\mathbf{U}}}^{{{\mathbf{(0)}}}}} = (0,0,U_{3}^{{(0)}}({{x}_{1}},{{x}_{2}}))$ – задача об антиплоских колебаниях, каждая из которых имеет свой спектр.
Согласно методам теории возмущений линейных операторов [23] структура точек дисперсионного множества может быть определена в окрестности частот запирания в виде регулярного разложения ${{\omega }^{2}} = {{\omega }_{{kj}}}^{2} + {{a}_{j}}{{\gamma }^{2}} + O({{\gamma }^{4}}),$ j = 1, 2 аналогично [11].
2.1. Вязкоупругий случай. При исследовании волновых процессов в волноводах, где необходим учет затухания, наиболее простым способом его учета является использование моделей линейной вязкоупругости [19, 20] и концепции комплексных модулей.
Учитывая операторные соотношения вязкоупругости типа Олдройда, при помощи которых можно смоделировать вязкоупругие свойства материала:
В результате получаем, что в случае установившихся колебаний вязкоупругие свойства материала можно задать при помощи следующих комплексных модулей:
(2.4)
$C_{{mk}}^{*}(\omega ) = {{C}_{{mk}}}((1 + {{\omega }^{2}}{{\tau }_{1}}{{\tau }_{2}}){\text{/}}(1 + {{\omega }^{2}}\tau _{1}^{2}) + i\omega \left( {{{\tau }_{1}} - {{\tau }_{2}}} \right){\text{/}}(1 + {{\omega }^{2}}\tau _{1}^{2}))$Отметим некоторые свойства введенных комплексных функций. Пусть $C_{{mk}}^{*}(\omega )$ = = Cmkf(ω), $f(\omega )\, = \,{{f}_{1}}(\omega )\, + \,i{{f}_{2}}(\omega ),$ ${{f}_{1}}(\omega )\, = \,(1\, + \,{{\omega }^{2}}{{\tau }_{1}}{{\tau }_{2}}){\text{/}}(1\, + \,{{\omega }^{2}}\tau _{1}^{2}),$ f2(ω) = ω(τ1 – ${{\tau }_{2}}){\text{/}}(1 + {{\omega }^{2}}\tau _{1}^{2}).$ Тогда имеют место следующие соотношения $\mathop {\lim }\limits_{\omega \to 0} {{f}_{1}}\left( \omega \right) = 1$ и $\mathop {\lim }\limits_{\omega \to 0} {{f}_{2}}\left( \omega \right) = 0$, $\mathop {\lim }\limits_{\omega \to \infty } {{f}_{1}}(\omega )$ = = τ2/τ1 и $\mathop {\lim }\limits_{\omega \to \infty } {{f}_{2}}\left( \omega \right) = 0$.
Таким образом, в рамках концепции комплексных модулей достаточно в соответствующем операторных пучках (2.1)–(2.3) заменить упругие характеристики их комплексными модулями.
2.2. Слабая постановка задачи. В изотропной теории упругости для исследования сформулированной спектральной задачи для цилиндрических волноводов традиционно применяются методы, связанные с заменой переменных в уравнениях движения, цель которых – переход к полярной системе координат и разделение переменных. Однако в анизотропном случае отсутствует возможность разделения переменных. Поэтому традиционный способ решения задач, связанных с исследованием спектра, оказывается неприменимым. Для изучения волновых процессов в рассматриваемом случае построим приближенные модели деформирования, для чего сформулируем слабую постановку задачи. Введем гладкий вектор ${\mathbf{V}} = ({{V}_{1}},{{V}_{2}},{{V}_{3}})$, ${{V}_{j}} \in С_{0}^{2}(S)$ удовлетворяющий граничным условиям на части ∂S1${{\left. {{{V}_{j}}} \right|}_{{\partial {{S}_{1}}}}} = 0$ и компоненты ${{t}_{{mj}}}(\gamma )$ согласно соотношениям ${{\sigma }_{{mj}}} = {{t}_{{mj}}}\exp (i(\gamma {{x}_{3}} - \omega t))$.
Тогда после отделения экспоненциального множителя уравнения движения запишутся в виде:
Умножая (2.5) на $\overline {{{V}_{m}}} $, где $\overline {{{V}_{m}}} $ – комплексно-сопряженные к компонентам Vm, интегрируя по S, и, используя формулу Грина, получим
Таким образом, учитывая однородные граничные условия на границе ∂S, получим, что слабая постановка исследуемой задачи имеет вид следующего равенства:
(2.6)
$\int\limits_S {({{t}_{{mj}}}\overline {{{V}_{m}}} {{,}_{j}} - \rho {{\omega }^{2}}{{U}_{m}}{{{\overline V }}_{m}})} dS = 0$Из (2.6) можно получить как вариационный принцип, аналогичный принципу Гамильтона–Остроградского для установившихся колебаний [23], так и линейную систему для определения компонент вектора Vm и нахождения точек дисперсионного множества.
1. Если положить ${{V}_{m}} = \delta {{U}_{m}}$, то из (12) получим $\delta M = 0$, где
2. Если выбрать систему линейно независимых координатных функций φk, таких что ${{\left. {{{\varphi }_{k}}} \right|}_{{\partial {{S}_{1}}}}} = 0$ и отыскивать решение Um в виде ${{U}_{m}} = \sum\limits_{k = 1}^N {{{A}_{{km}}}} {{\varphi }_{k}}$, то относительно Akm можно получить однородную систему, приравняв ее определитель к нулю, и, найдя его корни, получим приближение для точек дисперсионного множества.
Полагая τ1 = τ2 в (2.4), можно осуществить переход к упругому случаю, исследование которого представлено в работе [16], где было показано, что задача о распространении волны вдоль упругого топографического волновода может быть сведена к определению стационарного значения квадратичного функционала M:
При этом подынтегральная функция в (2.7) есть квадратичная функция амплитуд и их производных и имеет следующий вид:
Используя принцип соответствия, исследование особенностей распространения волновых полей в вязкоупругом волноводе может быть сведено к решению задачи о нахождении стационарного значения функционала
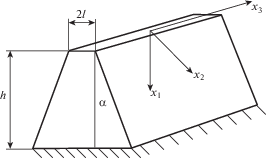
где подынтегральное выражение в (2.8) представляет собой квадратичную функцию амплитуд и их производных, строится аналогично упругому случаю с заменой γj на $\gamma _{j}^{*}$(ω) согласно (2.4).Рассмотрим частный случай: исследуем распространение волн в вязкоупругом волноводе с поперечным сечением S, которое представляет собой равнобочную трапецию с высотой h, меньшим основанием, равным $2l$, и градусной мерой угла при основании составляющей $\pi {\text{/}}2 - \alpha $ (рис. 2).
Для дальнейшего исследования и численных расчетов будем считать, что ${{\tau }_{1}} = m{{\tau }_{2}}$, $m > 1$, и введем безразмерный параметр A:
Тогда выражения для комплексных модулей (2.4) принимают вид:
(2.9)
$C_{{ij}}^{*} = {{C}_{{ij}}}\left( {\frac{{1 + m{{A}^{2}}\beta }}{{1 + {{A}^{2}}\beta }} - i\frac{{(m - 1)\sqrt \beta A}}{{1 + {{A}^{2}}\beta }}} \right)$При A = 0 задача о колебаниях вязкоупругого топографического волновода сводится к исследованию упругого случая, который был ранее изучен в работе [16].
3. Модель вязкоупругой пластины типа Кирхгофа. Как и в упругом случае, описанном в работах [12–16], рассматриваются антисимметричные колебания.
Учитывая спектральную задачу для упругого волновода, для упрощения основного функционала (2.8) примем, что для изучаемой модели при малых углах α компоненты амплитуд смещений удовлетворяют гипотезам, аналогичным гипотезам теории пластин для модели переменной жесткости Кирхгофа:
Внося это представление в (2.8) и интегрируя по x2, сделаем замену переменных $z = {{{{x}_{1}}} \mathord{\left/ {\vphantom {{{{x}_{1}}} h}} \right. \kern-0em} h}$. Таким образом, найдем упрощенное значение функционала, и задача об анализе волновых полей для топографических волноводов сводится к задаче об исследовании стационарного значения функционала M:
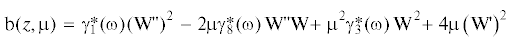
При µ = 0 функционал M[W] аналогичен соответствующему функционалу для балки [24].
Решение о нахождении стационарного значения функционала (3.1) будем искать согласно методу Ритца в следующем виде:
(3.2)
$W = {{\left( {1 - z} \right)}^{2}}\sum\limits_{n = 1}^N {{{a}_{n}}{{\varphi }_{n}}\left( z \right)} $4. Вычислительные эксперименты. Выполнены вычислительные эксперименты для вязкоупругого материала типа барит с параметрами α = 5°, s = 0.01 и m = 1.2 и упругими постоянными для нахождения комплексных модулей (2.9), которые описаны в [25] для барита. Результаты вычислительных экспериментов отражены в следующих таблицах. Отметим, что все точки дисперсионного множества в рассматриваемом случае, в отличие от упругого варианта, являются комплексными.
Из табл. 1 и табл. 2 можно заметить, что для стабилизации решений и описания первых двух мод достаточно взять 7 координатных функций.
Таблица 1.
Первая мода колебаний для волновода с трапециевидным сечением с параметрами: A = 0.01, α = 5°, s = 0.01 и m = 1.2
| N = 5 | N = 6 | N = 7 | N = 8 | |||||
|---|---|---|---|---|---|---|---|---|
| Re µ | Im µ | Re µ | Im µ | Re µ | Im µ | Re µ | Im µ | |
| β = 1 | 21.6651 | 0.0207 | 21.6773 | 0.0207 | 21.6795 | 0.0207 | 21.6796 | 0.0207 |
| β = 2 | 38.7483 | 0.0480 | 38.7880 | 0.0481 | 38.7984 | 0.0481 | 38.7991 | 0.0481 |
| β = 3 | 53.1212 | 0.0789 | 53.1897 | 0.0790 | 53.2144 | 0.0791 | 53.2169 | 0.0791 |
| β = 4 | 65.9868 | 0.1118 | 66.0781 | 0.1119 | 66.1216 | 0.1121 | 66.1273 | 0.1121 |
| β = 5 | 77.8078 | 0.1464 | 77.9139 | 0.1464 | 77.9787 | 0.1466 | 77.9889 | 0.1466 |
Таблица 2.
Вторая мода колебаний для волновода с трапециевидным сечением с параметрами: A = 0.01, α = 5°, s = 0.01 и m = 1.2
| N = 5 | N = 6 | N = 7 | N = 8 | |||||
|---|---|---|---|---|---|---|---|---|
| Re µ | Im µ | Re µ | Im µ | Re µ | Im µ | Re µ | Im µ | |
| β = 3 | 8.1071 | 0.0734 | 8.2368 | 0.0736 | 8.2605 | 0.0737 | 8.2623 | 0.0737 |
| β = 4 | 15.6940 | 0.0801 | 15.8602 | 0.0805 | 15.8972 | 0.0807 | 15.9005 | 0.0807 |
| β = 5 | 21.9185 | 0.0924 | 22.1213 | 0.0929 | 22.1749 | 0.0933 | 22.1803 | 0.0933 |
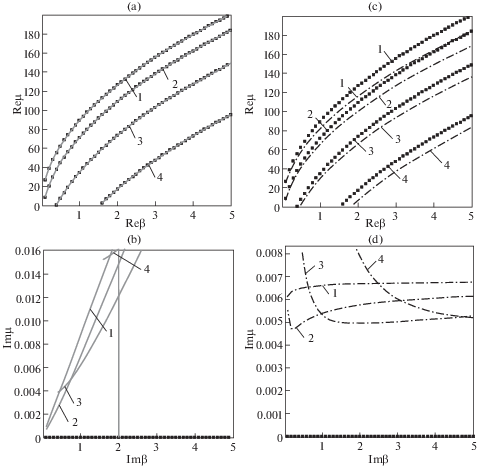
Графики дисперсионных зависимостей на рис. 3 и 4, где точками изображен упругий случай ($A = 0$), сплошной линией обозначены точки дисперсионного множества при $A = 0.001$, штрихпунктирной линией – при $A = 1000$, а метками обозначены соответствующие моды колебаний.
Рис. 3.
Дисперсионные зависимости (N = 7, s = 0.01, α = π/36) с трапециевидным (a, b) и треугольным (c, d) сечением.
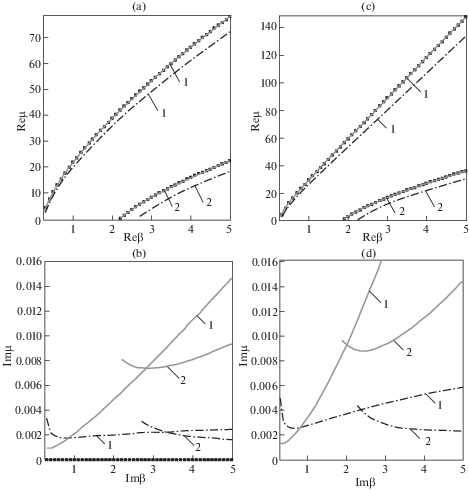
Можно заметить, что для первой и второй мод колебаний действительные части дисперсионных множеств, которые характеризуют скорости волн, для упругого случая и вязкоупругого случая с параметром $A = 0.001$, практически не отличаются. Что касается мнимых частей, характеризующих затухание, то их расхождение гораздо более выражено.
Для вязкоупругого случая при $A = 0.001$ и $A = 1000$ для волновода с трапециевидным сечением действительные части дисперсионного множества первой моды отличаются на 7.7%, а мнимые – на 79%, для второй моды действительные части дисперсионного множества первой моды отличаются на 24.2%, а мнимые – на 78%. Результаты вычислительных экспериментов свидетельствуют о том, что все моды являются затухающими, что учет вязкости не очень сильно влияет на скорости распространения волн, однако достаточно сильно влияет на затухание и уменьшение амплитуд.
5. Заключение. Рассмотрены особенности распространения волновых процессов в топографических волноводах из ортотропных вязкоупругих материалов. Для упругого волновода, поперечное сечение которого произвольно, представлена постановка задачи, сформулировано операторное уравнение, которое зависит от двух спектральных параметров. Сформулирована слабая постановка задачи, при использовании гипотез типа Кирхгофа пластин переменной жесткости построен функционал, стационарное значение которого найдено методом Ритца. В ходе вычислительных экспериментов для вязкоупругого топографического волновода с трапециевидным поперечным сечением построены дисперсионные соотношения для первых двух мод. Проведено сравнение с результатами, полученными ранее результатами для упругого случая, представлены виды дисперсионных зависимостей для волноводов с различными профилями сечения.
Благодарности. Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 19-31-90079.
Список литературы
Ash E.A., Rue R.M.D.L., Humphryes R.F. Microsound Surface Waveguide // IEEE Trans. Microw. Theory. Tech. 1969. V. 17. № 11. P. 882–892. https://doi.org/10.1109/TMTT.1969.1127078
Lagasse P.E., Mason I.M., Ash E.A. Acoustic surface waveguides – analysis and assessment // IEEE Trans. Microw. Theory Tech. 1973. V. MTT-21. P. 225–226. https://doi.org/10.1109/TMTT.1973.1127973
Lagasse P.E. Higher-order finite-element analysis of topographic guides supporting elastic surface waves // J. Acoust. Soc. Am. 1973. V. 53. № 4. P. 1116–1122. https://doi.org/10.1016/0041-624X(73)90248-5
Maradudin A.A., Wallis R.F., Mills D.L. et al. Vibrational edge modes in finite crystals // Phys. Rev. B. 1972. V. 6. P. 1106–1111. https://doi.org/10.1103/PhysRevB.6.1106
Moss S.L., Maradudin A.A., Cunningham S.L. Vibrational edge modes for wedges with arbitrary interior angles // Phys. Rev. B. 1973. V. 8. P. 2999–3008. https://doi.org/10.1103/PhysRevB.8.2999
Бирюков С.В., Гуляев Ю.В., Крылов В.В., Плесский В.П. Поверхностные акустические волны в неоднородных средах. М.: Наука, 1991. 414 с.
Можаев В.Г. Лучевая теория клиновых акустических волн // Вестник Моск. ун. Сер. 3: Физика. Астрономия. 1989. № 5. С. 40–45.
Wagers R.S. Phase-velocity relation for an acoustic wedge guide mode // J. Appl. Phys. 1973. V. 44. № 11. P. 4813–4815. https://doi.org/10.1063/1.1662049
Гринченко В.Т., Мелешко В.В. Свойства гармонических волн, распространяющихся вдоль ребра прямоугольного клина // Акуст. журн. 1981. Т. 27. № 2. С. 206–212.
Ворович И.И., Бабешко В.А. Динамические смешанные задачи теории упругости для неклассических областей. М.: Наука, 1979. 320 с.
Гетман И.П., Устинов Ю.А. Математическая теория нерегулярных твердых волноводов. Ростов нa Дону: Изд-во РЕУ, 1993. 144 с.
Ватульян А.О., Паринова Л.И. Исследование клиновых волн в ортотропной среде // Вестник ДГТУ. 2005. Т. 5. № 4 (26). С. 491–499.
Vatulyan A.O., Parinova L.I. On the elastic waves propagating along the edge of the wedge with small opening angle // Advanced Materials - Techniques, Physics, Mechanics and Applications, Springer Proceeding in Physics, Mechanics and Applications, Springer Proceeding in Physics V. 193 / Ed. bu Ivan A. Parinov, Shun-Hsyung Chang. Springer, 2017. P. 309–319. https://doi.org/10.1007/978-3-319-56062-5_26
Ватульян А.О., Паринова Л.И. Об исследовании дисперсионных свойств топографических волноводов // Изв. вузов. Сев-Кавк. регион. Естеств. науки. 2018. № 3. С. 10–17.
Vatulyan A., Parinova L. On the use of models of the tymoshenko type in the analysis of wave processes in wedge-shaped waveguides // Advanced Materials – Proceedings of the International Conference on “Physics and Mechanics of New Materials and Their Applications”, PHENMA 2019, Springer Proceedings in Materials, V. 6 / Ed by Parinov I.A., Shun-Hsyung Chang, Banh Tien Long. Cham, Switzerland: Springer Nature, 2020. P. 383–389. https://doi.org/10.1007/978-3-030-45120-2_31
Ватульян А.О., Паринова Л.И. Исследование волновых процессов в упругих топографических волноводах // Акуст. журн. 2021. Т. 67. № 2. С. 119–125. https://doi.org/10.31857/S0320791921020106
Камоцкий И.В. О поверхностной волне, бегущей вдоль ребра упругого клина // Алгебра и анализ. 2008. Т. 20. № 1. С. 86–92.
Заворохин Г.Л., Назаров А.И. Об упругих волнах в клине // Записки научных семинаров ЛОМИ. 2010. Т. 380. С. 45–52.
Работнов Ю.Н. Ползучесть элементов конструкций. М.: Наука, 1966. 752 с.
Кристенсен Р. Введение в теорию вязкоупругости. М.: Мир, 1974. 340 с.
Saravanan T. Jothi. Guided ultrasonic wave-based investigation on the transient response in an axisymmetric viscoelastic cylindrical waveguide // Ultrasonics. 2021. V. 117. P. 106543. https://doi.org/10.1016/j.ultras.2021.106543
Mazzotti M., Marzani A., Bartoli I., Viola E. Guided waves dispersion analysis for prestressed viscoelastic waveguides by means of the SAFE method // Int. J. Solids Struct. 2012. V. 49. № 18. P. 2359–2372 https://doi.org/10.1016/j.ijsolstr.2012.04.041
Като Т. Теория возмущений линейных операторов. М.: Мир, 1972. 740 с.
Филиппов А.П. Колебания деформируемых систем. М.: Машиностроение, 1970. 734 с.
Блистанов В.С., Бондаренко В.С., Перемолова Н.В. и др. Акустические кристаллы: Справочник / Под ред. Шаскольской М.П. М.: Наука, 1982. 632 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела