Известия РАН. Механика твердого тела, 2022, № 6, стр. 140-147

1. Введение. Рассмотрение трансляционно-инвариантных и циклических систем основывается на фундаментальных свойствах линейных дифференциальных операторов и краевых задач для систем дифференциальных уравнений [1–3]. Развитый аппарат линейных алгебраических систем и теории функций комплексного переменного [4–7] позволяют применять при решении периодических систем эффективные представления искомых решений. Особую роль при этом играют разрабатываемые методы декомпозиции [8–10]. Широкий класс задач [11, 12], исследуемых с применением данных методов, составляют проблемы механики деформируемого твердого тела, возникающие при изучении устойчивости сжатых циклических конструкций.

Данная работа содержит решение задач о спектре циклических систем, описываемых в операторной форме, в виде краевых задач на собственные значения. Получены представления для собственных функций в случае простого и кратного собственных значений. Разработана декомпозиция спектральных задач, упрощающая анализ поведения рассматриваемой механической системы. При этом решение описанной проблемы сводится к решению спектральных задач на элементарной ячейке. Метод декомпозиции применен также для вариационного анализа возникающих задач на собственные значения. В качестве примера приводится решение задачи устойчивости циклически сжимаемого неразрезного упругого кольца.

2. Основные соотношения задачи. Рассматриваются задачи о спектре циклических систем, поведение которых описывается краевыми задачами на собственные значения, записываемыми в операторной форме [1–3]

где $A$ и $B$ – симметричные вещественные операторы, включающие граничные условия, $\lambda $ – собственное значение, $w\left( {q;\theta } \right)$ – собственная функция, описывающая состояние системы и отвечающая собственному значению. Через q в аргументах функции $w$ и операторов $A$, $B$ обозначен набор всех отличных от $\theta $ независимых переменных. Предполагается, что операторы в уравнении (2.1) инвариантны относительно операции поворота на углы, кратные периоду ${{\theta }_{n}} = 2\pi {\text{/}}n$, то есть операторы $A$, $B$ и собственная функция $w$ не меняют своего вида при замене аргумента

Величина угла поворота $\theta $ меняется в пределах $0 \leqslant \theta \leqslant 2\pi $, и, следовательно, можно считать, что в (2.2) целая величина j удовлетворяет условию$j \in \left[ {1,n} \right]$, где $n$ – заданное значение. Заметим также, что в постановку спектральной краевой задачи (2.1) включено требование ограниченности решения $w\left( {q;\theta } \right)$.

Введем в рассмотрение функцию

Непосредственная подстановка функции $\tilde {w}\left( {q;\theta } \right)$ из (2.3) в уравнение (2.1) с последующей заменой (2.2) с  j = 1 и учетом свойства циклической инвариантности рассматриваемой системы показывает, что функция $\tilde {w}\left( {q;\theta } \right)$ также является собственной функцией краевой спектральной задачи (2.1), соответствующей собственному значению $\lambda $.

Рассмотрим сначала случай некратного (простого) собственного значения $\lambda $ и соответствующей ему с точностью до произвольной постоянной C единственной собственной функции $Cw\left( {q;\theta } \right)$ [4, 5]. Для функции $\tilde {w}\left( {q;\theta } \right) = Cw\left( {q;\theta } \right)$ согласно (2.3) имеем

Свойство (2.4) собственных функций циклических задач показывает, что при определении собственных функций, отвечающих простым собственным значениям, достаточно ограничиться интервалом изменения $\theta \in \left[ {0,{{\theta }_{n}}} \right]$. При этом значения функции в интервале $\left[ {{{\theta }_{n}},2\pi } \right]$ получаются продолжением функций из интервала $\left[ {0,{{\theta }_{n}}} \right]$ с использованием соотношения (2.4). В частности,

а при произвольном $j \in \left[ {1,n} \right]$ выполняется соотношение

С учетом равенства $n{{\theta }_{n}} = 2\pi $ будем иметь

Таким образом, входящая в равенство (2.4) постоянная $C$ удовлетворяет уравнению

С использованием выражений [6, 7] для корней уравнения (2.5)

получим представление для собственных функций в случае простого собственного значения

Рассмотрим теперь случай r-кратного собственного значения $\lambda $ и соответствующей ему системы собственных функций

Предполагается, что система линейно независимых функций (2.7) удовлетворяет условиям ортонормированности [4, 5]

где $\left( {q;\theta } \right)$ – символ Кронекера, а выражение в левой части равенства (2.8) – скалярное произведение. При этом функции ${{\tilde {w}}_{j}}\left( {q;\theta } \right) \equiv {{w}_{j}}\left( {q;\theta + {{\theta }_{n}}} \right)$ ($j = 1,2,...,r$) могут быть представлены в форме разложений по системе собственных функций (2.7)

причем в силу условий ортонормированности (2.8), записанных для функций, приведенных в (2.9), коэффициенты разложений ${{K}_{{jl}}}$ удовлетворяют уравнениям

Матрица K, составленная из коэффициентов разложений ${{K}_{{jl}}}$, является унитарной, т.е. $\tilde {K}{\text{*}}K$ – единичная матрица. Заметим, что матрица K может быть приведена к диагональному виду [4, 5]

с диагональной матрицей $\Lambda $. Для этого используется преобразование U базиса собственных функций ${{w}_{j}}\left( {q;\theta } \right)$, сохраняющее условие ортонормированности. Таким образом, собственные функции, принадлежащие кратному собственному значению, инвариантны относительно преобразования сдвига $\theta \to \theta + {{\theta }_{n}}$ краевой задачи (2.1) и могут быть выбраны в виде, удовлетворяющем условию (2.4), т.е.

Аналогично тому, как это делалось в случае некратных собственных значений, приходим к общему свойству собственных функций инвариантной относительно свойств спектральной краевой задачи (безотносительно кратности r)

Предположим, что собственная функция ${{w}_{{{{\alpha }_{k}}}}}(q;\theta )$ обладает свойством (2.13). Введем в рассмотрение вспомогательную функцию $w_{{{{\alpha }_{k}}}}^{0}(q;\theta )$, определяемую формулой

и рассмотрим эту функцию при $\theta \to \theta + {{\theta }_{n}}$. Будем иметь

Следовательно, $w_{{{{\alpha }_{k}}}}^{0}(q;\theta )$ является периодической функцией с периодом ${{\theta }_{n}}$. В итоге проведенного анализа приходим к общему представлению для собственных функций циклических систем, инвариантных относительно конечных вращений $\theta \to \theta + k{{\theta }_{n}}$ при рассмотрении проблемы (2.1):

Значение ${{\alpha }_{k}}$ является характеристикой собственных функций периодических задач, и в связи с этим значение этого параметра указывается в обозначениях собственных функций. Соответственно этому, собственные значения краевой задачи (2.1) также представляют собой некоторые зависимости от параметра ${{\alpha }_{k}}$, т.е. $\lambda = \lambda \left( {{{\alpha }_{k}}} \right)$. Отметим, что $\lambda \left( {{{\alpha }_{k}}} \right)$ – периодическая функция параметра ${{\alpha }_{k}}$, т.е. $\lambda \left( {{{\alpha }_{k}}} \right) = \lambda \left( {{{\alpha }_{k}} + 2\pi k} \right)$, $k = 1,2,...$, так как сдвигу параметра ${{\alpha }_{k}}$ на величины, кратные $2\pi $, отвечают целочисленные повороты механической системы вокруг ее оси симметрии.

3. Декомпозиция. Представление собственных функций периодической краевой задачи в форме (2.16) позволяет существенно упростить анализ поведения рассматриваемой механической системы, сводя решение исходной задачи к ее решению в секторе ${{\Omega }_{0}}:0 \leqslant \theta \leqslant {{\theta }_{n}}$, где ${{\Omega }_{0}}$ – элементарная ячейка исходной области $\Omega :0 \leqslant \theta \leqslant 2\pi $. Значения собственных функций ${{w}_{{{{\alpha }_{k}}}}}\left( {q;\theta } \right)$ на границах элементарной ячейки $\theta = 0$ и $\theta = {{\theta }_{n}}$ генерируются условиями периодичности (2.13) и в случае дифференцируемости решений (2.1) по угловой переменной $\theta $ принимают вид

Порядок производных по переменной $\theta $ отмечается верхним индексом $\left( s \right)$, записываемым в круглых скобках, причем максимальный порядок производной согласуется с операторами $A$ и $B$.

В результате используемой декомпозиции [8] решение исходной задачи (2.1), определенной в области $\Omega $, заменяется серией $n$ краевых задач, определенных в элементарной ячейке ${{\Omega }_{0}}$

Отметим, что краевая задача о собственных значениях (3.2) является однопараметрической с параметром ${{\alpha }_{k}}$, входящим в граничные условия и принимающим $n$ дискретных значений. Собственные значения краевой задачи (3.2) можно интерпретировать как некоторые функции этого параметра. Относительно взаимного поведения этих функций можно высказать общее утверждение (см. [9, 10]), что для систем общего положения пересечение графиков этих функций невозможно при любых значениях α_k.

С использованием метода декомпозиции приведем также вариационную формулировку спектральных краевых задач (3.2). Будем исходить из вариационной формулировки первоначальной задачи на собственные значения (2.1)

где $w$, удовлетворяет заданным условиям на границе $\Gamma $ области $\Omega $. Нижний индекс $\Omega $ указывает, что обозначаемое круглыми скобками в (3.3) скалярное произведение вычисляется в области $\Omega $. Минимум отношения Рэлея в (3.3) разыскивается в классе функций, удовлетворяющих общему свойству (2.13) решений периодических задач. С учетом этого, числитель и знаменатель в (3.3) преобразуются к виду где индексом ${{\Omega }_{0}}$ отмечено, что выражение в скобках определяется в области ${{\Omega }_{0}}:0 \leqslant \theta \leqslant {{\theta }_{n}}$ (“элементарной ячейке”). С использованием равенств (3.4) и (3.5) в (3.3) приходим к декомпозированному выражению для собственного значения

При этом на границах области ${{\Omega }_{0}}$:$\theta = 0$,$\theta = {{\theta }_{n}}$ значения искомой функции удовлетворяют условиям (3.2).

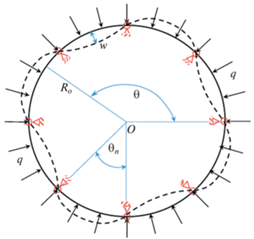
4. Устойчивость сжимаемого упругого кольца. В качестве примера применения развитых представлений и декомпозиции циклических систем рассмотрим задачу о сжатии и потере устойчивости кругового неразрезного упругого кольца, находящегося под равномерным давлением P и шарнирно закрепленного в точках ${{\theta }_{j}} = j{{\theta }_{n}}$, θ_n = $2\pi {\text{/}}n$, $j = 0,1,2,...,n - 1$ (рис. 1). Для описания упругого выпучивания кольца радиуса $R$ (в недеформированном состоянии) и жесткости на изгиб $EI$ воспользуемся уравнением и граничными условиями [11, 12]

С использованием переменной $\theta = {{\theta }_{n}}\tilde {\theta }$ (тильда в дальнейшем опускается) будем иметь

Граничные условия для используемой элементарной ячейки запишутся в виде

Удовлетворяя общее решение дифференциального уравнения (4.2)

граничным условиям краевой задачи (4.3), стандартным образом приходим к уравнению для определения критических сил потери устойчивости

Так как $\left| {\cos \alpha } \right| \leqslant 1$, то критические силы потери устойчивости удовлетворяют условию $\left| {f\left( \lambda \right)} \right| \leqslant 1$.

Непосредственные вычисления приводят к уравнениям для определения границ спектральных полос

Уравнению (4.6) удовлетворяют корни уравнений

а уравнение (4.7) имеет решение

Решение $\lambda = 0$ исключается из рассмотрения.

Таким образом, спектр критических сил потери устойчивости неразрезного упругого кольца, сжатого равномерным давлением и шарнирно закрепленного в равноотстоящих точках, состоит из полос с непрерывным спектром. Нижние границы полос описываются выражением

а верхние границы полос определяются корнями уравнения ${\text{tan}}\left( {\sqrt \lambda {\text{/}}2} \right) = \sqrt \lambda {\text{/}}2$ с асимптотическим представлением где ${{\varepsilon }_{k}} \approx 2{\text{/}}\left( {2k + 1} \right)\pi $ при $k \gg 1$. Расстояние между границами соседних полос $\Delta {{\lambda }_{k}}$ = = 2ε_k с ростом $k$ стремится к нулю.

5. Заключение и некоторые замечания. В работе представлены результаты исследования задач о спектре циклических систем, описываемых краевыми задачами на собственные значения. В предположении об инвариантности определяющих соотношений относительно поворота на углы, кратные периоду аргумента, и ограниченности решения спектральной задачи получены представления для собственных функций в случае простого и кратного собственных значений.

Представлена декомпозиция собственных функций, упрощающая анализ поведения рассматриваемой механической системы за счет сведения решения исходной задачи к ее решению на элементарной ячейке. С использованием метода декомпозиции дана также вариационная формулировка рассматриваемой задачи на собственные значения.

На примере рассмотрения задачи об устойчивости сжимаемого упругого кольца показана эффективность применения развитых представлений и декомпозиции циклических систем. Приведем некоторые замечания.

Замечание 1. Континуальные механические системы характеризуются наличием оси симметрии n-го порядка, при вращении вокруг которой на углы, кратные углу $2\pi {\text{/}}n$, эти системы совмещаются сами с собой. При $n \to \infty $ циклические системы трансформируются в системы с круговой симметрией.

Замечание 2. Данная работа посвящена циклическим механическим системам. Другим видом периодических систем служат трансляционно-инвариантные системы, являющиеся бесконечно протяженными и используемыми в качестве асимптотических моделей реальных механических объектов, находящихся в условиях свободных колебаний или в состоянии потери устойчивости при сжатии. Общие представления для трансляционно-инвариантных систем, включая собственные функции и собственные значения, получаются из представленных в работе для циклических систем заменой угла $\theta $ на осевую координату $x$ и периода ${{\theta }_{n}}$ на параметр периодичности $a$, фигурирующий в операции сдвига системы: $x \to x + a$.

Замечание 3. Помимо трансляционно-инвариантных и циклических систем к инвариантным относятся также случаи, когда операторы $A$ и $B$, а также и решение спектральной задачи $w$ характеризуются инверсией относительно операции $x \to a - x$ (инверсионный случай). В частности, условия инверсии выполняются, когда операторы A и $B$ содержат только четные производные по $x$, а варьируемые коэффициенты задачи являются четными функциями аргумента $a{\text{/}}2 - x$. При наличии данной инверсии вводится функция $\hat {w}\left( {q;x} \right) \equiv w\left( {q;a - x} \right)$, удовлетворяющая уравнению

и учитываются граничные условия. При этом и в результате имеем представление для уравнения и производных

Опуская проведенные дальнейшие элементарные операции (включая операции комплексного сопряжения), приходим к представлениям

где вещественная часть функции ${{w}_{\alpha }}\left( {q;x} \right)$ является четной, а мнимая часть – нечетной по отношению к $x = a{\text{/}}2$. Это позволяет уменьшить число операций, используя переходы к интервалам $x \in \left[ {0,a{\text{/}}2} \right]$ или$x \in \left[ {a{\text{/}}2,a} \right]$.

Автор благодарит А.А. Барсука и С.Ю. Иванову за полезные обсуждения и помощь в оформлении статьи.

Работа выполнена по теме госзадания (номер госрегистрации АААА-А20-120011690132-4) и при частичной финансовой поддержке Российским фондом фундаментальных исследований (проект № 20-08-00082а).