Известия РАН. Механика твердого тела, 2023, № 2, стр. 42-54

Введение. Задачи качения колеса, как основного элемента конструкции транспортного средства, в условиях сухого трения представляются весьма важными и полезными в настоящее время. Такие задачи встречаются, например, при исследовании шимми колеса шасси самолетной стойки [1–3] или устойчивости вертикального движения экипажа [4, 5]. Необходимо при этом учитывать, что контакт колеса с дорогой не является точечным, а происходит по некоторой (пусть и малой) площадке. Тогда классическая (по Эйлеру–Кулону) модель сухого трения должна быть заменена более реальной моделью Контенсу–Журавлева [6]. Это обстоятельство усложняет решение задач устойчивости, но приводит к более точным результатам и выводам.

Другая сторона задач о качении колеса заключается в исследовании нарушения контакта (односторонней связи) колеса с дорогой, в частности, при наезде колеса на препятствие или, наоборот, съезде с препятствия (например, это может быть выбоина или крышка канализационного люка). В этих случаях необходимо использовать теорию удара с трением [7]. Ясно, что в таких случаях сила трения, приложенная к колесу, существенно меняется (в частности, она может и равняться нулю). Такие критические ситуации, конечно, крайне нежелательны при движении транспортных средств или других колесных устройств. Поэтому исследование таких критических ситуаций представляется полезным с практической точки зрения.

В настоящей работе сделана попытка полного аналитического решения и анализа таких задач на достаточно простых моделях качения колеса. Предполагается, что контакт колеса с дорогой точечный, а модель сухого трения является классической по Эйлеру–Кулону. Рассмотрены некоторые задачи теоретической механики с ударами и односторонними связями, которые ранее были решены некорректно или неполно [8, 9]. В статье приведены полные решения таких задач, указаны причины допущенных ошибок и неполных решений. Также рассмотрены решения указанных задач для случаев их более широкой постановки. Отдельное внимание уделено возможности реализации движения тел с учетом действующих сил трения.

В частности, в задаче о скатывании колеса с уступа рассмотрен весь спектр инерционных свойств колеса относительно центра масс, совпадающего с его геометрическим центром. Показано, что при конечном значении коэффициента трения колесо начнет проскальзывать до его отрыва от уступа. Исключение составляет случай, соответствующий системе, состоящей из точечной массы, закрепленной в центре колеса, инерционными свойствами которого можно пренебречь. В этой ситуации колесо, обладающее указанными свойствами, проскальзывать не будет при любом значении коэффициента трения скольжения.

В задаче о перекатывании колеса через уступ рассматриваются условия, при которых колесо может преодолеть препятствие без отрыва от поверхности и без проскальзывания относительно нее, а также определяются дополнительные ограничения, накладываемые на высоту уступа при условии конечности коэффициента трения скольжения.

В задаче о подкидной доске и шарах рассматриваются возможные варианты послеударного движения системы.

1. Задача о перекатывании колеса через уступ [8]. Пусть колесо массы $m$ и радиуса $r$, катясь без скольжения по горизонтальной направляющей $LL$, наталкивается на уступ высотой h и, огибая его, поднимается на горизонтальную направляющую $OM$. Удар колеса об уступ считается неупругим, скольжение при ударе и огибании уступа отсутствует.

Определим, какой должна быть скорость центра C колеса перед ударом, чтобы колесо вкатилось на верхнюю направляющую.

Пусть ${{S}_{x}}$ и ${{S}_{y}}$ – ударные импульсы, приложенные в точке контакта O (см. рис. 1). Обозначим через ${{\alpha }}$ угол, образуемый радиусом СО с вертикалью ($\alpha = \angle OCP$). Ясно, что:

Предударное состояние колеса является качением без проскальзывания, а послеударное – это вращение без проскальзывания вокруг точки O. В системе координат $Oxy$ (рис. 1) имеем для скорости центра масс С и угловой скорости $\omega $ колеса:

В (1.2) знак “–” относится к предударному состоянию, а знак “+” относится к состоянию, наступившему сразу после момента удара. Т.к., ударные импульсы ${{S}_{x}}$ и ${{S}_{y}}$ не создают момента относительно точки О, то сохраняется кинетический момент колеса относительно точки О. Имеем, используя (1.2):

Приравнивая полученные выражения, найдем ${{\omega }^{ + }}$:

Отметим, что для корректной реализации послеударного движения колеса необходимо, чтобы ${{{{\omega }}}^{ + }} > 0$. Согласно (1.3), это эквивалентно неравенству ${{\sigma }} > 0$, из которого следует неравенство ${{\varepsilon }} = h{\text{/}}r < 1.5$.

После удара колесо начинает вращаться вокруг точки О по часовой стрелке, т.е. поднимается вверх. Если не рассматривать процесс этого движения в деталях, то ясно, что колесо поднимется до уровня $OM$, если у него будет достаточный запас послеударной кинетической энергии. Ввиду того, что полная механическая энергия при таком движении без проскальзывания в точке О сохраняется, минимальное значение угловой скорости ${{{{\omega }}}_{1}}$, необходимое для такого подъема, находится из соотношения ${{T}^{ + }} = П$, где

Отсюда получим $\omega _{1}^{2} = 4gh{\text{/}}(3{{r}^{2}})$. Таким образом, для подъема до уровня OM, необходимо, чтобы:

Используя (1.3), из (1.4) получим соответствующее неравенство для:

Формула (1.5) приведена в [1], где дополнительно указано также и неравенство, при котором этот ответ справедлив.

Это неравенство ${{{v}}_{C}}$ очевидно из геометрических соображений, если считать уступ прямоугольным, как это изображено на рис. 1. Однако можно представлять себе уступ и криволинейным, а тогда указанное послеударное кинематическое движение колеса реализуется также и при $0 \leqslant {{\varepsilon }} = h{\text{/}}r \leqslant 1.5$.

Рассмотрим процесс послеударного движения колеса более детально, предполагая, что в точке О отсутствует проскальзывание. Пусть ${{\varphi }}$ – угол между радиусом СО и отрицательным направлением горизонтальной оси $Ox$ (рис. 1). Запишем уравнение движения центра масс $С$ колеса в проекции на радиус OC:

где N – нормальная реакция, действующая на колесо со стороны уступа О.

Для осуществимости безотрывного движения колеса необходимо, чтобы N > 0. Тогда из (1.6) имеем неравенство:

Ясно, что $\varphi \in [0.5\pi - {{\alpha }},0.5\pi ]$.

Запишем теорему об изменении кинетического момента колеса относительно точки O:

Отсюда следует, что ${{\ddot {\varphi }}} < 0$, т.е. ${{\dot {\varphi }(\varphi )}}$ – монотонно-убывающая функция от аргумента ${{\varphi }}$, а $\sin {{\varphi }}$ – монотонно возрастающая функция при ${{\varphi }} \in [0.5{{\pi }} - {{\alpha }},0.5{{\pi }}]$. Тогда, если неравенство (1.7) выполнено в начальный момент при $\varphi = {{\varphi }_{0}} = 0.5\pi - \alpha $, то оно будет выполнено вплоть до подъема колеса на OM. Таким образом, нарушение неравенства (1.7) (т.е. неосуществимость описанного движения) может произойти лишь при φ = = ${{\varphi }_{0}} = 0.5\pi - \alpha $, т.е., если сразу после удара выполняется соотношение:

Итак, получен следующий результат.

1) Если

то безотрывное перекатывание колеса через уступ возможно и реализуется при отсутствии проскальзывания в точке О.

2) Если ${{({{\omega }^{ + }})}^{2}} \leqslant \frac{4}{3}\frac{{gh}}{{{{r}^{2}}}}$, то преодоление уступа невозможно, а если ${{({{\omega }^{ + }})}^{2}} > \frac{g}{r}(1 - {{\varepsilon }})$, то безотрывное движение вообще невозможно реализовать при отсутствии проскальзывания в точке О.

Множество движений, удовлетворяющих неравенству (1.8), может быть не пусто только при соблюдении неравенства, вытекающего из (1.8):

Если $h > \frac{3}{7}r$, то перекатывание колеса при отсутствии проскальзывания в точке О, не реализуется. Таким образом, послеударное перекатывание колеса на верхнюю направляющую OM при отсутствии проскальзывания в точке контакта $O$ возможно только при соблюдении следующих неравенств:

Нарушение одного из этих неравенств свидетельствует о невозможности перекатывания колеса через уступ в рамках рассматриваемой модели движения с отсутствием проскальзывания колеса в точке О.

Следует отметить, что данный результат получен без каких-либо ограничений на коэффициент трения скольжения. Рассмотрим случай, когда коэффициент трения имеет конечное значение.

Для того чтобы в точке О отсутствовало проскальзывание, сила трения не должна превышать максимального значения, которое можно реализовать в данных условиях движения. Найдем силу трения, записав совместно уравнения движения центра масс и теорему об изменении кинетического момента колеса относительно точки О после соприкосновения колеса с уступом.

Откуда

Запишем условие безотрывного движения

Как уже отмечалось, наиболее опасным с точки зрения отрыва колеса от уступа является момент времени сразу после удара колеса об уступ, когда ${{\varphi }} = \pi {\text{/}}2 - {{\alpha }}.$ Подставив это значение ${{\varphi }}$ в выражения (1.11) получим

При отсутствии проскальзывания, согласно закону Кулона, коэффициент трения должен удовлетворять следующему неравенству.

Подставив из (1.8) в (1.12) минимальное значение угловой скорости колеса по условию перекатывания через уступ, получим

Из неравенства (1.13) видно, что при ε = 3/7 коэффициент трения ${{\mu }} = \infty $. Из полученного неравенства также можно сделать вывод о том, что значение параметра $\varepsilon $ имеет ограничения ввиду ограничений, накладываемых на значение коэффициента трения. Получим условие этого ограничения

Например, для значения μ = 1, получим следующее неравенство, которое определяет область значений параметра ${{\varepsilon }}$, при которых перекатывание колеса через уступ возможно без проскальзывания

Полученное значение $\varepsilon $ меньше 3/7.

Отсюда можно сделать вывод, что при конечном значении коэффициента трения появляются дополнительные условия, накладывающие ограничение на отношение высоты уступа к радиусу колеса, при котором возможно перекатывание колеса через уступ без отрыва и проскальзывания.

2. Задача о скатывании колеса с уступа без начальной скорости [9]. Рассмотрим процесс скатывания абсолютно твердого колеса с уступа без начальной скорости в предположении, что в начальный момент времени геометрический центр С колеса находился непосредственно над точкой О (см. рис. 2).

Пусть колесо является любым физически реализуемым диском, центр масс которого совпадает с его геометрическим центром С (рис. 2). То есть радиус инерции колеса находится в пределах от 0 до значения, равного радиусу колеса. Найдем угол, при котором произойдет отрыв колеса от уступа без учета ограничений, накладываемых на движение колеса вследствие конечного значения коэффициента трения. Для этого запишем совместно уравнения движения центра масс и теорему об изменении кинетического момента колеса относительно точки О

где ${{I}_{{Oz}}} = m({{{{\rho }}}^{2}} + {{r}^{2}})~$ – момент инерции колеса относительно оси, перпендикулярной плоскости движения и проходящей через точку О, ${{\rho }}$ и $r$ – радиус инерции и радиус колеса соответственно.

Найдем нормальную реакцию

Квадрат угловой скорости колеса найдем из закона сохранения полной механической энергии

Откуда

После подстановки (2.3) в (2.2) получим

где $k = {{\rho /}}r$. Параметр k находится в пределах от 0 до 1. Значение, равное нулю, соответствует системе, состоящей из точечной массы, закрепленной в центре колеса, инерционными свойствами которого можно пренебречь. Значение, равное единице, соответствует тонкостенной трубе.

Найдем косинус угла отрыва колеса от уступа, приравняв нулю нормальную реакцию

С учетом диапазона значений параметра k получим

Или

Отметим, что в случае однородного колеса при ${{\rho }} = r{\text{/}}\sqrt 2 $ косинус угла отрыва равен 4/7. Такой же результат получен в [9, 10].

Теперь определим, может ли колесо достичь указанных углов отрыва без проскальзывания относительно уступа. Для этого из уравнений (2.1) найдем силу трения

Для отсутствия проскальзывания должно выполняться следующее неравенство

С учетом выражений (2.4), (2.7) и (2.8) получим

Или с учетом того, что $1 + {{k}^{2}} > 0,$ перепишем неравенство (2.9) в следующем виде

Откуда

или

При ${{\mu }} = 0$ получим

То есть при отсутствии трения проскальзывание колеса относительно уступа начнется сразу с началом его движения. Исключение составляет случай $k = 0$, так как в этой ситуации сила трения равна нулю. В этом легко убедиться, записав теорему об изменении кинетического момента относительно центра масс колеса.

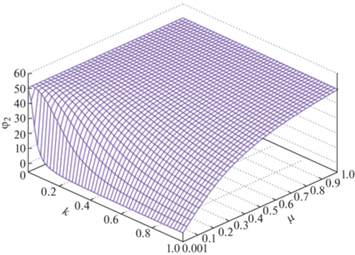
На рис. 3 приведено значение угла ${{{{\varphi }}}_{2}}$ в градусах, при котором колесо начнет проскальзывать, в зависимости от коэффициента трения и параметра k.

Для отсутствия проскальзывания колеса до момента его отрыва от уступа должно выполняться следующее неравенство

или

С учетом выражений (2.5) и (2.11) из неравенства (2.12) получим

После преобразований неравенство (2.13) можно переписать в следующем виде

При значении параметра k, равном нулю, это неравенство выполняется при любом значении коэффициента трения. Напомним, что случай k = 0 соответствует системе, состоящей из точечной массы, закрепленной в центре колеса, инерционными свойствами которого можно пренебречь.

При значениях параметра k, отличных от нуля, последнее неравенство можно переписать в следующем виде

При всех значениях параметра k, отличных от нуля, выражение в левой части последнего неравенства меньше нуля, а выражение в правой части больше нуля. То есть при таких значениях k неравенство не может быть удовлетворено при любом ${{\mu }}$. Следовательно, скатывание колеса с уступа без начальной скорости до момента отрыва невозможно без проскальзывания при всех значениях $k \ne 0$.

На рис. 4 приведены значения разности углов ${{{{\varphi }}}_{1}}$ и ${{{{\varphi }}}_{2}}$ в градусах при различных значениях коэффициента трения ${{\mu }}$ и параметра k.

Определим к какому значению стремится угол ${{{{\varphi }}}_{2}}$ с увеличением коэффициента трения ${{\mu }}$. Для этого найдем предел косинуса угла ${{{{\varphi }}}_{2}}$ при стремлении коэффициента трения к бесконечности

Применив правило Лопиталя, этот предел можно привести к следующему виду

Очевидно, что ${{M}_{2}}$

То есть $\cos {{{{\varphi }}}_{2}}$ стремится к $\cos {{{{\varphi }}}_{1}}$ справа при стремлении коэффициента трения ${{\mu }}$ к бесконечности. Следовательно, при ${{\mu }} \to \infty $ угол ${{{{\varphi }}}_{2}}$, при котором начнется проскальзывание колеса, стремится слева к углу ${{{{\varphi }}}_{1}}$ отрыва колеса от уступа.

3. Задача о подкидной доске [8]. В цирковом аттракционе используется подкидная доска, на правый конец которой с высоты $H$ падает шар А массы ${{M}_{1}}$ и остается на доске в точке контакта. На другом конце доски находится шар В массы M₂, который, приобретя скорость, отделяется от доски при повороте ее вокруг горизонтальной оси. Момент инерции доски относительно горизонтальной оси вращения, проходящей через точку О, равен $J$, угол наклона доски к горизонту равен ${{\alpha }}$.

Определим наибольшую высоту подъема шара В, если $О{{А}_{1}} = {{l}_{1}},\,OB = {{l}_{2}}$. Также рассмотрим случай, когда шару В сообщена в конце удара относительная по отношению к доске скорость ${v}$, направленная перпендикулярно к доске.

Состояние системы “доска + шары А и В” до удара известно. Доска и шар В находятся в покое. Тогда ${{{{\omega }}}^{ - }}$ = 0, где ω^– – угловая скорость доски до удара, а шар А непосредственно перед ударом имеет направленную вниз вертикальную скорость ${v}_{1}^{ - }\, = \,\sqrt {2gH} $ (эта скорость определяется из закона сохранения полной механической энергии для процесса свободного падания шара А с высоты $H$: ${{M}_{1}}gH = 0.5{{M}_{1}}{{({v}_{1}^{ - })}^{2}}$). Послеударное состояние системы также определено: доска вместе с шарами А и В начинает поворачиваться вокруг точки О. Неизвестна послеударная угловая скорость этого поворота, которую обозначим ${{{{\omega }}}^{ + }}$.

Подчеркнем еще раз, что непосредственно после удара оба шара сохраняют свой контакт с доской (шар А по условию абсолютно неупругого удара “прилипает к доске”, а шар В может оторваться от доски только при дальнейшем ее вращении). Для определения ${{{{\omega }}}^{ + }}$, применяем теорему об изменении кинетического момента при ударе относительно точки О. Выбор точки О связан с тем, что внешние ударные импульсы возникают только в шарнире О, тогда их момент относительно этой точки равен нулю, а поэтому кинетический момент всей системы относительно точки О сохраняется. До удара $K_{O}^{ - } = {{M}_{1}}{v}_{1}^{ - }{{l}_{1}}\cos {{\alpha }}$. После удара $K_{O}^{ + } = (J + {{M}_{1}}l_{1}^{2} + {{M}_{2}}l_{2}^{2}){{{{\omega }}}^{ + }}$. Используя условие $K_{O}^{ - } = K_{O}^{ + }$, получим

Исследуем теперь вопрос отрыва шара В от доски. Будем предполагать, что доска абсолютно шероховатая, или шар B помещен в небольшом желобе доски, чтобы исключить возможность перемещения его вдоль доски при ее вращении. Введем систему координат $Bxy$ с началом в точке В и осью y, перпендикулярной доске (см. рис. 5). Основным критерием безотрывного движения груза В на доске является положительность нормальной (т.е. вдоль оси By) силы, действующей на шар со стороны доски. Запишем уравнение динамики для груза В вдоль оси y при его безотрывном движении (т.е., вместе с доской):

В (3.2) введены обозначения: $N - $ нормальная реакция, ${{\dot {\omega }}}$ – угловое ускорение доски, ${{\varphi }}$ – угол наклона доски к горизонту, причем ${{\varphi }} \in ( - {{\alpha }},{{\alpha }})$. Здесь мы для простоты предполагаем, что граничные положения доски симметричны при опоре на A и B, т.е. угол наклона ${{\varphi }}$ доски к горизонтали меняется в пределах от $ - {{\alpha }}$ до $ + {{\alpha }}$. Этого всегда можно добиться, подняв или опустив уровень пола под одной из точек A или B.

Пусть ${{M}_{3}}$ – масса доски, ${{x}_{3}}$ – координата центра ее масс в системе $Bxy$. Тогда уравнение моментов для системы (доска с шарами) относительно точки О в послеударном движении имеет вид

Из (3.2) и (3.3) получим следующую формулу для $N$

В (3.3) и (3.4) величина ${{J}_{0}}$ дается выражением из (3.1).

Изучим следующие две возможные ситуации.

1. Отрыв происходит сразу, т.е., при $\varphi = - \alpha $.

2. Отрыва при ${{\varphi }} \in [ - {{\alpha }},{{\alpha }})$ нет, и он происходит “естественным” образом при ${{\varphi }} = {{\alpha }}$, когда конец А доски ударится об опорную горизонтальную плоскость, и доска начнет обратное вращение.

Из формулы (3.4) видно, что случай 1 имеет место при выполнении неравенства

В этом случае выражение в фигурных скобках в равенстве (3.4) является отрицательным, а нормальная реакция для шара B сразу (в начальный момент послеударного движения доски) становится отрицательной, и шар B сразу перестает контактировать с доской.

Если выполнено противоположное неравенство

то имеет место случай 2, что также следует из (3.4).

Пусть, например, доска является однородной, тогда

Неравенства (3.5) и (3.6) принимают вид

Из этих формул видно, что если ${{M}_{3}}$ достаточно велико и ${{l}_{2}} > 2{{l}_{1}}$, то груз В отскочит сразу, а если ${{l}_{2}} < 2{{l}_{1}}$, то груз В отскочит лишь в момент удара конца А доски о землю.

Пусть выполнено неравенство (3.5). Тогда груз В, получив скорость ${v}_{2}^{ + } = {{{{\omega }}}^{ + }}{{l}_{2}}$ перпендикулярно к доске, сразу после удара не будет контактировать с доской и полетит по параболе влево от доски (как указывалось выше, предположение наличия контакта приводит к отрицательности нормальной реакции, действующей на шар В вдоль оси By). Наибольшую высоту его подъема определим из закона сохранения полной механической энергии, записанного в неподвижных осях $O{{x}_{1}}{{y}_{1}}$ (см. рис. 5)

Этот же ответ приведен в задачнике [8], но, однако, без неравенства (3.5), при котором этот ответ справедлив.

Пусть выполнено неравенство (3.6). Тогда груз В оторвется лишь при ${{\varphi }} = {{\alpha }}$, т.е. в момент удара конца доски А о землю. В этот момент он будет иметь скорость ${{{v}}_{2}} = {{{{\omega }}}_{2}}{{l}_{2}}$, где ${{{{\omega }}}_{2}} \ne {{{{\omega }}}^{ + }},{{{{\omega }}}_{2}} > {{{{\omega }}}^{ + }}$. Эта скорость будет перпендикулярна доске и направлена уже вправо. Скорость ${{{{\omega }}}_{2}}$ мы найдем из закона сохранения полной механической энергии для системы “доска + шары А и В” в процессе ее вращательного движения.

Из последнего уравнения получаем

Теперь нетрудно (аналогично приведенной выше выкладке (3.9)) найти максимальную высоту подъема для новых условий. Ясно, что при малых ${{\alpha }}$ эта высота количественно будет мало отличаться от уже полученного ответа (3.9). Однако качественно результаты отличаются существенно: в одном случае шар В (по параболе) полетит налево, а в другом – направо.

Отметим еще одну возможную (несколько вырожденную) ситуацию, которая может реализоваться в случае выполнения неравенства (3.6). Пусть вместе с неравенством (3.6) выполнено неравенство

Тогда доска с шарами совершает замедленное вращение, а ситуация 2 будет иметь место при выполнении неравенства

Используя формулу (3.1), отсюда получим следующее неравенство

Пусть выполнено неравенство, противоположное последнему

Тогда после удара доска с шарами будет совершать замедленное вращение. Кроме того, будет существовать такое $\varphi {\text{*}} \in ( - \alpha ,\alpha )$, при котором $\omega (\varphi {\kern 1pt} *) = 0$ (т.е., доска на мгновение остановится). После этого доска начнет вращаться назад, против часовой стрелки, и ударится о землю уже концом В вместе с шаром B. Если удары доски о пол абсолютно упруги, то никаких отрывов вообще не будет, а будут наблюдаться периодические колебания доски вместе с шарами.

Покажем, что множество, задаваемое одновременно неравенствами (3.6) и (3.11), не пусто. Пусть доска однородная. Тогда имеем неравенства

Ясно, что при выборе достаточно большой массы ${{M}_{2}}$ эти неравенства заведомо имеют общие решения.

Таким образом, имеются следующие три случая послеударного поведения шара В.

Ι. После удара шар В отрывается от доски и летит по параболе влево от нее.

ΙΙ. После удара шар В вращается вместе с доской, и этот процесс длится вплоть до удара конца А о землю, после чего шар В отрывается от доски и летит по параболе вправо от нее.

ΙΙΙ. После удара шар В вращается по часовой стрелке вместе с доской замедленно вплоть до того момента, когда доска остановится в своем вращении (не ударившись концом А). Затем продолжается ускоренное вращение против часовой стрелки вплоть до момента удара доски о землю концом В. В этом случае, в предположении абсолютной упругости ударов доски о пол, никаких отрывов вообще не будет, а будут наблюдаться периодические колебания доски вместе с шарами.