Известия РАН. Механика твердого тела, 2023, № 2, стр. 136-146

О ВЯЗКОПЛАСТИЧЕСКОМ ТЕЧЕНИИ В МАТЕРИАЛЕ ЦИЛИНДРИЧЕСКОГО СЛОЯ, НАСАЖЕННОГО НА ЖЕСТКИЙ ВАЛ В УСЛОВИЯХ ЕГО ПЕРЕМЕННОГО ВРАЩЕНИЯ

С. В. Фирсов^a, *

^a ИМиМ, ХФИЦ ДВО РАН
Комсомольск-на-Амуре, Российская Федерация

Поступила в редакцию 21.05.2022
После доработки 24.05.2022
Принята к публикации 26.05.2022

EDN: DFVULC
DOI: 10.31857/S0572329922600359

Аннотация

Расчитывается развитие вязкопластического течения в материале цилиндрического слоя, помещенного на жесткий цилиндрический вал, и вращающегося вместе с ним вокруг их общей оси. Определяются в зависимости от возрастающей скорости вращения до максимальной место и моменты времени начала вязкопластического течения, закономерности продвижения области течения, изменяющиеся деформации и напряжения в деформируемом материале. В качестве условия вязкопластического течения принимается соответствующее обобщение условия максимальных октаэдрических напряжений. Для целей тестирования программ расчетов получено точное решение задачи об установившемся вязкопластическом течении материала при вращении составного цилиндра с постоянной скоростью.

Ключевые слова: упругость, вязкопластичность, вращающийся цилиндр, деформирование за счет инертностных сил

1. Введение. С тех пор как был сформулирован практический интерес к задачам о приобретении материалом вращающихся цилиндров и дисков необратимых деформаций [1, 2] такая задача становится одной из классических для теории ползучести и теории пластического течения. Рассматривалась она неоднократно [3–7]. При использовании кусочно-линейных потенциалов (классических поверхностей нагружения) удалось получить точные или численно-аналитические решения задачи [8–10]. Совместное производство необратимых деформаций за счет инертностных массовых сил как в медленном процессе ползучести материала, так и в более быстром процессе пластического течения рассматривалось в [10, 11].

2. Исходные соотношения принимаемой математической модели. Деформируемый материал полагаем упруговязкопластическим, допускающим лишь малые деформации. Полные деформации ${\mathbf{d}}$ в материале считаем представленными суммой его обратимых (упругих) деформаций ${\mathbf{e}}$ и необратимых вязкопластических ${\mathbf{p}}$ деформаций

(2.1)

${\mathbf{d}} = {\mathbf{e}} + {\mathbf{p}} = \frac{1}{2}(\nabla {\mathbf{u}} + {{\nabla }^{T}}{\mathbf{u}})$

В (2.1) ${\mathbf{u}}$ – вектор перемещений. Упругие деформации задают напряжения $\sigma $ в деформируемом материале.

(2.2)

$\sigma = \lambda {\text{tr}}({\mathbf{e}}){\mathbf{I}} + 2\mu {\mathbf{e}}$

Здесь λ, μ – параметры Ламе, ${\mathbf{I}}$ – единичный тензор составленный из символов Кронекера. Пластические деформации производятся в материале в условиях принадлежности напряжений поверхности нагружений (текучести) в пространстве напряжений $f(\sigma ,k) = 0$ (k – предел текучести). В условиях принятия принципа Мизеса [12] функция $f(\sigma ,k)$ оказывается пластическим потенциалом со следованием ассоциированного с поверхностью нагружения закона пластического течения

(2.3)

${{\varepsilon }^{p}} = \frac{{d{\mathbf{p}}}}{{dt}} = \Phi \frac{{\partial f}}{{\partial \sigma }},\quad \Phi > 0$

В качестве условия пластического течения (поверхности нагружения) будем использовать следующее обобщение условия максимальных октаэдрических напряжений Мизеса [13, 14]

(2.4)

$\left( {\tau - \eta \theta } \right) \cdot (\tau - \eta \theta ) = \frac{8}{3}{{k}^{2}},\quad \tau = \sigma - \frac{1}{3}tr\sigma ,\quad \theta = {{\varepsilon }^{p}} - \frac{1}{3}{\text{tr}}{{\varepsilon }^{p}}$

Вместе с уравнением движения (равновесия) система уравнений (2.1)–(2.4) составляет замкнутую систему уравнений, которой подчинено деформирование упруговязкопластического тела.

3. Постановка задачи. Первоначальное упругое деформирование. Рассматриваем двухслойный вал конечной длинны. Внутреннюю часть вала $0 \leqslant r \leqslant {{R}_{1}}$ полагаем абсолютно жесткой, а часть ${{R}_{1}} \leqslant r \leqslant {{R}_{2}}$ деформируемой. Считаем, что вал вращается вокруг своей оси с переменной угловой скоростью ${\mathbf{\omega }} = {\mathbf{\omega }}(t)$. Для деформаций материала такого составного цилиндра имеем в цилиндрической системе координат r, φ, z, связанной с вращающимся цилиндром

(3.1)

$\begin{array}{*{20}{c}} {{{u}_{r}} = {{u}_{r}}(r,t),\quad {{u}_{\varphi }} = {{u}_{\varphi }}(r,t),\quad {{u}_{z}} = 0,\quad {{d}_{{rr}}} = {{e}_{{rr}}} + {{p}_{{rr}}} = {{u}_{{r,r}}}} \\ {{{d}_{{\varphi \varphi }}} = {{e}_{{\varphi \varphi }}} + {{p}_{{\varphi \varphi }}} = {{r}^{{ - 1}}}{{u}_{r}},\quad {{d}_{{zz}}} = {{e}_{{zz}}} + {{p}_{{zz}}},\quad {{d}_{{\varphi r}}} = \frac{1}{2}({{u}_{{\varphi ,r}}} - {{r}^{{ - 1}}}{{u}_{\varphi }})} \end{array}$

Когда торцы жестко закреплены, тогда ${{d}_{{zz}}} = 0$. Если они свободны, то считаем d_zz = = $f(t)$. Такой случай называют обобщенной плоской деформацией и для определения ${{d}_{{zz}}}$ вводят ограничения на осевую нагрузку

(3.2)

$2\pi \int\limits_{{{R}_{1}}}^{{{R}_{2}}} r{{\sigma }_{{zz}}}(r,t){\kern 1pt} dr = 0$

Далее рассматривается такой случай. Уравнение движения во введенной системе координат принимают форму

(3.3)

$\begin{gathered} {{\sigma }_{{rr,r}}} + {{r}^{{ - 1}}}\left( {{{\sigma }_{{rr}}} - {{\sigma }_{{\varphi \varphi }}}} \right) = - \rho r{{\omega }^{2}} \\ {{\sigma }_{{\varphi r,r}}} + 2{{r}^{{ - 1}}}{{\sigma }_{{\varphi r}}} = - \rho r\dot {\omega } \\ \end{gathered} $

Здесь, также как и в (3.1) индекс после запятой обозначает дифференцирование по данной пространственной переменной; точкой обозначается производная по времени. Введем безразмерные зависимые и независимые переменные

(3.4)

$\begin{array}{*{20}{c}} {r = {{R}_{2}}{\mathbf{\xi }},\quad {{\sigma }_{{ij}}} = {{\sigma }_{0}}{{{\tilde {\sigma }}}_{{ij}}},\quad {{u}_{r}} = {{R}_{2}}{{{\tilde {u}}}_{r}},\quad {{u}_{\varphi }} = {{R}_{2}}{{{\tilde {u}}}_{\varphi }}} \\ {\psi = {{R}_{2}}\sqrt {\frac{\rho }{{{{\sigma }_{0}}}}} \omega ,\quad t = {{R}_{2}}\sqrt {\rho \sigma _{0}^{{ - 1}}} \tau } \end{array}$

Для постоянных задачи принимаем

(3.5)

${{{\mathbf{\xi }}}_{0}} = \frac{{{{R}_{1}}}}{{{{R}_{2}}}} = 0.2,\quad \alpha = \frac{\lambda }{{{{\sigma }_{0}}}} = 250,\quad \beta = \frac{\mu }{{{{\sigma }_{0}}}} = 195,\quad {\mathbf{\zeta }} = \frac{\eta }{{{{R}_{2}}\sqrt {\rho {{\sigma }_{0}}} }} = 100$

Здесь ρ – плотность деформируемого материала. Далее знак “^~” опускаем, так как будут использоваться только безразмерные переменные. В безразмерных переменных уравнение (3.3) принимает форму

(3.6)

$\begin{gathered} {{{\mathbf{\xi }}}^{2}}{{u}_{{r,{\mathbf{\xi \xi }}}}} + {\mathbf{\xi }}{{u}_{{r,{\mathbf{\xi }}}}} - {{u}_{r}} = - \frac{{{{{\mathbf{\xi }}}^{3}}{{\psi }^{2}}}}{{\alpha + 2\beta }} \\ {{{\mathbf{\xi }}}^{2}}{{u}_{{\varphi ,{\mathbf{\xi \xi }}}}} + \xi {{u}_{{\varphi ,{\mathbf{\xi }}}}} - {{u}_{\varphi }} = - \frac{{{{{\mathbf{\xi }}}^{3}}\dot {\psi }}}{\beta } \\ \end{gathered} $

В (3.6) следует иметь ввиду, что $\dot {\psi } = \frac{{d\psi }}{{d\tau }}$. Проинтегрировав (3.6), запишем

(3.7)

$\begin{gathered} {{u}_{r}} = {{c}_{1}}{\mathbf{\xi }} + {{c}_{2}}{{{\mathbf{\xi }}}^{{ - 1}}} - \frac{1}{8}\frac{{{{{\mathbf{\xi }}}^{3}}{{\psi }^{2}}}}{{\alpha + 2\beta }} \\ {{u}_{\varphi }} = {{c}_{3}}{\mathbf{\xi }} + {{c}_{4}}{{{\mathbf{\xi }}}^{{ - 1}}} - \frac{{{{{\mathbf{\xi }}}^{3}}\dot {\psi }}}{{8\beta }} \\ \end{gathered} $

Для напряжений, следуя (2.2) найдем

(3.8)

$\begin{gathered} {{\sigma }_{{rr}}} = 2\left( {\alpha + \beta } \right){{c}_{1}} - 2\beta {{c}_{2}}{{{\mathbf{\xi }}}^{{ - 2}}} + \alpha {{d}_{{zz}}} - \frac{1}{4}\frac{{2\alpha + 3\beta }}{{\alpha + 2\beta }}{{{\mathbf{\xi }}}^{2}}{{\psi }^{2}} \\ {{\sigma }_{{\varphi \varphi }}} = 2\left( {\alpha + \beta } \right){{c}_{1}} + 2\beta {{c}_{2}}{{{\mathbf{\xi }}}^{{ - 2}}} + \alpha {{d}_{{zz}}} - \frac{1}{4}\frac{{2\alpha + \beta }}{{\alpha + 2\beta }}{{{\mathbf{\xi }}}^{2}}{{\psi }^{2}} \\ {{\sigma }_{{zz}}} = 2\alpha {{c}_{1}} + \left( {\alpha + 2\beta } \right){{d}_{{zz}}} - \frac{1}{2}\frac{\alpha }{{\alpha + 2\beta }}{{{\mathbf{\xi }}}^{2}}{{\psi }^{2}} \\ {{\sigma }_{{\varphi r}}} = - 2\beta {{c}_{4}}{{{\mathbf{\xi }}}^{{ - 2}}} - \frac{1}{4}{{{\mathbf{\xi }}}^{2}}{{\psi }^{2}} \\ \end{gathered} $

Из (3.2) находим d_zz, зависящую только от безразмерного времени $\tau $

(3.9)

${{d}_{{zz}}} = \frac{\alpha }{{\alpha + 2\beta }}\left( {\frac{1}{4}\frac{{{\mathbf{\xi }}_{0}^{2} + 1}}{{\alpha + 2\beta }}{{\psi }^{2}} - 2{{c}_{1}}} \right)$

Постоянные в каждый момент времени ${{c}_{1}}$, ${{c}_{2}}$, ${{c}_{3}}$, ${{c}_{4}}$ находим из граничных условий. Последние имеют вид

(3.10)

${{u}_{r}}({{{\mathbf{\xi }}}_{0}},\tau ) = 0,\quad {{u}_{\varphi }}({{{\mathbf{\xi }}}_{0}},\tau ) = 0,\quad {{\sigma }_{{rr}}}(1,\tau ) = 0,\quad {{\sigma }_{{\varphi r}}}(1,\tau ) = 0$

Выполняя условия (3.10), находим

(3.11)

$\begin{gathered} {{c}_{1}} = \frac{{\beta (\alpha + 2\beta ){\mathbf{\xi }}_{0}^{4} - {{\alpha }^{2}}{\mathbf{\xi }}_{0}^{2} + (\alpha + \beta )(\alpha + 6\beta )}}{{8\beta (\alpha + 2\beta )((\alpha + 2\beta ){\mathbf{\xi }}_{0}^{2} + (3\alpha + 2\beta ))}}{{\psi }^{2}} \\ {{c}_{2}} = \frac{1}{{8\beta }}\frac{{\alpha + \beta }}{{\alpha + 2\beta }}\frac{{(\alpha + 2\beta ){\mathbf{\xi }}_{0}^{2} - (\alpha + 6\beta )}}{{(\alpha + 2\beta ){\mathbf{\xi }}_{0}^{2} + (3\alpha + 2\beta )}}{\mathbf{\xi }}_{0}^{2}{{\psi }^{2}} \\ {{c}_{3}} = \frac{{{\mathbf{\xi }}_{0}^{4} + 1}}{{8\beta {\mathbf{\xi }}_{0}^{2}}}\dot {\psi },\quad {{c}_{4}} = - \frac{1}{{8\beta }}\dot {\psi } \\ \end{gathered} $

Решение задачи (3.7)–(3.11) справедливо до моментов времени до наступления вязкопластического течения.

4. Вязкопластическое течение. Начало вязкопластического течения связано с выполнением в некоторый расчитываемый момент времени условия (2.4). В такой начальный момент времени в (2.4) скорости необратимых деформаций θ следует положить равными нулю ($\theta = 0$). Во введенных безразмерных переменных условие (2.4) принимает форму

(4.1)

${\mathbf{\Sigma }} = \sqrt {\sigma _{{rr}}^{2} + \sigma _{{\varphi \varphi }}^{2} + \sigma _{{zz}}^{2} - {{\sigma }_{{rr}}}{{\sigma }_{{\varphi \varphi }}} - {{\sigma }_{{rr}}}{{\sigma }_{{zz}}} - {{\sigma }_{{\varphi \varphi }}}{{\sigma }_{{zz}}} - 3\sigma _{{\varphi r}}^{2}} = 1$

После подстановки в (4.1) напряжений, вычисленных согласно (3.8) и (3.11), находим, что это условие первоначально выполнится на поверхности ${\mathbf{\xi }} = {{{\mathbf{\xi }}}_{0}}$ (${\mathbf{\Sigma }}({{{\mathbf{\xi }}}_{0}},\tau ) = 1$). Это произойдет при следующих безразмерных значениях для угловой скорости ${{\psi }_{p}}$ и углового ускорения ${{\dot {\psi }}_{p}}$

(4.2)

$\begin{gathered} \psi _{p}^{2} = \frac{{\alpha + 2\beta }}{{2{\mathbf{\xi }}_{0}^{2}(1 - {\mathbf{\xi }}_{0}^{2})}}((\alpha + 2\beta ){\mathbf{\xi }}_{0}^{2} + 3\alpha + 2\beta )\sqrt {16{\mathbf{\xi }}_{0}^{4} - 9{{{(1 - {\mathbf{\xi }}_{0}^{4})}}^{2}}\dot {\psi }_{p}^{2}} (3{{\alpha }^{4}} + 27{{\alpha }^{3}}\beta + \\ \; + 85{{\alpha }^{2}}{{\beta }^{2}} + 96\alpha {{\beta }^{3}} + 36{{\beta }^{4}} + \beta (\alpha + 2\beta ){\mathbf{\xi }}_{0}^{2}(\beta (\alpha + 2\beta ){\mathbf{\xi }}_{0}^{2} + (3{{\alpha }^{2}} + 16\alpha \beta + 12{{\beta }^{2}})){{)}^{{ - \frac{1}{2}}}} \\ \end{gathered} $

(4.3)

$\dot {\psi } < \frac{4}{{\sqrt 3 }}\frac{{{\mathbf{\xi }}_{0}^{2}}}{{1 - {\mathbf{\xi }}_{0}^{2}}}$

Вязкопластическое течение на поверхности ${\mathbf{\xi }} = {{{\mathbf{\xi }}}_{0}}$ может наступить при предельном значении ${{\dot {\psi }}_{p}}$, когда неравенство (4.3) обратится в равенство. При равноускоренном (с самого начала) вращении, когда задаваемая функция линейная $\left( {\psi (\tau ) = a\tau } \right)$ вязкопластическое течение наступает с момента начала вращения, если

$a = \pm \frac{{{\mathbf{\xi }}_{0}^{2}}}{{\sqrt 3 (1 - {\mathbf{\xi }}_{0}^{2})}}$

Такой случай иллюстрируется зависимостями $\psi = \psi (\tau )$ и $\dot {\psi } = \dot {\psi }(\tau )$ на рис. 1.a, где ψ_max – предельно допустимая угловая скорость вращения, τ* – момент времени, когда такая угловая скорость достигается. Здесь будем задавать вращение цилиндра, постулируя зависимости

(4.4)

$\psi (\tau ) = {{\psi }_{{{\text{max}}}}}\left( {\frac{\tau }{{\tau {\text{*}}}} - \frac{1}{{2\pi }}\sin \frac{{2\pi \tau }}{{\tau {\text{*}}}}} \right),\quad \dot {\psi }(\tau ) = \frac{{{{\psi }_{{\max }}}}}{{\tau {\text{*}}}}\left( {1 - \cos \frac{{2\pi \tau }}{{\tau {\text{*}}}}} \right)$

Эти функции иллюстрируются графически на рис. 1b.

Уравнения равновесия в перемещениях с учетом сил инерции (аналог (3.6)) теперь будут включать в себя неизвестные пластические деформации.

(4.5)

$\begin{array}{*{20}{c}} {{{{\mathbf{\xi }}}^{2}}{{u}_{{r,{\mathbf{\xi \xi }}}}} + {\mathbf{\xi }}{{u}_{{r,{\mathbf{\xi }}}}} - {{u}_{r}} = \frac{{2\beta }}{{\alpha + 2\beta }}{\mathbf{\xi }}({{p}_{{\varphi \varphi }}} - {{p}_{{rr}}}) + {{{\mathbf{\xi }}}^{2}}{{p}_{{rr,{\mathbf{\xi }}}}} + {{{\mathbf{\xi }}}^{2}}\frac{\alpha }{{\alpha + 2\beta }}({{p}_{{\varphi \varphi ,{\mathbf{\xi }}}}} + {{p}_{{zz,{\mathbf{\xi }}}}}) - \frac{{{{{\mathbf{\xi }}}^{3}}{{\psi }^{2}}}}{{\alpha + 2\beta }}} \\ {{{{\mathbf{\xi }}}^{2}}{{u}_{{\varphi ,{\mathbf{\xi \xi }}}}} + {\mathbf{\xi }}{{u}_{{\varphi ,{\mathbf{\xi }}}}} - {{u}_{\varphi }} = 4{\mathbf{\xi }}{{p}_{{\varphi r}}} + 2{{{\mathbf{\xi }}}^{2}}{{p}_{{\varphi r,{\mathbf{\xi }}}}} - \frac{{{{{\mathbf{\xi }}}^{3}}\psi '}}{\beta }} \end{array}$

Запишем решение (4.5) в форме

${{u}_{r}} = {{C}_{1}}{\mathbf{\xi }} + {{C}_{2}}{{{\mathbf{\xi }}}^{{ - 1}}} + \frac{{\beta \beta }}{{\alpha + 2\beta }}{{\Phi }_{1}} + {{{\mathbf{\xi }}}^{{ - 1}}}{{\Phi }_{2}} - \frac{1}{8}\frac{{{{{\mathbf{\xi }}}^{3}}{{\psi }^{2}}}}{{\alpha + 2\beta }}$

(4.6)

$\begin{gathered} {{u}_{{\mathbf{\varphi }}}} = {{C}_{3}}{\mathbf{\xi }} + {{C}_{4}}{{{\mathbf{\xi }}}^{{ - 1}}} + 2{\mathbf{\xi }}{{I}_{3}} - \frac{{{{{\mathbf{\xi }}}^{3}}\psi {\kern 1pt} '}}{{8\beta }} \\ {{\Phi }_{1}}({\mathbf{\xi }},\tau ) = \int\limits_{{{{\mathbf{\xi }}}_{0}}}^{\mathbf{\xi }} {{x}^{{ - 1}}}({{p}_{{rr}}}(x,\tau ) - {{p}_{{\varphi \varphi }}}(x,\tau ))dx \\ {{\Phi }_{2}}({\mathbf{\xi }},\tau ) = \int\limits_{{{{\mathbf{\xi }}}_{0}}}^{\mathbf{\xi }} x\left( {\frac{{\alpha + \beta }}{{\alpha + 2\beta }}({{p}_{{rr}}}(x,\tau ) + {{p}_{{\varphi \varphi }}}(x,\tau )) + \frac{\alpha }{{\alpha + 2\beta }}{{p}_{{zz}}}(x,\tau )} \right)dx \\ \end{gathered} $

${{\Phi }_{3}}({\mathbf{\xi }},\tau ) = \int\limits_{{{{\mathbf{\xi }}}_{0}}}^{\mathbf{\xi }} {{x}^{{ - 1}}}{{p}_{{\varphi r}}}(x,\tau )dx$

В (4.6) следует учитывать, что постоянные в рассматриваемый момент времени C_j ($j = 1,2,3,4$) являются все же функциями безразмерного времени τ, а Φ_i ($i = 1,2,3$) определяются неизвестными пластическими деформациями. Для компонент тензора напряжений из (2.2) и (4.6) следуют зависимости

${{\sigma }_{{rr}}} = 2(\alpha + \beta ){{C}_{1}} - 2\beta {{{\mathbf{\xi }}}^{{ - 2}}}{{C}_{2}} + \alpha {{d}_{{zz}}} + \frac{{2\beta (\alpha + \beta )}}{{\alpha + 2\beta }}{{\Phi }_{1}} - 2\beta {{{\mathbf{\xi }}}^{{ - 2}}}{{\Phi }_{2}} - \frac{1}{4}\frac{{2\alpha + 3\beta }}{{\alpha + 2\beta }}{{{\mathbf{\xi }}}^{2}}{{\psi }^{2}}$

(4.7)

$\begin{gathered} {{\sigma }_{{\varphi \varphi }}} = 2(\alpha + \beta ){{C}_{1}} + 2\beta {{{\mathbf{\xi }}}^{{ - 2}}}{{C}_{2}} + \alpha {{d}_{{zz}}} - 2\beta \left( {\frac{\alpha }{{\alpha + 2\beta }}{{p}_{{zz}}} + 2\frac{{\alpha + \beta }}{{\alpha + 2\beta }}{{p}_{{\varphi \varphi }}}} \right) + \\ \; + 2\beta \frac{{\alpha + \beta }}{{\alpha + 2\beta }}{{\Phi }_{1}} + 2\beta {{{\mathbf{\xi }}}^{{ - 2}}}{{\Phi }_{2}} - \frac{1}{4}\frac{{2\alpha + \beta }}{{\alpha + 2\beta }}{{{\mathbf{\xi }}}^{2}}{{\psi }^{2}} \\ {{\sigma }_{{zz}}} = 2\alpha {{C}_{1}} + (\alpha + 2\beta ){{d}_{{zz}}} - 4\beta \frac{{\alpha + \beta }}{{\alpha + 2\beta }}{{p}_{{zz}}} + \frac{{2\alpha \beta }}{{\alpha + 2\beta }}({{\Phi }_{1}} - {{p}_{{\varphi \varphi }}}) - \frac{1}{2}\frac{\alpha }{{\alpha + 2\beta }}{{{\mathbf{\xi }}}^{2}}{{\psi }^{2}} \\ \end{gathered} $

${{\sigma }_{{\varphi r}}} = - 2\beta {{C}_{4}}{{{\mathbf{\xi }}}^{{ - 2}}} - \frac{1}{4}{{{\mathbf{\xi }}}^{2}}\dot {\psi }$

Выполняя ограничение (3.2), налагаемое на значение осевых усилий, находим

(4.8)

$\begin{array}{*{20}{c}} {{{d}_{{zz}}} = \frac{\alpha }{{\alpha + 2\beta }}\left( {\frac{1}{4}\frac{{{\mathbf{\xi }}_{0}^{2} + 1}}{{\alpha + 2\beta }}{{\psi }^{2}} - 2{{C}_{1}}} \right) + \frac{{2\beta }}{{(\alpha + 2\beta )({\mathbf{\xi }}_{0}^{2} - 1)}}\left( {\frac{\alpha }{{\alpha + 2\beta }}{{\Phi }_{1}}(1,\tau ) - {{\Phi }_{4}}(1,\tau )} \right)} \\ {{{\Phi }_{4}}({\mathbf{\xi }},\tau ) = \int\limits_{{{{\mathbf{\xi }}}_{0}}}^{\mathbf{\xi }} x\left( {\frac{\alpha }{{\alpha + 2\beta }}({{p}_{{rr}}}(x,\tau ) + {{p}_{{\varphi \varphi }}}(x,\tau )) + 4\frac{{\alpha + \beta }}{{\alpha + 2\beta }}{{p}_{{zz}}}(x,\tau )} \right)dx} \end{array}$

Исходя из граничных условий (3.10), вычисляем постоянные в этот момент времени C_j ($j = 1,2,3,4$)

$\begin{gathered} {{C}_{1}} = \left( {(\alpha + 2\beta )({{I}_{2}}(1,\tau ) - {{I}_{1}}(1,\tau )) + \frac{\alpha }{{\alpha + 2\beta }}{{{(1 - \xi _{0}^{2})}}^{{ - 1}}}(\alpha {{I}_{1}}(1,\tau ) - {{I}_{4}}(1,\tau ))} \right. + \\ \; + \left. {\left( {\beta {\mathbf{\xi }}_{0}^{4} - \frac{{{{\alpha }^{2}}{\mathbf{\xi }}_{0}^{2}}}{{\alpha + 2\beta }} + \frac{{\alpha + \beta }}{{\alpha + 2\beta }}(\alpha + 6\beta )} \right)\frac{{{{\psi }^{2}}}}{{8\beta }}} \right){{((\alpha + 2\beta ){\mathbf{\xi }}_{0}^{2} + (3\alpha + 2\beta ))}^{{ - 1}}} \\ \end{gathered} $

(4.9)

${{C}_{2}} = {\mathbf{\xi }}_{0}^{2}\left( {(\alpha + 2\beta )({{I}_{1}}(1,\tau ) - {{I}_{2}}(1,\tau )) + \frac{\alpha }{{\alpha + 2\beta }}\frac{{{{I}_{4}}(1,\tau ) - \alpha {{I}_{1}}(1,\tau )}}{{1 - {\mathbf{\xi }}_{0}^{2}}}} \right. + $

$\begin{gathered} \; + \left. {\frac{{\alpha + \beta }}{{\alpha + 2\beta }}\left( {(\alpha + 2\beta ){\mathbf{\xi }}_{0}^{2} - (\alpha + 6\beta )} \right)\frac{{{{\psi }^{2}}}}{{8\beta }}} \right){{((\alpha + 2\beta ){\mathbf{\xi }}_{0}^{2} + (3\alpha + 2\beta ))}^{{ - 1}}} \\ {{C}_{3}} = \frac{{{\mathbf{\xi }}_{0}^{4} + 1}}{{8\beta {\mathbf{\xi }}_{0}^{2}}}\dot {\psi },\quad {{C}_{4}} = - \frac{1}{{8\beta }}\dot {\psi } \\ \end{gathered} $

В соотношениях (4.6)–(4.9) компоненты пластических деформаций остаются неизвестными. Для отыскания распределения этих деформаций в каждый рассматриваемый момент времени следует воспользоваться ассоциированным с выбранной поверхностью нагружения (2.4) законом вязкопластического течения (2.3). Таким способом получаем

${{\varepsilon }_{{rr}}} = \frac{{\partial {{p}_{{rr}}}}}{{\partial \tau }} = \frac{1}{{3{\mathbf{\zeta }}}}\frac{{\Sigma - 1}}{\Sigma }\left( {2{{\sigma }_{{rr}}} - {{\sigma }_{{\varphi \varphi }}} - {{\sigma }_{{zz}}}} \right)$

(4.10)

$\begin{gathered} {{\varepsilon }_{{\varphi \varphi }}} = \frac{{\partial {{p}_{{\varphi \varphi }}}}}{{\partial \tau }} = \frac{1}{{3{\mathbf{\zeta }}}}\frac{{\Sigma - 1}}{\Sigma }\left( {2{{\sigma }_{{\varphi \varphi }}} - {{\sigma }_{{rr}}} - {{\sigma }_{{zz}}}} \right) \\ {{\varepsilon }_{{zz}}} = \frac{{\partial {{p}_{{zz}}}}}{{\partial \tau }} = \frac{1}{{3{\mathbf{\zeta }}}}\frac{{\Sigma - 1}}{\Sigma }\left( {2{{\sigma }_{{zz}}} - {{\sigma }_{{rr}}} - {{\sigma }_{{\varphi \varphi }}}} \right) \\ \end{gathered} $

${{\varepsilon }_{{\varphi r}}} = \frac{{\partial {{p}_{{\varphi r}}}}}{{\partial \tau }} = \frac{1}{{\mathbf{\zeta }}}\frac{{\Sigma - 1}}{\Sigma }{{\sigma }_{{\varphi r}}}$

В момент начала вязкопластического течения при Σ = 1 пластические деформации в деформируемом материале равны нулю. Для расчетов следующих шагов по времени представляем (4.10) его конечно-разностным аналогом, включая последний в общий алгоритм расчетов последовательными шагами по времени.

5. Некоторые результаты расчетов. Далее, если это специально не оговорено, результаты расчетов будут представляться при следующем выборе для постоянных деформируемого материала и его геометрии

(5.1)

Согласно (4.4) параметрами задачи являются ψ_max и τ* – момент времени, в который значение ψ_max достигается. С целью задания (оценки) значения ψ_max в (4.4) имеем возможность вычислить его в момент начала вязкопластического течения, если не учитывать угловое ускорение. Такое значение, согласно (4.2), оказалось равным ψ_max = ${{\psi }_{p}} \approx 1.45893$. Другое значение ψ_max моно связать с переходом всего материала деформируемой части вращающегося цилиндра в пластическое состояние. Тогда, полагая угловое ускорение нулевым, получаем значение ${{\psi }_{{{\text{max}}}}} = {{\psi }_{{fp}}} \approx 2.06118$. Дальнейшие результаты расчетов связываются с такими двумя значениями ψ_max в (4.4).

На рис. 2,a и рис. 2,b указывается безразмерное время τ начала вязкопластического течения в зависимости от назначаемого параметра τ*. При этом на рис. 2,a данная зависимость получена при равноускоренном начальном вращении, а на рис. 2,b для закона вращения (4.4). Сплошная линия соответствует ${{\psi }_{{{\text{max}}}}} = {{\psi }_{p}}$, пунктирная ψ_max = ${{\psi }_{{fp}}}$.

В (5.1) геометрический параметр ξ₀ также является параметром задачи. Если фиксировать τ*, то можно указать время начала вязкопластического течения в зависимости от назначаемого параметра ξ₀. Такие графические зависимости представлены для ψ_max = = ψ_p на рис. 2,c и для ${{\psi }_{{{\text{max}}}}} = {{\psi }_{{fp}}}$ на рис. 2,d при $\tau {\text{*}} = 30$ (сплошная линия) и $\tau {\text{*}} = 50$ (пунктирная линия).

Распределение напряжений по деформируемому материалу перед началом пластического течения иллюстрируют графические зависимости рис. 2,e ($\tau {\text{*}} = 30$) и рис. 2,f ($\tau {\text{*}} = 50$). При этом в (4.4) принимается, что ${{\psi }_{{{\text{max}}}}} = {{\psi }_{{fp}}}$.

6. Установившееся вязкопластическое течение. Согласно (4.4) при $\tau \geqslant \tau {\text{*}}$ $\psi (\tau ) = {{\psi }_{{{\text{max}}}}}$ – const и $\dot {\psi }(\tau ) = 0$. Если ${{\psi }_{{{\text{max}}}}} \geqslant {{\psi }_{{fp}}}$, то деформируемая часть ${{\xi }_{0}} \leqslant \xi \leqslant 1$ вращающегося цилиндра будет находиться в пластическом состоянии. Возможно ли в таком случае предельное установившееся пластическое течение? Расчетом параметров такого течения, покажем, что оно осуществляется. Из (3.1) в случае установившегося вязкопластического течения с учетом того, что скорости пластических деформаций отождествляются со скоростями полных деформаций, получаем

(6.1)

${{\varepsilon }_{{rr}}} = {{{v}}_{{r,{\mathbf{\xi }}}}},\quad {{\varepsilon }_{{\varphi \varphi }}} = {{{\mathbf{\xi }}}^{{ - 1}}}{{{v}}_{r}},\quad {{\varepsilon }_{{zz}}} = {\text{const}},\quad {{\varepsilon }_{{\varphi r}}} = \frac{1}{2}({{{v}}_{{\varphi ,{\mathbf{\xi }}}}} - {{{\mathbf{\xi }}}^{{ - 1}}}{{{v}}_{\varphi }})$

Учитывая, что согласно выбранному условию пластического течения деформируемый материал пластически несжимаем, запишем

(6.2)

${{{v}}_{{r,{\mathbf{\xi }}}}} + {{{\mathbf{\xi }}}^{{ - 1}}}{{{v}}_{r}} + {{{\mathbf{\varepsilon }}}_{{zz}}} = 0,\quad {{{v}}_{r}} = {{{\mathbf{\xi }}}^{{ - 1}}}{{C}_{1}} - \frac{1}{2}{\mathbf{\xi }}{{{\mathbf{\varepsilon }}}_{{zz}}}$

Если учесть кинематику такого установившегося вязкопластического течения (6.1) и (6.2), то из (4.10) следуют соотношения

${{C}_{1}} = {{{\mathbf{\xi }}}^{2}}\frac{{\Sigma - 1}}{{2{\mathbf{\zeta }}\Sigma }}({{\sigma }_{{rr}}} - {{\sigma }_{{\varphi \varphi }}})$

(6.3)

$\begin{gathered} {{\varepsilon }_{{zz}}} = \frac{{\Sigma - 1}}{{3{\mathbf{\zeta }}\Sigma }}\left( {2{{\sigma }_{{zz}}} - {{\sigma }_{{rr}}} - {{\sigma }_{{\varphi \varphi }}}} \right) \\ {{v}_{{\varphi ,{\mathbf{\xi }}}}} - {{{\mathbf{\xi }}}^{{ - 1}}}{{v}_{{\mathbf{\sigma }}}} = 2\frac{{\Sigma - 1}}{{{\mathbf{\zeta }}\Sigma }}{{\sigma }_{{\varphi r}}} \\ \end{gathered} $

${{\sigma }_{{zz}}} = \left( {\frac{1}{2} - \frac{{3{{{\mathbf{\xi }}}^{2}}{{{\mathbf{\varepsilon }}}_{{zz}}}}}{{4{{C}_{1}}}}} \right){{\sigma }_{{rr}}} + \left( {\frac{1}{2} + \frac{{3{{{\mathbf{\xi }}}^{2}}{{{\mathbf{\varepsilon }}}_{{zz}}}}}{{4{{C}_{1}}}}} \right){{\sigma }_{{\varphi \varphi }}}$

Проинтегрировав уравнение равновесия (3.3), получим

(6.4)

$\begin{gathered} {{\sigma }_{{rr}}} = {{C}_{2}} - {\mathbf{\zeta }}{{{\mathbf{\xi }}}^{{ - 2}}}{{C}_{1}} + \frac{1}{{\sqrt 3 }}\left( {2\ln {\mathbf{\xi }} - \ln \left( {2 + \sqrt {4 + 3\frac{{{{{\mathbf{\xi }}}^{4}}{\mathbf{\varepsilon }}_{{zz}}^{2}}}{{C_{1}^{2}}}} } \right)} \right) - \frac{1}{2}{{{\mathbf{\xi }}}^{2}}{{\psi }^{2}} \\ {{\sigma }_{{\varphi \varphi }}} = 2{\mathbf{\zeta }}{{{\mathbf{\xi }}}^{{ - 2}}}{{C}_{1}} + {{\sigma }_{{rr}}} + 4{{\left( {12 + 9\frac{{{{{\mathbf{\xi }}}^{4}}{\mathbf{\varepsilon }}_{{zz}}^{2}}}{{C_{1}^{2}}}} \right)}^{{ - \frac{1}{2}}}},\quad {{\sigma }_{{\varphi r}}} = {{{\mathbf{\xi }}}^{{ - 2}}}{{C}_{3}} \\ \end{gathered} $

Постоянные интегрирования в рассматриваемый момент времени находим при выполнении граничных условий (3.10)

(6.5)

$\begin{gathered} {{C}_{1}} = \frac{1}{2}{\mathbf{\xi }}_{0}^{2}{{{\mathbf{\varepsilon }}}_{{zz}}},\quad {{C}_{3}} = 0,\quad {{C}_{4}} = 0 \\ {{C}_{2}} = \frac{1}{{\sqrt 3 }}\ln (2 + \sqrt {4 + 12{\mathbf{\xi }}_{0}^{{ - 4}}} ) + \frac{1}{2}{\mathbf{\zeta \xi }}_{0}^{2}{{\varepsilon }_{{zz}}} + \frac{1}{2}{{\psi }^{2}} \\ \end{gathered} $

Неизвестное ε_zz в (6.2)–(6.5) вычисляется при выполнении условия (3.2)

(6.6)

${{{\mathbf{\varepsilon }}}_{{zz}}} = \frac{1}{{2{\mathbf{\zeta }}}}\frac{{{{{(1 - {\mathbf{\xi }}_{0}^{2})}}^{2}}}}{{{\mathbf{\xi }}_{0}^{4} + 2{\mathbf{\xi }}_{0}^{2} - 3}}{{\psi }^{2}} + \frac{2}{{\sqrt 3 {\mathbf{\zeta }}}}\frac{{{\mathbf{\xi }}_{0}^{2}}}{{{\mathbf{\xi }}_{0}^{4} + 2{\mathbf{\xi }}_{0}^{2} - 3}}\left( {\sqrt {1 + 3{\mathbf{\xi }}_{0}^{{ - 4}}} - \ln \left( {\frac{1}{3}({\mathbf{\xi }}_{0}^{2} + \sqrt {{\mathbf{\xi }}_{0}^{4} + 3} )} \right) - 2} \right)$

Для того, чтобы установившее вязкопластическое течение в соответствии с точным решением (6.2)–(6.6) осуществилось необходимо, чтобы угловая скорость достигла значения ${{\psi }_{{fp}}}$. Для этого ψ_max в (4.4) должно быть не меньше этого значения. Зависимости (6.4)–(6.5) позволяют вычислить данное значение условием ${\mathbf{\Sigma }}(1,\tau ) \geqslant 1$

(6.7)

${{\psi }_{{fp}}} \geqslant \frac{2}{{1 - {\mathbf{\xi }}_{0}^{2}}}\sqrt {\frac{1}{{\sqrt 3 }}} \sqrt {\frac{{3 - 3{\mathbf{\xi }}_{0}^{4} - 4{\mathbf{\xi }}_{0}^{2}}}{{\sqrt {{\mathbf{\xi }}_{0}^{4} + 3} }} + {\mathbf{\xi }}_{0}^{2}\left( {2 - \ln \frac{3}{{{\mathbf{\xi }}_{0}^{2} + \sqrt {{\mathbf{\xi }}_{0}^{4} + 3} }}} \right)} $

Наименьшее из возможных ψ_fp использовалось при задании вращения в (4.4) ${{\psi }_{{{\text{max}}}}} = {{\psi }_{{fp}}} \approx 2.06118$, когда проводились численные расчеты (рис. 3).

Сравнение результатов численных расчетов с аналогичными, получаемыми при точном решении задачи, приведено на рис. 3,d и e соответственно, где представлено распределение напряжений в материале. Сравнение показывает, что численное решение оказывается близким к точному, за исключением значений для безразмерной σ_zz. Несовпадение тем больше, чем ближе подходим к жесткой поверхности ${{{\mathbf{\xi }}}_{0}} = 0.2$. На том же рис. 3,a,b представлено развитие области вязкопластического течения при $\tau {\text{*}} = 30$ и $\tau {\text{*}} = 50$ соответственно. Очень часто [4–9] угловым ускорением при начале вращения пренебрегают, что делает задачу зависящей от одной переменной и приводит к значительным ее упрощениям. На рис. 3,a графиком предстает закон продвижения упруговязкопластической границы в двух случаях: при учете в расчетах изменяющегося углового ускорения $\dot {\psi }(\tau )$ (сплошная линия) и без такого учета (пунктирная). Учет в расчетах углового ускорения приводит не только к более быстрому возникновению области вязкопластического течения, но и появлению области обратимого деформирования в окрестности поверхности ξ₀. Однако такой эффект характерен только при быстром разгоне (например при $\tau {\text{*}} = 30$, как на рис. 3,a); при $\tau {\text{*}} = 50$ он уже не проявляется (рис. 3,b).

Изменение безразмерного Σ при разгоне вращения графически показано на рис. 3,c. В качестве времени данного разгонного участка принято $\tau {\text{*}} = 30$. Заштрихованные области – области где происходит вязкопластическое течение материала. ψ_max в (4.4) выбрано ${{\psi }_{{{\text{max}}}}} = {{\psi }_{{fp}}}$, что обеспечивает распространение вязкопластического течения на всю деформируемую часть цилиндра $0.2 \leqslant \xi \leqslant 1$.

7. Заключение. В отличие от большинства публикаций [4–9] где на разгонном участке вращения дисков и цилиндров пренебрегается угловым ускорением, считая, что угловая скорость меняется достаточно медленно, здесь рассмотрен именно быстрый разгон вращения. В некоторых случаях приводится сравнение со случаем медленного разгона и указываются качественные отличия в процессе деформирования, вызываемые быстрым изменением угловой скорости вращения. Необходимо отметить работу [10], где также учитывались окружные силы инерции, определяемые угловым ускорением, но в иной постановке.

Основным средством тестирования программ расчетов являются точные решения упругой задачи, задающие изменения напряжений и деформаций на начальной стадии процесса, и, что более важно, точное решение задачи об установившемся вязкопластическом течении. В последнем случае весь деформируемый материал подвержен вязкопластическому течению в условии постоянства угловой скорости вращения.

Работа выполнена в рамках госзадания ХФИЦ ДВО РАН.

Рис. 1.

Варианты задания угловой скорости ψ(τ) и ускорения ${\mathbf{\dot {\psi }}}({\mathbf{\tau }})$: линейная (a) и гладкая (b).

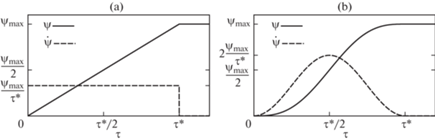
Рис. 2.

Зависимость времени начала пластического течения от времени разгона τ* при линейном росте угловой скорости (a) и при плавном (b), а также от положения внутренней границы ξ₀ для линейной зависимости при ${{\psi }_{{{\text{max}}}}} = {{\psi }_{{fp}}}$ (c) и ${{\psi }_{{{\text{max}}}}} = {{\psi }_{{fp}}}$ (d). Распределение напряжений в материале перед началом пластического течения при плавном разгоне и ${{\psi }_{{{\text{max}}}}} = {{\psi }_{{fp}}}$ для τ* = 30 (e) и τ* = 50 (f).

Рис. 3.

Результаты численных расчетов. Движение границ областей пластического течения при τ* = 30 (a) и τ* = 50 (b). Распределение интенсивности напряжений Σ в различные моменты времени при τ* = 30 и с учетом углового ускорения (c). Распределение напряжений в среде при установившемся вязкопластическом течении при численном (d) и аналитическом (e) решениях.

Список литературы

Работнов Ю.Н. Ползучесть элементов конструкций. М.: Наука, 2014. 752 p.
Nadai A. Theory of Flow and Fracture of Solids. McGraw Hill, 1950. 572 p.
Gamer U., Sayir M. Elastic-plastic stress distribution in a rotating solid shaft // ZAMP. 1984. V. 35. № 5. P. 601–617. https://doi.org/10.1007/BF00952107
Mack W. The rotating elastic-plastic solid shaft with free ends // Tech. Mech. 1991. № 12. P. 119–124.
Mack W. Rotating elastic-plastic tube with free ends // Int. J. Solids Struct. 1991. V. 27. № 11. P. 1461–1476. https://doi.org/10.1016/0020-7683(91)90042-E
Gamer U., Mack W., Varga I. Rotating elastic-plastic solid shaft with fixed ends // Int. J. Eng. Sci. 1997. V. 35. № 3. P. 253–267. https://doi.org/10.1016/S0020-7225(96)00085-7
Прокудин А.Н., Фирсов С.В. Вязкопластическое течение вращающегося полого цилиндра // Дальневосточный математический журнал. 2018. V. 18. № 2. P. 242–260.
Прокудин А.Н., Буренин А.А. Упругопластическое деформирование вращающегося сплошного цилиндра из линейно-упрочняющегося материала // ПММ. 2021. V. 85. № 2. P. 172–192. https://doi.org/10.31857/S0032823521020077
Прокудин А.Н., Буренин А.А. Анализ упругопластического деформирования вращающегося сплошного цилиндра при общем кусочно-линейном условии пластичности // ПМТФ. 2021. V. 62. № 5 (369). P. 68–79. https://doi.org/10.15372/PMTF20210507
Begun A.S., Burenin A.A., Kovtanyuk L.V., Prokudin A.N. Irreversible deformation of a rotating disk having angular acceleration // Acta Mech. 2021. V. 232. № 5. P. 1917–1931. https://doi.org/10.1007/s00707-021-02942-5
Firsov S.V., Prokudin A.N., Burenin A.A. Creep and plastic flow in a rotating cylinder with a rigid inclusion // J. Appl. Industr. Math. 2019. V. 13. № 4. P. 642–652. https://doi.org/10.1134/S199047891904001X
Быковцев Г.И., Ивлев Д.Д. Теория пластичности. Владивосток: Дальнаука, 1998. 528 p.
Мосолов П.П., Мясников В.П. Механика жесткопластических сред. М.: Наука, 1988. 208 p.
Ковтанюк Л.В., Шитиков А.В. О теории больших упругопластических деформаций материалов при учете температурных и реологических эффектов // Вестник ДВО РАН. 2006. № 4. P. 87–93.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал