Известия РАН. Механика твердого тела, 2023, № 2, стр. 166-175

Введение. Расчет радиального подшипника скольжения на износ является предметом многочисленных работ, в которых учитывались различные факторы процесса изнашивания: смазка, поверхностная шероховатость, наличие покрытия, фрикционный разогрев, перекос вала и др. [1–5].

Ниже описывается метод расчета процесса изнашивания антифрикционного покрытия (тонкого вкладыша) в радиальном подшипнике скольжения в условиях случайно изменяющихся температуры и внешней нагрузки (величина, направление). Подобные условия характерны, например, для узлов трения, работающих в открытом космосе на околоземных орбитальных станциях [6–9]. Изменение температуры узла трения в этом случае обусловлено его заходом в тень Земли или станции и по разным оценкам лежит в диапазоне от $ - 150^\circ {\text{C}}$ до $ + 150^\circ {\text{C}}$. Для таких узлов трения также следует ожидать значительного разброса величины и направления внешней нагрузки, что обуславливается отсутствием постоянной силы тяжести, как основного фактора нагружения.

Отметим, что ранее был выполнен расчет изнашивания радиального подшипника скольжения применительно к условиям работы на орбитальных станциях, который учитывал периодическое изменение температуры подшипника, однако нагрузка при этом считалась постоянной [10]. Также был предложен метод расчета радиального подшипника скольжения на износ в условиях случайно изменяющейся внешней нагрузки при неизменной температуре [3].

Цель описываемых ниже исследований состоит в учете и оценке значимости факторов случайного изменения температуры и внешней нагрузки при моделировании процесса изнашивания радиального подшипника скольжения с покрытием.

1. Постановка задачи и основные уравнения. Рассмотрим радиальный подшипник скольжения (далее – подшипник), в котором вращающийся вал 1 взаимодействует с тонким покрытием 3, связанным с обоймой 2 (рис. 1). Контактное взаимодействие вала с покрытием определяется величиной Q внешней нагрузки на вал и углом $\xi \in [ - \pi ,\pi ]$ ее приложения, который отсчитывается от вертикали (рис. 1). Соответствующая область контакта задается угловым размером a. Все элементы подшипника имеют одинаковую температуру $T$ и при ее изменении размеры подшипника меняются вследствие теплового расширения тел. Точки поверхности покрытия задаются с помощью угловой координаты $x$.

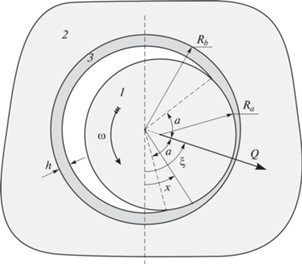
Считается, что покрытие в исходном состоянии, т.е. при $t = 0$, имеет постоянную толщину ${{h}_{0}}$. В результате взаимодействия с валом покрытие изнашивается и это приводит к изменению его толщины $h$ как по координате $x$, так и во времени $t$. В каждый момент процесса изнашивания покрытия величины $T,\;\xi ,\;Q$ могут принимать случайные значения, т.е. они являются случайными функциями времени $t$ (процессами) [11, 12].

Скорость износа покрытия в точке $x$ в каждый момент времени $t$ определяется величиной контактного давления $p(x,t)$, скоростью $V$ скольжения и температурой $T$ подшипника согласно закону изнашивания [1, 3]:

где $W(x,t) = {{h}_{0}} - h(x,t)$ – линейный износ покрытия, вид функции $F(p,V,T)$ будет конкретизирован ниже при численном анализе.

Скорость скольжения определяется по формуле $V = \omega {{R}_{a}}$, в которой $\omega $ – угловая скорость вращения вала, считающаяся постоянной, ${{R}_{a}}$ – радиус вала, износом которого будем пренебрегать. Отметим, что при изменении температуры радиус ${{R}_{a}}$ может меняться вследствие теплового расширения вала. Однако это изменение мало по сравнению с самим радиусом ${{R}_{a}}$ и не оказывает заметного влияния на скорость скольжения $V = \omega {{R}_{a}}$, которую, как и угловую скорость $\omega $, можно считать постоянной.

Допустим, что случайные изменения величин $T,\;\xi ,\;Q$ приводят к тому, что на поверхности изнашиваемого покрытия отсутствует приработанная к форме вала лунка износа. Вместо этого износ распределяется достаточно равномерно по поверхности покрытия, и это позволяет пренебречь изменением толщины изношенного покрытия в пределах области контакта по сравнению с самой толщиной, положив

Толщину $h$ тонкого покрытия можно считать малой по сравнению с размером $2a{{R}_{a}}$ области контакта. Кроме того, предполагая, что модуль упругости покрытия значительно меньше модулей упругости вала и обоймы подшипника, будем считать вал и обойму абсолютно жесткими.

Ставится задача: построить стохастическую модель процесса изнашивания покрытия в подшипнике, учитывающую случайный характер величин $T,\;\xi ,\;Q$.

Для построения такой модели рассмотрим вначале контактное взаимодействие вала и покрытия при некоторых фиксированных значениях $T,\;\xi ,\;Q$ и заданной толщине $h(x,t)$.

Учитывая сделанные выше допущения относительно толщины и модуля упругости покрытия, а также пренебрегая силой трения, воспользуемся моделью Винклера [13] для описания упругого поведения покрытия. В результате можно прийти к следующему выражению для контактного давления [3]

где – радиальный зазор подшипника, $\Delta \ll {{R}_{a}}(T)$, – коэффициент податливости покрытия, $E$ и $\nu $ – модуль упругости (Юнга) и коэффициент Пуассона покрытия, размер $a$ области контакта находится из уравнения

В представленных выражениях не учитывается изменение толщины $h$ покрытия в результате его теплового расширения, что допустимо для тонкого покрытия – соответствующее обоснование дано ниже (раздел 2). Кроме того, без ограничения общности рассмотрения, коэффициент Пуассона в выражении (1.5) считается независимым от температуры.

Примем теперь во внимание случайный характер величин $T,\;\xi ,\;Q$ и введем в рассмотрение соответствующую функцию плотности вероятности $\rho (T,\xi ,Q,t)$ [11]. В дальнейшем, для упрощения записи формул будут использоваться обозначения:

Для описания рассматриваемого процесса изнашивания покрытия воспользуемся известным подходом, основанным на статистическом осреднении закона изнашивания (1.1) по параметрам $T,\;\xi ,\;Q$ [3]. Результатом такой операции является равенство

в котором $h$ уже представляет собой среднее статистическое значение толщины покрытия. Для краткости символом $X$ здесь обозначается совокупность величин ${{X}_{1}},{{X}_{2}},{{X}_{3}}$, запись $\{ X\} $ обозначает множество допустимых значений этих величин, dX = $d{{X}_{1}}{\kern 1pt} d{{X}_{2}}{\kern 1pt} d{{X}_{3}}$.

Если случайные величины ${{X}_{1}},{{X}_{2}},{{X}_{3}}$ в каждый момент времени $t$ являются независимыми и стационарными как случайные процессы, то [11, 12]:

где ${{\rho }_{i}}({{X}_{i}}),\;\,i = 1,2,3$ – функция плотности вероятности величины ${{X}_{i}}$. Если дополнительно какая-либо из величин ${{X}_{i}}$ не является случайной и принимает постоянное значение ${{\hat {X}}_{i}}$, то в равенстве (1.8) следует формально положить где $\delta (X)$ – дельта-функция.

Указанная выше функция $\mathcal{P}(x,t;X)$ определяется равенствами (1.3)–(1.6) с учетом обозначений (1.7), поэтому равенство (1.8) представляет собой дифференциальное уравнение, которое при начальном условии

описывает кинетику изменения толщины изнашиваемого покрытия в терминах средних значений. Равенства (1.3)–(1.6), (1.8) составляют стохастическую модель процесса изнашивания покрытия в подшипнике и тем самым решают поставленную выше задачу.

Одной из важнейших характеристик процесса изнашивания покрытия является его долговечность, которая определяется как время ${{t}_{ * }}$ полного изнашивания покрытия в некоторой точке, т.е.

В дальнейшем для сравнения будут использоваться результаты расчета процесса изнашивания покрытия в подшипнике при детерминированной постановке, т.е. при неизменной температуре и постоянной по величине и направлению внешней нагрузке. Для решения такой задачи необходимо учитывать локальный характер изнашивания покрытия, который выражается в существовании приработанной к валу лунки износа с монотонно возрастающим размером $a(t)$ области контакта [2, 3, 13]. Такой процесс описывается уравнением (1.1) с начальным условием (1.11) и равенствами

первое из которых является следствием условия контакта вала и покрытия, а второе представляет собой условие равновесия вала [3]. Подстановка выражения (1.13) для контактного давления в равенство (1.14) при $t = 0,h(x,0) = {{h}_{0}},W(x,0) = 0$ позволяет получить для начального размера ${{a}_{0}} = a(0)$ области контакта уравнение, имеющее вид (1.6). Отметим, что здесь все величины являются детерминированными.

Замечание. Для решения задачи об изнашивании покрытия при детерминированной постановке, т.е. при ${{X}_{1}} = {{\hat {X}}_{1}}$, ${{X}_{2}} = {{\hat {X}}_{2}}$, ${{X}_{3}} = {{\hat {X}}_{3}}$, недопустимо использовать описанную выше стохастическую модель с функциями плотности вероятности вида (1.10) для всех величин ${{X}_{1}},{{X}_{2}},{{X}_{3}}$. Действительно, в таком виде стохастическая модель приводит к образованию приработанной лунки износа и, следовательно, к нарушению допущения (1.2).

2. Численный анализ. Излагаемый далее материал связан с анализом результатов расчетов процесса изнашивания покрытия в подшипнике. Целью анализа является оценка важности учета случайных изменений температуры и внешней нагрузки для прогнозирования износа и, в частности, долговечности подшипника. Для проведения соответствующих расчетов следует конкретизировать некоторые аспекты описанных выше стохастической и детерминированной моделей процесса изнашивания покрытия.

При выборе параметров материала покрытия для расчетов будем ориентироваться на использование самосмазывающихся композитов, в том числе, на полимерной основе. Подобные композиты успешно используются в качестве антифрикционных материалов в узлах трения, работающих в открытом космосе на околоземных орбитальных станциях в условиях вакуума и при значительных перепадах температуры [6–9].

Как показывают эксперименты [14–16], для полимерных композитов характерно существенное снижение модуля упругости с ростом температуры, которое может достигать нескольких порядков. По этой причине для расчетов воспользуемся экспоненциальной зависимостью [15]

с отрицательным параметром ${{k}_{E}}$, в которой $\theta = T - {{T}_{0}}$ – температура, отсчитываемая от нормальной температуры ${{T}_{0}}$. Подстановка выражения (2.1) в равенство (1.5) определяет температурную зависимость $B(T)$ коэффициента податливости покрытия.

Будем использовать линейный закон изнашивания (1.1), т.е. допустим, что

где $\alpha $ – коэффициент износа, величина которого зависит от температуры.

Результаты трибологических испытаний свидетельствуют о том, что с ростом температуры скорость $\partial W{\text{/}}\partial t$ износа полимерных композитов может претерпевать значительные изменения, достигающие нескольких порядков [15, 17–19]. В отличие от температурной зависимости (2.1) модуля упругости, зависимость скорости износа от температуры может быть как возрастающей, так и убывающей. С учетом указанных обстоятельств, примем экспоненциальную зависимость коэффициента износа от температуры:

в которой параметр ${{n}_{\alpha }}$ может принимать как отрицательные, так и положительные значения.

При увеличении температуры подшипника происходит тепловое расширение вала и обоймы, учитываемое в равенстве (1.4). В рассматриваемом случае тонкого и мягкого покрытия можно пренебречь его влиянием на расширение обоймы, полагая [10, 20]:

где ${{k}_{a}}$ и ${{k}_{b}}$ – коэффициенты линейного теплового расширения вала и обоймы. Отметим, что, если в подшипнике вместо тонкого покрытия используется толстый вкладыш, то для определения теплового расширения обоймы следует использовать решение соответствующей термоупругой задачи [10].

Для функции плотности вероятности $\rho (X,t)$ случайных величин ${{X}_{1}},{{X}_{2}},{{X}_{3}}$ воспользуемся выражением (1.9), считая эти величины независимыми и стационарными во времени. Соответствующие функции плотности вероятности зададим выражениями

в которых параметры ${{T}^{ \pm }}$ и ${{Q}_{m}}$ определяют диапазоны изменений температуры T и нагрузки Q. Выражения (2.4)–(2.6) удовлетворяют нормировочному условию, налагаемому на функцию плотности вероятности [11], а определяемые по ним средние значения случайных величин ${{X}_{1}},{{X}_{2}},{{X}_{3}}$ составляют:

Отметим, что функция ${{\rho }_{1}}({{X}_{1}})$ вида (2.4) описывает равновероятное распределение температуры $T = {{X}_{1}}$, тогда как функции ${{\rho }_{2}}({{X}_{2}})$ и ${{\rho }_{3}}({{X}_{3}})$ вида (2.5) и (2.6) допускают повышенную вероятность значений угла $\xi = {{X}_{2}}$ и нагрузки $Q = {{X}_{3}}$ вблизи их средних значений $0$ и ${{Q}_{m}}{\text{/}}2$ соответственно.

С учетом экспериментальных данных по полимерным композитам из упомянутых выше литературных источников, для расчетов процесса изнашивания покрытия были выбраны следующие значения трибофизических параметров:

$E$ = 1 ГПа, $\nu $ = 0.3, ${{k}_{E}}$ = –0.01 К^–1, ${{\alpha }_{0}}$ = 10^–15 Па^–1, ${{n}_{\alpha }}$ = 0.02 К^–1, ${{k}_{a}} = 2$ × 10^–5 К^–1, ${{k}_{b}} = 3$ × 10^–5 К^–1, ${{T}_{0}}$ = 293 К ($20^\circ \operatorname{C} $).

Геометрические параметры подшипника и условия его работы определялись значениями

${{h}_{{{\kern 1pt} 0}}}$ = 0.5 мм, ${{R}_{{a0}}}$ = 10 мм, ${{R}_{{b0}}}$ = 10.55 мм, $\omega = 2\pi $ с^–1, ${{A}_{\xi }}$ = 1 или 2, ${{A}_{Q}}$ = 1, ${{Q}_{m}}$ = 50 кН/м, $\bar {Q}$ = 25 кН/м, T^– = 143 К ($ - 130^\circ \operatorname{C} $), T⁺ = 443 К ($170^\circ \operatorname{C} $), $\bar {T} = {{T}_{0}}$.

Отметим, что при выбранных значениях ${{h}_{{{\kern 1pt} 0}}}$, ${{R}_{{a0}}}$, ${{R}_{{b0}}}$ начальный зазор подшипника составляет ${{\Delta }_{0}} = {{R}_{{b0}}} - {{R}_{{a0}}} - {{h}_{0}}$ = 0.05 мм, а указанные значения коэффициентов линейного теплового расширения вала ${{k}_{a}}$ и обоймы ${{k}_{b}}$ характерны для алюминиевых и магниевых сплавов [21]. Выбранный диапазон изменения температуры соответствует условиям работы узлов трения в открытом космосе на околоземных орбитальных станциях.

В качестве оценки коэффициента ${{k}_{c}}$ линейного теплового расширения полимерных композитов можно использовать значение 10^–5 К^–1 [21]. При таком значении ${{k}_{c}}$ и выбранном диапазоне изменения температуры относительное изменение толщины $h$ покрытия из полимерного композита в результате теплового расширения не превышает $ \pm 1.5$ × 10^–3, а относительное изменение зазора Δ не превышает $ \pm 2.5$ × 10^–2. Приведенные оценки обосновывают сделанное в предыдущем разделе допущение о возможности не учитывать изменение толщины $h$ покрытия, обусловленное тепловым расширением.

Расчеты процесса изнашивания покрытия проводились с использованием стохастической (1.3)–(1.6), (1.8) и детерминированной (1.1), (1.13), (1.14) моделей. Численное решение соответствующих дифференциальных уравнений строилось на основе явной по времени разностной схемы [22], при этом для детерминированной постановки задачи монотонно возрастающий размер a области контакта использовался в качестве временного параметра [3].

С целью оценки важности учета случайных изменений температуры и внешней нагрузки при расчете износа покрытия, рассматривались различные варианты с одной или двумя постоянными величинами из числа $T,\;\xi ,\;Q$. Для таких величин использовались соответствующие представления (1.10) функции плотности вероятности. Для варианта, допускающего постоянство всех трех величин $T,\;\xi ,\;Q$, расчет процесса изнашивания проводился на основе детерминированной модели.

Полученные результаты расчетов представлены ниже с использованием безразмерных величин $\tilde {h} = h{\text{/}}{{h}_{{{\kern 1pt} 0}}}$ и $\tilde {t} = t{\text{/}}{{t}_{c}}$, ${{t}_{c}}$= 10⁵ с ≈ 27.8 ч.

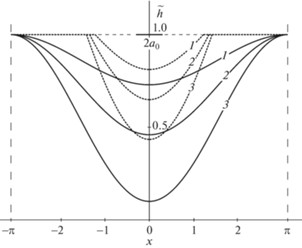
На рис. 2 показаны профили изношенного покрытия в различные моменты времени $\tilde {t}$: 8.03 (1), 16.1 (2), 26.8 (3). Расчеты проводились в предположении, что все величины $T,\;\xi ,\;Q$ случайные с функциями плотности вероятности вида (2.4)–(2.6) и ${{A}_{{\,\xi }}}$= 1. Для сравнения пунктирными линиями показаны профили изношенного покрытия в те же моменты времени, но при постоянных значениях $T = \bar {T},\;\;\xi = \bar {\xi } = 0,\;\;Q = \bar {Q}$. Соответствующая этим значениям начальная длина $2{{a}_{0}} = 0.601$ области контакта обозначена на рисунке отдельным отрезком.

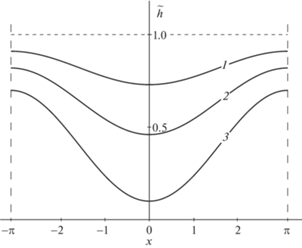
На рис. 3 показаны профили изношенного покрытия в различные моменты времени $\tilde {t}$: 10.7 (1), 21.4 (2), 35.8 (3). Все величины $T,\;\xi ,\;Q$ здесь считались случайными, однако, в отличие от рис. 2, расчеты проводились при ${{A}_{{\,\xi }}}$ = 2.

В таблице представлены значения долговечности $\tilde {t}_{*}^{{}} = t_{*}^{{}}{\text{/}}{{t}_{c}}$ покрытия, определяемой из условия (1.12), для вариантов с различными сочетаниями постоянных и случайных величин из числа $T,\;\xi ,\;Q$. Постоянный характер величины при этом отмечается символом “c”, а случайный – символом “r”. Для сравнения в таблице указана долговечность покрытия при всех трех постоянных величинах $T,\;\xi ,\;Q$, рассчитанная на основе детерминированной модели (вариант 4).

3. Обсуждение результатов. Представленные на рис. 2 и 3 графики показывают, что максимальное изнашивание покрытия, как и следовало ожидать, происходит при $x = 0$, т.е. в центральной части подшипника. Именно эта часть, согласно выражению (2.5), с наибольшей вероятностью подвержена контактному взаимодействию с валом. При детерминированной постановке задачи износ покрытия также концентрируется в центральной части подшипника в направлении $\xi = 0$ ($x = 0$) приложения постоянной нагрузки Q (пунктирные линии на рис. 2). Однако в отличие от стохастической постановки задачи, здесь износ носит локальный характер и представляет собой монотонно растущую лунку износа.

Сопоставление сплошных линий (стохастическая постановка задачи) и соответствующих им по времени пунктирных линий (детерминированная постановка задачи) на рис. 2, а также вариантов 3 и 4 в таблице позволяет сделать общий вывод о важности учета факторов случайности величин $T,\;\xi ,\;Q$ при расчете износа подшипника. Действительно, использование детерминированной модели (вариант 4) приводит к оценке долговечности $t_{*}^{{}}$ покрытия в 1.63 раза завышенной по сравнению с оценкой по стохастической модели (вариант 3).

Наиболее значимым представляется фактор случайности направления $\xi $ внешней нагрузки. Это проявляется, например, в том, что значение параметра ${{A}_{{\,\xi }}}$ функции плотности вероятности (2.5) величины $\xi $ оказывает качественное влияние на распределение износа по поверхности покрытия (рис. 2 и 3) и существенно влияет на оценку долговечности $t_{*}^{{}}$ покрытия (таблица). Однако фактор случайности величины нагрузки Q представляется малозначимым. Например, сравнение вариантов 2 и 3 таблицы показывает, что учет случайного изменения величины нагрузки Q не оказывает заметного влияния на оценку долговечности $t_{*}^{{}}$ покрытия.

Существенное влияние на результаты расчета износа покрытия оказывает фактор случайности температуры $T$ – это, например, следует из сравнения значений долговечности $t_{*}^{{}}$ покрытия для вариантов 1 и 3 таблицы. Такое влияние обусловлено тем, что модуль упругости $E$ и коэффициент износа $\alpha $ в значительной степени зависят от температуры согласно равенствам (2.1) и (2.2).

4. Выводы. 1. Предложена стохастическая модель процесса изнашивания тонкого покрытия в радиальном подшипнике скольжения, учитывающая случайные изменения температуры подшипника и внешней нагрузки.

2. Выполнен численный анализ процесса изнашивания покрытия, ориентированный на условия работы узлов трения в открытом космосе на околоземных орбитальных станциях.

3. Дана оценка значимости факторов случайного изменения температуры и внешней нагрузки при расчете износа подшипника. В частности, установлено, что наибольшую значимость имеют факторы случайности температуры подшипника и направления внешней нагрузки.

Работа выполнена при финансовой поддержке Российского научного фонда, грант № 22-49-02010.