Известия РАН. Механика жидкости и газа, 2019, № 1, стр. 44-57
Анализ гистерезиса перестройки конфигурации мыльной пленки на двух круглых рамках
М. М. Алимов a, *, К. Г. Корнев b
a Казанский (Приволжский) федеральный университет
Казань, Россия
b Clemson University
SC Clemson, USA
* E-mail: Mars.Alimov@kpfu.ru
Поступила в редакцию 12.03.2018
После доработки 14.06.2018
Принята к публикации 20.06.2018
Аннотация
Представлены результаты анализа поведения минимальной поверхности на системе двух круглых соосных рамок разного радиуса в процессе увеличения – уменьшения расстояния между рамками. Подтверждено предположение о метастабильности некоторых конфигураций минимальной поверхности, позволяющее объяснить наблюдаемый в экспериментах гистерезис перестройки мыльной пленки из одной конфигурации в другую. Показана эффективность использования аналитических методов теории фильтрации аномальных жидкостей в задачах определения конфигурации минимальной поверхности на рамках.
Пленки на различных рамках, извлеченных их мыльного раствора, представляют собой минимальные поверхности, конфигурация которых определяется условием минимума поверхностной энергии или, фактически, минимума площади поверхности [1]. Несмотря на прозрачный физический механизм, давнюю историю вопроса, начинающуюся с работы [2], и множества математических исследований по этому вопросу (см. [3–5] и библиографию в них), предсказать поведение пленок на рамках удается только в простейших случаях. В частности – это случай круглых, одинаковых и соосных рамок, когда минимальная поверхность представляет собой фигуру вращения, профиль которой – цепная линия. Такая минимальная поверхность называется катеноидом [4], ее полный анализ имеется, например, в [6].
Надо сказать, что даже в этом простейшем случае поведение минимальной поверхности нетривиально. Вместо регулярного катеноида, т.е. всюду гладкой поверхности с сужением – горловиной – в средней части, иногда наблюдаются катеноиды с плоской пленкой в его горловине. Такой катеноид будет уже сингулярным, поскольку представляет собой совокупность трех гладких сегментов, которые стыкуются по некоторой линии – сингулярному ребру минимальной поверхности [4].
Если же взять две круглые рамки разного радиуса, то пленка образует несимметричный катеноид – его горловина будет не в средней части. Как показали эксперименты, это приводит к неожиданным результатам в поведении пленки: при увеличении – уменьшении расстояния между рамками происходит перестройка регулярного несимметричного катеноида в сингулярный и обратно, и, более того, прямая и обратная перестройка происходят на различных расстояниях, т.е. имеет место гистерезис перестройки конфигурации [7].
Проводя аналогию между перестройкой минимальных поверхностей и фазовыми переходами, авторы [7] высказали предположение о метастабильности одной из возможных конфигураций пленки на такой системе рамок, что позволило им объяснить и сам гистерезис. Однако никаких оценок поверхностной энергии, отвечающей различным конфигурациям катеноида, в работе [7] проведено не было. Соответственно все объяснение носит гипотетический характер.
Настоящая работа преследует двоякую цель. Во-первых, объяснить экспериментальные результаты работы [7] путем проведения полного анализа поведения минимальной поверхности на системе двух круглых соосных рамок разного диаметра. Во-вторых, предложить новую схему анализа конфигураций минимальных поверхностей на рамках, использующую обнаруженную в работе [8] аналогию между теорией минимальных поверхностей и теории фильтрации аномальных жидкостей [9]. Примененная непосредственно к катеноиду такая схема анализа несколько сложнее классической [6], но обладает тем преимуществом, что легко может быть распространена на случай некруглых и негладких рамок.
Сначала разберем случай одинаковых круглых рамок и соответственно симметричного регулярного и сингулярного катеноида.
1. ПОСТАНОВКА ЗАДАЧИ О СИММЕТРИЧНОМ КАТЕНОИДЕ
Радиус рамок выберем за характерную длину. Приняв обозначение ${{R}_{{up}}}$ для радиуса верхней рамки и соответственно ${{R}_{{dn}}}$ для радиуса нижней рамки, можно считать, что
Примем, что плоскости рамок горизонтальны, и плоскость нижней рамки – это плоскость $x,y$. Ось $z$, направленная по вертикали вверх, будет для рамок осью симметрии. На фиг. 1a, 1б схематически представлены регулярный катеноид – гладкая поверхность ${{\Sigma }_{0}}$, и соответственно сингулярный катеноид – совокупность гладких сегментов $\Sigma _{0}^{ + } \cup \Sigma _{0}^{ - } \cup \Sigma _{0}^{'}$, где $\Sigma _{0}^{'}$ – круглая плоская пленка в горловине катеноида.
Фиг. 1.
Симметричный регулярный катеноид ${{\Sigma }_{0}}$ (а) и симметричный сингулярный катеноид $\Sigma _{0}^{ + } \cup \Sigma _{0}^{ - } \cup \Sigma _{0}^{'}$, т.е. катеноид с плоской пленкой $\Sigma _{0}^{'}$ в его горловине (б)
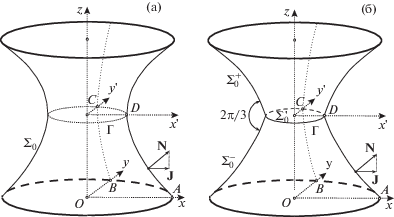
Являясь фигурой вращения, симметричный катеноид обладает еще и симметрией относительно горизонтальной плоскости $x{\text{'}}y{\text{'}}$, проходящей через геометрический центр катеноида. Поэтому как для регулярного, так и для сингулярного катеноида достаточно восстановить конфигурацию элемента симметрии минимальной поверхности, например, ее сегмента $ABCDA$, см. фиг. 1a, 1б.
Конфигурация сегмента $ABCDA$ минимальной поверхности может быть задана функцией высоты точки (x, y, z) минимальной поверхности над уровнем плоскости xy
Эта функция определена в области $\Omega $, которая является проекцией элемента симметрии $ABCDA$ минимальной поверхности на плоскость xy, см. фиг. 2a.
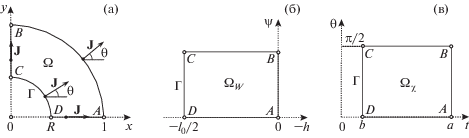
Фиг. 2.
Вид области течения в плоскости $x,z$ (а), в плоскости комплексного потенциала W (б), и в плоскости годографа скорости $\chi $ (в) для симметричного катеноида
Для нахождения функции $h(x,y)$ надо решить краевую задачу
(1.1)
$\Omega {\text{:}}\,\,\,\nabla \cdot [{{(1 + {{\left| {\nabla h} \right|}^{2}})}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\nabla h] = 0,$(1.6)
$\Gamma {\text{:}}\,\,\,h = \frac{{{{l}_{0}}}}{2},\quad {{(1 + {{\left| {\nabla h} \right|}^{2}})}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}\left| {\nabla h} \right| = \cos \left( {\frac{\pi }{6}} \right)$Здесь (1.1) – дифференциальное уравнение минимальной поверхности [3], (1.2), (1.3) – условие гладкого симметричного продолжения функции $h(x,y)$, а значит и минимальной поверхности ${{\Sigma }_{0}}$, через границу AD и BC соответственно; (1.4) – граничное условие на нижней рамке.
Граница $\Gamma = CD$ в обоих случаях – это сечение горловины минимальной поверхности ${{\Sigma }_{0}}$ горизонтальной срединной плоскостью $x{\text{'}}y{\text{'}}$, см. фиг. 1a. В сингулярном случае – это еще и сингулярное ребро поверхности $\Sigma _{0}^{ + } \cup \Sigma _{0}^{ - } \cup \Sigma _{0}^{'}$, см. фиг. 1б. В обоих случаях граница $\Gamma $ – окружность, однако ее радиус R неизвестен и формально она является свободной границей. Поэтому на ней задается два условия (1.5) в регулярном и соответственно два условия (1.6) – в сингулярном случаях. Первое условие и в (1.5), и в (1.6) – постоянство высоты $h(x,y)$. Второе условие в (1.5) для регулярного катеноида отражает факт ортогональности плоскости $x{\text{'}}y{\text{'}}$ и минимальной поверхности ${{\Sigma }_{0}}$.
Для сингулярного катеноида угол между каждой парой сегментов $\Sigma _{0}^{ + }$, $\Sigma _{0}^{ - }$, $\Sigma _{0}^{'}$ на линии их стыковки $\Gamma $ должен быть равен $2\pi {\text{/}}3$ [4] и, следовательно, нормаль ${\mathbf{N}}$ к минимальной поверхности будет составлять с горизонтальной плоскостью $x{\text{'}}y{\text{'}}$ угол $\pi {\text{/}}6$. Именно этот факт отражает второе условие в (1.6) для сингулярного катеноида, поскольку величина ${{(1 + {{\left| {\nabla h} \right|}^{2}})}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}\left| {\nabla h} \right|$ представляет собой проекцию ${\mathbf{N}}$ на плоскость $x{\text{'}}y{\text{'}}$ [10].
Таким образом, для определения конфигурации симметричного регулярного катеноида надо решить краевую задачу (1.1)–(1.5), а для определения конфигурации симметричного сингулярного катеноида – краевую задачу (1.1)–(1.4), (1.6). Расстояние между плоскостями рамок l0 представляет собой единственный управляющий параметр задачи, от которого зависит конфигурация минимальной поверхности.
2. АНАЛОГИЯ С ФИЛЬТРАЦИЕЙ АНОМАЛЬНО ВЯЗКИХ ЖИДКОСТЕЙ
В работе [8] установлено, что для анализа задач о минимальной поверхности можно эффективно использовать аналогию с задачами фильтрации аномально вязких жидкостей в пористой среде [9]. Определим фиктивный гидродинамический поток ${\mathbf{J}}$ жидкости следующим образом:
(2.1)
${\mathbf{J}} = - \frac{{\nabla h}}{{\left| {\nabla h} \right|}}J,\quad J = \frac{{\left| {\nabla h} \right|}}{{\sqrt {1 + {{{\left| {\nabla h} \right|}}^{2}}} }}$Вектор потока ${\mathbf{J}}$ характеризуется своей величиной $J = \left| {\mathbf{J}} \right|$ и углом наклона ${\theta }$ к оси $x$. Связь (2.1) между величинами J и $\left| {\nabla h} \right|$ можно записать в другой форме
(2.2)
$\left| {\nabla h} \right| = \Phi (J),\quad \Phi (J) = J{{(1 - {{J}^{2}})}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$(2.3)
$\Omega {\text{:}}\,\,\,\nabla h = - \frac{{\mathbf{J}}}{J}\Phi (J),\quad \nabla \cdot {\mathbf{J}} = 0$При этом $h(x,y)$ является аналогом напора, а ${\mathbf{J}}(x,y)$ – аналогом скорости фильтрации. Характер течения представлен на фиг. 2a. Закон фильтрации (2.2) был впервые рассмотрен В.В. Соколовским [11].
Второе дифференциальное уравнение (2.3) означает, что жидкость несжимаема и, следовательно, можно ввести функцию тока $\psi (x,y)$ [12]. Тогда
Как показано Христиановичем [13], для фильтрационных течений, удовлетворяющих закону (2.3), целесообразно использовать преобразование Чаплыгина [14] к переменным годографа скорости t, $\theta $. Для закона Соколовского (2.2) переменная t будет связана с J выражением [11]
(2.4)
$J = {{\operatorname{ch} }^{{ - 1}}}t,\quad t = {\text{arch}}\,{{J}^{{{\kern 1pt} - 1}}},\quad \Phi (J) = {{\operatorname{sh} }^{{ - 1}}}t$В результате такого преобразования придем к соотношениям Коши–Римана (подробности см. [11, 15])
Следовательно, можно ввести комплексные переменные W и $\chi $
и использовать функцию комплексного переменного $\chi (W)$ или $W(\chi )$ [16]. Условно W называется комплексным потенциалом течения, а $\chi $ – годографом скорости [9].Когда функция $\chi (W)$ будет найдена, вернуться на физическую плоскость $x,y$ можно, выписав формулы Христиановича полных дифференциалов от функций $x(h,\psi )$, $y(h,\psi )$ [9, 13]
(2.5)
$dx = - \cos \theta \operatorname{sh} tdh - \sin \theta \operatorname{ch} td\psi ,\quad dy = - \sin \theta \operatorname{sh} t\,dh + \cos \theta \operatorname{ch} td\psi $Как показано в [9], задача определения функции $\chi (W)$ может эффективно решаться методом годографа скорости [17] при условии, что плоскости $\chi $ и W имеют канонический вид.
3. АНАЛИЗ ВИДА ПЛОСКОСТЕЙ КОМПЛЕКСНОГО ПОТЕНЦИАЛА И ГОДОГРАФА СКОРОСТИ
Сначала проанализируем вид плоскости комплексного потенциала $W = - h + i\psi $. Границы $AD$ и $BC$ области $\Omega $ являются линиями тока, см. фиг. 2a, а границы $AB$ и $CD$ – линиями постоянства h, см. формулы (1.4)–(1.6). Поэтому в плоскости потенциала $W = - h + i\psi $ области течения $\Omega $ отвечает прямоугольник ${{\Omega }_{W}}$, представленный на фиг. 2б.
Чтобы проанализировать вид плоскости годографа скорости $\chi = t + i\theta $, помимо представления J, как вектора потока несжимаемой жидкости, удобно использовать и геометрическую его интерпретацию: в соответствии с [10] вектор потока ${\mathbf{J}}(x,y)$ вида (2.1) будет проекцией вектора нормали ${\mathbf{{\rm N}}}(x,y)$ на плоскость $x,y$, см. фиг. 1.
С учетом картины течения, см. фиг. 2а, на линиях тока $AD$ и $BC$ имеем
На границах $AB$ и $CD$ используем тот факт, что вектор нормали ${\mathbf{{\rm N}}}(x,y)$ будет ортогонален к самим границам. Тогда и вектор потока J будет ортогонален к ним, см. фиг. 2a. Далее, из соображений осевой симметрии течения следует, что величина потока J будет постоянной на каждой из границ $AB$ и $CD$.
Величина потока J на границе $\Gamma = CD$ устанавливается в регулярном случае из второго граничного условия в (1.5): J = 1 и соответственно в сингулярном случае – из граничного условия (1.6): $J = \cos (\pi {\text{/}}6)$. Введем обозначения ${{b}_{r}}$, ${{b}_{s}}$ для параметра $b$ в регулярном и сингулярном случае соответственно:
(3.2)
$b = \left\{ {\begin{array}{*{20}{l}} {{{b}_{r}} = 0} \\ {{{b}_{s}} = {\text{arch}}\left[ {{{{\cos }}^{{ - 1}}}\left( {\frac{\pi }{6}} \right)} \right]} \end{array}} \right.$Тогда, с учетом связи (2.4) между J и $t$, условие на $\Gamma $ в обоих случаях может быть выписано в общем виде
Поток J на границе $AB$ постоянен, но неизвестен по величине. Вследствие той же самой формулы (2.4) величина $t$ на границе $AB$ также будет постоянной, но неопределенной. Обозначим ее через $a$
С учетом формул (3.1)–(3.4) приходим к выводу, что в плоскости годографа скорости $\chi $ области течения $\Omega $ отвечает прямоугольник ${{\Omega }_{\chi }}$, представленный на фиг. 2в. Определяющий отношение сторон прямоугольника параметр $a$ будет основным вспомогательным параметром задачи. Очевидно, что $a > b$.
Учитывая вид комплексных плоскостей $W = - h + i\psi $ и $\chi = t + i\theta $, легко находим конформное отображение $W(\chi )$
которое непосредственно определяет функции $h(t,\theta )$ и $\psi (t,\theta )$4. ВОССТАНОВЛЕНИЕ КОНФИГУРАЦИИ МИНИМАЛЬНОЙ ПОВЕРХНОСТИ
Радиус R окружности $\Gamma $ можно определить из соображений материального баланса. Действительно, в силу несжимаемости жидкости ее суммарные потоки через границы $AB$ и $CD$ должны совпадать. Вектор J ортогонален к этим границам, а его величина J постоянна на каждой из границ. С учетом этого будем иметь
В результате, используя условия (3.3), (3.4), получим
Найти конфигурации всей минимальной поверхности можно, определив функцию $h(x,y)$. Поскольку задача была параметризована введением вспомогательной плоскости $\chi = t + i\theta $, функция $h(x,y)$ опосредованно определяется функциями $h(t,\theta )$, $x(t,\theta )$ и $y(t,\theta )$. Функция $h(t,\theta )$ нам уже известна, см. формулу (3.5). Чтобы найти функции $x(t,\theta )$ и $y(t,\theta )$, используем дифференциальные формулы Христиановича общего вида (2.5). Подставляя в них вытекающие из (3.5) выражения для частных производных функций $h(t,\theta )$ и $\psi (t,\theta )$
(4.2)
$\begin{gathered} dx = \frac{{{{l}_{0}}}}{{2\left( {a - b} \right)}}\left[ {\cos \theta \operatorname{sh} tdt - \sin \theta \operatorname{ch} td\theta } \right], \hfill \\ dy = \frac{{{{l}_{0}}}}{{2\left( {a - b} \right)}}\left[ {\sin \theta \operatorname{sh} tdt + \cos \theta \operatorname{ch} td\theta } \right] \hfill \\ \end{gathered} $В частности, для границы $\Gamma $ из формул (4.2) с учетом условия (3.3) следует
Соответственно можно связать приращения дуговой абсциссы ${{s}_{\Gamma }}$ границы $\Gamma $ и угла наклона $\theta $ к оси $x$ нормали к этой границе
Поскольку $\Gamma $ – окружность, из последнего выражения следует еще одна формула для величины радиуса $R$ окружности $\Gamma $
Сравнивая ее с формулой (4.1), получим связь единственного управляющего параметра задачи l0 с основным вспомогательным параметром задачи $a$
Далее, из формул (4.2) дифференциалов функций $x(t,\theta )$ и $y(t,\theta )$ можно восстановить и сами функции, но поскольку и регулярный, и сингулярный катеноиды являются фигурами вращения, достаточно установить их профиль AD в плоскости xz, как функции $x = x(z)$. Для границы AD из формул (4.2) при учете первого условия (3.1) и формулы (4.3) получим соотношение, связывающее дифференциалы $t$ и $x$
Проинтегрируем его от точки $D$, где $t = b$ и $x = R$. С учетом выражения (4.1) найдем функцию $x(t)$ на границе AD
Функцию $z(t)$ на границе AD по сути дает первое выражение в формуле (3.5). Перепишем его с учетом выражения (4.3)
Обращая функцию $z(t)$, найдем функцию $t(z)$ на на границе $AD$
Подставляя формулу (4.5) в формулу (4.4), получим искомый профиль $x(z)$ границы AD
(4.6)
$AD{\text{:}}\,\,\,x(z) = \frac{{\operatorname{ch} \left( {a - z\operatorname{ch} a} \right)}}{{\operatorname{ch} a}}$Этот профиль является цепной линией и отличается от известных формул [6] только выбором начала координат и масштаба.
5. ОПРЕДЕЛЕНИЕ ПЛОЩАДИ МИНИМАЛЬНОЙ ПОВЕРХНОСТИ
Часть катеноида, заключенная между плоскостями $z = 0$ и $z = z{\text{'}}$, представляет собой фигуру вращения с заданным профилем $x(z)$ и осью вращения $z$. Поэтому для вычисления ее площади $S(z')$ можно использовать формулу [18]
(5.1)
$S(z{\text{'}}) = 2\pi \int\limits_0^{z'} {x(z)\sqrt {1 + {{{\left( {\frac{{dx}}{{dz}}} \right)}}^{2}}} dz} $Профиль $x(z)$ представлен выражением (4.6). Его непосредственное дифференцирование дает выражение для $dx{\text{/}}dz$
Подставляя его формулу (5.1) и проводя интегрирование, получим
(5.2)
$S(z{\text{'}}) = \pi \frac{{2z{\text{'}}\operatorname{ch} a - \operatorname{sh} \left( {2a - 2z{\text{'}}\operatorname{ch} a} \right) + \operatorname{sh} \left( {2a} \right)}}{{2{{{\operatorname{ch} }}^{2}}a}}$Тогда площадь всего катеноида в регулярном и в сингулярном случаях можно выразить единой формулой
(5.3)
${{S}_{0}} = {{\left. {{}^{}2S(z{\text{'}})} \right|}_{{z{\text{'}} = {{l}_{0}}{\text{/}}2}}} + (bb_{s}^{{ - 1}})\pi {{R}^{2}}$Второе слагаемое здесь подчеркивает, что площадь сингулярного катеноида отличается от площади регулярного катеноида не только другим значением $b$ в формуле (4.3) для ${{l}_{0}}$, но и добавлением площади пленки $\Sigma _{0}^{'}$ в горловине катеноида. Проводя вычисления по формуле (5.3) с учетом выражений (4.3), (5.2), найдем площадь симметричного катеноида ${{S}_{0}}$ в зависимости от параметра $a$
(5.4)
${{S}_{0}}(a) = \pi \frac{{2\left( {a - b} \right) + \operatorname{sh} \left( {2a} \right) - \operatorname{sh} \left( {2b} \right) + (bb_{s}^{{ - 1}}){{{\operatorname{ch} }}^{2}}b}}{{{{{\operatorname{ch} }}^{2}}a}}$Здесь в регулярном и сингулярном случаях надо выбирать свое значение $b$ в соответствии с формулой (3.2).
6. АНАЛИЗ РЕЗУЛЬТАТОВ ДЛЯ СИММЕТРИЧНОГО КАТЕНОИДА
На фиг. 3a представлена рассчитанная по формуле (4.3) зависимость ${{l}_{0}}(a)$: кривая 1 – для регулярного катеноида, кривая 2 – для сингулярного катеноида. Обе кривые немонотонны и имеют максимумы, отмеченные звездочкой: у кривой 1 это критическое значение $l_{{0,r}}^{*} = 1.3255$, которое достигается при a, равном $a_{r}^{*} = 1.1997$; у кривой 2 это критическое значение $l_{{0,s}}^{*} = 0.8156$, которое достигается при $a$, равном $a_{s}^{*} = 1.6293$. Следовательно, и в регулярном, и в сингулярном случаях при l0, больше критического значения, связной конфигурации минимальной поверхности не существует, а при l0, меньше критического значения, возможны две конфигурации катеноида.
Фиг. 3.
Зависимости от параметра a величин l0 (а) и $R$ (б) для симметричного катеноида в регулярном (кривые 1) и в сингулярном (кривые 2) случаях. Зависимости площади симметричного катеноида ${{S}_{0}}$ от величины l0 (в): 1, 2 – внешняя (устойчивая), и 1', 2' – внутренняя (неустойчивая) конфигурация катеноида в регулярном и сингулярном случае соответственно; 3 – устойчивое состояние системы “регулярный катеноид с пленкой на одной из рамок”; 4 – две отдельные пленки на рамках
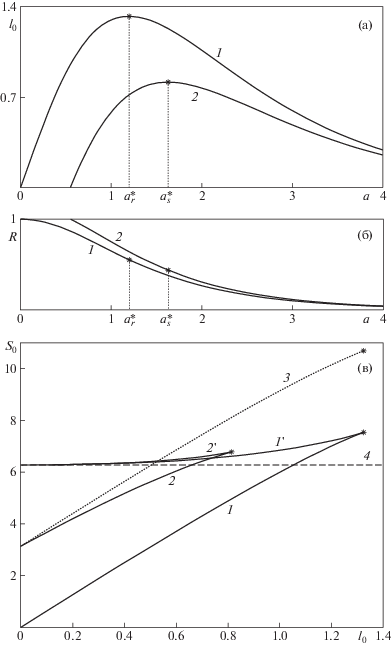
На фиг. 3б представлена рассчитанная по формуле (4.1) зависимость $R(a)$: кривая 1 – для регулярного катеноида, кривая 2 – для сингулярного катеноида. Звездочками отмечены критические значения $R$: для кривой 1 – это значение, равное $R_{r}^{*} = 0.5524$ при $a = a_{r}^{*}$; для кривой 2 – это значение, равное $R_{s}^{*} = 0.4360$ при $a = a_{s}^{*}$. Видим, что в обоих случаях зависимость $R(a)$ монотонно убывает и соответственно упомянутые выше две конфигурации катеноида можно различать по величине R окружности $\Gamma $: когда значения параметра a меньше критического, это будет внешний катеноид с величиной R, больше критической; когда значения параметра a больше критического, это будет внутренний катеноид с величиной R, меньше критической.
Известно, что и регулярном, и в сингулярном случае только внешний катеноид устойчив, поскольку отвечает минимуму свободной энергии [6]. Чтобы убедиться в этом, приведем рассчитанную по формуле (5.4) зависимость площади поверхности катеноида ${{S}_{0}}$ от расстояния между рамками l0, см. фиг. 3в. Сплошные линии 1 и 2 отвечают устойчивым, а 1' и 2' – неустойчивым ветвям регулярного и сингулярного катеноида соответственно. Звездочками отмечены критические значения, в которых зависимости ${{S}_{0}}({{l}_{0}})$ имеют точки возврата. Им отвечают значения ${{l}_{0}} = l_{{0,r}}^{*}$, ${{S}_{0}} = S_{{0,r}}^{*} = 7.5378$ – в регулярном случае, и значения ${{l}_{0}} = l_{{0,s}}^{*}$, ${{S}_{0}} = S_{{0,s}}^{*} = 6.7856$ – в сингулярном случае. Штриховой линией 4 отмечено решение ${{S}_{0}} = 2\pi $, отвечающее случаю разрывного решения задачи – две отдельные пленки на рамках.
В этой связи также возникает вопрос о возможности перестройки регулярного катеноида в сингулярный и обратно. Ограничиваясь рассмотрением только устойчивых конфигураций внешнего катеноида, см. линии 1 и 2 на фиг. 3в, можно заключить, что при фиксированном l0 площадь сингулярного катеноида всегда больше площади регулярного катеноида. Поэтому регулярный катеноид не может самопроизвольно перестроиться в сингулярный. Остается вопрос – возможна ли обратная перестройка?
Если расстояние между рамками l0 будет больше $l_{{0,s}}^{*}$, очевидно, что катеноид не сможет оставаться сингулярным и, в частности, может стать регулярным, если срединная пленка $\Sigma _{0}^{'}$ хлопнется. Однако это лишь один из вероятных исходов, возможны и другие: например, переход системы к разрывному решению – двум отдельным пленкам на каждой рамке, или к схлопыванию всех пленок.
В то же время, если расстояние между рамками l0 будет меньше $l_{{0,s}}^{*}$, то на первый взгляд представляется, что системе энергетически более выгодно перейти от сингулярного катеноида к регулярному. Однако это не так, поскольку на сингулярном катеноиде есть срединная пленка $\Sigma _{0}^{'}$. Если отбросить возможность ее устранения путем внешнего вмешательства, то для такого перехода необходимо, чтобы пленка $\Sigma _{0}^{'}$ перешла на одну из рамок. Очевидно, свободная энергия такой системы – “регулярный катеноид плюс пленка на рамке”, будет характеризоваться уже не просто площадью ${{S}_{{0,r}}}$ регулярного катеноида в устойчивой внешней конфигурации (линия 1), а суммой $({{S}_{{0,r}}} + \pi )$, см. линию 3 на фиг. 3в. Эта линия проходит уже выше сингулярного катеноида в устойчивой внешней конфигурации (линии 2) и переход от сингулярного катеноида к системе “регулярный катеноид плюс пленка на рамке” невозможен.
Рассмотрим также обратную ситуацию, когда к регулярному катеноиду дополнительно на одну из рамок подсаживается пленка. Если расстояние между рамками l0 будет больше $l_{{0,s}}^{*}$, то система будет оставаться в этом состоянии, поскольку альтернативы – сингулярного катеноида – при таком l0 нет. Однако, если в момент подсадки расстояние между рамками l0 будет меньше $l_{{0,s}}^{*}$, подсаженная пленка соскользнет в горловину регулярного катеноида, и состоится переход системы из состояния “регулярный катеноид с пленкой на одной из рамок” к сингулярному катеноиду.
Как замечено в [7], такая перестройка катеноида происходит в два этапа: сначала пленка соскальзывает с рамки в горловину катеноида, а затем катеноид, ставший уже сингулярным, приходит к равновесному состоянию. Соответственно необходимым условием этой перестройки является не только более выгодное конечное состояние (с меньшей свободной энергией), но и более выгодное промежуточное состояние, после соскальзывания пленки в горловину катеноида. Здесь оба эти условия соблюдаются, поскольку площадь пленки при переходе с рамки в горловину уменьшается. Поэтому целый отрезок ${{l}_{0}} \in (0,l_{{0,s}}^{*}]$ линии 3 фиг. 3в отвечает неустойчивому состоянию системы “регулярный катеноид с пленкой на одной из рамок” – последняя сразу переходит в состояние сингулярного катеноида (линия 2).
Еще более неожиданные особенности таких перестроек катеноидов проявляются в случае несимметричных рамок [7]. Перейдем к его анализу.
7. СЛУЧАЙ НЕСИММЕТРИЧНЫХ РАМОК
В этом случае можно принять, что
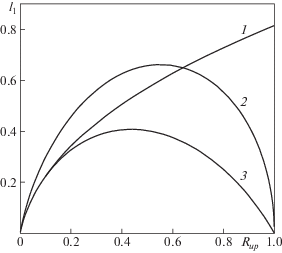
Конфигурацию регулярного и сингулярного несимметричного катеноиды можно найти простым отсечением плоскостью $z = z{\text{'}}$ нужной части от рассмотренного выше симметричного катеноида: регулярного Σ0 (фиг. 4а) или сингулярного $\Sigma _{0}^{ + } \cup \Sigma _{0}^{ - } \cup \Sigma _{0}^{'}$ (фиг. 4б).
Фиг. 4.
Схема определения несимметричного катеноида по заданной величине ${{R}_{{up}}} < 1$ с помощью сечения симметричного катеноида ${{\Sigma }_{0}}$ – в регулярном (а) и $\Sigma _{0}^{ + } \cup \Sigma _{0}^{ - } \cup \Sigma _{0}^{'}$ – в сингулярном случае (б): решение I – катеноид без горловины, решение II – катеноид с горловиной
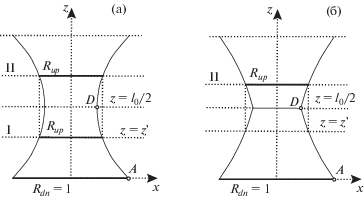
Найдем сечение катеноида $z = z{\text{'}}$ из интервала $0 < z{\text{'}} < {{l}_{0}}{\text{/}}2$, радиус которого равен ${{R}_{{up}}} < 1$. Для этого разрешим уравнение профиля $AD$ катеноида (4.6) относительно $z$
где через $F(x,a)$ обозначена функция(7.2)
$F(x,a) = \frac{{a - {\text{arch}}\left( {x\operatorname{ch} a} \right)}}{{\operatorname{ch} a}}$Полагая $x = {{R}_{{up}}}$ в выражении (7.1) найдем искомое сечение катеноида $z = z{\text{'}}$
При этом надо ограничиться только теми $z{\text{'}}$, которые удовлетворяют условию
Очевидно, что это условие накладывает дополнительное ограничение на диапазон изменения параметра $a$
Это сужает ранее указанный диапазон изменения параметра $a$: $a > b$, поскольку ввиду условия ${{R}_{{up}}} < 1$ выполняется неравенство ${\text{arch}}(R_{{up}}^{{ - 1}}\operatorname{ch} b) > b$.
Таким образом, искомое сечение катеноида $z = z{\text{'}}$ из интервала $0 < z{\text{'}} < {{l}_{0}}{\text{/}}2$, радиус которого равен ${{R}_{{up}}}$, определяется формулой (7.3) при условии (7.4). Площадь сегмента катеноида, лежащего между плоскостями $z = 0$ и $z = z{\text{'}} < {{l}_{0}}{\text{/}}2$, по сути уже найдена: ${{S}_{1}} = S(z{\text{'}})$, см. выражение (5.2).
Поскольку найденные ранее катеноиды ${{\Sigma }_{0}}$ и $\Sigma _{0}^{ + } \cup \Sigma _{0}^{ - } \cup \Sigma _{0}^{'}$ симметричны относительно плоскости $z = {{l}_{0}}{\text{/}}2$, помимо найденного в интервале $0 < z{\text{'}} < {{l}_{0}}{\text{/}}2$ сечения $z = z{\text{'}}$, радиус которого равен ${{R}_{{up}}}$, в интервале ${{l}_{0}}{\text{/}}2 < z{\text{'}} < {{l}_{0}}$ будет еще одно сечение такого же радиуса. Таким образом, задача определения в симметричном регулярном катеноиде ${{\Sigma }_{0}}$ расстояния l1 между круглыми рамками радиуса ${{R}_{{dn}}} = 1$ и ${{R}_{{up}}} < 1$ имеет два решения, которые назовем решением I (без горловины) и решением II (с горловиной), см. фиг. 4а
(7.5)
${\text{I}}:\quad \left\{ {\begin{array}{*{20}{l}} {{{l}_{1}} = F({{R}_{{up}}},a)} \\ {{{S}_{1}} = {{{\left. {{}^{}S(z{\text{'}})} \right|}}_{{z{\text{'}} = {{l}_{1}}}}}} \end{array}} \right.$(7.6)
${\text{II}}:\quad \left\{ {\begin{array}{*{20}{l}} {{{l}_{1}} = {{{\left. {{{l}_{0}}(a)} \right|}}_{{b = {{b}_{r}}}}} - F({{R}_{{up}}},a)} \\ {{{S}_{1}} = {{{\left. {{{S}_{0}}(a)} \right|}}_{{b = {{b}_{r}}}}} - {{{\left. {{}^{}S(z{\text{'}})} \right|}}_{{z{\text{'}} = {{l}_{1}}}}}} \end{array}} \right.$В то же время аналогичная задача в симметричном сингулярном катеноиде $\Sigma _{0}^{ + } \cup \Sigma _{0}^{ - } \cup \Sigma _{0}^{'}$ имеет только решение II, см. фиг. 4б
(7.7)
${\text{II}}:\quad \left\{ {\begin{array}{*{20}{l}} {{{l}_{1}} = {{{\left. {{{l}_{0}}(a)} \right|}}_{{b = {{b}_{s}}}}} - F({{R}_{{up}}},a)} \\ {{{S}_{1}} = {{{\left. {{{S}_{0}}(a)} \right|}}_{{b = {{b}_{s}}}}} - {{{\left. {{}^{}S(z{\text{'}})} \right|}}_{{z{\text{'}} = {{l}_{1}}}}}} \end{array}} \right.$В выражениях (7.5)–(7.7) необходимо учесть формулы (3.2), (5.2), (7.2) при условии (7.4).
Ниже приведены рассчитанные по формулам (7.5)–(7.7) графики зависимостей ${{S}_{1}}({{l}_{1}})$ для несимметричных регулярного и сингулярного катеноидов при ${{R}_{{up}}} = 0.5$ (фиг. 5a) и ${{R}_{{up}}} = 0.8$ (фиг. 5б). Линии 1 и 2 отвечают устойчивым, а 1' и 2' – неустойчивым ветвям регулярного и соответственно сингулярного катеноида.
Фиг. 5.
Зависимости площади несимметричного катеноида S1 от величины l1 в регулярном и сингулярном случае при ${{R}_{{up}}} = 0.5$ (a) и ${{R}_{{up}}} = 0.8$ (б). Кривые 1 и 2 отвечают устойчивым, а 1' и 2' – неустойчивым ветвям в регулярном и сингулярном случае соответственно
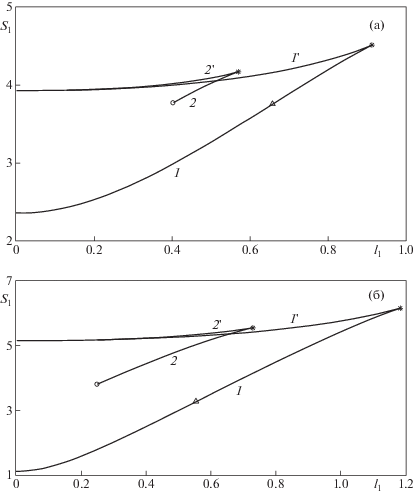
Как и ранее, символами “*” обозначим правые концы устойчивых веток регулярного и сингулярного катеноида, а отвечающие им значения максимально возможных ${{l}_{{1,r}}}$ и ${{l}_{{1,s}}}$ обозначим соответственно через $l_{{1,r}}^{*}$ и $l_{{1,s}}^{*}$. Символом “o” обозначим левый конец устойчивой ветви сингулярного катеноида, который определяется ограничением (7.4), а соответствующее ему значение минимально возможного ${{l}_{{1,s}}}$ обозначим через $l_{{1,s}}^{{\text{o}}}$.
Значение ${{l}_{{1,r}}}$, при котором у регулярного катеноида появляется (или исчезает) горловина, обозначим через $l_{{1,r}}^{\vartriangle }$. Соответствующую ему точку на устойчивой ветви ${{S}_{1}}({{l}_{1}})$ регулярного катеноида обозначим символом “$\vartriangle $”, так что при ${{l}_{1}} < l_{{1,r}}^{\vartriangle }$ катеноид будет без горловины (решение I), а при ${{l}_{1}} < l_{{1,r}}^{\vartriangle }$ – будет с горловиной (решение II), см. фиг. 4а.
Видно, что для любых ${{R}_{{up}}} < 1$ графики ${{S}_{1}}({{l}_{1}})$ качественно схожи между собой и также схожи с первоначальным графиком ${{S}_{0}}({{l}_{0}})$ для симметричного регулярного и сингулярного катеноида, см. фиг. 3в. Также, аналогично симметричному случаю, регулярный катеноид не может самопроизвольно перейти в сингулярный катеноид, поскольку зависимость ${{S}_{1}}({{l}_{1}})$ для последнего всегда ниже. В то же время здесь, в отличие от случая симметричных рамок, возможен непрерывный обратный переход – при уменьшении расстояния l1 между рамками плоскость срединной пленки сингулярного катеноида приближается к плоскости меньшей рамки и при ${{l}_{1}} = l_{{1,s}}^{{\text{o}}}$ эти плоскости просто совмещаются. Соответственно пленка $\Sigma _{0}^{'}$ в горловине становится пленкой на верхней (меньшей) рамке, а сам катеноид становится регулярным. Однако обсуждать это надо в рамках анализа системы “регулярный несимметричный катеноид с пленкой на меньшей рамке”.
8. СЛУЧАЙ, КОГДА К РЕГУЛЯРНОМУ НЕСИММЕТРИЧНОМУ КАТЕНОИДУ ПОДСАЖИВАЕТСЯ ПЛЕНКА НА МЕНЬШЕЙ РАМКЕ
Свободная энергия системы “регулярный катеноид плюс пленка на меньшей рамке” пропорциональна ее суммарной площади ${{S}_{{1,r}}}({{l}_{1}}) + \pi R_{{up}}^{2}$. Зависимость этой площади от расстояния l1 между рамками представлена пунктирными линиями 3 на фиг. 6а при ${{R}_{{up}}} = 0.5$ и на фиг. 6б при ${{R}_{{up}}} = 0.8$. Символом “$\vartriangle $”, как и ранее, отмечена точка возникновения (исчезновения) горловины на регулярном катеноиде. Линии 2 представляют устойчивые ветви для сингулярного катеноида – те же самые, что и на фиг. 5а, 5б. Левые и правые концы этих линий, как и ранее, обозначены символами “${\text{o}}$” и “*”.
Фиг. 6.
Устойчивые ветви зависимости S1 от l1 для несимметричного сингулярного катеноида (кривые 2) и зависимости $({{S}_{1}} + \pi R_{{up}}^{2})$ от l1 для системы “регулярный несимметричный катеноид с пленкой на меньшей рамке” (3) при: ${{R}_{{up}}} = 0.5$ (a) и ${{R}_{{up}}} = 0.8$ (б); стрелки вдоль кривых обозначают квазистационарное изменение состояния системы с изменением расстояния l1, вертикальные стрелки обозначают переход системы из неустойчивого положения в устойчивое
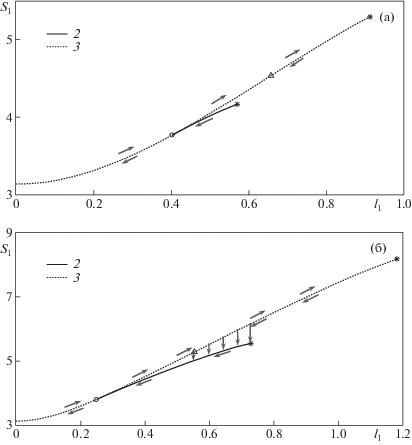
Как видно из фиг. 6а, 6б, при уменьшении расстояния l1 между рамками и достижении l1 величины $l_{{1,s}}^{{\text{o}}}$ действительно происходит непрерывный и даже гладкий (в смысле значений свободной энергии) переход от сингулярного несимметричного катеноида к системе “регулярный несимметричный катеноид с пленкой на меньшей рамке”. Понятно, что расстояние ${{l}_{1}}$ можно уменьшать и далее, система будет оставаться в этом устойчивом состоянии. Но, что случится, если начать увеличивать расстояние ${{l}_{1}}$ до величины $l_{{1,s}}^{{\text{o}}}$ и далее?
На первый взгляд, при достижении l1 величины $l_{{1,s}}^{{\text{o}}}$ система должна выбрать наиболее выгодный путь с меньшей свободной энергией, т.е. перейти к сингулярному несимметричному катеноиду, но это не так [7]. В отличие от случая симметричных рамок, когда у регулярного катеноида всегда была горловина, здесь участки ${{l}_{1}} \in (0,l_{{1,r}}^{\vartriangle }]$ пунктирных линий 3 фиг. 6а, 6б отвечают решению I для регулярного несимметричного катеноида (без горловины), фиг. 4а. Чтобы в таком катеноиде заставить пленку сойти с меньшей рамки, ее площадь необходимо увеличить. В соответствии с описанной в [7] двухэтапной схемой перестройка катеноида, первый этап перестройки – сход пленки с меньшей рамки – оказывается невыгоден системе, поскольку сопряжен с затратами энергии. В результате участкам ${{l}_{1}} \in (0,l_{{1,r}}^{\vartriangle }]$ пунктирных линий 3 фиг. 6а, 6б будет отвечать метастабильное состояние системы, и без дополнительных затрат энергии находиться в нем система может неограниченно долго.
Сценарий развития событий при дальнейшем увеличении l1 зависит от величины радиуса ${{R}_{{up}}}$ меньшей рамки. Для ${{R}_{{up}}} = 0.5$, см. фиг. 6а, система так и останется в состоянии “регулярный несимметричный катеноид с пленкой на меньшей рамке” вплоть до достижения l1 величины $l_{{1,r}}^{*}$. Для ${{R}_{{up}}} = 0.8$ картина совсем другая. Здесь значение ${{l}_{1}} = l_{{1,r}}^{\vartriangle }$ достигается раньше, чем ${{l}_{1}} = l_{{1,s}}^{*}$, см. фиг. 6б. Это значит, что целый отрезок ${{l}_{1}} \in [l_{{1,r}}^{\vartriangle },l_{{1,s}}^{*}]$ пунктирной линии 3 отвечает уже решению II для несимметричного регулярного катеноида (с горловиной), см. фиг. 4а. Поэтому первый этап перестройки регулярного катеноида в сингулярный – сход пленки с меньшей рамки в горловину – становится выгоден системе и такая перестройка имеет место. Следовательно, весь отрезок ${{l}_{1}} \in [l_{{1,r}}^{\vartriangle },l_{{1,s}}^{*}]$ пунктирной линии 3 отвечает неустойчивой конфигурации.
В результате, если менять расстояние между рамками l1, то увеличивая, то уменьшая его, можно добиться перестройки катеноида, причем перестройка регулярного в сингулярный будет происходить при значении ${{l}_{1}} = l_{{1,r}}^{\vartriangle }$, а обратная перестройка сингулярного катеноида в регулярный – при значении ${{l}_{1}} = l_{{1,s}}^{{\text{o}}}$, т.е. в перестройке катеноидов наблюдается гистерезис [7]. Очевидно, что такой гистерезис возможен не всегда, а только при условии $l_{{1,s}}^{{\text{o}}} < l_{{1,r}}^{\vartriangle } < l_{{1,s}}^{*}$.
На фиг. 7 приведены найденные в результате анализа системы (7.5)–(7.7) зависимости $l_{{1,s}}^{*}({{R}_{{up}}})$ – линия 1, $l_{{1,r}}^{\vartriangle }({{R}_{{up}}})$ – линия 2, и $l_{{1,s}}^{{\text{o}}}({{R}_{{up}}})$ – линия 3. В частности, найдено критическое значение ${{R}_{{up}}} \approx 0.641$, для которого $l_{{1,r}}^{\vartriangle } = l_{{1,s}}^{*}$. Соответственно гистерезис перестройки регулярного катеноида в сингулярный и обратно возможен только, если радиус меньшей рамки удовлетворяет условию ${{R}_{{up}}} > 0.641$. С точностью до обозначений это согласуется с результатами работы [7].
ЗАКЛЮЧЕНИЕ
Проведен полный анализ возможных перестроек конфигурации минимальной поверхности, образующейся на системе двух круглых соосных рамок разного радиуса. В частности, для разных конфигураций построены графики зависимости ее площади (поверхностной энергии) от расстояния между рамками. Только с привязкой к этим графикам выдвинутое в [7] предположение об метастабильности одной из конфигураций получает обоснование, а предложенное в [7] объяснение гистерезиса перестройки конфигураций катеноида приобретает ясный физический смысл. Использованная схема анализа на основе методов теории фильтрации аномальных жидкостей может быть распространена на случай некруглых и негладких рамок.
Работа выполнена за счет средств субсидии, выделенной в рамках государственной поддержки Казанского (Приволжского) федерального университета в целях повышения его конкурентоспособности среди ведущих мировых научно-образовательных центров (М.М.А.) и National Science Foundation IOS-1354956 (К.Г.К).
Список литературы
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. VI. Гидродинамика. М.: Наука, 1988. 736 с.
Plateau J. Statique experimentale et theorique des liquides soumis aux seules forees moleculaires. Paris: Gauthier-Villars, 1873.
Courant R. Dirichlet’s principle, conformal mapping, and minimal surfaces. New York: Dover Publications, 2005 = Курант Р. Принцип Дирихле, конформные отображения и минимальные поверхности. М.: Изд. иностр. лит-ры, 1953. 313 с.
Дао Чонг Тхи, Фоменко А.Т. Минимальные поверхности и проблема Плато. М.: Наука, 1987. 312 с.
Hoffman D., Meeks W.H. Minimal Surfaces Based on the Catenoid // The American Mathematical Monthly. Special Geometry Issue (Oct., 1990). V. 97. № 8. P. 702–730.
Arfken G.B., Weber H.J., Harris F.E. Mathematical Methods for Physicists. Amsterdam: r Elsevier Acad. Press, 2013.
Salkin L., Schmit A., Panizza P., Courbin L. Influence of boundary conditions on the existence and stability of minimal surfaces of revolution made of soap films // American J. Phys. 2014. V. 82. № 9. P. 839–849.
Alimov M.M., Kornev K.G. Meniscus on a shaped fibre: singularities and hodograph formulation // Proc. R. Soc. A. 2014. V. 470. P. 20140113.
Бернадинер М.Г., Ентов В.М. Гидродинамическая теория фильтрации аномальных жидкостей. М.: Наука, 1975. 199 с.
Новиков С.П., Фоменко А.Т. Элементы дифференциальной геометрии и топологии. М.: Наука, 1987. 432 с.
Соколовский В.В. О нелинейной фильтрации грунтовых вод // ПММ. 1949. Т. 13. Вып. 5. С. 525–536.
Lamb H. Hydrodynamics. Cambridge: Univ. Press, 1932 = Ламб Г. Гидродинамика. М.; Л.: Гостехиздат, 1947. 928 с.
Христианович С.А. Движение подземных вод, не следующее закону Дарси // ПММ. 1940. Т. 4. Вып. 1. С. 33–52.
Чаплыгин С.А. О газовых струях. М.; Л.: Гостехиздат, 1949. 160 с.
Алимов М.М., Корнев К.Г. Внешний мениск на тонком волокне с овоидальным профилем (случай полного смачивания) // Изв. РАН. МЖГ. 2017. № 4. С. 97–112.
Лаврентьев М.А., Шабат Б.В. Методы теории функции комплексного переменного. М.: Наука, 1973. 736 с.
Гуревич М.И. Теория струй идеальной жидкости. М.: Наука, 1979. 536 с.
Смирнов В.И. Курс высшей математики. Т. 1. М.: Наука, 1974. 479 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика жидкости и газа