Известия РАН. Механика жидкости и газа, 2019, № 1, стр. 58-67

ТОЧНОЕ РЕШЕНИЕ УРАВНЕНИЙ ОСЕСИММЕТРИЧНОГО ДВИЖЕНИЯ ВЯЗКОЙ ЖИДКОСТИ МЕЖДУ ПАРАЛЛЕЛЬНЫМИ ПЛОСКОСТЯМИ ПРИ ИХ СБЛИЖЕНИИ И РАЗДВИЖЕНИИ

А. Г. Петров^*

Институт проблем механики РАН им. А.Ю. Ишлинского
Москва, Россия

Поступила в редакцию 05.04.2018
После доработки 20.06.2018
Принята к публикации 20.06.2018

DOI: 10.1134/S0568528119010109

Аннотация

Исследуются точные решения уравнений Навье–Стокса в слое между параллельными пластинами, расстояние между которыми меняется по произвольному степенному закону. На границе пластин ставится условие прилипания. Точные решения уравнений Навье–Стокса строятся как ряды по степеням числа Рейнольдса. Подробно изучены случаи замедленного движения по закону квадратного корня из времени, равномерного движения и равномерно ускоренного движения плоскостей. Для первого случая ряды сходятся, в других случаях решение определяется с помощью асимптотических рядов. Определено критическое число Рейнольдса, соответствующее появлению противотока.

Ключевые слова: Уравнения Навье–Стокса, точные решения, движущиеся параллельно пластины, осевая симметрия

Рассматривается задача о нестационарном осесимметричном течении вязкой жидкости между двумя параллельными пластинами, расстояние между которыми меняется по степенному закону. Это естественное продолжение работ [1–3], где была решена плоская краевая задача. Нестационарные уравнения Навье–Стокса с некоторыми специальными подстановками сведены к системе обыкновенных дифференциальных уравнений. Его решения построены в виде рядов по степеням числа Рейнольдса.

В [4] обсуждается плоское и осесимметричное течения между двумя параллельными пластинами, где расстояние между пластинами изменяется во времени в соответствии со степенным законом: $h \sim {{t}^{{1/2}}}$. Исследование такого течения сведено к краевой задаче для обыкновенного дифференциального уравнения четвертого порядка, однако его решение не приводится.

В [5, 6] решаются аналогичные задачи плоского и осесимметричного течений между двумя пластинами также для случая, когда расстояние между пластинами изменяется по степенному закону: $h \sim {{t}^{{1/2}}}$. Решение сведено к построению ряда по степеням числа Рейнольдса ${\text{Re}} = h'h{\text{/}}\nu $.

Достаточно полный обзор точных решений краевых задач для уравнений Навье–Стокса представлен в [7].

В настоящей работе рассматривается более общая задача осесимметричного течения между двумя пластинами, когда расстояние между пластинами изменяется по степенному закону с произвольным степенным законом $h \sim {\text{|}}t{{{\text{|}}}^{s}}$. Кроме того, аналогично решению плоской задачи [3], уравнение краевой задачи упрощается до обыкновенного дифференциального уравнения третьего порядка и приводится полный анализ ее решения. Решение построено в виде ряда по степеням числа Рейнольдса. Подробно изучены случаи замедленных, устойчивых и равномерно ускоренных движений ($s = 0.5,1,2$). В частности, во всех рассмотренных случаях наблюдается эффект противотока.

1. ФОРМУЛИРОВКА КРАЕВОЙ ЗАДАЧИ

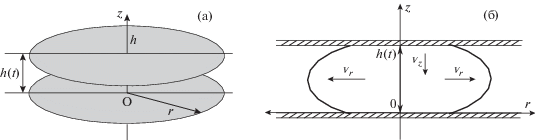
Рассматривается осесимметричное вязкое течение с компонентами скорости ${{v}_{r}}(t,r,z)$, ${{v}_{z}}(t,r,z)$ и давлением $p(t,r,z)$ в слое жидкости $0 < z < h$, $0 < r < \infty $ между двумя параллельными плоскостями. Нижняя плоскость z = 0 неподвижна, а верхняя движется по закону $h(t) \sim {\text{|}}t{{{\text{|}}}^{s}}$ (фиг. 1). Верхняя плоскость приближается к нижней, когда $h{\text{'}}(t) > 0$ и в случае $h'(t) < 0$ удаляется от нее.

Фиг. 1.

Геометрия задачи (а) и схема (б)осесимметричного течения жидкости между двумя пластинами (диски бесконечных радиусов $0 < r < \infty $, $0 < z < h$). Нижняя плоскость (z = 0) неподвижна, а верхняя ($z = h(t)$) движется к ней или от нее по произвольному степенному закону $h \sim {\text{|}}t{{{\text{|}}}^{s}}$

Запишем уравнения Навье–Стокса в цилиндрической системе координат для осесимметричного течения с условиями прилипания

(1.1)

$\begin{array}{*{20}{c}} {\frac{{{{v}_{r}}}}{r} + \frac{{\partial {{v}_{r}}}}{{\partial r}} + \frac{{\partial {{v}_{z}}}}{{\partial z}} = 0} \\ {\frac{{\partial {{v}_{r}}}}{{\partial t}} + {{v}_{r}}\frac{{\partial {{v}_{r}}}}{{\partial r}} + {{v}_{z}}\frac{{\partial {{v}_{r}}}}{{\partial z}} + \frac{{\partial p}}{{\partial r}} = \nu \left( {\frac{{{{\partial }^{2}}{{v}_{r}}}}{{\partial {{r}^{2}}}} + \frac{1}{r}\frac{{\partial {{v}_{r}}}}{{\partial r}} + \frac{{{{\partial }^{2}}{{v}_{r}}}}{{\partial {{z}^{2}}}} - \frac{{{{v}_{r}}}}{{{{r}^{2}}}}} \right)} \\ {\frac{{\partial {{v}_{z}}}}{{\partial t}} + {{v}_{r}}\frac{{\partial {{v}_{z}}}}{{\partial r}} + {{v}_{z}}\frac{{\partial {{v}_{z}}}}{{\partial z}} + \frac{{\partial p}}{{\partial z}} = \nu \left( {\frac{{{{\partial }^{2}}{{v}_{z}}}}{{\partial {{r}^{2}}}} + \frac{1}{r}\frac{{\partial {{v}_{z}}}}{{\partial r}} + \frac{{{{\partial }^{2}}{{v}_{z}}}}{{\partial {{z}^{2}}}}} \right)} \\ {{{v}_{r}}(t,r,0) = {{v}_{r}}(t,r,h) = 0,\quad {{v}_{z}}(t,r,0) = 0,\quad {{v}_{z}}(t,r,h) = h'} \end{array}$

где $\nu $ – коэффициент кинематической вязкости; плотность жидкости принимается за единицу (ρ = 1). Решение задачи (1.1) ищем в виде, аналогичном решению плоской задачи [3]:

(1.2)

$\begin{array}{*{20}{c}} {{{v}_{r}} = \frac{{h'}}{h}rU(\eta ,{\text{Re}}),\quad {{v}_{z}} = h'V(\eta ,{\text{Re}}),\quad {\text{Re}} = hh'{\text{/}}\nu } \\ {p = \mathop {h'}\nolimits^2 \left[ {b\frac{{{{r}^{2}}}}{{2{{h}^{2}}}} + P(t,\eta )} \right] + {{p}_{0}}(t),\quad \eta = \frac{z}{h},\quad \eta \in (0,1)} \end{array}$

При заменах (1.2) уравнения Навье–Стокса (1.1) будут сведены к новой форме, которые упрощают построение точных решений уравнений Навье–Стокса (1.1). Для степенного закона движения $h(t)$ число Рейнольдса зависит от времени, ${\text{Re}} = hh'{\text{/}}\nu $, и эта зависимость должна учитываться при вычислении частных производных по времени в уравнении (1.1)

(1.3)

$\begin{array}{*{20}{c}} {\frac{{\partial {{v}_{r}}}}{{\partial t}} = \frac{{\mathop {h'}\nolimits^2 }}{{{{h}^{2}}}}r\left( { - \eta U{\text{'}} - aU + (2 - a){\text{Re}}\frac{{\partial U}}{{\partial {\text{Re}}}}} \right)} \\ {\frac{{\partial {{v}_{z}}}}{{\partial t}} = \frac{{\mathop {h'}\nolimits^2 }}{h}\left( {(1 - a)V - \eta V{\text{'}} + (2 - a){\text{Re}}\frac{{\partial V}}{{\partial {\text{Re}}}}} \right)} \end{array}$

Здесь штрихом обозначена производная по переменной $\eta $, а параметр $a = 1 - h{\text{''}}h{\text{/}}h{{{\text{'}}}^{2}} = 1{\text{/}}s$ является постоянным числом.

После подстановки (1.2) в первые два уравнения Навье–Стокса (1.1) с учетом уравнений (1.3) мы приходим к следующей краевой задаче для системы обыкновенных дифференциальных уравнений с неизвестными функциями $U(\eta ),V(\eta )$

(1.4)

$\begin{array}{*{20}{c}} {2U + V{\text{'}} = 0} \\ { - \;aU - \eta U{\text{'}} + {{U}^{2}} + VU{\text{'}} + b - \frac{1}{{Re}}U{\text{''}} + (2 - a){\text{Re}}\frac{{\partial U}}{{\partial {\text{Re}}}} = 0} \\ {U(0) = V(0) = 0,\quad U(1) = 0,\quad V(1) = 1} \\ {a = 1 - \frac{{h{\text{''}}h}}{{\mathop {h'}\nolimits^2 }},\quad {\text{Re}}(t) = \frac{{hh'}}{\nu }} \end{array}$

В выражение для $a$ входит зависимость расстояния $h$ от времени согласно степенному закону, с произвольной степенью $s$. Число Рейнольдса все еще зависит от времени. Таким образом, получаем

(1.5)

$h = k{\text{|}}t - {{t}_{0}}{{{\text{|}}}^{s}},\quad a = \frac{1}{s},\quad {\text{Re}}(t) = \frac{1}{\nu }s{{k}^{2}}{\text{|}}t - {{t}_{0}}{{{\text{|}}}^{{2s - 1}}}{\text{sign}}(t - {{t}_{0}})$

где k – произвольная постоянная в степенном законе. Без потери общности предполагается, что ${{t}_{0}} = 0$. Следует заметить, что $t$ может быть отрицательным. Система уравнений (1.4) имеет третий порядок, поэтому четыре граничных условия в (1.4) вместе с законом движения пластин позволяют найти функции $U(\eta ),V(\eta )$ и параметр b, определяющий давление. Условие Re > 0 соответствует увеличению зазора между пластинами, а Re < 0 – уменьшению.

Третье уравнение Навье–Стокса (1.1) после подстановки (1.2) принимает вид

$(1 - a)V - \eta V{\text{'}} + VV{\text{'}} - \frac{1}{{Re}}V{\text{''}} + \frac{{dP(t,\eta )}}{{d\eta }} + (2 - a){\text{Re}}\frac{{\partial V}}{{\partial {\text{Re}}}} = 0$

Отсюда находится функция $P(t,\eta )$, определяющая давление:

(1.6)

$P = (a - 2)\int\limits_0^\eta {\left( {V - {\text{Re}}\frac{{\partial V}}{{\partial {\text{Re}}}}} \right)} d\eta + \eta V - \frac{{{{V}^{2}}}}{2} + \frac{1}{{{\text{Re}}}}V'(\eta )$

С помощью подстановок

(1.7)

$\eta = \frac{1}{2}(Y + 1),\quad U = - \frac{1}{2} + u,\quad V = \eta + \frac{1}{2}v$

для функций $u(Y)$, $v(Y)$, $Y \in ( - 1,1)$ получаем систему обыкновенных дифференциальных уравнений

(1.8)

$\begin{array}{*{20}{c}} {2u + v{\text{'}} = 0} \\ {vu{\text{'}} + {{u}^{2}} - (1 + a)u + \frac{1}{4} + \frac{a}{2} + b - \frac{{4u''}}{{Re}} + (2 - a){\text{Re}}\frac{{\partial u}}{{\partial {\text{Re}}}} = 0} \end{array}$

с условиями на границе

(1.9)

$u( - 1) = u(1) = \frac{1}{2},\quad v( - 1) = v(1) = 0$

Штрихом обозначена производная по Y. Размерные компоненты скорости жидкости выражаются через $u$ и $v$

(1.10)

$\begin{array}{*{20}{c}} {{{v}_{r}} = \frac{{h'}}{h}r\left( {u(Y,{\text{Re}}) - \frac{1}{2}} \right),\quad {{v}_{z}} = \frac{{h'}}{2}(Y + 1 + v(Y,{\text{Re}})),\quad Y = 2\frac{z}{h} - 1} \end{array}$

Формулировка краевой задачи (1.8), помимо граничных условий, должна включать и начальное условие, определенное для некоторого Re. Решение начально-краевой задачи здесь не рассматривается. Целью последующего исследования является построение семейства частных решений уравнений (1.8) в виде рядов по степеням числа Рейнольдса.

2. РАЗЛОЖЕНИЯ ПО СТЕПЕНЯМ ЧИСЛА РЕЙНОЛЬДСА

Сформулируем краевую задачу (1.8) и (1.9) в виде одного уравнения для $v(Y,{\text{Re}})$ с граничными условиями

(2.1)

$\begin{array}{*{20}{c}} { - vv{\text{''}} + \frac{{{{{(v')}}^{2}}}}{2} + (1 + a)v{\text{'}} + c + \frac{{4v{\text{'''}}}}{{{\text{Re}}}} + (a - 2){\text{Re}}\frac{{\partial v{\text{'}}}}{{\partial {\text{Re}}}} = 0} \\ {v( - 1) = v(1) = 0,\quad v{\text{'}}( - 1) = v'(1) = - 1} \end{array}$

где $c = 1{\text{/}}2 + a + 2b$. Для малого числа Рейнольдса решение этой краевой задачи может быть найдено в виде следующего ряда:

(2.2)

$\begin{array}{*{20}{c}} {c = \frac{1}{{{\text{Re}}}}{{c}_{{ - 1}}} + {{c}_{0}} + {\text{Re}}{{c}_{1}} + ...} \\ {v = {{v}_{0}} + {\text{Re}}{{v}_{1}} + {\text{R}}{{{\text{e}}}^{2}}{{v}_{2}} + ...} \end{array}$

Откуда находим

${\text{Re}}\frac{{\partial v{\text{'}}}}{{\partial {\text{Re}}}} = {\text{Re}}v_{1}^{'} + 2{\text{R}}{{{\text{e}}}^{2}}v_{2}^{'} + ...$

Из (2.1) и (2.2) следует

(2.3)

${{c}_{{ - 1}}} = 12,\quad {{v}_{0}}(Y) = \frac{1}{2}Y(1 - {{Y}^{2}})$

Формулы для пары следующих ${{c}_{n}}$ и ${{v}_{n}}$ приведены в приложении A .

Из (2.2) коэффициент давления $b = (c - a){\text{/}}2 - 1{\text{/}}4$ найден в виде ряда по числу Рейнольдса

(2.4)

$\begin{array}{*{20}{c}} {b = \frac{{{{b}_{{ - 1}}}}}{{{\text{Re}}}} + {{b}_{0}} + {{b}_{1}}{\text{Re}} + {{b}_{2}}{\text{R}}{{{\text{e}}}^{2}} + ...} \\ {{{b}_{{ - 1}}} = {{c}_{{ - 1}}}{\text{/}}2,\quad {{b}_{0}} = ({{c}_{0}} - a - 0.5){\text{/}}2,\quad {{b}_{1}} = {{c}_{1}}{\text{/}}2,\quad {{b}_{2}} = {{c}_{2}}{\text{/}}2, \ldots } \end{array}$

Каждый коэффициент ${{b}_{n}}(a)$ является многочленом степени n + 1 параметра a с рациональными коэффициентами.

Очевидно, что решение краевой задачи (2.1) зависит от времени только через число Рейнольдса.

Аналогично [3], самые интересные случаи движения верхней плоскости соответствуют значениям: a = 2 (расстояние между плоскостями $h$ меняется по закону $h = k\sqrt {{\text{|}}t{\text{|}}} $); a = 1 (равномерное изменение расстояния $h = k{\text{|}}t{\text{|}}$); $a = 1{\text{/}}2$ (равноускоренное изменение расстояния $h = k{{t}^{2}}$).

3. СЛУЧАЙ a = 2. РАССТОЯНИЕ МЕЖДУ ПЛОСКОСТЯМИ МЕНЯЕТСЯ ПО ЗАКОНУ $h = k\sqrt {{\text{|}}t{\text{|}}} $

В случае a = 2 расстояние между пластинами изменяется как $h = k\sqrt {{\text{|}}t - {{t}_{0}}{\text{|}}} $. Заметим, что если Re < 0, то $t < {{t}_{0}}$. Частная производная по числу Рейнольдса в уравнение (2.1) не входит. Таким образом, мы приходим к краевой задаче для обыкновенных дифференциальных уравнений, которая легко решается численно

(3.1)

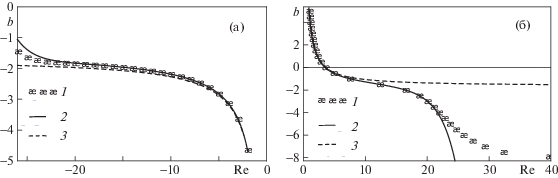
$\begin{array}{*{20}{c}} { - vv{\text{''}} + \frac{{{{{(v{\text{'}})}}^{2}}}}{2} + 3v{\text{'}} + c + \frac{4}{{Re}}v{\text{'''}} = 0,\quad c = 2.5 + 2b} \\ {v( - 1) = v(1) = 0,\quad v{\text{'}}( - 1) = v{\text{'}}(1) = - 1} \end{array}$

Задача (3.1) может быть решена численно, методом, описанным в [2]. Для заданного числа ${\text{Re}}$ этот метод позволяет определить параметр c и функцию $v(Y)$. Фиг. 2 показывает зависимости $b({\text{Re}})$, найденные из численного решения задачи (точки 1) и приблизительно с помощью частичной суммы 17 членов ряда (2.4) (сплошные линии 2), и асимптотическое решение $b = 6{\text{/Re}} - 117{\text{/}}70$ (штриховые линии 3).

Фиг. 2.

Зависимости коэффициента давления $b({\text{Re}},a)$ в уравнении (1.2) от числа Рейнольдса: – численные решения, – решение в виде ряда $b = \sum\nolimits_{n = - 1}^N {{b}_{n}}{\text{R}}{{{\text{e}}}^{n}}$ из 17 членов (N = 15), – двухчленное разложение $b = 6{\text{/Re}} - 117{\text{/}}70$; (а) Re < 0, (б) Re > 0; a = 2

Первые 17 членов ряда b (2.4) перечислены в таблице 1 приложения Б. Радиус сходимости этого ряда бесконечен.

Для появления противотока критическое число Рейнольдса (${\text{R}}{{{\text{e}}}_{{back}}}$) можно найти как корень уравнения [3]

(3.2)

${{\left. {\frac{{\partial u}}{{\partial Y}}} \right|}_{{Y = 1,{\text{Re}} = {\text{R}}{{{\text{e}}}_{{back}}}}}} = 0$

Таблица 1.

n	b_n (a = 2) Reⁿ	b_n (a = 1) Reⁿ	b_n (a = 0.5) Reⁿ
−1	6Re⁻¹	6Re⁻¹	6Re⁻¹
0	−1.67143Re⁰	−1.07143Re⁰	−7.71429 × 10⁻¹Re⁰
1	−1.20439 × 10⁻²Re¹	−5.13915 × 10⁻³Re¹	−2.75819 × 10⁻³Re¹
2	−5.07318 × 10⁻⁴Re²	−8.18858 × 10⁻⁵Re²	−1.6704 × 10⁻⁵Re²
3	−2.24626 × 10⁻⁵Re³	−8.55423 × 10⁻⁷Re³	4.78493 × 10⁻⁸Re³
4	−9.99064 × 10⁻⁷Re⁴	−3.79077 × 10⁻⁹Re⁴	−6.64576 × 10⁻¹⁰Re⁴
5	−4.42352 × 10⁻⁸Re⁵	2.90881 × 10⁻¹¹Re⁵	6.09809 × 10⁻¹¹Re⁵
6	−1.94616 × 10⁻⁹Re⁶	3.64733 × 10⁻¹³Re⁶	−6.06048 × 10⁻¹²Re⁶
7	−8.50400 × 10⁻¹¹¹Re⁷	5.75514 × 10⁻¹⁵Re⁷	7.12402 × 10⁻¹³Re⁷
8	−3.68935 × 10⁻¹²Re⁸	−2.82184 × 10⁻¹⁶Re⁸	−9.65286 × 10⁻¹⁴Re⁸
9	1.58827 × 10⁻¹³Re⁹	2.53429 × 10⁻¹⁷Re⁹	1.47967 × 10⁻¹⁴Re⁹
10	−6.77982 × 10⁻¹⁵Re¹⁰	−2.63842 × 10⁻¹⁸Re¹⁰	−2.53226 × 10⁻¹⁵Re¹⁰
11	−2.86668 × 10⁻¹⁶Re¹¹	3.0351 × 10⁻¹⁹Re¹¹	4.78819 × 10⁻¹⁶Re¹¹
12	−1.19901 × 10⁻¹⁷Re¹²	−3.85162 × 10⁻²⁰Re¹²	−9.91821 × 10⁻¹²Re¹²
13	−4.95195 × 10⁻¹⁹Re¹³	−3.85162 × 10⁻²¹Re¹³	2.23432 × 10⁻¹⁷Re¹³
14	−2.01471 × 10⁻²⁰Re¹⁴	−8.06329 × 10⁻²²Re¹⁴	−5.44013 × 10⁻¹⁸Re¹⁴
15	−8.04837 × 10⁻²²Re¹⁵	1.31318 × 10⁻²²Re¹⁵	1.4239 × 10⁻¹⁵Re¹⁵

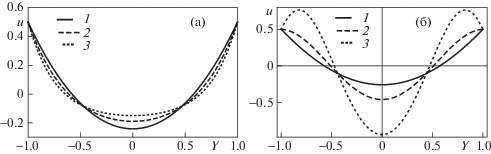
В рассматриваемом случае ($a = 2,s = 1{\text{/}}2$) число Рейнольдса не зависит от времени: Re = = ${{k}^{2}}{\text{/}}(2\nu ){\text{sign}}(t - {{t}_{0}})$ и соответственно профиль скорости сохраняет свою форму в течение всего времени движения пластины. Профили скоростей при отрицательных и положительных значениях числа Рейнольдса изображены на фиг. 3.

Фиг. 3.

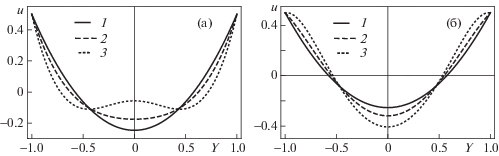
Профиль скорости $u(Y) = \sum\nolimits_{n = 0}^{15} {{u}_{n}}{\text{R}}{{{\text{e}}}^{n}}$ соответствующий компоненте скорости ${{v}_{r}}$ (1.10), a = 2: для раздвижения (а) ${\text{Re}} = - 1(1), - 10(2), - 21(3)$ и сближения (б) ${\text{Re}} = 1(1),13(2),20(3)$ плоскостей $Y = \pm 1$

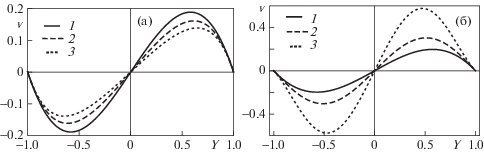
На фиг. 4 показаны профили скорости $v(Y)$, найденные из серии решений $\sum\nolimits_{n = 0}^N {{v}_{n}}(Y,a){\text{R}}{{{\text{e}}}^{n}}$, N = 15. Числа Рейнольдса соответствуют увеличению (Re < 0) и уменьшению (Re > 0) расстояния между плоскостями.

Фиг. 4.

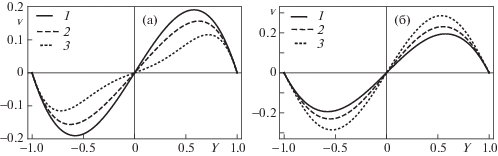
Поперечная скорость $v(Y) = \sum\nolimits_{n = 0}^{15} {{v}_{n}}{\text{R}}{{{\text{e}}}^{n}}$ соответствующая ${{v}_{z}}$ (1.10), $a = 2$: при увеличении (а) ${\text{Re}} = - 1(1), - 10(2), - 21(3)$ и уменьшения ${\text{Re}} = 1(1),13(2),20(3)$ расстояния между плоскостями

Видно, что для положительных чисел Рейнольдса, больше критических (${\text{Re}} > {\text{R}}{{{\text{e}}}_{{back}}} \approx 20$), скорость $u$ вблизи границ $Y = \pm 1$ имеет относительно средней скорости противоположное направление, что означает, что вблизи границы появляется противоток. Однако при большом отрицательном числе Рейнольдса (${\text{Re}} < - 21$) течение сохраняет исходное направление; встречного течения не наблюдается. Таким образом, можно сделать вывод, что встречный поток возникает только при движении пластины с положительными числами Рейнольдса ${\text{Re}} > {\text{R}}{{{\text{e}}}_{{back}}}$, т.е. только при увеличении расстояния между пластинами.

4. СЛУЧАЙ РАВНОМЕРНОГО ДВИЖЕНИЯ ПЛОСКОСТИ $h = k{\text{|}}t{\text{|}}$

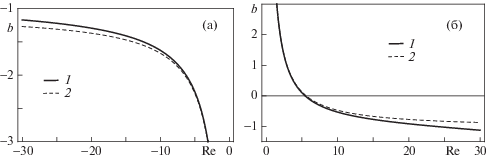
В случае $a = 1$ уравнения (2.1) и их последовательные решения (2.2) соответствуют изменению расстояния между пластинами по закону $h = k{\text{|}}t{\text{|}}$. Этот случай отличается от предыдущего: уравнения Навье–Стокса не могут быть сведены к обыкновенному дифференциальному уравнению, как это было сделано в предыдущем случае, и автомодельных решений этой задачи не существует. Ряд b(Re) при a = 1 расходится, но является асимптотическим, см. [3]. Зависимости b(Re) для положительных и отрицательных чисел Рейнольдса показаны на фиг. 5.

Фиг. 5.

Зависимости b(Re) при Re < 0 (а) и Re > 0 (б): – серия решений $b({\text{Re}},a)$ с 11 членами (N = 9), – двухчленные разложения $b = 6{\text{/Re}} - 15{\text{/}}14$; а=1

Для лучшей аппроксимации зависимости b(Re) асимптотическим рядом нужно взять N, равное значению, при котором выражение ${{b}_{N}}{\text{R}}{{{\text{e}}}^{N}}$ минимально. Оно зависит от числа Рейнольдса Re. Например, для случая, рассматриваемого здесь ($a = 1$) при ${\text{Re}} = 10,20$ и 30, минимум выражения ${{b}_{N}}{\text{R}}{{{\text{e}}}^{N}}$ достигается при $N = 9,8$ и 7 соответственно (см. таблицу в приложении Б). Для асимптотических рядов погрешность аппроксимации b(Re) частичной суммой $b = \sum\nolimits_{n = - 1}^N {{b}_{n}}{\text{R}}{{{\text{e}}}^{n}}$ имеет тот же порядок следующего отброшенного члена ряда, т.е. $b = \sum\nolimits_{n = - 1}^N {{b}_{n}}{\text{R}}{{{\text{e}}}^{n}} \pm {{b}_{{N + 1}}}{\text{R}}{{{\text{e}}}^{{N + 1}}}$.

Критическое число Рейнольдса ${\text{R}}{{{\text{e}}}_{{back}}}$, найденное из уравнения (3.2), таково ${\text{R}}{{{\text{e}}}_{{back}}} \approx 26.5$ (N = 11). Числа членов $N$ в выражении $u_{n}^{'}(Y = 1,a = 1){\text{R}}{{{\text{e}}}^{n}}$ при Re = 10, Re = 20 и Re = 30 равны 11, 7 и 5 соответственно.

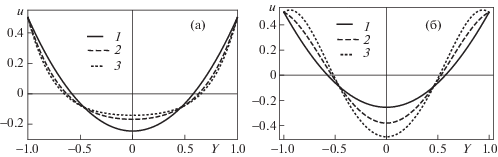
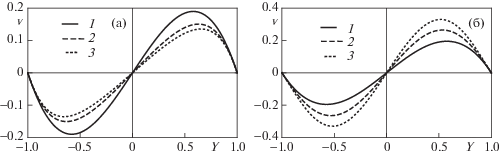
На фиг. 6 и 7 изображены профили скорости $u(Y)$, $v(Y)$ при движении верхней пластины по закону $h = k{\text{|}}t{\text{|}}$ в моменты времени, соответствующие числам Рейнольдса $ \pm 1,\; \pm 21,\; \pm 35$. Другими словами, кривые на указанных фигурах демонстрируют эволюции во времени профилей скорости при раздвижении и сближении пластин. Они были построены с использованием сумм с числами членов, равных 15, 11, 7 соответственно.

Фиг. 6.

Зависимости $u(Y) = \sum\nolimits_{n = 0}^N {{u}_{n}}{\text{R}}{{{\text{e}}}^{n}}$ ($N = 11,$, 7, 5) соответствующие компоненте скорости ${{v}_{r}}$ (1.10) при $a = 1$ и увеличении (а) ${\text{Re}} = - 1, - 21, - 35$ и уменьшении (б) ${\text{Re}} = 1,21,35$ расстояния между плоскостями (–3)

Фиг. 7.

Зависимости $v(Y) = \sum\nolimits_{n = 0}^N {{v}_{n}}{\text{R}}{{{\text{e}}}^{n}}$ (N = 15, 11, 7) соответствующие компоненте скорости ${{v}_{z}}$ (1.10) при $a = 1$ и увеличении (а) ${\text{Re}} = - 1, - 21, - 35$ (–3) и уменьшении (б) ${\text{Re}} = 1,21,35$ (–3) расстояния между плоскостями

5. СЛУЧАЙ РАВНОУСКОРЕННОГО ДВИЖЕНИЯ ПЛАСТИНЫ $h = k{{t}^{2}}$

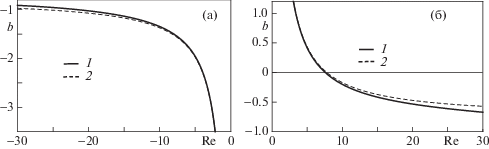
При a = 0.5 уравнения (2.1) и их последовательные решения (2.2) соответствуют равномерно ускоренному движению верхней пластины $h = k{{t}^{2}}$. Этот случай аналогичен случаю a = 1. Ряд с коэффициентами b_n, представленными в третьем столбце таблицы, также расходится. Слагаемые ${\text{|}}{{b}_{n}}{\text{R}}{{{\text{e}}}^{n}}{\text{|}}$ уменьшаются в абсолютном значении до минимального значения. Его номер N зависит от числа Рейнольдса. При Re = 10, 20 и 30 значения $N = 6,4$ и 4, потом с ростом ${\text{Re}}$ они растут. Таким образом, при исследовании данного случая будем использовать частичную сумму 7 слагаемых (N = 5). Зависимости b(Re) при положительных и отрицательных числах Рейнольдса показаны на фиг. 8. Напомним, что эти графики не изменяются, если число слагаемых, используемых в расчете, изменяется на 2 ($N \pm 2$); однако после Re = 30 разница заметна.

Фиг. 8.

Зависимость b(Re) для Re < 0 (а) и Re > 0 (б): – ряд $b({\text{Re}},a)$ состоящий из 7 членов (N = 5); – двухчленное разложение $b = 6{\text{/Re}} - 27{\text{/}}35$; $a = 0.5$

Количество членов ряда $u'$ для Re = 10, 20, 30 равно 7, 5 и 4 соответственно. Критическое число Рейнольдса ${\text{R}}{{{\text{e}}}_{{back}}}$ находится так же, как это было сделано в разделе 4 из уравнения (3.2) c 6-тью членами ($N = 5$) и равно ${\text{R}}{{{\text{e}}}_{{back}}} \approx 43.5$.

Профили скоростей $u(Y)$ и $v(Y)$ для некоторых чисел Рейнольдса показаны на фиг. 9 и фиг. 10. Видно, что для чисел Рейнольдса, больших критических ${\text{Re}} = 48 > {\text{R}}{{{\text{e}}}_{{back}}}$, при раздвижении плоскостей появился противоток вблизи плоскостей. Также при приближении пластин в центре зазора наблюдается умеренное снижение скорости. Ошибка для профиля скорости ${{u}_{4}}{\text{/}}{{u}_{0}}$ (Re = 48), меньше 1%.

Фиг. 9.

Профили скорости $u(Y) = \sum\nolimits_{n = 0}^N {{u}_{n}}{\text{R}}{{{\text{e}}}^{n}}$ ($N = 14$, 3, 3) соответствующие ${{v}_{r}}$ (1.10): при раздвижении (a) ${\text{Re}} = - 1, - 20, - 48$ (–3) и сближении (б) (${\text{Re}} = 1,20,48$) (–3) плоскостей; a = 0.5

Фиг. 10.

Поперечная скорость $v(Y) = \sum\nolimits_{n = 0}^N {{v}_{n}}{\text{R}}{{{\text{e}}}^{n}}$ ($N = 14$, 3, 3) соответствующая ${{v}_{z}}$ (1.10) для a = 0.5: при раздвижении (а) ${\text{Re}} = - 1, - 20, - 48$ (–3) и сближении (б) ${\text{Re}} = 1,20,48$ (–3) плоскостей

6. ОБСУЖДЕНИЕ

Рассматривается задача о вязком осесимметричном сжатии между двумя параллельными плоскостями (дисками с бесконечным радиусом). Одна плоскость неподвижна, в то время как другая приближается или движется от нее так, что расстояние между плоскостями изменяется в соответствии со степенным законом $h \sim {\text{|}}t{{{\text{|}}}^{S}}$, где s – произвольный индекс.

Целью исследования является определение течения между пластинами. Сформулирована краевая задача с реализацией условий скольжения на пластинах (1.1). При изменении переменных исходные уравнения Навье–Стокса были сведены к уравнению в частных производных третьего порядка с двумя переменными ($u$, $v$), которые вместе с граничными условиями образуют новую краевую задачу (1.8), (1.9). Были построены множество частных решений в виде рядов по степеням числа Рейнольдса.

Аналогично [1–3] в случае $s = 1{\text{/}}2$ начальная задача была сведена к обыкновенному дифференциальному уравнению (3.1), что позволило легко определить решение численными методами (см. фиг. 2). В этом случае решение в виде ряда по степеням числа Рейнольдса сходится с бесконечным радиусом сходимости. Построены профили скоростей для этого случая (фиг. 3 и 4 ).

Для других исследуемых показателей ($s = 1,2$) ряды решений были асимптотическими. Для наилучшего приближения ряда в этих случаях были предложены частичные суммы асимптотического ряда с определенным числом членов (см. фиг. 5, 8 ). Также для этих случаев были построены профили скорости потока между пластинами (см. фиг. 6, 7, 9, 10 ).

Обнаружен эффект противотока при раздвигании пластин, скорость потока вблизи поверхности пластин имеет противоположное направление относительно средней скорости между ними. Встречный поток произойдет, когда число Рейнольдса превысит критическое значение ${\text{Re}} \geqslant {\text{R}}{{{\text{e}}}_{{back}}}$, а ${\text{R}}{{{\text{e}}}_{{back}}}$ было определено для различных режимов движения верхней пластины. Теоретические числа Рейнольдса для наблюдения эффекта противотока следующие: для $s = 1{\text{/}}2$, ${\text{R}}{{{\text{e}}}_{{back}}} \approx 13.4$ (см. фиг. 3б), для s = 1, ${\text{R}}{{{\text{e}}}_{{back}}} \approx 26.5$ (см. фиг. 6б), и для s = 2, ${\text{R}}{{{\text{e}}}_{{back}}} \approx 43.5$ (см. фиг. 9б).

Несмотря на то что для осесимметричной и плоской задач использовались аналогичные методы решения, решения отличаются качественно. В случае плоского течения существует несколько непрерывных семейств решений (несколько кривых b(Re), удовлетворяющих начальным уравнениям). В настоящем исследовании существует только одно семейство решений (одна кривая b(Re), удовлетворяющая начальным уравнениям). Кроме того, осесимметричный поток более реалистичен и легче воспроизводится в лабораторных экспериментах.

ЗАКЛЮЧЕНИЕ

Исходные уравнения Навье–Стокса сведены к уравнению в частных производных третьего порядка с двумя переменными ($u$, $v$), которые вместе с граничными условиями образуют новую краевую задачу (1.8), (1.9). Построены множество частных решений в виде рядов по степеням числа Рейнольдса.

Работа выполнена при финансовой поддержке РФФИ, проект 17–01–00901 и по теме гос. задания (№ госрегистрации АААА-А17-117021310382-5).

ПРИЛОЖЕНИЕ А. РАЗЛОЖЕНИЯ ДЛЯ КОМПОНЕНТ ${{v}_{n}}$ и ${{c}_{n}}$

Размерные компоненты скорости среды ${{v}_{r}}(t,r,z)$, ${{v}_{z}}(t,r,z)$ выражаются через $u(Y)$ и $v(Y)$, см. (1.10), где $v$ рассчитывается по (2.2) и $u = - 0.5dv{\text{/}}dY$. Компоненты ${{c}_{0}}$ и ${{v}_{1}}$ вычисляются из краевой задачи второго порядка:

$\begin{array}{*{20}{c}} { - {{v}_{0}}{{v}_{0}}{\text{''}} + \frac{1}{2}{{{({{v}_{0}}{\text{'}})}}^{2}}(a + 1){{v}_{0}}{\text{'}} + {{c}_{0}} + 4{{v}_{1}}{\text{'''}} = 0} \\ {{{v}_{1}}( - 1) = {{v}_{1}}(1) = 0,\quad v_{1}^{'}( - 1) = v_{1}^{'}(1) = 0} \end{array}$

его решение имеет вид

${{c}_{0}} = - \frac{{( - 31 - 14a)}}{{70}}\quad {{v}_{1}}(Y) = - \frac{{Y{{{({{Y}^{2}} - 1)}}^{2}}}}{{2240}}(9 + 14a + {{Y}^{2}})$

Коэффициент ${{c}_{1}}$ и компонент скорости ${{v}_{2}}$ вычисляются из краевой задачи (2.1) следующего порядка. Они имеют вид:

$\begin{array}{*{20}{c}} {{{c}_{1}} = - \frac{{( - 353 - 847a - 462{{a}^{2}})}}{{161\,\,700}},\quad {{v}_{2}}(Y) = - \frac{{Y{{{({{Y}^{2}} - 1)}}^{2}}}}{{248\,\,\,371\,\,200}} \times } \\ { \times \;(3696{{a}^{2}}( - 11 + 5{{Y}^{2}}) + 77a( - 39 - 122{{Y}^{2}} + 65{{Y}^{4}}) + 2(7785 - 6121{{Y}^{2}} + 763{{Y}^{4}} + 189{{Y}^{6}})).} \end{array}$

ПРИЛОЖЕНИЕ Б. КОЭФФИЦИЕНТЫ ${{b}_{n}}(a)$ СЕРИИ $b({\text{Re}},a)$ ДЛЯ РАЗЛИЧНЫХ ЗНАЧЕНИЙ ПАРАМЕТРА $a$

В таблице представлены слагаемые ${{b}_{n}}(a){\text{R}}{{{\text{e}}}^{n}}$ ряда $b({\text{Re}},a)$ (2.4) при $a = 0.5,1,2$. Подчеркнутые слагаемые – минимальные по абсолютной величине слагаемые при Re = 10. Ряды серий $b({\text{Re}},a)$ для a = 1 и 0.5 являются асимптотическими расходящимися рядами. Достаточно точное приближение аналитических функций такими рядами возможно. Для наилучшего приближения функции необходимо взять N – членов, так что при этом значении N – слагаемое ${\text{|}}{{b}_{n}}{\text{R}}{{{\text{e}}}^{n}}{\text{|}}$ – минимально. Число N зависит от Re; подчеркнутые члены таблицы минимальны для Re = 10. Для больших Re минимальными слагаемыми члены имеют меньший порядковый номер N. Таким образом, для наилучшего приближения коэффициента давления b и компонент скорости ($u,v$) для малых чисел Рейнольдса необходимо взять большое число членов асимптотических рядов, а для больших чисел Re достаточно нескольких коэффициентов. Ошибка аппроксимации частичной суммы имеет тот же порядок, что и член, следующий за минимальным, т.е. b = $\sum\nolimits_{n = - 1}^N {{b}_{n}}{\text{R}}{{{\text{e}}}^{n}}\, \pm \,{{b}_{{N + 1}}}{\text{R}}{{{\text{e}}}^{{N + 1}}}$.

Список литературы

Петров А.Г. Точное решение уравнений Навье–Стокса в слое жидкости между движущимися параллельно пластинами // ПМТФ. 2012. Т. 53. № 5. С. 13–18. = Petrov A.G. Exact solution of the Navier-Stokes equations in a fluid layer between the moving parallel plates // J. Appl. Mech. and Tech. Physics. 2012. V. 53. P. 642–646.
Петров А.Г. О точных и асимптотических решениях уравнений Навье–Стокса в слое жидкости между сближающимися и удаляющимися пластинами // ИЗВ. РАН. МЖГ. 2014. № 2. С. 44–57. Petrov A.G. Exact and Asymptotic Solutions of the Navier-Stokes Equations in a Fluid Layer between Plates Approaching and Moving Apart from One Another // Fluid Dynamics. 2014. V. 49. P. 174–187.
Petrov A.G., Kharlamova I.S. The solutions of Navier–Stokes equations in squeezing flow between parallel plates // Europ. J. of Mechanics B-Fluids. 2014. V. 48. P. 40–48.
Thorpe J.F. Further Investigation of Squeezing Flow Between Parallel Plates // Develop. in Theor. and Appl. Mech. 1967. V. 3. P. 635–648.
Wang C.Y., Watson L.T. Squeezing of a Viscous Fluid Between Elliptic Plates // Appl. Scient. Res. 1979. V. 35. P. 195–207.
Wang C.Y. Exact solution of the steady Navier–Stokes equations // Annu. Rev. Fluid Mech. 1991. V. 23. P. 159–177.
Пухначев В.В. Симметрии в уравнениях Навье–Стокса // Успехи механики. 2006. Т. 4. № 1. С. 6–76.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал