Известия РАН. Механика жидкости и газа, 2019, № 1, стр. 17-35

Волновое движение в ледяном покрове с трещиной при равномерном движении нагрузки

Л. А. Ткачева^a, *

^a Институт гидродинамики им. М.А. Лаврентьева СО РАН
Новосибирск, Россия

Поступила в редакцию 14.03.2018
После доработки 14.06.2018
Принята к публикации 20.06.2018

DOI: 10.1134/S0568528119010158

Аннотация

Методом Винера–Хопфа получено аналитическое решение задачи о поведении ледяного покрова с прямолинейной трещиной при равномерном движении области давления прямоугольного вида, моделирующей судно на воздушной подушке. Ледяной покров моделируется тонкими упругими полубесконечными пластинами постоянной толщины на поверхности идеальной несжимаемой жидкости конечной глубины. Рассмотрены две конфигурации: 1) две полубесконечные пластины со свободными краями (толщины которых могут быть различными) разделены трещиной; 2) жидкость ограничена вертикальной стенкой, и край ледяного покрова может быть как свободным, так и примороженным к стенке. В случае контакта пластин одинаковой толщины, а также при наличии стенки решение получено в явном виде. Показано, что в случае контакта идентичных пластин со свободными краями при движении нагрузки со сверхкритической скоростью возбуждаются краевые волноводные моды вдоль трещины. Исследованы волновые силы, действующие на движущееся тело, а также прогибы пластин в зависимости от их толщин и скорости движения нагрузки при докритическом и сверхкритическом режимах.

Ключевые слова: тонкая упругая плавающая пластина, изгибно-гравитационные волны, критическая скорость, краевая мода, преобразование Фурье, метод Винера–Хопфа

В настоящее время ведутся активные работы по освоению Арктики. При этом ледяной покров используется для создания дорог, взлетных полос, причалов и плавающих платформ для разведочного бурения. Для безопасности работ на льду необходимо изучать закономерности его поведения при механическом воздействии. Имеется большое число исследований о поведении бесконечного ледяного покрова, полностью покрывающего поверхность воды, при разных видах нагрузки. Начало исследований о поведении ледяного покрова при движущейся нагрузке было положено в работах [1, 2]. Обзоры полученных результатов можно найти в [3–9]. В работе [10] приведены результаты экспериментального, а в [2, 11–13] теоретических исследований прогиба льда при равномерном движении нагрузки в дальнем и ближнем поле.

Известно [1], что существует критическая скорость, совпадающая с минимальной фазовой скоростью изгибно-гравитационных волн. Стационарное решение при равномерном движении нагрузки с критической скоростью по упругой плавающей пластине в линейном приближении не существует. Для определения ограниченного решения при критической скорости необходимо привлекать нелинейные модели или учитывать структурное демпфирование пластины. Силы волнового сопротивления при движении нагрузки по упругой бесконечной плавающей пластине изучались в работах [14–16].

В действительности ледяной покров неоднороден. В нем существуют трещины, торосы, полыньи. Дифракция изгибно-гравитационных волн на таких неоднородностях изучена достаточно хорошо [17–24]. В работах [17, 18] показано, что при наличии линейных неоднородностей типа трещин или торосов в однородном ледяном покрове существуют краевые волноводные моды – решения однородной задачи дифракции типа бегущих волн, распространяющихся вдоль трещины и затухающих в перпендикулярных направлениях. Показано в [23], что волноводная краевая мода существует при наличии трещины и для пластин с различной толщиной, однако отличие их толщин должно быть небольшим.

Краевая мода в ледяном покрове с трещиной не может непосредственно возбуждаться набегающими плоскими волнами, так как она не удовлетворяет дисперсионному соотношению для изгибно-гравитационных волн. Однако она может возбуждаться динамическими нагрузками, действующими на пластину. В статье [24] исследовано возбуждение краевых мод периодическим по времени внешним воздействием на ледяной покров с трещиной. В работе [25] описан эффект усиления краевых мод при их нелинейном резонансном взаимодействии с набегающими плоскими волнами.

Задача о поведении ограниченного ледяного покрова под действием движущейся нагрузки еще требует изучения. В [26] проведено численное исследование напряженно-деформированного состояния полубесконечного ледяного покрова под действием движущейся нагрузки методом конечных элементов. Решена задача о поведении очень большой упругой плавающей пластины, моделирующей плавающий аэропорт, при взлете и посадке самолета [27]. В работе [28] исследовались генерируемые движущейся нагрузкой изгибно-гравитационные волны в полубесконечной пластине, жестко прикрепленной к вертикальной стенке, в линейном приближении и в нелинейной постановке. Построено решение задачи о движении нагрузки по ледяному покрову в канале с помощью преобразования Фурье и метода нормальных мод [29]. Исследовано поведение полубесконечного ледяного покрова, контактирующего со свободной поверхностью жидкости, при равномерно движущейся нагрузке [30] методами Винера-Хопфа и сращивания разложений по собственным функциям.

В данной статье приведено решение задачи о поведении ледяного покрова, состоящего из двух полубесконечных пластин со свободными краями, под действием равномерно движущейся нагрузки. Методом отражения получено также решение задачи для случая контакта ледяного покрова с вертикальной стенкой.

1. ПОСТАНОВКА ЗАДАЧИ

Ледяной покров моделируется двумя упругими полубесконечными пластинами постоянной толщины, разделенными прямолинейной трещиной. Пластины могут иметь различную толщину ${{h}_{1}}$, ${{h}_{2}}$. Жидкость глубины H предполагается идеальной несжимаемой.

Рассматривается движение пластин и жидкости под действием равномерно движущейся области давления вдоль края ледяного поля. Задача решается в линейной постановке. Введем декартову систему координат $Oxyz$ с осью Ox, перпендикулярной к трещине, осью Oy вдоль трещины и осью Oz, направленной вертикально вверх. Пластины занимают области $x > 0$ и $x < 0$. Давление предполагается равномерно распределенным по прямоугольной области S шириной $2a$ и длиной $2b$. Область давления движется со скоростью V в положительном направлении оси $Oy$, S = $\{ (x,y),{\text{|}}x - {{x}_{0}}{\text{|}} < a,{\text{|}}y - Vt{\text{|}} < b\} $, давление равно $q(x,y,t) = {{q}_{0}} = gM{\text{/}}(4ab)$, где M – масса движущегося тела, $g$ – ускорение свободного падения, ${{x}_{0}}$ – расстояние центра области нагрузки от края пластины. Данная нагрузка моделирует судно на воздушной подушке.

Перейдем в подвижную систему координат $y{\text{'}} = y - Vt$, в которой движение пластин и жидкости предполагается установившимся. Штрихи далее опускаем. Потенциал течения жидкости удовлетворяет уравнению Лапласа

(1.1)

$\frac{{{{\partial }^{2}}\varphi }}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}\varphi }}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}\varphi }}{{\partial {{z}^{2}}}} = 0$

Прогиб пластин описывается уравнениями изгиба тонких упругих пластин

(1.2)

${{D}_{n}}{{\left( {\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}}} \right)}^{2}}w + {{\rho }_{0}}{{h}_{n}}{{\left( {\frac{\partial }{{\partial t}} - V\frac{\partial }{{\partial y}}} \right)}^{2}}w = p - U(x)q(x,y)$

(1.3)

$\frac{p}{\rho } = - \left( {\frac{\partial }{{\partial t}} - V\frac{\partial }{{\partial y}}} \right)\varphi - gw,\quad {{D}_{n}} = \frac{{Eh_{n}^{3}}}{{12(1 - {{\nu }^{2}})}},\quad n = 1,2$

Здесь $w(x,y)$ – нормальный прогиб пластин, ρ₀, $\rho $ – плотности льда и жидкости, p – гидродинамическое давление, ${{D}_{1}}$, ${{D}_{2}}$ – цилиндрические жесткости пластин, E – модуль Юнга, $\nu $ – коэффициент Пуассона, $U(x)$ – функция Хевисайда, $t$ – время.

Осадка пластин в воду не учитывается. Граничные условия на верхней границе жидкости сносятся на плоскость z = 0. Предполагается, что нижняя поверхность ледяного покрова все время находится в контакте с жидкостью, отрыва не происходит, на верхней границе выполнено кинематическое соотношение

(1.4)

$\left( {\frac{\partial }{{\partial t}} - V\frac{\partial }{{\partial y}}} \right)w = {{\varphi }_{z}}\quad (z = 0)$

на дне – условие непротекания

(1.5)

${{\varphi }_{z}} = 0\quad (z = - H)$

Граничные условия для пластин со свободными краями имеют вид

(1.6)

$\left( {\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} + \nu \frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}}} \right)w( \pm 0,y) = 0,\quad \frac{\partial }{{\partial x}}\left( {\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} + (2 - \nu )\frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}}} \right)w( \pm 0,y) = 0$

В случае примороженного края ледяного покрова $w(0,y) = \partial w{\text{/}}\partial x(0,y) = 0$. При контакте пластины с вертикальной стенкой ставится краевое условие $\partial \varphi {\text{/}}\partial x = 0$ $(x = 0)$. На бесконечности ставится условие излучения – волны являются уходящими от источника возмущений.

При движении тела по свободной поверхности или по ледяному покрову на него действуют сила волнового сопротивления ${{F}_{y}}$ и боковая сила ${{F}_{x}}$, которые находятся по формулам

$({{F}_{x}},{{F}_{y}}) = - {{q}_{0}}\int\limits_{ - b}^b \,\int\limits_{{{x}_{0}} - a}^{{{x}_{0}} + a} ({{w}_{x}},{{w}_{y}})dxdy$

Безразмерные коэффициенты волновых сил ${{A}_{x}}$, ${{A}_{y}}$ вычисляются по формулам [15]

$({{A}_{x}},{{A}_{y}}) = - \frac{{\rho g}}{{2aq_{0}^{2}}}({{F}_{x}},{{F}_{y}})$

2. РЕШЕНИЕ ЗАДАЧИ В СЛУЧАЕ ПЛАСТИН РАЗЛИЧНОЙ ТОЛЩИНЫ

Введем безразмерные переменные и параметры

$(x{\text{'}},y{\text{'}},z{\text{'}}) = \frac{{(x,y,z)}}{H},\quad (x_{0}^{'},a{\text{'}},b{\text{'}}) = \frac{{({{x}_{0}},a,b)}}{H},\quad F = \frac{V}{{\sqrt {gH} }},\quad q_{0}^{'} = \frac{{{{q}_{0}}}}{{\rho gH}},$

${{\beta }_{n}} = \frac{{{{D}_{n}}}}{{\rho g{{H}^{4}}}},\quad {{\sigma }_{n}} = \frac{{{{\rho }_{0}}{{h}_{n}}}}{{\rho H}}$

Штрихи в дальнейшем будем опускать. Будем искать прогиб пластины и потенциал течения жидкости в виде

$w = HW(x,y),\quad \varphi = VH\phi (x,y,z)$

Тогда для функций $\phi $, W из (1.1)–(1.6) получим уравнения

$\frac{{{{\partial }^{2}}\phi }}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}\phi }}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}\phi }}{{\partial {{z}^{2}}}} = 0\quad ( - 1 < z < 0)$

${{\phi }_{z}} = 0\quad (z = - 1),\quad {{\phi }_{z}} = - {{W}_{y}}\quad (z = 0)$

(2.1)

$({{\beta }_{1}}\Delta _{2}^{2} + 1 - {{\sigma }_{1}}{{F}^{2}}{{s}^{2}})\frac{{\partial \phi }}{{\partial z}} + {{F}^{2}}\frac{{{{\partial }^{2}}\phi }}{{\partial {{y}^{2}}}} = 0\quad (z = 0,x < 0)$

$({{\beta }_{2}}\Delta _{2}^{2} + 1 - {{\sigma }_{2}}{{F}^{2}}{{s}^{2}})\frac{{\partial \phi }}{{\partial z}} + {{F}^{2}}\frac{{{{\partial }^{2}}\phi }}{{\partial {{y}^{2}}}} = \frac{{\partial q}}{{\partial y}}\quad (z = 0,x > 0)$

$\left( {\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} + \nu \frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}}} \right){{\phi }_{z}}( \pm 0,y,0) = 0,\quad \frac{\partial }{{\partial x}}\left( {\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} + (2 - \nu )\frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}}} \right){{\phi }_{z}}( \pm 0,y,0) = 0$

где ${{\Delta }_{2}}$ – оператор Лапласа по горизонтальным координатам.

Дисперсионное соотношение для плоских волн вида ${{{\text{e}}}^{{i(kx - \omega t)}}}$ под бесконечным ледяным покровом имеет вид [3]

${{\omega }^{2}} = \frac{{k({{\beta }_{n}}{{k}^{4}} + 1)}}{{{{\sigma }_{n}}k + {\text{cth}}k}}$

Графики фазовой скорости $c = \omega {\text{/}}k$ (толстые линии) и групповой скорости $U = \partial \omega {\text{/}}\partial k$ (тонкие линии) приведены на фиг. 1 для бесконечного ледяного покрова толщиной $h = 1,\;2,\;3$ м при следующих значениях входных параметров

(2.2)

$E = 5\;{\text{Г П а }},\quad \rho = 1000\;{\text{к г /}}{{{\text{м }}}^{3}},\quad {{\rho }_{0}} = 900\;{\text{к г /}}{{{\text{м }}}^{3}},\quad \nu = 1{\text{/}}3,\quad H = 350\;{\text{м }}$

Фиг. 1.

Зависимости фазовых скоростей $c(k)$ (толстые кривые) и групповых скоростей $U(k)$ (тонкие кривые) изгибно-гравитационных волн от волнового числа $k$: 1 –3 – $h = 1$, 2, 3 м

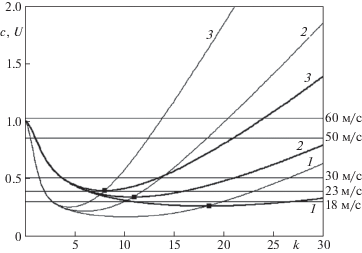
Из графиков следует, что фазовая скорость достигает минимума при некотором значении волнового числа $k$, и в этой точке происходит пересечение кривых фазовой и групповой скоростей. Точка минимума разделяет графики фазовой и групповой скоростей на две ветви. Волны левой ветви имеют групповую скорость меньше фазовой, они распространяются сзади нагрузки и являются длинными, так как волновые числа малы. Волны правой ветви короче, они имеют групповую скорость больше фазовой и распространяются перед нагрузкой.

Вводим преобразование Фурье по переменным x и y

${{\Phi }_{ - }}(\alpha ,s,z) = \int\limits_{ - \infty }^\infty {{{\text{e}}}^{{ - isy}}}dy\int\limits_{ - \infty }^0 \phi (x,y,z){{{\text{e}}}^{{i\alpha x}}}dx$

${{\Phi }_{ + }}(\alpha ,s,z) = \int\limits_{ - \infty }^\infty {{{\text{e}}}^{{ - isy}}}dy\int\limits_0^\infty \phi (x,y,z){{{\text{e}}}^{{i\alpha x}}}dx,\quad \Phi (\alpha ,s,z) = {{\Phi }_{ - }}(\alpha ,s,z) + {{\Phi }_{ + }}(\alpha ,s,z)$

Из уравнения Лапласа и условия непротекания получаем

${{\partial }^{2}}\Phi {\text{/}}\partial {{z}^{2}} - ({{\alpha }^{2}} + {{s}^{2}})\Phi = 0\quad ( - 1 < z < 0)$

${{\Phi }_{z}} = 0\quad (z = - 1)$

Отсюда находим

(2.3)

$\Phi (\alpha ,s,z) = C(\alpha ,s)Z(\alpha ,s,z),\quad Z(\alpha ,s,z) = {\text{ch}}((z + 1)\sqrt {{{\alpha }^{2}} + {{s}^{2}}} ){\text{/ch}}(\sqrt {{{\alpha }^{2}} + {{s}^{2}}} )$

Применяем метод Винера–Хопфа и вводим функции ${{G}_{{n \pm }}}$, $n = 1,2$ следующим образом

${{G}_{{n - }}}(\alpha ,s) = \int\limits_{ - \infty }^\infty {{{\text{e}}}^{{ - isy}}}dy\int\limits_{ - \infty }^0 {{\left. {[({{\beta }_{n}}\Delta _{2}^{2} + 1 + {{\sigma }_{n}}{{F}^{2}}{{\partial }^{2}}{\text{/}}\partial {{y}^{2}}){{\phi }_{z}} + {{F}^{2}}{{\phi }_{{yy}}}]} \right|}_{{z = 0}}}{{{\text{e}}}^{{i\alpha x}}}dx$

${{G}_{{n + }}}(\alpha ,s) = \int\limits_{ - \infty }^\infty {{{\text{e}}}^{{ - isy}}}dy\int\limits_0^\infty {{\left. {[({{\beta }_{n}}\Delta _{2}^{2} + 1 + {{\sigma }_{n}}{{F}^{2}}{{\partial }^{2}}{\text{/}}\partial {{y}^{2}}){{\phi }_{z}} + {{F}^{2}}{{\phi }_{{yy}}}]} \right|}_{{z = 0}}}{{{\text{e}}}^{{i\alpha x}}}dx$

Функции с индексами +/– аналитичны по α соответственно в верхней/нижней полуплоскостях. Из уравнений (2.1) имеем

(2.4)

${{G}_{{1 - }}}(\alpha ,s) \equiv 0,\quad {{G}_{{2 + }}}(\alpha ,s) = isQ(\alpha ,s)$

$Q(\alpha ,s) = \int\limits_{ - \infty }^\infty dy\int\limits_{ - \infty }^\infty q(x,y){{{\text{e}}}^{{i(\alpha x - sy)}}}dx = \frac{{4{{q}_{0}}{{{\text{e}}}^{{i\alpha {{x}_{0}}}}}sin(\alpha a)sin(sb)}}{{\alpha s}}$

Из представления (2.3) находим

(2.5)

${{G}_{n}}(\alpha ,s) = {{G}_{{n - }}}(\alpha ,s) + {{G}_{{n + }}}(\alpha ,s) = C(\alpha ,s){{K}_{n}}(\alpha ,s),\quad n = 1,2$

где ${{K}_{n}}(\alpha ,s)$ – дисперсионные функции для изгибно-гравитационных волн при равномерном движении источника возмущений

${{K}_{n}}(\alpha ,s) = [{{\beta }_{n}}{{({{\alpha }^{2}} + {{s}^{2}})}^{2}} + 1 - {{\sigma }_{n}}{{F}^{2}}{{s}^{2}}]\sqrt {{{\alpha }^{2}} + {{s}^{2}}} {\text{th}}(\sqrt {{{\alpha }^{2}} + {{s}^{2}}} ) - {{F}^{2}}{{s}^{2}}$

Известно, что дисперсионное соотношение для изгибно-гравитационных волн

${{K}_{1}}(\gamma ) \equiv ({{\beta }_{1}}{{\gamma }^{4}} + 1 - {{\sigma }_{1}}{{F}^{2}}{{s}^{2}})\gamma {\text{th}}\gamma - {{F}^{2}}{{s}^{2}} = 0$

имеет два действительных корня $ \pm {{\gamma }_{0}}(s)$, четыре комплексных корня, которые обозначим $ \pm {{\gamma }_{{ - 1}}}(s)$, $ \pm {{\gamma }_{{ - 2}}}(s)$, ${{\gamma }_{{ - 2}}} = - \mathop {\bar {\gamma }}\nolimits_{ - 1} $ (черта означает комплексное сопряжение), и счетное множество мнимых корней $ \pm {{\gamma }_{m}}(s)$, $m = 1,2,\; \ldots $. Аналогично второе дисперсионное соотношение

${{K}_{2}}(\mu ) \equiv ({{\beta }_{2}}{{\mu }^{4}} + 1 - {{\sigma }_{2}}{{F}^{2}}{{s}^{2}})\mu {\text{th}}\mu - {{F}^{2}}{{s}^{2}} = 0$

имеет два действительных корня $ \pm {{\mu }_{0}}(s)$, четыре комплексных корня $ \pm {{\mu }_{{ - 1}}}(s)$, $ \pm {{\mu }_{{ - 2}}}(s)$, ${{\mu }_{{ - 2}}} = - \mathop {\bar {\mu }}\nolimits_{ - 1} $ и счетное множество чисто мнимых корней $ \pm {{\mu }_{m}}(s)$, $m = 1,2,\; \ldots $. Тогда корни дисперсионных соотношений ${{K}_{n}}(\alpha ,s) = 0$ соответственно равны $ \pm {{\chi }_{m}}$, $ \pm {{\alpha }_{m}}$

${{\chi }_{m}} = \sqrt {\gamma _{m}^{2} - {{s}^{2}}} ,\quad {{\alpha }_{m}} = \sqrt {\mu _{m}^{2} - {{s}^{2}}} $

В последних выражениях условимся брать значения комплексных корней в верхней полуплоскости, действительных корней – на положительной полуоси.

Функция ${{\Phi }_{ - }}(\alpha ,s,z)$ аналитична по $\alpha $ в нижней полуплоскости ${\text{Im}}(\alpha ) < {{\lambda }_{1}}$, за исключением возможных вещественных полюсов в точках $ \pm {{\chi }_{0}}$, ${{\lambda }_{1}} = {\text{min}}\left| {{\text{Im}}({{\chi }_{m}})} \right|$ $m \ne 0$ при $\left| s \right| \leqslant {{\gamma }_{0}}$, ${{\lambda }_{1}} = \left| {{{\chi }_{0}}} \right|$ при $\left| s \right| > {{\gamma }_{0}}$. Функция ${{\Phi }_{ + }}(\alpha ,s,z)$ аналитична по $\alpha $ в верхней полуплоскости ${\text{Im}}(\alpha ) > - {{\lambda }_{2}}$, за исключением возможных вещественных полюсов в точках $ \pm {{\alpha }_{0}}$, ${{\lambda }_{2}} = {\text{min}}\left| {{\text{Im}}({{\alpha }_{m}})} \right|$, $m \ne 0$ при $\left| s \right| \leqslant {{\mu }_{0}}$, ${{\lambda }_{2}} = \left| {{\text{Im}}({{\alpha }_{0}})} \right|$ при $\left| s \right| > {{\mu }_{0}}$.

Исключая из соотношений (2.4), (2.5) $C(\alpha ,s)$, выводим уравнение

(2.6)

${{G}_{{2 - }}}(\alpha ,s) + isQ(\alpha ,s) = {{G}_{{1 + }}}(\alpha ,s)K(\alpha ,s),\quad K(\alpha ,s) = \frac{{{{K}_{2}}(\alpha ,s)}}{{{{K}_{1}}(\alpha ,s)}}$

В соответствии с методом Винера–Хопфа факторизуем функцию $K(\alpha ,s)$

$K(\alpha ,s) = {{K}_{ - }}(\alpha ,s){{K}_{ + }}(\alpha ,s)$

где функции ${{K}_{ - }}$ и ${{K}_{ + }}$ аналитичны по $\alpha $ соответственно в нижней и верхней полуплоскостях и определяются формулами

${{K}_{ \pm }}(\alpha ,s) = \prod\limits_{j = - 2}^\infty \frac{{{{\gamma }_{j}}(\alpha \pm {{\alpha }_{j}})}}{{{{\mu }_{j}}(\alpha \pm {{\chi }_{j}})}}$

Разделим уравнение (2.6) на ${{K}_{ - }}(\alpha ,s)$, получим

$\frac{{{{G}_{{2 - }}}(\alpha ,s)}}{{{{K}_{ - }}(\alpha ,s)}} + 2{{q}_{0}}sin(sb)\frac{{\psi (\alpha )}}{{{{K}_{ - }}(\alpha ,s)}} = {{G}_{{1 + }}}(\alpha ,s){{K}_{ + }}(\alpha ,s),\quad \psi (\alpha ) = \frac{{{{{\text{e}}}^{{i\alpha ({{x}_{0}} + a)}}} - {{{\text{e}}}^{{i\alpha ({{x}_{0}} - a)}}}}}{\alpha }$

Используя представление [31]

$\frac{{\psi (\alpha )}}{{{{K}_{ - }}(\alpha ,s)}} = {{L}_{ - }}(\alpha ,s) + {{L}_{ + }}(\alpha ,s),\quad {{L}_{ \pm }}(\alpha ,s) = \pm \frac{1}{{2\pi i}}\int\limits_{ - \infty \mp i\lambda }^{\infty \mp i\lambda } \frac{{\psi (\zeta )d\zeta }}{{{{K}_{ - }}(\zeta ,s)(\zeta - \alpha )}}$

где функции ${{L}_{ \pm }}$ аналитичны по α соответственно в верхней и нижней полуплоскостях, $\lambda < {\text{min}}({{\lambda }_{1}},{{\lambda }_{2}})$, получаем уравнение

$\frac{{{{G}_{{2 - }}}(\alpha ,s)}}{{{{K}_{ - }}(\alpha ,s)}} + 2{{q}_{0}}sin(sb){{L}_{ - }}(\alpha ,s) = {{G}_{{1 + }}}(\alpha ,s){{K}_{ + }}(\alpha ,s) - 2{{q}_{0}}sin(sb){{L}_{ + }}(\alpha ,s)$

Имеем в левой части функцию аналитическую в нижней полуплоскости, а в правой части – аналитическую в верхней полуплоскости. Следовательно эти функции представляют аналитическую функцию во всей комплексной плоскости. По теореме Лиувилля эта функция является полиномом, степень которого определяется поведением этой функции на бесконечности по $\alpha $. Имеем

$\left| {{{K}_{ \pm }}(\alpha ,s)} \right| = O(1),\quad \left| {{{L}_{ \pm }}(\alpha ,s)} \right| = O({{\left| \alpha \right|}^{{ - 1}}}),\quad \alpha \to \infty $

Вблизи кромки пластины градиент потенциала имеет интегрируемую особенность $O({{r}^{{ - \eta }}})$, ($\eta < 1$, $r$ – расстояние до кромки пластины). Тогда [32] при $\left| \alpha \right| \to \infty $

$\left| {{{G}_{{n \pm }}}(\alpha ,s)} \right| = O({{\left| \alpha \right|}^{{\eta + 3}}})$

Следовательно, степень полинома равна трем и

${{G}_{{1 + }}}(\alpha ,s){{K}_{ + }}(\alpha ,s) - 2{{q}_{0}}sin(sb){{L}_{ + }}(\alpha ,s) = 2{{q}_{0}}sin(sb)\sum\limits_{n = 0}^3 {{a}_{n}}(s){{\alpha }^{n}}$

где ${{a}_{n}}(s)$ – неизвестные функции, которые определяются из условий на кромках пластин.

Получаем

$\Phi (\alpha ,s,z) = 2{{q}_{0}}sin(sb)\frac{{({{a}_{0}} + {{a}_{1}}\alpha + {{a}_{2}}{{\alpha }^{2}} + {{a}_{3}}{{\alpha }^{3}} + {{L}_{ + }}(\alpha ,s))Z(\alpha ,s,z)}}{{{{K}_{ + }}(\alpha ,s){{K}_{1}}(\alpha ,s)}}$

$\Phi (x,s,z) = \frac{{{{q}_{0}}sin(sb)}}{\pi }\int\limits_{ - \infty }^\infty \frac{{{{{\text{e}}}^{{ - i\alpha x}}}({{a}_{0}} + {{a}_{1}}\alpha + {{a}_{2}}{{\alpha }^{2}} + {{a}_{3}}{{\alpha }^{3}} + {{L}_{ + }}(\alpha ,s))Z(\alpha ,s,z)d\alpha }}{{{{K}_{ + }}(\alpha ,s){{K}_{1}}(\alpha ,s)}}$

(2.7)

$\frac{{\partial \Phi }}{{\partial z}}(x,s,0) = \frac{{{{q}_{0}}sin(sb)}}{\pi }\int\limits_{ - \infty }^\infty \frac{{{{{\text{e}}}^{{ - i\alpha x}}}\sqrt {{{\alpha }^{2}} + {{s}^{2}}} {\text{th}}(\sqrt {{{\alpha }^{2}} + {{s}^{2}}} )}}{{{{K}_{ + }}(\alpha ,s){{K}_{1}}(\alpha ,s)}}\left( {\sum\limits_{n = 0}^3 {{a}_{n}}{{\alpha }^{n}} + {{L}_{ + }}(\alpha ,s)} \right)d\alpha $

При вычислении интегралов важно правильно выбрать правило обхода полюсов на действительной оси, при этом используется условие излучения аналогично тому, как изложено в [33]. Установлено, что полюса на положительной полуоси обходятся снизу, а на отрицательной полуоси – сверху.

Все интегралы по $\alpha $ вычисляем с помощью теории вычетов. При $x < 0$

$\frac{{\partial \Phi }}{{\partial z}}(x,s,0) = i2{{q}_{0}}sin(sb)\sum\limits_{j = - 2}^\infty \frac{{{{{\text{e}}}^{{ - i{{\chi }_{j}}x}}}{{\gamma }_{j}}{\text{th}}{{\gamma }_{j}}}}{{{{K}_{ + }}({{\chi }_{j}},s)K_{1}^{'}({{\chi }_{j}},s)}}\left( {\sum\limits_{n = 0}^3 {{a}_{n}}\chi _{j}^{n} + {{L}_{ + }}({{\chi }_{j}},s)} \right)$

${{L}_{ - }}(\alpha ,s) = - \sum\limits_{m = - 2}^\infty \frac{{\psi ({{\alpha }_{m}})}}{{K_{ - }^{'}({{\alpha }_{m}},s)({{\alpha }_{m}} - \alpha )}}$

${{L}_{ + }}(\alpha ,s) = \frac{{\psi (\alpha )}}{{{{K}_{ - }}(\alpha ,s)}} - {{L}_{ - }}(\alpha ,s),\quad K_{ - }^{'}({{\alpha }_{m}},s) = \frac{{K_{2}^{'}({{\alpha }_{m}},s)}}{{{{K}_{ + }}({{\alpha }_{m}},s){{K}_{1}}({{\alpha }_{m}},s)}}$

где штрих означает производную по первой переменной.

Подставляем эти выражения в краевые условия при $x = - 0$. Граничные условия на левой пластине записываются в виде

(2.8)

$\sum\limits_{j = - 2}^\infty \frac{{(\gamma _{j}^{2} - (1 - \nu ){{s}^{2}})[{{a}_{0}} + {{a}_{1}}{{\chi }_{j}} + {{a}_{2}}\chi _{j}^{2} + {{a}_{3}}\chi _{j}^{3} + {{L}_{ + }}({{\chi }_{j}},s)]{{\gamma }_{j}}{\text{th}}{{\gamma }_{j}}}}{{{{K}_{ + }}({{\chi }_{j}},s)K_{1}^{'}({{\chi }_{j}},s)}} = 0$

$\sum\limits_{j = - 2}^\infty \frac{{{{\chi }_{j}}(\gamma _{j}^{2} + (1 - \nu ){{s}^{2}})[{{a}_{0}} + {{a}_{1}}{{\chi }_{j}} + {{a}_{2}}\chi _{j}^{2} + {{a}_{3}}\chi _{j}^{3} + {{L}_{ + }}({{\chi }_{j}},s)]{{\gamma }_{j}}{\text{th}}{{\gamma }_{j}}}}{{{{K}_{ + }}({{\chi }_{j}},s)K_{1}^{'}({{\chi }_{j}},s)}} = 0$

При $x > 0$ домножим числитель и знаменатель подынтегрального выражения в (2.7) на ${{K}_{ - }}(\alpha ,s)$, получим

$\frac{{\partial \Phi }}{{\partial z}}(x,s,0) = \frac{{{{q}_{0}}sin(sb)}}{\pi }\int\limits_{ - \infty }^\infty \frac{{{{{\text{e}}}^{{ - i\alpha x}}}({{a}_{0}} + {{a}_{1}}\alpha + {{a}_{2}}{{\alpha }^{2}} + {{a}_{3}}{{\alpha }^{3}} - {{L}_{ - }}(\alpha ,s)){{K}_{ - }}(\alpha ,s)}}{{{{K}_{2}}(\alpha ,s)}} \times $

$ \times \;\sqrt {{{\alpha }^{2}} + {{s}^{2}}} {\text{th}}(\sqrt {{{\alpha }^{2}} + {{s}^{2}}} )d\alpha + \frac{{{{q}_{0}}sin(sb)}}{\pi }\int\limits_{ - \infty }^\infty \frac{{{{{\text{e}}}^{{ - i\alpha x}}}\psi (\alpha )\sqrt {{{\alpha }^{2}} + {{s}^{2}}} {\text{th}}(\sqrt {{{\alpha }^{2}} + {{s}^{2}}} )d\alpha }}{{{{K}_{2}}(\alpha ,s)}}$

При $0 < x < {{x}_{0}} - a$ находим

$\frac{{\partial \Phi }}{{\partial z}}(x,s,0) = i2{{q}_{0}}sin(sb)\left( {\sum\limits_{j = - 2}^\infty \frac{{{{{\text{e}}}^{{ - i{{\alpha }_{j}}x}}}\psi ({{\alpha }_{j}}){{\mu }_{j}}{\text{th}}{{\mu }_{j}}}}{{K_{2}^{'}({{\alpha }_{j}},s)}}} \right. + $

$ + \;\left. {\sum\limits_{j = - 2}^\infty \frac{{{{{\text{e}}}^{{i{{\alpha }_{j}}x}}}{{K}_{ + }}({{\alpha }_{j}},s){{\mu }_{j}}{\text{th}}{{\mu }_{j}}}}{{K_{2}^{'}({{\alpha }_{j}},s)}}[{{a}_{0}} - {{a}_{1}}{{\alpha }_{j}} + {{a}_{2}}\alpha _{j}^{2} - {{a}_{3}}\alpha _{j}^{3} - {{L}_{ - }}( - {{\alpha }_{j}},s)]} \right)$

Получаем краевые условия на кромке правой пластины в виде

$\sum\limits_{j = - 2}^\infty \frac{{(\alpha _{j}^{2} + \nu {{s}^{2}})({{a}_{0}} - {{a}_{1}}{{\alpha }_{j}} + {{a}_{2}}\alpha _{j}^{2} - {{a}_{3}}\alpha _{j}^{3} - {{L}_{ - }}( - {{\alpha }_{j}},s)){{K}_{ + }}({{\alpha }_{j}},s){{\mu }_{j}}{\text{th}}{{\mu }_{j}}}}{{K_{2}^{'}({{\alpha }_{j}},s)}} = $

(2.9)

$ = \; - \sum\limits_{j = - 2}^\infty \frac{{(\alpha _{j}^{2} + \nu {{s}^{2}})\psi ({{\alpha }_{j}}){{\mu }_{j}}{\text{th}}{{\mu }_{j}}}}{{K_{2}^{'}({{\alpha }_{j}},s)}}$

$\sum\limits_{j = - 2}^\infty \frac{{{{\alpha }_{j}}(\alpha _{j}^{2} + (2 - \nu ){{s}^{2}})({{a}_{0}} - {{a}_{1}}{{\alpha }_{j}} + {{a}_{2}}\alpha _{j}^{2} - {{a}_{3}}\alpha _{j}^{3} - {{L}_{ - }}( - {{\alpha }_{j}},s)){{K}_{ + }}({{\alpha }_{j}},s)}}{{K_{2}^{'}({{\alpha }_{j}},s)}} \times $

$ \times \;{{\mu }_{j}}{\text{th}}{{\mu }_{j}} = \sum\limits_{j = - 2}^\infty \frac{{{{\alpha }_{j}}(\alpha _{j}^{2} + (2 - \nu ){{s}^{2}})\psi ({{\alpha }_{j}}){{\mu }_{j}}{\text{th}}{{\mu }_{j}}}}{{K_{2}^{'}({{\alpha }_{j}},s)}}$

Для определения коэффициентов ${{a}_{n}}(s)$ получили систему уравнений (2.8), (2.9).

После решения системы находим прогибы пластин с помощью обратного преобразования Фурье. При $x > 0$

(2.10)

$W(x,y) = - \frac{{{{q}_{0}}}}{\pi }\int\limits_{ - \infty }^\infty \frac{{{{{\text{e}}}^{{isy}}}sin(sb)}}{s}\left( {{{S}_{ + }}(x,s) + \Lambda (x,s)} \right)ds$

${{S}_{ + }}(x,s) = \sum\limits_{j = - 2}^\infty \frac{{{{{\text{e}}}^{{i{{\alpha }_{j}}x}}}({{a}_{0}} - {{a}_{1}}{{\alpha }_{j}} + {{a}_{2}}\alpha _{j}^{2} - {{a}_{3}}\alpha _{j}^{3} - {{L}_{ - }}( - {{\alpha }_{j}},s)){{K}_{ + }}({{\alpha }_{j}},s){{\mu }_{j}}{\text{th}}{{\mu }_{j}}}}{{K_{2}^{'}({{\alpha }_{j}},s)}}$

$\Lambda (x,s) = \frac{1}{{2\pi i}}\int\limits_{ - \infty }^\infty \frac{{{{{\text{e}}}^{{ - i\alpha x}}}\psi (\alpha )\sqrt {{{\alpha }^{2}} + {{s}^{2}}} {\text{th}}(\sqrt {{{\alpha }^{2}} + {{s}^{2}}} )d\alpha }}{{{{K}_{2}}(\alpha ,s)}}$

При $x < 0$

(2.11)

$W(x,y) = - \frac{{{{q}_{0}}}}{\pi }\int\limits_{ - \infty }^\infty \frac{{{{{\text{e}}}^{{isy}}}sin(sb){{S}_{ - }}(x,s)}}{s}ds$

${{S}_{ - }}(x,s) = \sum\limits_{j = - 2}^\infty \frac{{{{{\text{e}}}^{{ - i{{\chi }_{j}}x}}}({{a}_{0}} + {{a}_{1}}{{\chi }_{j}} + {{a}_{2}}\chi _{j}^{2} + {{a}_{3}}\chi _{j}^{3} + {{L}_{ + }}({{\chi }_{j}},s)){{\gamma }_{j}}{\text{th}}{{\gamma }_{j}}}}{{{{K}_{ + }}({{\chi }_{j}},s)K_{1}^{'}({{\chi }_{j}},s)}}$

Функция $\Lambda (x,s)$ вычисляется с помощью теории вычетов, контур интегрирования замыкается в верхней или нижней полуплоскости, в зависимости от значения $x$, при этом необходимо учитывать полюс в нуле. При ${{x}_{0}} - a < x < {{x}_{0}} + a$ получаем

$\Lambda (x,s) = \sum\limits_{j = - 2}^\infty \frac{{({{{\text{e}}}^{{i{{\alpha }_{j}}({{x}_{0}} + a - x)}}} + {{{\text{e}}}^{{i{{\alpha }_{j}}(x + a - {{x}_{0}})}}} - 2){{\mu }_{j}}{\text{th}}{{\mu }_{j}}}}{{{{\alpha }_{j}}K_{2}^{'}({{\alpha }_{j}},s)}} = $

$ = \;\sum\limits_{j = - 2}^\infty \frac{{({{{\text{e}}}^{{i{{\alpha }_{j}}({{x}_{0}} + a - x)}}} + {{{\text{e}}}^{{i{{\alpha }_{j}}(x + a - {{x}_{0}})}}}){{\mu }_{j}}{\text{th}}{{\mu }_{j}}}}{{{{\alpha }_{j}}K_{2}^{'}({{\alpha }_{j}},s)}} + \frac{{s{\text{th}}s}}{{{{K}_{2}}(0,s)}}.$

Подынтегральные функции в выражениях (2.10), (2.11) экспоненциально затухают при $s \to \infty $.

Для каждой пластины существует своя минимальная фазовая скорость $c_{n}^{ * }$, $n = 1,\;2$ изгибно-гравитационных волн. Если $V < c_{2}^{ * }$, то ${{\mu }_{0}}(s) < \left| s \right|$ при любых значениях параметра s и нет действительных корней дисперсионного соотношения ${{K}_{2}}(\alpha ,s) = 0$. Если $V < c_{1}^{ * }$, то это справедливо для другой пластины – ${{\gamma }_{0}}(s) < \left| s \right|$ и нет действительных корней дисперсионного соотношения ${{K}_{1}}(\alpha ,s)$ = 0. При $V < min\{ c_{1}^{ * },c_{2}^{ * }\} $ волновых движений в пластинах не возбуждается, наблюдаются локальные возмущения вблизи области действия нагрузки. Если $c_{2}^{ * } < V < \sqrt {gH} $, то существуют два значения ${{s}_{{2 - }}}$ и ${{s}_{{2 + }}}$ такие, что ${{\mu }_{0}}(s) > \left| s \right|$ при ${{s}_{{2 - }}} < \left| s \right| < {{s}_{{2 + }}}$. Аналогичное утверждение справедливо для другой пластины, при $c_{1}^{ * } < V < \sqrt {gH} $ существуют два значения ${{s}_{{1 - }}}$ и ${{s}_{{1 + }}}$ такие, что ${{\gamma }_{0}}(s) > \left| s \right|$ при ${{s}_{{1 - }}} < \left| s \right| < {{s}_{{1 + }}}$. С увеличением скорости движения нагрузки значение ${{s}_{{n - }}}$ уменьшается, а ${{s}_{{n + }}}$ возрастает, $n = 1,\;2$. При скорости, большей второй критической скорости, $V \geqslant \sqrt {gH} $ ${{s}_{{1 - }}} = {{s}_{{2 - }}} = 0$, то есть ${{\mu }_{0}}(s) > \left| s \right|$ при $\left| s \right| < {{s}_{{2 + }}}$, ${{\mu }_{0}}(s) < \left| s \right|$ при $\left| s \right| > {{s}_{{2 + }}}$ и ${{\gamma }_{0}}(s) > \left| s \right|$ при $\left| s \right| < {{s}_{{1 + }}}$, ${{\gamma }_{0}}(s) < \left| s \right|$ при $\left| s \right| > {{s}_{{1 + }}}$.

Так как ${{\alpha }_{0}} = 0$ при ${{\mu }_{0}}(s) = s$, то при $V > c_{2}^{ * }$ выражение для ${{L}_{ - }}( - {{\alpha }_{0}},s)$ содержит корневую интегрируемую особенность вида ${{(\mu _{0}^{2}(s) - {{s}^{2}})}^{{ - 1/2}}}$. С помощью замены переменной интегрирования можно подынтегральную функцию сделать регулярной. Замена переменной проводится следующим образом. В случае $c_{2}^{ * } < V < \sqrt {gH} $ область интегрирования делится на три участка:

1) $0 < s < {{s}_{{2 - }}}{\text{:}}\quad s = {{s}_{{2 - }}}{\text{sin}}\zeta ,\quad 0 < \zeta < \pi {\text{/}}2$

2) ${{s}_{{2 - }}} < s < {{s}_{{2 + }}}$: $s = {{s}_{0}} + dsin\zeta ,$ $ - \pi {\text{/}}2 < \zeta < \pi {\text{/}}2$, ${{s}_{0}} = \tfrac{{{{s}_{{2 - }}} + {{s}_{{2 + }}}}}{2},$ $d = \tfrac{{{{s}_{{2 + }}} - {{s}_{{2 - }}}}}{2}$

3) $s > {{s}_{{2 + }}}{\text{:}}\quad s = {{s}_{{2 + }}}{\text{ch}}\zeta ,\quad 0 < \zeta < \infty $

Если $V > \sqrt {gH} $, то первый участок отсутствует.

3. РЕШЕНИЕ В СЛУЧАЕ ОДИНАКОВЫХ ПЛАСТИН

Рассмотрим случай одинаковых пластин. Тогда ${{K}_{1}}(\alpha ,s) \equiv {{K}_{2}}(\alpha ,s)$, $K(\alpha ,s) \equiv 1$, ${{K}_{ \pm }}(\alpha ,s) \equiv 1$, ${{L}_{ - }}(\alpha ,s) \equiv 0$,

$\phi (x,y,z) = \frac{{{{q}_{0}}}}{{2{{\pi }^{2}}}}\int\limits_{ - \infty }^\infty {{{\text{e}}}^{{isy}}}sin(sb)ds\int\limits_{ - \infty }^\infty \frac{{{{{\text{e}}}^{{ - i\alpha x}}}Z(\alpha ,s,z)}}{{{{K}_{2}}(\alpha ,s)}}\left( {\sum\limits_{n = 0}^3 {{a}_{n}}{{\alpha }^{n}} + \psi (\alpha )} \right)d\alpha $

$\frac{{\partial \Phi }}{{\partial z}}(x,s,0) = \frac{{{{q}_{0}}sin(sb)}}{\pi }\int\limits_{ - \infty }^\infty \frac{{{{{\text{e}}}^{{ - i\alpha x}}}\sqrt {{{\alpha }^{2}} + {{s}^{2}}} {\text{th}}(\sqrt {{{\alpha }^{2}} + {{s}^{2}}} )}}{{{{K}_{2}}(\alpha ,s)}}\left( {\sum\limits_{n = 0}^3 {{a}_{n}}{{\alpha }^{n}} + \psi (\alpha )} \right)d\alpha $

При $x < {{x}_{0}} - a$

$\frac{{\partial \Phi }}{{\partial z}}(x,s,0) = i2{{q}_{0}}sin(sb)\sum\limits_{j = - 2}^\infty \frac{{{{{\text{e}}}^{{i{{\alpha }_{j}}|x|}}}({{a}_{0}} \mp {{a}_{1}}{{\alpha }_{j}} + {{a}_{2}}\alpha _{j}^{2} \mp {{a}_{3}}\alpha _{j}^{3}) + {{{\text{e}}}^{{ - i{{\alpha }_{j}}x}}}\psi ({{\alpha }_{j}})}}{{K_{2}^{'}({{\alpha }_{j}},s)}}{{\mu }_{j}}{\text{th}}{{\mu }_{j}}$

где знак –/+ берется соответственно при $x > 0{\text{/}}x < 0$.

Для пластин со свободными краями из граничных условий на кромках имеем

(3.1)

$\sum\limits_{j = - 2}^\infty \frac{{(\alpha _{j}^{2} + \nu {{s}^{2}})({{a}_{0}} \mp {{a}_{1}}{{\alpha }_{j}} + {{a}_{2}}\alpha _{j}^{2} \mp {{a}_{3}}\alpha _{j}^{3} + \psi ({{\alpha }_{j}})){{\mu }_{j}}{\text{th}}{{\mu }_{j}}}}{{K_{2}^{'}({{\alpha }_{j}},s)}} = 0$

$\sum\limits_{j = - 2}^\infty \frac{{(\alpha _{j}^{2} + (2 - \nu ){{s}^{2}})( \pm i{{\alpha }_{j}}({{a}_{0}} \mp {{a}_{1}}{{\alpha }_{j}} + {{a}_{2}}\alpha _{j}^{2} \mp {{a}_{3}}\alpha _{j}^{3}) - i{{\alpha }_{j}}\psi ({{\alpha }_{j}})){{\mu }_{j}}{\text{th}}{{\mu }_{j}}}}{{K_{2}^{'}({{\alpha }_{j}},s))}} = 0$

где верхние/нижние знаки берутся соответственно при $x > 0{\text{/}}x < 0$.

Коэффициенты ${{a}_{0}}(s)$, ${{a}_{2}}(s)$ определяют симметричную часть соответственно ${{a}_{1}}(s)$, ${{a}_{3}}(s)$ – антисимметричную часть вклада трещины в решение. Систему уравнений (3.1) можно разделить на две независимые подсистемы для четных и нечетных коэффициентов. Сложим и вычтем попарно первое и второе уравнения, третье и четвертое. Используем подстановку

(3.2)

${{\mu }_{j}}{\text{th}}{{\mu }_{j}} = \frac{{{{F}^{2}}{{s}^{2}}}}{{\beta \mu _{j}^{4} + 1 - \delta }},\quad \delta = \sigma {{F}^{2}}{{s}^{2}}$

которая следует из дисперсионного соотношения, и получаем

(3.3)

$\sum\limits_{j = - 2}^\infty \frac{{{{\alpha }_{j}}(\alpha _{j}^{2} + (2 - \nu ){{s}^{2}})({{a}_{1}}{{\alpha }_{j}} + {{a}_{3}}\alpha _{j}^{3})}}{{K_{2}^{'}\left( {{{\alpha }_{j}},s} \right)(\beta \mu _{j}^{4} + 1 - \delta )}} = - \sum\limits_{j = - 2}^\infty \frac{{{{\alpha }_{j}}(\alpha _{j}^{2} + (2 - \nu ){{s}^{2}})\psi ({{\alpha }_{j}})}}{{K_{2}^{'}\left( {{{\alpha }_{j}},s} \right)(\beta \mu _{j}^{4} + 1 - \delta )}}$

$\sum\limits_{j = - 2}^\infty \frac{{(\alpha _{j}^{2} + \nu {{s}^{2}})({{a}_{0}} + {{a}_{2}}\alpha _{j}^{2})}}{{K_{2}^{'}\left( {{{\alpha }_{j}},s} \right)(\beta \mu _{j}^{4} + 1 - \delta )}} = \sum\limits_{j = - 2}^\infty \frac{{(\alpha _{j}^{2} + \nu {{s}^{2}})\psi ({{\alpha }_{j}})}}{{K_{2}^{'}({{\alpha }_{j}},s)(\beta \mu _{j}^{4} + 1 - \delta )}}$

(3.4)

С помощью теории вычетов преобразуем выражение в левой части первого уравнения системы (3.3) через вычеты в корнях полинома, стоящего в знаменателе, замыкая контур интегрирования сначала в верхней полуплоскости, а затем в нижней,

$\sum\limits_{j = - 2}^\infty \frac{{(\alpha _{j}^{2} + \nu {{s}^{2}})({{a}_{1}}{{\alpha }_{j}} + {{a}_{3}}\alpha _{j}^{3})}}{{K_{2}^{'}\left( {{{\alpha }_{j}},s} \right)(\beta \mu _{j}^{4} + 1 - \delta )}} = \frac{1}{{2\pi i}}\int\limits_{ - \infty }^\infty \frac{{({{\alpha }^{2}} + \nu {{s}^{2}})({{a}_{1}}\alpha + {{a}_{3}}{{\alpha }^{3}})d\alpha }}{{{{K}_{2}}(\alpha ,s)(\beta {{{({{\alpha }^{2}} + {{s}^{2}})}}^{2}} + 1 - \delta )}} - $

$ - \;\sum\limits_{k = 1}^2 \frac{{(\eta _{k}^{2} + \nu {{s}^{2}})({{a}_{1}}{{\eta }_{k}} + {{a}_{3}}\eta _{k}^{3})}}{{{{K}_{2}}({{\eta }_{k}})4\beta {{\eta }_{k}}(\eta _{k}^{2} + {{s}^{2}})}} = \sum\limits_{j = - 2}^\infty \frac{{(\alpha _{j}^{2} + \nu {{s}^{2}})( - {{a}_{1}}{{\alpha }_{j}} - {{a}_{3}}\alpha _{j}^{3})}}{{K_{2}^{'}\left( { - {{\alpha }_{j}},s} \right)(\beta \mu _{j}^{4} + 1 - \delta )}} + $

$ + \;\frac{1}{{4\beta {{F}^{2}}{{s}^{2}}}}\sum\limits_{k = 1}^4 \frac{{(\eta _{k}^{2} + \nu {{s}^{2}})({{a}_{1}}{{\eta }_{k}} + {{a}_{3}}\eta _{k}^{3})}}{{{{\eta }_{k}}(\eta _{k}^{2} + {{s}^{2}})}},\quad {{\eta }_{k}} = \pm {{\left( { \pm i{{{\left( {\frac{{1 - \delta }}{\beta }} \right)}}^{{1/2}}} - {{s}^{2}}} \right)}^{{1/2}}}$

Отсюда находим

(3.5)

$\sum\limits_{j = - 2}^\infty \frac{{(\alpha _{j}^{2} + \nu {{s}^{2}})({{a}_{1}}{{\alpha }_{j}} + {{a}_{3}}\alpha _{j}^{3})}}{{K_{2}^{'}\left( {{{\alpha }_{j}},s} \right)(\beta \mu _{j}^{4} + 1 - \delta )}} = \frac{1}{{4\beta {{F}^{2}}{{s}^{2}}}}\sum\limits_{k = 1}^2 \frac{{(\eta _{k}^{2} + \nu {{s}^{2}})({{a}_{1}} + {{a}_{3}}\eta _{k}^{2})}}{{(\eta _{k}^{2} + {{s}^{2}})}} = 0$

Подставляя значения корней ${{\eta }_{k}}$ в соотношение (3.5), после преобразований получаем

${{a}_{1}}(s) = (2 - \nu ){{s}^{2}}{{a}_{3}}(s)$

Из второго уравнения системы (3.3) выводим

${{a}_{3}}(s)\sum\limits_{j = - 2}^\infty \frac{{\alpha _{j}^{2}{{{(\alpha _{j}^{2} + (2 - \nu ){{s}^{2}})}}^{2}}{{\mu }_{j}}{\text{th}}{{\mu }_{j}}}}{{K_{2}^{'}\left( {{{\alpha }_{j}},s} \right)}} = - \sum\limits_{j = - 2}^\infty \frac{{{{\alpha }_{j}}(\alpha _{j}^{2} + (2 - \nu ){{s}^{2}})\psi ({{\alpha }_{j}}){{\mu }_{j}}{\text{th}}{{\mu }_{j}}}}{{K_{2}^{'}\left( {{{\alpha }_{j}},s} \right)}}$

Аналогичным образом преобразуем выражение в левой части последнего уравнения системы (3.4). Получаем

$\sum\limits_{j = - 2}^\infty \frac{{{{\alpha }_{j}}(\alpha _{j}^{2} + (2 - \nu ){{s}^{2}})({{a}_{0}} + {{a}_{2}}\alpha _{j}^{2})}}{{K_{2}^{'}\left( {{{\alpha }_{j}},s} \right)(\beta \mu _{j}^{4} + 1 - \delta )}} = \frac{1}{{4\beta {{F}^{2}}{{s}^{2}}}}\sum\limits_{k = 1}^2 \frac{{(\eta _{k}^{2} + (2 - \nu ){{s}^{2}})({{a}_{0}} + {{a}_{2}}\eta _{k}^{2})}}{{\eta _{k}^{2} + {{s}^{2}}}} = 0$

Подставляя значения ${{\eta }_{k}}$, после преобразований находим

(3.6)

${{a}_{0}}(s) = \nu {{s}^{2}}{{a}_{2}}(s)$

Из первого уравнения системы (3.4) имеем

(3.7)

${{a}_{2}}(s)\Delta (s) = - \sum\limits_{j = - 2}^\infty \frac{{(\alpha _{j}^{2} + \nu {{s}^{2}})\psi ({{\alpha }_{j}}){{\mu }_{j}}{\text{th}}{{\mu }_{j}}}}{{K_{2}^{'}({{\alpha }_{j}},s)}},\quad \Delta (s) = \sum\limits_{j = - 2}^\infty \frac{{{{{(\alpha _{j}^{2} + \nu {{s}^{2}})}}^{2}}{{\mu }_{j}}{\text{th}}{{\mu }_{j}}}}{{K_{2}^{'}({{\alpha }_{j}},s)}}$

Таким образом, коэффициенты ${{a}_{n}}(s)$ найдены в явном виде.

Прогиб пластин определяется выражением

(3.8)

$W(x,y) = - \frac{{{{q}_{0}}}}{\pi }\int\limits_{ - \infty }^\infty {{{\text{e}}}^{{isy}}}\frac{{sin(bs)}}{s}\left[ {\Lambda (x,s) + {{U}_{2}}(x,s) + {{U}_{3}}(x,s)} \right]ds$

${{U}_{2}}(x,s) = {{a}_{2}}(s)\sum\limits_{j = - 2}^\infty \frac{{{{{\text{e}}}^{{i{{\alpha }_{j}}|x|}}}(\alpha _{j}^{2} + \nu {{s}^{2}}){{\mu }_{j}}{\text{th}}{{\mu }_{j}}}}{{K_{2}^{'}({{\alpha }_{j}},s)}}$

${{U}_{3}}(x,s) = \mp {{a}_{3}}(s)\sum\limits_{j = - 2}^\infty \frac{{{{{\text{e}}}^{{i{{\alpha }_{j}}|x|}}}{{\alpha }_{j}}(\alpha _{j}^{2} + (2 - \nu ){{s}^{2}}){{\mu }_{j}}{\text{th}}{{\mu }_{j}}}}{{K_{2}^{'}({{\alpha }_{j}},s)}}$

где знак –/+ берется соответственно при $x > 0{\text{/}}x < 0$. Функция $\Lambda (x,s)$ представляет решение, соответствующее бесконечной упругой плавающей пластине без трещины, а функции ${{U}_{2}}(x,s)$ и ${{U}_{3}}(x,s)$ описывают соответственно симметричную и антисимметричную части вклада трещины в решение. Подынтегральные функции экспоненциально затухают при $\left| s \right| \to \infty $.

Если скорость нагрузки меньше критической, то ${{\mu }_{0}}(s) < \left| s \right|$ при любых значениях параметра $s$, тогда ${{\alpha }_{0}}(s)$ имеет мнимые значения и волн в этом случае не наблюдается. Если скорость нагрузки больше критической, то существуют значения ${{s}_{ - }}$ и ${{s}_{ + }}$ такие, что ${{\mu }_{0}}(s) > \left| s \right|$ при ${{s}_{ - }} < \left| s \right| < {{s}_{ + }}$. Проведенные расчеты показали, что при скорости нагрузки, большей критической, в случае пластин одинаковой толщины существуют два значения $s_{ - }^{ * }$ и $s_{ + }^{ * }$, экстремально близкие к значениям ${{s}_{ - }}$ и ${{s}_{ + }}$, $s_{ - }^{ * } < {{s}_{ - }}$, $s_{ + }^{ * } > {{s}_{ + }}$, при которых функция $\Delta (s)$ обращается в нуль. Таким образом, подынтегральная функция ${{U}_{2}}(x,s)$ имеет полюсы в этих точках. Вычеты подынтегральной функции в этих точках определяют краевые волноводные моды с волновыми числами $s_{ - }^{ * }$ и $s_{ + }^{ * }$. Если скорость нагрузки больше второй критической скорости, равной $\sqrt {gH} $ и совпадающей с максимальным значением фазовой и групповой скоростей поверхностных волн в жидкости, то ${{s}_{ - }} = s_{ - }^{ * } = 0$. В этом случае сзади области давления образуется зона тени, где волн нет [11].

При вычислении прогиба пластин при скорости, большей критической, важно правильно выбрать путь обхода полюсов функции ${{U}_{2}}(s)$: волны с волновым числом $s_{ - }^{ * }$ имеют групповую скорость меньше фазовой скорости и распространяются сзади области нагрузки, а волны, соответствующие волновому числу $s_{ + }^{ * }$, имеют групповую скорость больше фазовой и распространяются перед нагрузкой. Легко показать, что при $\left| s \right| < {{s}_{ - }}$ и $\left| s \right| > {{s}_{ + }}$ функции $\Lambda (x,s)$, ${{U}_{2}}(x,s)$, ${{U}_{3}}(x,s)$ являются действительными, при ${{s}_{ - }} < \left| s \right| < {{s}_{ + }}$ – комплексными. Формула для прогиба пластин принимает вид

$W(x,y) = - \frac{{2{{q}_{0}}}}{\pi }{\text{v}}.{\text{p}}.\int\limits_0^{{{s}_{ - }}} \frac{{cos(sy)sin(bs)}}{s}\left[ {\Lambda (x,s) + {{U}_{2}}(x,s) + {{U}_{3}}(x,s)} \right]ds - $

$ - \;\frac{{2{{q}_{0}}}}{\pi }{\text{v}}.{\text{p}}.\int\limits_{{{s}_{ + }}}^\infty \frac{{cos(sy)sin(bs)}}{s}\left[ {\Lambda (x,s) + {{U}_{2}}(x,s) + {{U}_{3}}(x,s)} \right]ds - $

$ - \;\frac{{2{{q}_{0}}}}{\pi }\int\limits_{{{s}_{ - }}}^{{{s}_{ + }}} \frac{{sin(bs)}}{s}{\text{Re}}\left\{ {{{{\text{e}}}^{{isy}}}[\Lambda (x,s) + {{U}_{2}}(x,s) + {{U}_{3}}(x,s)]} \right\}ds + $

(3.9)

$ + \;2{{q}_{0}}\left( {\frac{{sin(s_{ + }^{ * }y)sin(bs_{ + }^{ * })}}{{s_{ + }^{ * }}}{\text{Res}}{{U}_{2}}(x,s_{ + }^{ * }) - \frac{{sin(s_{ - }^{ * }y)sin(bs_{ - }^{ * })}}{{s_{ - }^{ * }}}{\text{Res}}{{U}_{2}}(x,s_{ - }^{ * })} \right)$

где символы v.p. обозначают интеграл в смысле главного значения. При интегрировании, чтобы избежать корневой особенности при $s = {{\mu }_{0}}$, вводится замена переменной, указанная выше. Тогда подынтегральная функция становится регулярной на всей действительной оси за исключением полюсов в точках $s_{ - }^{ * }$, $s_{ + }^{ * }$. Отметим, что амплитуда краевой моды пропорциональна величине $sin(s_{ - }^{ * }b)$ или $sin(s_{ + }^{ * }b)$. Поэтому при соответствующих значениях параметра $b$ она может быть равной нулю.

4. РЕШЕНИЕ ЗАДАЧИ ПРИ НАЛИЧИИ ВЕРТИКАЛЬНОЙ СТЕНКИ

В случае контакта плавающей упругой пластины с вертикальной стенкой решение можно получить с помощью метода отражения. В силу симметрии ${{a}_{1}}(s) = {{a}_{3}}(s) = 0$. В случае свободного края для коэффициентов ${{a}_{0}}(s)$, ${{a}_{2}}(s)$ получаются соотношения (3.6), (3.7), только в (3.7) правая часть увеличивается в два раза, а в формуле (3.9) к члену $\Lambda (x,s)$ добавляется аналогичный член ${{\Lambda }_{1}}(x,s)$, соответствующий отраженной области давления с центром в точке $( - {{x}_{0}},0)$.

В случае примороженного края из граничных условий получаем систему уравнений для коэффициентов ${{a}_{0}}(s)$, ${{a}_{2}}(s)$

(4.1)

$\sum\limits_{j = - 2}^\infty \frac{{({{a}_{0}} + {{a}_{2}}\alpha _{j}^{2}){{\mu }_{j}}{\text{th}}{{\mu }_{j}}}}{{K_{2}^{'}({{\alpha }_{j}},s)}} = - 2\sum\limits_{j = - 2}^\infty \frac{{\psi ({{\alpha }_{j}}){{\mu }_{j}}{\text{th}}{{\mu }_{j}}}}{{K_{2}^{'}({{\alpha }_{j}},s)}}$

$\sum\limits_{j = - 2}^\infty \frac{{{{\alpha }_{j}}({{a}_{0}} + {{a}_{2}}\alpha _{j}^{2}){{\mu }_{j}}{\text{th}}{{\mu }_{j}}}}{{K_{2}^{'}({{\alpha }_{j}},s)}} = 0$

Используем подстановку (3.2) и преобразуем выражение в левой части второго уравнения системы (4.1) через вычеты в корнях полинома в знаменателе, замыкая контур интегрирования сначала в верхней полуплоскости, а затем в нижней. Подставляя в полученные выражения значения корней, находим ${{a}_{2}}(s) = 0$. Из первого уравнения системы (4.1) выражаем ${{a}_{0}}(s)$

${{a}_{0}}(s)\sum\limits_{j = - 2}^\infty \frac{{{{\mu }_{j}}{\text{th}}{{\mu }_{j}}}}{{K_{2}^{'}({{\alpha }_{j}},s)}} = - 2\sum\limits_{j = - 2}^\infty \frac{{\psi ({{\alpha }_{j}}){{\mu }_{j}}{\text{th}}{{\mu }_{j}}}}{{K_{2}^{'}({{\alpha }_{j}},s)}}$

Прогиб ледяного покрова определяется формулами

$W(x,y) = - \frac{{{{q}_{0}}}}{\pi }\int\limits_{ - \infty }^\infty {{{\text{e}}}^{{isy}}}\frac{{sin(bs)}}{s}\left( {\Lambda (x,s) + {{\Lambda }_{1}}(x,s) + {{a}_{0}}(s)\sum\limits_{j = - 2}^\infty \frac{{{{{\text{e}}}^{{i{{\alpha }_{j}}x}}}{{\mu }_{j}}{\text{th}}{{\mu }_{j}}}}{{K_{2}^{'}({{\alpha }_{j}},s)}}} \right)ds$

${{\Lambda }_{1}}(x,s) = \frac{1}{{2\pi i}}\int\limits_{ - \infty }^\infty \frac{{{{{\text{e}}}^{{ - i\alpha (x + {{x}_{0}})}}}({{{\text{e}}}^{{i\alpha a}}} - {{{\text{e}}}^{{ - i\alpha a}}})\sqrt {{{\alpha }^{2}} + {{s}^{2}}} {\text{th}}(\sqrt {{{\alpha }^{2}} + {{s}^{2}}} )d\alpha }}{{\alpha {{K}_{2}}(\alpha ,s)}}$

5. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ

Проведены численные расчеты для полубесконечного ледяного покрова с прямолинейной трещиной при входных параметрах (2.2) и ${{q}_{0}} = 1000$ Н/м², $a = 10$ м, $b = 20$ м, ${{x}_{0}} = 50$ м. Толщина нагруженной пластины ${{h}_{2}} = 2$ м, толщина второй пластины принималась ${{h}_{1}} = 1,\;2$ или 3 м. Минимальные фазовые скорости изгибно-гравитационных волн в пластинах толщиной 1, 2 и 3 м равны соответственно 15.59, 20.14 и 23.38 м/с. Скорость движения нагрузки менялась.

Скорость V = 15 м/с является докритической при выбранных параметрах, прогиб нагруженной пластины локализован вблизи области нагрузки, вдали от нее затухает. Прогиб второй пластины во всех случаях (при толщинах ${{h}_{1}} = 1,\;2,\;3$ м) значительно меньше и локализован у кромки вблизи области нагрузки, волн нет.

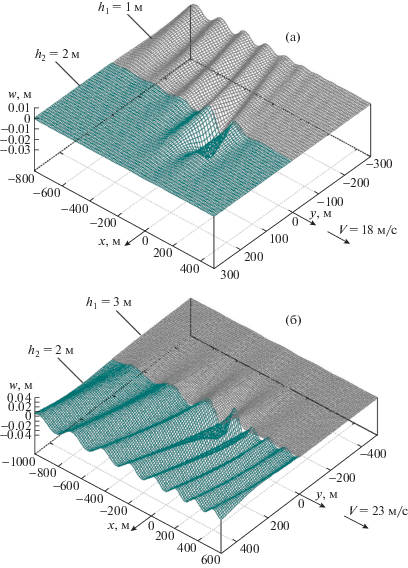
Скорость V = 18 м/с является сверхкритической для пластины толщиной 1 м и докритической для пластины толщиной 2 м. На фиг. 2a представлены трехмерные графики вертикальных смещений пластин толщиной ${{h}_{1}} = 1$ м и ${{h}_{2}} = 2$ м при скорости V = 18 м/с. Видно, что в тонкой пластине появляется волновое движение, которое возбуждает в толстой пластине волны вблизи края, затухающие вдали от кромки. На фиг. 2б изображены аналогичные графики для пластин толщиной ${{h}_{2}} = 2$ м и ${{h}_{1}} = 3$ м при скорости V = 23 м/с. В этом случае для пластины толщиной ${{h}_{2}}$ = 2 м скорость $V = 23$ м/с является сверхкритической, а для пластины толщиной ${{h}_{1}} = 3$ м – докритической. В нагруженной пластине перед нагрузкой распространяются короткие изгибные волны, а сзади нее – длинные гравитационные волны. Они возбуждают во второй пластине волны вблизи кромки, затухающие вдали от края.

Фиг. 2.

Вертикальные смещения пластин – (а) с толщинами ${{h}_{1}} = 1$ м и ${{h}_{2}} = 2$ м при V = 18 м/с и (б) с толщинами ${{h}_{2}} = 2$ м и ${{h}_{1}} = 3$ м при V = 23 м/с

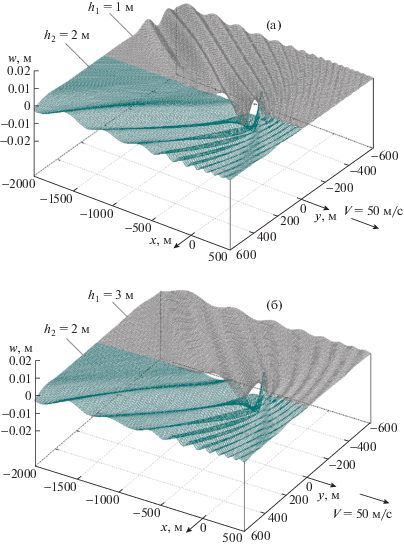
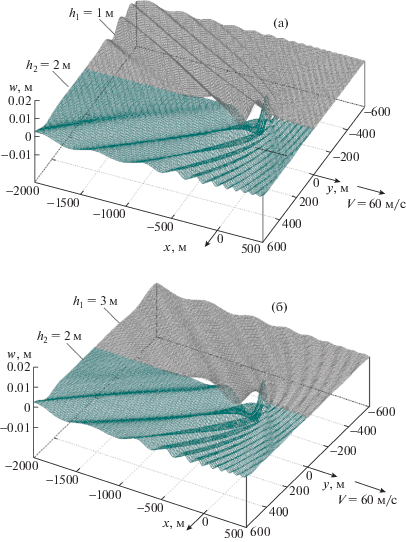
Скорости V = 30, 50 и 60 м/с являются сверхкритическими для изгибно-гравитационных волн в пластинах толщиной 1, 2 и 3 м. На фиг. 3 приведены трехмерные графики вертикальных смещений пластин толщиной ${{h}_{1}} = 1$ м и ${{h}_{2}} = 2$ м (а), а также ${{h}_{2}} = 2$ м и ${{h}_{1}} = 3$ м (б) при скорости V = = 30 м/с. Движущаяся нагрузка вызывает волновое движение в обеих пластинах впереди и сзади нагрузки. Волны сзади нагрузки имеют приблизительно одинаковую длину, так как левые ветви кривых фазовых скоростей пластин разной толщины практически совпадают (фиг. 1). А волны, распространяющиеся перед нагрузкой, имеют различные длины по разные стороны трещины, в тонкой пластине они короче. На фиг. 4 показаны трехмерные графики вертикальных смещений пластин толщиной ${{h}_{1}} = 1$ м и ${{h}_{2}} = 2$ м (a), а также ${{h}_{2}} = 2$ м и ${{h}_{1}} = 3$ м (б) при скорости V = 50 м/с, а на фиг. 5 – аналогичные графики при скорости V = 60 м/с. Увеличение скорости приводит к тому, что волны перед нагрузкой становятся короче, а сзади нее – длиннее. Скорость V = 60 м/с является сверхкритической по отношению к характерной скорости волн в жидкости $\sqrt {gH} $ = 58.16 м/с. В этом случае в нагруженной пластине сзади области нагрузки образуется зона тени, где волн нет [11].

Фиг. 3.

Вертикальные смещения пластин при V = 30 м/с – (а) с толщинами h₁ = 1 м и h₂ = 2 м и (б) с толщинами h₂ = 2 м и ${{h}_{1}} = 3$ м

Фиг. 4.

Вертикальные смещения пластин при V = 50 м/с – (а) с толщинами h₁ = 1 м и h₂ = 2 м и (б) с толщинами h₂ = 2 м и ${{h}_{1}} = 3$ м

Фиг. 5.

Вертикальные смещения пластин при V = 60 м/с – (а) с толщинами h₁ = 1 м и h₂ = 2 м и (б) с толщинами h₂ = 2 м и ${{h}_{1}} = 3$ м

В случае контакта пластин одинаковой толщины прогиб пластин подобен соответствующему прогибу для бесконечной пластины. В проведенных расчетах амплитуды краевых мод были небольшими, амплитуда краевой волны с меньшим волновым числом была во много раз меньше, чем амплитуда краевой моды с большим волновым числом. На фиг. 6 приведены графики прогиба кромки нагруженной пластины в зависимости от координаты $y$ при различных соотношениях толщин пластин, а также для пластины со свободным краем вблизи вертикальной стенки при скоростях нагрузки $V = 21,\;24,\;30$ м/с. Отметим, что масштаб горизонтальных размеров выбран разный при $y < 0$ и $y > 0$, чтобы лучше представить отличие графиков в различных случаях. Видно, что при наличии стенки амплитуды волн значительно выше.

Фиг. 6.

Прогиб кромки нагруженной пластины в зависимости от координаты y при различных скоростях движения нагрузки – (а) V = 21 м/с, (б) V = 24 м/с, (в) V = 30 м/с

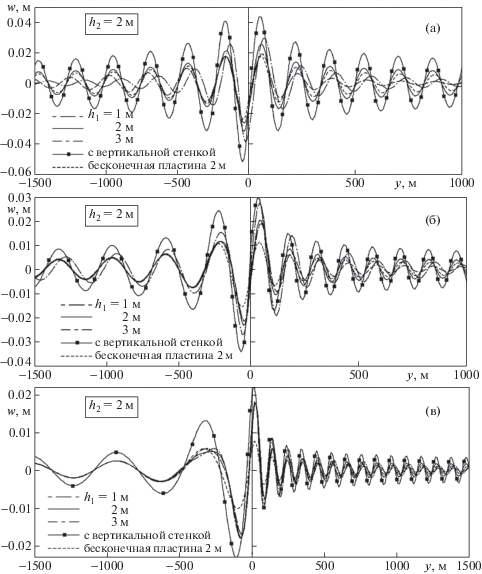
Сравним теперь амплитуды волн в других случаях (при отсутствии стенки). Скорость V = 21 м/с является околокритической для пластины толщиной $h = 2$ м. Известно из предшествующих исследований, что в случае бесконечной пластины максимальные амплитуды изгибно-гравитационных волн достигаются на околокритических режимах. Из графиков видно, что вблизи области нагрузки амплитуды волн в случае пластин толщиной ${{h}_{2}} = 2$ м и ${{h}_{1}} = 3$ м выше, чем в других случаях, т.е. влияние толстой пластины подобно роли вертикальной стенки. Вдали от области нагрузки амплитуды волн впереди и сзади движущегося тела максимальны для случая пластин одинаковой толщины (фиг. 6а) – проявляется влияние краевой моды.

Скорость V = 24 м/с является околокритической для пластины толщиной 3 м. При этой скорости максимальные амплитуды волн при отсутствии стенки наблюдаются в случае пластин толщиной h₂ = 2 м и ${{h}_{1}} = 3$ м вблизи области давления и в некоторой области впереди и сзади нее. Однако дальше впереди нагрузки амплитуды волн пластин одинаковой толщины становятся преобладающими, проявляет себя краевая мода (фиг. 6б). Сзади области нагрузки амплитуды волн в случае пластин ${{h}_{2}} = 2$ м и ${{h}_{1}} = 3$ м существенно больше, чем в других случаях.

Скорость V = 30 м/с удалена от значений критических скоростей. В этом случае вблизи области нагрузки и сзади нее амплитуды волн пластин с различным соотношением толщин при отсутствии стенки приблизительно равны. Впереди нагрузки на небольших расстояниях преобладающими являются амплитуды волн пластин толщиной ${{h}_{2}} = 2$ м и ${{h}_{1}} = 3$ м, а при удалении от области давления амплитуды волн пластин одинаковой толщины становятся максимальными (фиг. 6в).

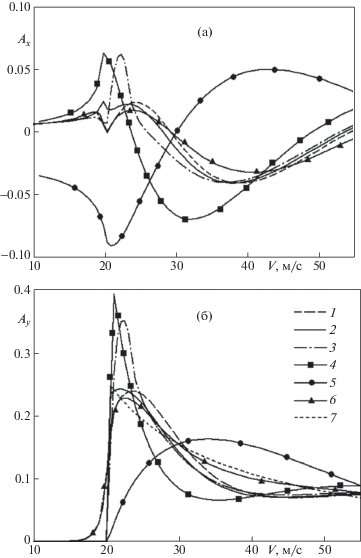
На фиг. 7 представлены зависимости безразмерных коэффициентов сил волнового сопротивления ${{A}_{y}}$ и боковой силы ${{A}_{x}}$ от скорости движения нагрузки для пластин различной толщины и при наличии стенки, а также для ледяной пластины, контактирующей со свободной поверхностью жидкости [30]. Отметим, что в работе [30] график зависимости боковой силы от скорости приведен с ошибкой. Видно, что для пластины со свободным краем максимальные значения силы волнового сопротивления достигаются при значениях скорости движения нагрузки, близкой к критической скорости волн в пластине. В случае пластин толщиной ${{h}_{2}} = 2$ м и ${{h}_{1}} = 3$ м, а также для пластины со свободным краем вблизи стенки максимальные значения волновых сил значительно больше, чем в других случаях. Воздействие толстой пластины, по-видимому, аналогично отражению от твердой стенки. Для пластины с примороженным краем вблизи стенки графики зависимости сил от скорости сильно отличаются от всех других случаев.

Фиг. 7.

Зависимости безразмерных коэффициентов волновых сил ${{A}_{x}}$ (a) и ${{A}_{y}}$ (б) от скорости движения нагрузки в различных случаях: 1–3 – ${{h}_{1}} = 1,\;2,\;3$ м, 4 – для пластины со свободным краем вблизи стенки, 5 – для пластины с примороженным краем вблизи стенки, 6 – для пластины, контактирующей со свободной поверхностью жидкости, 7 – для бесконечной пластины толщиной $h = 2$ м

ЗАКЛЮЧЕНИЕ

Построено аналитическое решение задачи о генерации изгибно-гравитационных волн в ледяном покрове с прямолинейной трещиной равномерно движущейся нагрузкой. Проанализировано влияние скорости и толщины пластин на характер волнового движения при докритическом и сверхкритическом режимах, а также на волновые силы, действующие на движущееся тело.

Показано, что в случае пластин одинаковой толщины, а также для пластины со свободным краем вблизи вертикальной стенки при сверхкритических скоростях существуют две краевые моды с разными волновыми числами. Мода с меньшим волновым числом имеет групповую скорость меньше фазовой и распространяется сзади нагрузки, мода с большим волновым числом имеет групповую скорость выше фазовой и распространяется перед нагрузкой. С наибольшей амплитудой краевые волны распространяются при контакте пластины с твердой вертикальной стенкой.

Список литературы

Хейсин Д.Е. Перемещение нагрузки по упругой пластинке, плавающей на поверхности идеальной жидкости // Изв. АН СССР. ОТН. Мех. и Машиностр. 1963. № 1. С. 178–180.
Доценко С.Ф. Установившиеся гравитационно-упругие трехмерные волны от движущихся возмущений // Цунами и внутренние волны. Севастополь: Изд. МГИ АН УССР, 1976. С. 144–155.
Хейсин Д.Е. Динамика ледяного покрова. Л.: Гидрометеоиздат, 1967. 215 с.
Черкесов Л.В. Поверхностные и внутренние волны. Киев: Наук. думка, 1973. 247 с.
Squire V.A., Hosking R.J., Kerr A.D. et al. Moving Loads on Ice Plates. Dordrecht: Kluwer, 1996. 244 p.
Козин В.М., Жесткая В.Д., Погорелова А.В., Чижиумов С.Д., Джабраилов М.Р., Морозов В.С., Кустов А.Н. Прикладные задачи динамики ледяного покрова. М.: Изд-во “Академия Естествознания”, 2008. 329 с.
Bukatov A.E., Zharkov V.V. Formation of the Ice Cover’s Flexural Oscillations by Action of Surface and Internal Ship Waves. Part I. Surface Waves // Intern. J. Offshore Polar Engng. 1997. V. 7. № 1. P. 1–12.
Squire V.A. Synergies between VLFS Hydroelasticity and Sea Ice Research // Int. J. Offshore Polar Eng. ISOPE. 2008. V. 18. № 4. P. 241–253.
Козин В.М., Погорелова А.В., Земляк В.Л., Верещагин В.Ю., Рогожникова В.Е., Кипин Д.Ю., Матюшина А.А. Экспериментально-теоретические исследования зависимости параметров, распространяющихся в плавающей пластине изгибно-гравитационных волн от условий их возбуждения. Новосибирск: Изд-во СО РАН, 2016. 221 с.
Takizawa T. Deflection of a floating sea ice sheet induced by moving load // Cold Regions Sci. Tech. 1985. V. 11. P. 171–180.
Davys J.W., Hosking R.J., Sneyd A.D. Waves due to steadily moving source on a floating ice plate // J. Fluid Mech. 1985. V. 158. P. 269–287.
Milinazzo F., Shinbrot M., Evans N.W. A mathematical analysis of the steady response of floating ice to the uniform motion of a rectangle load // J. Fluid Mech. 1995. V. 287. P. 173–197.
Schulkes R.M.S.M., Hosking R.J., Sneyd A.D. Waves due to a steadily moving source on a floating ice plate. Part 2 // J . Fluid Mech. 1987. V. 180. P. 297–318.
Yeung R.W., Kim J.W. Effects of a translating load on a floating plate-structural drag and plate deformation // J. Fluids Struct. 2000. V. 14. № 7. P. 993–1011.
Козин В.М., Погорелова А.В. Волновое сопротивление амфибийных судов на воздушной подушке при движении по ледяному покрову // ПМТФ. 2003. Т. 44. № 2. С. 49–55.
Погорелова А.В. Особенности волнового сопротивления СВПА при нестационарном движении по ледяному покрову // ПМТФ. 2008. Т. 49. № 1. С. 89–99.
Гольдштейн Р.В., Марченко А.В., Семенов А.Ю. Краевые волны в жидкости под упругой пластиной с трещиной // ДАН. 1994. Т. 339. № 3. С. 331–334.
Evans D.V., Porter R. Wave scattering by narrow cracks in ice sheets floating on water of finite depth // J. Fluid Mech. 2003. V. 484. P. 143–165.
Марченко А.В. Собственные колебания гряды торосов в упругом ледяном покрове, плавающем на поверхности бесконечно глубокой жидкости // Изв. РАН. МЖГ. 1995. № 6. С. 99–105.
Chung H., Linton C.M. Reflection and transmission of waves across a gap between two semi-infinite elastic plates on water // Quart. J. Appl. Math. 2005. V. 58. № 1. P. 1–15.
Waughan G.L., Williams T.D., Squire V.A. Perfect transmission and asymptotic solutions for reflection of ice-coupled waves by inhomogeneities // Wave Motion. 2007. V. 44. P. 371–384.
Chung H., Fox C. A direct relationship between bending waves and transition conditions of floating plates // Wave Motion. 2009. V. 46. P. 468–479.
Williams T.D., Porter R. The effect of submergence on the scattering by the interface between two semi-infinite sheets // J. Fluids Struct. 2009. V. 25. P. 777–793.
Ткачева Л.А. Воздействие локальной периодической по времени нагрузки на ледяной покров с трещиной // ПМТФ. 2017. Т. 58. № 6. С. 133–148.
Mapчeнкo A.B. Parametric excitation of flexural-gravity edge waves in the fluid beneath an elastic ice sheet with a crack // Europ. J. Mech., B/Fluids. 1999. V. 18. № 3. P. 511–525.
Жесткая В.Д., Козин В.М. Исследования напряженно-деформированного состояния полубесконечного ледяного покрова под действием движущейся нагрузки // ПМТФ. 1994. Т. 35. № 5. С. 112–117.
Kashiwagi M. Transient responses of a VLFS during landing and take-off of an airplane // J. Mar. Sci. Technol. 2004. V. 9. № 1. P. 14–23.
Brocklehurst P. Hydroelastic Waves and their Interaction with Fixed Structures (PhD thesis). University of East Anglia. UK, 2012.
Shishmarev K., Khabakhpasheva T., Korobkin A. The response of ice cover to a load moving along a frozen channel // Appl. Ocean Res. 2016. V. 59. P. 313–326.
Sturova I.V., Tkacheva L.A. Wave motion in a fluid under an inhomogeneous ice cover // J. Phys.: Conf. Ser. 2017. V. 894. P. 1–8. https://doi. org/10.1088/1742-6596/894/1/012092
Нобл Б. Метод Винера–Хопфа для решения дифференциальных уравнений в частных производных. М.: Изд-во Иностр. лит., 1962. 279 с.
Гельфанд И.М., Шилов Г.Е. Обобщенные функции и действия над ними. М.: Физматгиз, 1958.
Лайтхилл Дж. Волны в жидкостях. М.: Изд-во Мир, 1981.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал