Известия РАН. Механика жидкости и газа, 2019, № 2, стр. 48-58

НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ ПЛАВАЮЩЕЙ ПРОДОЛЬНО СЖАТОЙ УПРУГОЙ ПЛАСТИНКИ ПРИ ВЗАИМОДЕЙСТВИИ ВОЛНОВЫХ ГАРМОНИК КОНЕЧНОЙ АМПЛИТУДЫ

А. А. Букатов^*

Морской гидрофизический институт РАН
Севастополь, Россия

Поступила в редакцию 14.05.2018
После доработки 25.06.2018
Принята к публикации 18.10.2018

DOI: 10.1134/S056852811902004X

Аннотация

Методом многих масштабов получены уравнения для трех нелинейных приближений изгибно-гравитационных колебаний продольно сжатой упругой пластинки, учитывающие нелинейность ускорения ее вертикальных смещений. Неограниченная в горизонтальных направлениях ледовая пластинка плавает на поверхности однородной идеальной жидкости. На основе полученных уравнений построены асимптотические разложения до величин третьего порядка малости для возвышения поверхности пластинка–жидкость и потенциала скорости движения жидких частиц при нелинейном взаимодействии двух гармоник прогрессивных поверхностных периодических волн. Выполнен анализ зависимости амплитудно-фазовых характеристик формируемого возвышения поверхности от глубины бассейна, параметров ледовой пластинки и взаимодействующих гармоник, нелинейности ускорения вертикальных смещений льда.

Ключевые слова: колебания плавающей пластинки, продольное сжимающее усилие, изгибно-гравитационные волны, волны конечной амплитуды, нелинейное взаимодействие волн

Исследования колебаний упругой плавающей пластинки в линейной постановке при отсутствии сжимающего усилия выполнено в [1–7], а при его наличии в [8–12]. Оценка нелинейных колебаний абсолютно гибкой плавающей пластинки проведена в работе [13]. Колебания конечной амплитуды без учета нелинейности ускорения вертикальных смещений плавающей упругой пластинки, обусловленных ее изгибом, рассматривались в [14–16]. Изучение влияния нелинейности ускорения вертикальных смещений упругой ледовой пластинки на распространение периодических поверхностных волн при отсутствии продольного сжатия проведено в [17], а при его наличии в [18]. Анализ нелинейных колебаний абсолютно гибкой пластинки сформированных при взаимодействии прогрессивных поверхностных волн конечной амплитуды выполнен в [19].

Цель настоящей работы – исследование колебаний продольно сжатой упругой пластинки, формируемых при нелинейном взаимодействии бегущих периодических поверхностных волн.

1. ПОСТАНОВКА ЗАДАЧИ

Рассмотрим однородную идеальную несжимаемую жидкость, заполняющую неограниченный бассейн конечной глубины H. Поверхность жидкости покрыта тонкой продольно сжатой упругой пластинкой. В горизонтальных направлениях пластинка и жидкость неограниченны. Предполагая движение жидкости потенциальным, а колебания пластинки безотрывными в безразмерных величинах $x = k{{x}_{1}}$, $z = k{{z}_{1}}$, $t = \sqrt {kg} {{t}_{1}}$, $\zeta = k\zeta {\text{*}}$, $\varphi = ({{k}^{2}}{\text{/}}\sqrt {kg} )\varphi {\text{*}}$ (k – волновое число) задача заключается в решении уравнения Лапласа

(1.1)

${{\varphi }_{{xx}}} + {{\varphi }_{{zz}}} = 0,\quad - \infty < x < \infty ,\quad - H \leqslant z \leqslant \zeta $

для потенциала скорости φ(x, z, t) с граничными условиями на поверхности z = ζ пластинка–жидкость

(1.2)

$P = \frac{{\partial \varphi }}{{\partial t}} - \zeta - \frac{1}{2}\left[ {{{{\left( {\frac{{\partial \varphi }}{{\partial x}}} \right)}}^{2}} + {{{\left( {\frac{{\partial \varphi }}{{\partial z}}} \right)}}^{2}}} \right]$

и на дне (z = –H) бассейна

(1.3)

$\frac{{\partial \varphi }}{{\partial z}} = 0$

В начальный момент времени (t = 0)

(1.4)

$\zeta = f(x),\quad \frac{{\partial \zeta }}{{\partial t}} = 0$

Здесь ${{D}_{1}} = \frac{D}{{\rho g}}$, $D = \frac{{E{{h}^{3}}}}{{12(1 - {{\nu }^{2}})}}$, ${{Q}_{1}} = \frac{Q}{{\rho g}}$, $\kappa = h\frac{{{{\rho }_{1}}}}{\rho }$, где Е, h, ρ₁, ν – модуль нормальной упругости, толщина, плотность, коэффициент Пуассона пластинки; Q – продольное сжимающее усилие, приходящееся на единицу ширины пластинки; ζ(x, t) – возвышение поверхности пластинка–жидкость; ρ – плотность жидкости; g – ускорение силы тяжести.

Потенциал скорости φ(x, z, t) и возмущение поверхности пластинка–жидкость ζ(х, t) связаны кинематическим условием

(1.5)

$\frac{{\partial \zeta }}{{\partial t}} - \frac{{\partial \zeta }}{{\partial x}}\frac{{\partial \varphi }}{{\partial x}} + \frac{{\partial \varphi }}{{\partial z}} = 0$

В динамическом условии (1.2) полная производная с множителем κ может быть преобразована следующим образом

$\kappa k\frac{{{{d}^{2}}\zeta }}{{d{{t}^{2}}}} = \kappa k\frac{d}{{dt}}\left( {\frac{{d\zeta }}{{dt}}} \right) = \kappa k\frac{d}{{dt}}\left( {\frac{{\partial \zeta }}{{\partial t}} + \frac{{\partial \zeta }}{{\partial x}}u} \right) = \kappa k\left[ {\frac{\partial }{{\partial t}}\left( {\frac{{\partial \zeta }}{{\partial t}} + \frac{{\partial \zeta }}{{\partial x}}u} \right) + \frac{\partial }{{\partial x}}\left( {\frac{{\partial \zeta }}{{\partial t}} + \frac{{\partial \zeta }}{{\partial x}}u} \right)u} \right]$

Заменим горизонтальную составляющую скорости u производной от потенциала скорости φ(x, z, t) по горизонтальной координате х: $u = - \partial \varphi {\text{/}}\partial x$. Следовательно,

$\kappa k\frac{{{{d}^{2}}\zeta }}{{d{{t}^{2}}}} = \kappa k\left[ {\frac{\partial }{{\partial t}}\left( {\frac{{\partial \zeta }}{{\partial t}} - \frac{{\partial \zeta }}{{\partial x}}\frac{{\partial \varphi }}{{\partial x}}} \right) - \frac{\partial }{{\partial x}}\left( {\frac{{\partial \zeta }}{{\partial t}} - \frac{{\partial \zeta }}{{\partial x}}\frac{{\partial \varphi }}{{\partial x}}} \right)\frac{{\partial \varphi }}{{\partial x}}} \right]$

Из кинематического условия (1.5) находим

$\frac{{\partial \zeta }}{{\partial t}} - \frac{{\partial \zeta }}{{\partial x}}\frac{{\partial \varphi }}{{\partial x}} = - \frac{{\partial \varphi }}{{\partial z}}$

В результате

$\kappa k\frac{{{{d}^{2}}\zeta }}{{d{{t}^{2}}}} = \kappa k\left[ { - \frac{\partial }{{\partial t}}\frac{{\partial \varphi }}{{\partial z}} + \frac{\partial }{{\partial x}}\left( {\frac{{\partial \varphi }}{{\partial z}}} \right)\frac{{\partial \varphi }}{{\partial x}}} \right] = \kappa k\frac{\partial }{{\partial z}}\left[ {\frac{1}{2}{{{\left( {\frac{{\partial \varphi }}{{\partial x}}} \right)}}^{2}} - \frac{{\partial \varphi }}{{\partial t}}} \right]$

Таким образом, динамическое условие (1.2) в нелинейном случае принимает вид

(1.6)

${{D}_{1}}{{k}^{4}}\frac{{{{\partial }^{4}}\zeta }}{{\partial {{x}^{4}}}} + {{Q}_{1}}{{k}^{2}}\frac{{{{\partial }^{2}}\zeta }}{{\partial {{x}^{2}}}} + \kappa k\frac{\partial }{{\partial z}}\left[ {\frac{1}{2}{{{\left( {\frac{{\partial \varphi }}{{\partial x}}} \right)}}^{2}} - \frac{{\partial \varphi }}{{\partial t}}} \right] = P$

Выражение с множителем κ в (1.6) представляет собой инерцию вертикальных смещений льда, где первое слагаемое в скобках этого выражения характеризует нелинейность вертикального ускорения пластинки.

2. УРАВНЕНИЯ ДЛЯ НЕЛИНЕЙНЫХ ПРИБЛИЖЕНИЙ

Решение задачи (1.1), (1.3)–(1.6), сформулированной в безразмерных величинах, найдем методом многих масштабов [20].

Введем две новые медленно меняющиеся по сравнению с t = Т₀ переменные ${{T}_{1}} = \varepsilon t$, ${{T}_{2}} = {{\varepsilon }^{2}}t$, где ε малое, но конечное, и предположим, что

(2.1)

$\zeta = \varepsilon {{\zeta }_{0}},\quad \varphi = \varepsilon {{\varphi }_{0}},\quad f = \varepsilon {{f}_{0}},\quad {{\zeta }_{0}} = {{\zeta }_{1}} + \varepsilon {{\zeta }_{2}} + {{\varepsilon }^{2}}{{\zeta }_{3}} + O({{\varepsilon }^{3}})$

${{\varphi }_{0}} = {{\varphi }_{1}} + \varepsilon {{\varphi }_{2}} + {{\varepsilon }^{2}}{{\varphi }_{3}} + O({{\varepsilon }^{3}}),\quad {{f}_{0}} = {{f}_{1}} + \varepsilon {{f}_{2}} + {{\varepsilon }^{2}}{{f}_{3}} + O({{\varepsilon }^{3}})$

Подставив φ из (2.1) в (1.1) и (1.3), с точностью до величин третьего порядка малости получим

$\varepsilon \Delta {{\varphi }_{1}} + {{\varepsilon }^{2}}\Delta {{\varphi }_{2}} + {{\varepsilon }^{3}}\Delta {{\varphi }_{3}} = 0,\quad \varepsilon \frac{{\partial {{\varphi }_{1}}}}{{\partial z}} + {{\varepsilon }^{2}}\frac{{\partial {{\varphi }_{2}}}}{{\partial z}} + {{\varepsilon }^{3}}\frac{{\partial {{\varphi }_{3}}}}{{\partial z}} = 0,\quad \Delta = \frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{z}^{2}}}}$

Рассмотрим теперь динамическое (1.6), кинематическое (1.5) и начальное (1.4) условия.

Представим потенциал скорости поверхности пластинка–жидкость $z = \varepsilon {{\zeta }_{0}}$ в виде

(2.2)

$\varphi (x,\varepsilon {{\zeta }_{0}},t) = \varphi (x,0,t) + \varepsilon {{\zeta }_{0}}{{\varphi }_{z}}(x,0,t) + \frac{1}{2}{{\varepsilon }^{2}}\zeta _{0}^{2}{{\varphi }_{{zz}}}(x,0,t) + \ldots ..$

Подставим $\zeta = \varepsilon {{\zeta }_{0}}$, $f = \varepsilon {{f}_{0}}$ $\varphi (x,\varepsilon {{\zeta }_{0}},t)$ и ${{\varphi }_{z}}(x,\varepsilon {{\zeta }_{0}},t)$ в соответствующие условия (1.6) и (1.5), учитывая, что по правилу дифференцирования сложной функции частная производная по времени определяется выражением

$\frac{\partial }{{\partial t}} = \frac{\partial }{{\partial {{T}_{0}}}} + \varepsilon \frac{\partial }{{\partial {{T}_{1}}}} + {{\varepsilon }^{2}}\frac{\partial }{{\partial {{T}_{2}}}}$

и принимая во внимание зависимость ζ₀ от х и t в (2.2). Тогда, собрав коэффициенты при одинаковых степенях ε и приравняв их нулю, найдем следующие уравнения для определения нелинейных приближений [18]

(2.3)

$\frac{{{{\partial }^{2}}{{\varphi }_{n}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}{{\varphi }_{n}}}}{{\partial {{z}^{2}}}} = 0,\quad - \infty < x < \infty ,\quad - H \leqslant z \leqslant 0$

(2.4)

${{D}_{1}}{{k}^{4}}\frac{{{{\partial }^{4}}{{\zeta }_{n}}}}{{\partial {{x}^{4}}}} + {{Q}_{1}}{{k}^{2}}\frac{{{{\partial }^{2}}{{\zeta }_{n}}}}{{\partial {{x}^{2}}}} - \kappa k\frac{{{{\partial }^{2}}{{\varphi }_{n}}}}{{\partial z\partial {{T}_{0}}}} - \frac{{\partial {{\varphi }_{n}}}}{{\partial {{T}_{0}}}} + {{\zeta }_{n}} = F_{n}^{*},\quad z = 0$

(2.5)

$\frac{{\partial {{\zeta }_{n}}}}{{\partial {{T}_{0}}}} + \frac{{\partial {{\varphi }_{n}}}}{{\partial z}} = {{L}_{n}},\quad z = 0$

(2.6)

$\frac{{\partial {{\varphi }_{n}}}}{{\partial z}} = 0,\quad z = - H$

(2.7)

${{\zeta }_{n}} = {{f}_{n}}(x),\quad \frac{{\partial {{\zeta }_{n}}}}{{\partial {{T}_{0}}}} = {{G}_{n}},\quad t = 0$

Здесь

$F_{n}^{*} = {{F}_{n}} + F_{n}^{0},\quad {{F}_{1}} = F_{1}^{0} = {{L}_{1}} = {{G}_{1}} = 0,\quad n = 1,\;2,\;3$

${{F}_{2}} = {{\zeta }_{1}}\frac{{{{\partial }^{2}}{{\varphi }_{1}}}}{{\partial {{T}_{0}}\partial z}} + \frac{{\partial {{\varphi }_{1}}}}{{\partial {{T}_{1}}}} + \frac{{\partial {{\zeta }_{1}}}}{{\partial {{T}_{0}}}}\frac{{\partial {{\varphi }_{1}}}}{{\partial z}} - \frac{1}{2}\left[ {{{{\left( {\frac{{\partial {{\varphi }_{1}}}}{{\partial x}}} \right)}}^{2}} + {{{\left( {\frac{{\partial {{\varphi }_{1}}}}{{\partial z}}} \right)}}^{2}}} \right] + \kappa kN$

$N = \frac{{\partial {{\zeta }_{1}}}}{{\partial {{T}_{0}}}}\frac{{{{\partial }^{2}}{{\varphi }_{1}}}}{{\partial {{z}^{2}}}} + {{\zeta }_{1}}\frac{{{{\partial }^{3}}{{\varphi }_{1}}}}{{\partial {{T}_{0}}\partial {{z}^{2}}}} + \frac{{{{\partial }^{2}}{{\varphi }_{1}}}}{{\partial {{T}_{1}}\partial z}},\quad {{L}_{2}} = \frac{{\partial {{\zeta }_{1}}}}{{\partial x}}\frac{{\partial {{\varphi }_{1}}}}{{\partial x}} - {{\zeta }_{1}}\frac{{{{\partial }^{2}}{{\varphi }_{1}}}}{{\partial {{z}^{2}}}} - \frac{{\partial {{\zeta }_{1}}}}{{\partial {{T}_{1}}}}$

${{F}_{3}} = {{\zeta }_{1}}{{N}_{1}} + {{\zeta }_{2}}\frac{{{{\partial }^{2}}{{\varphi }_{1}}}}{{\partial {{T}_{0}}\partial z}} + \frac{{\partial {{\varphi }_{2}}}}{{\partial {{T}_{1}}}} + \frac{{\partial {{\varphi }_{1}}}}{{\partial {{T}_{2}}}} - \frac{{\partial {{\varphi }_{1}}}}{{\partial x}}\frac{{\partial {{\varphi }_{2}}}}{{\partial x}} - \frac{{\partial {{\varphi }_{1}}}}{{\partial z}}\frac{{\partial {{\varphi }_{2}}}}{{\partial z}} + {{N}_{2}} + \kappa k{{N}_{3}}$

${{N}_{1}} = \frac{{{{\partial }^{2}}{{\varphi }_{1}}}}{{\partial {{T}_{1}}\partial z}} + \frac{{{{\partial }^{2}}{{\varphi }_{2}}}}{{\partial {{T}_{0}}\partial z}} - \frac{{{{\partial }^{2}}{{\varphi }_{1}}}}{{\partial z\partial x}}\frac{{\partial {{\varphi }_{1}}}}{{\partial x}} + \frac{{{{\partial }^{2}}{{\varphi }_{1}}}}{{\partial {{z}^{2}}}}\left( {\frac{{\partial {{\zeta }_{1}}}}{{\partial {{T}_{0}}}} - \frac{{\partial {{\varphi }_{1}}}}{{\partial z}}} \right) + \frac{1}{2}{{\zeta }_{1}}\frac{{{{\partial }^{3}}{{\varphi }_{1}}}}{{\partial {{T}_{0}}\partial {{z}^{2}}}}$

${{N}_{2}} = \frac{{\partial {{\zeta }_{1}}}}{{\partial {{T}_{0}}}}\frac{{\partial {{\varphi }_{2}}}}{{\partial z}} + \frac{{\partial {{\varphi }_{1}}}}{{\partial z}}\left( {\frac{{\partial {{\zeta }_{2}}}}{{\partial {{T}_{0}}}} + \frac{{\partial {{\zeta }_{1}}}}{{\partial {{T}_{1}}}} - \frac{{\partial {{\zeta }_{1}}}}{{\partial x}}\frac{{\partial {{\varphi }_{1}}}}{{\partial x}}} \right)$

${{N}_{3}} = {{\zeta }_{1}}{{N}_{4}} + \frac{1}{2}\zeta _{1}^{2}\frac{{{{\partial }^{4}}{{\varphi }_{1}}}}{{\partial {{T}_{0}}\partial {{z}^{3}}}} + {{\zeta }_{2}}\frac{{{{\partial }^{3}}{{\varphi }_{1}}}}{{\partial {{T}_{0}}\partial {{z}^{2}}}} + \frac{{{{\partial }^{2}}{{\varphi }_{1}}}}{{\partial {{z}^{2}}}}\left( {\frac{{\partial {{\zeta }_{2}}}}{{\partial {{T}_{0}}}} + \frac{{\partial {{\zeta }_{1}}}}{{\partial {{T}_{1}}}}} \right) + \frac{{{{\partial }^{2}}{{\varphi }_{1}}}}{{\partial z\partial {{T}_{2}}}} + {{N}_{5}}$

${{N}_{4}} = \frac{{{{\partial }^{3}}{{\varphi }_{2}}}}{{\partial {{T}_{0}}\partial {{z}^{2}}}} + \frac{{\partial {{\zeta }_{1}}}}{{\partial {{T}_{0}}}}\frac{{{{\partial }^{3}}{{\varphi }_{1}}}}{{\partial {{z}^{3}}}} + \frac{{{{\partial }^{3}}{{\varphi }_{1}}}}{{\partial {{z}^{2}}\partial {{T}_{1}}}},\quad {{N}_{5}} = \frac{{\partial {{\zeta }_{1}}}}{{\partial {{T}_{0}}}}\frac{{{{\partial }^{2}}{{\varphi }_{2}}}}{{\partial {{z}^{2}}}} + \frac{{{{\partial }^{2}}{{\varphi }_{2}}}}{{\partial z\partial {{T}_{1}}}}$

${{L}_{3}} = {{\zeta }_{1}}{{N}_{6}} - {{\zeta }_{2}}\frac{{{{\partial }^{2}}{{\varphi }_{1}}}}{{\partial {{z}^{2}}}} + \frac{{\partial {{\zeta }_{2}}}}{{\partial x}}\frac{{\partial {{\varphi }_{1}}}}{{\partial x}} + \frac{{\partial {{\zeta }_{1}}}}{{\partial x}}\frac{{\partial {{\varphi }_{2}}}}{{\partial x}} - \frac{{\partial {{\zeta }_{2}}}}{{\partial {{T}_{1}}}} - \frac{{\partial {{\zeta }_{1}}}}{{\partial {{T}_{2}}}} + \frac{{\partial {{\varphi }_{1}}}}{{\partial z}}{{\left( {\frac{{\partial {{\zeta }_{1}}}}{{\partial x}}} \right)}^{2}}$

${{N}_{6}} = \frac{{\partial {{\zeta }_{1}}}}{{\partial x}}\frac{{{{\partial }^{2}}{{\varphi }_{1}}}}{{\partial z\partial x}} - \frac{{{{\partial }^{2}}{{\varphi }_{2}}}}{{\partial {{z}^{2}}}} - \frac{1}{2}{{\zeta }_{1}}\frac{{{{\partial }^{3}}{{\varphi }_{1}}}}{{\partial {{z}^{3}}}},\quad F_{2}^{0} = - \kappa k\frac{{{{\partial }^{2}}{{\varphi }_{1}}}}{{\partial x\partial z}}\frac{{\partial {{\varphi }_{1}}}}{{\partial x}}$

$F_{3}^{0} = - \kappa k\left[ {{{\zeta }_{1}}{{N}_{7}} + \frac{{{{\partial }^{2}}{{\varphi }_{1}}}}{{\partial x\partial z}}\left( {\frac{{\partial {{\varphi }_{2}}}}{{\partial x}} + \frac{{\partial {{\zeta }_{1}}}}{{\partial x}}\frac{{\partial {{\varphi }_{1}}}}{{\partial z}}} \right) + \frac{{\partial {{\varphi }_{1}}}}{{\partial x}}\left( {\frac{{{{\partial }^{2}}{{\varphi }_{2}}}}{{\partial x\partial z}} + \frac{{\partial {{\zeta }_{1}}}}{{\partial x}}\frac{{{{\partial }^{2}}{{\varphi }_{1}}}}{{\partial {{z}^{2}}}}} \right)} \right]$

${{N}_{7}} = {{\left( {\frac{{{{\partial }^{2}}{{\varphi }_{1}}}}{{\partial x\partial z}}} \right)}^{2}} + \frac{{\partial {{\varphi }_{1}}}}{{\partial x}}\frac{{{{\partial }^{3}}{{\varphi }_{1}}}}{{\partial x\partial {{z}^{2}}}},\quad {{G}_{2}} = - \frac{{\partial {{\zeta }_{1}}}}{{\partial {{T}_{1}}}},\quad {{G}_{3}} = - \frac{{\partial {{\zeta }_{1}}}}{{\partial {{T}_{2}}}} - \frac{{\partial {{\zeta }_{2}}}}{{\partial {{T}_{1}}}}$

Отметим, что слагаемые $F_{2}^{0}$, $F_{3}^{0}$, входящие в правые части динамических условий (2.4) для второго (n = 2) и третьего (n = 3) приближений, обусловлены учетом нелинейности ускорения вертикальных смещений льда.

3. ВЫРАЖЕНИЯ ДЛЯ ПОТЕНЦИАЛА СКОРОСТИ ДВИЖЕНИЯ ЖИДКОСТИ И ВОЗВЫШЕНИЯ ПОВЕРХНОСТИ ПЛАСТИНКА–ЖИДКОСТЬ

Уравнения (2.3)–(2.7) получены для общего случая неустановившихся колебаний конечной амплитуды. Найдем решение этих уравнений в случае взаимодействия бегущих периодических волн.

Зададим первое приближение (n = 1) возвышения поверхности пластинка–жидкость в виде

(3.1)

${{\zeta }_{1}} = \cos \theta + {{a}_{1}}\cos 2\theta ,\quad \theta = x + \tau {{T}_{0}} + \beta ({{T}_{1}},{{T}_{2}})$

где a₁ постоянная порядка единицы, а β = 0 при t = 0.

Удовлетворяя условию на дне и учитывая взаимосвязь волновых характеристик через граничные условия (2.4) и (2.5), запишем

(3.2)

${{\varphi }_{1}} = \tau \left[ {\frac{{{\text{ch}}\left( {z + H} \right)}}{{{\text{sh}}H}}\sin \theta + {{a}_{1}}\frac{{{\text{ch}}2\left( {z + H} \right)}}{{{\text{sh}}2H}}\sin 2\theta } \right]$

${{\tau }^{2}} = (1 - {{Q}_{1}}{{k}^{2}} + {{D}_{1}}{{k}^{4}}){{\left( {1 + \kappa k\,{\text{th}}H} \right)}^{{ - 1}}}{\text{th}}H$

Амплитуду a₁ и фазовый сдвиг β(Т₁, Т₂) определим из последующих приближений.

Подставив ζ₁, φ₁ из (3.1), (3.2) в правые части динамического (2.4) и кинематического (2.5) граничных условий для второго приближения и, решив задачу (2.3)–(2.7) при n = 2 с учетом требования отсутствия первой и второй гармоник в частном решении, получим

(3.3)

${{\zeta }_{2}} = {{a}_{2}}\cos 2\theta + \sum\limits_{i = 3}^4 {{{a}_{{2i}}}\cos i\theta } $

(3.4)

${{\varphi }_{2}} = {{b}_{{20}}}t + \sum\limits_{i = 2}^4 {{{b}_{{2i}}}{\text{ch}}i\left( {z + H} \right)} \sin i\theta $

(3.5)

${{a}_{1}} = \pm {{\left( {\frac{{{{\mu }_{2}}{{r}_{1}}}}{{4{{r}_{2}}(2{{\tau }^{2}}{\text{cth}}2H + 4{{\tau }^{2}}\kappa k + {{\mu }_{2}})\left( {1 + 2\kappa k{\kern 1pt} {\text{th}}2H} \right)}}} \right)}^{{1/2}}}$

${{r}_{1}} = \left( {2{\text{cth}}H + {\text{th}}2H\left( {{\text{cth}}H\left( {\frac{1}{2}{\text{cth}}H + 3\kappa k} \right) - \frac{5}{2}} \right)} \right)({{\tau }^{2}}\left( {{\text{cth}}H + \kappa k} \right) + {{\mu }_{1}})$

${{r}_{2}} = {{\tau }^{2}}\left( {\frac{1}{2} + {\text{cth}}2H{\text{cth}}H - \kappa k\left( {{\text{cth}}2H - \frac{5}{2}{\text{cth}}H} \right)} \right) + {{\mu }_{1}}\left( {\frac{1}{2}{\text{cth}}H + {\text{cth}}2H} \right)$

${{\sigma }_{1}} = \frac{{\tau {{\mu }_{2}}\left( {2{\text{cth}}H + {\text{th}}2H\left( {{\text{cth}}H\left( {\frac{1}{2}{\text{cth}}H + 3\kappa k} \right) - \frac{5}{2}} \right)} \right)}}{{4{{a}_{1}}(2{{\tau }^{2}}{\text{cth}}2H + 4{{\tau }^{2}}\kappa k + {{\mu }_{2}})\left( {1 + 2\kappa k{\text{th}}2H} \right)}},\quad {{b}_{{12}}} = {{a}_{1}}\frac{\tau }{{{\text{sh}}2H}}$

${{l}_{3}} = - \frac{3}{2}{{a}_{1}}\tau \left( {2{\text{cth}}2H + {\text{cth}}H} \right),\quad {{l}_{4}} = - 4a_{1}^{2}{\text{cth}}2H$

${{l}_{7}} = {{a}_{1}}{{\tau }^{2}}\left( {\frac{{11}}{2} - {\text{cth}}2H{\text{cth}}H + \kappa k\left( {5{\text{cth}}2H - \frac{1}{2}{\text{cth}}H} \right)} \right)$

${{l}_{8}} = a_{1}^{2}{{\tau }^{2}}(5 - {\text{ct}}{{{\text{h}}}^{2}}2H + 4\kappa k{\text{cth}}2H),\quad {{\mu }_{i}} = 1 - {{i}^{2}}{{Q}_{1}}{{k}^{2}} + {{i}^{4}}{{D}_{1}}{{k}^{4}},\quad i = 1 \ldots 4$

${{b}_{{23}}} = \frac{{{{l}_{3}}{{\mu }_{3}} + 3{{l}_{7}}\tau }}{{3{\text{sh}}3H({{\mu }_{3}} - 9\kappa k{{\tau }^{2}} - 3{{\tau }^{2}}{\text{cth}}3H)}},\quad {{b}_{{24}}} = \frac{{{{l}_{4}}{{\mu }_{4}} + 4{{l}_{8}}\tau }}{{3{\text{sh}}4H({{\mu }_{4}} - 16\kappa k{{\tau }^{2}} - 4{{\tau }^{2}}{\text{cth}}4H)}}$

${{a}_{{23}}} = \mu _{3}^{{ - 1}}\left( {{{l}_{7}} + 3\tau {{b}_{{23}}}\left( {{\text{ch}}3H - \kappa k3{\text{sh}}3H} \right)} \right)$, ${{a}_{{24}}} = \mu _{4}^{{ - 1}}\left( {{{l}_{8}} + 4\tau {{b}_{{24}}}\left( {{\text{ch}}4H - \kappa k4{\text{sh}}4H} \right)} \right)$

${{b}_{{20}}} = {{\tau }^{2}}\left( {a_{1}^{2}(1 + {\text{ct}}{{{\text{h}}}^{2}}2H) + \frac{1}{4}(1 + {\text{ct}}{{{\text{h}}}^{2}}H) + \kappa k\left( {\frac{1}{2}{\text{cth}}H + 4a_{1}^{2}{\text{cth}}2H} \right)} \right)$

Полученные решения (3.1), (3.2) и (3.3), (3.4) для первого и второго приближений соответственно определяют правые части динамического (2.4) и кинематического (2.5) условий задачи для третьего приближения. Исключив из них слагаемые, порождающие секулярность, для ζ₃ и φ₃ получим

(3.6)

${{\zeta }_{3}} = {{a}_{3}}\cos 2\theta + \sum\limits_{i = 3}^6 {{{a}_{{3i}}}\cos i\theta } $

(3.7)

${{\varphi }_{3}} = {{b}_{{30}}}t + \sum\limits_{i = 2}^6 {{{b}_{{3i}}}} {\text{ch}}i\left( {z + H} \right)\sin i\theta $

${{j}_{3}} = - \frac{5}{8}\tau - \frac{3}{8}a_{1}^{2}\tau - 6{{b}_{{24}}}{\text{ch}}4H - \frac{3}{2}{{a}_{{24}}}\tau {\kern 1pt} {\text{cth}}H + 3{{a}_{{23}}}{{\sigma }_{1}}$

${{j}_{4}} = - \frac{9}{2}{{a}_{1}}\tau - 6{{b}_{{23}}}{\text{ch}}3H - 2{{a}_{{23}}}\tau {\text{cth}}H + 4{{a}_{{24}}}{{\sigma }_{1}}$

${{j}_{5}} = - \frac{{69}}{8}a_{1}^{2}\tau - 10{{b}_{{24}}}{\text{ch}}4H - \frac{5}{2}{{a}_{{24}}}\tau {\text{cth}}H - 5{{a}_{1}}\left( {\frac{3}{2}{{b}_{{23}}}{\text{ch}}3H - {{a}_{{23}}}\tau {\text{cth}}2H} \right)$

${{j}_{6}} = - 5a_{1}^{3}\tau - 6{{a}_{1}}\left( {2{{b}_{{24}}}{\text{ch}}4H - {{a}_{{24}}}\tau {\text{cth}}2H} \right)$

$\begin{gathered} {{m}_{3}} = \tau \left( {\frac{9}{2}{{a}_{1}}{{\sigma }_{1}} + 2{{b}_{{24}}}{\text{ch}}4H\left( {2{\text{th}}4H - {\text{cth}}H} \right)} \right) + \frac{1}{2}{{\tau }^{2}}\left( {\frac{1}{4}{\text{cth}}H(1 - 23a_{1}^{2}) + 7a_{1}^{2}{\text{cth}}2H} \right. - \\ \left. { - \;3{{a}_{{24}}}} \right) + 3{{b}_{{23}}}{{\sigma }_{1}}{\text{ch}}3H + \kappa k\left( {\tau \left( {2{{b}_{{24}}}{\text{sh}}4H\left( {11{\text{cth}}4H - 4{\text{cth}}H} \right) + 3{{a}_{1}}{{\sigma }_{1}}\left( {{\text{2cth}}2H} \right. + } \right.} \right. \\ \left. { + \;\frac{1}{2}{\text{cth}}H} \right) + {{\tau }^{2}}\left( {a_{1}^{2}\left( {\frac{{21}}{8} - 2{\text{ct}}{{{\text{h}}}^{2}}2H - \frac{7}{2}{\text{cth}}H{\kern 1pt} {\text{cth}}2H} \right) - \frac{1}{8} - \frac{3}{2}{{a}_{{24}}}{\text{cth}}H - } \right. \\ - \;\left. {\left. {\frac{1}{2}{\text{ct}}{{{\text{h}}}^{2}}H} \right) + 9{{b}_{{23}}}{{\sigma }_{1}}{\text{sh}}3H} \right) \\ \end{gathered} $

$\begin{gathered} {{m}_{4}} = \tau \left( {4{{\sigma }_{1}}a_{1}^{2} + \frac{3}{2}{{b}_{{23}}}{\text{ch}}3H\left( {5{\text{th}}3H - {\text{cth}}H} \right)} \right) + 2{{\tau }^{2}}\left( {{{a}_{1}}{\text{cth}}2H - \frac{1}{4}{{a}_{1}}{\text{cth}}H + {{a}_{{23}}}} \right) + \\ + \;4{{b}_{{24}}}{{\sigma }_{1}}{\text{ch}}4H + \kappa k\left( {\tau \left( {\frac{3}{2}{{b}_{{23}}}{\text{sh}}3H\left( {11{\text{cth}}3H - 3{\text{cth}}H} \right) + 8a_{1}^{2}{{\sigma }_{1}}{\text{cth}}2H} \right)} \right. + \\ \left. { + \;{{\tau }^{2}}\left( {{{a}_{1}}\left( {\frac{{37}}{4} - 4{\text{cth}}2H{\text{cth}}H - \frac{3}{4}{\text{ct}}{{{\text{h}}}^{2}}H} \right) + 2{{a}_{{23}}}{\text{cth}}H} \right) + 16{{b}_{{24}}}{{\sigma }_{1}}{\text{sh}}4H} \right) \\ \end{gathered} $

$\begin{gathered} {{m}_{5}} = \tau \left( {2{{b}_{{24}}}{\kern 1pt} {\text{ch}}4H\left( {6{\text{th}}4H - {\text{cth}}H} \right) + 3{{b}_{{23}}}{{a}_{1}}{\text{ch}}3H\left( {\frac{7}{2}{\text{th}}3H - {\text{cth}}2H} \right)} \right) + \\ + \;{{\tau }^{2}}\left( {\frac{7}{2}a_{1}^{2}\left( {{\text{cth}}2H - \frac{1}{4}{\text{cth}}H} \right) + 5{{a}_{{23}}}{{a}_{1}} + \frac{5}{2}{{a}_{{24}}}} \right) + \kappa k\left( {\tau \left( {2{{b}_{{24}}}{\text{sh}}4H\left( {19{\text{cth}}4H - 4{\text{cth}}H} \right) + } \right.} \right. \\ \left. { + \;3{{b}_{{23}}}{{a}_{1}}{\text{sh}}3H\left( {\frac{{11}}{2}{\text{cth}}3H - 3{\text{cth}}2H} \right)} \right) + {{\tau }^{2}}\left( {a_{1}^{2}\left( {\frac{3}{8} - 6{\text{cth}}2H - \frac{{11}}{2}{\text{cth}}2H{\text{cth}}H} \right) + } \right. \\ \left. {\left. { + \;10{{a}_{{23}}}{{a}_{1}}{\text{cth}}2H + \frac{5}{2}{{a}_{{24}}}{\text{cth}}H} \right)} \right) \\ \end{gathered} $

$\begin{gathered} {{m}_{6}} = 4\tau {{b}_{{24}}}{{a}_{1}}{\text{ch}}4H\left( {4{\text{th}}4H - {\text{cth}}2H} \right) + {{\tau }^{2}}{{a}_{1}}(a_{1}^{2}{\text{cth}}2H + 6{{a}_{{24}}}) + \\ + \;2\kappa k{{a}_{1}}(4\tau {{b}_{{24}}}{\text{sh}}4H\left( {5{\text{cth}}4H - 2{\text{cth}}2H} \right) + {{\tau }^{2}}(6{{a}_{{24}}}{\text{cth}}2H - a_{1}^{2}(1 + 4{\text{ct}}{{{\text{h}}}^{2}}2H))) \\ \end{gathered} $

$\begin{gathered} {{q}_{1}} = {{\mu }_{1}}\left( {\frac{3}{2}{{b}_{{23}}}{{a}_{1}}{\text{ch}}3H - \tau \left( {\frac{3}{8} - \frac{{15}}{4}a_{1}^{2} + {{a}_{{23}}}{{a}_{1}}{\text{cth}}2H} \right)} \right) + {{\tau }^{2}}{{a}_{1}}\left( { - \frac{1}{2}{{\sigma }_{1}} + } \right. \\ \left. { + \;3{{b}_{{23}}}{\text{ch}}3H\left( {\frac{1}{2}{\text{th}}3H + {\text{cth}}2H} \right)} \right) + {{\tau }^{3}}\left( {9a_{1}^{2}{\text{cth}}2H + {{a}_{1}}{{a}_{{23}}} + \frac{1}{4}{\text{cth}}H\left( {\frac{5}{2} - a_{1}^{2}} \right)} \right) + \\ + \;\kappa k\left( {{{\tau }^{2}}{{a}_{1}}\left( {3{{b}_{{23}}}{\text{sh}}3H\left( {\frac{1}{2}{\text{cth}}3H + 3{\text{cth}}2H} \right) - 2{{\sigma }_{1}}{\text{cth}}2H + \frac{1}{2}{{\sigma }_{1}}{\text{cth}}H} \right) + } \right. \\ \left. { + \;{{\tau }^{3}}\left( {2{{a}_{{23}}}{{a}_{1}}{\text{cth2}}H + \frac{1}{2}{{\tau }^{2}}{\text{ct}}{{{\text{h}}}^{2}}H + \frac{3}{8} + a_{1}^{2}\left( {8{\text{ct}}{{{\text{h}}}^{2}}2H + {\text{cth}}H{\text{cth}}2H + \frac{{39}}{4}} \right)} \right)} \right) \\ \end{gathered} $

$\begin{gathered} {{q}_{2}} = {{\mu }_{2}}(3{{b}_{{23}}}{\text{ch}}3H + 4{{b}_{{24}}}{{a}_{1}}{\text{ch}}4H + \tau ({{a}_{{23}}}{\text{cth}}H + 2{{a}_{{24}}}{{a}_{1}}{\text{cth}}2H - 3a_{1}^{3})) + \\ + \;2{{\tau }^{2}}\left( {\frac{3}{2}{{b}_{{23}}}{\text{ch}}3H\left( {{\text{cth}}H - {\text{th}}3H} \right) + 4{{b}_{{24}}}{{a}_{1}}{\text{cth}}2H{\text{ch}}4H - {{\sigma }_{1}}} \right) + \\ + \;2{{\tau }^{3}}({{a}_{{23}}} + {{a}_{1}}(3{{a}_{1}}{\text{cth}}H + 2{{a}_{{24}}} + {\text{cth}}2H(5a_{1}^{2} - 2))) + \\ + \;\kappa k\left( {2{{\tau }^{2}}\left( {\frac{3}{2}{{b}_{{23}}}{\text{sh}}3H\left( {{\text{3cth}}H - 5{\text{cth}}3H} \right) + 8{{b}_{{24}}}{{a}_{1}}{\text{sh}}4H\left( {{\text{2cth}}2H - {\text{cth}}4H} \right) - {{\sigma }_{1}}{\text{cth}}H} \right) + } \right. \\ \left. { + \;2{{\tau }^{3}}\left( {2a_{1}^{3}\left( {3 + 4{\text{cth}}2H} \right) + {{a}_{1}}\left( {4{\text{cth}}2H\left( {{{a}_{{24}}} + {\text{cth}}H} \right) + \frac{1}{2}{\text{ct}}{{{\text{h}}}^{2}}H - \frac{3}{2}} \right) + {{a}_{{23}}}{\text{cth}}H} \right)} \right) \\ \end{gathered} $

${{\sigma }_{2}} = \frac{1}{4}\left( {\frac{{{{q}_{1}}}}{{{{\mu }_{1}}}} + \frac{{{{q}_{2}}}}{{2{{a}_{1}}{{\mu }_{2}}}}} \right),\quad {{b}_{{3i}}} = \frac{{{{j}_{i}}{{\mu }_{i}} + i{{m}_{i}}\tau }}{{i{\text{sh}}iH({{\mu }_{i}} - {{i}^{2}}{{\tau }^{2}}\kappa k - i{{\tau }^{2}}{\text{cth}}iH)}},\quad i = 3 \ldots 6$

${{a}_{{3i}}} = (i\tau {{b}_{{3i}}}({\text{ch}}iH + i\kappa k{\text{sh}}iH) + {{m}_{i}})\mu _{i}^{{ - 1}},\quad i = 3 \ldots 6$, ${{\mu }_{i}} = 1 - {{i}^{2}}{{Q}_{1}}{{k}^{2}} + {{i}^{4}}{{D}_{1}}{{k}^{4}},\quad i{\text{ }} = {\text{ 5}} \ldots {\text{6}}$

${{b}_{{30}}} = {{a}_{1}}{{\tau }^{2}}\left( {2{\text{cth}}2H + \frac{1}{2}{\text{cth}}H + \kappa k\left( {\frac{9}{4} + 2{\text{cth}}2H{\text{cth}}H - \frac{1}{4}{\text{ct}}{{{\text{h}}}^{2}}H} \right)} \right)$

Здесь ${{b}_{{22}}} = {{b}_{{32}}} = {{a}_{2}} = {{a}_{3}} = {{l}_{1}} = {{l}_{2}} = {{l}_{5}} = {{l}_{6}} = {{j}_{1}} = {{j}_{2}} = {{m}_{1}} = {{m}_{2}} = 0$.

Таким образом, для определения возвышения поверхности пластинка–жидкость ζ и потенциала скорости движения жидкости φ в безразмерных величинах до третьего порядка малости имеем

(3.8)

$\zeta = \varepsilon \cos \theta + \sum\limits_{n = 1}^3 {{{\varepsilon }^{n}}{{a}_{n}}\cos 2\theta + \sum\limits_{n = 2}^3 {{{\varepsilon }^{n}}} \sum\limits_{j = 3}^4 {{{a}_{{nj}}}\cos j\theta } + } {{\varepsilon }^{3}}\sum\limits_{n = 5}^6 {{{a}_{{3n}}}\cos n\theta } $

(3.9)

$\begin{gathered} \varphi = \varepsilon \frac{\tau }{{{\text{sh}}H}}{\text{ch}}\left( {z + H} \right)\sin \theta + \sum\limits_{n = 1}^3 {{{\varepsilon }^{n}}{{b}_{{n2}}}{\text{ch}}2\left( {z + H} \right)\sin 2\theta } + \\ + \;\sum\limits_{n = 2}^3 {{{\varepsilon }^{n}}} \sum\limits_{j = 3}^4 {{{b}_{{nj}}}{\text{ch}}j\left( {z + H} \right)\sin j\theta + } {{\varepsilon }^{3}}\sum\limits_{n = 5}^6 {{{b}_{{3n}}}{\text{ch}}n\left( {z + H} \right)\sin n\theta } + \sum\limits_{n = 2}^3 {{{\varepsilon }^{n}}{{b}_{{n0}}}} t \\ \end{gathered} $

где $\theta = x + \sigma t$, $\sigma = \tau + \varepsilon {{\sigma }_{1}} + {{\varepsilon }^{2}}{{\sigma }_{2}}$, $\varepsilon = ak$, а – амплитуда начальной гармоники.

Фазовая скорость волновых возмущений определяется по формуле

$\text{v} = (\tau + \varepsilon {{\sigma }_{1}} + {{\varepsilon }^{2}}{{\sigma }_{2}}){{k}^{{ - 1}}}$

В размерных величинах ($\zeta * = \zeta {\text{/}}k$, $\varphi * = \varphi \sqrt {kg} {\text{/}}{{k}^{2}}$, ${{x}_{1}} = x{\text{/}}k$, ${{z}_{1}} = z{\text{/}}k$, ${{t}_{1}} = {t \mathord{\left/ {\vphantom {t {\sqrt {kg} }}} \right. \kern-0em} {\sqrt {kg} }}$, $\varepsilon = ak$) выражения (3.8) и (3.9) принимают вид

(3.10)

$\begin{gathered} \zeta = a\cos \theta + a{{a}_{1}}\cos 2\theta + ({{a}^{2}}k{{a}_{{23}}} + {{a}^{3}}{{k}^{2}}{{a}_{{33}}})\cos 3\theta + \\ \, + ({{a}^{2}}k{{a}_{{24}}} + {{a}^{3}}{{k}^{2}}{{a}_{{34}}})\cos 4\theta + {{a}^{3}}{{k}^{2}}{{a}_{{35}}}\cos 5\theta + {{a}^{2}}{{k}^{2}}{{a}_{{36}}}\cos 6\theta \\ \end{gathered} $

$\begin{gathered} \varphi = a{{\left( {\frac{g}{k}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\left( {\frac{\tau }{{{\text{sh}}H}}{\text{ch}}\left( {z + H} \right)\sin \theta + {{b}_{{12}}}{\text{ch}}2\left( {z + H} \right)\sin 2\theta } \right) + {{a}^{2}}\sqrt {kg} \left( {{{b}_{{23}}}{\text{ch}}3\left( {z + H} \right) + } \right. \\ \left. { + \;{{b}_{{24}}}{\text{ch}}4\left( {z + H} \right)\sin 4\theta + {{b}_{{20}}}t} \right) + {{a}^{3}}k\sqrt {kg} \left( {{{b}_{{33}}}{\text{ch}}3\left( {z + H} \right)\sin 3\theta + {{b}_{{34}}}{\text{ch}}4\left( {z + H} \right)\sin 4\theta + } \right. \\ + \;\left. {{{b}_{{35}}}{\text{ch}}5\left( {z + H} \right)\sin 5\theta + {{b}_{{36}}}{\text{ch}}6\left( {z + H} \right) + {{b}_{{30}}}t} \right) \\ \end{gathered} $

$\theta = kx + \sqrt {kg} (\tau + ak{{\sigma }_{1}} + {{a}^{2}}{{k}^{2}}{{\sigma }_{2}}{\text{)}}t$

Здесь и далее индекс 1 у латинских символов x, z, t и знак звездочки у греческих ζ и φ опущены.

Формулы (3.8)–(3.9) для ζ и φ определяют формируемое волновое возмущение и без учета нелинейности ускорения вертикальных смещений льда в динамическом условии (2.4). Однако в таком случае следует учесть, что $F_{2}^{0} = F_{3}^{0} = 0$.

4. АНАЛИЗ РЕЗУЛЬТАТОВ

Найденное решение (3.10) справедливо вне малых окрестностей резонансных значений волнового числа k₁, k₂, k₃, k₄, являющихся положительными действительными корнями уравнения

(4.1)

${{\mu }_{i}} - {{i}^{2}}{{\tau }^{2}}\kappa k - i{{\tau }^{2}}{\text{cth}}iH = 0,\quad i = 3 \ldots 6$

Левая часть (4.1) входит в знаменатель выражения для b_3i, причем k₁ > k₂ > k₃ > k₄. Отметим, что резонансное значение k = k₁, получаемое из (4.1) при i = 3, совпадает с меньшим из двух резонансных значений волнового числа, получаемых, когда первое приближение ζ₁ задается в виде cosθ [18]. Увеличение сжимающего усилия приводит к росту значений k_i при фиксированных h и E. С ростом толщины h ледовой пластинки величина k₁ уменьшается при постоянных E и Q₁. Уменьшение величины модуля упругости при фиксированных h и Q₁ увеличивает значения k_i.

Для количественной оценки влияния ледовой пластинки, глубины бассейна на амплитудно-фазовые характеристики формируемого возмущения проводились расчеты при значениях модуля упругости E = 0.5 × 10⁹∼ 3 × 10⁹ Н/м², коэффициента Пуассона ν = 0.34 и плотности ρ₁/ρ = 0.87. Продольное сжимающее усилие выбиралось при условии ${{Q}_{1}} < 2\sqrt {{{D}_{1}}} $, необходимом для устойчивости ледяной пластинки [8, 21].

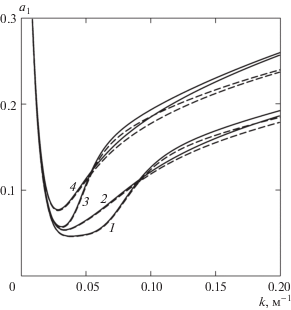
Графики на рис. 1 иллюстрируют зависимость амплитуды второй взаимодействующей гармоники (3.5) от волнового числа при толщине h ледовой пластинки 0.5 м (линии 1, 2) и 1 м (3, 4) при H = 100 м, E = 3 × 10⁹ Н/м². Кривые (1, 3) и (2, 4) соответствуют значениям ${{Q}_{1}} = 1.5\sqrt D $ и 0. При k = 0 амплитуда a₁ принимает значение 1/√2. Видно, что а₁(k) имеет локальный минимум, величина которого растет с увеличением толщины льда. Отметим, что сжимающее усилие уменьшает его величину. С увеличением волнового числа усиливается влияние нелинейности ускорения вертикальных смещений льда.

Рис. 1.

Распределение а₁ по волновому числу k при H = 100 м, E = 3 × 10⁹ Н/м²: (1, 2) и (3, 4) – h = 0.5 и 1 м; (1, 3) и (2, 4) – ${{Q}_{1}} = 1.5\sqrt D $ и 0. Сплошные линии – без учета, штриховые – с учtтом нелинейности ускорения вертикальных смещений пластинки

Численные расчеты по формуле (3.10) распределений вертикальных смещений поверхности пластинка–жидкость (изгиб пластины) вдоль направления движения волны (отрицательное направление оси х) показали зависимость структуры возмущений от глубины бассейна, характеристик начальной основной гармоники, а также цилиндрической жесткости ледовой пластины, сжимающего усилия и амплитуды второй взаимодействующей гармоники. О влиянии этих параметров можно судить по зависимостям на рис. 2 и 3 .

Рис. 2.

Профили волны изгибной деформации ледяной пластинки при E = 3 × 10⁹ Н/м², H = 100 м, h = 1.2 м, а = 2 м, λ = 2π × 10⁴/51 м: а, б – а₁ > 0, а₁ < 0; (1, 2) и (3, 4) – без учета и с учетом нелинейности ускорения вертикальных смещений пластинки; (2, 3) и (1, 4) – Q₁ = 0 и $\sqrt D $

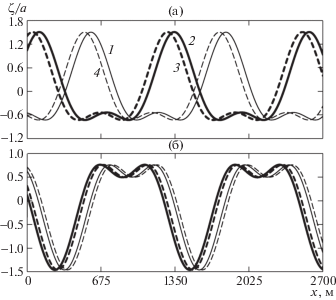
Рис. 3.

Профили волны изгибной деформации ледяной пластинки при E = 3 × 10⁹ Н/м², H = 20 м, h = 0.5 м, а = 1.3 м, λ = π × 10²/13 м: а, б – а₁ > 0, а₁ < 0; (1, 2) и (3, 4) – без учета и с учетом нелинейности ускорения вертикальных смещений пластинки; (2, 3) и (1, 4) – Q₁ = 0 и $\sqrt D $

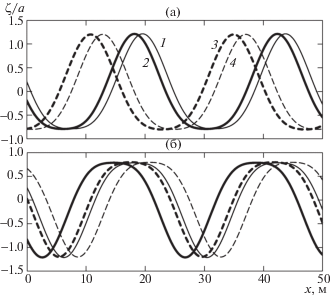
В случае E = 3 × 10⁹ Н/м² распределения профиля изгиба ледовой пластинки при а₁ > 0 представлены на рис. 2а и 3а, а при а₁ < 0 – на рис. 2б и 3б. Из изображений профилей следует, что при а₁ > 0 и Q₁ = 0 учет нелинейности ускорения вертикальных смещений ледовой пластинки при нелинейном взаимодействии волновых гармоник увеличивает фазовую скорость сформированного возмущения и незначительно влияет на его амплитуду. При Q₁ ≠ 0 наблюдается отставание фазы колебания от профиля сформированного при Q₁ = 0. Однако учет нелинейности ускорения пластинки сохраняет влияние, т.е. ускоряет смещение профиля волны относительно профиля, полученного без учета. Максимальные смещения относительно невозмущенного состояния поверхности наблюдаются в виде гребней, а минимальные – в виде ложбин. При а₁ < 0 профиль возмущения деформируется качественно и количественно. К примеру, в местах наблюдавшихся гребней (рис. 2б) фиксируются двухгорбые профили изгиба. Проявление высших гармоник здесь более заметно, чем на рис. 3б. Направленность фазовых изменений при изменении начальной фазы второй гармоники (изменение знака а₁) так же меняется. Для профилей, полученных с учетом нелинейности ускорения вертикальных смещений ледовой пластинки, наблюдается уменьшение фазовой скорости.

Распределение фазовой скорости v по волновому числу k (k > k₁) сформировавшейся изгибно-гравитационной волны конечной амплитуды показано на рис. 4. Из представленных данных следует, что учет нелинейности при a₁ > 0 приводит к увеличению скорости перемещения волны изгиба. Наличие продольного сжимающего усилия уменьшает фазовую скорость как при учете нелинейности вертикальных смещений, так и без учета. Отметим, что с ростом толщины пластинки или модуля ее упругости значение фазовой скорости растет [2, 17, 21].

Рис. 4.

Распределение фазовой скорости v сформировавшейся изгибно-гравитационной волны по волновому числу k при E = 3 × 10⁹ Н/м², h = 1 м, H = 100 м: (1, 2) и (3, 4) – a₁ > 0 и a₁ < 0; (1, 3) и (2, 4) – Q₁ = 0 и $\sqrt D $; 5 – фазовая скорость в линейном приближении. Сплошные линии без учета, а штриховые – с учетом нелинейности ускорения вертикальных смещений пластинки

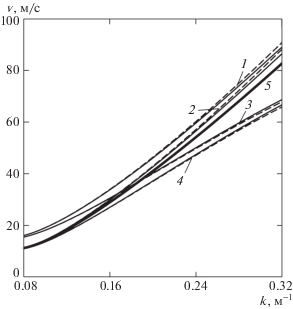
При а₁ < 0 фазовая скорость, полученная с учетом нелинейности вертикального ускорения меньше, чем без учета. Влияние сжимающего усилия сохраняет свою направленность на уменьшение v(k). При этом видно, что существует такое k, начиная с которого значения фазовой скорости при a₁ > 0 как при Q₁ = 0, так и при Q₁ ≠ 0 больше линейного приближения, а при a₁ < 0 меньше. Для волновых чисел k < k₄ (длинные волны) влияние характеристик пластинки на распределения v(k) слабое [2, 21]. Зависимости v(k) с учетом и без учета слагаемых $F_{2}^{0}$ и $F_{3}^{0}$ в (2.4) при Q₁ = 0 и при Q₁ ≠ 0 практически совпадают между собой как для a₁ > 0, так и для a₁ < 0.

ЗАКЛЮЧЕНИЕ

На основе метода многих масштабов получены асимптотические разложения до величин третьего порядка малости для возвышения поверхности пластинка–жидкость и потенциала скорости движения жидких частиц, формируемых при нелинейном взаимодействии двух гармоник прогрессивных поверхностных волн. Построенные разложения справедливы вне малых окрестностей резонансных значений волнового числа.

Выполнен анализ зависимости амплитудно-фазовых характеристик волновых возмущений от модуля упругости, продольного сжимающего усилия, толщины ледовой пластины и параметров взаимодействующих гармоник. Дана оценка скорости перемещения волны изгиба.

Показано, что при взаимодействии волновых гармоник вклад учета нелинейности ускорения вертикальных смещений упругой пластинки в фазу колебаний зависит от знака амплитуды второй взаимодействующей гармоники. Наличие сжимающего усилия выражается в отставании фазы колебаний от фазы, полученной при отсутствии сжатия, и в незначительном уменьшении амплитуды.

Работа выполнена в рамках государственного задания по теме № 0827-2018-0003.

Список литературы

Хейсин Д.Е. Нестационарная задача о колебаниях бесконечной пластинки, плавающей на поверхности идеальной жидкости // Изв. АН СССР. Механика и машиностроение. 1962. № 1. С. 163–167.
Букатов А.Е., Черкесов Л.В. Неустановившиеся колебания упругой пластинки, плавающей на поверхности потока жидкости // Прикл. механика. 1970. Т. 6. № 8. С. 89–96.
Ткаченко В.А., Яковлев В.В. Неустановившиеся изгибно-гравитационные волны в системе жидкость–пластинка // Прикл. механика. 1984. Т. 20. № 3. С. 70–75.
Daffy D.G. The response of floating ice to a moving, vibrating load // Cold Regions Science and Technology. 1991. V. 20. P. 51–64.
Squire V.A., Hosking R.J., Kerr A.D., Langhorne P.J. Moving loads on ice plates. Dordrecht: Kluwer, 1996. 236 p.
Стурова И.В. Генерация волн колеблющимся погруженным цилиндром при наличии плавающей полубесконечной упругой пластины // Изв. РАН. МЖГ. 2014. № 4. С. 98–108.
Батяев Е.А., Хабахпашева Т.И. Гидроупругие волны в канале со свободным ледовым покровом // Изв. РАН. МЖГ. 2015. № 6. С. 71–88.
Букатов А.Е. Влияние продольного сжатия на неустановившиеся колебания упругой пластинки, плавающей на поверхности жидкости // Прикл. механика. 1981. Т. 17. № 1. С. 93–98.
Пожуев В.И., Полякова Н.П. Нестационарная задача о воздействии подвижной нагрузки на ледяной покров // Строительная механика и расчет сооружений. 1990. № 6. С. 46–50.
Bukatov A.E., Zharkov V.V. Formation of the ice cover’s flexural oscillations by action of surface and internal ship waves – Part 1. Surface waves // Int. J. Offshore and Polar engineering. 1997. V. 7. № 1. P. 1–12.
Kerr A.D. The critical velocities of a moving on a floating ice plate that is sub-jected to in – plane forces // Cold Regions Science and Technology. 1983. V. 6. P. 267–276.
Schulkes R.M.S.M., Hosking R.J., Sneyd A.D. Waves due to a steadily moving source on a floating ice plate. Part 2 // J. Fluid Mech. 1987. V. 180. P. 297–318.
Bukatov A.E., Bukatov A.A. Propagation of surface wave of finite amplitude in a basin with floating broken ice // Int. J. Offshore and Polar Engineering. 1999. V. 9. № 3. P. 161–166.
Гладун О.М., Федосенко В.С. Нелинейные установившиеся колебания упругой пластины, плавающей на поверхности жидкости конечной глубины // Изв. АН СССР. МЖГ. 1989. № 3. С. 146–154.
Гольдштейн Р.В., Марченко А.В. О длинных волнах в системе ледяной покров–жидкость при наличии ледового сжатия / Электрофизические и физико-механические свойства льда: Сб. научн. тр. ГК СССР по гидрометеорологии. ААНИИ. Л.: Гидрометеоиздат, 1989. С. 188–205.
Ильичев А.Т. Солитоноподобные структуры на поверхности раздела вода–лед // Успехи мат. наук. 2015. Т. 70. Вып. 6. С. 85–138.
Букатов А.Е., Букатов А.А. Волны конечной амплитуды в однородной жидкости с плавающей упругой пластиной // ПМТФ. 2009. Т. 50. № 5. С. 67–74.
Букатов А.Е., Букатов А.А. О нелинейных колебаниях плавающей упругой пластинки // Прикл. механика. 2010. Т. 46. № 10. С. 62–70.
Букатов А.Е., Букатов А.А. Взаимодействие поверхностных волн в бассейне с плавающим битым льдом // Морской гидрофизический журн. 2003. № 6. С. 3–22.
Найфе А.Х. Методы возмущений. М.: Мир, 1976. 455 с.
Хейсин Д.Е. Динамика ледяного покрова. Л.: Гидрометеоиздат, 1967. 215 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал